Как найти концентрацию протонов

В общем, задача звучит так:  Произведение растворимости Mg(OH)2 (свежеосажденного) составляет 6,010-10. Рассчитайте растворимость Mg(OH)2 в г/л и концентрацию протонов в растворе (без учета диссоциации молекул воды).

Растворимость нашел. Как решал,  на фото есть. Вопрос только в том, как найти концентрацию протонов. Знаю, как это сделать, если известен pH, а как отсюда выпутаться? Кто-нибудь может помочь?

Растворимость 0,03 г/л. А то сейчас посмотрел, сам бы не понял почерк.

Приближенный
расчет кислотности среды в растворах
слабых электролитов выполняется с
учетом концентрации электролита и
значения константы его диссоциации.
Они выводятся на основе закона действия
масс примененного к уравнению диссоциации.
Как и в рассмотренных выше случаях,
решение уравнения полного материального
баланса приводит к усложнению задачи.
Поэтому, при выводе формул, не будем
учитывать роль автопротолиза воды, что
вполне корректно при значениях констант
диссоциации К_д 
10^6.

а) Слабая кислота.

Запишем уравнение
диссоциации слабой одноосновной кислоты
НХ и формулу константы диссоциации
К_кис:

НХ 
Н⁺ + Х^
(4.33)

К_кис =

(4.34)

Принимая во
внимание, что для одноосновной кислоты
[H⁺] = [X^]
и учитывая, что [HX] 
С₀, где С₀ – исходная
концентрация кислоты (это справедливо
для значений К_кис 
10^2),
получаем

[H⁺]²
= К_кисС₀
(4.35)

[H⁺]
=

(4.36)

б) Слабое основание.

Вывод формул для
приближенного расчета кислотности
среды слабого кислотного основания
выполняется аналогично слабым кислотам,
но при этом учитывают, что при диссоциации
слабого основания в растворе идет
накопление гидроксид-ионов, концентрация
которых вычисляется по формуле

[OH^]
=

(4.37)

Учитывая, что
концентрации [H⁺] и
[OH^]
связаны между собой через значение
константы автопротолиза воды К_w,
можно записать:

[H⁺]
=

=

(4.38)

4.8.4 Расчет концентрации протонов в кислотных и основных буферах

Значение рН в
буферных растворах определяется как
концентрацией соли, так и кислоты
(основания), что легко доказать, исходя
из закона действия масс. Приближенное
значение концентрации протонов в
растворе можно найти следующим образом:

[H⁺] =

– кислотный буфер (4.39)

[H⁺] =

– основный буфер (4.40)

где К_кис и
К_осн – константы диссоциации
кислоты и основания; Кw –
константа автопротолиза воды; С_х (х
= кис, осн, соли) – молярная концентрация
кислоты, основания или соли соответственно,
моль/л; _х –
количество вещества кислоты, основания
или соли в растворе, моль.

В
таблице 4.4 приведены формулы для
приближенного вычисления концентрации
протонов в различных типах растворов
электролитов. Они справедливы для слабых
электролитов, у которых значение К_дис
составляет порядка 10^2

10^5.
Если К_дис10^2,
то электролит считается сильным, а его
диссоциация в растворе – полной. Значение
рН в растворах любого типа находят по
общей формуле:

рН
=

lg
[H⁺].
(4.41)

Таблица. 4.4 Формулы
приближенного расчета концентрации
протонов

в
растворах электролитов и буферах.

№	тип электролита	пример электролита	формула расчета [H+]
1	Сильная кислота	HCl	[H+]  nCк-ты*
2	Сильное основание	KOH	[H+] 
3	Слабая кислота	HCOOH	[H+] =
4	Слабое основание	NH4OH	[H+] =
5	Соль слабой кислоты и сильного основания	KCN	[H+] =
6	Соль сильной кислоты и слабого основания	NH4Cl	[H+] =
7	Соль слабой кислоты и слабого основания	HCOONH4	[H+] =
	рН буферных систем
8	Кислотный буфер: слабая кислота и соль слабой кислоты и сильного основания	CH3COOH + CH3COONa	[H+]= =
9	Основный буфер: слабое основание и соль слабого основания и сильной кислоты.	NH4OH + NH4Cl	[H+] = =
10	Вода	H2O	[H+] = [OH] = 107

^*n
– основность кислоты или кислотность
щелочи.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

You need more than a hint. You need a hard shove…

The overall notion here is that water dissociates

$$ce{H2O <=> H+ + OH-}$$

and that the equilibrium is given by

$$K_w = 1.00times10^{-14} = ce{[H+][OH-]}$$

where $ce{[H+]}$ is the molar concentration of $ce{H+}$ ions and $ce{[OH-]}$ is the molar concentration of $ce{OH-}$ ions.

NOTE: The pH of a solution is defined as the negative log of the $ce{H+}$ ion concentration, and pOH of a solution is defined as the negative log of the $ce{OH-}$ ion concentration. So

$$14 = text{pH + pOH}$$

Sodium hydroxide is a strong base, so the assumption is that it completely dissociates.

$$ce{NaOH(solid) <=> Na+(aq) + OH-(aq)}$$

The molecular mass of sodium hydroxide is 40.00 grams/mole.

$$ce{[OH-]} = dfrac{0.60text{ g}}{40.00text{ g/mole}times0.80text{ liter}} = 0.01875text{ mole/liter}$$

Rearranging the $K_w$ equation

$$ce{[H+]} = dfrac{K_w}{ce{[OH-]}} = dfrac{1.00times10^{-14}}{1.875times10^{-2}} = 5.3times10^{-13}text{ mole/liter}$$

Изобретение относится к физической химии и электрохимии твердых электролитов и может быть использовано для определения концентрации протонов в протон-проводящих оксидных материалах в атмосфере сухого водорода. Способ определения концентрации протонов в протон-проводящих оксидах заключается в том, что образец оксида помещают в реактор, соединенный с газовым контуром, сушат при нагреве до температуры 900÷1000°C. Затем меняют газовую фазу на атмосферу, содержащую водород, регистрируют изменение во времени значения параметра оксида, напрямую связанного с изменением количества протонов в оксиде, достигая состояния равновесия оксида с газовой фазой, и на основании полученного равновесного значения параметра оксида производят расчет концентрации протонов в протон-проводящем оксиде как количества вещества водорода в оксиде, отнесенного к одному молю оксида. При этом в качестве параметра оксида, напрямую связанного с изменением количества протонов в протон-проводящем оксиде, используют значение давления водорода над оксидом в замкнутом газовом контуре постоянного объема, для этого образец помещают в реактор, вакуумплотно соединенный с газовым контуром, изолированным от атмосферы. Далее откачивают газовый контур с реактором на высокий вакуум и сушат образец, выдерживая его при температуре осушки до установления остаточного давления не более 10^-7 Па. Затем перекрывают вакуумплотное соединение реактора с газовым контуром, напускают в контур водород высокой чистоты до заданного давления, открывают вакуумплотное соединение реактора с газовым контуром и после мгновенного установления общего давления водорода в системе «реактор-газовый контур» регистрируют изменение значения давления водорода над образцом во времени, достигая состояния равновесия оксида с газовой фазой, и на основании разницы давления водорода, установившегося сразу после открытия вакуумплотного соединения, и полученного равновесного значения давления водорода над образцом производят расчет концентрации протонов в протон-проводящем оксиде. Техническим результатом является повышение степени осушки исследуемых образцов, повышение точности измерения концентрации протонов в атмосфере сухого водорода, а также сокращение расхода водорода. 2 ил.

Изобретение относится к физической химии и электрохимии твердых электролитов и может быть использовано для определения концентрации протонов в протон-проводящих оксидных материалах в атмосфере сухого водорода.

Известен способ определения концентрации протонов в протон-проводящих оксидных материалах в атмосфере «вода-водород», то есть в атмосфере влажного водорода, включающий использование метода термогравиметрического анализа с генератором водяного пара (Kreuer, K.D. Proton-Conducting Oxides. Annual Review of Material Research (2003) 33: 333-359) [1]. Согласно этому способу, исследуемый образец оксидного протон-проводящего материала помещают в реактор, соединенный с газовым контуром термоанализатора, сообщающимся с атмосферой, до начала эксперимента по растворимости водорода образец исследуемого материала сушат, продувая воздух или кислород над образцом через трубку с каким-либо из адсорбентов водяного пара, например цеолитами, пентоксидом фосфора и др. Температура осушки составляет 900÷1000°C. После осушки посредством регуляторов расхода газов проточную систему «реактор-газовый контур» продувают газовой смесью, содержащей водород и водяные пары, создаваемые парогенератором. Задавая скорость движения газов с помощью регуляторов расхода газов, можно добиться получения смеси с необходимым соотношением концентраций водорода и паров воды.

В результате происходит растворение водорода в оксиде, что влечет за собой увеличение массы образца. С помощью весов регистрируют изменение массы образца во времени, дожидаясь состояния равновесия, а затем производят расчет концентрации протонов в оксиде, численно равной количеству вещества протонов в одном моле оксида. Использование в качестве осушителей адсорбентов водяного пара, таких как цеолиты, пентоксид фосфора и других, позволяет получить остаточное давление водяных паров не менее нескольких единиц, а то и десятков паскалей, что бывает крайне недостаточно для полной осушки образцов, особенно для тех, в которых растворимость водорода довольно низкая. Не досушенные таким образом образцы могут содержать растворенный водород, что может привести к существенному «занижению» результатов измерений.

Кроме того, проточная система «реактор-газовый контур» требует большого расхода газов для длительной продувки водородсодержащей смеси при организации эксперимента.

Описанный способ с использованием метода термогравиметрического анализа позволяет определять концентрацию протонов в атмосфере влажного водорода, однако не дает возможности провести измерения в атмосфере сухого водорода, т.е. не содержащего пары воды, поскольку технически невозможно в достаточной степени высушить газовый контур, термоанализатор, а также газовые магистрали. Таким образом, всегда остается слабо контролируемое количество воды, точное количество которой определить практически невозможно.

Задача настоящего изобретения заключается в создании возможности измерения концентрации протонов в протон-проводящих оксидных материалах в атмосфере сухого водорода при повышении точности измерения концентрации протонов за счет глубокой степени осушки образца, а также в снижении расхода водорода.

Для решения поставленной задачи в способе определения концентрации протонов в протон-проводящих оксидных материалах образец исследуемого оксида помещают в реактор, соединенный с газовым контуром, сушат при нагреве до температуры 900÷1000°C, затем меняют газовую фазу на атмосферу, содержащую водород, регистрируют изменение во времени значения параметра оксида, напрямую связанного с изменением количества протонов в оксиде, достигая состояния равновесия оксида с газовой фазой, и на основании полученного равновесного значения параметра оксида производят расчет концентрации протонов в протон-проводящем оксиде как количества вещества водорода в оксиде, отнесенного к одному молю оксида, отличающийся тем, что в качестве параметра оксида, напрямую связанного с изменением количества протонов в протон-проводящем оксиде, используют значение давления водорода над оксидом в замкнутом газовом контуре постоянного объема, для этого образец помещают в реактор, вакуумплотно соединенный с газовым контуром, изолированным от атмосферы, откачивают газовый контур с реактором на высокий вакуум и сушат образец, выдерживая его при температуре осушки до установления остаточного давления не более 10 Па, затем перекрывают вакуумплотное соединение реактора с газовым контуром, напускают в контур водород высокой чистоты до заданного давления, открывают вакуумплотное соединение реактора с газовым контуром и после мгновенного установления общего давления водорода в системе «реактор-газовый контур» регистрируют изменение значения давления водорода над образцом во времени, достигая состояния равновесия оксида с газовой фазой, и на основании разницы давления водорода, установившегося сразу после открытия вакуумплотного соединения, и полученного равновесного значения давления водорода над образцом производят расчет концентрации протонов в протон-проводящем оксиде.

В отличие от способа по прототипу с применением метода термогравиметрического анализа, где в качестве параметра, напрямую указывающего на изменение концентрации протонов в протон-проводящем оксиде, используется изменение массы образца во времени, добиваясь состояния равновесия образца с газовой фазой, в заявленном способе в качестве такого параметра используется величина давления водорода над образцом в замкнутом газовом контуре постоянного объема. Метод релаксации давления водорода заключается в том, что вначале проводят глубокую осушку образца протон-проводящего оксида, для этого образец нагревают до температуры 900÷1100°C и выдерживают при постоянной откачке на высокий вакуум, оставляя открытым вакуумплотное соединение, добиваясь установления остаточного давления не более 10^-7 Па. Затем вакуумплотное соединение перекрывают и в оставшуюся часть контура напускают водород высокой чистоты до заданного давления, после чего вакуумплотное соединение открывают. Величина давления, которую задают для проведения измерений, может быть любой в диапазоне от 10^-1 до 10⁵ Па.

В результате после мгновенного установления общего давления водорода в системе «реактор-газовый контур» происходит медленное растворение водорода в протон-проводящем оксиде, при этом водород проникает в образец оксида, а давление водорода уменьшается.

Таким образом, с помощью метода релаксации давления водорода регистрируют изменение во времени значения давления водорода, напрямую связанного с изменением количества протонов в оксиде, так как образец находится в замкнутом газовом контуре постоянного объема. Однако, в отличие от метода термогравиметрического анализа, где используют проточную систему для продувки водородсодержащей газовой смеси, метод релаксации давления водорода реализуют с использованием реактора, вакуумплотно соединенного с газовым контуром, изолированным от атмосферы, в котором можно создать высокий вакуум и любое давление водорода в диапазоне от 10^-1 до 10⁵ Па. Откачка газового контура с реактором на высокий вакуум при открытом вакуумплотном соединении реактора с газовым контуром позволяет произвести осушку образца протон-проводящего оксида при температуре 900÷1100°C до остаточного давления 10 Па, что существенно ниже по сравнению с сушкой в проточной системе в атмосфере воздуха над адсорбентами водяного пара, такими как цеолиты, пентоксид фосфора и др. Это предотвращает искажение результатов измерений, обусловливаемое недостаточной осушкой образцов, что важно особенно для образцов с низкой растворимостью водорода.

Вакуумплотно перекрывая сообщение реактора с газовым контуром и напуская в контур водород высокой чистоты, задают необходимое давление водорода над образцом после открытия вакуумплотного соединения.

Использование водорода высокой чистоты вместо водородсодержащей смеси, применяемой в термогравиметрическом методе анализа, позволяет проводить измерение в атмосфере сухого водорода. В методе релаксации давления парциальное давление водорода равно абсолютному, поэтому в заявленном способе применим датчик общего давления, работающий с абсолютными давлениями при комнатной температуре. Это позволяет регистрировать изменения давления водорода в атмосфере сухого водорода. Использование для реализации метода релаксации замкнутого газового контура, изолированного от атмосферы с возможностью его откачивания на высокий вакуум, позволяет экономно расходовать водород.

Таким образом, новый технический результат, достигаемый заявленным способом, заключается в повышении степени осушки исследуемых образцов, повышении точности измерения концентрации протонов в атмосфере сухого водорода, сокращении расхода водорода.

Изобретение иллюстрируется чертежами, где на фиг.1 приведена принципиальная схема экспериментальной установки для реализации способа; на фиг.2 приведена кривая зависимости давления от времени, иллюстрирующая метод релаксации давления.

Экспериментальная установка состоит из двух частей: газовый контур 1, который посредством вакуумного крана 2 вакуумплотно соединен с кварцевым реактором 3. В реактор 3 помещают образец 4. Реактор помещен в печь (не показана). Газовый контур 1 имеет трехступенчатую систему откачки. Откачку на форвакуум осуществляют с помощью диафрагменного насоса 5, остаточное давление при этом составляет порядка 10^-1 Па. Вторую ступень откачки осуществляют с помощью турбомолекулярного насоса 6, остаточное давление при этом составляет порядка 10^-5 Па. Третью ступень откачки осуществляют с помощью высоковакуумного магниторазрядного насоса 7, при этом достигается остаточное давление порядка 10^-8 Па. Установка содержит датчики давления Баярда-Альперта Пирани 8, систему напуска водорода 9, баллон с кислородом высокой чистоты 10.

Давление газа в контуре 1 измеряли с помощью датчиков Баярда-Альперта Пирани 8, откалиброванных на диапазон давлений от 10^-8 до 10⁵ Па. Напуск водорода в контур 1 осуществляли с помощью системы напуска 9 из баллона 10. Для вакуумплотного соединения реактора с газовым контуром использовали вакуумные краны типа All-Metal UHV Valves с натеканием по гелию не более чем 10^-4 Па·см³/с. Работу печи реактора 3 обеспечивали с помощью терморегулятора Термодат-19Е5. Тип использованной термопары – ТПП.

В ходе эксперимента использовали водород высокой чистоты. После размещения исследуемого образца в реакторе при комнатной температуре проводили откачку газового контура на высокий вакуум.

До начала эксперимента по реализации метода релаксации давления водорода проводили глубокую осушку образца протон-проводящего оксида. Для этого образец нагревали до температуры 900°C и выдерживали в течение трех-четырех суток при постоянной откачке на высокий вакуум, оставляя открытым вакуумплотное соединение, добиваясь остаточного давления не более 10^-7 Па. Затем вакуумплотное соединение перекрывали и в оставшуюся часть контура напускали водород высокой чистоты до нужного давления. После этого вакуумплотное соединение открывали и регистрировали изменение во времени значения давления водорода (фиг. 2), добиваясь состояния равновесия образца оксида с газовой фазой. Критерием установившегося состояния равновесия служило значение стандартного отклонения давления для 1000 последних записанных точек от их среднего значения, которое не превышало 1 Па. На основании разницы давления водорода, установившегося сразу после открытия вакуумплотного соединения, и полученного равновесного значения давления водорода над образцом, производят расчет концентрации протонов в протон-проводящем оксиде, как количества вещества водорода в оксиде, отнесенного к одному молю оксида.

Момент открытия реактора считается началом эксперимента с применением метода релаксации давления водорода.

Заявленный способ позволяет расширить диапазон средств для измерения концентрации протонов в протон-проводящих оксидных материалах в атмосфере сухого водорода, повысить точность измерения концентрации протонов за счет глубокой степени осушки образца, сократить расход водорода.

Способ определения концентрации протонов в протон-проводящих оксидах, в котором образец исследуемого оксида помещают в реактор, соединенный с газовым контуром, сушат при нагреве до температуры 900÷1000°C, затем меняют газовую фазу на атмосферу, содержащую водород, регистрируют изменение во времени значения параметра оксида, напрямую связанного с изменением количества протонов в оксиде, достигая состояния равновесия оксида с газовой фазой, и на основании полученного равновесного значения параметра оксида производят расчет концентрации протонов в протон-проводящем оксиде как количества вещества водорода в оксиде, отнесенного к одному молю оксида, отличающийся тем, что в качестве параметра оксида, напрямую связанного с изменением количества протонов в протон-проводящем оксиде, используют значение давления водорода над оксидом в замкнутом газовом контуре постоянного объема, для этого образец помещают в реактор, вакуумплотно соединенный с газовым контуром, изолированным от атмосферы, откачивают газовый контур с реактором на высокий вакуум и сушат образец, выдерживая его при температуре осушки до установления остаточного давления не более 10^-7 Па, затем перекрывают вакуумплотное соединение реактора с газовым контуром, напускают в контур водород высокой чистоты до заданного давления, открывают вакуумплотное соединение реактора с газовым контуром и после мгновенного установления общего давления водорода в системе «реактор-газовый контур» регистрируют изменение значения давления водорода над образцом во времени, достигая состояния равновесия оксида с газовой фазой, и на основании разницы давления водорода, установившегося сразу после открытия вакуумплотного соединения, и полученного равновесного значения давления водорода над образцом производят расчет концентрации протонов в протон-проводящем оксиде.



Большинство химических реакций, протекающих в разбавленных растворах слабых электролитов, основаны на равновесных процессах с участием ионов. Правильный расчет физико-химических равновесий позволяет контролировать и управлять химическими реакциями, а также создавать необходимые условия для оптимального протекания технологических процессов, качественных и количественных аналитических определений.

В данной статье приведены основы математического расчета различных химических равновесий, условий и полноты протекания реакций и определения равновесных концентраций веществ в реагирующих системах.

Ключевые слова: химическое равновесие, равновесная концентрация, константа ионизации, слабая кислота, слабое основание, ступенчатая диссоциация, материальный баланс, фосфорная кислота, гидрат аммиака, константа автопротолиза, ионное произведение воды, гидролиз солей, константа гидролиза, произведение растворимости солей

Keywords. Chemical equilibrium, equilibrium concentration, ionization constant, weak acid, weak base, stepwise dissociation, material balance, phosphoric acid, ammonium hydroxide, autoprotolysis constant, ionic product of water, hydrolysis of salts, hydrolysis constant, solubility product of salts.

Рассмотрение вопросов о расчете химических равновесий начнем с конкретных примеров.

Задача 1. Вычислить концентрацию продуктов ступенчатой диссоциации ортофосфорной кислоты в 0,1 М водном растворе. Рассчитать степень диссоциации кислоты в этом растворе.

Решение. Вразбавленных водных растворах ортофосфорная кислота ведет себя как сильная кислота, однако только один из протонов отщепляется легко, и константа ионизации по первой ступени достаточно высокая. Вторая и третья константы ионизации последовательно снижаются на пять порядков.

Запишем уравнения ступенчатой диссоциации ортофосфорной кислоты:

(I ступень) H₃PO₄ + H₂O H₃O⁺ + H₂PO₄^–, ;

(II ступень) H₂PO₄^– + H₂O H₃O⁺ + HPO₄^2–, ;

(III ступень) HPO₄^2– + H₂O H₃O⁺ + PO₄^3–, .

Здесь и далее pK = — lgK_равн — логарифмический показатель констант равновесия, а все расчеты проводятся для стандартных состояний веществ и t=25°C.

С учетом всех трех стадий ступенчатой диссоциации фосфорной кислоты можно составить уравнение материального баланса. Одним из условий материального баланса является неизменность содержания определенного вида атомов (или групп атомов) в процессе химического превращения веществ в изолированной системе. Например, водород в рассматриваемой системе находится в виде гидратированных ионов H₃O⁺ и входит в состав ионов H₂PO₄^–, HPO₄^2–, а также электронейтральных молекул H₃PO₄. Математическая запись этого условия выглядит следующим образом:

.

Баланс по числу атомов фосфора можно представить в следующем виде:

.

Каждое химическое равновесие характеризуется своей константой равновесия. Для рассматриваемых случаев — это ступенчатые константы ионизации:

;

;

.

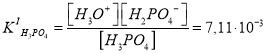
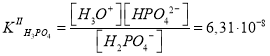
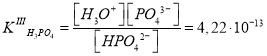
Поскольку значения и различаются приблизительно в 10⁵ раз, концентрацию протонов можно вычислить с учетом диссоциации H₃PO₄ только по первой ступени. Данное допущение не вызывает больших погрешностей расчетов, если многоосновной кислоты превышает примерно в 10³ раз и более.

Предположим, что в процессе диссоциации фосфорной кислоты по первой ступени образуется равное количество ионов H⁺ и H₂PO₄^–, а их равновесную концентрацию обозначим x моль/л. Тогда равновесная концентрация фосфорной кислоты составит (0,1 — x), моль/л:

H₃PO₄ + H₂O H₃O⁺ + H₂PO₄^–

(0,1 – x) xx

Подставим равновесные концентрации этих ионов в выражение для константы равновесия :

,

или .

Решая квадратное уравнение, получаем:

моль/л.

В том случае, если кислота очень слабая, то [H⁺]<0_HA и C⁰_HA — [H⁺] ≈ C⁰_HA. Равновесную концентрацию протонов в таких растворах вычисляют по следующей формуле:

.

Данное допущение оправдано для кислот с pK≥4 (при условии, что C⁰_HA˃˃K_HA). Концентрация иона H₂PO₄^– практически определяется диссоциацией фосфорной кислоты по I ступени: [H₂PO₄^–] = [H₃O⁺] = 2,33·10^–2 моль/л.

Значения и различаются в 10⁵ раз, поэтому концентрацию иона HPO₄^2– определим с учетом диссоциации кислоты по II ступени:

моль/л.

Концентрация аниона, образующегося в результате диссоциации слабой кислоты H₂A по II ступени, численно равна , т. е. [A^2–] =·(H₂A).

Зная равновесные концентрации ионов H₃O⁺ и HPO₄^2–, вычислим концентрацию иона PO₄^3–:

(или 1,14·10^–18моль/л).

По равновесным концентрациям продуктов диссоциации фосфорной кислоты найдем степень диссоциации (α) по всем трем ступеням:

или 23,3 %;

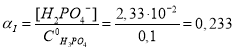
или 2,7·10^–4 %;

или 1,8·10^–9 %.

В растворах, где [H₃O⁺]<0_HA, степень диссоциации (α) можно определить по следующему уравнению:

.

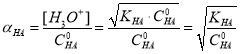
Математическими расчетами были определены области преобладания частиц в водном растворе ортофосфорной кислоты в зависимости от pH среды: H₃PO₄: 0 ≤ pH ≤ 2,12; H₂PO₄^–: 2,12 ≤ pH ≤ 7,21; HPO₄^2–: 7,21 ≤ pH ≤ 12; PO₄^3–: 12 ≤ pH ≤ 14.

Задача 2. Определите, какие продукты будут образовываться при взаимодействии ортофосфорной кислоты и гидрата аммиака в разбавленном водном растворе.

Решение. Для ответа на вопрос рассчитаем константу равновесия следующей реакции в предположении того, что гидрат аммиака (NH₃·H₂O) как основание отщепляет от фосфорной кислоты сразу три протона:

H₃PO₄ + 3 NH₃·H₂O 3 NH₄⁺ + PO₄^3– + 3 H₂O.

С учетом закона действующих масс константу равновесия можно записать в следующем виде:

;

или .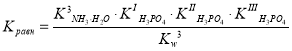

К данному выражению мы пришли с учетом следующих допущений:

а) в водном растворе происходит диссоциация гидрата аммиака:

3 NH₃·H₂O 3 NH₄⁺ + 3 OH^–.

Запишем выражение для константы равновесия данной реакции:

;

выражение носит название константы диссоциации (ионизации) основания NH₃·H₂O.

б) В водном растворе происходит ионизация молекул фосфорной кислоты:

H₃PO₄ + 3 H₂O 3 H₃O⁺ + PO₄^3–.

Запишем выражение для константы равновесия данной реакции с учетом выражений для констант диссоциации фосфорной кислоты по трем ступеням:

.

После преобразований получаем следующее равенство:

,

.

в) Вода (H₂O) — слабый электролит и в незначительной степени подвергается ионизации. Этот процесс называется автопротолизом. Схематично его можно представить так:

H₂O + H₂O H₃O⁺ + OH^–.

Константу равновесия автопротолиза представим в следующем виде:

.

Посредствам измерения электропроводности абсолютно чистой воды было показано, что концентрации ионов H₃O⁺ и OH^– составляют 10^–7 моль/л, а концентрация молекул H₂O составляет 1000/18 = 55,56 моль/л. Отсюда была вычислена константа автопротолиза воды:

.

Диссоциация воды весьма незначительна, поэтому ее концентрацию считают практически неизменной, и выражение для константы диссоциации воды можно представить в следующем виде:

.

Иными словами, произведение концентрации ионов, образующихся в процессе диссоциации воды — есть величина постоянная при данной температуре (25°C), и данная константа называется ионным произведением воды K_w.

С учетом приведенных выше уточнений (а — в) рассчитаем константу равновесия реакции:

.

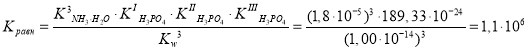
Величина Kравн служит характеристикой необратимости реакции в данных условиях. Так, если значение Kравн очень велико, то это означает, что при равновесии, концентрации продуктов реакции намного превышают концентрации исходных веществ, и реакция прошла почти до конца, — слева направо.

Предположим, что гидрат аммиака отщепляет от фосфорной кислоты один протон. Рассчитаем константу равновесия данной реакции с учетом представленных выше допущений.

H₃PO₄ + NH₃·H₂O H₂PO₄^– + NH₄⁺ + H₂O.

,

.

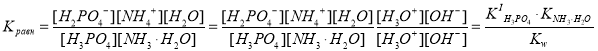
Расчет показал, что химическое равновесие существенно смещено вправо, и реакция в стандартных условиях идет до конца, поскольку значение константы равновесия этой реакции также достаточно велико (K_равн˃˃1).

Пусть на следующей стадии процесса происходит отщепление второго протона. Рассчитаем вероятность этого процесса и сравним с рассмотренными случаями.

H₂PO₄^– + NH₃·H₂O HPO₄^2– + NH₄⁺ + H₂O.

,

.

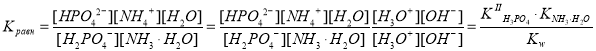
Расчет показывает, что данная стадия также термодинамически вероятна, поскольку значение константы равновесия положительное, и равновесие существенно смещено вправо, однако величина константы равновесия на пять порядков ниже. Это свидетельствует о меньшей вероятности протекания данного процесса по сравнению с предыдущей реакцией.

Наконец, если предположить отщепление третьего протона на следующей стадии, то реакцию можно представить в следующем виде:

HPO₄^2– + NH₃·H₂O PO₄^3– + NH₄⁺ + H₂O.

,

.

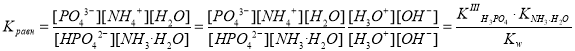
Величина константы равновесия данной реакции свидетельствует о ее неполном прохождении. Равновесие существенно смещено влево.

Таким образом, взаимодействие фосфорной кислоты с гидратом аммиака в основном протекает по схемам:

1) H₃PO₄ + NH₃·H₂O NH₄H₂PO₄ + H₂O,

2) NH₄H₂PO₄ + NH₃·H₂O (NH₄)₂HPO₄ + H₂O;

или H₃PO₄ + 2 NH₃·H₂O 2 (NH₄)₂HPO₄ + 2 H₂O.

Задача 3. Рассчитайте концентрации ионов H₂PO₄^– и PO₄^3– в растворе, в котором общая концентрация фосфат-ионов C⁰_n составляет 0,5 моль/л, а pH раствора равен 5.

Решение. Зная pH раствора, находим концентрацию протонов: [H₃O⁺]=10^–5 моль/л.

Для любого слабого электролита состава AH_n с учетом уравнения материального баланса (например, по числу атомов A) и выражений констант равновесия (пусть n=2 и диссоциация AH_n идет по двум ступеням), после несложных математических преобразований можно записать следующее выражение для концентрации :

.

Если – доля недиссоциированных молекул, то с учетом выражения для , получим:

.

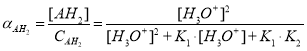
Доли продуктов диссоциации не зависят от общей концентрации электролита, а зависят от концентрации ионов H₃O⁺ и — через константы диссоциации — от природы электролита. Поэтому, если известен pH раствора, то легко можно рассчитать концентрации продуктов диссоциации.

Для любого слабого электролита состава AB₂ можно написать общее выражение знаменателя в формуле для расчета долей продуктов диссоциации (α):

[B]ⁿ + K₁· [B]^n-1 + K₁·K₂· [B]^n-2 + … + K₁·K₂…K_n-1· [B] + K₁·K₂…K_n.

Например, долю ионов AB_n-2 можно определить по следующей формуле:

.

Если из выражений констант ступенчатой диссоциации фосфорной кислоты выразить концентрации соответствующих ионов (H₂PO₄^–, HPO₄^2–, PO₄^3–) и подставить в выражение материального баланса по атомам фосфора, то можно получить следующее уравнение для истинной концентрации фосфорной кислоты :

, , ;

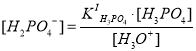
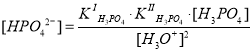
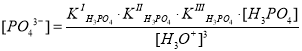
Если перед нами встала задача определения мольной доли, например, фосфорной кислоты, оставшейся в недиссоциированном (молекулярном) состоянии, нам необходимо найти отношение концентрации частиц [H₃PO₄] к суммарной концентрации всех частиц :

.

Вернемся к нашему примеру. Зная значения констант диссоциации фосфорной кислоты аналогичным образом определим долю ионов, образующихся по первой ступени (H₂PO₄^–):

;

;

.

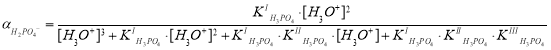
Тогда концентрацию ионов H₂PO₄^– определим следующим образом:

[H₂PO₄^–] = · C⁰_n = 0,99·0,5 = 0,495 моль/л.

Доля ионов, образующихся по второй ступени, определяется по выведенной выше формуле и после подстановки соответствующих значений составит . Концентрацию ионов PO₄^3– определим аналогично:

[PO₄^3–] = · C⁰_n = 3,3·10^–10·0,5 = 16,5·10^–11 моль/л.

Задача 4. Определить pH 0,1 М водных растворов ортогидрофосфата и ортофосфата натрия с учетом процесса гидролиза солей. Возможно ли растворение цинка в данных растворах?

Решение. а)Соль Na₂HPO₄ в водном растворе диссоциирована практически полностью:

Na₂HPO₄ → 2 Na⁺ + HPO₄^2–.

Гидрофосфат-ион (HPO₄^2–) подвергается гидролизу по первой ступени в соответствии со следующей схемой:

HPO₄^2– + H₂O H₂PO₄^– + OH^–,

далее дигидрофосфат-ион подвергается гидролизу по второй ступени:

H₂PO₄^– + H₂O H₃PO₄ + OH^–.

Запишем выражения для констант гидролиза и определим их значения:

,

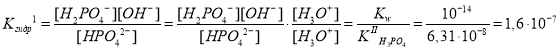
где , так как H₂PO₄^– + H₂O HPO₄^2– + H₃O⁺, а , так как H₂O + H₂O H₃O⁺ + OH^–.

.

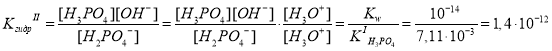
В данных расчетах, как и в предыдущих мы использовали следующий прием: умножили числитель и знаменатель дроби на концентрацию ионов H₃O⁺, тем самым пришли к выражениям для константы ионизации и константы автопротолиза.

K^I_гидр превышает K^II_гидр практически в 10⁵ раз, поэтому гидролизом по второй ступени можно пренебречь.

Гидрофосфат-ион (HPO₄^2–) диссоциирует в водном растворе по следующей схеме:

HPO₄^2– + H₂O H₃O⁺ + PO₄^3–.

Для данного процесса запишем выражение для константы равновесия:

.

Протоны, появляющиеся в результате диссоциации гидрофосфат-ионов, реагируют с OH^–-ионами, образующимися при гидролизе HPO₄^2–-иона. Учитывая, что [H₃O⁺] = [PO₄^3–] и [OH^–] = [H₂PO₄^–], равновесная концентрация протонов в растворе Na₂HPO₄ определяется разностью [H₃O⁺]= = [PO₄^3–] — [H₂PO₄^–] или [OH^–] = [H₂PO₄^–] — [PO₄^3–].

Выразим концентрацию ионов H₂PO₄^– и PO₄^3– через константы равновесий реакций гидролиза и диссоциации иона H₂PO₄^–:

,

.

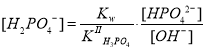
Из ионного произведения воды следует, что , поэтому после подстановки соотношение примет следующий вид:

.

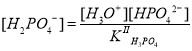
Теперь, зная концентрации фосфат- и дигидрофосфат-ионов, определим равновесную концентрацию протонов:

.

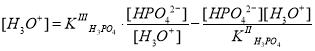
Далее, после преобразований получаем следующее уравнение:

,

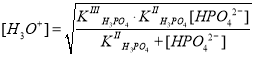
где ; она намного меньше концентрации ионов HPO₄^2– и практически равна начальной концентрации соли Na₂HPO₄, т. е. 0,1 моль/л. Поэтому сумма упрощается: , и уравнение примет следующий вид:

.

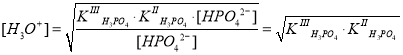
В итоге, величину pH можно определить следующим образом:

.

По данной формуле рассчитаем величину pH в 0,1 М растворе Na₂HPO₄:

.

Аналогично можно показать, что в растворе соли NaH₂PO₄ pH вычисляется по формуле:

.

б) Рассчитаем pH 0,1 М раствора Na₃PO₄. Здесь приведем упрощенный расчет. В данном случае также после диссоциации соли протекает протолиз аниона:

Na₃PO₄ 3 Na⁺ + PO₄^3–,

PO₄^3– + H₂O HPO₄^2– + OH^–.

Запишем выражение для константы равновесия:

,

откуда ,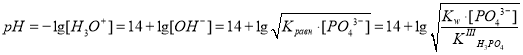

.

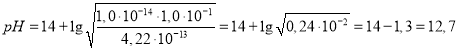
Высокие значения pH среды в данных растворах (0,1 М Na₂HPO₄ pH=9,8; 0,1 М Na₃PO₄ pH=12,7) свидетельствуют о сильнощелочной среде. В задаче стоял вопрос о растворимости цинка в этих растворах. Основываясь на знании химических свойств цинка, в частности, его способности взаимодействовать с растворами щелочей, можно предложить следующие реакции для процессов растворения цинка в растворах Na₂HPO₄ и Na₃PO₄:

2 Na₂HPO₄ + Zn + 4 H₂O = Na₂ [Zn(OH)₄] + 2 NaH₂PO₄ + H₂↑,

2 Na₃PO₄ + Zn + 4 H₂O = Na₂ [Zn(OH)₄] + 2 Na₂HPO₄ + H₂↑.

Задача 5. Вычислить без учета гидролиза и с учетом гидролиза произведение растворимости фосфата серебра , если растворимость этой соли в воде при комнатной температуре равна 4,68·10^–6 моль/л. Вычислить pH насыщенного раствора Ag₃PO₄.

Решение. Внасыщенном растворе Ag₃PO₄ существует равновесие:

Ag₃PO₄ (крист.) 3 Ag⁺ + PO₄^3–

3·4,68·10^–6 моль/л 4,68·10^–6 моль/л.

а) Если растворимость соли составляет 4,68·10^–6 моль/л, то в соответствии с уравнением процесса, но без учета гидролиза получим следующее: [PO₄^3–] = 4,68·10^–6 моль/л, а [Ag⁺] = 3· [PO₄^3–] = 3·4,68·10^–6 моль/л.

По этим данным вычислим :

.

Справочная величина составляет: .

б) Вычислим с учетом процесса гидролиза фосфата серебра.

Образующийся при растворении в воде Ag₃PO₄ ион PO₄^3– подвергается гидролизу:

PO₄^3– + H₂O HPO₄^{2 —} + OH^–

Пусть подверглось гидролизу x моль/л иона PO₄^3–, а образовалось в результате гидролиза по (4,68·10^–6 — x) моль/л ионов HPO₄^{2 –} и OH^–, соответственно.

Запишем выражение для константы гидролиза:

.

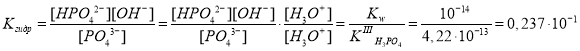
Гидролиз иона PO₄^3– по первой ступени при концентрации 4,68·10^–6 моль/л протекает практически полностью, поэтому за наименьшую равновесную концентрацию x принимаем равновесную концентрацию ионов PO₄^3–, т. е. [PO₄^3–] = x, [HPO₄^2–] = [OH^–] = 4,68·10^–6 — x, моль/л.

Подставим равновесные концентрации в выражение для константы гидролиза:

.

Допустим, что 4,68·10^–6 — x ≈ 4,68·10^–6. Тогда 2,37·10^–2 · x = (4,68·10^–6)² и x = 9,24·10^–10 моль/л. Эта величина достаточно мала и в приближенных расчетах ей можно пренебречь.

Следовательно, [OH^–] ≈ 4,68·10^–6 моль/л и pH = 14 + lg 4,68·10^–6 = 8,67.

Гидролиз Ag₃PO₄ по катиону протекает незначительно. Константа гидролиза Ag⁺ очень мала (). При [Ag⁺] = 3·4,68·10^–6 = 1,4·10^–5 моль/л и [OH^–] = 4,68·10^–6 моль/л концентрация AgOH составит: [AgOH] = β_AgOH [Ag⁺] [OH^–] = 2·10²·1,4·10^–5·4,68·10^–6 = 1,31·10^–8 моль/л, т. е. всего около 0,1 % от начальной концентрации ионов Ag⁺. Здесь β — общая константа устойчивости AgOH, которая определяет следующее равновесие:

Ag⁺ + OH^– AgOH,

.

Следовательно, поправка к pH, учитывающая гидролиз соли по катиону в насыщенном растворе Ag₃PO₄, невелика.

Рассчитаем значение произведения растворимости соли с учетом гидролиза:

.

Данное значение существенно отличается от величины, найденной без учета гидролиза соли.

На простых примерах мы убедились, что расчет химических равновесий с применением простейших алгебраических алгоритмов и приемов, позволяет предсказать принципиальную возможность (вероятность) протекания химической реакции, а также сделать вывод о влиянии тех или иных факторов на смещение химического равновесия с целью достижения необходимого положительного эффекта процесса. На основании значений констант химического равновесия конкурентно протекающих реакций можно сделать вывод о преобладающем значении той или иной реакции в общем массиве термодинамически вероятных процессов.

Литература:

1. Гольбрайх З. Е., Маслов Е. И. Сборник задач и упражнений по химии: Учебное пособие для хим.-технол. спец. вузов. — М.: Высш. шк., 1997.
2. Михайлов В. А. Химическое равновесие: учебное пособие / В. А. Михайлов, О. В. Сорокина, Е. В. Савинкина, М. Н. Давыдова; Под ред. А. Ю. Цевадзе. — М.: БИНОМ. Лаборатория знаний, 2011.
3. Сборник вопросов и задач по аналитической химии. Учебное пособие для вузов / В. П. Васильев, В. Е. Калинина, Л. А. Кочергина и др. Под ред. В. П. Васильева. — М.: Высш. шк., 1976.