Как найти концентрацию раствора ch3cooh

Чему равна концентрация раствора уксусной кислоты, pH которого равен 3,2(К_д=1,8*10^-5)?

Я решал так:

pH=-lg[H⁺], следовательно lg[H⁺]=-pH

[H⁺]=10^-pH=10^-3,2=6,3*10^-4;

1. [H⁺]=α*C, следовательноα=[H⁺]/С
2. К_д=α²*C(так как CH3COOH-слабая кислота)

Из 1. и 2. следует: К_д=([H⁺]/С)²*C=[H⁺]²/С,следовательно С=[H⁺]²/К_д

С=6,3²/1,8*10^-5=0,022

ответ:0,022

Верно?если нет, то где ошибка?

Рассчитайте концентрацию уксусной кислоты (CH₃COOH) в винном уксусе (рН=2,80), полагая, что кислотность определяется только уксусной кислотой (CH₃COOH).

Решение задачи

Запишем уравнение диссоциации уксусной кислоты (CH₃COOH):

Водородный показатель (pH) раствора численно равен отрицательному десятичному логарифму концентрации ионов водорода в этом растворе.

Используя, формулу, найдем концентрацию ионов водорода (H⁺):

-lg С(H⁺) = 2,8

С(H⁺) = 10^-2,8 = 0,0016 (моль/л).

Учитывая, что концентрация уксусной кислоты (CH₃COOH) равна концентрации ионов водорода (смотри уравнение диссоциации уксусной кислоты), следовательно, концентрация уксусной кислоты (CH₃COOH) равна 0,0016 моль/л.

Ответ:

концентрация уксусной кислоты 0,0016 моль/л.

Вычисление концентрации электролита по значению его рН

Задача 545. 
Чему равна концентрация раствора уксусной кислоты, рН которого равен 5,2?
Решение: 
K_D(CH₃COOH) = 1,8 ^. 10^-5.
Согласно условию задачи -lg[H⁺] = 5,2. Следовательно, -lg[H⁺] = 5,2 = 6,8. По таблице логарифмов находим:

[H⁺] = 6,31 ^. 10^-5 моль/л. 

Концентрации ионов [H⁺] и ионов [CH₃COO^–] в растворе CH₃COOH равны:

CH₃COOH ⇔ CH₃COO^– + H⁺

Обозначим искомую концентрацию уксусной кислоты через x и найдём его значение из выражения константы диссоциации, получим:

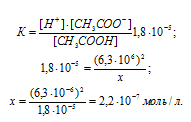
Ответ: C_M = 2,2 ^. 10^-7 моль/л.

---

Задача 546.
Вычислить значения (OH^–)  и p(OH)  в 0,2 н. растворе NaОН, считая f(OH^–) = 0,80.
Решение:
Для электролитов, состоящих из однозарядных ионов, значение ионной силы раствора численно равно концентрации раствора, в данном случае: I(NaOH) = 0,20. При ионной силе равной 0,2 и при коэффициенте активности иона равному 0,80 можно рассчитать значения активностей ионов по формуле  (ион) = fC_M, получим:

(OH^–) = 0,80 ^. 0,20 = 0,16 моль/л.

Теперь рассчитаем значение  p(OH^–):

p(OH^–) = –(OH^–) = -lg1,6 . 10-1 = 1 – lg1,6 = 0,8.

Ответ: p(OH-) = 0,8, (OH^–) = 1,6 ^. 10^-1 моль/л.

---

Задача 547.
Используя данные табл. 7 приложения, найти p(H⁺) 0,005 н. раствора НСI, содержащего, кроме того, 0,015 моль/л NаС1.
Решение:
Для электролитов, состоящих из однозарядных ионов, значение ионной силы раствора численно равно концентрации раствора, в данном случае: I = 0,005 + 0,015 = 0,02. 

При этой ионной силе коэффициент активности однозарядного иона равен 0,90. Активную концентрацию иона водорода рассчитаем по формуле  (ион) = fC_M, где f – коэффициент активности иона, С_М – концентрация раствора, получим:

(H⁺) = 0,02 ^. 0,9 = 1,8 ^. 10^-2 моль/л.

Теперь находим значение p(H+):

p(H⁺) = –(H⁺) = -lg1,8 ^. 10^-2 = 2 – lg1,8 = 2 – 0,255 = 1,75.

Ответ: p(H⁺) = 1,75.

---

Задачи 548.
Степень диссоциации слабой одноосновной кислоты в 0,2 н. растворе равна 0,03. Вычислить значения  [H⁺], [OH^–] и pOH для этого раствора.
Решение:
Находим концентрацию ионов водорода:

[H⁺] = ^. C_M = 0,2 ^. 0,03 = 6 ^. 10^-3 моль/л.

Концентрацию гидроксид-ионов находим из соотношения:  

pH₂O = [H⁺] ^. [OH^–] = 10^-14; [OH^–] = (10^-14)/(6 ^. 10^-3) = 1,7 ^. 10^-12.              

Отсюда

pОН = lg[OH^–] = -lg1,7 ^. 10^-12 = 12 – lg1,7 = 12 – 0,23 = 11,77.

Ответ:  [H⁺] = 6 ^. 10^-3 моль/л; [OH^–] = 1,7 ^. 10^-12; pОН = 11,77.

---

         Растворы. Способы выражения концентрации растворов

         Важной
характеристикой раствора является концентрация.

         Концентрация – это величина, измеряемая количеством растворенного
вещества, содержащегося в определенной массе или объеме раствора или
растворителя.

         Наиболее
часто применяемые способы выражения концентрации: массовая доля,
молярная концентрация, молярная концентрация эквивалента, моляльность,
молярная доля, объемная доля, титр.

         Массовую
долю w(X) выражают в долях единицы, процентах (%), промилле (тысячная
часть процента) и в миллионных долях (млн^–1) . Массовую долю
рассчитывают по формулам:

,

где m(X) – масса растворенного
вещества Х, кг (г);

m_р-ра – масса
раствора, кг (г).

         Например:
дан 0.85% раствор хлорида натрия. Это означает, что в 100 г раствора содержится
0.85 г NaCl.

         Молярную
концентрацию с(Х) выражают в моль/л. Молярную концентрацию находят
по формуле:

,

где n(X) – количество
растворенного вещества, моль;

M(X) – молярная
масса растворенного вещества, кг/моль, или г/моль;

m(X) – масса
растворенного вещества, соответственно, кг или г; 

V_р-ра – объем
раствора, л.

         Например:
дан 0.2 М раствор BaCl₂. Это означает, что в 1 л (1000 мл) раствора содержится 0.2
моль BaCl₂ и масса хлорида бария m (BaCl₂) = с·M·V = 0.2 моль/л·208
г/моль·1 л = 41.6 г.

         Моляльность
с_m(X) или b(X) выражают в единицах моль/кг. Рассчитываем моляльность по
формуле:

,

где m (р-ль) – масса
растворителя, кг.

         Моляльность
показывает, сколько моль растворенного вещества Х приходится на 1 кг
растворителя.

         В
химии широко используют понятие эквивалента и фактора
эквивалентности.

         Эквивалентом называют реальную или условную частицу вещества Х, которая в
данной обменной реакции обменивает один однозарядный ион или в данной
окислительно–восстановительной реакции переносит один электрон.

         Фактор эквивалентности  f_экв(Х) – число, обозначающее, какая доля реальной частицы
вещества Х эквивалентна одному иону водорода в данной кислотно–основной реакции
или одному электрону в данной окислительно-восстановительной реакции.

         Фактор
эквивалентности рассчитывают на основе стехиометрии данной реакции из
равенства:

f_экв(Х) = 1/z,

где z – основность кислоты или
кислотность основания данной кислотно-основной реакции, или число электронов,
присоединяемых или теряемых частицей в данной окислительно-восстановительной
реакции.

         Фактор
эквивалентности зависит от реакции, в которой участвует данное вещество; так
для фосфорной кислоты в реакциях:

H₃PO₄ + NaOH → NaH₂PO₄ + H₂O;           f_экв = 1/1.

H₃PO₄ + 2 NaOH → Na₂HPO₄
+ 2H₂O;      f_экв = 1/2.

H₃PO₄ + 3 NaOH → Na₃PO₄
+ 3H₂O;                  f_экв = 1/3.

         Для
перманганата калия в реакциях:

MnO₄^– + 8H⁺ + 5ē → Mn²⁺ + 4 H₂O;           f_экв = 1/5.

MnO₄^– + 2 H₂O + 3ē → Mno₂ + 4 OH^–;       f_экв = 1/3.

MnO₄^– + 1ē → MnO₄^2-;                               f_экв = 1/1.

         Для
иодид-иона и иода в реакции:

2I^–
– 2ē → I₂⁰;                                             f_экв(I^–) = 1/1; f_экв(I₂) = 1/2.

         Молярной массой эквивалента
вещества Х (масса одного моль эквивалента вещества) называют величину,
измеряемую произведением фактора эквивалентности на молярную массу вещества Х.

М(f_экв(Х)) =  f_экв·М(Х),

где М(f_экв(Х)) – молярная масса эквивалента.

         Единица
измерения молярной массы эквивалента – г/моль.

         Соответственно
для растворов используют понятие молярной концентрации эквивалента (нормальная
концентрация).

         Молярную
концентрацию эквивалента (нормальность) с(f_экв(Х)) рассчитывают
по формуле:

,

где n (f_экв (Х)) – количество
вещества эквивалента, моль;

V_р-ра – объем
раствора, л;

M (f_экв(Х)) – молярная масса эквивалента.

         Молярную
концентрацию эквивалента (нормальную концентрацию) обозначают c(f_экв(Х)). Единицы ее измерения – моль/м³, моль/дм³,
моль/л. В медицине чаще используют единицу моль/л. Форма записи, например,
с KMnO₄ (¹/₅) = 0.1 моль/л или 0.1 н. KMnO₄. Это означает, что в 1 л раствора содержится 0.1 моль
эквивалента перманганата калия.

         Молярная
концентрация эквивалента (нормальность) связана с молярной концентрацией
(молярностью) следующим выражением:

.

         Молярную
долю x(X_i) выражают в
долях единицы или в процентах. Молярную долю рассчитывают по формуле:

,

где n(X_i)– количество вещества данного компонента, моль;

 – суммарное количество всех компонентов раствора, моль.

         Объемную
долю φ(Х) выражают в долях единицы или в процентах, ее рассчитывают
по формуле

,

где V(Х)– объем данного
компонента Х, л; 

V_р-ра – общий
объем раствора, л.

         Титр
раствора обозначают T(X), единица
измерения – г/см³, г/мл. Титр раствора можно рассчитать по формуле:

 ,

где m(Х) – масса вещества,
обычно г;

V_р-ра – объем
раствора, мл.

         Титр
показывает, какая масса вещества содержится в 1 мл его раствора.

         В клинической практике нередко выражают концентрацию
ионов в миллиграмм–процентах (мг %). Это масса вещества, выраженная в
миллиграммах на 100 мл раствора.

         Формулы перехода от одних способов выражения
концентрации к другим см. прил., табл. №2.

Задача 1.

В 180 г воды растворили H₃PO₄ массой 9.8 г. Определите молярную долю (Х) и моляльную
концентрацию (С_m)
ортофосфорной кислоты.

Решение:

;

n (H₃PO₄)=  = 0.1 моль;

n (H₂O) =  = 10 моль;

Х (H₃PO₄) =  = 0.0099;

С_m (H₃PO₄)  ₌   = 0.556 моль/кг.

Ответ: Х (H₃PO₄) = 0.0099; С_m (H₃PO₄) = 0.0566 моль/кг.

Задача 2.

Массовая доля хлорида натрия в физиологическом растворе 0.9%
(ρ = 1 г/мл). Вычислите: а) молярную концентрацию и титр NaCl в этом растворе; б)
массу соли, веденной в организм при вливании 500 мл данного раствора.

Решение:

с(X)  = ; T = ; Т = ;

с(NaCl) =  = 0.154 моль/л;

Т (NaCl) =  = 0.00900 г/мл;

m(NaCl) = 0.00900 г/мл · 500
мл  = 4.5 г.

Ответ: с(NaCl) = 0.154 моль/л; Т(NaCl) = 0.00900 г/мл.

        Задача 3.

        Сколько мл
80% раствора CH₃COOH (ρ = 1.070 г/см³)
необходимо для приготовления 500 мл 0.1 М раствора?

Решение:

Найдем, сколько граммов уксусной кислоты содержится в 500 мл
раствора:

   .

Определим, в какой массе 80% раствора уксусной кислоты
содержится 3.0 г CH₃COOH:

.

Найдем объем 80% раствора CH₃COOH:

.

         Ответ:
V = 3.5 мл.

Считаем концентрацию ионов водорода
Из уравнения диссоциации концентрация ацетат-ионов, а значит и продиссоциировавшей кислоты такая же
Считаем равновесную концентрацию кислоты

Сложим равновесную концентрацию кислоты и концентрацию продиссоциировавшей кислоты