vk.com/club152685050 | vk.com/id446425943
ОБЩИЕ СВЕДЕНИЯ
Ведение. Видимый свет, как известно, представляет собой электромагнитные волны с длинами волн от 4 10-7 до 7 10-7 м. В электромагнитной волне векторы напряженности
электрического поля Е и магнитного поля Н взаимно перпендикулярны и одновременно перпендикулярны направлению распространения волны. Волны с такими свойствами называют поперечными.
Плоскость, проведенную через направления векторов напряженности электрического поля и световой луч, называют плоскостью колебаний электрического вектора.
Если для некоторого пучка света плоскость колебаний электрического вектора не изменяет своего положения в пространстве, то такой свет называют линейно (или плоско) поляризованным.
Для получения линейно поляризованного света используют специальные призмы, изготовленные из исландского шпата, и эти призмы называют поляризаторами. Аналогичные по устройству призмы, используемые для анализа поляризованного света, называют анализаторами.
Ряд веществ обладает способностью поворачивать плоскость колебаний вектора Е,
проходящего через них светового луча. Это явление называется оптической активностью. К оптически активным веществам относятся некоторые кристаллы и растворы (например кварц и раствор сахара в дистиллированной воде).
Вращение плоскости поляризации объясняется особым расположением атомов в пределах молекулы оптически активного вещества.
Если между скрещенными поляризатором и анализатором поместить оптически активное вещество, то плоскость поляризации света, вышедшего из поляризатора, повернется вокруг светового луча на некоторый угол, и анализатор пропустит свет. Чтобы вновь погасить свет, необходимо повернуть анализатор на угол α, равный углу вращения плоскости поляризации. Угол поворота плоскости поляризации при прохождении поляризованного света через кристалл пропорционален толщине активного слоя . Для
активного раствора угол поворота пропорционален длине пути луча в растворе и концентрации раствора с.
Для кристалла
|
‚ |
|
|
для раствора |
|
|
с ‚ |
|
|
где ρ′ и ρ″ – удельное вращение соответственно для |
|
|
кристалла и раствора. |
|
|
Удельное вращение (коэффициент ρ″) численно равен |
|
|
углу поворота плоскости поляризации при длине пути в 1 м и |
|
|
единичной концентрации активного раствора. Удельное |
|
|
вращение зависит от рода активного вещества и длины волны |
|
|
проходящего света. |
|
|
Целью лабораторной работы является определение |
|
|
величины удельного вращения ρ″ для раствора сахара (для |
Рис.1 |
|
чего используется эталонный раствор), а также определение |
|
|
концентрации сахара в некотором исследуемом растворе. |
1
vk.com/club152685050 | vk.com/id446425943
ОПИСАНИЕ УСТАНОВКИ
Концентрация раствора сахара определяется прибором, который называется сахариметром. Его основными частями являются поляризатор и анализатор, между которыми помещается трубка с раствором сахара
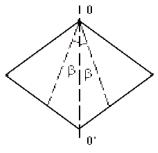
Так как точно установить поляризатор и анализатор “на темноту “ невозможно, то в сахариметре применяется полутеневой поляризатор. Получается он из поляризационной призмы Николя, разрезанной по двум плоскостям, симметричным плоскости главного сечения ОО′ (рис.1) и составляющими между собой небольшой угол 2β. Лежащий между этими плоскостями клин вырезается, и обе половинки склеиваются. Каждая половинка представляет собой самостоятельный поляризатор, причем плоскости колебаний электрического вектора Р1 и Р2 лучей света, прошедших через них, образуют угол 2β.
При прохождении через анализатор обоих лучей правая и левая половины поля зрения освещены одинаково только в том случае, если плоскость поляризации анализатора составляет одинаковые углы с плоскостями поляризации обоих лучей. Последнему условию удовлетворяет плоскость ОС (рис. 2а). Если на пути луча, вышедшего из поляризатора, поместить трубку с раствором сахара, то плоскости поляризации Р1 и Р2 повернутся на
|
С |
С |
|||||||
|
а)Р1 |
Р2 |
б) |
Р1 |
Р2 |
||||
|
2 |
||||||||
некоторый угол (рис.2,б), и освещенности правого и левого поля зрения будут различными. Для уравнивания освещенности полей в сахариметре имеется компенсирующий кварцевый клин, вращающий плоскость поляризации в сторону, обратную той, в которую вращает ее раствор сахара. Двигая клин, можно подобрать толщину кварца, при которой вращение, вызванное раствором, полностью компенсируется.
Оптическая схема сахариметра (рис.3) следующая: свет от источника 1 проходит через фильтр 2, выделяющий узкую спектральную область. За фильтром расположены
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Рис.3 поляризатор 3, трубка с раствором сахара 4, кварцевый клин 5 и анализатор 6.
|
На рис.4 показан внешний вид |
|||||||||
|
сахариметра. Источником света 1 служит лампа |
|||||||||
|
накаливания, укрепленная внутри прибора. |
|||||||||
|
Фильтр (красный) может быть введён в |
|||||||||
|
1 |
2 |
3 |
5 |
6 |
оптический |
канал с |
помощью |
вращения |
|
|
держателя 2. Трубка с исследуемым раствором |
|||||||||
|
4 |
|||||||||
|
сахара вкладывается в прибор через продольный |
|||||||||
|
вырез 3, закрывающийся шторкой. Две |
|||||||||
|
Рис.4 |
половинки поля зрения наблюдаются в окуляр |
||||||||
|
зрительной |
трубки |
4. |
Кварцевый |
||||||
2
vk.com/club152685050 | vk.com/id446425943
компенсирующий клин перемещается винтом 5. С подвижным кварцевым клином связана шкала, которую можно наблюдать с помощью окуляра 6.
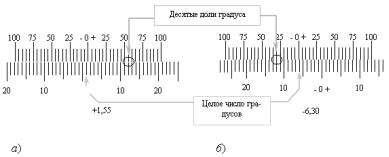
В поле зрения окуляра 6 видна основная шкала (верхняя часть шкалы) и нониус (нижняя часть шкалы). Ноль основной шкалы (рис.5) расположен в центре. Отсчеты вправо от него берутся со знаком плюс, влево – со знаком минус. Нониус также имеет ноль посередине. Целое число градусов отсчитывается по основной шкале против нулевого деления нониуса. Десятые доли градуса определяются по нониусу обычным способом.
Однако, если ноль нониуса сдвинут в положительную часть основной шкалы, то для нахождения десятых долей градуса используется правая часть нониуса; если же он сдвинут в отрицательную часть основной шкалы, то используется левая часть нониуса. Например, на рисунке 5,а отсчет равен + 1,55 градуса, а на рисунке 5,б – 6,30 градуса. Шкала прибора проградуирована в международных сахарных градусах. Сто градусов этой шкалы соответствуют 34,62 дуговых градуса.
– 0 +
Рис.5
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Устанавливаем резкую границу между правой и левой половинками поля зрения передвижением окуляра зрительной трубки (4 на рис.4). Вращая ручку 6, перемещающую кварцевый клин, уравниваем освещенности полей зрения в области полутени при темном поле зрения окуляра, так как лишь при этом условии малейший поворот рукоятки вызывает резкую смену соотношения освещенности обеих половинок поля зрения окуляра. Снимаем
нулевой отсчет α0 по шкале, видимой в лупу. Измерения проводим 3 раза с красным
светофильтром.
2.Помещаем в сахариметр трубку с раствором сахара известной концентрации и закрываем шторку. Уравниваем освещенности полей зрения при темном поле зрения
окуляра. Для красного светофильтра 3 раза определяем α1, соответствующий равенству
освещенностей. Находим среднее α
3.Вычисляем угол поворота плоскости поляризации для красного света и затем определяем удельное вращение по формуле:
ρ″═α ∕ ℓС,
где α═α1 – α0.
Значения ℓ и С указаны на трубке.
4.Помещаем в сахариметр трубку с раствором сахара, концентрацию которого надо определить. Повторяем все измерения, описанные выше. Получаем α2 .
5.Вычисляем αX ═α2 – α0 для красного света. Подставив полученные значения в
формулу
СX = αX ∕ ρ″ιX,
3
vk.com/club152685050 | vk.com/id446425943
определяем концентрацию сахара в растворе, а затем находим Схср . Все измерения записываем в таблицу 1.
|
Таблица 1 |
|||||||||||||||
|
Определениеудельноговращения |
Определениеконцентрациисахарного |
||||||||||||||
|
Светофильтр |
раствора |
||||||||||||||
|
№ |
О |
Оср |
1 |
1ср |
2 |
2ср |
Х |
СХ |
СХср |
||||||
|
1. |
|||||||||||||||
|
Красный |
2. |
||||||||||||||
|
3. |
|||||||||||||||
|
Без |
1. |
||||||||||||||
|
2. |
|||||||||||||||
|
светофильтра |
|||||||||||||||
|
3. |
|||||||||||||||
6. Вычисляем погрешность определения концентрации сахара в растворе.
4
vk.com/club152685050 | vk.com/id446425943
8. ИЗУЧЕНИЕ ПРЕЛОМЛЕНИЯ СВЕТА ПРИЗМОЙ, ИЗУЧЕНИЕ ДИСПЕРСИИ СВЕТА.
|
ξ |
Введение. |
Абсолютным |
показателем |
||
|
n |
преломления некоторого вещества в электромагнитной |
||||
|
А |
теории называется число, показывающее, во сколько |
||||
|
раз скорость волны в вакууме больше скорости волны в |
|||||
|
В |
веществе: N = C/V. |
||||
|
1 |
Абсолютный показатель преломления связан с |
||||
|
диэлектрической и магнитной проницаемостями среды |
|||||
|
следующим |
образом: |
||||
|
k |
N = . |
||||
|
Дисперсией |
электромагнитного |
излучения |
|||
|
λ0 |
называют явление, обусловленное зависимостью |
||||
|
Рис. 1 |
показателя преломления вещества от длины волны |
(частоты) n = f(λ0), где λ0 – длина волны излучения в
вакууме.
Дисперсией вещества называют производную показателя преломления по длине волны DN/Dλ0.
Теория дисперсии построена на представлении об электроне, квазиупруго связанном в атоме и испытывающем со стороны среды действие сил, аналогичных силам трения (модель Г.А.Лоренца). В поле электромагнитной волны электрон, находящийся в электронной оболочке атома, совершает вынужденные колебания под действием гармонической силы с частотой, равной частоте волны. Колебания сопровождаются появлением гармонических ускорений в движении электрона. Ускоренно движущийся электрон, как известно из теории излучает электромагнитную волну, частота которой равна частоте колебаний. Таким образом, ускоренно движущийся электрон излучает вторичную волну, отличающуюся по фазе от первичной. Первичная электромагнитная волна и волна, излученная электронами, складываются, и образуют результирующую волну, фазовая скорость которой оказывается при этом отличной от её скорости в вакууме. Чем ближе частота электромагнитного излучения к “собственной” частоте колебаний электрона в атоме, тем больше амплитуда колебаний электрона, и больше это различие.
Зависимость показателя преломления N от частоты электромагнитной волны ω (т.н.
дисперсионная зависимость) приближенно определяется следующим соотношением:
N2 = 1 + N/ε0 E 2 / M( 2 0K 2 ) ,
K
где N – концентрация молекул вещества, E и M – заряд и масса электрона, ω0k – собственная частота колебаний электрона в атоме. На тех же частотах ω0k (они ещё носят
название резонансных) происходит наиболее интенсивное поглощение излучения веществом.
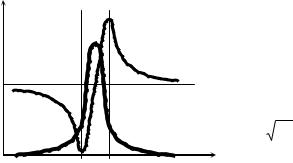
Зависимость показателя преломления N от длины волны 0 представлена на рис. 1. Здесь же приведена зависимость коэффициента поглощения k от длины волны.
|
Прозрачные бесцветные вещества имеют в видимой части спектра функцию N (λ0) как |
|
|
на участке АВ. Здесь дисперсия вещества DN/Dλ0 отрицательна и возрастает по модулю с |
|
|
уменьшением |
λ0. |
|
В этом случае дисперсию называют нормальной. |
|
|
В области сильного поглощения (в полосе поглощения) дисперсия DN/Dλ0 наоборот |
|
|
положительна. Возрастание показателя преломления с ростом λ0 называют |
аномальной |
дисперсией (закрашенный участок на рис.1).
Рассмотрим преломление света призмой. Пусть на грань АВ трёхгранной призмы АВС (рис. 2, а) падает луч света. После двукратного преломления на гранях луч выходит из призмы отклонённым от первоначального направления на угол δ, называемый
1
vk.com/club152685050 | vk.com/id446425943
углом отклонения. Угол при вершине призмы – γ называют преломляющим углом призмы. Угол отклонения зависит от угла падения α1, преломляющего угла призмы γ и показателя преломления материала призмы N.
Рассмотрим случай симметричного хода луча через призму (рис. 2, б). При этом α1 =
|
В |
В |
|||||
|
γ |
γ |
|||||
|
δ |
D |
K |
δ |
E |
||
|
α1 |
α – β |
|||||
|
β1 |
α2 |
α |
β |
β |
α |
|
|
β2 |
||||||
|
А |
а) |
С |
А |
б) |
С |
|
|
Рис. 2 |
||||||
α2 = α, и β1 = β2 = β, а угол отклонения δ принимает наименьшее значение и называется углом наименьшего отклонения.
Свяжем угол наименьшего отклонения δ с преломляющим углом призмы и показателем преломления. По закону преломления,
|
sin α/ sin β = N |
(1) |
|
Из треугольника DBE: γ + 2(90о – β) = 180о, откуда |
|
|
β = γ/2. |
(2) |
|
Угол δ – внешний для треугольника DKE, следовательно, δ = 2(α – β), или, с учётом |
|
|
равенства (2), |
|
|
α = (γ + δ)/ 2. |
(3) |
Подставив (2) и (3) в (1), получим рабочую формулу для расчета показателя преломления:
N = (sin (γ + δ)/ 2)/(sin (γ/2)).
|
Таким образом измерив преломляющий угол |
|
|
призмы γ и угол наименьшего отклонения δ, можно |
|
|
определить показатель преломления стекла, из которого |
|
|
изготовлена призма. |
|
|
Поскольку показатель преломления зависит от |
|
|
длины волны, лучи, соответствующие волнам разной |
|
|
длины, будут преломляться в призме под разными |
α |
|
углами (рис. 3). Поэтому наблюдаемое изображение |
|
|
входной щели прибора в разных длинах волн видно под |
|
|
разными углами как набор вертикальных отрезков |
А |
|
разного цвета. Это т.н. дисперсионный спектр. |
|
|
В работе требуется измерить показатель |
|
|
преломления стекла для нескольких длин волн и |
|
|
построить график зависимости показателя преломления |
|
|
от длины волны (кривую дисперсии). |
(4)
В
γ
δ(λ)
β(λ)
α2(λ)
С
Рис. 3
2
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
ОПРЕДЕЛЕНИЕ Цель работы: Приборы и принадлежности: сахариметр, кювета поляриметрическая, растворы сахара. 1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕБыстрота и точность определения концентрации Это явление было открыто Араго (1811 г.) при изучении им двойного Вещества, способные вращать плоскость
Естественный Для данной длины волны угол поворота плоскости поляризации пропорционален
где φ – угол поворота плоскости поляризации; d – толщина пластины; α – удельное вращение. Удельное вращение зависит от длины волны, природы вещества и
При распространении
На рис. 2, а обозначены: Если скорости распространения обеих волн Различие |
||||||||||||||||||||||||||||||||
2.
|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
Рис. 3 |
||||||||||||||||||||||||||||||||
|
Если плоскость колебания светового вектора Если плоскость пропускания анализатора АА расположена перпендикулярно |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
Все вышесказанное относится к случаю, когда на поляриметр падает В работе используется сахариметр СУ-4, внешний Сахариметр состоит из узла измерительной головки 2 и осветительного узла 9, С лицевой стороны измерительной головки расположена лупа 1 для отсчета показаний по шкале и |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
В нижней части измерительной головки расположена рукоятка 19 клинового компенсатора, вращением Осветительный узел состоит из патрона с лампой (патрон устанавливается На крышке 14 установлены Внутри основания вмонтирован понижающий трансформатор. На тыльной Оптическая схема сахариметра изображена на рис. 6. Световой поток, При установке кюветы с раствором между поляризатором и анализатором Рис. 6Для уравнивания По нулевому делению нониуса 18 3.
|
|
Концентрация С, г/см3 |
Номер опыта |
Деление шкалы N, ºS |
Среднее значение |
Угол φ,˚ |
Примечание |
|
С1 |
1 2 3 |
Длина трубки Удельное вращение дм·г |
|||
|
С2 |
1 2 3 |
||||
|
С3 |
1 2 3 |
||||
|
С4 |
1 2 3 |
||||
|
Сх |
1 2 3 |
3.6. По данным таблицы выполняют зависимость N = f (С), откладывая по оси ординат деления
шкалы прибора, а по оси абсцисс – концентрацию раствора С.
3.7. Помещают между поляризатором и анализатором раствор сахара
неизвестной концентрации Сх и вновь производят измерения,
записывая деления шкалы Nх в момент
исчезновения границ половин поля зрения.
3.8. По диаграмме N = f (С) определяют концентрацию Сх раствора
сахара.
ВОПРОСЫ
ДЛЯ ДОПУСКА К РАБОТЕ
1. Сформулируйте цель работы.
2. Объясните принцип действия сахариметра. Опишите порядок выполнения
работы.
3. Какие вещества называются оптически активными?
4. От чего зависит поворот плоскости поляризации света в оптически активном
веществе?
ВОПРОСЫ
ДЛЯ ЗАЩИТЫ РАБОТЫ
1. Оптическая схема сахариметра.
2. Объяснение по Френелю поворота плоскости поляризации света.
3. Зависимость удельного вращения от агрегатного состояния вещества.
4. Анализ диаграммы зависимости N = f (С).
5. Практическое использование данного метода и рабочей установки.
6. Критические замечания к рабочей установке и методу измерений.
ЛИТЕРАТУРА
1. Ландсберг Г.С. Оптика. – М:
Наука, 1976. – 926 с.
2. Майсова Н.Н. Практикум по курсу общей
физики. – М: Высш. шк., 1970. – 448 с.
3. Руководство к лабораторным работам по
физике / под. ред. В.Е. Аверичевой. – Томск: ТПИ, 1973. – 129 с.
Профи
(879),
закрыт
10 лет назад
rafael ahmetov
Высший разум
(122431)
10 лет назад
Возьми небольшую деревянную палочку (можно кусок карандаша) . На один конец намотай медной проволоки и опусти в раствор, так, чтобы палочка приняла вертикальное положение. Подбери такую длину проволочки, чтобы палочка погрузилась примерно наполовину. Отметь на палочке уровень раствора. Теперь взвесь на обычных бытовых весах пустой стакан (запиши массу m1). Налей в стакан столько воды, чтобы нижняя часть палочки (до отметки) целиком помещалась в воде. Взвесь стакан с водой (запиши массу m2). Опусти палочку в стакан с водой. В чистой воде палочка утонет глубже, чем в растворе сахара, так как плотность раствора больше плотности воды. Теперь понемногу присыпай в стакан сахар, растворяй его и время от времени опускай палочку. Когда палочка будет погружаться до метки, значит концентрация полученного тобой раствора равна концентрации исследуемого. Взвесь стакан с раствором (масса m3). Процентная концентрация сахара равна (m3-m2)/(m3-m1). Желаю успеха.
Николай Горелов
Искусственный Интеллект
(114096)
10 лет назад
А ху-ху не хо-хо? . Концентрация, это масса в единице объёма. Оставь надежду.
А бытовые весы есть? Тебе же не надо с точностью до 0.00001%? Я думаю, с тебя и 10% точности хватит. Берёшь 200 мл (по бытовой мензурке, по стакану, в конце-концов) , взвешиваешь и упариваешь (посуду найдёшь?) , пока кисель не получится, помешиваешь. Желательно взвешивать и упаривать в одной бочке.
Думаю, у тебя не получится: с такими вопросами.
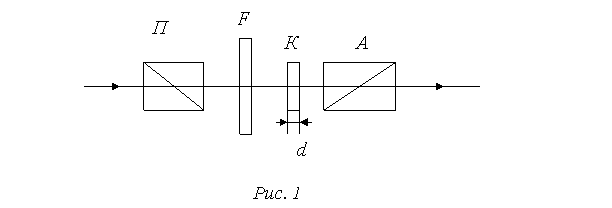



 Рис. 4
Рис. 4


