| Концентрация | |
|---|---|
 |
|
| Размерность | L−3 |
| Единицы измерения | |
| СИ | м−3 |
| СГС | см−3 |
Концентра́ция части́ц — физическая величина, равная отношению числа частиц N к объёму V, в котором они находятся:
Размерность в СИ [n] = 1/м3, в системе СГС — [n] = 1/см3.
Если концентрация является функцией координаты 
Таким образом,
Однако такое представление является в некоторой степени условным, поскольку концентрация (как, например, и температура) относится к макропараметрам и при переходе к бесконечно малому объёму, по большому счёту, теряет смысл. Бесконечно малый объём в данном случае должен определяться как объём, число частиц в котором велико, однако изменение макропараметров в пределах объёма мало́.
Концентрация имеет следующую связь с плотностью и насыщенностью:
Формулы, в которых присутствует концентрация[править | править код]
[1] — давление идеального газа (см. уравнение Клапейрона).
— средняя длина свободного пробега молекулы газа (здесь D — эффективный диаметр молекулы).
— число ударов молекул газа о единицу поверхности стенки за единицу времени (здесь
— средняя скорость молекул).
— плотность тока (здесь q — заряд носителя,
— средняя скорость носителей заряда в данной точке).
См. также[править | править код]
- Концентрация смеси
Примечания[править | править код]
- ↑ Клапейрона уравнение // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 371. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
Формулы молекулярной физики
Формула концентрации молекул
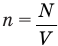
Здесь n — концентрация  , N — количество молекул (безразмерное), V — объем
, N — количество молекул (безразмерное), V — объем  .
.
Формула плотности
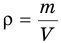
Здесь  — плотность вещества
— плотность вещества  , m — масса вещества (кг), V — объем
, m — масса вещества (кг), V — объем  .
.
Формула относительной молекулярной массы
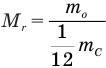
Здесь 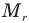 — относительная молекулярная масса (безразмерная),
— относительная молекулярная масса (безразмерная),  — масса одной молекулы (кг),
— масса одной молекулы (кг), 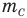 — масса атома углерода (кг).
— масса атома углерода (кг).
Формула количества вещества (количества молей)
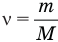
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
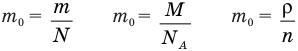
Здесь 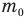 — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль),
— масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), 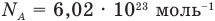 — число Авогадро,
— число Авогадро,  — плотность вещества
— плотность вещества  , n — концентрация молекул
, n — концентрация молекул  .
.
Формулы количества молекул
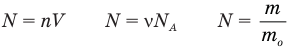
Здесь A — количество молекул (безразмерное), п — концентрация молекул  , V— объем
, V— объем  , v — количество вещества (количество молей) (моль),
, v — количество вещества (количество молей) (моль), 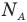 — число Авогадро
— число Авогадро 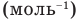 , m — масса вещества (кг),
, m — масса вещества (кг),  — масса одной молекулы.
— масса одной молекулы.
Формулы средней квадратичной скорости молекул
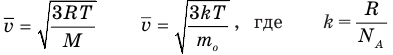
Здесь 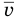 — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль),
— средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), 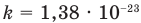 Дж/К — постоянная Больцмана,
Дж/К — постоянная Больцмана,  — масса одной молекулы (кг).
— масса одной молекулы (кг).
Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па),  — масса одной молекулы (кг), n — концентрация молекул
— масса одной молекулы (кг), n — концентрация молекул  ,
, 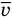 — средняя квадратичная скорость молекул (м/с),
— средняя квадратичная скорость молекул (м/с),  — средняя кинетическая энергия молекул (Дж).
— средняя кинетическая энергия молекул (Дж).
Формула средней кинетической энергии молекул
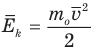
Здесь 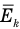 — средняя кинетическая энергия молекул (Дж),
— средняя кинетическая энергия молекул (Дж), 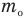 — масса одной молекулы (кг),
— масса одной молекулы (кг), 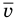 — средняя квадратичная скорость молекул (м/с).
— средняя квадратичная скорость молекул (м/с).
Связь шкал Цельсия и Кельвина
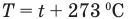
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
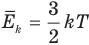
Здесь  — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
— средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
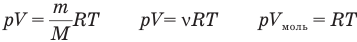
Здесь р — давление газа (Па), V — объем  , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль),
, т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), 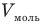 — объем моля
— объем моля 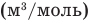 .
.
Объединенный газовый закон — уравнение Клапейрона
при 
Здесь 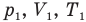 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 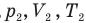 — давление (Па), объем
— давление (Па), объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Бойля — Мариотта (изотермический процесс)
при 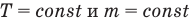
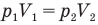
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 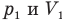 — давление (Па) и объем газа
— давление (Па) и объем газа  в первом состоянии,
в первом состоянии, 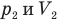 — давление (Па) и объем
— давление (Па) и объем  газа во втором состоянии.
газа во втором состоянии.
Закон Гей-Люссака (изобарный процесс)
при 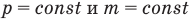
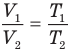
Здесь р — давление газа (Па), m — масса газа (кг), 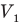 и
и 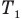 — объем
— объем  и абсолютная температура (К) газа в первом состоянии,
и абсолютная температура (К) газа в первом состоянии, 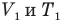 — объем
— объем  и абсолютная температура (К) газа во втором состоянии.
и абсолютная температура (К) газа во втором состоянии.
Закон Шарля
при 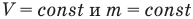
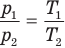
Здесь V — объем газа  , m — масса газа (кг),
, m — масса газа (кг), 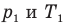 — давление (Па) и абсолютная температура (К) газа в первом состоянии,
— давление (Па) и абсолютная температура (К) газа в первом состоянии, 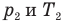 — давление (Па) и абсолютная температура (К) газа во втором состоянии.
— давление (Па) и абсолютная температура (К) газа во втором состоянии.
Связь давления идеального газа с концентрацией его молекул и температурой
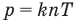
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа  , абсолютная температура Т (К).
, абсолютная температура Т (К).
Формулы относительной влажности
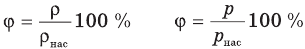
Здесь 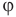 — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре
— относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре 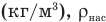 — плотность насыщенного водяного пара при той же температуре
— плотность насыщенного водяного пара при той же температуре 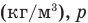 — давление водяного пара в воздухе при данной температуре (Па),
— давление водяного пара в воздухе при данной температуре (Па), 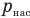 — давление насыщенного водяного пара в воздухе при той же температуре (Па).
— давление насыщенного водяного пара в воздухе при той же температуре (Па).
Работа при изобарном изменении объема газа
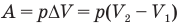
Здесь А — работа (Дж), р — давление газа (Па), 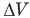 — изменение объема газа
— изменение объема газа 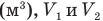 — соответственно начальный и конечный объемы газа
— соответственно начальный и конечный объемы газа  .
.
Внутренняя энергия идеального одноатомного газа
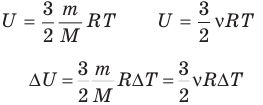
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 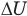 — изменение внутренней энергии (Дж),
— изменение внутренней энергии (Дж), 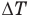 — изменение температуры (К).
— изменение температуры (К).
Первый закон термодинамики
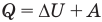
Здесь Q — количество теплоты, переданное термодинамической системе (Дж),  — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
— изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при 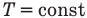
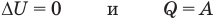
к изохорному: при V = const
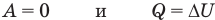
к изобарному: при р = const
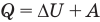
к адиабатному: при Q = 0

Здесь Т — абсолютная температура (К),  — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем
— изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем 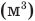 , р — давление (Па).
, р — давление (Па).
Формулы количества теплоты при нагревании или охлаждении тел
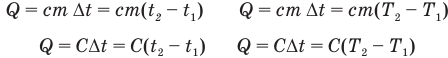
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 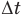 — изменение температуры тела по шкале Цельсия,
— изменение температуры тела по шкале Цельсия, 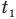 и
и 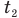 — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия,
— температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, 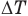 — изменение абсолютной температуры тела (К),
— изменение абсолютной температуры тела (К), 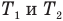 — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К),
— абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), 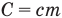 — теплоемкость тела (Дж/К).
— теплоемкость тела (Дж/К).
Формула количества теплоты при плавлении или кристаллизации
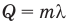
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 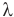 — удельная теплота плавления вещества (Дж/кг).
— удельная теплота плавления вещества (Дж/кг).
Формула количества теплоты при парообразовании или конденсации
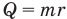
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
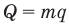
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
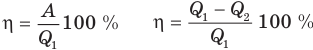
Здесь  — коэффициент полезного действия (безразмерный или в %),
— коэффициент полезного действия (безразмерный или в %), 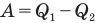 — работа, совершенная двигателем (Дж),
— работа, совершенная двигателем (Дж), 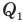 — количество теплоты, полученное рабочим веществом от нагревателя (Дж),
— количество теплоты, полученное рабочим веществом от нагревателя (Дж), 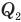 — количество теплоты, отданное рабочим веществом холодильнику (Дж).
— количество теплоты, отданное рабочим веществом холодильнику (Дж).
Коэффициент полезного действия идеального теплового двигателя
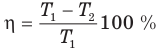
Здесь  — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %),
— коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), 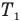 — абсолютная температура нагревателя (К),
— абсолютная температура нагревателя (К), 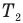 — абсолютная температура холодильника(К).
— абсолютная температура холодильника(К).
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:

Концентрация
частиц (молекул, атомов и т. п.) однородной
системы
n=N/V,
где
V
— объем
системы.
Основное уравнение
кинетической теории газов
p=2/зn<п>,
где р
— давление
газа; <п>—
средняя кинетическая энергия*
поступательного
движения молекулы.
Средняя
кинетическая энергия:
приходящаяся на
одну степень свободы молекулы
<1>=½kT;
-
Здесь и далее
кинетическая энергия молекул и других
частиц обозначается .
приходящаяся на
все степени свободы молекулы (полная
энергия молекулы)
![]() ;
;
поступательного
движения молекулы
![]() ,
,
где
k
—
постоянная Больцмана; Т
—
термодинамическая температура;
i — число
степеней свободы молекулы;
вращательного
движения молекулы
![]()
Зависимость
давления газа от концентрации молекул
и температуры
p=nkT.
Скорость
молекул:
средняя квадратичная
![]() ,
,
или
![]() ;
;
средняя арифметическая
![]() ,
,
или
![]() ;
;
наиболее вероятная
![]() ,
,
или
![]() ,
,
где
m1
—
масса одной
молекулы.
Примеры решения задач
Пример
1. В
баллоне вместимостью
V=6,9 л
находится азот массой m=2,3
г. При нагревании часть молекул
диссоциировали на атомы. Коэффициент
диссоциации*
=0,2.
Определить:
1) общее
число
N1
молекул и концентрацию
n1
молекул азота до нагревания;
2) концентрацию
n2
молекул и n3
атомов азота после нагревания.
Решение.
По определению, концентрация частиц
газа есть отношение числа частиц к
вместимости сосуда, занимаемого газом:
n=N/V.
(1)
1.
Число
N1
молекул газа до нагревания найдем из
соотношения
![]() .
.
(2)
где
v
— количество
вещества азота;
na
—
постоянная Авогадро;
М
— молярная
масса азота;
Mr
—
относительная молекулярная масса азота;
k=10-3
кг/моль (см. пример
1 на с.
114). Подставив
значения величин в
(2), получим
![]() .
.
*
См. примечание к задаче
8.15.
Концентрацию
n1
найдем, подставив значения величин в
(1):
![]() .
.
2.
Концентрацию после нагревания найдем
из соотношения
![]() , (3)
, (3)
где
N
— число
молекул, не распавшихся на атомы.
После подстановки
значений величин в
(3) получим
![]() .
.
Концентрация
атомов после нагревания азота
![]() . (4)
. (4)
Число
2 в формуле
(4) выражает
тот факт, что каждая молекула после
распада дает два атома.
Подставим в
(4) значения
величин и произведем вычисления:
![]() .
.
Пример
2. В колбе
вместимостью V=0,5
л находится кислород при нормальных
условиях. Определить среднюю энергию
![]() поступательного движения всех молекул,
поступательного движения всех молекул,
содержащихся в колбе.
Решение.
Средняя энергия
![]() поступательного
поступательного
движения всех молекул может быть
выражена соотношением
![]() ,
,
(1)
где <п>—
средняя энергия поступательного движения
одной молекулы;
N
— число
всех молекул, содержащихся в колбе.
Как известно,
![]() ,
,
(2)
где
k
—
постоянная Больцмана; Т
—
термодинамическая температура.
Число молекул,
содержащихся в колбе, найдем по формуле
N=vNA,
(3)
где
v
— количество
вещества кислорода; NA
— постоянная
Авогадро.
Количество
вещества v найдем из таких соображений:
известно, что при нормальных условиях
молярный объем Vm равен 22,410-3
м3/моль. Так как, по условию задачи,
кислород в колбе находится при нормальных
условиях, то количество вещества
кислорода в колбе выражается
соотношением
v=V/Vm.
(4)
Подставив выражение
v
по
(4) в
(3), получим
N=VNA/Vm.
(5)
С учетом
(2) и
(5) выражение
(1) энергии
поступательного движения молекул
примет вид
![]()
Проверим, дает ли
правая часть расчетной формулы единицу
энергии (джоуль). Для этого вместо
символов величин подставим единицы, в
которых эти величины выражаются:
![]() .
.
Подставив значения
величин в
(6) и произведя
вычисления, найдем
![]()
Пример
3. Найти
среднюю кинетическую энергию одной
молекулы аммиака
NH3
при температуре
t=27 °С и
среднюю энергию вращательного движения
этой молекулы при той же температуре.
Решение.
Средняя полная энергия молекулы
определяется по
формуле
![]()
(1)
где
i
— число
степеней свободы молекулы;
k
—
постоянная Больцмана; Т—термодинамическая
температура газа: T=t+Т0,
где Т0=273
К.
Число степеней
свободы
i
четырехатомной молекулы, какой является
молекула аммиака, равно
6.
Подставим значения
величин в
(l):
![]() .
.
Средняя энергия
вращательного движения молекулы
определяется по формуле
![]() ,
,
(2)
где число
3 означает
число степеней свободы поступательного
движения.
Подставим в
(2) значения
величин и вычислим:
![]() .
.
Заметим, что энергию
вращательного движения молекул аммиака
можно было получить иначе, разделив
полную энергию ()
на две равные части. Дело в том, что у
трех (и более) атомных молекул число
степеней свободы, приходящихся на
поступательное и вращательное
движение, одинаково (по
3), поэтому
энергии поступательного и вращательного
движений одинаковы. В данном случае
![]()
Газ обладает высокой реакционной способностью по сравнению с жидкими и твердыми телами ввиду большой площади его активной поверхности и высокой кинетической энергии образующих систему частиц. При этом химическая активность газа, его давление и некоторые другие параметры зависят от концентрации молекул. Рассмотрим в данной статье, что это за величина и как ее можно вычислить.
О каком газе пойдет речь?
В данной статье будут рассмотрены так называемые идеальные газы. В них пренебрегают размерами частиц и взаимодействием между ними. Единственным процессом, который происходит в идеальных газах, являются упругие столкновения между частицами и стенками сосуда. Результатом этих столкновений является возникновение абсолютного давления.
Любой реальный газ приближается по своим свойствам к идеальному, если уменьшать его давление или плотность и увеличивать абсолютную температуру. Тем не менее существуют химические вещества, которые даже при низких плотностях и высоких температурах далеки от идеального газа. Ярким и всем известным примером такого вещества является водяной пар. Дело в том, что его молекулы (H2O) являются сильно полярными (кислород оттягивает на себя электронную плотность от атомов водорода). Полярность приводит к появлению существенного электростатического взаимодействия между ними, что является грубым нарушением концепции идеального газа.
Универсальный закон Клапейрона-Менделеева
Чтобы уметь рассчитывать концентрацию молекул идеального газа, следует познакомиться с законом, который описывает состояние любой идеальной газовой системы независимо от ее химического состава. Этот закон носит фамилии француза Эмиля Клапейрона и русского ученого Дмитрия Менделеева. Соответствующее уравнение имеет вид:
P*V = n*R*T.
Равенство говорит о том, что произведение давления P на объем V всегда для идеального газа должно быть прямо пропорционально произведению температуры абсолютной T на количество вещества n. Здесь R – это коэффициент пропорциональности, который получил название универсальной газовой постоянной. Она показывает величину работы, которую 1 моль газа выполняет в результате расширения, если его на 1 К нагреть (R=8,314 Дж/(моль*К)).
Концентрация молекул и ее вычисление
Согласно определению под концентрацией атомов или молекул понимают количество частиц в системе, которое приходится на единицу объема. Математически можно записать:
cN = N/V.
Где N – общее число частиц в системе.
Прежде чем записать формулу для определения концентрации молекул газа, вспомним определение количества вещества n и выражение, которое связывает величину R с постоянной Больцмана kB:
n = N/NA;
kB = R/NA.
Используя эти равенства, выразим отношение N/V из универсального уравнения состояния:
P*V = n*R*T =>
P*V = N/NA*R*T = N*kB*T =>
cN = N/V = P/(kB*T).
Таким образом мы получили формулу для определения концентрации частиц в газе. Как видно, она прямо пропорционально зависит от давления в системе и обратно пропорционально от абсолютной температуры.
Поскольку количество частиц в системе велико, то концентрацией cN пользоваться неудобно при выполнении практических расчетов. Вместо нее чаще используют молярную концентрацию cn. Она для идеального газа определяется так:
cn = n/V = P/(R *T).
Пример задачи
Необходимо рассчитать молярную концентрацию молекул кислорода в воздухе при нормальных условиях.

Для решения этой задачи вспомним, что в воздухе находится 21 % кислорода. В соответствии с законом Дальтона кислород создает парциальное давление 0,21*P0, где P0 = 101325 Па (одна атмосфера). Нормальные условия также предполагают температуру 0 oC (273,15 К).
Мы знаем все необходимые параметры для вычисления молярной концентрации кислорода в воздухе. Получаем:
cn(O2) = P/(R *T) = 0,21*101325/(8,314*273,15) = 9,37 моль/м3.
Если эту концентрацию привести к объему 1 литр, то мы получим значение 0,009 моль/л.
Чтобы понять, сколько молекул O2 содержится в 1 литре воздуха, следует умножить рассчитанную концентрацию на число NA. Выполнив эту процедуру, получим огромное значение: N(O2) = 5,64*1021 молекул.




