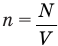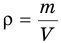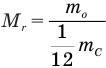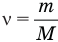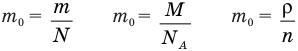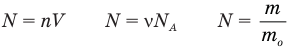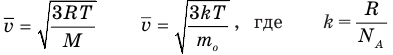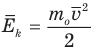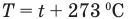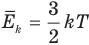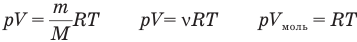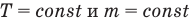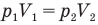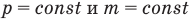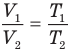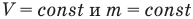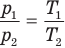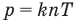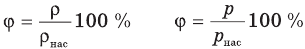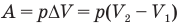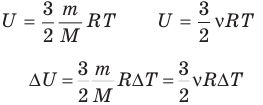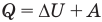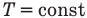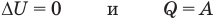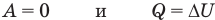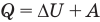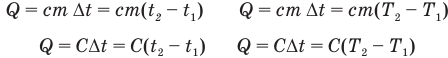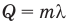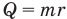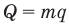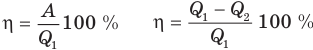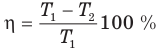Как найти концентрацию вещества в физике формула

Формулы молекулярной физики

Формула концентрации молекул

Здесь n — концентрация , N — количество молекул (безразмерное), V — объем .

Формула плотности

Здесь — плотность вещества , m — масса вещества (кг), V — объем .

Формула относительной молекулярной массы

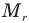
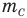
Здесь — относительная молекулярная масса (безразмерная), — масса одной молекулы (кг), — масса атома углерода (кг).

Формула количества вещества (количества молей)

Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).

Формулы массы одной молекулы

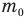
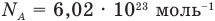
Здесь — масса одной молекулы (кг), т — масса вещества (кг), N — количество молекул (безразмерное), М — молярная масса (кг/моль), — число Авогадро, — плотность вещества , n — концентрация молекул .

Формулы количества молекул

Здесь A — количество молекул (безразмерное), п — концентрация молекул , V— объем , v — количество вещества (количество молей) (моль), — число Авогадро , m — масса вещества (кг), — масса одной молекулы.

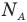
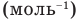
Формулы средней квадратичной скорости молекул

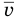
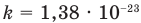
Здесь — средняя квадратичная скорость молекул (м/с), R = 8,31 Дж/(моль • К) — молярная газовая постоянная, Т — абсолютная температура (К), М — молярная масса (кг/моль), Дж/К — постоянная Больцмана, — масса одной молекулы (кг).

Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па), — масса одной молекулы (кг), n — концентрация молекул , — средняя квадратичная скорость молекул (м/с), — средняя кинетическая энергия молекул (Дж).

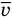
Формула средней кинетической энергии молекул

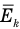
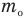
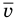
Здесь — средняя кинетическая энергия молекул (Дж), — масса одной молекулы (кг), — средняя квадратичная скорость молекул (м/с).

Связь шкал Цельсия и Кельвина

Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.

Связь средней кинетической энергии молекул идеального газа с абсолютной температурой

Здесь — средняя кинетическая энергия молекул (Дж), k — постоянная Больцмана (Дж/К), Т — абсолютная температура (К).

У равнение состояния идеального газа — уравнение Клапейрона — Менделеева

Здесь р — давление газа (Па), V — объем , т — масса газа (кг), М — молярная масса (кг/моль), R — молярная газовая постоянная (ДжДмоль • К), Т — абсолютная температура (К), v — количество вещества (количество молей) (моль), — объем моля .

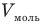
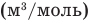
Объединенный газовый закон — уравнение Клапейрона

при

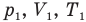
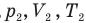
Здесь — давление (Па), объем и абсолютная температура (К) газа в первом состоянии, — давление (Па), объем и абсолютная температура (К) газа во втором состоянии.

Закон Бойля — Мариотта (изотермический процесс)

при

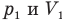
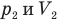
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), — давление (Па) и объем газа в первом состоянии, — давление (Па) и объем газа во втором состоянии.

Закон Гей-Люссака (изобарный процесс)

при

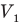
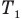
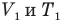
Здесь р — давление газа (Па), m — масса газа (кг), и — объем и абсолютная температура (К) газа в первом состоянии, — объем и абсолютная температура (К) газа во втором состоянии.

Закон Шарля

при

Здесь V — объем газа , m — масса газа (кг), — давление (Па) и абсолютная температура (К) газа в первом состоянии, — давление (Па) и абсолютная температура (К) газа во втором состоянии.

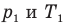
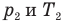
Связь давления идеального газа с концентрацией его молекул и температурой

Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа , абсолютная температура Т (К).

Формулы относительной влажности

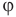
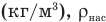
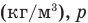
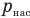
Здесь — относительная влажность (безразмерная или в %), р — плотность водяного пара в воздухе при данной температуре — плотность насыщенного водяного пара при той же температуре — давление водяного пара в воздухе при данной температуре (Па), — давление насыщенного водяного пара в воздухе при той же температуре (Па).

Работа при изобарном изменении объема газа

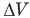
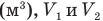
Здесь А — работа (Дж), р — давление газа (Па), — изменение объема газа — соответственно начальный и конечный объемы газа .

Внутренняя энергия идеального одноатомного газа

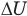
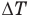
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), — изменение внутренней энергии (Дж), — изменение температуры (К).

Первый закон термодинамики

Здесь Q — количество теплоты, переданное термодинамической системе (Дж), — изменение внутренней энергии системы (Дж), А — работа против внешних сил (Дж)

Применение первого закона термодинамики к термодинамическим процессам

к изотермическому: при

к изохорному: при V = const

к изобарному: при р = const

к адиабатному: при Q = 0

Здесь Т — абсолютная температура (К), — изменение внутренней энергии (Дж), Q — количество теплоты (Дж), А — работа (Дж), V — объем , р — давление (Па).

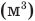
Формулы количества теплоты при нагревании или охлаждении тел

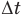
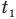
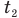
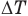
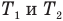
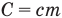
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), — изменение температуры тела по шкале Цельсия, и — температуры тела в начале и в конце процесса передачи теплоты по шкале Цельсия, — изменение абсолютной температуры тела (К), — абсолютные температуры тела в начале и в конце процесса передачи теплоты (К), — теплоемкость тела (Дж/К).

Формула количества теплоты при плавлении или кристаллизации

Здесь Q — количество теплоты (Дж), т — масса тела (кг), 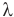— удельная теплота плавления вещества (Дж/кг).

Формула количества теплоты при парообразовании или конденсации

Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).

Формула количества теплоты при сгорании топлива

Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).

Коэффициент полезного действия теплового двигателя

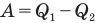
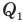
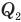
Здесь — коэффициент полезного действия (безразмерный или в %), — работа, совершенная двигателем (Дж), — количество теплоты, полученное рабочим веществом от нагревателя (Дж), — количество теплоты, отданное рабочим веществом холодильнику (Дж).

Коэффициент полезного действия идеального теплового двигателя

Здесь — коэффициент полезного действия идеального теплового двигателя (безразмерный или в %), — абсолютная температура нагревателя (К), — абсолютная температура холодильника(К).

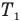
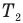
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти страницы:

Концентрация
Размерность	L−3
Единицы измерения
СИ	м−3
СГС	см−3

Концентра́ция части́ц — физическая величина, равная отношению числа частиц N к объёму V, в котором они находятся:

Размерность в СИ [n] = 1/м³, в системе СГС — [n] = 1/см³.

Если концентрация является функцией координаты то под концентрацией понимают отношение:

Таким образом,

Однако такое представление является в некоторой степени условным, поскольку концентрация (как, например, и температура) относится к макропараметрам и при переходе к бесконечно малому объёму, по большому счёту, теряет смысл. Бесконечно малый объём в данном случае должен определяться как объём, число частиц в котором велико, однако изменение макропараметров в пределах объёма мало́.

Концентрация имеет следующую связь с плотностью и насыщенностью:

Формулы, в которых присутствует концентрация[править | править код]

^[1] — давление идеального газа (см. уравнение Клапейрона).

 — средняя длина свободного пробега молекулы газа (здесь D — эффективный диаметр молекулы).

 — число ударов молекул газа о единицу поверхности стенки за единицу времени (здесь  — средняя скорость молекул).

— плотность тока (здесь q — заряд носителя, — средняя скорость носителей заряда в данной точке).

См. также[править | править код]

• Концентрация смеси

Примечания[править | править код]

Как найти концентрацию молекул

Концентрация частиц – это величина, показывающая, сколько частиц вещества находится в каком-либо объеме. Она вычисляется по формуле: c = N/V, ее размерность 1/м^3. Часто возникает необходимость определить концентрацию молекул, причем исследуемое вещество может быть в любом агрегатном состоянии: твердом, жидком или газообразном.

Инструкция

Представьте, что любознательный царь Гиерон дал своему придворному математику еще одну корону, приказав: «Вот она-то точно из чистого золота. Определи, Архимед, какова концентрация молекул в ней». Гениального ученого такая задача поставила бы в тупик. Ну, а вы решите ее очень быстро. Предположим, корона весила бы ровно 1,93 килограмма, занимая при этом объем в 100 см^3.

Прежде всего найдите, сколько молей золота содержится в таком количестве вещества. С помощью таблицы Менделеева вы узнаете молекулярную массу золота: 197 а.е.м. (атомных единиц массы). А масса одного моля любого вещества (в граммах) численно равна его молекулярной массе. Следовательно, один моль золота весит 197 грамм. Разделив фактическую массу короны на молярную массу золота, вы получите: 1930/197 = 9,79. Или, округленно, 9,8 молей золота.

Умножьте количество молей на универсальное число Авогадро, показывающее, сколько элементарных частиц содержится в моле любого вещества. 9,8*6,022*10^23 = 5,9*10^24. Вот сколько молекул золота приблизительно содержится в короне.

Ну, а теперь найти концентрацию молекул проще простого. 100 кубических сантиметров – это 0,0001 м^3. Разделим: 5,9*10^24/0,0001 = 5,9*10^28. Концентрация молекул золота равна 5,9*10^28/м3.

Теперь предположим, что вам задана такая задача: при давлении Р, средняя квадратичная скорость молекул углекислого газа равна V. Требуется определить концентрацию его молекул. И здесь нет ничего сложного. Существует так называемое основное уравнение кинетической теории идеального газа: Р = V^2m0C/3, где C – концентрация молекул газа, а m0 – масса одной его молекулы. Следовательно, искомая концентрация С находится так: С = 3P/m0V^2.

Единственная неизвестная величина – m0. Ее можно узнать в справочнике по химии или физике. Можно также вычислить по формуле: m0 = M/Na, где М – молярная масса углекислого газа (44 грамм/моль), а Na – число Авогадро (6,022х1023). Подставив все величины в формулу, вычислите искомую концентрацию С.

Видоизмените условие задачи. Предположим, вам известны только температура Т и давление Р углекислого газа. Как по этим данным найти концентрацию его молекул? Давление и температура газа связаны формулой: P = CkT, где С – концентрация молекул газа, а К – постоянная Больцмана, равная 1,38*10^-23. То есть С = P/kT. Подставив в формулу известные величины, вы вычислите концентрацию С.

§ 20. Атомы и молекулы, их характеристики (окончание)

Концентрация молекул

7. Постоянная Авогадро. Поскольку молекулы имеют малые размеры, их число в любом макроскопическом теле очень велико.

Число молекул в единице объёма называют концентрацией. Концентрация n вычисляется по формуле

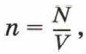
где N — число молекул в теле, V — его объём.

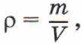
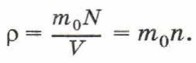
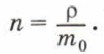
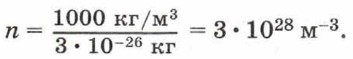
Концентрацию молекул в теле также можно определить, зная плотность вещества ρ и массу молекулы этого вещества m₀. Поскольку где m — масса тела, и m = m₀N, то

Чтобы представить себе, насколько велико это число, предположим, что в воздушном шаре сделали настолько тонкий прокол, что за каждую секунду через него проходит 10 молекул. В этом случае, для того чтобы вышли все молекулы, потребуется 30 миллиардов лет.

Из определения моля следует, что 1 моль любого вещества содержит одинаковое число молекул (атомов). Это число называют постоянной Авогадро.

Постоянная Авогадро N_А — число молекул или атомов в количестве вещества 1 моль.

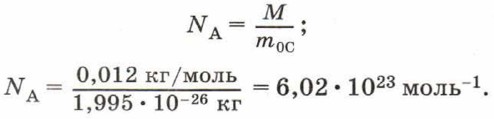
Поскольку в одном моле любого вещества содержится одинаковое число молекул, то при одинаковых условиях 1 моль любого газа занимает одинаковый объём.

Вопросы для самопроверки

1. Сформулируйте первое положение молекулярно-кинетической теории строения вещества.

2. Поясните выражение: «Молекула — мельчайшая частица вещества, сохраняющая его химические свойства».

3. Опишите опыт, позволяющий оценить размеры молекулы. Предложите способ измерения объёма капли масла.

4. Что называют относительной молекулярной массой; количеством вещества; молярной массой; концентрацией молекул; постоянной Авогадро?

5. Что такое один моль?

6. Каков порядок значений размеров, массы молекул, их концентрации, числа молекул в одном моле вещества?

1_Д. Подготовьте краткое сообщение об исследованиях М. В. Ломоносова, результаты которых внесли вклад в развитие учения о строении вещества. Воспользуйтесь для этого интернет-ресурсами и другими источниками информации. Докажите, что результаты исследований М. В. Ломоносова имели принципиальное значение для развития взглядов на строение вещества.

2. Сравните количество вещества, содержащееся в телах равной массы из алюминия и железа.

3. Найдите число атомов в алюминиевой ложке массой 30 г.

4. Деталь площадью 30 см 2 покрыли слоем серебра толщиной 2 мкм. Сколько атомов серебра содержится в покрытии?

5. Сравните массы и объёмы двух тел, сделанных из свинца и меди, если в них содержатся равные количества вещества.

Вопросы для дискуссии

Почему мы уверены в существовании молекул и атомов, ведь мы их не видим?

Источник

Идеальный газ. Формула концентрации молекул газа. Пример задачи

В физике текучих субстанций большое внимание уделяется изучению газов, которое осуществляют при помощи использования модели идеального газа. В этой области было открыто много законов. В приведенной ниже статье изучим формулу концентрации молекул газа (идеального) и покажем, как ее следует применять при решении практической проблемы.

Идеальный газ

Что же это такое? Прежде чем записать формулу концентрации молекул газа, расскажем, что собой представляет модель идеального газа. В соответствии с кинетической теорией текучих субстанций, в таких веществах молекулы и атомы движутся хаотически по прямым траекториям. Расстояния между ними намного больше, чем их собственные линейные размеры, поэтому последними пренебрегают при выполнении вычислений. Кроме того, считают, что взаимодействий между молекулами не существует, поскольку их кинетическая энергия слишком велика по сравнению со слабыми потенциальными взаимодействиями.

Любые реальные газы, которые находятся при низких давлениях и достаточно высоких абсолютных температурах, по своему поведению приближаются к описанной модели. Тем не менее существуют текучие субстанции, у которых помимо ван-дер-ваальсовых взаимодействий между частицами действуют взаимодействия более сильного характера. Примером является водяной пар, у которого молекулы друг с другом связаны водородными (полярными) связями. Для описания поведения таких субстанций нельзя использовать модель идеального газа.

Универсальное уравнение

Модель идеального газа удобна при выполнении практических расчетов тем, что уравнение состояния вещества, полученное на ее основе, связывает три термодинамических параметра: температуру T, объем системы V и абсолютное давление P. Это уравнение записано ниже:

Современная молекулярно-кинетическая теория газов позволяет путем несложных рассуждений и математических выкладок получить теоретически это уравнение. Впервые же оно было записано в результате анализа многочисленных экспериментов, которые в течение двух веков выполняли европейские ученые, начиная от Роберта Бойля (вторая половина XVII века) и заканчивая Амедео Авогадро (начало XIX века).

Считается, что уравнение состояния идеального газа первым получил Эмиль Клапейрон, а к современной форме его привел русский химик Дмитрий Менделеев, поэтому его часто называют законом Клапейрона-Менделеева.

Понятие о концентрации молекул: виды концентраций

Когда изучают текучие субстанции, то знать концентрации компонентов, которые их образуют, является важным при решении многих практических задач. Например, от этого показателя и размеров молекул зависит общая площадь поверхности активного вещества, а значит, его реакционная способность. Другой пример, концентрация некоторых веществ в воздухе определяет допустимые их пределы для нормального протекания жизненно необходимых процессов в организме человека.

В случае газов, как правило, пользуются тремя следующими концентрациями:

Заметим, что все виды концентраций вычисляются по отношению к объему системы. Справедливость этих величин действительна, поскольку каждый компонент системы полностью заполняет ее объем.

Среди всех типов концентраций наиболее удобной на практике является молярная. Ниже в статье приведем формулу именно для нее.

Формула концентрации молекул газа

В соответствии с приведенным в предыдущем пункте определением, молярная концентрация i-го компонента системы c_n(i) вычисляется так:

Предположим, что мы имеем однокомпонентный (чистый) газ. Это может быть кислород, азот, гелий и так далее. В этом случае можно применить формулу Клапейрона-Менделеева и выразить из нее молярную концентрацию молекул. Имеем:

Из записанной формулы концентрации молекул газа легко получить атомную (молекулярную) концентрацию. Покажем, как это делается:

Пример задачи

В результате изобарного нагрева закрытой системы с идеальным газом его температура увеличилась на 100 К и стала равной 400 К. Как изменится концентрация молекул газа, если давление в системе составляет 1,5 атмосферы.

Поскольку давление в процессе нагрева не изменилось, а температура была равна 300 К согласно условию задачи, то молярная концентрацию молекул до нагрева системы составляла:

Число молекул в системе не изменилось при нагреве, так как система является закрытой. После нагрева газа его концентрация составила:

Изменение концентрации составило:

Отрицательный знак говорит, что концентрация уменьшилась, что является очевидным, поскольку увеличился объем системы после нагрева, а число частиц в ней осталось прежним.

Источник

Концентрация растворов. Способы выражения концентрации растворов.

Концентрация раствора может выражаться как в безразмерных единицах (долях, процентах), так и в размерных величинах (массовых долях, молярности, титрах, мольных долях).

Способы выражения концентрации растворов.

1. Массовая доля (или процентная концентрация вещества) – это отношение массы растворенного вещества m к общей массе раствора. Для бинарного раствора, состоящего из растворённого вещества и растворителя:

,

ω – массовая доля растворенного вещества;

m_в-ва – масса растворённого вещества;

Массовую долю выражают в долях от единицы или в процентах.

2. Молярная концентрация или молярность – это количество молей растворённого вещества в одном литре раствора V:

,

C – молярная концентрация растворённого вещества, моль/л (возможно также обозначение М, например, 0,2 М HCl);

n – количество растворенного вещества, моль;

V – объём раствора, л.

Раствор называют молярным или одномолярным, если в 1 литре раствора растворено 1 моль вещества, децимолярным – растворено 0,1 моля вещества, сантимолярным – растворено 0,01 моля вещества, миллимолярным – растворено 0,001 моля вещества.

3. Моляльная концентрация (моляльность) раствора С(x) показывает количество молей n растворенного вещества в 1 кг растворителя m:

,

С (x) – моляльность, моль/кг;

n – количество растворенного вещества, моль;

4. Титр – содержание вещества в граммах в 1 мл раствора:

,

T – титр растворённого вещества, г/мл;

m_в-ва – масса растворенного вещества, г;

5. Мольная доля растворённого вещества – безразмерная величина, равная отношению количества растворенного вещества n к общему количеству веществ в растворе:

,

N – мольная доля растворённого вещества;

n – количество растворённого вещества, моль;

n_р-ля – количество вещества растворителя, моль.

Сумма мольных долей должна равняться 1:

Иногда при решении задач необходимо переходить от одних единиц выражения к другим:

М(Х) – молярная масса растворенного вещества;

ρ= m/(1000V) – плотность раствора. 6. Нормальная концентрация растворов (нормальность или молярная концентрация эквивалента) – число грамм-эквивалентов данного вещества в одном литре раствора.

Грамм-эквивалент вещества – количество граммов вещества, численно равное его эквиваленту.

Эквивалент – это условная единица, равноценная одному иону водорода в кислотоно-основных реакциях или одному электрону в окислительно – восстановительных реакциях.

Для записи концентрации таких растворов используют сокращения н или N. Например, раствор, содержащий 0,1 моль-экв/л, называют децинормальным и записывают как 0,1 н.

,

С_Н – нормальная концентрация, моль-экв/л;

z – число эквивалентности;

Коэффициент растворимости – отношение массы вещества, образующего насыщенный раствор при конкретной температуре, к массе растворителя:

Источник

Определение молярной концентрации и формулы для её расчёта

В природе практически невозможно найти вещество в чистом виде. Тела соприкасаются, перемешиваются образуя смеси. Одним из видов описания растворов является молярная концентрация. Это важное понятие в химии, характеризующее количественную часть. Выражается чаще всего эта величина через массовую долю, показывающую чистоту раствора. Измеряется она в единичных долях или процентах и находится по химической формуле.

Основные понятия и определения

Под раствором в химии понимают твёрдую или жидкую однородную систему, состоящую из нескольких компонентов. Вещества образующие раствор разделяются на растворители и растворённые.

Например, сахар, находящийся в воде — такая смесь называется двухгомогенная. Если же в сахарную воду добавить уксус, то полученный раствор уже будет трёхгомогенный. Количество в смеси того или иного разжиженного компонента называется концентрацией. Изменяться она может в широких пределах.

Существует несколько способов выражения концентрации растворов:

Молярная масса и доли

Для измерения массы используются граммы, килограммы, тонны, но для обозначения количества вещества они не подходят. В химических процессах принимают участие различные частицы, такие как молекулы, атомы, ионы. Поэтому для того чтобы определить, сколько вещества содержится в той или иной смеси, ввели специальную единицу — моль. Иными словами — это множество, в котором объединены масса с числом.

Концентрация — это значение количества объёма раствора к растворенному в нём телу. Наиболее часто для измерения применяется массовая доля разжиженного вещества, молярная и нормальная концентрация. Массовая часть — это неизмеряемая величина. Складывается она из двух масс:

Способность же вещества поглощаться другим называют растворимостью. При определении результата взаимодействия растворов находится массовая доля каждого из них.

N = Na * n, где Na — постоянная Авогадро, n — количество вещества. То есть моль — это количество в котором содержится 6 * 10 23 молекул. Молярная концентрация определяет, сколько моль разжиженного вещества содержится в одном литре раствора.

Массовая доля растворимого часто называется процентной концентрацией. При этом вместо процентного определения используется молярная концентрация. Другими словами, отношение количества к объёму в литрах. Зная число молей в одном литре довольно просто подобрать необходимое число молей используя специальную посуду.

Формулы перехода

Расчёт количества той или иной части концентрированной смеси, возможно, выполнить в различных единицах. Но между тем существуют формулы перехода от одних выражений к другим. При пересчёте происходит округление знака после запятой, поэтому при переходе с одной величины на другую появляется определённая погрешность.

Конвертация от массовой доли к молярной массе выполняется по формуле: Cb = (p * ɷb) / M (B), где: Cb — молярная концентрация, p — плотность, ɷb — массовая доля, M (B) — молярная масса. При этом когда плотность раствора изначально обозначается в грамм на миллилитр, а молярная в грамм на моль, то ответ необходимо умножить на 1 тыс. мл/л. Если же значение доли указано в процентах, то ответ необходимо разделить на 100%.

Для перехода от молярной к нормальной концентрации (молярной концентрации эквивалента), используется выражение: c * ((1 / z) * B) = Cb * z. Где молярность измеряется в моль на литр, а z — число эквивалентности (сопоставимое с одним молем катионов водорода в проходящей реакции). В определённых ситуациях выполняется и перевод массовой доли к титру. Выполняют это по формуле: T = p * ɷ, где p — плотность, измеряемая в граммах, делённых на миллилитры, а ɷ — массовая часть растворённого, в долях.

Перевести можно и молярность к титру. Используют для этого следующую формулу перехода: Т = Cb * M, в которой М — молярная масса разжиженного вещества. В случае же когда концентрация выражается в моль на литр, а масса в грамм на моль, ответ нужно разделить на 1 тыс. миллилитров на литр. Молярность связана с моляльностью формулой: mb = Cb / p, где р — плотность раствора, измеряемая в граммах, делённых на миллилитры.

Самый же сложный перевод происходит при конвертации моляльности к мольной доле. Для решения такой задачи используется формула для мольного элемента: Yb = mb / (mb + 1/ M (A)). В выражении mb обозначает моляльность, а M (A) — молярную массу растворителя. Чтобы ответ получился в одинаковых единицах измерения, цифра один в формуле представляется как 1000 г/кг. Это необходимо, когда моляльность подставляется в моль на килограмм, а масса в грамм на моль.

Вычисление концентрации

Чтобы получить раствор, необходимо между собой смешать растворитель и растворимое. Для того чтобы вычислить концентрацию, нужно знать или найти общий объём смеси, который будет равен сумме элементов, используемых при создании раствора. Измеряться концентрация может в различных величинах. Основные из них:

Найти молярность, характеризуемую числом доли растворенных элементов, зная массу и формулу вещества несложно. Если количество растворённой части задано в других единицах, то их преобразуют в граммы.

Каждый элемент характеризуется молярной массой и определяется отношением массы к числу моль. Равна она атомной массе, которую можно взять из таблицы Менделеева. Для нахождения молярной величины нужно сложить все атомные числа элементов, смешанных в растворе.

Найдя молекулярное значение можно перейти к вычислению количества молей. Делается это с помощью формулы для молярной концентрации: масса растворённого вещества умножается на обратную молярную часть. Результат должен получиться в моль. На следующем этапе находится молярность. Полученное число молей делится на объём, измеряемого в литрах раствора. Обычно объёмом растворённой части пренебрегают.

По аналогии вычисляется концентрация и в процентном составе. Для этого нужно найти массу частей, составляющих раствор. На первом этапе все единицы измерения переводятся в граммы. Находится плотность, затем она умножается на объём и получается масса вещества в граммах. Вычисление концентрации в процентном составе находится как масса растворённого вещества, делённая на сумму массы растворяемого и растворителя, а после результат умножается на сто.

Так как проценты являются сотой долей, то для получения ответа в миллионной доле результат нужно умножить ещё на 10 тысяч.

Примеры расчёта

Определением молярности раствора занимается химия. В процессах участвуют различные частицы, количество которых даже в малых объёмах велико. Значение молярной концентрации определяется не только количественным, но и качественным составом. Самые простые задачи связаны с нахождением молярной массы. Например, для соединения CH4 она наводится следующим образом:

Мr (CH4) = Ar + 4Ar (H) = 12 + 4 =16

Получается, что масса метана содержит 16 г/моль или 6,02Ч * 10 23 молекул. Буква «Ч» используется для обозначения части.

Теперь можно найти массу в объёмном количестве. Например, нужно определить массу метана смешанном в количестве двух моль. Так как для метана его масса составляет 16 г/моль, то ответом будет:

м (метан) = 2 * 16 = 32 г

Много задач встречается на нахождение массовой доли в растворе. Например, в 200 грамм соли добавили 80 грамм воды. Чтобы определить часть соли в полученной смеси необходимо найти первоначальную её долю в растворе: M1 = w * m = 0,14 * 200 = 28 гамм. Затем вычислить массу нового раствора: М2 = 200 + 80 = 280 грамм. И воспользовавшись формулой получить ответ: W = M1 / M2 = 28 / 280 = 0,100.

Немного сложнее задачи на расчёт грамм-эквивалента. Пусть нужно найти нормальность серной кислоты, смешанной с раствором щёлочи. При смешении образуется соединение: NaSO4. Так как при реакции серная кислота нейтрализует гидросульфат натрия только частично то можно записать: Н2SO4 + NaOH = NaHSO4 + Н2О. Серная кислота представляет основу равную единице, поэтому и фактор эквивалентности также будет составлять единицу.

Экв (H2SO4) =1 * ф = 1/1 = 1

Отсюда следует, что значение молярности эквивалента кислоты:

Мэкв (H2SO4) = M * Ф = M/1 = 98/1 = 98 г/экв

Нужно найти массовую часть и молярность эквивалента смеси, полученной при смешивании 400 мл раствора серной кислоты (p =1, 18 г/мл) и 400 мл восьмипроцентного раствора серной кислоты (p = 1,05 г/мл).

Вначале следует вычислить массу первого раствора и содержание в нём серной кислоты:

m (р-ра) = p (р-ра) * V (р-ра) = 1,18 * 400 = 720 г

m (H2SO4) = V (H2SO4) * м (H2SO4)= С (H2SO4) * V (р-ра) * М (H2SO4) = 720 * 0,2 — 98 = 46 г

Затем определить массу второго раствора и содержание в нём количества серной кислоты:

m (р-ра) = р (р-ра) * V (р-ра) = 1,05 * 400 = 420 г

m = m (р-ра) * (H2SO4)= 420 * 0,08 = 24 г

Часть полученного раствора находится по формуле:

ɷ (H2SO4) = m (H2SO4) / m (р-ра) = (46 + 24) / (720+420) = 0,146

Ответ удобнее записать в процентном соотношении — 14,6%.

Источник

Концентрация объемная

Концентрация растворов является важной характеристикой, показывающей содержание растворенного вещества и растворителя в его составе. Выражается концентрация, как правило, в массовых (вес) и объемных (объем) процентах или долях.

Растворы и их концентрация

Под раствором следует понимать однородную (гомогенную систему), в состав которой входит один или несколько компонентов. Растворы могут быть газовыми, жидкими, твердыми. Концентрация раствора бывает качественной и количественной. Качественная концентрация определяет растворы насыщенные, ненасыщенные, перенасыщенные. Количественная концентрация показывает массу или объем содержания веществ в составе раствора.

Самый простой состав – это растворитель и растворенное вещество. Растворитель представляет собой вещество, которое при растворении не меняет свое состояние. Если смешиваются вещества в одинаковом агрегатном состоянии, к примеру, жидкость с жидкостью или газ с газом, растворителем будет компонент, которого больше. Образование раствора зависит от характера взаимодействия между частицами растворителя и растворенного вещества, их природой.

Чтобы определить соотношение растворенного вещества и растворителя в составе смеси и применяется такая характеристика, как концентрация. В зависимости от того, какая единица измерения выбрана, концентрация может быть объемной (содержание вещества в объеме раствора) или массовой (содержание вещества в единице массы раствора).

Объемные концентрации

Объемная доля вещества в общем объеме раствора выражается соотношением между объемом компонента, который нужно определить, и общим объемом всего раствора. Для измерения объемной концентрации используются доли или проценты. Значение концентрации указывается при определенных показателях температурного режима и давления.

Для выражения объемной доли используется следующая формула:

V(А) – объем вещества, V (смеси) – общий объем раствора.

Объемная доля, как правило, применяется в отношении газовых смесей. К примеру, содержание кислорода в воздухе составляет 21%, что означает объемную долю кислорода: φ(O2) = 21%. Применение объемной доли удобно потому, что объемное содержание газа в составе раствора газов, которые химически не взаимодействуют между собой, такая же, как молярная доля смеси. Это в достаточной мере точно выполняется, когда показатели давления и температуры не слишком высокие.

Для определения концентрации растворов определенных веществ используется ареометр. Он проградуирован непосредственно в концентрации смеси, а не в показателях ее плотности.

Объемная концентрация и объемная доля – безразмерные величины. Чтобы их выражать в большинстве случаев используются проценты, но могут также применяться такие единицы, как промилле, миллионные доли. Возможно также отображение единиц в таком виде: «% об.» или «об.%» (объемные проценты), однако рекомендуется писать конкретное указывать величину, к которой относится значение.

Источник

В статье рассмотрена модель идеального газа, приведено основное уравнение молекулярно-кинетической теории и его вывод.

Чтобы объяснить свойства материи в газообразном состоянии, в физике применяется модель идеального газа. Идеальный газ — разреженный, состоящий из одного типа атомов газ, частицы которого не взаимодействуют между собой. Помимо основных положений МКТ эта модель предполагает, что:

• молекулы имеют пренебрежимо малый объем в сравнении с объемом емкости
• при сближении частиц друг с другом и с границами емкости имеют место силы отталкивания

Основное уравнение молекулярно-кинетической теории

Физический смысл основного уравнения МКТ заключается в том, что давление идеального газа — это совокупность всех ударов молекул о стенки сосуда. Это уравнение можно выразить через концентрацию частиц, их среднюю скорость и массу одной частицы:

• p – давление молекул газа на границы емкости,
• m0 – масса одной молекулы,
• n — концентрация молекул, число частиц N в единице объема V;
• v2 — средне квадратичная скорость молекул.

Вывод основного уравнения МКТ

Частицы идеального газа при соударениях с границами емкости ведут себя как упругие тела. Такое взаимодействие описывается согласно законам механики. При соприкосновении частицы с границей емкости проекция vx скоростного вектора на ось ОХ, проходящую под прямым углом к границе сосуда, меняет свой знак на противоположный, но сохраняется неизменной по модулю:

Поэтому после соударения частицы с границей емкости проекция импульса молекулы на ось ОХ меняется с mv1x = –mvx на mv2x = mvx.

Изменение импульса молекулы ΔP равняется удвоенному произведению массы молекулы на ее скорость:

Поскольку в каждом из шести основных направлений декартовой системы координат (вверх, вниз, вперед, назад, вправо, влево) движется одна шестая часть частиц N/6. Тогда число частиц, которые сталкиваются с каждой стенкой за время Δt равно:

1. S – площадь этой стенки
2. n — концентрация частиц
3. Давление p равно отношению силы F к площади S, на которую действует эта сила:

Суммарная сила, с которой частицы давят на стенку равна отношению произведения числа этих частиц N и изменения импульса ΔP ко времени, в течение которого происходит давление:

Исходя из вышенаписанного получаем:

Тогда

Если заменить среднее значение кинетической энергии поступательного движения молекул — E:

и подставить эту формулу в основное уравнение МКТ, получим давление идеального газа:

Давление идеального газа равняется двум третям средней кинетической энергии поступательного движения молекул на единицу объема. При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.

Источник: https://people-ask.ru/nauki/fizika/osnovnoe-uravnenie-molekulyarno-kineticheskoj-teorii-mkt-s-vivodom

II. Молекулярная физика

Вещество состоит из частиц.

Молекула — это самая маленькая частица вещества, которая обладает его основными химическими свойствами.

Молекула состоит из атомов. Атом — наименьшая частица вещества, которая не делится при химических реакциях.

Многие молекулы состоят из двух или больше атомов, удерживаемых вместе химическими связями. Некоторые молекулы состоят из сотен тысяч атомов.

Второе положение молекулярно-кинетической теории

Молекулы находятся в непрерывном хаотическом движении. Это движение не зависит от внешних воздействий. Движение происходит в непредсказуемом направлении из-за столкновения молекул. Доказательством является броуновское движение частиц (открыто Р.Броуном 1827г). Частицы помещают в жидкость или газ и наблюдают их непредсказуемое движение из-за соударений с молекулами вещества.

Броуновское движение

Доказательством хаотического движения является диффузия — проникновение молекул одного вещества в промежутки между молекулами другого вещества. Например, запах освежителя воздуха мы ощущаем не только в том месте, где его распылили, но он постепенно перемешивается с молекулами воздуха во всей комнате.

Агрегатное состояние вещества

В газах среднее расстояние между молекулами в сотни раз превышает их размеры. В основном молекулы движутся поступательно и равномерно. После столкновений начинают вращаться.

В жидкостях расстояние между молекулами значительно меньше. Молекулы совершают колебательное и поступательное движения. Молекулы через малые промежутки времени скачкообразно переходят в новые положения равновесия (мы наблюдаем текучесть жидкости).

В твердых телах молекулы колеблются и очень редко перемещаются (только при увеличении температуры).

Третье положение молекулярно-кинетической теории

Между молекулами существуют силы взаимодействия, которые имеют электромагнитную природу. Эти силы позволяют объяснить возникновение сил упругости. Когда вещество сжимают, молекулы сближаются, между ними возникает сила отталкивания, когда внешние силы отдаляют молекулы друг от друга (растягивают вещество), между ними возникает сила притяжения.

Плотность вещества

Это скалярная величина, которая определяется по формуле

Плотность веществ — известные табличные значения

Химические характеристики вещества

Постоянная Авогадро NA — число атомов, содержащихся в 12г изотопа углерода

Количество вещества — это отношение числа элементов этого вещества к постоянной Авогадро

• 1 моль любого вещества содержит одинаковое число частиц, это число равно постоянной Авогадро.
• Молярная масса M — это масса одного моля вещества
• Если тело состоит из N молекул массой m0, то масса тела
• Концентрация частиц — это количество частиц в объеме
• Можно вывести формулы

Источник: http://fizmat.by/kursy/molekuljarnaja/polozhenija_mkt

Молекулярно-кинетическая теория идеального газа. Основные положения

Молекулы в идеальном газе движутся хаотически. Движение одной молекулы характеризуют микроскопические параметры (масса молекулы, ее скорость, импульс, кинетическая энергия).

Свойства газа как целого описываются с помощью макроскопических параметров (масса газа, давление, объем, температура).

Молекулярно-кинетическая теория устанавливает взаимосвязь между микроскопическими и макроскопическими параметрами.

Число молекул в идеальном газе столь велико, что закономерности их поведения можно выяснить только с помощью статистического метода. Равномерное распределение в пространстве молекул идеального газа является наиболее вероятным состоянием газа, т. е. наиболее часто встречающимся.

Распределение молекул идеального газа по скоростям при определенной температуре является статистической закономерностью.

Наиболее вероятная скорость молекул — скорость, которой обладает максимальное число молекул. Стационарное равновесное состояние газа — состояние, в котором число молекул в заданном интервале скоростей остается постоянным.

Температура тела — мера средней кинетической энергии поступательного движения его молекул:

• где черта сверху — знак усреднения по скоростям, k = 1,38 • 10-23 Дж/К — постоянная Больцмана.
• Единица термодинамической температуры — кельвин (К).
• При абсолютном нуле температуры средняя кинетическая энергия молекул равна нулю.
• Средняя квадратичная (тепловая) скорость молекул газа

где М — молярная масса, R = 8,31 Дж/(К • моль) — молярная газовая постоянная.

Давление газа — следствие ударов движущихся молекул:

где n — концентрация молекул (число молекул в единице объема), Ek — средняя кинетическая энергия молекулы.

Давление газа пропорционально его температуре:

Постоянная Лошмидта — концентрация идеального газа при нормальных условиях (атмосферное давление р= 1,01 • 105 Па и температура Т = 273 К):

Уравнение Клапейрона—Менделеева — уравнение состояния идеального газа, связывающее три макроскопических параметра (давление, объем, температуру) данной массы газа.

Изопроцесс — процесс, при котором один из макроскопических параметров состояния данной массы газа остается постоянным. Изотермический процесс — процесс изменения состояния определенной массы газа при постоянной температуре.

Закон Бойля—Мариотта: для газа данной массы при постоянной температуре:

где р1, р2, V1, V2 — давление и объем газа в начальном и конечном состояниях

Изотерма — график изменения макроскопических параметров газа при изотермическом процессе. Изобарный процесс — процесс изменения состояния определенной массы газа при постоянном давлении.

Закон Гей-Люссака: для газа данной массы при постоянном давлении

1. где V1, V2, T1, Т2— объем и температура газа в начальном и конечном состояниях.
2. Изобара — график изменения макроскопических параметров газа при изобарном процессе.
3. Изохорный процесс — процесс изменения состояния определенной массы газа при постоянном объеме. Закон Шарля: для газа данной массы при постоянном объеме

где p1, р2, T1, Т2 — давление и температура газа в начальном и конечном состояниях.

Изохора — график изменения макроскопических параметров газа при изохорном процессе.

Источник: https://5terka.com/molekulyarno-kineticheskaya-teoriya-idealnogo-gaza-osnovnye-polozheniya

Идеальный газ. Формула концентрации молекул газа. Пример задачи :

В физике текучих субстанций большое внимание уделяется изучению газов, которое осуществляют при помощи использования модели идеального газа. В этой области было открыто много законов. В приведенной ниже статье изучим формулу концентрации молекул газа (идеального) и покажем, как ее следует применять при решении практической проблемы.

Идеальный газ

Что же это такое? Прежде чем записать формулу концентрации молекул газа, расскажем, что собой представляет модель идеального газа. В соответствии с кинетической теорией текучих субстанций, в таких веществах молекулы и атомы движутся хаотически по прямым траекториям. Расстояния между ними намного больше, чем их собственные линейные размеры, поэтому последними пренебрегают при выполнении вычислений. Кроме того, считают, что взаимодействий между молекулами не существует, поскольку их кинетическая энергия слишком велика по сравнению со слабыми потенциальными взаимодействиями.

Любые реальные газы, которые находятся при низких давлениях и достаточно высоких абсолютных температурах, по своему поведению приближаются к описанной модели.

Тем не менее существуют текучие субстанции, у которых помимо ван-дер-ваальсовых взаимодействий между частицами действуют взаимодействия более сильного характера.

Примером является водяной пар, у которого молекулы друг с другом связаны водородными (полярными) связями. Для описания поведения таких субстанций нельзя использовать модель идеального газа.

Универсальное уравнение

• Модель идеального газа удобна при выполнении практических расчетов тем, что уравнение состояния вещества, полученное на ее основе, связывает три термодинамических параметра: температуру T, объем системы V и абсолютное давление P. Это уравнение записано ниже:
• P * V = n * R * T.
• Где R — постоянная, равная 8,314 Дж/(моль*К), n — количество вещества.

Современная молекулярно-кинетическая теория газов позволяет путем несложных рассуждений и математических выкладок получить теоретически это уравнение.

Впервые же оно было записано в результате анализа многочисленных экспериментов, которые в течение двух веков выполняли европейские ученые, начиная от Роберта Бойля (вторая половина XVII века) и заканчивая Амедео Авогадро (начало XIX века).

Считается, что уравнение состояния идеального газа первым получил Эмиль Клапейрон, а к современной форме его привел русский химик Дмитрий Менделеев, поэтому его часто называют законом Клапейрона-Менделеева.

Понятие о концентрации молекул: виды концентраций

Когда изучают текучие субстанции, то знать концентрации компонентов, которые их образуют, является важным при решении многих практических задач.

Например, от этого показателя и размеров молекул зависит общая площадь поверхности активного вещества, а значит, его реакционная способность.

Другой пример, концентрация некоторых веществ в воздухе определяет допустимые их пределы для нормального протекания жизненно необходимых процессов в организме человека.

В случае газов, как правило, пользуются тремя следующими концентрациями:

• Атомная. Она определяется, как процентное содержание количества атомов или молекул компонента по отношению к объему всей системы.
• Массовая. Показывает отношение массы компонента к объему газа.
• Молярная. Она равна отношению количества вещества изучаемого компонента к объему системы.

Заметим, что все виды концентраций вычисляются по отношению к объему системы. Справедливость этих величин действительна, поскольку каждый компонент системы полностью заполняет ее объем.

Среди всех типов концентраций наиболее удобной на практике является молярная. Ниже в статье приведем формулу именно для нее.

Формула концентрации молекул газа

В соответствии с приведенным в предыдущем пункте определением, молярная концентрация i-го компонента системы cn(i) вычисляется так:

cn(i) = ni / V.

Предположим, что мы имеем однокомпонентный (чистый) газ. Это может быть кислород, азот, гелий и так далее. В этом случае можно применить формулу Клапейрона-Менделеева и выразить из нее молярную концентрацию молекул. Имеем:

1. P * V = n * R * T =>
2. cn = n / V = P / (R * T).
3. Из записанной формулы концентрации молекул газа легко получить атомную (молекулярную) концентрацию. Покажем, как это делается:
4. cn = n / V = N / (NA * V) = cN / NA =>
5. cN = cn * NA = NA * P / (R * T) = P / (kB * T).

Здесь NA и kB — число Авогадро и постоянная Больцмана. Соответственно, N — число молекул в системе. Поскольку величина kB имеет маленькое значение (1,38 * 10-23), то cN принимает огромные значения, что неудобно для ее практического использования.

Пример задачи

В результате изобарного нагрева закрытой системы с идеальным газом его температура увеличилась на 100 К и стала равной 400 К. Как изменится концентрация молекул газа, если давление в системе составляет 1,5 атмосферы.

• Поскольку давление в процессе нагрева не изменилось, а температура была равна 300 К согласно условию задачи, то молярная концентрацию молекул до нагрева системы составляла:
• cn1 = 1,5 * 101 325 / (8,314 * 300) = 60,9 моль/м3.
• Число молекул в системе не изменилось при нагреве, так как система является закрытой. После нагрева газа его концентрация составила:
• cn2 = 1,5 * 101 325 / (8,314 * 400) = 45,7 моль/м3.
• Изменение концентрации составило:
• Δcn = cn2 — cn1 = 45,7 — 60,9 = -15,2 моль/м3.
• Отрицательный знак говорит, что концентрация уменьшилась, что является очевидным, поскольку увеличился объем системы после нагрева, а число частиц в ней осталось прежним.

Источник: https://www.syl.ru/article/459392/idealnyiy-gaz-formula-kontsentratsii-molekul-gaza-primer-zadachi

Урок 15. Моляльность и молярность – HIMI4KA

Архив уроков › Основные законы химии

В уроке 15 «Моляльность и молярность» из курса «Химия для чайников» рассмотрим понятия растворитель и растворенное вещество научимся выполнять расчет молярной и моляльной концентрации, а также разбавлять растворы. Невозможно объяснить что такое моляльность и молярность, если вы не знакомы с понятием моль вещества, поэтому не поленитесь и прочитайте предыдущие уроки. Кстати, в прошлом уроке мы разбирали задачи на выход реакции, посмотрите если вам интересно.

Химикам нередко приходится работать с жидкими растворами, так как это благоприятная среда для протекания химических реакций. Жидкости легко смешивать, в отличие от кристаллических тел, а также жидкость занимает меньший объем, по сравнению с газом.

Благодаря этим достоинствам, химические реакции могут осуществляться гораздо быстрее, так как исходные реагенты в жидкой среде часто сближаются и сталкиваются друг с другом.

В прошлых уроках мы отмечали, что вода относится к полярным жидкостям, и потому является неплохим растворителем для проведения химических реакций.

Молекулы H2O, а также ионы H+ и OH—, на которых вода диссоциирована в небольшой степени, могут способствовать запуску химические реакций, благодаря поляризации связей в других молекулах или ослаблению связи между атомами. Вот почему жизнь на Земле зародилась не на суше или в атмосфере, а именно в воде.

Растворитель и растворенное вещество

Раствор может быть образован путем растворения газа в жидкости или твердого тела в жидкости.

В обоих случаях жидкость является растворителем, а другой компонент — растворенное вещество.

Когда раствор образован путем смешивания двух жидкостей, растворителем считается та жидкость, которая находится в большем количестве, иначе говоря имеет бОльшую концентрацию.

Расчет концентрации раствора

Молярная концентрация

Концентрацию можно выражать по разному, но наиболее распространенный способ — указание его молярности. Молярная концентрация (молярность) — это число молей растворенного вещества в 1 литре раствора.

Единица молярности обозначается символом M. Например два моля соляной кислоты на 1 литр раствора обозначается 2 М HCl. Кстати, если на 1 литр раствора приходится 1 моль растворенного вещества, тогда раствор называется одномолярным.

Молярная концентрация раствора обозначается различными символами:

• cx, Смx, [x], где x — растворенное вещество

Формула для вычисления молярной концентрации (молярности):

где n — количество растворенного вещества в молях, V — объем раствора в литрах.

Пару слов о технике приготовления растворов нужной молярности. Очевидно, что если добавить к одному литру растворителя 1 моль вещества, общий объем раствора будет чуть больше одного литра, и потому будет ошибкой считать полученный раствор одномолярным.

Чтобы этого избежать, первым делом добавляем вещество, а только потом доливаем воду, пока суммарный объем раствора не будет равным 1 л.

Полезно будет запомнить приближенное правило аддитивности объемов, которое гласит, что объем раствора приближенно равен сумме объемов растворителя и растворенного вещества. Растворы многих солей приближенно подчиняются данному правилу.

Пример 1. Химичка дала задание растворить в литре воды 264 г сульфата аммония (NH4)2SO4, а затем вычислить молярность полученного раствора и его объем, основываясь на предположении об аддитивности объемов. Плотность сульфата аммония равна 1,76 г/мл.

Решение:

Определим объем (NH4)2SO4 до растворения:

• 264 г / 1,76 г/мл = 150 мл = 0,150 л

Пользуясь правилом аддитивности объемов, найдем окончательный объем раствора:

• 1,000 л + 0,150 л = 1,150 л

Число молей растворенного сульфата аммония равно:

• 264 г / 132 г/моль = 2,00 моля (NH4)2SO4

Завершающий шаг! Молярность раствора равна:

• 2,000 / 1,150 л = 1,74 моль/л, т.е 1,74 М (NH4)2SO4

Приближенным правилом аддитивности объемов можно пользоваться только для грубой предварительной оценки молярности раствора. Например, в примере 1, объем полученного раствора на самом деле имеет молярную концентрацию равную 1,8 М, т.е погрешность наших расчетов составляет 3,3%.

Моляльная концентрация

Наряду с молярностью, химики используют моляльность, или моляльную концентрацию, в основе которой учитывается количество использованного растворителя, а не количество образующегося раствора.

Моляльная концентрация — это число молей растворенного вещества в 1 кг растворителя (а не раствора!). Моляльность выражается в моль/кг и обозначается маленькой буквой m.

Формула для вычисления моляльной концентрации:

где n — количество растворенного вещества в молях, m — масса растворителя в кг

Для справки отметим, что 1 л воды = 1 кг воды, и еще, 1 г/мл = 1 кг/л.

Пример 2. Химичка попросила определить моляльность раствора, полученного при растворении 5 г уксусной кислоты C2H4O2 в 1 л этанола. Плотность этанола равна 0,789 г/мл.

Решение:

Число молей уксусной кислоты в 5 г равно:

• 5,00 г / 60,05 г/моль = 0,833 моля C2H4O2

Масса 1 л этанола равна:

• 1,000 л × 0,789 кг/л = 0,789 кг этанола

Последний этап. Найдем моляльность полученного раствора:

• 0,833 моля / 0,789 кг растворителя = 0,106 моль/кг

Единица моляльности обозначается Мл, поэтому ответ также можно записать 0,106 Мл.

Разбавление растворов

В химической практике часто занимаются разбавлением растворов, т.е добавлением растворителя. Просто нужно запомнить, что число молей растворенного вещества при разбавлении раствора остается неизменным. И еще запомните формулу правильного разбавления раствора:

• Число молей растворенного вещества = c1V1 = c2V2

где с1 и V1 — молярная концентрация и объем раствора до разбавления, с2 и V2 — молярная концентрация и объем раствора после разбавления. Рассмотрите задачи на разбавление растворов:

Пример 3. Определите молярность раствора, полученного разбавлением 175 мл 2,00 М раствора до 1,00 л.

Решение:

В условие задача указаны значения с1, V1 и V2, поэтому пользуясь формулой разбавления растворов, выразим молярную концентрацию полученного раствора с2

• с2 = c1V1 / V2 = (2,00 М × 175 мл) / 1000 мл = 0,350 М

Пример 4 самостоятельно. До какого объема следует разбавить 5,00 мл 6,00 М раствора HCl, чтобы его молярность стала 0,1 М?

Ответ: V2 = 300 мл

Без сомнения, вы и сами догадались, что урок 15 «Моляльность и молярность» очень важный, ведь 90% все лабораторных по химии связаны с приготовлением растворов нужной концентрации. Поэтому проштудируйте материал от корки до корки. Если у вас возникли вопросы, пишите их в комментарии.

Источник: https://himi4ka.ru/arhiv-urokov/urok-15-moljalnost-i-moljarnost.html

ФизМат

Основные положения молекулярно-кинетической теории и их экспериментальное обоснование.

 Молекулярно-кинетическая теория — это раздел физики, изучающий свойства различных состояний вещества, основывающийся на представлениях о существовании молекул и атомов как мельчайших частиц вещества. В основе МКТ лежат три основных положения:

Размеры и массы молекул. 

 Средняя масса молекул обычно определяется химическими методами, постоянная Авогадро с высокой точностью определена несколькими физическими методами. Массы молекул и атомов со значительной степенью точности определяются с помощью масс-спектрографа.

Моль. 

   Единицей количества вещества является моль. Моль — это количество вещества, содержащее столько же структурных элементов любого вещества, сколько содержится атомов в 12 г углерода С12. 

Число Авогадро. 

Опыт Штерна.

Опыт Штерна — опыт, впервые проведённый немецким физиком Отто Штерном в 1920 году. Опыт являлся одним из первых практических доказательств состоятельности молекулярно-кинетической теории строения вещества. В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям.

Для проведения опыта Штерном был подготовлен прибор, состоящий из двух цилиндров разного радиуса, ось которых совпадала и на ней располагалась платиновая проволока с нанесённым слоем серебра. В пространстве внутри цилиндров посредством непрерывной откачки воздуха поддерживалось достаточно низкое давление.

При пропускании электрического тока через проволоку достигалась температура плавления серебра, из-за чего атомы начинали испаряться и летели к внутренней поверхности малого цилиндра равномерно и прямолинейно со скоростью v, соответствующей подаваемому на концы нити напряжению.

Во внутреннем цилиндре была проделана узкая щель, через которую атомы могли беспрепятственно пролетать далее. Стенки цилиндров специально охлаждались, что способствовало оседанию попадающих на них атомов.

В таком состоянии на внутренней поверхности большого цилиндра образовывалась достаточно чёткая узкая полоса серебряного налёта, расположенная прямо напротив щели малого цилиндра. Затем всю систему начинали вращать с некой достаточно большой угловой скоростью ω.

При этом полоса налёта смещалась в сторону, противоположную направлению вращения, и теряла чёткость. Измерив смещение sнаиболее тёмной части полосы от её положения, когда система покоилась, Штерн определил время полёта, через которое нашёл скорость движения молекул:

,

где s — смещение полосы, l — расстояние между цилиндрами, а u — скорость движения точек внешнего цилиндра.

Найденная таким образом скорость движения атомов серебра совпала со скоростью, рассчитанной по законам молекулярно-кинетической теории, а тот факт, что получившаяся полоска была размытой, свидетельствовал в пользу того, что скорости атомов различны и распределены по некоторому закону — закону распределения Максвелла: атомы, двигавшиеся быстрее, смещались относительно полосы, полученной в состоянии покоя, на меньшие расстояния, чем те, которые двигались медленнее.

Модель идеального газа.

Основные уравнения молекулярно-кинетической теории идеального газа.

Идеальный газ

Идеальный газ — это физическая модель газа, взаимодействие между молекулами которого пренебрежительно мало.
— вводится для математического описания поведения газов. Реальные разреженные газы ведут себя как идеальный газ!

Свойства идеального газа:

— взаимодействие между молекулами пренебрежительно мало
— расстояние между молекулами много больше размеров молекул
— молекулы — это упругие шары
— отталкивание молекул возможно только при соударении
— движение молекул — по законам Ньютона

— давление газа на стенки сосуда — за счет ударов молекул газа

Скорость молекул газа

В теории газов скорость молекул принято определять через среднее значение квадрата скорости молекул. Хотя скорости различных молекул сильно отличаются друг от друга, но среднее значение квадрата скорости молекул есть величина постоянная.

Формула для расчета среднего значения квадрата скорости молекул газа:

V^2 = (v1^2 + v2^2 +…+vn^2)/n

где
n — число молекул в газе
v — модули скоростей отдельных молекул в газе В теории газов часто используется понятие кинетической энергии молекул.

Используя среднее значение квадрата скорости молекул, получаем формулу для определения средней кинетической энергии молекул:

Основное уравнение МКТ газа

Основное уравнение МКТ связывает микропараметры частиц ( массу молекулы, среднюю кинетическую энергию молекул, средний квадрат скорости молекул) с макропараметрами газа (р — давление, V — объем, Т — температура). 
Давление газа на стенки сосуда пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы. Ниже приведены различные выражения для основного уравнения МКТ:

  P=F/s=1/3 * n * m0 * V^2 = 1/3 * ρ * v^2 = 2/3*n*Ek

где P — давление газа на стенки сосуда(Па) n — концентрация молекул, т.е. число молекул в единице объема ( 1/м3) m0 — масса молекулы (кг) V^2 — средний квадрат скорости молекул ( м2/с2) ρ — плотность газа (кг/м3) Ek — средняя кинетическая энергия молекул (Дж)

Давление идеального газа на стенки сосуда зависит от концентрации молекул и пропорционально средней кинетической энергии молекул.

• Дополнительные расчетные формулы по теме

• Формула для расчета концентрации молекул:

• n=N/V

где N — число молекул газа
V — объем газа (м3)

Формула для расчета плотности газа:

ρ = m0*n

где mo — масса молекулы (кг)

n — концентрация молекул (1/м3)

Закон Дальтона.

Давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений.

При постоянной температуре растворимость в данной жидкости каждого из компонентов газовой смеси, находящейся над жидкостью, пропорциональна их парциальному давлению.

Источник: http://fizmatinf.blogspot.com/2013/05/20.html

Идеальный газ. Основное уравнение МКТ. Молекулярная физика — Класс!ная физика

Идеальный газ — это просто!

Идеальный газ

Идеальный газ — это физическая модель газа, взаимодействие между молекулами которого пренебрежительно мало. Понятие «идеальный газ» вводится для математического описания поведения газов.

Реальные разреженные газы ведут себя как идеальный газ!

• Свойства идеального газа:
• — давление газа на стенки сосуда — за счет ударов молекул газа
• Скорость молекул газа

— взаимодействие между молекулами пренебрежительно мало — расстояние между молекулами много больше размеров молекул — молекулы — это упругие шары — отталкивание молекул возможно только при соударении — движение молекул — по законам Ньютона

В теории газов скорость молекул принято определять через среднее значение квадрата скорости молекул. Хотя скорости различных молекул сильно отличаются друг от друга, но среднее значение квадрата скорости молекул есть величина постоянная.

Формула для расчета среднего значения квадрата скорости молекул газа:

1. где n — число молекул в газе v — модули скоростей отдельных молекул в газе В теории газов часто используется понятие кинетической энергии молекул.
2. Используя среднее значение квадрата скорости молекул, получаем формулу для определения средней кинетической энергии молекул:

Основное уравнение МКТ связывает микропараметры частиц (массу молекулы, среднюю кинетическую энергию молекул, средний квадрат скорости молекул) с макропараметрами газа (р — давление, V — объем, Т — температура). Давление газа на стенки сосуда пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Ниже приведены различные выражения для основного уравнения МКТ:

где р — давление газа на стенки сосуда(Па)

n — концентрация молекул, т.е. число молекул в единице объема ( 1/м3)

— масса молекулы (кг) — средний квадрат скорости молекул (м2/с2) ρ — плотность газа (кг/м3) — средняя кинетическая энергия молекул (Дж)

• Давление идеального газа на стенки сосуда зависит от концентрации молекул и пропорционально средней кинетической энергии молекул.
• Дополнительные расчетные формулы по теме
• Формула для расчета концентрации молекул:

1. где N — число молекул газа
2. V — объем газа (м3)
3. Формула для расчета плотности газа:

где mo — масса молекулы (кг) n — концентрация молекул (1/м3)

Назад в раздел «10-11 класс»

Молекулярная физика. Термодинамика — Класс!ная физика

Основные положения МКТ. Масса и размер молекул. Количество вещества. — Взаимодействие молекул. Строение твердых тел, жидкостей и газов. — Идеальный газ. Основное уравнение МКТ. — Температура. Тепловое равновесие.

Абсолютная шкала температур. — Уравнение состояния идеального газа. — Изопроцессы. Газовые законы. — Взаимные превращения жидкостей и газов. Влажность воздуха. — Твердые тела. Кристаллические тела. Аморфные тела.

Источник: http://class-fizika.ru/10_27.html

Урок 18. основное уравнение мкт — Физика — 10 класс — Российская электронная школа

• Физика, 10 класс
• Урок 18. Основное уравнение МКТ
• Перечень вопросов, рассматриваемых на уроке:
• 1) средняя кинетическая энергия молекулы;
• 2) давление газа;
• 3) основное уравнение МКТ;
• Глоссарий по теме:
• Давление идеального газа пропорционально произведению концентрации молекул и средней кинетической энергии поступательного движения молекул.
• Средняя кинетическая энергия молекул – усреднённая величина, равная половине произведения массы молекулы на среднюю величину квадрата её скорости.
• Концентрация – число молекул в единице объёма.
• Масса молекулы (или атома) – чрезвычайно маленькая величина в макроскопических масштабах (граммах и килограммах), вычисляется через отношение массы вещества к количеству содержащихся в ней молекул (или атомов).

Изменение импульса тела – произведение силы на время действия силы. Импульс силы всегда показывает, как изменяется импульс тела за данное время.

Основная и дополнительная литература по теме урока:

1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 188 – 192.
2. Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. С. 111.
3. Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. С. 65 – 67.

Открытые электронные ресурсы по теме урока:

Теоретический материал для самостоятельного изучения

Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами — массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа.

Давление газа на стенку сосуда обусловлено ударами молекул, давление газа пропорционально концентрации молекул: чем больше молекул в единице объема, тем больше ударов молекул о стенку за единицу времени. Каждая молекула при ударе о стенку передает ей импульс, пропорциональный импульсу молекулы m0v.

1. Давление пропорционально второй степени скорости, так как, чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории идеального газа имеет вид:
2. , где m0 — масса одной молекулы газа,
3. n- концентрация молекул,

Средняя кинетическая энергия поступательного движения

тогда уравнение примет вид:

• Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
• Примеры и разбор решения заданий.
• 1. К каждой позиции первого столбца подберите соответствующую позицию второго:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
1) импульс тела	А)
2) средняя кинетическая энергия молекул	Б)
3) давление газа на стенку сосуда	В)
4) концентрация молекул	Г)

Правильный ответ: вспомнив формулы величин, устанавливаем соответствие:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
1) импульс тела	В)
2) средняя кинетическая энергия молекул	А)
3) давление газа на стенку сосуда	Г)
4) концентрация молекул	Б)

2. Кислород находится при нормальных условиях. Средняя квадратичная скорость молекул кислорода в этом случае равна ___ м/с.

1. Решение:
2. Ответ: 460 м/с.

Источник: https://resh.edu.ru/subject/lesson/6291/conspect/