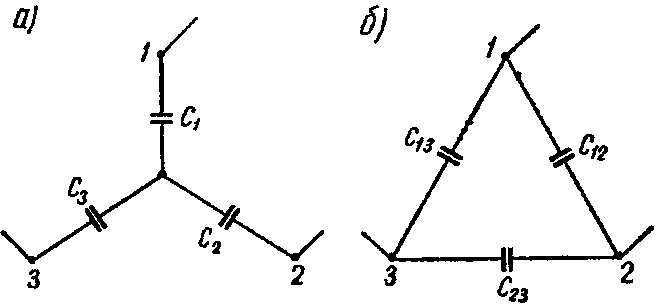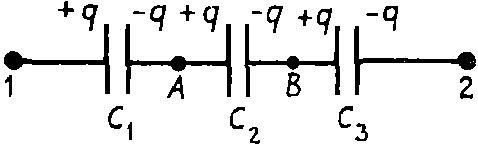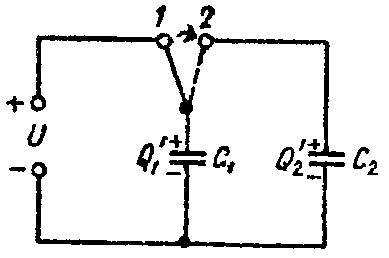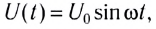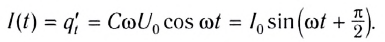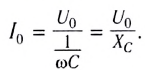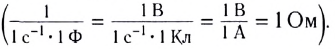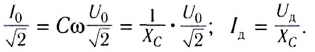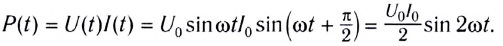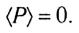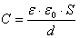Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами
Расчет электрической цепи постоянного тока с конденсаторами
Расчет электрической цепи постоянного тока с конденсаторами
Основные положения и соотношения
1. Общее выражение емкости конденсатора
C= Q U .
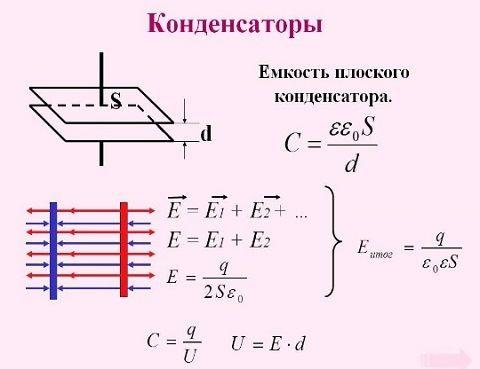
2. Емкость плоского конденсатора
C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,
здесь
S — поверхность каждой пластины конденсатора;
d — расстояние между ними;
εa = εr·ε0 — абсолютная диэлектрическая проницаемость среды;
εr — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);
ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12 Ф м – электрическая постоянная.
3. При параллельном соединении конденсаторов С1, С2, …, Сn эквивалентная емкость равна
C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .
4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .
Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:
C= C 1 ⋅ C 2 C 1 + C 2 ,
а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:
U 1 =U⋅ C 2 C 1 + C 2 ; U 2 =U⋅ C 1 C 1 + C 2 .
5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)
Рис. 0
осуществляется по формулам:
Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ; C 13 = C 1 ⋅ C 3 ΣC ; C 23 = C 2 ⋅ C 3 ΣC , где ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .
6. Энергия электростатического поля конденсатора:
W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .
7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:
1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:
ΣQ=Σ Q ′ .
2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:
∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .
Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.
Решение задач на расчет электрической цепи постоянного тока с конденсаторами
Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).
Рис. 1
Решение
На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U12, то на левую пластину конденсатора С1 перейдет заряд +q, на правую пластину конденсатора С3 заряд –q.
Вследствие электризации через влияние правая пластина конденсатора С1 будет иметь заряд –q, а так как пластины конденсаторов С1 и С2 соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C2 будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.
Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.
Разность потенциалов U12 = φ1 — φ2 складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов
U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .
Воспользовавшись формулой напряжения на конденсаторе
U= q C ,
запишем
q C = q C 1 + q C 2 + q C 3 .
Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов
1 C = 1 C 1 + 1 C 2 + 1 C 3 .
В общем случае эквивалентная емкость при последовательном соединении конденсаторов
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .
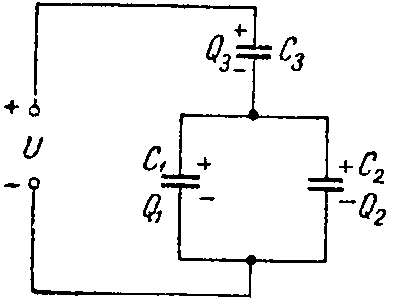
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.
Рис. 2
Емкости конденсаторов: C1 =50 мкФ; C2 =150 мкФ; C3 =300 мкФ.
Решение
Эквивалентная емкость конденсаторов C1 и C2, соединенных параллельно
C12 = C1 + C2 = 200 мкФ,
эквивалентная емкость всей цепи равна
C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120 мкФ.
Заряд на эквивалентной емкости
Q = C·U = 120·10–6·240 = 288·10–4 Кл.
Той же величине равен заряд Q3 на конденсаторе C3, т.е. Q3 = Q = 288·10–4 Кл; напряжение на этом конденсаторе
U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96 В.
Напряжение на конденсаторах C1 и C2 равно
U1 = U2 = U — U3 = 240 — 96 = 144 В.
их заряды имеют следующие значения
Q1 = C1·U1 = 50·10–6·144 = 72·10–4 Кл;
Q2 = C2·U2 = 150·10–6·144 = 216·10–4 Кл.
Энергии электростатического поля конденсаторов равны
W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52 Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56 Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38 Дж.
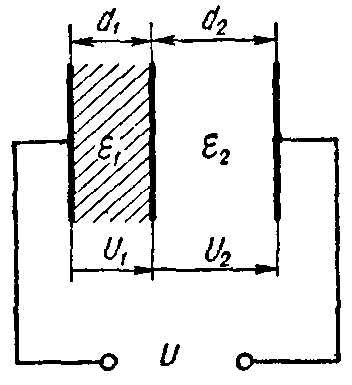
Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см2, имеет диэлектрик, состоящий из слюды (εr1 = 6) толщиною d1 = 0,3 мм и стекла (εr2 = 7) толщиною d2 =0,4 мм.
Пробивные напряженности слюды и стекла соответственно равны E1 = 77 кВ/мм, E2 = 36 кВ/мм.
Рис. 3
Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.
Решение
Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов
C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .
Подставляя сюда числовые значения, предварительно заменив εa1 = εr1·ε0 и εa2 = εr2·ε0, получим
C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12 Ф.
Обозначим общее напряжение, подключаемое к слоистому конденсатору, через Uпр, при этом заряд конденсатора будет равен
Q = C·Uпр.
Напряжения на каждом слое будут равны
U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .
Напряженности электростатического поля в каждом слое
E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .
Здесь U’np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U”np — общее напряжение, при котором происходит пробой второго слоя.
Из последнего выражения находим
U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5 кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0 кВ.
Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное
27,0 кВ / 2 = 13,5 кВ.
Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d1 = 1 см друг от друга. Площадь обкладок S = 50 см2. Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.
Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d2 = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.
Решение
Энергия заряженного плоского конденсатора равна
W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,
где С1 — емкость до раздвижения обкладок.
Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения
Q = C2·U2,
где C2 — емкость конденсатора после раздвижения обкладок, следует, что, так как C2 = ε0·S/d2 стало меньше в 10 раз (d2 увеличилось в 10 раз), то напряжение на конденсаторе U2 увеличилось в 10 раз, т. е. U2 = 10U.
Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d2 будет больше первоначальной
W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .
Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.
Таким образом, надо совершить работу, равную
W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7 Дж.
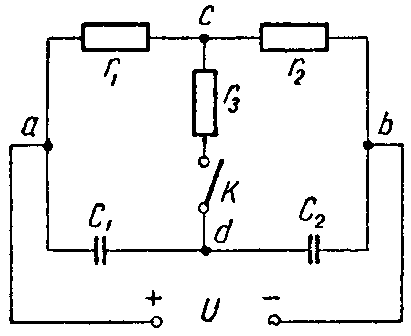
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.
Даны: C1 = 30 мкФ; C2 = 20 мкФ; r1 = 100 Ом. r2 = 400 Ом. r3 = 600 Ом, U = 20 В.
Решение
Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям
U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8 В; U 2 =U− U 1 =20−8=12 В.
Рис. 4
Ключ К замкнут. Через сопротивления r1 и r2 протекает ток
I= U r 1 + r 2 = 20 500 =0,04 А,
а через сопротивление r3 ток не протекает.
Поэтому точки c и d равнопотенциальны (φc = φd). Следовательно, напряжение между точками a и c (Uac = φa — φc) равно напряжению между точками a и d (Uad = φa — φd).
Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r1
UC1 = I·r1 = 0,04·100 = 4 В.
Аналогично напряжение на втором конденсаторе равно
UC2 = I·r2 = 0,04·400 = 16 В.
Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C1 = 5 мкФ; C2 = 120 мкФ. Конденсатор C2 предварительно не был заряжен.
Рис. 5
Решение
Когда рубильник находится в положении 1, то конденсатор C1 заряжен до напряжения U и его заряд равен
Q = C1·U = 5·10–6·25 = 125·10–6 Кл.
После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C1 и C2 (рис. 5). Обозначим эти заряды через Q’1 и Q’2.
На основании закона сохранения электричества имеем
Q = Q’1 + Q’2 = 125 10–6 Кл. (1)
По второму закону Кирхгофа имеем
0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,
или
Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0. (2)
Решая уравнения (1) и (2), найдем
Q’1 = 5 10–6 Кл; Q’2 = 120 10–6 Кл.
Доставка свежих и аппетитных японских суши в Новороссийске – ям ям..
Напряжение на зажимах конденсаторов станет равным
U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1 В.
Энергия обоих конденсаторов будет равна
W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6 Дж.
Подсчитаем энергию, которая была запасена в конденсаторе С1, при его подключении к источнику электрической энергии
W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6 Дж.
Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10–6 — 62,5·10–6 = 1500·10–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C1 в конденсатор C2 после перевода рубильника в положение 2.
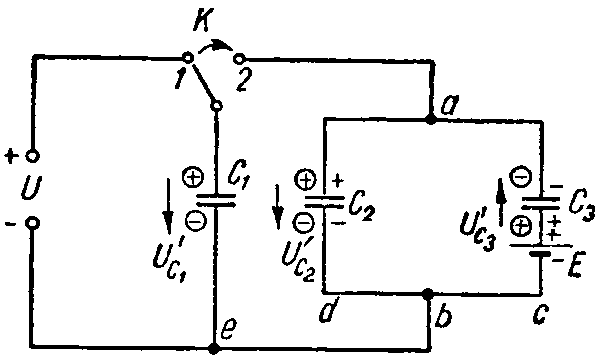
Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.
Емкости конденсаторов равны: C1 = 10 мкФ; C2 = 30 мкФ; C3 = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.
Рис. 6
Решение
Рубильник находится в положении 1. Заряд конденсатора C1 равен
Q1 = C1·U = 10·10–6·30 = 0,3·10–3 Кл.
В указанном положении рубильника конденсаторы C2 и C3 соединены последовательно друг с другом, поэтому их заряды равны: Q2 = Q3. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем
E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,
откуда
Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3 Кл.
При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’1, Q’2 и Q’3. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.
Для узла a
Q’1 + Q’2 — Q’3 = Q1 + Q2 — Q3. (1)
Для контура 2ebda2
0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .
Для контура bcadb
E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .
Уравнения (1) — (3), после подстановки числовых значений величин, примут вид
Q’1 + Q’2 — Q’3 = 0,3·10–3; (4)
3Q’1 — Q’2 = 0; (5)
2Q’2 + Q’3 = 3·10–3. (6)
Решая совместно уравнения (4) — (6), получим
Q’1 = 0,33·10–3 Кл; Q’2 = 0,99·10–3 Кл; Q’3 = 1,02·10–3 Кл.
Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.
Напряжения на конденсаторах после перевода рубильника будут равны
U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33 В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33 В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17 В.
Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C1 = 5 мкФ; C2 = 4 мкФ; C3 = 3 мкФ; э. д. с. источников E1 = 20 В и E2 = 5 В.
Рис. 7
Решение
Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках
− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .
Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q1 = 50 мкКл; Q2 = 20 мкКл; Q3 = –30 мкКл.
Таким образом, истинная полярность зарядов на обкладках конденсаторов C1 и C2 соответствует выбранной, а у конденсатора C3 — противоположна выбранной.
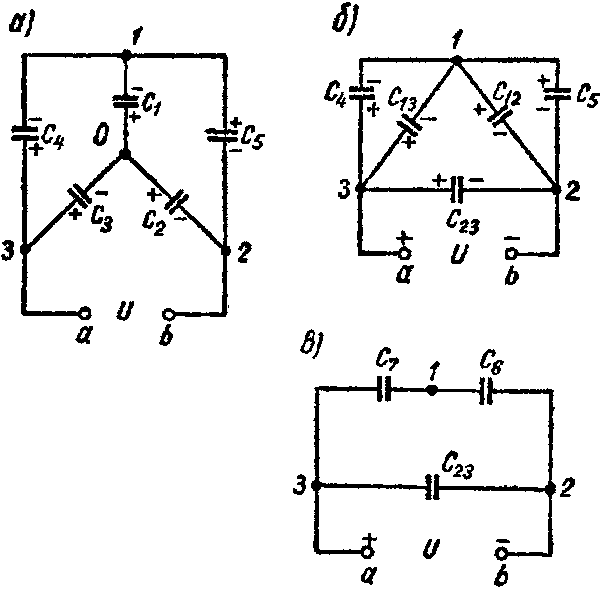
Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C1 = 2 мкФ; C2 = 3 мкФ; C3 = 5 мкФ; C4 = 1 мкФ; C5 = 2,4 мкФ.
Рис. 8
Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол.
Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.
Решение
1-й способ. Звезду емкостей C1, C2 и C3 (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)
C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6 мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0 мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5 мкФ.
Емкости C12 и C5 оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость
C6 = C12 + C5 = 3 мкФ.
Аналогично
C7 = C13 + C4 = 2 мкФ.
Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется
C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7 мкФ.
Вычислим напряжение на каждом из конденсаторов.
На конденсаторе C7 напряжение равно
U 7 = C 6 C 6 + C 7 ⋅U=6 В.
Таково же напряжение и на конденсаторах C4 и C13
U4 = U31 = 6 В.
Напряжение на конденсаторе C6 равно
U6 = U — U7 = 4 В;
U5 = U12 = 4 В.
Вычислим заряды
Q4 = C4·U4 = 6·10–6 Кл;
Q5 = C5·U5 = 9,6·10–6 Кл;
Q12 = C12·U12 = 6·10–6 Кл;
Q13 = C13·U31 = 2,4·10–6 Кл.
По закону сохранения электричества для узла 1 схем 8, а и б имеем
–Q4 — Q1 + Q5 = –Q4 — Q13 + Q12 + Q5,
отсюда
Q1 = Q13 — Q12 = 3,6·10–6 Кл,
а напряжение на конденсаторе, емкостью C1 составляет
U 1 = Q 1 C 1 =1,8 В.
Далее находим напряжения и заряды на остальных конденсаторах
U31 = U1 + U3,
отсюда
U3 = U31 — U1 = 4,2 В;
Q3 = C3·U3 = 21·10–6 Кл,
также
U12 = U2 — U1 = 4,2 В,
откуда
U2 = U12 + U1 = 5,8 В;
Q2 = C2·U2 = 17,4·10–6 Кл.
Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.
2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)
для узла 1
Q5 — Q1 — Q4 = 0; (1)
для узла О
Q1 + Q2 — Q3 = 0; (2)
для контура О13О
Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0; (3)
для контура О12О
Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0; (4)
для контура a3О2b
Q 3 C 3 + Q 2 C 2 =U. (5)
Система уравнений (1) — (5) — содержит пять неизвестных: Q1, Q2, Q3, Q4 и Q5. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы Сab можно найти из отношения
C ab = Q U ,
где Q = Q3 + Q4, или Q = Q2 + Q5.
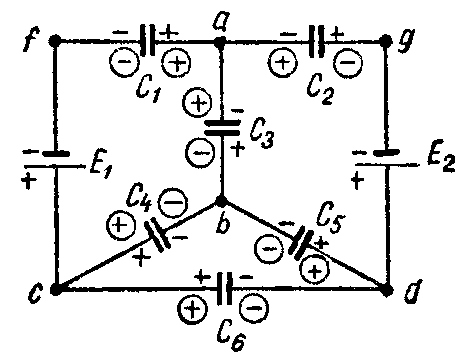
Задача 9. В схеме рис. 9 найти распределение зарядов, если E1 = 20 В; E2 = 7 В; C1 = 7 мкФ; C2 = 1 мкФ; C3 = 3 мкФ; C4 = 4 мкФ; C5 = C6 = 5 мкФ.
Рис. 9
Решение
При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:
для узла а
Q1 + Q2 + Q3 = 0;
для узла b
–Q3 — Q4 — Q5 = 0;
для узла c
–Q1 + Q4 + Q6 = 0;
для контура afcba
E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;
ля контура gdbag
E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;
для контура cbdc
0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .
Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды
Q1 = 35 мкКл; Q2 = –5 мкКл; Q3 = –30 мкКл;
Q4 = 20 мкКл; Q5 = 10 мкКл; Q6 = 15 мкКл.
Таким образом, истинные знаки зарядов Q1, Q4, Q5 и Q6 соответствуют выбранным, а знаки Q2 и Q3 противоположны выбранным.
Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.
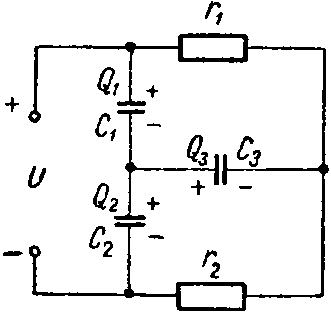
Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C1 = 6 мкФ; C2 = 2 мкФ; C3 = 3 мкФ; r1 = 500 Ом; r2 = 400 Ом; U = 45 В.
Рис. 10
Решение
Через сопротивления протекает ток
I= U r 1 + r 2 =0,05 А.
Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:
− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,
или
Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .
Решив эту систему уравнений, найдем, что
Q1 = 90 мкКл; Q2 = 60 мкКл; Q3 = 30 мкКл.

параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами
Комментарии
Для учащихся (для лучшего понимания физики).
Вспомним основное из предыдущей статьи.
Плоский конденсатор представляет собой устройство, состоящее из двух металлических пластин (обкладок), между которыми находится диэлектрик.
На практике конденсаторы нашли очень широкое применение благодаря их способности накапливать на обкладках значительные электрические заряды. При этом между обкладками возникает разность потенциалов (напряжение).
Конденсаторы характеризуются электрической ёмкостью С:
Ёмкость конденсатора численно равна отношению заряда на одной из обкладок к напряжению между обкладками
или
ёмкость конденсатора численно равна заряду, который надо сообщить обкладке конденсатора, чтобы повысить напряжение между обкладками на единицу напряжения.
Надо помнить, что заряд конденсатора и его напряжение зависят друг от друга, а ёмкость конденсатора не зависит ни от заряда, ни от напряжения, она только численно равна их отношению.
Ёмкость плоского конденсатора зависит лишь от его размеров (от площади пластин, расстояния между ними) и от диэлектрической проницаемости среды между обкладками:
Заряжаются конденсаторы от источников постоянного тока (см. статью “Зарядка конденсатора. Зарядный и разрядный ток проводимости”
На рисунке ниже показана электрическая цепь, состоящая из источника постоянного напряжения, конденсатора и сопротивления:
В момент замыкания ключа К возникший в цепи ток (рисунок справа) имеет максимальное значение, так как разность потенциалов между полюсом источника и обкладкой конденсатора (она не была заряжена) максимальна.
По мере роста заряда на обкладке ток в цепи уменьшается, обращаясь в нуль в момент, когда напряжение на конденсаторе станет равным напряжению на клеммах источника:
Если заряженный конденсатор отключить от источника (следующий рисунок) и замкнуть его обкладки через сопротивление, то по цепи пойдёт разрядный ток, направленный в сторону обратную зарядному току.
Ниже на одном рисунке показаны кривые зависимости зарядного и разрядного тока от времени, из которого видно, что и зарядный, и разрядный токи имеют максимальные значения в моменты замыкания цепей.
При разрядке конденсатор является источником электрической энергии, отдаваемой во внешнюю цепь.
Чтобы энергия конденсаторов постоянно пополнялась, их включают в электрические цепи, содержащие источники постоянного тока. Такие цепи называют ещё конденсаторными цепями.
Дальше рассмотрим некоторые задачи на расчёт таких цепей. Расчёт сводится, как правило, к нахождению заряда конденсаторов или напряжения на конденсаторах.
Задача.
При решении задач на конденсаторные цепи можно кроме способов, применённых при решении рассмотренных выше задач, пользоваться первым, вторым, третьим и четвёртым правилами.
Сейчас на примере качественного решения следующей задачи рассмотрим перечисленные правила.
Задача
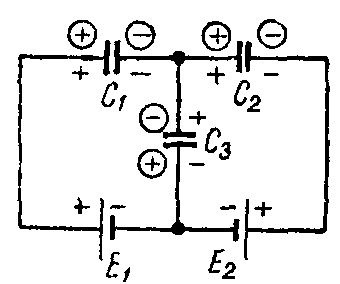
Найти заряд каждого конденсатора в изображённой на рисунке цепи, если известны ЭДС источников постоянного тока и ёмкости конденсаторов.
Сначала подумаем, какие обкладки конденсаторов заряжены положительно, а какие – отрицательно.
Левая обкладка первого конденсатора и правая обкладка третьего конденсатора заряжены отрицательно, так как они соединены с отрицательными полюсами источников. По этой же причине верхняя обкладка второго конденсатора заряжена положительно. Другие обкладки конденсаторов имеют противоположные знаки.
Первое правило
Если в цепи есть точки, в которых сходятся провода обкладок конденсаторов, не соединённых с источником, то их общий заряд равен нулю.
В нашей задаче такой точкой является точка В.
Второе правило
В цепи находим точки равного потенциала и соединяем их в узлы. Потенциал одного из узлов принимаем за нуль. Заряд каждого конденсатора выражаем через его ёмкость и разность потенциалов (напряжение).
Наша цепь содержит два узла А и В. Примем потенциал узла В за нуль.
Третье правило
Для любого замкнутого контура в конденсаторной цепи алгебраическая сумма ЭДС, входящих в контур, равна алгебраической сумме напряжений на конденсаторах в контурах.
В статье “Как найти заряды конденсаторов в цепи …” всё это проделано для нашей задачи и получен ответ.
Все четыре правила расчёта конденсаторных цепей подробно с примерами рассмотрены в статье Занятии 54 и следующих за ней четырёх статьях.
Итак, пользуясь изложенными здесь методами и правилами можно решать сложные задачи на расчёт цепей постоянного тока, содержащих конденсаторы.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Для школьников предлагаются подборки материала по темам:
!. Механика. Кинематика. Равномерное прямолинейное движение.
2. Равнопеременное прямолинейное движение.
Предыдущая запись: Ёмкость уединённого проводника. Ёмкость конденсатора. Почему диэлектрик повышает ёмкость конденсатора?
Следующая запись: Явление электростатической индукции в задачах.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
Как работает конденсатор и катушка в цепи переменного тока
Содержание
- 1 Особенности работы конденсатора
- 2 Формула ёмкости
- 3 Особенности электроцепи с емкостью и индуктивностью
- 4 Виды конденсаторов
- 5 Различные характеристики конденсаторов
- 6 Где используются конденсаторы
- 7 Видео по теме
Работа многих электрических схем строится на использовании конденсаторов. Основной особенностью этих радиоэлементов является то, что они хорошо проводят переменный ток, но не пропускают постоянный.
Особенности работы конденсатора
Радиодеталь представляет собой две пластины, к которым прикреплены металлические выводы. Пластины не соприкасаются между собой. Обычно между ними проложен слой изолятора. Постоянный электроток через конденсатор проходить не может, так как нет контакта между проводниками, но для переменного он не является препятствием.
Когда конденсатор включен в цепь переменного тока, частота напряжения меняется по закону синусоиды. Сначала электродвижущая сила растёт до своего максимума. После этого она уменьшается до нуля, а затем переходит в отрицательную область, где постепенно возрастает до амплитуды, взятой со знаком минус. Затем отрицательная ЭДС уменьшается по абсолютной величине до нуля и начинает возрастать в положительной области до наибольшего значения. Описанный цикл изменений повторяется снова и снова.
Когда конденсатор работает в цепи переменного тока, в нем циклически происходят следующие процессы:
- При возрастании амплитуды от нулевого значения до максимального происходит накопление заряда. Пластины накапливают равные по абсолютной величине, но противоположные по знаку заряды.
- При уменьшении до нуля накопление прекращается, заряд уменьшается, так как начинает стекать с пластин конденсатора.
- Когда напряжение меняется на противоположное, на пластины начинают поступать заряды, которые имеют знаки, противоположные тем, что были раньше.
- Как только ЭДС достигнет максимального отрицательного значения и станет уменьшаться по абсолютной величине, начнётся разрядка конденсатора.
Описанный здесь цикл повторится с началом возрастания ЭДС. Он будет осуществляться до тех пор, пока переменный ток не будет отключён.
Формула ёмкости
Одна из самых важных характеристик конденсатора — ёмкость. Её обозначают символом C. Несмотря на то, что контакта между пластинами нет, ток будет идти через конденсатор в цепи переменного тока то к пластинам, то от них. Это обусловлено циклически происходящими процессами зарядки и разрядки конденсатора.
Величина ёмкости характеризует способность конденсатора накапливать заряд при поступлении на обкладки определённой разности потенциалов. Ее можно найти по формуле:
Используя эту формулу наряду с законом изменения напряжения, можно узнать силу тока, возникающего в процессе зарядки или разрядки пластин конденсатора в цепи переменного тока. Но для этого необходимо сделать соответствующие преобразования.
Сначала находим напряжение, возникающее на конденсаторе в цепи переменного тока, воспользовавшись формулами для определения ёмкости и разности потенциалов. После преобразований получаем выражение:
Из него находим величину заряда:
Теперь можно получить выражение для электротока в цепи с конденсатором:
Надо сказать, что при выводе формулы для нахождения силы электрического тока были использованы следующие приемы:
- От выражения для заряда была взята производная по времени.
- Затем было выполнено эквивалентное тригонометрическое преобразование.
- Um соответствует максимальному значению амплитуды колебаний электронапряжения.
Полученное выражение позволяет узнать ток зарядки и разрядки конденсатора в любой момент. Изменения тока опережают напряжение на половину «пи». Величина тока будет максимальной при нулевом напряжении. И, наоборот, значение тока станет нулевым, когда напряжение достигнет максимума.
Для определения ёмкости может быть использована еще такая формула:
Как видно из формулы, ёмкость конденсатора увеличивается при увеличении площади пластин и уменьшении расстояния между ними.
Емкостное сопротивление — ещё одна важная характеристика конденсатора. Его можно найти по формуле:
Если взять формулу для определения амплитуды электротока:
И подставить в нее значение ХС, то получим:
После изучения данной формулы становится понятно, что емкостное и активное сопротивление из закона Ома играют одну и ту же роль. Поэтому емкостное можно считать сопротивлением конденсатора переменному электротоку.
Пример использования формул для решения простых задач по нахождению емкости конденсатора можно увидеть на изображении ниже:
Особенности электроцепи с емкостью и индуктивностью
Рассматривая ранее цепь переменного тока с включенным конденсатором, мы могли видеть, что частота колебаний электротока на конденсаторе опережает частоту колебаний электронапряжения на π/2. При включении катушки индуктивности наблюдается обратное явление, то есть, электроток отстает от электронапряжения на π/2. Его амплитуда определяется по формуле:
Знаменатель в данной формуле представляет собой выражение, используемое для определения индуктивного сопротивления:
В итоге получаем формулу для силы электротока:
Индуктивное сопротивление, как и емкостное, зависит от частоты электротока. Поэтому катушка, включенная в постоянную цепь, будет иметь нулевое индуктивное сопротивление.
Конденсатор и катушка индуктивности в цепи переменного тока образуют, так называемый, колебательный контур. Его колебания определяются по формуле:
При вынужденных колебаниях сила элетротока достигает максимума, если колебания электронапряжения и самого контура становятся равными:
Виды конденсаторов
На данный момент существует огромный выбор конденсаторов:
- Наиболее распространены радиодетали с двумя обкладками, но их может быть и больше.
- Плоский конденсатор состоит из двух пластин, между которыми расположен тонкий слой диэлектрика. Его толщина должна быть небольшой по сравнению с размерами пластин.
- В цилиндрическом конденсаторе обе пластины имеют цилиндрическую форму. Одна из них находится внутри другой. Между цилиндрами имеется равномерный тонкий промежуток, который заполнен диэлектриком.
- Существуют сферические конденсаторы, обкладки которых представляют собой сферы, одна из которых находится внутри другой.
Конденсаторы различаются в зависимости от вида диэлектрика. В частности, может использоваться не только твёрдый, но и жидкий или газообразный диэлектрик. Есть также вакуумные конденсаторы, в которых внутри между обкладками находится вакуум.
Существуют оксидно-полупроводниковые конденсаторы. Один из их электродов является анодом. Диэлектриком выступает покрывающий его оксид. Катодом является полупроводниковый слой, который наносится на слой оксида.
Для изолирующего слоя могут использоваться как органические, так и неорганические материалы. В первом случае применяются бумажные или плёночные материалы. Неорганический диэлектрик выполняется из керамики, стекла, слюды или неорганических синтетических плёнок. Есть и такие, внутри которых содержится электролитический раствор. Конденсаторы с подобным диэлектриком характеризуются относительно высокой ёмкостью.
Еще одна разновидность конденсаторов — подстроечные. Их использование предоставляет возможность изменять значение емкости в определенных пределах, чтобы деталь могла работать наиболее эффективно.
Наряду с конденсаторами общего назначения существуют и те, которые предназначены для специального применения. Примерами таких видов являются дозиметрические, высоковольтные, пусковые, импульсные, помехоподавляющие и некоторые другие радиоэлементы.
Различные характеристики конденсаторов
Основной характеристикой конденсатора является ёмкость. Но при выборе необходимо учитывать и другие.
Для каждого конденсатора существует номинальное напряжение. Если эксплуатация детали будет осуществляться исключительно при таком значении, производитель гарантирует качественную работу в течение всего срока службы.
При увеличении подаваемого на пластины напряжения заряд будет увеличиваться. Если разность потенциалов станет слишком большой, произойдёт пробой радиодетали. В результате между обкладками пройдёт искра, а сам конденсатор станет неисправной. Конденсатор в цепи переменного тока необходимо эксплуатировать в строго заданных параметрах. Иначе срок его эксплуатации существенно сокращается.
Ещё одна характеристика — удельная ёмкость. Она равна отношению ёмкости и массы используемого диэлектрика. С её повышением улучшаются характеристики, но возрастает вероятность пробоя.
В формуле для определения ёмкости используется понятие диэлектрической проницаемости диэлектрика, который находится между пластинами. Эта характеристика определяет то, насколько сильно данное вещество ослабляет влияние электрического поля между обкладками.
В диэлектриках электроны сильно привязаны к ядрам атомов, из-за чего они не перемещаются под действием электрического поля и не образуют электрический ток. Однако при воздействии электрического поля осуществляется поляризация атомов за счет смещения электронов внутри них. Следствием этого является ослабление электрического поля. Его величина зависит от того, какое вещество используется в качестве диэлектрика. Возмущение электрического поля, создаваемое диэлектриком, ослабляет то, которое было приложено к пластинам, и препятствует притоку заряда к пластинам.
Где используются конденсаторы
Радиодетали этого вида находят применение в разных сферах деятельности современного человека:
- Конденсатор и катушка индуктивности в цепи переменного тока образуют колебательный контур, его используют во многих устройствах.
- Конденсаторы меняют свои характеристики в зависимости от температуры или влажности окружающей среды, поэтому применяются в самых разных измерительных приборах.
- Еще одна сфера применения— блоки питания.
- Используются в цепях с преобразователями переменного тока в постоянный.
- Применяются в частотных фильтрах.
- Без конденсатора трудно представить усилитель.
- Конденсатор является важным элементом для процессоров и других микросхем.
Здесь приведены только некоторые варианты использования. На самом деле их гораздо больше.
Видео по теме
Преподаватель который помогает студентам и школьникам в учёбе.
Конденсатор в цепях переменного тока – формулы и определение с примерами
Конденсатор в цепях переменного тока:
Рассмотрим конденсатор емкостью С в цепи переменного тока. Заряд конденсатора q(t) = CU(t) изменяется с течением времени вследствие изменения напряжения на нем. Если напряжение в цепи переменного тока
Согласно определению мгновенное значение силы тока в цепи равно производной заряда по времени, т. е. скорости изменения заряда:
Следовательно, колебания силы тока опережают по фазе колебания напряжения на угол 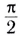
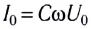
Таким образом, для амплитудных значений переменного тока и напряжения закон Ома можем записать в виде
Величину 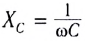
обратно пропорционально емкости конденсатора и
цепи
Для действующих значений напряжения и тока, так же как и для амплитудных значений, выполняется закон Ома:
В цепи постоянного тока 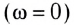
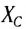
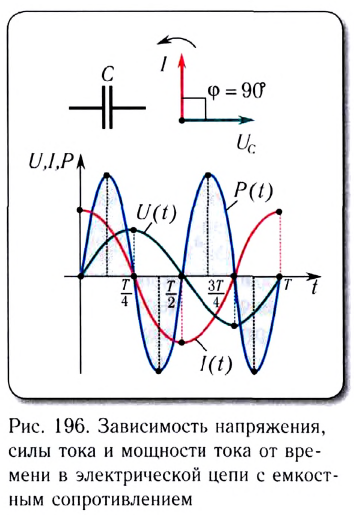
Так же как и для цепи с катушкой индуктивности, для цепи с конденсатором закон Ома не применим для мгновенных значений силы тока и напряжения, поскольку они не совпадают по фазе (см. рис. 196).
Мгновенная мощность в цепи переменного тока, содержащей конденсатор, определяется по формуле
Как и в случае с катушкой индуктивности, средняя за период мощность равна
нулю:
В первой и третьей четвертях периода конденсатор заряжается, превращая энергию источника в энергию электростатического поля конденсатора 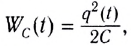
Можно сказать, что в этой цепи происходит без потерь периодический обмен энергией между «генератором» и конденсатором. По этой причине (как и в случае с катушкой индуктивности) емкостное сопротивление называют реактивным.
- Электрический ток в различных средах
- Электромагнитная индукция в физике
- Правило Ленца для электромагнитной индукции
- Магнитные свойства вещества
- Постоянный электрический ток
- Законы постоянного тока
- Переменный электрический ток
- Катушка индуктивности в цепях переменного тока
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
В чем измеряется емкость конденсатора
Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.
Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме.
Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10-12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.
Формула энергии конденсатора
С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU2/2.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Формула тока утечки конденсатора
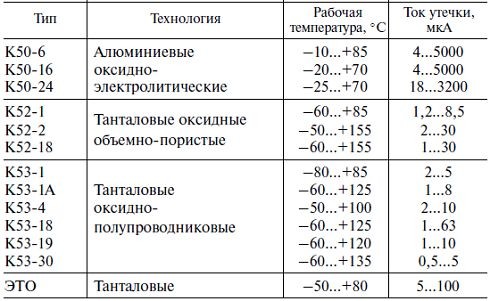
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.
Основная формула для расчета выглядит следующим образом: Iут = U/Rd, где Iут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а Rd – сопротивление изоляции.