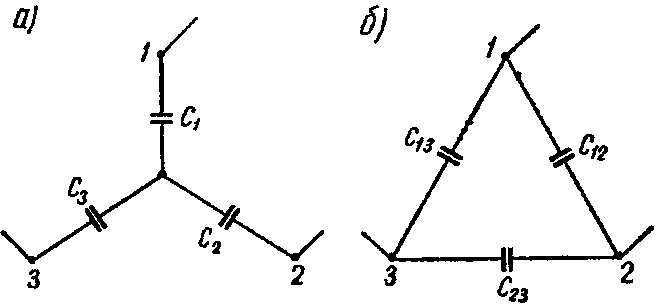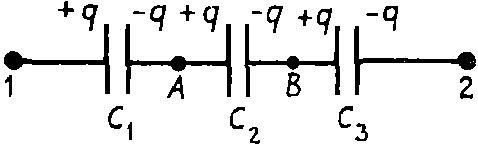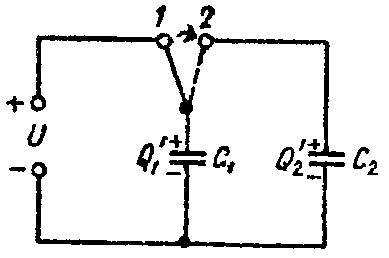Как найти конденсатор в электротехнике

Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами

Расчет электрической цепи постоянного тока с конденсаторами

Расчет электрической цепи постоянного тока с конденсаторами

Основные положения и соотношения

1. Общее выражение емкости конденсатора

C= Q U .

2. Емкость плоского конденсатора

C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,

здесь

S — поверхность каждой пластины конденсатора;

d — расстояние между ними;

ε_a = ε_r·ε₀ — абсолютная диэлектрическая проницаемость среды;

ε_r — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);

ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12    Ф м  – электрическая постоянная.

3. При параллельном соединении конденсаторов С₁, С₂, …, С_n эквивалентная емкость равна

C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .

4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:

C= C 1 ⋅ C 2 C 1 + C 2 ,

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:

U 1 =U⋅ C 2 C 1 + C 2 ;    U 2 =U⋅ C 1 C 1 + C 2 .

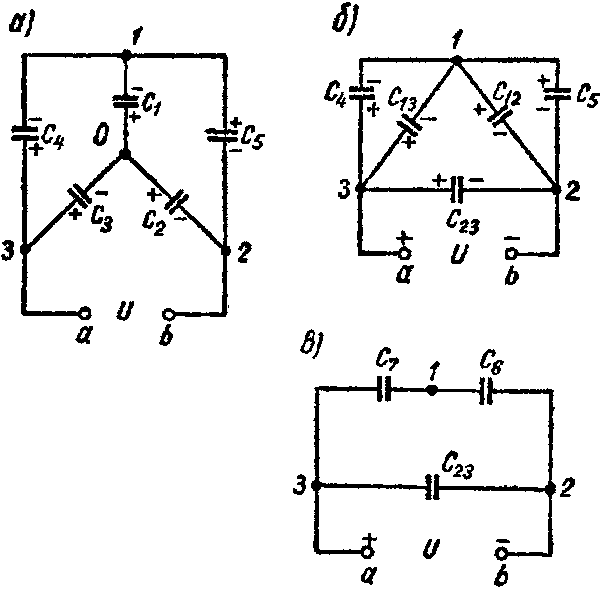
5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)

Рис. 0

осуществляется по формулам:

Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ;   C 13 = C 1 ⋅ C 3 ΣC ;   C 23 = C 2 ⋅ C 3 ΣC , где          ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .

6. Энергия электростатического поля конденсатора:

W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .

7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:

1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:

ΣQ=Σ Q ′ .

2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:

∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .

Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.

Решение задач на расчет электрической цепи постоянного тока с конденсаторами

Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).

Рис. 1

Решение

На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U₁₂, то на левую пластину конденсатора С₁ перейдет заряд +q, на правую пластину конденсатора С₃ заряд –q.

Вследствие электризации через влияние правая пластина конденсатора С₁ будет иметь заряд –q, а так как пластины конденсаторов С₁ и С₂ соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C₂ будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.

Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.

Разность потенциалов U₁₂ = φ₁ — φ₂ складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов

U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .

Воспользовавшись формулой напряжения на конденсаторе

U= q C ,

запишем

q C = q C 1 + q C 2 + q C 3 .

Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов

1 C = 1 C 1 + 1 C 2 + 1 C 3 .

В общем случае эквивалентная емкость при последовательном соединении конденсаторов

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

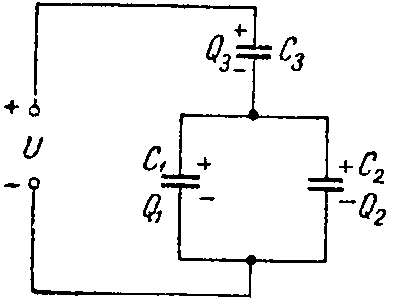
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.

Рис. 2

Емкости конденсаторов: C₁ =50 мкФ; C₂ =150 мкФ; C₃ =300 мкФ.

Решение

Эквивалентная емкость конденсаторов C₁ и C₂, соединенных параллельно

C₁₂ = C₁ + C₂ = 200 мкФ,

эквивалентная емкость всей цепи равна

C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120  мкФ.

Заряд на эквивалентной емкости

Q = C·U = 120·10^–6·240 = 288·10^–4 Кл.

Той же величине равен заряд Q₃ на конденсаторе C₃, т.е. Q₃ = Q = 288·10^–4 Кл; напряжение на этом конденсаторе

U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96  В.

Напряжение на конденсаторах C₁ и C₂ равно

U₁ = U₂ = U — U₃ = 240 — 96 = 144 В.

их заряды имеют следующие значения

Q₁ = C₁·U₁ = 50·10^–6·144 = 72·10^–4 Кл;

Q₂ = C₂·U₂ = 150·10^–6·144 = 216·10^–4 Кл.

Энергии электростатического поля конденсаторов равны

W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52  Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56  Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38  Дж.

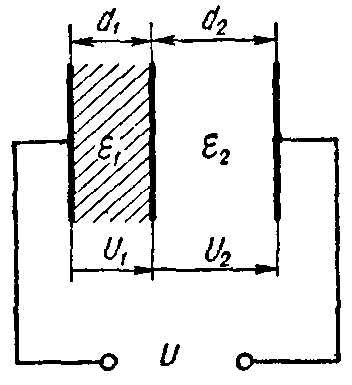
Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см², имеет диэлектрик, состоящий из слюды (ε_r1 = 6) толщиною d₁ = 0,3 мм и стекла (ε_r2 = 7) толщиною d₂ =0,4 мм.

Пробивные напряженности слюды и стекла соответственно равны E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

Рис. 3

Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.

Решение

Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов

C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .

Подставляя сюда числовые значения, предварительно заменив ε_a1 = ε_r1·ε₀ и ε_a2 = ε_r2·ε₀, получим

C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12   Ф.

Обозначим общее напряжение, подключаемое к слоистому конденсатору, через U_пр, при этом заряд конденсатора будет равен

Q = C·U_пр.

Напряжения на каждом слое будут равны

U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .

Напряженности электростатического поля в каждом слое

E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .

Здесь U’_np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U”_np — общее напряжение, при котором происходит пробой второго слоя.

Из последнего выражения находим

U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5  кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0  кВ.

Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное

27,0 кВ / 2 = 13,5 кВ.

Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d₁ = 1 см друг от друга. Площадь обкладок S = 50 см². Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.

Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d₂ = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.

Решение

Энергия заряженного плоского конденсатора равна

W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,

где С₁ — емкость до раздвижения обкладок.

Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения

Q = C₂·U₂,

где C₂ — емкость конденсатора после раздвижения обкладок, следует, что, так как C₂ = ε₀·S/d₂ стало меньше в 10 раз (d₂ увеличилось в 10 раз), то напряжение на конденсаторе U₂ увеличилось в 10 раз, т. е. U₂ = 10U.

Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d₂ будет больше первоначальной

W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .

Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.

Таким образом, надо совершить работу, равную

W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7   Дж.

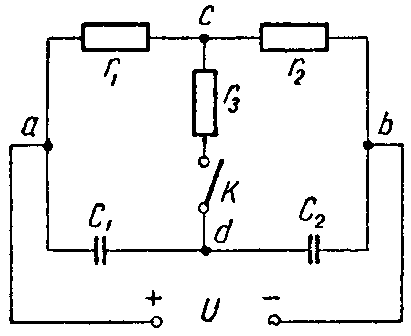
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.

Даны: C₁ = 30 мкФ; C₂ = 20 мкФ; r₁ = 100 Ом. r₂ = 400 Ом. r₃ = 600 Ом, U = 20 В.

Решение

Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям

U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8  В; U 2 =U− U 1 =20−8=12  В.

Рис. 4

Ключ К замкнут. Через сопротивления r₁ и r₂ протекает ток

I= U r 1 + r 2 = 20 500 =0,04  А,

а через сопротивление r₃ ток не протекает.

Поэтому точки c и d равнопотенциальны (φ_c = φ_d). Следовательно, напряжение между точками a и c (U_ac = φ_a — φ_c) равно напряжению между точками a и d (U_ad = φ_a — φ_d).

Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r₁

U_C1 = I·r₁ = 0,04·100 = 4 В.

Аналогично напряжение на втором конденсаторе равно

U_C2 = I·r₂ = 0,04·400 = 16 В.

Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C₁ = 5 мкФ; C₂ = 120 мкФ. Конденсатор C₂ предварительно не был заряжен.

Рис. 5

Решение

Когда рубильник находится в положении 1, то конденсатор C₁ заряжен до напряжения U и его заряд равен

Q = C₁·U = 5·10^–6·25 = 125·10^–6 Кл.

После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C₁ и C₂ (рис. 5). Обозначим эти заряды через Q’₁ и Q’₂.

На основании закона сохранения электричества имеем

Q = Q’₁ + Q’₂ = 125 10^–6 Кл. (1)

По второму закону Кирхгофа имеем

0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,

или

Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0.   (2)

Решая уравнения (1) и (2), найдем

Q’₁ = 5 10^–6 Кл; Q’₂ = 120 10^–6 Кл.

Доставка свежих и аппетитных японских суши в Новороссийске – ям ям..

Напряжение на зажимах конденсаторов станет равным

U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1  В.

Энергия обоих конденсаторов будет равна

W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6   Дж.

Подсчитаем энергию, которая была запасена в конденсаторе С₁, при его подключении к источнику электрической энергии

W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6   Дж.

Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10^–6 — 62,5·10^–6 = 1500·10^–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C₁ в конденсатор C₂ после перевода рубильника в положение 2.

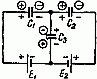
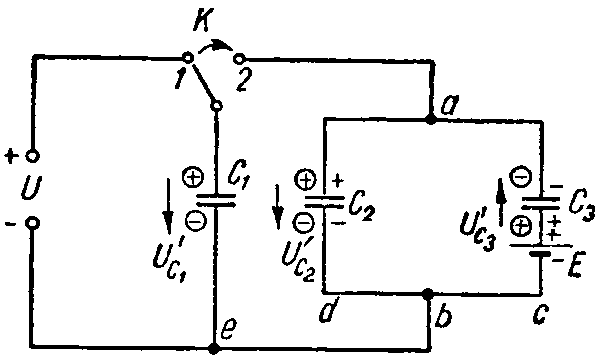
Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.

Емкости конденсаторов равны: C₁ = 10 мкФ; C₂ = 30 мкФ; C₃ = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.

Рис. 6

Решение

Рубильник находится в положении 1. Заряд конденсатора C₁ равен

Q₁ = C₁·U = 10·10^–6·30 = 0,3·10^–3 Кл.

В указанном положении рубильника конденсаторы C₂ и C₃ соединены последовательно друг с другом, поэтому их заряды равны: Q₂ = Q₃. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем

E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,

откуда

Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3   Кл.

При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’₁, Q’₂ и Q’₃. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.

Для узла a

Q’₁ + Q’₂ — Q’₃ = Q₁ + Q₂ — Q₃. (1)

Для контура 2ebda2

0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .

Для контура bcadb

E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .

Уравнения (1) — (3), после подстановки числовых значений величин, примут вид

Q’₁ + Q’₂ — Q’₃ = 0,3·10^–3; (4)

3Q’₁ — Q’₂ = 0; (5)

2Q’₂ + Q’₃ = 3·10^–3. (6)

Решая совместно уравнения (4) — (6), получим

Q’₁ = 0,33·10^–3 Кл; Q’₂ = 0,99·10^–3 Кл; Q’₃ = 1,02·10^–3 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.

Напряжения на конденсаторах после перевода рубильника будут равны

U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33  В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33  В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17  В.

Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C₁ = 5 мкФ; C₂ = 4 мкФ; C₃ = 3 мкФ; э. д. с. источников E₁ = 20 В и E₂ = 5 В.

Рис. 7

Решение

Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках

− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .

Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q₁ = 50 мкКл; Q₂ = 20 мкКл; Q₃ = –30 мкКл.

Таким образом, истинная полярность зарядов на обкладках конденсаторов C₁ и C₂ соответствует выбранной, а у конденсатора C₃ — противоположна выбранной.

Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C₁ = 2 мкФ; C₂ = 3 мкФ; C₃ = 5 мкФ; C₄ = 1 мкФ; C₅ = 2,4 мкФ.

Рис. 8

Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол.

Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.

Решение

1-й способ. Звезду емкостей C₁, C₂ и C₃ (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)

C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6  мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0  мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5  мкФ.

Емкости C₁₂ и C₅ оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость

C₆ = C₁₂ + C₅ = 3 мкФ.

Аналогично

C₇ = C₁₃ + C₄ = 2 мкФ.

Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется

C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7  мкФ.

Вычислим напряжение на каждом из конденсаторов.

На конденсаторе C₇ напряжение равно

U 7 = C 6 C 6 + C 7 ⋅U=6  В.

Таково же напряжение и на конденсаторах C₄ и C₁₃

U₄ = U₃₁ = 6 В.

Напряжение на конденсаторе C₆ равно

U₆ = U — U₇ = 4 В;

U₅ = U₁₂ = 4 В.

Вычислим заряды

Q₄ = C₄·U₄ = 6·10^–6 Кл;

Q₅ = C₅·U₅ = 9,6·10^–6 Кл;

Q₁₂ = C₁₂·U₁₂ = 6·10^–6 Кл;

Q₁₃ = C₁₃·U₃₁ = 2,4·10^–6 Кл.

По закону сохранения электричества для узла 1 схем 8, а и б имеем

–Q₄ — Q₁ + Q₅ = –Q₄ — Q₁₃ + Q₁₂ + Q₅,

отсюда

Q₁ = Q₁₃ — Q₁₂ = 3,6·10^–6 Кл,

а напряжение на конденсаторе, емкостью C₁ составляет

U 1 = Q 1 C 1 =1,8  В.

Далее находим напряжения и заряды на остальных конденсаторах

U₃₁ = U₁ + U₃,

отсюда

U₃ = U₃₁ — U₁ = 4,2 В;

Q₃ = C₃·U₃ = 21·10^–6 Кл,

также

U₁₂ = U₂ — U₁ = 4,2 В,

откуда

U₂ = U₁₂ + U₁ = 5,8 В;

Q₂ = C₂·U₂ = 17,4·10^–6 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.

2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)

для узла 1

Q₅ — Q₁ — Q₄ = 0; (1)

для узла О

Q₁ + Q₂ — Q₃ = 0; (2)

для контура О13О

Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0;  (3)

для контура О12О

Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0;  (4)

для контура a3О2b

Q 3 C 3 + Q 2 C 2 =U.  (5)

Система уравнений (1) — (5) — содержит пять неизвестных: Q₁, Q₂, Q₃, Q₄ и Q₅. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы С_ab можно найти из отношения

C ab = Q U ,

где Q = Q₃ + Q₄, или Q = Q₂ + Q₅.

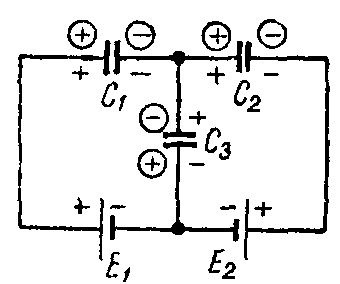
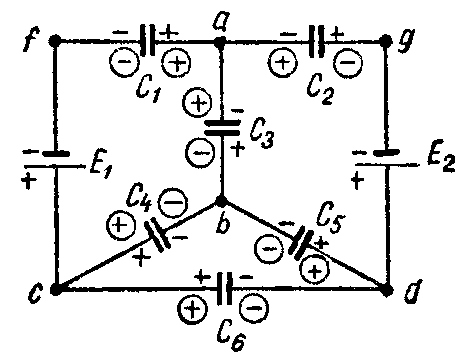
Задача 9. В схеме рис. 9 найти распределение зарядов, если E₁ = 20 В; E₂ = 7 В; C₁ = 7 мкФ; C₂ = 1 мкФ; C₃ = 3 мкФ; C₄ = 4 мкФ; C₅ = C₆ = 5 мкФ.

Рис. 9

Решение

При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:

для узла а

Q₁ + Q₂ + Q₃ = 0;

для узла b

–Q₃ — Q₄ — Q₅ = 0;

для узла c

–Q₁ + Q₄ + Q₆ = 0;

для контура afcba

E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;

ля контура gdbag

E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;

для контура cbdc

0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .

Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды

Q₁ = 35 мкКл; Q₂ = –5 мкКл; Q₃ = –30 мкКл;

Q₄ = 20 мкКл; Q₅ = 10 мкКл; Q₆ = 15 мкКл.

Таким образом, истинные знаки зарядов Q₁, Q₄, Q₅ и Q₆ соответствуют выбранным, а знаки Q₂ и Q₃ противоположны выбранным.

Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.

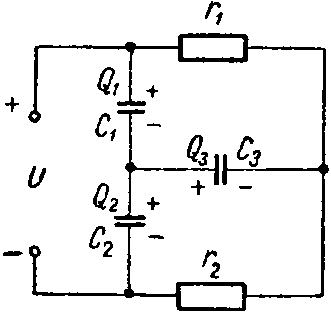
Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C₁ = 6 мкФ; C₂ = 2 мкФ; C₃ = 3 мкФ; r₁ = 500 Ом; r₂ = 400 Ом; U = 45 В.

Рис. 10

Решение

Через сопротивления протекает ток

I= U r 1 + r 2 =0,05  А.

Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:

− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,

или

Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .

Решив эту систему уравнений, найдем, что

Q₁ = 90 мкКл; Q₂ = 60 мкКл; Q₃ = 30 мкКл.

---

последовательное соединение конденсаторов,
параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами

Комментарии

Что такое конденсатор

Конденсатор или как в народе говорят — «кондер», образуются от латинского «condensatus», что означает как «уплотненный, сгущенный». Он представляет из себя пассивный радиоэлемент, который обладает таким свойством, как сохранение электрического заряда на своих обкладках, если, конечно, перед этим его зарядить каким-нибудь источником питания.

Грубо говоря, конденсатор можно рассматривать как батарейку или аккумулятор электрической энергии. Но вся разница в том, что аккумулятор или батарейка имеют в своем составе источник ЭДС, тогда как конденсатор лишен этого внутреннего источника.

Из чего состоит конденсатор

Любой конденсатор состоит из двух или более металлических обкладок, которые не соприкасаются друг с другом. Для более полного понимания, как все это устроено в конденсаторе, давайте представим себе блин.

намажем его сгущенкой

 и сверху положим точно такой же блин

Должно выполняться условие: эти два блина не должны прикасаться  друг  с другом. То есть верхний блин должен лежать на сгущенке и не прикасаться с нижним блином. Тут, думаю, все понятно. Перед вами типичный «блинный конденсатор» :-). Вот таким образом устроены все конденсаторы, только вместо блинов используются тонкие металлические пластины, а вместо сгущенки различный диэлектрик. В качестве диэлектрика может быть воздух, бумага, электролит, слюда, керамика, и так далее. К каждой металлической пластине подсоединены проводки — это выводы конденсатора.

Схематически все это выглядит примерно вот так.

Как вы могли заметить, из-за диэлектрика конденсатор не может проводить ток. Но это относиться только к постоянному току. Переменный ток конденсатор пропускает через себя без проблем с небольшим сопротивлением, номинал которого зависит от частоты тока и емкости самого конденсатора.

Емкость конденсатора

Электрические заряды

Как вы знаете, существует два типа зарядов: положительный заряд и отрицательный заряд. Ну и все как обычно, одноименные заряды отталкивается, а разноименные  — притягиваются. Физика седьмой класс).

Давайте еще раз рассмотрим простую модель конденсатора.

Если мы соединим наш конденсатор с каким-нибудь источником питания постоянного тока, то мы его зарядим. В этот момент положительные заряды, которые идут от плюса источника питания, осядут на одной пластине, а отрицательные заряды с минуса источника питания — на другой.

Самое интересное то, что количество положительных зарядов будет равняться количеству отрицательных зарядов.

Даже если мы отсоединим источник питания постоянного тока, то у нас конденсатор так и останется заряженным.

Почему так происходит?

Во-первых, заряду некуда течь. Хотя с течением времени он все равно будет разряжаться. Это  зависит от материала диэлектрика.

Во-вторых, происходит взаимодействие зарядов. Положительные заряды притягиваются к отрицательным, но они не могут соединиться с друг другом, так как им мешает диэлектрик, который, как вы знаете, не пропускает электрический ток. В это время между обкладками конденсатора возникает электрическое поле, которое как раз и запасает энергию конденсатора.

Когда конденсатор заряжается, электрическое поле между обкладками становится сильнее. Соответственно, когда конденсатор разряжается, электрическое поле слабеет. Но как много заряда мы можем «впихнуть» в конденсатор? Вот здесь и применяется такое понятие, как емкость конденсатора.

Что такое емкость

Но ведь емкость может быть не только у конденсатора. Например, емкость бутылки 1 литр, или емкость бензобака — 100 литров и так далее. Мы ведь не можем впихнуть в бутылку емкость в 1 литр больше, чем рассчитана эта бутылка, так ведь? Иначе остатки жидкости просто не влезут в бутылку и будут выливаться из нее. Точно такие же дела и обстоят с конденсатором. Мы не сможем впихнуть в него заряда больше, если он не рассчитан на это. Поэтому, емкость конденсатора выражается формулой:

где

С — это емкость, Фарад

Q — количество заряда на одной из обкладок конденсатора, Кулоны

U — напряжение между пластинами, Вольты

Получается, 1 Фарад — это когда на обкладках конденсатора хранится заряд в 1 Кулон и напряжение между пластинами 1 Вольт. Емкость может принимать только положительные значения.

Значение в 1 Фарад — это слишком много. На практике в основном пользуются значениями микрофарады, нанофарады и пикофарады. Хочу вам напомнить, что приставка «микро» — это 10^-6 , «нано» — это 10^-9 , пико — это 10^-12 .

Плоский конденсатор и его емкость

Плоским конденсатором называют конденсатор, который состоит из двух одинаковых пластин, которые параллельны друг другу. Пластины могут быть разной формы. На практике чаще всего можно встретить квадратные, прямоугольные и круглые пластины. Давайте рассмотрим простой плоский квадратный конденсатор.

где

d — расстояние между пластинами конденсатора, м

S — площадь самой наименьшей пластины, м²

ε — диэлектрическая проницаемость диэлектрика между обкладками конденсатора

Готовая формула для плоского конденсатора будет выглядеть так:

где

С — емкость конденсатора, ф

ε — диэлектрическая проницаемость диэлектрика

ε₀ — диэлектрическая постоянная, ф/м

S — площадь самой наименьшей пластины, м²

d — расстояние между пластинами, м

Да, знаю, у вас сразу возникает вопрос: «А что такое диэлектрическая постоянная?» Диэлектрическая постоянная — это постоянная величина, которая нужная для вычислений в некоторых формулах электромагнетизма. Ее значение равняется 8, 854 × 10^-12 ф/м.

Диэлектрическая проницаемость — эта величина зависит от типа диэлектрика, который находится между обкладками конденсатора. Например, для воздуха и вакуума это значение равняется 1, для некоторых других веществ можете посмотреть в таблице.

Какой можно сделать вывод из этой формулы? Хотите сделать конденсатор с огромной емкостью, делайте площадь пластин как можно больше, расстояние между пластинами как можно меньше и заправляйте вместо диэлектрика дистиллированную воду.

В настоящее время конденсаторы делают из нескольких пластин в виде слоеного торта. Это примерно выглядит вот так.

В этом случае формула такого конденсатора примет вид:

где n — это количество пластин

Максимальное рабочее напряжение на конденсаторе

Все конденсаторы имеют какое-то предельное напряжение, которое можно на них подавать. Дело все в том, что может произойти пробой диэлектрика, и конденсатор выйдет из строя. Чаще всего это напряжение пишут на самом корпусе конденсатора. Например, на электролитическом конденсаторе.

В технической документации этот параметр чаще всего обозначается, как WV, что с английского Working Voltage (рабочее напряжение), или DC WV — Direct Current Working Voltage — постоянное рабочее напряжение конденсатора.

Здесь есть один нюанс, о котором часто забывают. Дело в том, что на конденсаторе написано именно на какое постоянное напряжение он рассчитан, а не переменное. Если такой конденсатор, как на рисунке выше, с максимальным рабочим напряжением в 50 Вольт вставите в цепь переменного тока с источником питания, который выдает 50 Вольт переменного тока, то ваш конденсатор взорвется. Так как 50 Вольт переменного тока — это действующее напряжение. Его максимальное значение будет 50 × √2 = 70,7 Вольт, что намного больше, чем 50 Вольт.

Ток утечки конденсатора

Дело все в том, что какой бы ни был диэлектрик, конденсатор все равно рано или поздно разрядится, так как через диэлектрик, как ни странно, все равно течет ток. Величина этого тока у разных конденсаторов тоже разная. Электролитические конденсаторы обладают самым большим током утечки.

Также ток утечки зависит от напряжения между обкладками конденсатора. Здесь уже работает закон Ома: I=U/R_{диэлектрика} . Поэтому, никогда не стоит подавать напряжение больше, чем максимально рабочее напряжение, прописанное в даташите или на самом конденсаторе.

Неполярные конденсаторы

К неполярным конденсаторам относят конденсаторы, для которых неважна полярность. Такие конденсаторы обладают симметричностью. Обозначение неполярных конденсаторов на электросхемах выглядит вот так.

Конденсаторы переменной емкости

Эти виды конденсаторов имеют воздушный диэлектрик и могут менять свою емкость под действием внешней силы, например, такой как рука человека. Ниже на фото советские типы таких переменных конденсаторов.

Современные выглядят чуточку красивее

Переменный конденсатор от подстроечного отличается лишь тем, что переменный конденсатор крутят чаще, чем подстроечный. Подстроечный крутят раз в жизни)

На схемах обозначаются так.

Слева -переменный, справа — подстроечный.

Пленочные конденсаторы

Пленочные конденсаторы являются самыми распространенными в большом семействе конденсаторов. Они названы так потому, что вместо диэлектрика здесь используется тонкая пленка, которая может состоять из полиэстера, полипропилена, поликарбоната, тефлона и много еще из чего. Такие конденсаторы идут от номинала 5 пФ и до 100 мкФ. Они могут быть сделаны по принципу бетерброда

А также по принципу рулета

Давайте рассмотрим К73-9 советский пленочный конденсатор.

Что же у него внутри? Смотрим.

Как и ожидалось, рулончик из фольги с диэлектриком-пленкой

Керамические конденсаторы

Керамические конденсаторы — это конденсаторы, которые изготавливают из керамики или фарфора, которые покрывают серебром. Берут диск квадратной или круглой формы, напыляют с с двух сторон серебро, выводят выводы и вуаля! Конденсатор готов! То есть и есть самый простой плоский конденсатор, о котором мы говорили выше в этой статье.

Хотите получишь емкость больше? Не вопрос! Складываем диски в бутерброд и увеличиваем емкость

Выглядеть керамические конденсаторы могут вот так:

SMD конденсаторы

SMD конденсаторы — это керамические конденсаторы, которые построены по принципу бутерброда.

Они используются в микроэлектронике, так как обладают крошечными размерами и удобны в плане промышленного производства с помощью роботов, которые автоматически расставляют SMD компоненты на плату.Такой тип конденсаторов вы без труда можете найти на платах своих мобильных телефонов, на материнских платах компьютеров, а также в современных гаджетах.

Полярные конденсаторы

Для полярных конденсаторов очень важно не путать выводы местами при монтаже. Плюсовая ножка должны подключаться к плюсу на схеме, а минусовая — к минусу. Обозначается полярные конденсаторы также, как и их собратья. Единственное отличие — это указание полярности такого конденсатора. Выглядеть на схемах они могут вот так.

Электролитические конденсаторы

Электролитические конденсаторы используется в электронике и электротехнике, где требуются большие значения емкости. Также повелось название «электролиты».

Строение электролитических конденсаторов очень похоже на пленочные конденсаторы, которые также собраны по принципу рулета, но с одной только разницей. Вместо диэлектрика здесь используется оксид алюминия.

Давайте разберем один из таких электролитических конденсаторов во благо науки.

Снимаем его корпус и видим тот самый рулетик

Разматываем «рулетик» и видим, что между двумя обкладками металлической фольги у нас находится бумага, пропитанная каким-то раствором.

Некоторые ошибочно полагают, что бумага — это и есть тот самый диэлектрик, хотя это в корне неверно. Как она может быть диэлектриком, если она смочена в растворе, который проводит электрический ток?

На самом же деле диэлектриком в данном случае является тончайший слой оксида алюминия, который производится электрохимическим способом еще на производстве. Все это выглядит приблизительно вот так:

Слой оксида алюминия настолько тонкий, что можно изготавливать конденсаторы бешеной емкости с малыми габаритами. Вы ведь не забыли формулу емкости для плоского конденсатора?

где d — это и есть тот самый слой оксида алюминия. Чем он тоньше, тем больше емкость.

На полярных конденсаторах часто можно увидеть вот такой значок-стрелку, которая указывает на минусовый вывод конденсатора.

То есть  в электрических схемах с постоянным током вы должны обязательно соблюдать правило: плюс на плюс, а минус на минус. Если перепутаете, то конденсатор может бахнуть.

Танталовые конденсаторы

Танталовые конденсаторы доступны как в мокром так и в сухом исполнении. Хотя, в сухом исполнении они намного более распространены. Здесь в качестве диэлектрика используется оксид тантала. Оксид тантала обладает более лучшими свойствами, по сравнению с оксидом алюминия. Если самый большой минус электролитических конденсаторов — это их большой ток утечки, то танталовые конденсаторы лишены такого недостатка. Минус танталовых конденсаторов в том, что они рассчитаны на более низкое напряжение, чем их собраться — электролиты. Танталовые конденсаторы также полярные, как и электролитические конденсаторы.

Выглядеть танталовые конденсаторы могут вот так

ну или так

Ионисторы

Есть также  особый класс конденсаторов — ионисторы. Иногда их еще называют суперконденсаторами или золотыми конденсаторами. Нет, не потому, что  там есть золото. Сам принцип работы ионистора ценее, чем золото.  Для того, чтобы получить максимальную емкость мы должны намазать «сгущенку»(диэлектрик)  тонким-тонким слоем или увеличить площадь блинов (металлических пластин). Так как без конца увеличивать слой блинов очень затратно, разработчики решили уменьшить слой диэлектрика. Так как диэлектрический слой между обкладками ионистора , то есть «слой сгущенки», составляет 5-10 нанометров, следовательно емкость ионистора достигает впечатляющих значений! Вы только представьте, какой заряд может накопить такой суперконденсатор!

Емкость таких конденсаторов может достигать до десятка фарад. Поверьте, это очень много. Ионисторы выглядят, как обычные таблетки, а  также могут выглядеть как цилиндрические конденсаторы. Для того, чтобы различить их от конденсаторов, достаточно взглянуть на емкость, которая на них указана. Если там единицы Фарад, то это однозначно ионистор!

В настоящее время ионисторы стали очень широко применяться в электронике и электротехнике. Они заменяют маленькие батарейки с малым напряжением, потому что ионистор конструктивно пока что не могут сделать на напряжение более нескольких Вольт. Но можно соединить их последовательно и набрать нужное напряжение. Но удовольствие это не дешевое :-).

Они также очень быстро заряжаются, так как их сопротивление ограничено только их выводами.  А исходя из закона Ома, чем меньше сопротивление проводника, тем большая сила тока течет по нему и следовательно тем быстрее заряжается ионистор. Заряжать и разряжать ионисторы можно почти бесконечно.

Конденсатор в цепи постоянного тока

Итак, берем блок питания постоянного напряжения и выставляем на его крокодилах напряжение 12 Вольт. Лампочку берем тоже на 12 Вольт. Теперь в разрыв цепи вставляем конденсатор.

Нет, лампочка не горит.

А  вот если исключить конденсатор из цепи и подключить напрямую к лампочке, то лампа горит.

Отсюда напрашивается вывод: постоянный ток через конденсатор не течет! То есть в цепи постоянного тока идеальный конденсатор оказывает бесконечно большое сопротивление.

Если честно, то в самый начальный момент подачи напряжения ток все-таки течет на доыли секунды. Все зависит от емкости конденсатора.

Конденсатор в цепи переменного тока

Для того, чтобы узнать, как ведет себя конденсатор в цепи переменного тока, нам надо собрать простейшую схему, которая представляет из себя делитель напряжения. Смысл опыта такой: с помощью генератора частоты мы будем менять только частоту, а амплитуду оставим неизменной. По сути красная точка нам будет показывать сигнал с генератора частоты, а желтая — сигнал на резисторе. Снимая сигнал с резистора, мы можем косвенно узнать, как ведет себя конденсатор исходя из законов делителя напряжения.

С помощью осциллографа мы будем снимать сигнал с красной и желтой точек относительно земли.

Думаю, этот генератор частоты вполне пойдет.

Для начала возьмем конденсатор на 1мкФ и резистор на 100 ом.

Далее за дело берется цифровой осциллограф OWON SDS 6062. Что такое осциллограф и с чем его едят, читаем здесь.  Будем использовать сразу два канала, то есть на одном экране будут высвечиваться сразу два сигнала. Здесь на экране уже видны наводки от сети 220 Вольт. Не стоит на это обращать внимание.

Красная осциллограмму снимаем с красной точки в цепи, а желтую — с желтой точки в цепи.

Зависимость сопротивления от частоты и сдвиг фаз

Поехали. Итак, если у нас частота нулевая, то это значит постоянный ток. Постоянный ток, как мы уже видели, конденсатор не пропускает. С этим вроде бы разобрались. Но что будет, если подать переменный ток с частотой в 100 Герц?

На дисплее осциллографа были выведены такие параметры, как частота сигнала и его амплитуда (эти параметры помечены белой стрелочкой).

F — это частота

Ma — амплитуда

Красная синусоида показывает сигнал, который выдает нам китайский генератор частоты. Желтая синусоида — это то, что мы уже получаем на нагрузке. В нашем случае нагрузкой является резистор. Ну вот, собственно, и все.

Как вы видите на осциллограмме, с генератора выходит синусоидальный сигнал с частотой в 100 Герц и амплитудой в 2 Вольта, а на резисторе напряжение всего каких-то 136 мВ.

Как вы могли заметить, амплитуда желтого сигнала стала меньше. Это говорит нам о том, что конденсатор стал пропускать переменный ток, но его сопротивление до сих пор очень большое.

Но здесь можно заметить еще одну особенность: осциллограмма напряжения на резисторе сигнала сдвинулась влево, то есть она опережает сигнал с генератора частоты, или научным языком, появляется сдвиг фаз. Опережает именно фаза, а не сам сигнал. Если бы опережал сам сигнал, то у нас бы тогда получилось, что сигнал на резисторе появлялся бы по времени раньше, чем сигнал, поданный на него через конденсатор. Получилось бы какое-те перемещение во времени :-), что конечно же, невозможно.

Сдвиг фаз — это разность между начальными фазами двух измеряемых величин. В данном случае — напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз:

Давайте увеличим частоту  на генераторе до 500 Гц

На резисторе уже получили 560 мВ. Сдвиг фаз уменьшается. Получается, что мы чуть-чуть увеличили частоту, и сопротивление конденсатора стало меньше.

Увеличиваем частоту до 1 КГц

На резисторе у нас напряжение 1 Вольт. Напряжение не резисторе растет с увеличением частоты. Это говорит о том, что сопротивление конденсатора стало еще меньше.

Ставим частоту 5 КГц

Амплитуда 1,84 Вольта и сдвиг фаз явно становится меньше

Увеличиваем до 10 КГц

Амплитуда уже почти  такая же как и на входе. Сдвиг фаз менее заметен.

Ставим 100 КГц.

Сдвига фаз почти нет. Напряжение не резисторе почти сравнялось с напряжением генератора частоты. Это говорит о том, что конденсатор почти не оказывает сопротивление на высоких частотах.

Получился парадокс. Постоянный ток конденсатор не пропускает, а вот токи высокой частоты — без проблем!

Отсюда делаем глубокомысленные выводы:

Чем больше частота, тем меньшее сопротивление конденсатор оказывает переменному току. Сдвиг фаз убывает с увеличением частоты почти до нуля. На бесконечно низких частотах его величина составляет 90 градусов или π/2.

Если построить обрезок графика, то получится типа что-то этого:

Зависимость сопротивления от номинала конденсатора

Итак, мы с вами узнали, что сопротивление конденсатора зависит от частоты. Но только ли от частоты? Давайте возьмем конденсатор емкостью в 0,1 микрофарад, то есть номиналом в 10 раз меньше, чем предыдущий и снова прогоним по  этим же частотам.

Смотрим и анализируем значения:

Внимательно сравните амплитудные значения желтого сигнала на одной и той же частоте, но с разными номиналами конденсатора. Например, на частоте в 100 Гц  и номиналом конденсатора в 1 мкФ амплитуда желтого сигнала равнялась 136 милливольт, а на этой же самой частоте амплитуда желтого сигнала, но с конденсатором в 0,1 мкФ уже была 101 милливольт (в реальности еще меньше из за помех). На частоте 500 Герц —  560 милливольт и 106 милливольт соответственно, на частоте в 1 Килогерц — 1 Вольт и 136 милливольт и так далее.

Отсюда вывод напрашивается сам собой: при уменьшении номинала конденсатора его сопротивление становится больше.

Формула сопротивления конденсатора

С помощью физико-математических преобразований физики и математики вывели формулу для расчета сопротивления конденсатора. Прошу любить и жаловать:

где, Х_С  — это сопротивление конденсатора, Ом

П — постоянная и равняется приблизительно 3,14 

F — частота, измеряется в Герцах

С — емкость,  измеряется в Фарадах

Так вот, поставьте в эту формулу частоту в  ноль Герц. Частота в ноль Герц — это и есть постоянный ток. Что получится? 1/0=бесконечность или очень большое сопротивление. Короче говоря, обрыв цепи.

Последовательное и параллельное соединение конденсаторов

При последовательном соединении  конденсаторов

Их общая емкость будет вычисляться по формуле

 а при параллельном соединении

их общая емкость будет вычисляться по формуле

Также в интернете нашел очень интересное видео по теме конденсаторов

Похожие статьи по теме «конденсатор»

ESR конденсатора

Как проверить конденсатор мультиметром

RC цепь

Электрический конденсатор (англ. capacitor) — это устройство, которое может накапливать электрический заряд и хранить его некоторое время. Конденсаторы можно найти практически в любом электронном устройстве. Они бывают разных типов и размеров.

На электрических схемах конденсаторы обозначают двумя параллельными черточками. При этом, у полярных конденсаторов около положительного электрода дополнительно ставится плюсик.

Для чего нужен конденсатор?

У этого прибора есть множество применений. Мы не будем перечислять их все, отметим лишь некоторые.

1) Фильтрация пульсаций в цепях питания. Конденсаторы часто ставят на входе и выходе преобразователей напряжения, на входе питания микросхем. В этом случае конденсаторы служат своего рода амортизаторами, которые могут сгладить неровности напряжения, подобно амортизаторам автомобиля, сглаживающим неровности дороги.

2) Времязадающие электрические цепи. Конденсаторы разной ёмкости заряжаются и разряжаются за разное время. Эту особенность используют в устройствах, где необходимо отсчитывать определенные промежутки времени. Например, с помощью резистора и конденсатора задается период и скважность импульса в микросхеме таймера 555 (урок про таймер 555).

3) Датчики прикосновения. В роли одной из обкладок конденсатора может выступить человек. Эту особенность нашего тела используют в своей работе сенсорные кнопки, тачскрины и тачпады некоторых видов.

4) Хранение данных. Конденсаторы применяются для хранения данных в оперативной памяти — ОЗУ (SRAM). Каждый модуль такой памяти содержит миллиарды отдельных конденсаторов, которые могут быть заряжены или разряжены, что интерпретируется как единица или ноль.

И это далеко не все варианты применения этого незаменимого прибора. Попробуем разобраться, как устройство конденсатора позволяет ему выполнять столько полезных функций!

Устройство простейшего конденсатора

Конденсатор состоит их двух металлических пластин — электродов, называемых также обкладками, между которыми находится тонкий слой диэлектрика.

Собственно, все конденсаторы устроены именно таким (или почти таким) образом, разве что меняется материал обкладок и диэлектрика.

Чтобы увеличить ёмкость конденсатора, не увеличивая его размеры, применяют разные хитрости. Например, если мы возьмем две обкладки в виде длинных полосок фольги, проложим между ними хотя бы тот же полиэтилен и свернем все это как рулет, то получится очень компактный прибор с большой ёмкостью. Именно так устроены плёночные конденсаторы.

Если вместо полиэтилена взять бумагу и пропитать её электролитом, то на поверхности фольги образуется тонкий слой оксида, который не проводит ток. Такой конденсатор будет называться электролитическим.

Существует много разных видов конденсаторов: бумажные, плёночные, оксидные алюминиевые и танталовые, вакуумные и т.п. В нашем уроке мы будем использовать оксидные электролитические конденсаторы из-за их большой ёмкости и доступности.

Полярные и неполярные конденсаторы

Очень важным является разделение конденсаторов на полярные и неполярные.

Приборы на основе оксидов: электролитические алюминиевые и танталовые обычно являются полярными, а значит если перепутать их полярность — они выйдут из строя. Причём этот выход из строя будет сопровождаться бурной электрохимической реакций вплоть до взрыва конденсатора.

На полярных конденсаторах всегда имеется маркировка. Как правило на электролитических конденсаторах на корпусе контрастной полосой отмечается отрицательный вывод (катод), у танталовых (в желтых прямоугольных корпусах) полоской помечается положительный вывод (анод). Если есть сомнения в маркировке, то лучше найти документацию на этот конденсатор и убедиться.

Неполярные же конденсаторы можно включать в цепь какой угодно стороной. К примеру, многослойные керамические конденсаторы — неполярные.

Ёмкость и напряжение конденсатора

Теперь обратим внимание на две важные характеристики конденсатора: ёмкость и номинальное напряжение.

Ёмкость конденсатора характеризует способность конденсатора накапливать заряд. Это как ёмкость банки, в которой хранится, к примеру, вода. Кстати, не зря одним из первых электрических конденсаторов была так называемая Лейденская банка. Она представляла собой обыкновенную стеклянную посуду, снаружи обмотанную фольгой. В банку была налита токопроводящая жидкость — электролит. Фольга и электролит играли роль обкладок, а стекло банки служило тем самым диэлектрическим барьером.

Ёмкость электрического конденсатора измеряют в фарадах. В схемах ёмкость обозначают латинской буквой C. Как правило, ёмкость классических конденсаторов варьируется от нескольких пикофарад (пФ) до нескольких тысяч микрофарад (мкФ). Ёмкость указывается на корпусе конденсатора. Если единицы не указаны — то это пикофарады. Микрофарады часто обозначают как uF — так как буква u внешне похожа на греческую букву мю, которую используют вместо приставки микро.

Существует и особый вид конденсаторов, называемых ионисторами (англ. supercapacitor), которые имеют ёмкость в несколько фарад!  Чем больше ёмкость конденсатора, тем больше энергии в нём может храниться и тем дольше он заряжается, при прочих равных условиях.

Номинальное напряжение — второй важный параметр. Это такое напряжение, при котором конденсатор будет работать весь срок службы без критичного изменения своих параметров. Нельзя применять в 12-вольтовой цепи конденсатор на 6 вольт — он быстро выйдет из строя.

Именно эти два параметра обычно наносят на поверхность корпуса конденсатора. На фотографии ниже изображён электролитический конденсатор ёмкостью 470 мкФ и номинальным напряжением 16 Вольт.

А вот на керамических конденсаторах часто указывают только ёмкость. На картинке ниже конденсатор имеет маркировку 104. Что бы это значило?

Последняя цифра в этом коде — количество нулей после двухзначного числа в начале. 104 = 10 0000 пФ = 100 нФ = 0,1 мкФ

Параллельное и последовательное подключение конденсаторов

Как и в случае резисторов, конденсаторы можно составлять в цепочки. Это бывает нужно, когда в схеме необходима какая-то конкретная ёмкость, а у вас нет такого конденсатора.

Параллельное подключение

В отличие от резисторов, при параллельном подключении конденсаторов их ёмкости складываются. Например, если нам нужно получить ёмкость 3000 мкФ, а у нас есть два конденсатора по 1000 мкФ, и 10 штук по 100 мкФ, смело ставим их параллельно и получаем: 1000*2+100*10 = 2000 + 1000 = 3000 мкФ

Последовательно подключение

При последовательном подключении конденсаторы ведут себя как резисторы, соединённые параллельно. Например, посчитаем суммарную ёмкость двух конденсаторов на 100 мкФ, соединённых последовательно:

Суммарная ёмкость Ctot = 50 мкФ.

Заряд и разряд конденсатора — RC-цепочка

Теперь разберёмся с процессами, происходящими внутри конденсатора во время заряда и разряда. Для этого рассмотрим самую простую электрическую цепь с конденсатором. С левой стороны схемы подключим источник питания. Сверху разместим ключ и резистор, а справа сам конденсатор. Участок цепи, на котором есть конденсатор и резистор называют RC-цепью.

При замыкании ключа, в такой цепи образуется электрический ток, сила которого зависит от сопротивления резистора и внутреннего сопротивления самого конденсатора. Заряженные частицы устремятся к конденсатору, но не смогут преодолеть слой диэлектрика (по крайней мере все разом). Вследствие чего, с одной стороны конденсатора накопятся отрицательно заряженные частицы, а с другой стороны — положительно заряженные. Концентрация заряженных частиц на обкладках создаст мощное электрическое поле между ними.

С течением времени, напряжение на конденсаторе растет, а сила тока падает. После завершения процесса заряда, ток в цепи упадет почти до нуля. Останется только очень маленький ток утечки, который образуется благодаря тому, что некоторым заряженным частицам всё же удается проскочить через слой диэлектрика. Напряжение, напротив, станет практически равным напряжению источника.

Когда мы отключим конденсатор от источника питания, этот самый ток утечки постепенно разрядит конденсатор. Эта особенность электрических конденсаторов не даёт нам сделать из них контейнер для длительного хранения энергии. Хотя частично эту проблему решают ионисторы.

Резистор и время заряда конденсатора

Зачем в цепи нужен резистор? Что на мешает подключить его напрямую к источнику? Тому есть две причины.

Резистор ограничивает ток, протекающий через конденсатор. Чем меньше заряженных частиц за единицу времени прибывает в конденсатор, тем больше времени для заряда ему потребуется.

Конденсатор заряжается и разряжается по экспоненциальному закону. Зная это, мы можем легко рассчитать время заряда/разряда в зависимости от его ёмкости и от сопротивления резистора.

По картинке можно понять, что за время T конденсатор заряжается на 63,2%. А вот за время 3T уже на 95%. Время T здесь равно произведению ёмкости конденсатора C на сопротивление R, последовательно соединенного резистора:

Например, у нас есть конденсатор ёмкостью 100 мкФ, соединенный с резистором 1 кОм. Посчитаем за сколько секунд он зарядится хотя бы до 95%:

Теперь умножаем это на 3 и получаем 3T = 0,3 секунды — за такое время конденсатор почти полностью будет заряжен.

Таким образом, меняя ёмкость конденсатора и резистора мы можем управлять временем его заряда, что нам ещё пригодится в будущем.

Вторая важная причина, по которой в цепи присутствует резистор — защита источника питания. Дело в том, что разряженные конденсаторы имеют очень низкое внутреннее сопротивление, которое составляет доли Ома. По сути, их можно рассматривать как обычные проводники. А что будет, если замкнуть выводы питания проводником? Будет короткое замыкание! Такой режим работы цепи является аварийным для источника питания, и его нужно всячески избегать.

Плавное выключение светодиода при помощи конденсатора

Проведем небольшой опыт. Для этого соберем на макетной плате цепь с кнопкой, конденсатором и светодиодом. В качестве источника питания используем контакты питания Ардуино Уно.

Принципиальная схема

Внешний вид макета

Подключим Ардуино  к питанию. Затем, нажмем кнопку и светодиод практически мгновенно загорится. Отпустим кнопку — светодиод медленно начнет гаснуть. Почему так происходит?

Сразу после подключения нашей схемы к источнику питания, в ней начинают происходит интересные процессы.

Как уже говорилось ранее, пока конденсатор пустой, ток через него максимален. Следовательно, конденсатор начинает стремительно набирать заряд. При этом светодиоду, который подключен параллельно, ничего не достается 🙁 Напряжение на нем близко к нулю.

С течением времени конденсатор насыщается, благодаря чему ток начинает постепенно переходить в параллельную цепь — через светодиод. Напряжение на светодиоде начинает расти. Наступает момент, когда напряжение на светодиоде принимает критическое значение (для красного светодиода около 1,8 В), при котором он стремительно отбирает остатки тока у конденсатора и вспыхивает!

Когда мы отпускаем кнопку, ситуация становится гораздо проще. Конденсатор становится источником питания для светодиода с резистором. Светодиод начинает медленно высасывать заряд из конденсатора, пока тот не разрядится. Тут мы и наблюдаем медленно угасание.

Меняя сопротивление R1, мы можем влиять на скорость вспыхивания светодиода. Однако, следует учитывать, что увеличивая R1 мы будем снижать ток в цепи, тем самым уменьшая максимальный заряд конденсатора и яркость светодиода.

Увеличивая C1, мы получим более длительное время работы светодиода после выключения источника. Это как поставить более ёмкую батарейку.

Наконец, меняя R2 можно регулировать яркость светодиода, и соответственно, время его работы. Ведь чем меньше тока мы забираем из конденсатора, тем на большее время его хватит.

К размышлению

Итак, мы познакомились с конденсатором — интересным и порой опасным жителем любой электронной платы. В следующих уроках уделим внимание резистору и индуктивности, а также более сложному их собрату — транзистору.