Как найти конечную скорость пули

В статье (Аливердиев А.А. Точный расчет дистанции выстрела в сверхзвуковом диапазоне изменения скорости движения снаряда // Актуальные проблемы теории и практики судебной экспертизы: Доклады и сообщения на международной конференции «Восток-Запад: партнерство в судебной экспертизе». — М.: РФЦСЭ, С. 97-100.) нами показано, что в сверхзвуковом диапазоне изменения скорости движения снаряда (от 340 м/с до 1000 м/с) можно точно рассчитать для ряда снарядов дистанцию выстрела в зависимости от конечной скорости снаряда и его баллистического коэффициента. В основе этих расчетов лежит предположение о том, что сила сопротивления воздуха, приходящаяся на единицу массы снаряда F(v), может быть представлена в виде (Определение расстояния выстрела: Методическое пособие для экспертов. — М.: РФЦСЭ, 1995. Вып. 1. — 154 с.) (Определение расстояния выстрела: Методическое пособие для экспертов. — М.: РФЦСЭ, 1995. Вып. 2. — 180 с.):

где:

• C — баллистический коэффициент снаряда;
• H(y) — функция плотности воздуха (для нормальных условий, при стрельбе параллельно горизонтальной плоскости H(y) = 1);
• Fc(v) — сила сопротивления воздуха, приходящаяся на единицу массы, для снаряда Сиаччи.

Логика расчетов в основывалась на том, что анализ табличных данных значений Fc(v), приведенных в (Сташенко Е.И. Способ расчета скорости снарядов (пуль) на различных расстояниях от дульного среза оружия // Экспертная техника. 1981. — Вып. 69. с. 59-77.), показывает, что изменение dFc (v) в сверхзвуковом диапазоне изменения скорости (от 340 м/с до 1000 м/с) пропорционально изменению скорости dv. Поэтому функциональная зависимость Fc(v) в указанном диапазоне изменения скорости — прямолинейная, вследствие чего ее можно представить в виде:

где:

• kc = 0,3625 с^-1, Bc = 258 м/с — постоянные.

Данные константы имеют следующий физико-математический смысл:

• kc — тангенс угла наклона прямой относительно оси скоростей;
• Bc — точка пересечения этой прямой с данной осью.

Экспериментальные и рассчитанные по формуле (2) значения Fc(v) даны в табл. 1. Как видно из приведенных данных, относительная погрешность расчетных и экспериментальных данных не превышает 0,7%. Если учесть, что в экспериментальных исследованиях погрешность измерения Fc(v) не может быть меньше 1%, то можно считать, что расчетные и экспериментальные данные практически совпадают.

Прямолинейность функции Fc(v) обусловлена физическим процессом поглощения энергии движущегося снаряда средой (воздухом) посредством звуковой волны, поэтому следует ожидать, что аналогичные зависимости (в этом диапазоне изменение скорости)

будут иметь место и для других (отличающихся между собой геометрической формой, размерами и массой) снарядов:

Из сравнения формул (2) и (3) следует, что условие (1) будет выполняться только для тех снарядов, для которых константа B = Bc = 258 м/с. В случае же неравенства констант B и Bc баллистический коэффициент С (отношение F(v) к Fс(v) при H(y) = const зависит от скорости) является функцией скорости. Поэтому уравнение (2) (при равенстве B = Bc = 258 м/с) является только частным случаем уравнения (3).

Сила сопротивления среды существенно зависит от геометрической формы движущегося в ней тела, то есть от констант k и В. В статье  нами рассмотрено движение двух остроконечных пуль: от промежуточного патрона, выстреленной из 7,62-мм самозарядного карабина Симонова, и от винтовочного патрона, выстреленной из 7,62-мм станкового пулемета конструкции Горюнова. Для этих пуль B = Bс = 258 м/с. Поэтому, в общем случае, необходимо рассмотреть движение пули, геометрическая форма которой отличается от остроконечной формы. С точки зрения судебной баллистики на сегодняшний день наибольший интерес представляет собой движение пули МЖВ13 от промежуточного патрона М74, выстреленной из 5,45-мм автомата Калашникова АК-74.

Поэтому нами были поставлены следующие задачи:

• рассмотреть общий случай движения снаряда в сверхзвуковом диапазоне изменения скорости;
• в качестве конкретного примера рассмотреть движение пули МЖВ13 от промежуточного патрона М74, выстреленной из 5,45-мм автомата Калашникова АК- С74У (АКС74У Н2).

Полагая, что функциональную зависимость F(v) можно представить в виде (3), рассчитаем дистанцию выстрела из энергетических соображений. Первоначально отметим, что во время полета из-за наличия силы тяжести снаряд притягивается к земле. Поэтому траектория полета снаряда всегда баллистическая. Однако при сравнительно коротких дистанциях выстрела (малом промежутке времени полета снаряда) сила тяжести несущественно влияет на движение снаряда, вследствие чего траектория полета практически прямолинейная. В этом случае силу тяжести можно не учитывать. Критерий необходимости учета силы тяжести нами будет дан ниже.

С учетом сделанного замечания допустим, что снаряд движется по прямолинейной траектории, параллельной горизонтальной плоскости (угол бросания равен нулю, H(y)=1). Из закона сохранения энергии следует, что энергия, необходимая на преодоление силы сопротивления среды (воздуха), тратится за счет уменьшения ки-нетической энергии движущегося снаряда, при этом сила сопротивления среды, при-ходящаяся на единицу массы снаряда F(v), численно равна ускорению торможения снаряда. Так как работа по перемещению снаряда массой m на величину dx должна быть равна изменению кинетической энергии данного снаряда, то закон сохранения энергии в дифференциальной форме запишется в виде:

Подставляя значение F(v) в (4) и проводя разделение переменных, получим интегральное уравнение:

Решая уравнение (5), получим значение дистанции выстрела, как функцию от начальной и конечной скорости снаряда:

Следует отметить, что решение (6) уравнения (5) — точное. Уравнение (6) получено из закона сохранения энергии. Поэтому проблема определения дистанции выстрела для плоской (зависящей от одной координаты) траектории движения снаряда в сверхзвуковом диапазоне изменения скоростей, при выполнении условия (3), разрешена полностью, а необходимость в использовании приближенных, ко всему еще и громоздких, расчетных методов, рекомендованных в, отпадает. Точность расчета дистанции выстрела по формуле (6) зависит только от точности определения констант В и k для данного вида снаряда, а также его начальной и конечной скорости.

Зная явный вид функции, описывающей силу сопротивления воздуха, можно рассчитать время пролета снаряда. Из закона сохранения количества движения (импульса силы), записанного в дифференциальной форме, следует:

Подставляя значение F(v) в (7) и проводя разделение переменных, получим интегральное уравнение:

Решая уравнение (8), получим значение времени пролета снаряда, как функцию от значений начальной и конечной скорости:

Решение (9) уравнения (8) точное. Уравнение (9) получено из закона сохранения количества движения. Следовательно, точность расчетного времени пролета снаряда зависит только от точности измерения начальной и конечной его скорости, разумеется, при выполнении условия (3).

Из формулы (9) следует, что конечная скорость снаряда связана со временем его пролета соотношением:

Следовательно, для расчета значений конечной скорости и дистанции выстрела достаточно знать начальную скорость снаряда и время его пролета. Формула (6), с учетом сделанного замечания, может быть преобразована к виду:

За время t, как указывалось выше, вследствие силы тяжести снаряд отклонится к Земле в вертикальном направлении на величину h = gt²/2. Поэтому, строго говоря, угол бросания Θ не может быть равен нулю. Однако расчеты по формулам (6), (9), (10) и (11) можно считать достоверными, если учет силы тяжести не превышает экспериментального разброса скорости снаряда (по крайней мере, не превышает 0,1% от скорости снаряда), что во всем сверхзвуковом диапазоне изменения скорости всегда будет выполнено, если

где максимально возможное значение угла Θ равно величине:

Расчетные скорости в этом случае определены с точностью не менее 99,9%.

Для практического применения формул (6) — (11) необходимо знать точные значения констант k и В. Данные константы в общем случае не могут быть рассчитаны теоретически. Однако их можно найти путем сравнения теории и эксперимента. В частности, зная начальную скорость снаряда, два промежутка времени и (соответствующие им) значения конечных скоростей, константу В можно определить, например, из формулы (9) путем деления одного промежутка времени на другой. В этом случае константа k исключается и имеет место логарифмическое уравнение с одним неизвестным — константой В. Далее, подставляя значение константы В в формулу (9), можно найти константу k.

В качестве конкретного примера приведем значения констант B и k для пули МЖВ13 от промежуточного патрона М74, выстреленной из 5,45-мм автомата Калашникова АКС-74У: B = 180 м/с, k = 1,17 с^-1. Значения данных констант получены в результате анализа экспериментальных данных, приведенных в (Руководство по 5,45-мм автомату Калашникова Укороченному АКС74У (АКС74У Н2). — М.: Воен. издат., 1992. — 160с.). Время пролета пули экспериментально измерялось с точностью до 0,01 с. Поэтому с целью уменьшения относительной погрешности измерения для промежутка времени, соответствующего 100 м дистанции выстрела, данное время пролета при оценке констант полагалось равным 0,145 с, а не 0,15 с. Значения данных констант оценивались по времени пролета и дистанции выстрела, то есть по формулам (6) и (9). Расчетные и экспериментальные данные приведены в табл. 2. Как видно из таблицы, расчетные и экспериментальные данные по крайней мере находятся в удовлетворительном согласии. Следует особо подчеркнуть, что конечная скорость полета пули экспериментально измеряется с точностью только до третьей значащей цифры, поэтому и дистанция выстрела рассчитана по формуле (6) с такой же точностью. Учитывая, что относительная погрешность между расчетными и экспериментально измеренными значениями дистанции выстрела составляет менее трех процентов, можно считать, что указанные константы оценены точно.

Необходимость учета силы тяжести снаряда, то есть достоверность расчетов, можно установить по формуле (12). Для этого необходимо рассчитать значения: дистанции выстрела и времени пролета снаряда для скорости, равной величине: v = 340 м/с. Подставляя значения: начальной скорости — vo = 735м/с и конечной скорости — v = 340 м/с, в формулы (6) и (9), соответственно получим: х = 528,4 м и t = 1,06 с. Из формулы (13) следует, что угол бросания равен величине: Θ = 0,01 рад.

Подставляя значение Θ = 0,01 рад в формулу: gt sinΘ, получим 0,109 м/с, что меньше значения 0,34 м/с. Следовательно, силу тяжести в расчетах можно не учитывать.

Таким образом, расчеты (без учета силы тяжести) по формулам (10) и (11) можно считать достоверными. Расчетные значения дистанции выстрела и скорости пули в зависимости от времени пролета снаряда приведены в таблице 3. Экспериментальные данные цитируются из . Как видно из приведенных данных, расчетные и экспериментально измеренные величины дистанции выстрела и конечной скорости практически совпадают (относительная погрешность между экспериментально измеренными и расчетными величинами менее одного процента), что однозначно свидетельствует о справедливости логики изложенных рассуждений.

Таким образом, условие (3) в сверхзвуковом диапазоне изменения скорости для снарядов, выстреленных из стрелкового оружия, выполняется, что позволяет рассчитать дистанцию выстрела, при этом расчеты будут настолько точными, насколько точно известны начальная скорость снаряда, а также время пролета или же конечная скорость снаряда.

Автор:

А. А. Аливердиев — зам. начальника Дагестанской ЛСЭ Минюста России, зав. отделом криминалистических исследований, к.ф.-м.н.

Сила тяжести, направленная вниз (F g), равна сдерживающей силе сопротивления (F d) плюс плавучесть. Чистая сила, действующая на объект, равна нулю, и в результате скорость объекта остается постоянной.

Конечная скорость – это максимальная скорость, достигаемая объектом при падении через жидкость (air – самый распространенный пример). Это происходит, когда сумма силы сопротивления (F d) и плавучести равна направляемой вниз силе силы тяжести (FG), действующей на объекте. Поскольку чистая сила на объекте равна нулю, объект имеет нулевое ускорение.

В гидродинамике объект движется со своей конечной скоростью, если его скорость постоянна из-за сдерживающей силы, оказываемой жидкостью, в которой она движется.

С увеличением скорости объекта увеличивается и сила сопротивления, действующая на него, которая также зависит от вещества, через которое он проходит (например, воздуха или воды). На некоторой скорости сопротивление или сила сопротивления будут равны гравитационному притяжению объекта (плавучесть рассматривается ниже). В этот момент объект перестает ускоряться и продолжает падать с постоянной скоростью, называемой конечной скоростью (также называемой скоростью установления). Объект, движущийся вниз со скоростью, превышающей предельную (например, потому что он был брошен вниз, упал из более тонкой части атмосферы или изменил форму), будет замедляться, пока не достигнет предельной скорости. Перетаскивание зависит от области проекции, в данном случае от поперечного сечения или силуэта объекта в горизонтальной плоскости. Объект с большой площадью проецирования относительно его массы, например парашют, имеет меньшую конечную скорость, чем объект с небольшой площадью проецирования относительно его массы, например дротик. В общем, для той же формы и материала конечная скорость объекта увеличивается с размером. Это потому, что направленная вниз сила (вес) пропорциональна кубу линейного размера, но сопротивление воздуха приблизительно пропорционально площади поперечного сечения, которая увеличивается только как квадрат линейного размера. Для очень маленьких объектов, таких как пыль и туман, конечная скорость легко преодолевается конвекционными потоками, которые не позволяют им достигать земли, и, следовательно, они остаются в воздухе в течение неопределенного времени. Загрязнение воздуха и туман являются примерами этого.

Содержание

• 1 Примеры
• 2 Физика
  • 2.1 Вывод для конечной скорости
  • 2.2 Конечная скорость в ползущем потоке
    • 2.2.1 Приложения
• 3 Конечная скорость при наличии плавучести force
• 4 См. также
• 5 Ссылки
• 6 Внешние ссылки

Примеры

График зависимости скорости парашютиста от времени, достигающего предельной скорости.

На основе сопротивления ветра, например, Предельная скорость парашютиста в положении «живот к земле» (т. е. лицом вниз) свободное падение составляет около 195 км / ч (120 миль / ч ; 54 м / с ). Эта скорость является асимптотическим предельным значением скорости, и силы, действующие на тело, уравновешивают друг друга все более и более по мере приближения к конечной скорости. В этом примере скорость 50% от скорости терминала достигается всего за 3 секунды, в то время как для достижения 90% требуется 8 секунд, для достижения 99% – 15 секунд и так далее.

Более высокая скорость может быть достигнута, если парашютист тянет свои конечности (см. Также свободный полет ). В этом случае конечная скорость увеличивается примерно до 320 км / ч (200 миль / ч или 90 м / с), что почти равно конечной скорости сапсана, ныряющего на свою добычу. Такая же конечная скорость достигается для типичной пули .30-06, падающей вниз – когда она возвращается на землю после выстрела вверх или падения с башни – согласно исследованию артиллерийского вооружения армии США 1920 года.

Соревнования парашютисты-парашютисты летают вниз головой и могут развивать скорость 530 км / ч (330 миль / ч; 150 м / с); текущий рекорд принадлежит Феликсу Баумгартнеру, который прыгнул с высоты 128 100 футов (39 000 м) и достиг 1357,6 км / ч (840 миль / ч; 380 м / с), хотя он достиг этой скорости на большой высоте. где плотность воздуха намного ниже, чем у поверхности Земли, поэтому создается низкая сила сопротивления.

Биолог Дж. Б. С. Холдейн писал:

Для мыши и любого более мелкого животного [гравитация] практически не представляет опасности. Вы можете бросить мышь в шахту длиной в тысячу ярдов; и, достигнув дна, он получает легкий шок и уходит. Убита крыса, сломан человек, брызжет конь. Поскольку сопротивление, оказываемое движению воздуха, пропорционально поверхности движущегося объекта.

Физика

Используя математические термины, конечная скорость – без учета эффектов плавучести – определяется выражением

V t = 2 мг ρ AC d { displaystyle V_ {t} = { sqrt { frac {2mg} { rho AC_ {d}}}}}

где

В действительности объект приближается к своей конечной скорости асимптотически.

Эффекты плавучести из-за направленной вверх силы, действующей на объект окружающей жидкостью, могут быть приняты во внимание используя Arc Принцип Химеда : масса m { displaystyle m}должна быть уменьшена на массу вытесненной жидкости ρ V { displaystyle rho V}с V { displaystyle V}объемом объекта. Поэтому вместо m { displaystyle m}используйте приведенную массу mr = m – ρ V { displaystyle m_ {r} = m- rho V}в этой и последующих формулах.

Конечная скорость объекта изменяется из-за свойств жидкости, массы объекта и его проекции поперечного сечения площадь поверхности.

Плотность воздуха увеличивается с уменьшением высоты, примерно на 1 % на 80 метров (260 футов) (см. барометрическую формулу ). Для объектов, падающих через атмосферу, на каждые 160 метров (520 футов) падения конечная скорость уменьшается на 1%. После достижения локальной конечной скорости, продолжая падение, скорость уменьшается, чтобы измениться с локальной конечной скоростью.

Вывод для предельной скорости

Используя математические термины, определяя вниз как положительное, результирующая сила, действующая на объект, падающий вблизи поверхности Земли, равна (согласно уравнению сопротивления ):

F net = ma = mg – 1 2 ρ v 2 AC d, { displaystyle F_ {net} = ma = mg- {1 over 2} rho v ^ {2} AC_ {d },}

с v (t) скорость объекта как функция времени t.

В равновесии, чистая сила равна нулю (F net = 0), и скорость становится конечной скоростью. t → ∞ v (t) = V t:

мг – 1 2 ρ V t 2 AC d = 0. { displaystyle mg- {1 over 2} rho V_ {t} ^ {2} AC_ {d} = 0.}

Решение для V t дает

(5) V t = 2 мг ρ AC d. { displaystyle V_ {t} = { sqrt { frac {2mg} { rho AC_ {d}}}}.}

Вывод решения для скорости v как функции времени t

Уравнение сопротивления – при условии, что ρ, g и C d являются постоянными: ma = mdvdt = mg – 1 2 ρ v 2 AC d. { displaystyle ma = m { frac { mathrm {d} v} { mathrm {d} t}} = mg – { frac {1} {2}} rho v ^ {2} AC_ {d}.} Хотя это уравнение Риккати, которое может быть решено путем сведения к линейному дифференциальному уравнению второго порядка, легче разделить переменные. Более практичная форма этого Уравнение может быть получено заменой α = ρAC d / 2mg. Деление обеих сторон на m дает d v d t = g (1 – α 2 v 2). { displaystyle { frac { mathrm {d} v} { mathrm {d} t}} = g left (1- alpha ^ {2} v ^ {2} right).} уравнение может быть преобразовано в dt = dvg (1 – α 2 v 2). { displaystyle mathrm {d} t = { frac { mathrm {d} v} {g (1- alpha ^ {2} v ^ {2})}}.} Взяв интеграл от обоих сторон дает ∫ 0 tdt ′ = 1 g ∫ 0 vdv ′ 1 – α 2 v ′ 2. { displaystyle int _ {0} ^ {t} { mathrm {d} t ^ { prime}} = {1 over g} int _ {0} ^ {v} { frac { mathrm { d} v ^ { prime}} {1- alpha ^ {2} v ^ { prime 2}}}.} После интегрирования это становится t – 0 = 1 g [ln ⁡ ( 1 + α v ′) 2 α – ln ⁡ (1 – α v ′) 2 α + C] v ′ = 0 v ′ = v = 1 g [ln ⁡ 1 + α v ′ 1 – α v ′ 2 α + C] v ‘= 0 v’ = v { displaystyle t-0 = {1 over g} left [{ ln (1+ alpha v ^ { prime}) over 2 alpha} – { гидроразрыв { ln (1- alpha v ^ { prime})} {2 alpha}} + C right] _ {v ^ { prime} = 0} ^ {v ^ { prime} = v} = {1 over g} left [{ ln { frac {1+ alpha v ^ { prime}} {1- alpha v ^ { prime}}} over 2 alpha} + C справа] _ {v ^ { prime} = 0} ^ {v ^ { prime} = v}} или в более простой форме t = 1 2 α g ln ⁡ 1 + α v 1 – α v знак равно arctanh (α v) α g, { displaystyle t = {1 over 2 alpha g} ln { frac {1+ alpha v} {1- alpha v}} = { frac { mathrm {arctanh} ( alpha v)} { alpha g}},} с arctanh функция обратного гиперболического тангенса. В качестве альтернативы 1 α tanh ⁡ (α gt) = v, { displaystyle { frac {1} { alpha}} tanh ( alpha gt) = v,} с tanh функция гиперболический тангенс. Предполагая, что g положительно (что было определено как), и подставляя обратно α, скорость v становится v = 2 m g ρ A C d tanh ⁡ (t g ρ A C d 2 m). { displaystyle v = { sqrt { frac {2mg} { rho AC_ {d}}}} tanh left (t { sqrt { frac {g rho AC_ {d}} {2m}}}) right).} Когда время стремится к бесконечности (t → ∞), гиперболический тангенс стремится к 1, в результате чего конечная скорость V t = lim t → ∞ v (t) = 2 mg ρ AC d. { displaystyle V_ {t} = lim _ {t to infty} v (t) = { sqrt { frac {2mg} { rho AC_ {d}}}}.}

Конечная скорость в ползущий поток

ползущий поток мимо сферы: линии тока, сила сопротивления F d и сила тяжести F g

Для очень медленного движения жидкости силы инерции жидкости незначительны (предположение безмассовой жидкости) по сравнению с другими силами. Такие потоки называются ползущими потоками, и условие, которое должно выполняться для потоков, которые должны быть ползучими потоками, – это число Рейнольдса, R e ≪ 1 { displaystyle Re ll 1 }. Уравнение движения для ползучего потока (упрощенное уравнение Навье – Стокса ) задается следующим образом:

∇ p = μ ∇ 2 v { displaystyle { mathbf { nabla}} p = mu nabla ^ {2} { mathbf {v}}}

где

Аналитическое решение для ползучего потока вокруг сферы был впервые дан Стокса в 1851 году. Из решения Стокса сила сопротивления, действующая на сферу, может быть получена как

(6) D = 3 π μ d V или C d = 24 R е { Displaystyle quad (6) qquad D = 3 pi mu dV qquad qquad { text {или}} qquad qquad C_ {d} = { frac {24} {Re} }}

где число Рейнольдса, R e = 1 μ ρ d V { displaystyle Re = { frac {1} { mu}} rho dV}. Выражение для силы лобового сопротивления, задаваемое уравнением (6), называется законом Стокса.

, когда значение C d { displaystyle C_ {d}}подставляется в уравнение (5), мы получаем выражение для предельной скорости сферического объекта, движущегося в условиях ползучего потока:

V t = gd 2 18 μ (ρ s – ρ), { displaystyle V_ {t} = { frac {gd ^ {2}} {18 mu}} left ( rho _ {s} – rho right),}

где ρ s { displaystyle rho _ {s}}– плотность объекта.

Приложения

Результаты ползучего потока могут применяться для изучения осаждения отложений у дна океана и падения капель влаги в атмосфере. Этот принцип также применяется в вискозиметре с падающей сферой, экспериментальном устройстве, используемом для измерения вязкости высоковязких жидкостей, например нефти, парафина, гудрона и т. Д.

Конечная скорость в присутствии выталкивающей силы

Скорость оседания W s песчинки (диаметр d, плотность 2650 кг / м) в воде при 20 ° C, вычисленная по формуле Soulsby (1997).

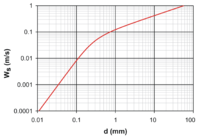
Если принять во внимание эффекты плавучести, объект, падающий через жидкость под собственным весом, может достичь предельной скорости (скорости оседания), если результирующая сила, действующая на объект, станет равной нулю. Когда достигается предельная скорость, вес объекта точно уравновешивается восходящей силой плавучести и силой сопротивления. То есть

(1) W = F b + D { displaystyle quad (1) qquad W = F_ {b} + D}

, где

Если падающий объект имеет сферическую форму, выражения для трех сил приведены ниже:

(2) W = π 6 d 3 ρ sg, (3) F б знак равно π 6 d 3 ρ г, (4) D знак равно C d 1 2 ρ V 2 A, { Displaystyle { begin {align} quad (2) qquad W = { frac { pi} { 6}} d ^ {3} rho _ {s} g, \ quad (3) qquad F_ {b} = { frac { pi} {6}} d ^ {3} rho g, \ quad (4) qquad D = C_ {d} { frac {1} {2}} rho V ^ {2} A, end {align}}}

где

Подстановка уравнений (2–4) в уравнение (1) и решение для конечной скорости, V t { displaystyle V_ {t}}, чтобы получить следующее выражение

(5) V t = 4 gd 3 C d (ρ s – ρ ρ). { displaystyle quad (5) qquad V_ {t} = { sqrt {{ frac {4gd} {3C_ {d}}} left ({ frac { rho _ {s} – rho} { rho}} right)}}.}

В уравнении (1) предполагается, что объект более плотный, чем жидкость. В противном случае знак силы сопротивления следует сделать отрицательным, поскольку объект будет двигаться вверх против силы тяжести. Примерами являются пузырьки, образующиеся на дне бокала с шампанским, и воздушные шары с гелием. Конечная скорость в таких случаях будет иметь отрицательное значение, соответствующее скорости подъема.

См. Также

• закон Стокса
• Терминальная баллистика

Ссылки

Внешние ссылки

• Конечная скорость – сайт НАСА
• Бортовое видео Space Shuttle Solid Ракетные ускорители быстро замедляются до предельной скорости при входе в более плотную атмосферу, с 2900 миль в час (3,8 Маха) в 5:15 на видео до 220 миль в час в 6:45, когда парашюты раскрываются через 90 секунд – Видео и звук НАСА, @ io9.com.

Методы определения скорости полета пули

Для
определения скорости полета пули, знание
которой необходимо для расчета
кинетической энергии, могут использоваться
различные методы и устройства.

Метод баллистического маятника

Этот
метод основывается на физическом законе
сохранения суммарного импульса системы
тел при их соударениях.

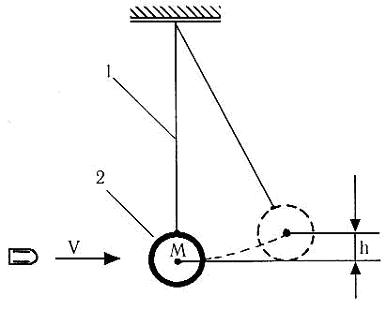
1-подвес;
2-маятник.

Баллистический
маятник представляет собой массивное
тело, укрепленное на подвесе (рис. 1).
Движущаяся пуля, попадая в неподвижный
маятник, вызывает его колебания. Зная
массу пули – m, массу маятника – М и
максимальную величину подъема центра
тяжести маятника – h, можно рассчитать
скорость пули V в момент соударения ее
с маятником по формуле:

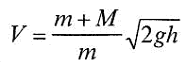
где
g =9,8м/с2 – ускорение свободного падения.

Идея
измерения скорости пуль с помощью
баллистического маятника была впервые
применена в 1707 году, однако, этот метод
до настоящего времени с успехом
применяется на практике.

Механический хронограф

Одна
из конструкций механического хронографа
представляет собой два диска, закрепленных
на одной вращающейся оси (рис. 5.9). Диски
можно изготовить, например, из плотной
бумаги и разместить на оси электромотора.
При выстреле пуля пробивает сначала
первый диск, затем второй. Время движения
пули между дисками определяют по величине
угла а, на который сместится пулевая
пробоина на втором диске относительно
пробоины на первом диске. Зная расстояние
между дисками и их скорость вращения,
скорость полета пули можно вычислить
по формуле:

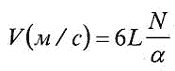
где
L – расстояние между дисками, измеренное
в метрах; N – число оборотов оси с дисками
в минуту; а – угол в градусах между
пулевыми пробоинами.

Чем
больше скорость вращения дисков, тем
выше точность измерения скорости пули.

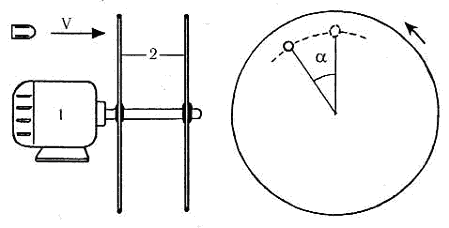
1-электромотор;
2-диски.

Электронные миллисекундомеры

Измерение
скорости полета пули с помощью электронных
миллисекундомеров основано на
непосредственном измерении времени,
за которое пуля проходит определенное
расстояние между двумя датчиками. При
пролете пули через датчики первый датчик
запускает миллисекунодомер, а второй
– останавливает.

Датчики
могут быть выполнены в различных
вариантах: .

– рамки с проволокой,
которая разрывается пулей, – тем самым
разрывается электрическая цепь
миллисекундомера;

– электромагнитные
датчики в виде соленоида, в которых
наводится ЭДС самоиндукции при прохождении
их пулей;

– оптоэлектронные датчики,
которые запускают отсчет времени при
пересечении пулей светового луча (рис.
3).

1
и 2 – рамки с блоками оптоэлектронных
датчиков.

Электронные
миллисекундомеры представляют собой
электронные схемы на основе высокоточных
генераторов и счетчиков импульсов.
Установки подобного типа снабжаются
жидкокристаллическими или газоразрядными
индикаторами, на которые выводится
время пролета или непосредственно
скорость полета пули.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

вот решил предложить тему для тех кто любит всё знать!!!!В данной статье рассмотрены основные математические зависимости позволяющие с практически значимой точностью определять основные баллистические характеристики пули на полетной траектории.
Первое, что интересует большинство охотников и просто любителей стрельбы, это как изменяется скорость пули и, соответственно, ее кинетическая энергия от расстояния до цели. Абсолютная скорость пули зависит от огромного количества внешних факторов, многие из них не поддаются строгому математическому описанию. Конечно, определяющим фактором является плотность окружающей атмосферы – воздуха (для любителей подводной охоты – воды). Математически для газа это можно записать так:
ρ = P/(RT) (1)
где ρ – плотность газа, [кг/м3],
P – абсолютное давление в газе, [Па], (среднее атмосферное давление 101,3 кПа)
R – газовая постоянная, [Дж/(кгК)], (в среднем для воздуха R=278,3 Дж/(кгК))
T – термодинамическая температура газа, [К]
(напомню, что температура по Кельвину есть температура по Цельсию плюс 273,15о, т.е. Т=273,15+оС).
Газовая постоянная R и атмосферное давление Р зависят от конкретных метеоусловий и химического состава среды, проще говоря, в эту самую минуту, когда Вы читаете этот текст плотность воздуха рядом с Вами и вашем любимом месте охоты различны. Справедливости ради надо отметить, что величины R и T сказываются на плотности воздуха мало, гораздо существенней влияние температуры. Тем не менее, этими вещами нельзя пренебрегать при особо точной стрельбе на большие расстояния. Профессионалы – снайперы подтвердят, что пристреливать точное оружие необходимо прямо на месте, а в рекомендациях (‘наставлениях’ и проч. войсковых документах) есть пункт о внесении поправок на прицеливание в зависимости от температуры воздуха. Также, температура воздуха сказывается на начальной скорости пули еще из-за того, что порох (метательные хим. вещества вообще) горят с разной скоростью при разной температуре, и, соответственно, развивают разные давления в стволе – отсюда дополнительные колебания скорости пули, но в данной статье это рассматриваться не будет.
Сила, тормозящая пулю Fc (при больших скоростях, т.е. 100..150 м/с и больше) пропорциональна скоростному напору, площади миделя пули и ее коэффициенту лобового сопротивления.

Fc= (ρV2/2)CxS (2)

В выражении (2) V – текущая скорость пули, Сx – коэффициент лобового сопротивления, S – площадь миделя пули. Запишем (2) в более удобной форме:
Fc=ξ V2 (3), где ξ=ρCxS/2

Далее можем записать, что работа силы сопротивления полету пули на расстоянии равна потери кинетической энергии (уравнение (4) в дифференциальной форме):
d(mV2/2)= -ξV2dx (4)

Преобразуем и решим это уравнение:
VdV/V2= – (ξ/m)dx
ln | V | =-ξx/(2m)+C0

Постоянную интегрирования определяем из того условия, что при нулевом пути скорость пули равна начальной V0:
ln | V | – ln | V0 | =-ξx/(2m)
ln | V/ V0 | =-ξx/(2m)

V=V0e(-ξx/(2m))
Или окончательно:
V=V0e(-xSρCx/(2m)) (5)

Уравнение (5) справедливо для любых типов пуль летящих в воздушной атмосфере со скоростями более 50..80 м/с. При выводе этого уравнения мы не учитывали вязкое трение в воздухе, ниже будет показано, что в этом нет необходимости, т.к. погрешность расчета остается незначительной с практической точки зрения. (Необходимо понимать принципиальную разницу между вязким трением и влиянием скоростного напора, для скоростей современного пневматического или огнестрельного оружия основная сила, тормозящая пулю почти строго пропорциональна скоростному напору.)
Оценим толщину пограничного слоя δ на поверхности пули при следующих условиях:
– атмосфера воздушная (ρ=1.2 кг/м3)
– температура Т=300 К (27 0С)
– вязкость μ=1,8510-6 кГсек/м2
– скорость пули V=250 м/с
– длина пули l=0.008 м
(δ/l) ~ 1/(ρUl/&#956 1/2
или:
δ ~ l /(ρUl/&#956 1/2 (6)

Из выражения (6) легко находим, что для заданных условий толщина пограничного слоя δ не превышает 7,02310-6 метра или 0.007 мм. При такой ничтожной толщине пограничного слоя говорить об эффективном торможении за счет трения не приходится. Уравнение (5) готово для практического использования.
Пример расчета:
определить скорость и кинетическую энергию пули ‘Gamo Pro Magnum’ на расстоянии 50 метров при начальной скорости 280 м/с:
Решение:
Для пули ‘Gamo Pro Magnum’ имеем площадь сечения миделя (т.е. площадь круга диаметром 4.5 мм) S=0.0000159038 м2, масса пули m=0.4810-3 кг, коэффициент лобового сопротивления Cx=0.51, плотность воздуха ρ=1.2 кг/м3, расстояние х=50 м, начальная скорость V0=280 м/с. Подставляем эти значения в выражение (5) и получаем конечную цифру V=168,7 м/с. Кинетическая энергия пули определяется как:
W=(mV2)/2

Для пули ‘Gamo Pro Magnum’ и V=168,7 м/с W=6,83 Дж. Такой кинетической энергии достаточно для охоты на животное или птицу весом не более 500..700 грамм. (Предполагается, что на килограмм массы тела объекта охоты необходимо около 10..15 Дж) Выбирайте соответствующую дистанцию стрельбы.
Для практической стрельбы также желательно знать время, за которое пуля подлетит к цели (для определения поправок при стрельбе по движущейся цели) и понижение (превышение) траектории при изменении расстояния. Решения также получаются также просто при принятых теоретических допущениях. Приведем только решение без подробных комментариев, обозначения переменных те же, что и выше, размерности всех величин в СИ.
Зависимость подлетного времени от расстояния:
dV/dt=a (a – ускорение, действующее на тело), на основании чего:
dV/dt=F/m, или d2x/dt2=F/m (7)

Сила, действующая на тело из выражения (3) Fc=ξ V2:
dV/dt= (ξ V2)/m; далее преобразуем это выражение к окончательному виду:
dV/V2= [ρSCx/(2m)]dt (8)

Решая уравнение (8) при граничных условиях t=0 → V=V0 находим решение (9). Интегрируя его по переменной t с граничными условиями t=0 → x=x0 находим зависимость пройденного расстояния от времени (10), или подлетного времени от пройденного расстояния (11).
Из равенства
H(x)=H0-gt(x)2/2
где Н(x) – текущая координата пули по высоте, Н0 – начальная координата пули по высоте, g – ускорение силы тяжести (9,81 м/с2), t(x) – подлетное время, определяемое выражением (11) получаем выражение (12) описывающее понижение траектории пули от пройденного расстояния. Все выше описанное относится как к пулям, так и к дроби, стой разницей, что в случае дробового выстрела рассматривать можно полет одной дробины (для катаной дроби Cx=0.55) и принять что скорость (энергия, подлетное время и проч.) других дробин такие же, средний диаметр дробовой осыпи в зависимости от расстояния и способа снаряжения патрона определяется только экспериментально.