Как найти конечную температуру формула количество теплоты

Все неприличные комментарии будут удаляться.

все для проектирования

Формула расчета конечной температуры воды после смещения холодной и горячей:

где: Тс — температура смещенной воды, град.

М1 — масса холодной воды, кг

М2 — масса горячей воды, кг

Т1 — температура холодной воды, град.

Т2 — температура горячей воды, град.

Пример 1:

холодная вода 10 литров температурой 5 град смешивается с горячей водой 8 литров 60 градусов.

Необходимо определить конечную температуру воды. Подставляем все значения в формулу 1:

Формула расчета количество холодной и горячей воды в зависимости от температуры:

Бывает задача стоит в обратном направлении. Когда наоборот известно какую температуру необходимо иметь на выходе и общий вес воды, но не известна масса холодной и горячей воды. Тогда из формула 1 выводим новую формулу:

Пример 2:

из циркуляционного душа воды выходит температурой 36 градусов и объемом 40 литров. Необходимо определить количество холодной и горячей воды.

Как правило холодная вода имеет расчетную температуру 5 градусов. Горячая вода — 60 градусов.

Подставляем значения в формулу 2 и 3:

М1=(36*40-60*40)/(5-60)=17,45 литров холодной воды

М2=40-17,45=22,55 литров горячей воды

Удачного Вам дня! И успешных проектов!

Выше конечной целью теплового расчете являлось определение поверхности нагрева и основных размеров теплообменника для его дальнейшего конструирования. Предположим теперь, что теплообменник уже имеется или по крайней мере спроектирован. В этом случае целью теплового расчета является определение конечных температур рабочих жидкостей. Это — так называемый поверочный расчет.

При решении такой задачи известными являются следующие величины: поверхность нагрева F, коэффициент теплопередачи k, водяные эквиваленты W₁ и W₂ и начальные температуры t₁’ и t₂’, а искомыми: конечные температуры t₁” и t₂” и количество переданного тепла Q.

В приближенных расчетах можно исходить из следующих представлений. Количество тепла, отдаваемое горячей жидкостью, равно:

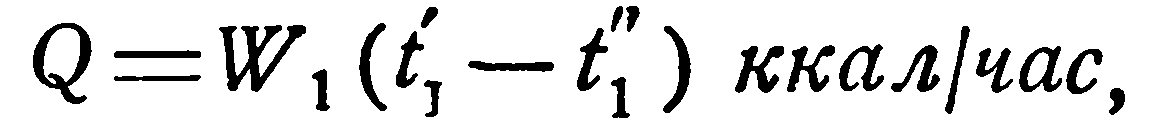(2.13)

откуда конечная температура ее t₁” определяется соотношением:

(a)

Соответственно для холодной жидкости имеем:

(2.14)

(b)

Если принять, что температуры рабочих жидкостей меняются по линейному закону, то

(с)

Вместо неизвестных t₁” и t₂” подставим их значения из уравнений (а) и (b), тогда получим:

(d)

Произведя дальнейшее преобразование, имеем:

(e)

откуда окончательно получаем:

(2.15)

Зная количество переданного тепла Q, очень просто формулам (а) и (b) определить и конечные температуры рабочих жидкостей t₁” и t₂”.

Приведенная схема расчета, хотя и проста, однако применима лишь для ориентировочных расчетов и в случае небольших изменений температур жидкостей. В общем же случае конечная температура зависит от схемы движения рабочих жидкостей. Поэтому для прямотока и противотока ниже приводится вывод более точных формул.

1. Прямоток. Выше было показано, что температурный напор изменяется по экспоненциальному закону:

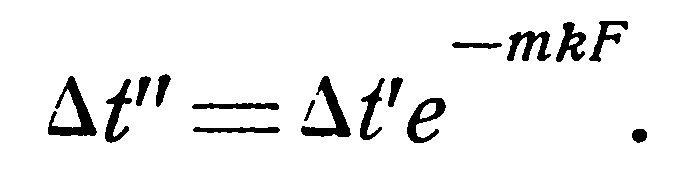(2.16)

Имея в виду, что

и, что в конце поверхности нагрева Δt” = t₁’ – t₂’, то, подставляя эти значения в уравнение (19), последнее можно представить в следующем виде:

(2.17)

Однако, это уравнение дает лишь разности температур. Чтобы отсюда получить конечные температуры в отдельности, необходимо обе части равенства вычесть из единицы:

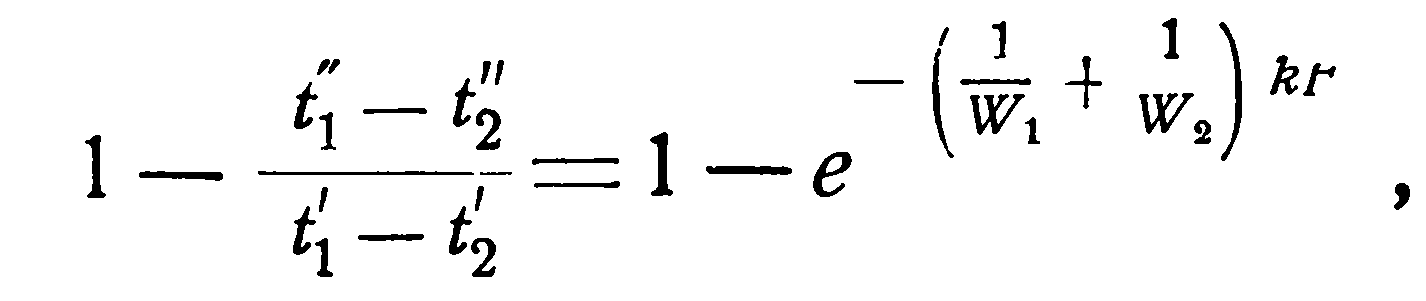(2.18)

(2.19)

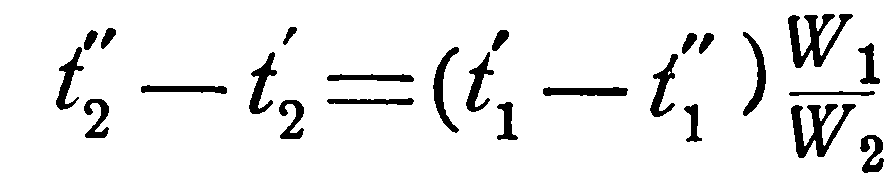
[см. разд.2.1 уравнение (2.5)].

то, подставляя это значение в левую часть уравнения (2.19), получаем:

(2.20)

Последнее уравнение, показывает, что изменение температуры горячей жидкости δt₁ равно некоторой доле П располагаемого начального температурного напора, t₁’ – t₂’; эта доля зависит только от двух безразмерных параметров 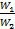и .

Аналогичным образом из уравнения (2.19) можно получить выражение и для изменения температуры холодной жидкости, а именно:

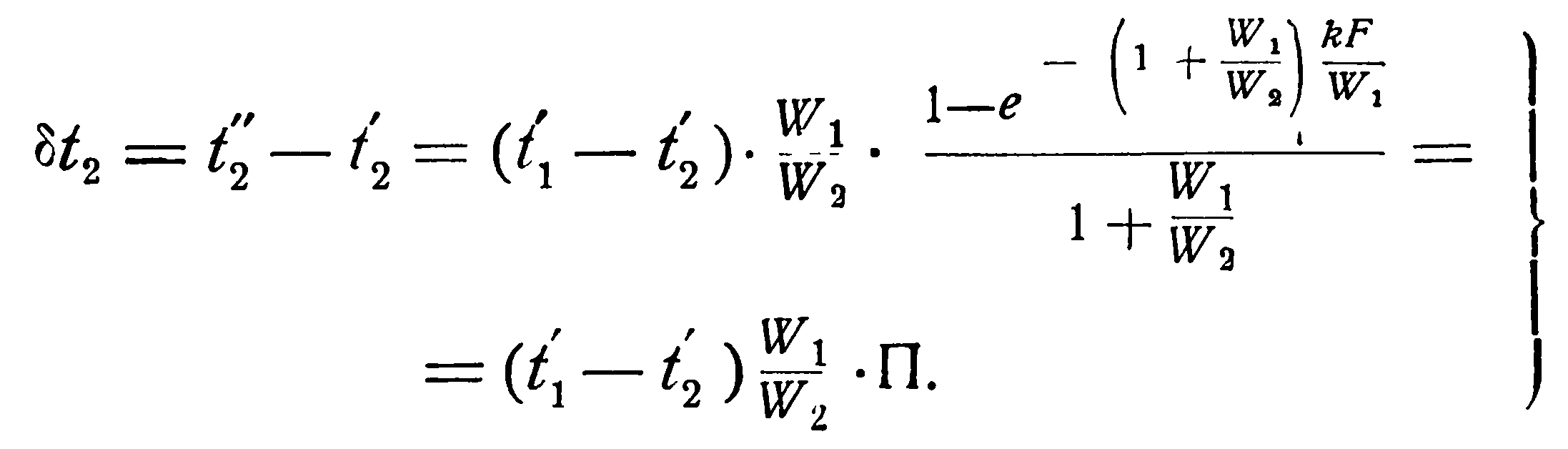(2.21)

Определив изменения температур рабочих жидкостей и зная их начальные температуры, легко определить конечные:

(2.22)

Расход тепла определяется путем умножения водяного эквивалента жидкости на изменение ее температуры:

(2.23)

Значение функции приведено на рис. 2.5. Формулы (2.21) – (2.23) могут быть применены и для расчета промежуточных значений температуры рабочих жидкостей и количества тепла. В этом случае в, расчетные формулы вместо F надо подставить значение F_x.

Пример 2.2. Имеется водяной холодильник с поверхностью нагрева F=8 м 2 . Определить конечные температуры жидкостей и часовое количество передаваемого тепла Q, если заданы следующие величины: V₁= 0,25 м 3 /час, γ₁ = 1100 кг/м 3 , c_p1 = 0,727 ккал/кг °С и t₁’ = 120 °С Для охлаждения в распоряжении имеется 1000 л воды в час при температуре t₂’ = 10 °С. Кроме того, известно значение коэффициента теплопередачи k = 30 ккал/м 2 час °С.

Соответствующее значение функции П находим из рис.2.5:

Рис. 2.5. — вспомогательная функция для расчета конечной температуры при прямотоке

Изменение (понижение) температуры горячей жидкости согласно уравнению (2.20) равно:

Следовательно, конечная температура ее равна:

Количество переданного тепла в час определится по уравнению (2.23)

Изменение температуры холодной жидкости определяется по уравнению (2.21). Но его можно также определить и из соотношения Q = W₂ (t₂” — t₂’), откуда

2. Противоток. Для противотока расчетные формулы выводятся так же, как и для прямотока. Окончательно они имеют следующий вид:

(2.24)

(2.25)

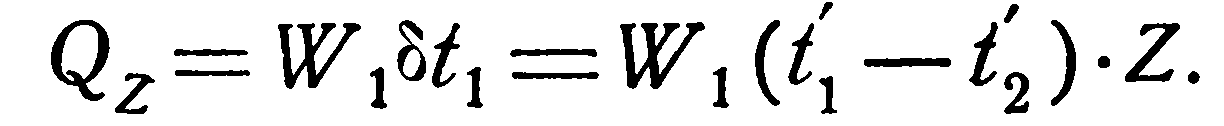(2.26)

В частном случае, когда формулы

(2.24) – (2.26) принимают вид:

(2.27)

(2.28)

(2.29)

Значение функции 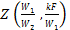приведено на рис. 2.6.

Рис. 2.6. — вспомогательная функция для расчета конечной температуры при противотоке

Для расчета промежуточных значений температуры рабочих жидкостей и количества переданного тепла в формулах (2.23) – (2.29) в числителе значение F заменяется на F_x, а в знаменателе остается значение полной поверхности F.

Пример 2.3. Если взять тот же теплообменник, который был рассмотрен в условиях прямотока, и допустить, что условия теплопередачи остаются без изменения (k = 30 ккал/м 2 час °С), то получим следующие соотношения:

Из рис. 2.6 находим значение функции Z:

Изменение температуры горячей жидкости равно [уравнение (2.24)]:

Конечная температура ее:

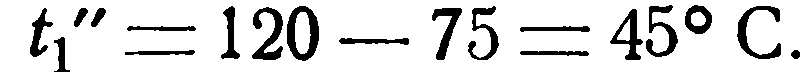
Изменение температуры холодной жидкости [уравнение (2.25)];

Конечная температура ее:

Количество переданного тепла в час [уравнение (2.26)]:

Таким образом, в случае противотока в теплообменнике происходит более глубокое охлаждение горячей жидкости.

3. Сравнение прямотока с противотоком. Чтобы выявить преимущество одной схемы перед другой, достаточно сравнить количество передаваемого тепла при прямотоке и противотоке при равенстве прочих условий. Для этого необходимо уравнение (2.23) разделить на уравнение (2.26). В результате этого действия мы получаем новую функцию тех же двух безразмерных аргументов

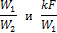
характер изменения которой графически показан на рис. 2.7.

Рис. 2.7. -сравнение прямотока с противотоком

Из рисунка следует, что схемы можно считать равноценными в том случае, если водяные эквиваленты обеих жидкостей значительно отличаются один от другого (при и при 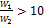) или если значение параметра — мало. Первое условие равнозначно тому, что изменение температуры одной жидкости незначительно по сравнению с изменением температуры другой. Далее, поскольку 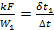, то второе условие соответствует случаю, когда средний температурный напор значительно превышает изменения температур рабочих жидкостей. Во всех остальных случаях при одной и той же поверхности нагрева и одинаковых крайних температурах теплоносителей при прямотоке передается меньше тепла, чем при противотоке. Поэтому с теплотехнической точки зрения всегда следует отдавать предпочтение противотоку, если какие-либо другие причины (например, конструктивные) не заставляют применять прямоток. При этом следует иметь в виду, что при противотоке создаются более тяжелые температурные условия для металла, ибо одни и те же участки стенок теплообменника с обеих сторон омываются рабочими жидкостями с наиболее высокой температурой.

При конденсации и кипении температура жидкости постоянна. Это означает, что водяной эквивалент такой жидкости бесконечно велик. В этом случае прямоток и противоток равнозначны, и уравнения (2.23) и (2.26) становятся тождественными. Конечная температура той жидкости, для которой водяной эквивалент имеет конечное значение, определяется следующим образом.

При конденсации паров;

(2.30)

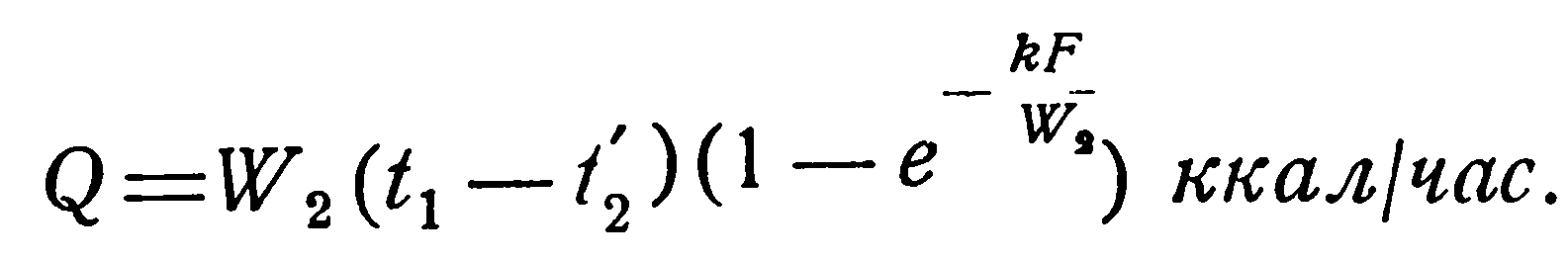(2.31)

При кипении жидкостей:

(2.32)

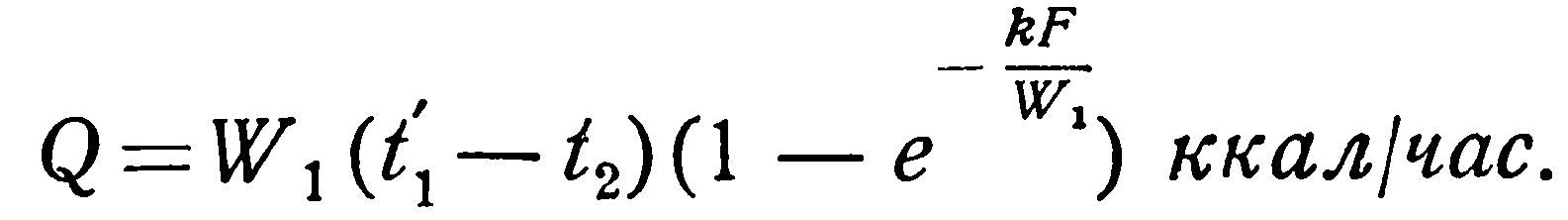(2.33)

Вместо t₁ и t₂ в уравнения (2.30) – (2.33) можно подставить температуру стенки, значение которой при этом также постоянно. Значения функции находятся из таблиц показательных функций.

В случае перекрестного тока конечные температуры рабочих жидкостей находятся между конечными температурами для прямотока и противотока. Поэтому в приближенных расчетах можно пользоваться методом расчета одной из указанных схем. Если одна из жидкостей движется навстречу другой зигзагообразно (смешанный ток), то расчет может быть произведен, как для противотока.

4. Влияние тепловых потерь и проницаемости стенок.Все вышеприведенные формулы справедливы для случая, когда тепловые потери во внешнюю среду равны нулю. В действительности они всегда имеются. Более или менее точно учесть их влияние, вообще говоря, возможно, однако расчетные формулы при этом становятся громоздкими. Поэтому для учета влияния тепловых потерь в практике обычно применяется приближенный метод, который состоит в следующем.

Тепловые потери со стороны горячей жидкости вызывают более сильное падение ее .температуры. Это равносильно случаю, когда теплоотдающая жидкость в аппарате без потерь в окружающую среду имела бы меньшее значение водяного эквивалента. Поэтому влияние потерь в окружающую среду можно учесть, изменив водяной эквивалент теплоотдающей жидкости в тепловом аппарате таким образом, чтобы в последнем происходило такое же понижение температуры, как и при потоке с действительным водяным числом при наличии тепловых потерь. Внешние тепловые потери со стороны холодной жидкости оказывают обратное влияние, они уменьшают повышение температуры жидкости, что приводит к кажущемуся увеличению ее водяного эквивалента.

Наличие присоса наружного холодного воздуха оказывает такое же влияние, как и внешняя потеря тепла. Присосанный вездух на горячей стороне понижает температуру горячей жидкости (газа) точно так же, как если бы теплообменный аппарат был абсолютно непроницаем, но жидкость имела меньшее значение водяного эквивалента. Присос вездуха на холодной стороне понижает температуру холодной жидкости, что равносильно увеличению значения водяного эквивалента.

Если потеря тепла составляет р% к общему количеству передаваемого тепла, то вместо действительного значения водяного эквивалента W в расчетные формулы следует подставить значение W’ которое определяется следующим образом:

(2.34)

Знак минус (-) берется для горячей, а знак плюс (+) для холодной жидкости.

При таком способе учета внешних тепловых потерь все приведенные выше формулы для расчета конечных температур можно применять без какого-либо их изменения.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Количество теплоты

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: количество теплоты, удельная теплоёмкость вещества, уравнение теплового баланса.

Как мы знаем, одним из способов изменения внутренней энергии является теплопередача (теплообмен). Предположим, что тело участвует в теплообмене с другими телами, и при этом не совершается механическая работа — ни самим телом, ни другими телами над этим телом.

Если в процессе теплообмена внутренняя энергия тела изменилась на величину , то говорят, что тело получило соответствующее количество теплоты: .

Если при этом величина отрицательна, т.е. тело отдавало энергию, то говорят также, что тело отдавало тепло. Например, вместо формально верной, но несколько нелепой фразы «тело получило —5 Дж тепла» мы скажем: «тело отдало 5 Дж тепла».

Удельная теплоёмкость вещества

Предположим, что в процессе теплообмена агрегатное состояние вещества тела не изменяется (не происходит плавление, кристаллизация, парообразование или конденсация). Начальную температуру тела обозначим , конечную температуру — .

Опыт показывает, что количество теплоты, полученное телом, прямо пропорционально массе тела и разности конечной и начальной температур:

Коэффициент пропорциональности c называется удельной теплоёмкостью вещества тела. Удельная теплоёмкость не зависит от формы и размеров тела. Удельные теплоёмкости различных веществ можно найти в таблицах.

Введя обозначение , получим также:

Чтобы понять физический смысл удельной теплоёмкости, выразим её из последней формулы:

Мы видим, что удельная теплоёмкость численно равна количеству теплоты, которое необходимо для нагревания 1кг данного вещества на (или, что то же самое, на ). Измеряется удельная теплоёмкость в Дж/(кг·C) или в Дж/(кг·K).

Чем больше удельная теплоёмкость вещества, тем большее количество теплоты требуется для нагревания тела данной массы на заданное количество градусов.

В задачах часто фигурируют вода и лёд. Их удельные теплоёмкости желательно помнить.

Вода: Дж/(кг·C).
Лёд: Дж/(кг·C).

Произведение удельной теплоёмкости вещества на массу тела называется теплоёмкостью тела и обозначается :

Соответственно, для количества теплоты имеем:

Уравнение теплового баланса

Рассмотрим два тела (обозначим их 1 и 2), которые образуют замкнутую систему. Это означает, что данные тела могут обмениваться энергией только друг с другом, но не с другими телами. Считаем также, что механическая работа не совершается — внутренняя энергия тел меняется только в процессе теплообмена.

Имеется фундаментальный закон природы, подтверждаемый всевозможными экспериментами — закон сохранения энергии. Он гласит, что полная энергия замкнутой системы тел не меняется со временем.

В данном случае закон сохранения энергии утверждает, что внутренняя энергия нашей системы будет оставаться одной и той же: . Если изменение внутренней энергии первого тела равно , а изменение внутренней энергии второго тела равно , то суммарное изменение внутренней энергии будет равно нулю:

Но — количество теплоты, полученное первым телом в процессе теплообмена; аналогично — количество теплоты, полученное вторым телом в процессе теплообмена. Стало быть,

(1)

Попросту говоря, сколько джоулей тепла отдало одно тело, ровно столько же джоулей получило второе тело. Так как система замкнута, ни один джоуль наружу не вышел. Соотношение (1) называется уравнением теплового баланса. В общем случае, когда тел образуют замкнутую систему и обмениваются энергией только с помощью теплопередачи, из закона сохранения энергии с помощью тех же рассуждений получаем общее уравнение теплового баланса:

(2)

В качестве простого примера применения уравнения теплового баланса рассмотрим следующую задачу.

Смешали г воды при температуре и г воды при температуре . Найти установившуюся температуру смеси.

Обозначим искомую установившуюся температуру через . Запишем уравнение теплового баланса (1):

где — удельная теплоёмкость воды. Раскрываем скобки и находим:

Расчет конечной температуры реакции по удельной теплоемкости

На чтение 2 мин. Просмотров 96 Опубликовано 04.06.2021

Этот пример задачи демонстрирует, как вычислить конечную температуру вещества, учитывая количество использованной энергии, массу и начальную температуру.

Содержание

1. Проблема
2. Решение
3. Конечная температура После смешивания
4. Задача
5. Решение

Проблема

300 граммов этанола при 10 ° C нагреваются с помощью 14640 джоулей энергии. Какова конечная температура этанола?

Полезная информация : удельная теплоемкость этанола составляет 2,44 Дж/г · ° C.

Решение

Используйте формулу

q = mcΔT

Где

• q = Нагрев Энергия
• m = Масса
• c = Удельная теплоемкость
• ΔT = Изменение температуры.

14640 Дж = (300 г) (2,44 Дж/г · ° C) ΔT

Решить для ΔT:

1. ΔT = 14640 Дж/(300 г) (2,44 Дж/г · ° C)
2. ΔT = 20 ° C
3. ΔT = T _final – T _{начальный}
4. T _final = T _{начальный} + ΔT
5. T _final = 10 ° C + 20 ° C
6. T _final = 30 ° C

Ответ : Конечная температура этанола составляет 30 ° C.

Конечная температура После смешивания

Когда вы смешиваете вместе два вещества с разными начальными температурами применяются одни и те же принципы. Если материалы не вступают в химическую реакцию, все, что вам нужно сделать для определения конечной температуры, – это предположить, что оба вещества в конечном итоге достигнут одинаковой температуры.

Задача

Найдите конечную температуру, когда 10,0 граммов алюминия при 130,0 ° C смешиваются с 200,0 граммами воды при 25 ° C. Предположим, что вода не теряется в виде водяного пара.

Решение

Опять же, вы используете q = mcΔT, но предполагаете, что q _aluminium = q _water и решите для T, которая является конечной температурой. Вам нужно найти значения удельной теплоемкости (c) для алюминия и воды. В этом решении используется 0,901 для алюминия и 4,18 для воды:

• (10) (130 – T) (0.901) = (200.0) ( T – 25) (4.18)
• T = 26,12 ° C

Лицей естественных
наук г. Кирова

Г.Г. Самарин

 

Решение
задач на теплообмен

с использованием уравнения
теплового баланса

(методические рекомендации)

Киров

2002

ББК
74.204.2

С
17

Печатается
по решению редакционно-издательского совета Лицея естественных наук г. Кирова

Рецензент:  К.А. Коханов, кандидат
педагогических наук, старший преподаватель кафедры дидактики физики Вятского
государственного гуманитарного университета, заместитель заведующего кафедрой
дидактики физики.

С 17  Самарин Г.Г.   Решение задач на теплообмен с использованием уравнения теплового
баланса:  Методические рекомендации. – Киров: Издательство Лицея естественных
наук, 2002. – 35 с.

Пособие рекомендовано учащимся,
желающим получить практические навыки в решении задач на теплообмен, и может
быть полезным для учителей и абитуриентов.

©
Лицей естественных наук, 2002

©
Г.Г. Самарин, 2002

При соприкосновении тел, имеющих
разные температуры, между этими телами происходит теплообмен. С точки зрения молекулярно-кинетической
теории, это объясняется так: молекулы более нагретого тела имеют большую
кинетическую энергию, чем молекулы тела, менее нагретого. При «столкновениях»
молекул соприкасающихся тел  происходит процесс выравнивания их средних кинетических
энергий. Молекулы более нагретого тела теряют часть своей кинетической энергии,
при этом нагретое тело будет остывать. Кинетическая энергия молекул холодного
тела  возрастает, поэтому температура этого тела будет увеличиваться.  В
конечном итоге кинетические энергии молекул обоих тел сравняются, и температуры
тел станут одинаковыми. На этом теплообмен прекращается.

Энергию, которую тело получает
или отдаёт в процессе теплообмена, называют количеством теплоты (Q).

Количество теплоты, как и все другие
виды энергии, измеряется в системе СИ в Джоулях: [Q] = Дж. *

Нагревание или охлаждение

 При нагревании или охлаждении тела
количество теплоты, поглощаемое или выделяемое им, рассчитывается по формуле:

Q = сm(t₂ – t₁), ⁽¹⁾

 где m – масса тела, кг;

(t₂ – t₁) – разность 
температур тела,°С (или К);

с – удельная теплоёмкость вещества, из
которого состоит тело,

 или .

Удельная теплоёмкость вещества – это количество теплоты, которое нужно
сообщить одному килограмму данного вещества, чтобы увеличить его температуру на
1°С (или
это количество теплоты, которое выделяет один килограмм данного вещества,
остывая на 1°С).

Например, С_воды = 4200,     С_{льда, водяного пара} =
2100,     С_свинца = 140, С_меди = 380, С_{железа, стали} = 460, С_{алюминия} = 920.

Значения удельных теплоемкостей других
веществ можно найти в справочниках, а также в школьном учебнике или задачнике.

При нагревании тела его внутренняя
энергия увеличивается. Это требует притока энергии к телу от других тел.
Значит, оно поглощает некоторое количество теплоты, принимая его от других тел,
участвующих в теплообмене.

При охлаждении тела его внутренняя
энергия уменьшается. Поэтому остывающее тело отдаёт кому-либо некоторое
количество теплоты.

 Обычно конечную температуру,
установившуюся в результате теплообмена, обозначают греческой буквой q (тэта).

В формуле (1) произведение cm для каждого конкретного тела есть величина постоянная. Её называют теплоёмкостью
тела и обозначают С:

C
= c×m.⁽²⁾

 Размерность теплоемкости: [С] = .  Теплоемкость
тела показывает, сколько энергии нужно подвести к данному телу, чтобы нагреть
его на 1°С
(или сколько энергии выделяет это тело, остывая на 1°С).

Теплообмен между телами, имеющими
одинаковые температуры, не происходит, даже если контактируют вещества,
находящиеся  в разных агрегатных состояниях. Например, при температуре
плавления (0°С) лёд и вода могут находиться бесконечно долго, при этом количество
льда и количество воды останутся неизменными. Аналогично ведут себя пар и
жидкость, находящиеся при температуре кипения. Теплообмен между ними не
происходит.

Плавление или кристаллизация

 Если при нагревании тела его
температура достигнет температуры плавления, то начинает происходить процесс
перехода этого вещества из твердого состояния в жидкое. При этом идут изменения
в расположении и характере взаимодействия молекул.    Температура при плавлении
не изменяется. Это означает, что средние кинетические энергии молекул жидкости
и твердого тела при температуре плавления одинаковы. Однако внутренняя энергия
тела при плавлении возрастает за счет увеличения энергии взаимодействия
молекул. Количество теплоты, поглощаемое телом при плавлении, рассчитывается по
формуле

 Q = l×m⁽³⁾,

где m
– масса тела, кг;

      l – удельная
теплота плавления, .

При кристаллизации, наоборот,
внутренняя энергия тела уменьшается на величину Q = l×m, и
эта теплота данным телом выделяется. Она поглощается другими телами,
участвующими в теплообмене.

Удельная теплота плавления показывает, сколько энергии нужно сообщить одному килограмму данного
вещества, взятого при температуре плавления, чтобы полностью превратить его при
этой температуре в жидкость (или сколько энергии выделяет 1
кг жидкости, взятой при температуре кристаллизации, если вся она при этой
температуре полностью превратится в твёрдое тело).

Удельную теплоту плавления любого
вещества можно найти в справочниках.  Для льда же l = 3,4×10⁵ .

Температура плавления у каждого
вещества своя. Её также можно найти в справочниках. Важно подчеркнуть, что
температура плавления вещества равна температуре кристаллизации этого же
вещества. У льда  t_пл = 0°С.

Кипение или конденсация

При достижении жидкостью температуры
кипения начинает происходить другой фазовый переход – кипение, при котором
расстояния между молекулами значительно увеличиваются, а силы взаимодействия
молекул уменьшаются. Вся подводимая к жидкости теплота идет на разрыв связей
между молекулами. При конденсации пара в жидкость, наоборот, расстояния между
молекулами значительно сокращаются, а силы взаимодействия молекул
увеличиваются. Для кипения жидкости энергию к жидкости нужно подводить, при
конденсации пара энергия выделяется. Количество теплоты, поглощаемое при
кипении или выделяемое при конденсации, рассчитывается по формуле:

Q = L×m ⁽⁴⁾,

 где m – масса тела, кг;

       L – удельная теплота парообразования, .

Удельная теплота парообразования показывает, сколько энергии нужно сообщить одному килограмму жидкости,
взятой при температуре кипения, чтобы при этой температуре полностью превратить
её в пар (для конденсации: сколько энергии выделяет один килограмм пара,
взятого при температуре конденсации, полностью превращаясь в жидкость).

При одинаковом давлении температура
кипения и температура конденсации  одного и того же вещества одинаковы.

Температуры кипения и удельные теплоты
парообразования также можно найти в справочниках. Для воды же они
соответственно равны: t_кип = 100°С,  L = 2,3×10⁶  (при нормальном атмосферном
давлении).

Уравнение теплового баланса

Тела, участвующие в теплообмене,
представляют собой термодинамическую систему. Термодинамическая система
называется теплоизолированной, если она не получает энергию извне и не
отдаёт её; теплообмен происходит только между телами, входящими в эту систему. 
Для любой теплоизолированной системы тел справедливо следующее утверждение: количество
теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими
телами.

Q_отд. = Q_получ.⁽⁵⁾

Это утверждение описывает частный
случай закона сохранения и превращения энергии в применении к процессу
теплообмена. А формула (5) является одним из видов уравнения теплового баланса.

При решении задач с помощью данного
вида уравнения теплового баланса в формуле (1) в качестве t₂ следует брать большую температуру, а в
качестве t₁ – меньшую.
Тогда разность (t₂ – t₁) будет положительна и всё произведение cm(t₂–t₁) также будет положительным. Все теплоты,
отданные и полученные, будут положительными.

Уравнение теплового баланса можно
записать и в таком виде:

Q₁+ Q₂+…+ Q_n=
0,⁽⁶⁾

Где n –
количество тел системы.

Алгебраическая сумма  всех
количеств теплоты  (поглощенных и выделенных) в теплоизолированной системе
равна нулю.

Q₁, Q₂, …, Q_n –
это  теплоты, поглощаемые или выделяемые участниками теплообмена. Очевидно, что
в этом случае какие-то теплоты должны быть положительны, а какие-то –
отрицательны. При записи уравнения теплового баланса в виде (6) всегда t₂ – конечная температура, а t₁ – начальная.

 Если тело нагревается, то разность (t₂ –  t₁) положительна и все произведение cm(t₂ – t₁) положительно. То есть Q > 0 тогда, когда
теплота к данному телу подводится.

 А если t₂ < t₁ (тело
остывает), то разность (t₂
– t₁) отрицательна, то
есть Q < 0. В этом случае тело энергию выделяет.

Если при фазовом переходе энергия к
телу подводится (плавление, кипение), то Q > 0; если
тело выделяет энергию (кристаллизация, конденсация), то Q
< 0.

В принципе уравнения (5) и (6)
равносильны. Результат решения задачи не зависит от того, каким видом уравнения
пользуемся. Выбор способа решения – за читателем.

Применим уравнение теплового баланса
для решения ряда задач.

Задача 1

В медном калориметре массой 100
г находится 1 кг воды при температуре 20°С. В воду опускают свинцовую
деталь массой 2 кг, имеющую температуру 90°С. До какой температуры
нагреется вода? Потерями теплоты пренебречь.*

Решение

m1 = 0,1 кг с1= 380 Дж/(кг×0С) t2 = 20°С m2 = 1 кг с2=4200 Дж/(кг×0С) m3 = 2 кг с3= 140 Дж/(кг×0С) t3 = 90°С     q  – ?	Проведём анализ: Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t1 =  t2 = 20°С. При опускании в воду с температурой 20°С свинцового тела с температурой 90°С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода – нагреваться. В этом же процессе  участвует  и калориметр, который, как и вода, будет тоже нагреваться.
	Изменение температур  тел с течением времени  удобно изображать на графике зависимости t(t). Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q3.
	Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q1 и Q2, которую они поглощают.
	Решим задачу с использованием уравнения теплового баланса в виде (5): Q1 + Q2 = Q3, c1m1(q – t1) + c2m2(q – t2) = c3m3(t3 – q). Выражаем температуру q: q =

 Решим
задачу с использованием уравнения теплового баланса в виде (6):

Q₁ + Q₂ + Q₃ = 0,

c₁m₁(q – t₁) + c₂m₂(q – t₂) + c₃m₃(q – t₃) = 0.

q =  = 24 (°С)

Ответ: Вода нагреется до 24 °С.

  Предлагаю читателю
самостоятельно сделать проверку размерности.

Задача
2

Три пластины: медную, имеющую массу m₁ = 1
кг и температуру t₁ = 100°С,
железную (m₂ = 1,2 кг, t₂ = 150°С)
и алюминиевую (m₃ = 0,8 кг, t₃ = 80°С)
сложили вплотную (см рис). Какую температуру будут иметь пластины, когда
теплообмен прекратится? Потерями теплоты в окружающую среду  пренебречь.

m1 = 1 кг с1= 380 Дж/(кг×0С) t1 = 100°С m2 = 1,2 кг с2= 460 Дж/(кг×0С) t2 = 150°С m3 = 0,8 кг с3= 920 Дж/(кг×0С) t3 = 80°С

Решение Решим задачу с помощью уравнения теплового баланса в виде (5). 1. Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная – нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая – нагреваться. Мысленно соединим сначала эти две пластины и найдём температуру t, которой они при этом достигнут: Q2 = Q3  Þ  c2m2(t2 – t) =  c3m3(t – t3)      t =

q – ?

t =

2. Теперь медная пластина вступает в
теплообмен с железной и алюминиевой. Медная будет нагреваться от температуры t₁ до температуры q, а железная и алюминиевая –
остывать от температуры t до температуры q. Тогда:

Q₁
= Q₂‘+ Q₃‘_,

c₁m₁(q – t₁) = (c₂m₂
+ c₃m₃)(t –
q),

c₁m₁q – c₁m₁t₁ = (c₂m₂
+ c₃m₃)t – (c₂m₂ + c₃m₃)q

q
=

3. Решим
задачу, применив уравнение теплового баланса в виде (6):

Q₁ + Q₂ + Q₃ = 0,

c₁m₁(q – t₁) + c₂m₂(q – t₂) + c₃m₃(q – t₃)
= 0,

q =  = 108 (°С)

Ответ: Пластины будут иметь температуру 108 °С.

  Как видим,
второй способ оказался и в данном случае более рациональным. Однако, первый
способ зачастую оказывается более  понятным, особенно при наличии фазовых
переходов. Поэтому в дальнейшем автор будет придерживаться первого способа
решения задач. Желательно, чтобы читатель пробовал решать их и  вторым
способом.

Задача
3

В
железном ведре массой 1,2 кг находится 5
кг воды при температуре 20°С. Сколько льда температурой –10°С надо положить в
ведро, чтобы температура воды понизилась до 12°С? Теплообменом с окружающей
средой пренебречь.

m1 = 1,2 кг с1=460 Дж/(кг×0С) m2 = 5 кг с2=4200 Дж/(кг×0С) t1 = t2 = 20°С t3 = –10°С с3=2100 Дж/(кг×0С) t4 = 0оС   q = 12°С

Решение Известна конечная температура, Значит, анализ ситуации довольно прост: вода и ведро будут остывать, не испытывая фазовых переходов, отдавая теплоты Q1 и Q2, а лёд сначала будет нагреваться до температуры плавления t4, поглощая теплоту Q3, затем плавиться, поглощая теплоту Q4, а затем вода, образовавшаяся из льда, будет нагреваться до конечной температуры q, поглощая теплоту Q5. Так как иных участников теплообмена нет, то можно так  записать уравнение теплового баланса:  Q1 + Q2 = Q3 + Q4 + Q5. (c1m1 + c2m2)(t1 – q) = = c3m3(t4 – t3) + lm3 + c2m3(q – t4)

m3 – ?

Ответ:  Потребуется 0,4
кг льда.

Задача
4

В алюминиевую кастрюлю массой 200
г, содержащую 3 кг воды при  20°С,
поместили стальную деталь массой 0,5 кг, нагретую до 500°С. При этом часть воды выкипела, а оставшаяся
вода нагрелась до 22°С.
Сколько воды выкипело?

m1 = 3 кг с1=4200Дж/(кг°С) m2 = 0,2 кг с2 =920 Дж/(кг°С) t1 = t2 = 20°С q = 22°С m3 = 0,5 кг с3 = 460 Дж/(кг0С) t3 = 500°С L = 2,3×106 Дж/кг	Решение 1.     Стальная деталь, не претерпевая фазовых переходов, остыла от 500°С до 22°С, выделив при этом количество теплоты        Q3 = c3m3(t3 – q). 2. Часть воды массой  m0 нагрелась до температуры кипения (100оС) и выкипела. При  этом была поглощена теплота               Q1  = c1m0(100 – t1) + Lm0. 3. Оставшаяся в кастрюле вода массой (m1 – m0) и сама кастрюля массой m2 нагрелись от 200С до 22°С. При этом была поглощена теплота Q2 = c1(m1 – m0)(q – t1) + c2m2(q – t1).
m0 – ?
4. Так как потерь тепла нет, то записываем уравнение теплового баланса: Q1 + Q2 = Q3, c1m0(100 – t1) + Lm0 + c1(m1 – m0)(q – t1) + + c2m2(q – t2) = c3m3(t3 – q). 5. Решая это уравнение, находим m0: m0 = , m0 =

Ответ: Выкипело 32
г воды.

Задача
5

Комок мокрого снега массой 400
г опустили в медный таз массой 500 г, содержащий 2
кг воды при температуре 20°С. После установления теплового равновесия температура воды в тазу
стала 10°С. Сколько воды было в комке снега?

m3 = 0,4 кг l = 3,4×105 Дж/кг t1 = t2 = 20°С t3 = 0°С m1 = 0,5 кг с1 = 380 Дж/(кг×0С) m2 = 2 кг с2=4200Дж/(кг×0С) q = 10°С	Решение 1. Медный таз и вода находятся в тепловом равновесии. Поэтому 20°С – их общая температура. При остывании от 20°С до 10°С ни медь, ни вода фазовых превращений не испытывают. При этом они отдают суммарную теплоту: Q1 + Q2  =  c1m1(t1 – q) + c2m2(t2 – q). 2. Мокрый снег – это снег, содержащий воду. Значит, снег и вода находятся в тепловом равновесии. Это возможно только при температуре фазового перехода, то есть при 0°С.
mв – ?
Итак, начальная температура мокрого снега 0°С. 3. На пути к температуре 10°С снег массой m3–mв будет сначала таять. Для этого требуется теплота Q3 = l(m3 – mв). А затем вся вода массой m3 будет нагреваться от 0°С до 10°С. Для этого ей надо получить количество теплоты Q4 = c2m3(q – t3). 4. Так как нет потерь тепла, то можно написать уравнение теплового баланса: Q1 + Q2 = Q3 + Q4, с1m1(t1 – q) + c2m2(t2 – q) = l(m3 – mв) + c2m2(q – t3). 5. Решая это уравнение, находим mв: mв = mв = Ответ: В комке мокрого снега было 0,2 кг воды.

Задача
6

В холодную воду массой 2
кг, имеющую температуру 10°С, находящуюся в кастрюле, влили 3
кг горячей воды при температуре 80°С. До какой температуры нагреется холодная вода,
если известно, что 25% теплоты, отданной горячей водой, пошло на нагревание
кастрюли? Какова теплоемкость кастрюли?

M1 = 2 кг t1 = 10°С m2  = 3 кг t2 = 80°С h1=0,25 (25%)

Решение Так как 25% теплоты отданы кастрюле, то 75% теплоты пошло на нагревание холодной воды.   Значит, можно говорить о КПД  процесса нагревания холодной воды: h2 =     (h2 = 0,75) Здесь  Qполез –  теплота, идущая на нагревание холодной воды: Qполез = c1m1(q – t1);             Qзатр –  теплота, отданная горячей водой: Qзатр = c2m2(t2 – q). Удельные теплоты с1 холодной и с2 горячей воды равны. h2 =  Þ h2m2(t2 – q) = m1(q – t2), h2m2t2 – h2m2q = m1q – m1t1,

q – ? С – ?

q =

q =

Так как 25% теплоты, отданной горячей водой, пошло на
нагревание кастрюли, то можно говорить и о КПД процесса нагревания кастрюли:

  ,

откуда:

Ответ: Холодная вода нагреется до температуры 47°С. Теплоемкость кастрюли 2809 Дж/⁰С.

Задача
7

Сколько керосина нужно сжечь, чтобы превратить
в пар 1 кг льда, взятого при температуре –40°С?
КПД нагревательного устройства равен 60%, удельная теплота сгорания керосина
46      МДж/кг.

m1 = 1 кг t1 = –40°С с1 =2100Дж/(кг×0С) l = 3,4×105 Дж/кг с2 =4200Дж/(кг×0С) L = 2,3×106 Дж/кг h = 0,6 (60%) q = 46×106 Дж/кг

Решение 1.  Изобразим на графике t(t) процессы: нагревание льда, плавление льда, нагревание получившейся из льда воды, кипение этой воды. Для осуществления каждого из этих процессов необходим подвод теплоты. Теплоту выделяет керосин в процессе сгорания (на графике не показано).  2.  Применим формулу КПД нагревателя: h = . Здесь Qполез = Q1 + Q2 + Q3 + Q4 = = m1[c1(0 – t1) + l + c2(100 – 0) + L], а Qзатр = qm2. Получаем: h = , откуда: m2 = .  m2 = = 114 г

m2 – ?

Ответ: Нужно сжечь 114
г керосина.

Задача 8

Сколько
водяного пара, имеющего температуру 120°С, надо впустить в калориметр,
содержащий 800 г льда при температуре –20°С, чтобы температура
образовавшейся воды оказалась 20°С? Теплоёмкостью калориметра пренебречь.

m1 = 0,8 кг t1 = –20°С с1 = с2 = 2100 Дж/(кг×0С) t2 = 120°С с3 =4200Дж/(кг×0С) q = 20°С

Решение 1. Так как теплоемкостью калориметра можно пренебречь, то  систему лед – пар можно считать теплоизолированной: теплообмен происходит только между паром и льдом. 2.  Получают теплоту тела: –           лёд, нагреваясь от –200С до температуры плавления: Q1 = c1m1(0 – t1); –           лёд, превращаясь в воду при температуре плавления: Q2 = lm1; –           вода, образовавшаяся из льда, нагреваясь от 0°С до 20°С: Q3 = с3m1(q – 0). 3. Отдают теплоту тела: –           пар, остывая от 120°С до температуры конденсации: Q4 = c2m2(t2 – 100); –           пар, превращаясь в воду при 100°С: Q5 = Lm2; –           вода, образовавшаяся из пара, остывая от 100°С до 20°С: Q6 = c3m2(100 – q). 4. Других участников теплообмена нет, поэтому записываем уравнение теплового баланса: Q1 + Q2 + Q3 =  Q4 + Q5 + Q6, c1m1(0 – t1) + lm1 + c3m1(q – 0) = c2m2(t2 – 100) + + Lm2 + c3m2(100 – q),

m2-?

Ответ: Потребуется 140 г водяного пара.

  Часто при
решении задач можно встретиться со следующей проблемой. В теплообмене участвуют
вещества, находящиеся в различных агрегатных состояниях, и конечная температура
теплообмена не известна. Тогда уравнение теплового баланса сразу написать не
удастся, так как его вид зависит от того, в каких агрегатных состояниях будут
находиться конечные продукты. В этом случае последовательность решения задачи
немного изменяется. Сначала нужно сделать предварительные расчеты: сколько
теплоты выделит или поглотит каждое вещество в предполагаемом процессе,
сравнить эти теплоты и сделать вывод о том, в каких агрегатных состояниях будут
находиться продукты теплообмена. И только после этого можно записывать
уравнение теплового баланса. Такие задачи значительно сложнее задач, в которых
конечная температура известна. Рассмотрим ряд таких задач.

Задача
9

В калориметр, содержащий воду массой 0,5
кг при температуре 25°С, впускают водяной пар массой 50
г при температуре 120°С. Какая температура установится в калориметре, если его теплоёмкость
1200 Дж/^оС?

m1 = 0,5 кг с1 =4200 Дж/(кг×0С) t1 = 25°С m2 = 0,05 кг t2 = 120°С c2=2100 Дж/(кг×0С) С = 1200 Дж/0С L = 2,3×106 Дж/кг	Решение 1. Если в конечном итоге весь пар остынет от 120°С до 100°С, затем сконденсируется в воду, затем образовавшаяся из пара  вода  остынет  от 100°С до q, то в калориметре будет находиться вода при температуре q, а уравнение теплового баланса примет вид:  .
q-?
	2. Если  пар остынет от 120°С до 100°С, а сконденсируется не весь, то в калориметре будет находиться смесь воды и пара при температуре 100°С, а уравнение теплового баланса будет таким: Здесь m¢ – масса сконденсировавшегося пара.
	3. Пар может остыть от 120°С до 100°С, а вода и калориметр уже нагреются до 100°С, и при этом часть воды даже выкипит. В калориметре будет смесь пара и воды при температуре 100°С. Уравнение теплового баланса будет иметь вид: , где m¢¢– масса превратившейся в пар воды.
Каким из трёх уравнений пользоваться? Cделаем предварительные расчёты. Вычислим: а) сколько теплоты нужно для того, чтобы нагреть воду и калориметр от 25°С до 100°С: Q1 = c1m1(100 – t1) + C(100 – t1) = 4200×0,5×75+1200×75 = 247500 (Дж). б) сколько теплоты выделится, если весь пар остынет от 120°С до 100°С: Q2 = c2m2(t2 – 100) =2100×0,05×20 = 2100 (Дж). в) сколько теплоты выделится, если весь пар сконденсируется в воду  при температуре 100°С: Q3 = Lm2 = 2300000×0,05 = 115000 (Дж).

 Выделяющаяся
теплота Q₂ + Q₃ = 2100 Дж + 115000 Дж = 117100 Дж при
охлаждении пара и его конденсации меньше теплоты, которая требуется для
нагревания «холодной» воды и калориметра. Значит, чтобы вода вместе с
калориметром смогла нагреться до 100°С, ей нужно больше энергии, чем может отдать пар,
остывая и конденсируясь. Поэтому 117100 Дж пар отдаст, став при этом «горячей»
водой при 100°С, а «холодная» вода при этом до 100°С ещё не нагреется. Тогда в
калориметре будут одновременно находиться сконденсировавшаяся из пара вода при
100°С и
подогретая «холодная» вода. В результате дальнейшего теплообмена «горячая» 
вода остынет, а «холодная» нагреется. И в итоге в калориметре будет вода,
температура которой ниже 100⁰С, но выше 25⁰С.

Уравнение
теплового баланса будет иметь вид (1):

c₁m₁(q – t₁) + C(q – t₁) = c₂m₂(t₂ – 100) + Lm₂ + c₁m₂(100 – q), откуда

c₁m₁q – c₁m₁t₁ + Сq
– Сt₁ = 117100 + c₁m₂×100
– c₁m₂q.

Ответ: В
калориметре установится температура 63°С.

Задача 10

В калориметре
находится вода массой 0,8 кг при температуре 20°С. В воду опустили 2
кг льда при температуре –30°С. Что будет в калориметре после того, как теплообмен прекратится?
Теплоёмкостью калориметра пренебречь.

1)   Весь лёд нагреется до температуры 0°С, весь расплавится и
образуется из льда вода, которая нагреется с 0°С до температуры q:

Уравнение
теплового баланса:

c₁m₁(t₁–q)=c₂m₂(0-t₂)+lm₂+c₁m²¢(q-0)

Тогда в
калориметре будет вода при температуре q.

m1 = 0,8 кг с1=4200 Дж/(кг×0С) t1 = 20°С m2 = 2 кг t2 = –30°С c2=2100 Дж/(кг×0С) l = 3,4×105 Дж/кг

Решение Рассмотрим варианты решения: 1. Вода остынет от 20°С до 0°С, затем эта вода замёрзнет и станет льдом при температуре 0°С, затем лёд, образовавшийся из воды, остынет до температуры q (см. график). А опущенный в воду лёд только нагреется от температуры –30°С до температуры q. В калориметре будет находиться лёд при температуре q. Уравнение теплового баланса запишется так: c1m1(t1 – 0) + lm1 + c2m1(0 – q) = c2m2(q – t2).

q, mв, mл – ?

2. Вода остынет от 20°С до 0°С, часть её замёрзнет и станет льдом при 0°С, остальная –
останется водой при 0°С.
Лёд при этом нагреется от –30°С до 0°С (см. график). И тогда в калориметре будет
находиться смесь воды со льдом при температуре 0°С. Уравнение
теплового баланса запишется так:

c₁m₁(t₁ – 0) + lm¢ = c₂m₂(q – t₂), где m¢ – масса превратившейся
в лед воды.

3. Вода
остынет от 20°С до 0°С. Лёд при этом нагреется от –30°С до 0°С, затем частично или полностью расплавится и станет водой при 0°С. В калориметре
будет смесь воды и льда при температуре 0°С. Уравнение теплового
баланса запишется так:

c₁m₁(t₁ – 0) = c₂m₂(0 – t₂) + lm², где m² – масса
превратившегося в воду льда.

4. Лёд нагреется от –30°С  до 0°С,  расплавится, и образовавшаяся из льда вода нагреется от 0°С до температуры q. А вода массой m₁ при этом остынет от 20°С до температуры q. Тогда в калориметре
будет находиться вода при температуре q. Уравнение теплового баланса запишется так:

c₁m₁(t₁ – q) = c₂m₂(0 – t₂) + lm₂ + c₁m₂(q –
0).

Проведем численный анализ ситуации. Сколько теплоты:

а) выделит вода при остывании от 20°С до 0°С:

Q₁ = c₁m₁(t₁
– 0) = 4200×0,8×20
= 67200 (Дж);

б) выделит вода при превращении в лед при 0°С:

Q₂ = lm₁ = 340000×0,8 = 272000 (Дж);

в) нужно получить льду, чтобы нагреться от –30°С до 0°С:

Q₃ = c₂m₂(0
– t₂) = 2100×2×30
= 126000 (Дж);

г) нужно получить льду, чтобы полностью
расплавиться при температуре 0°С:

Q₄ = lm₂ = 340000×2 = 680000 (Дж).

  Получаем: чтобы весь лёд нагрелся от –30°С  до 0°С, ему нужно передать
126000 Дж теплоты, а вода при этом, остывая от 20°С до 0°С, может дать только 67200
Дж. Значит, лёд эти 67200 Дж у воды «возьмет», но ему ещё не будет хватать Q¢ = 126000 Дж – 67200 Дж = 58800 Дж,
чтобы нагреться до 0°С. Он их «возьмёт» у превращающейся в лед  воды (если бы вода
полностью превратилась в лед, то она бы выделила 272000 Дж, а это больше, чем
«нужно» льду):

 Q¢ = lm¢ Þ  m¢ = Q¢/l = 58800/340000 » 0,2 (кг), где

m¢ – это масса воды, обратившейся в лёд при температуре 0°С.

 Как только лёд
нагреется до 0°С, теплообмен между льдом и водой прекратится, так как они будут иметь
одинаковые температуры.

 Итак, получили:
вода остынет до 0°С, часть её (а именно m¢ = 0,2 кг) замёрзнет и станет льдом при 0°С, а лёд нагреется до 0°С. И в результате в
калориметре будет находиться смесь воды и льда при 0°С.    При этом масса воды
будет равна:

m_в = m₁ – m¢= 0,8
кг – 0,2
кг  = 0,6 кг,

 а масса льда
равна: m_л = m₂ + m¢ = 2 кг + 0,2 кг = 2,2 кг.

Ответ: В калориметре
при 0°С 
находится смесь воды (0,6 кг) и льда (2,2
кг).

Задача 11

В калориметр,
содержащий 1 кг льда при –20°С, впускают 200 г водяного пара при 120°С. Что будет в калориметре,
когда теплообмен прекратится? Теплоёмкостью калориметра пренебречь.

m1 = 1 кг с1 = c2 = 2100 Дж/(кг×0С) t1 = –20°С m2 = 0,2 кг t2 = 120°С L = 2,3×106 Дж/кг l = 3,4×105 Дж/кг с3 =4200Дж/(кг×0С)	Решение 1. Вычислим, сколько теплоты нужно получить льду, чтобы нагреться от –20°С до 0°С: Q1¢ = c1m1(0 – t1) = 2100×1×20 = 42000 (Дж); 2. Вычислим, сколько теплоты нужно получить льду, чтобы при 0°С растаять: Q1² = lm1 = 340000×1 = 340000 (Дж); 3. Вычислим, сколько теплоты нужно получить  воде, образующейся из льда, чтобы нагреться от 0°С до 100°С: Q1²¢ = c3m1(100 – 0) = 4200×1×100 = 420000 (Дж); 4. Найдем, сколько теплоты выделит пар, остывая от 120°С до 100°С: Q2¢ = c2m2(t2 – 100) = 2100×0,2×20 = 8400 (Дж); 5. Найдем, сколько теплоты выделит пар, конденсируясь в воду  при 100°С: Q2² = Lm2 = 2300000×0,2 = 460000 (Дж); 6. Рассчитаем, сколько теплоты может выделить вода, образовавшаяся из пара, остывая от 100°С  до 0°С: Q2²¢ = c3m3(100 – 0) = 4200×0,2×100 = 84000 (Дж).
q – ? mв – ? mл – ?

Проведем анализ ситуации:

а) льду надо
получить 42000 Дж, чтобы нагреться от –20°С до 0°С, а пар, остывая от 120°С до 100°С, может отдать только 8400 Дж. Значит, лёд «возьмёт» у пара 8400 Дж,
но ещё не нагреется до 0°С. Льду не достает еще 42000 Дж – 8400 Дж = 33600 Дж, чтобы нагреться
до 0°С;

б)
недостающая энергия может быть получена от конденсации пара. Пар будет
конденсироваться при 100°С и выделит при этом 460000 Дж. Лёд за счёт этого сначала нагреется до
0°С, а
затем  будет плавиться. Для этого ему нужна энергия: 33600 Дж + 340000  Дж =
373600 Дж. Это меньше, чем выделит пар, превращаясь в воду;

в) значит,
лед растает и станет водой при 0°С. А у пара еще «останется» 460000 Дж – 373600 Дж = 86400 (Дж). Но
этого не хватит, чтобы вода, образующаяся из льда, нагрелась до 100°С. Но на сколько-то
она все же  нагреется. Поэтому можно сделать вывод: в калориметре будет
находиться только вода. Она будет состоять из воды, образованной из льда, и
воды, образованной из пара. Её масса: m_в = m₁ + m₂ = 1,2
кг.

Конечную
температуру воды q будем искать из уравнения теплового баланса:

c₁m₁(0 –
t₁) + lm₁ + c₃m₁(q –
0) =c₂m₂(t₂ – 100) + Lm₂ + c₃m₃(100 – q).

Используем результаты сделанных ранее вычислений:

c₃m₁(q – 0) – c₃m₂(100 – q) = 86400,

c₃m₁q –  c₃m₂100 + c₃m₂q = 86400,

q = .

Ответ: В калориметре будет находиться  1,2
кг воды при температуре 17°С.

Иногда в задачах говорится о
веществах, находящихся при указанных температурах в таких агрегатных
состояниях, которые не соответствуют указанной температуре. Например,
перегретая жидкость – жидкость, находящаяся при температуре выше температуры
кипения (при обычном давлении); переохлаждённая жидкость – жидкость,
находящаяся при температуре ниже температуры замерзания, но остающаяся ещё
жидкостью. Такое возможно в условиях, когда нет центров парообразования или
центров кристаллизации. При малейшем возмущении эти вещества самопроизвольно и
очень быстро переходят в то агрегатное состояние, которое соответствует
указанной температуре. В таких веществах энергия, необходимая для того или
иного процесса, заключена в самом веществе. При решении подобных задач строить
графики нет необходимости.

Задача 12

Колбу , содержащую 120
г перегретой воды при температуре 118°С и нормальном атмосферном
давлении, слегка встряхивают, отчего происходит бурное вскипание воды. Сколько
воды останется в колбе? Теплоёмкостью колбы и теплообменом с окружающей средой
пренебречь.

m = 0,12 кг t1 = 118°С t2 = 100°С с = 4200 Дж/(кг×0С) L = 2,3×106 Дж/кг

Решение Обозначим: m1 – масса выкипевшей воды. Q1 = Lm1 – энергия, необходимая для превращения в пар воды массой m1. Этот переход обычно происходит при 100°С. а вся вода находится при температуре 118°С. Значит, вся вода остывает до 100°С, выделяя при этом теплоту Q2 = cm(t1 – t2). Эта теплота и поглощается выкипающей водой. Уравнение теплового баланса: Q1 = Q2 Lm1 = cm(t1 – t2)  Þ  m1 = m m – m1 = m – m = m(1 – ) = = 0,12(1 – ) = 0,116 (кг) = 116 (г)

(m – m1) – ?

Ответ:  В колбе останется 116
г воды.

Задача 13

Пробирку, содержащую 100
г воды, переохлаждённой до температуры –10°С, слегка
встряхивают, отчего вода превращается в лёд с температурой 0°С. Какова масса
образовавшегося льда? Теплоёмкость пробирки мала.

m = 0,1 кг с =4200 Дж/(кг×0С) l = 3,4×105  Дж/кг t1 = –10°С t2 = 0°С	Решение  Вся вода нагревается от –10°С до 0°С, получая энергию Q за счёт того, что часть воды при этом превращается в лёд с температурой 0°С и выделяет при этом энергию Q1.
m1 – ?

Получается, что вся вода нагревается за счет теплоты,
выделяющейся при кристаллизации своей части. Поэтому:

Q = Q₁,

cm(t₂ – t₁)
= lm₁,

m₁ = ;

m₁ = .

Ответ:  Масса образовавшегося льда равна 12
г.

Задачи для самостоятельного
решения

1.          
Для приготовления ванны ёмкостью 100
л смешали холодную воду, имеющую температуру 12°С, и горячую, имеющую
температуру 72°С. Сколько той и другой воды надо взять, чтобы температура воды в ванне
была 36°С?^*

2.          
Когда в 2
кг воды, находящейся в калориметре при 20°С, опустили алюминиевое тело
массой 0,8 кг, имеющее температуру 100°С, температура воды поднялась до 25°С. Определить
теплоёмкость калориметра.

3.          
В 2 кг воды, имеющей температуру 20°С, опустили сначала
медное тело массой 2 кг, имеющее температуру 80°С. После того, как
температура перестала меняться, в воду опустили железное тело массой 3
кг, имеющее температуру –20°С. Какой после этого стала температура воды? Теплоёмкостью сосуда 
пренебречь.

4.          
После опускания в воду, имеющую температуру 100°С, тела с
температурой 20°С, установилась общая температура 80°С. Какой станет температура
воды, если, не вынимая первого тела, в нее опустить ещё два таких же тела,
имеющих температуру 20°С?

5.          
В чайник налили воду при температуре 20⁰С
и поставили на электроплитку. Через 13 минут вода закипела. Через какое время
половина воды выкипит?

6.          
Для того, чтобы на спиртовом нагревателе, с КПД 
70%, нагреть до кипения 1,4 кг воды и половину ее превратить в пар,  израсходовали
100 г спирта. Какова начальная температура воды? Удельная теплота сгорания
спирта 29×10⁶ Дж/кг.

7.          
В калориметре находится лёд массой 500
г  при температуре 0°С. В калориметр впускают  водяной пар температурой 100°С. Сколько воды
окажется в калориметре, когда весь лёд растает, а температура образовавшейся
воды будет равна 0°С?

8.          
В калориметр, содержащий 400
г воды и 200 г льда при 0°С, впустили водяной пар с температурой 100°С. Сколько пара было впущено
в калориметр, если в калориметре установилась температура 20°С? Теплоёмкость
калориметра 1000 Дж/⁰С.

 

9.          
В сосуд теплоёмкостью 1000 Дж/⁰С,
содержащий 5 кг воды при температуре 20°С, положили лёд, имеющий температуру –40°С. Температура
образовавшейся смеси оказалась равна –2°С. Сколько льда было положено в сосуд?

 

10.     
В алюминиевом калориметре массой 200
г находится кусок льда с температурой –20°С. В калориметр впустили водяной пар, имеющий температуру 100°С. Когда температура 
калориметра стала равна 20°С, измерили массу его содержимого. Она оказалась равной 400
г. Найти массу льда, находящегося в калориметре, и массу сконденсировавшегося
пара.

 

11.     
В калориметр, содержащий 3
кг воды при температуре 20°С, опустили 2 кг льда, имеющего температуру –10°С. Что будет в калориметре,
когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.

 

12.     
В калориметр, содержащий 1
кг льда и 800 г воды при 0°С впускают 100 г водяного пара при 100°С. Что будет в калориметре,
когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.

 

13.     
В калориметре находится вода массой 600
г при температуре 5°С. К ней долили ещё 300 г воды с температурой 10°С и положили 600
г льда с температурой –60°С. Что будет в калориметре после того, как теплообмен прекратится?
Теплоемкостью калориметра пренебречь.

14.     
В теплоизолированном медном сосуде массой 400
г находятся 2 кг льда при температуре –10°С. В сосуд помещают 400 г водяного пара при температуре 110°С. Что будет в сосуде
после того, как теплообмен прекратится?

 

15.     
В колбе находятся 200
г воды при температуре 0°С. Откачиванием паров всю воду в колбе заморозили. Сколько получилось
льда?

Ответы и решения

1.    60 л холодной и 40
л горячей воды.

t1 = 12°С t2 = 72°С q = 36°С V = 100 л	Решение Q1 = cm1(q – t1) – теплота, которую получит холодная вода, нагреваясь от 12°С до 36°С; Q2 = c(m – m1)(t2 – q) – теплота, которую отдаст горячая вода, остывая от 72°С до 36°С,
V1 – ?  V2 – ?

Q₁ = Q₂,

cm₁(q – t₁) = c(m – m₁)(t₂ – q),

m₁(q – t₁) + m₁(t₂ – q) = m(t₂ – q),

rV₁(q –
t₁ + t₂ – q) = rV (t₂ – q),

V₁ = V×;

V₁ = 100× = 60 (л),

V₂  = V – V₁ = 100 – 60 = 40 (л).

2. 2640 .

m1 = 2 кг t1 = 20°С с1=4200 Дж/(кг×0С) m2 = 0,8 кг t2 = 100°С с2 = 920 Дж/(кг×0С) q = 25°С_______ Ск – ?

Решение Q2  = Q + Q1, где Q2 – теплота, отданная алюминиевым телом; Q1 – теплота, полученная водой, Q – теплота, полученная калориметром. c2m2(t2 – q) = (Cк + c1m1)(q – t1), Cк = . Cк =   = 2640 (Дж/0С)

3. 19⁰С.

m1 = 2 кг c1=4200 Дж/(кг×0С) t1 = 20°С m2 = 2 кг c2 = 380 Дж/(кг×0С) t2 = 80°С m3 = 3 кг c3 = 460 Дж/(кг×0С) t3 = –20°С	Решение Здесь удобнее пользоваться уравнением теплового баланса в виде (6), так как при решении этим способом последовательность опускания в воду тел не важна: Q1 + Q2 + Q3 = 0, c1m1(q – t1) + c2m2(q – t2) + c3m3(q – t3) = 0, q = .
q – ?

4. 53°С

С1– теплоёмкость воды; t1 = 100°С С2– теплоёмкость тела; t2 = 20°С t3 = 80°С	Решение 1.    При опускании в воду с температурой t1 первого тела: С1(t1 – t3) = С2(t3 – t2). (1) 2.    При опускании в воду с температурой t2 сразу трех тел: С1(t1 – t4) = 3С2(t4 – t2). (2) 3.    Делим уравнение (1) на уравнение (2) и получаем: , Решая это уравнение, находим, что :  t4 » 53 °С.
t4 – ?

5.    44,5 мин.

t1 = 13 мин t1 = 20°С t2 = 100°С m2 = m1/2 с = 4200 Дж/(кг×0С) L = 2,3×106 Дж/кг

t2 – ?

Решение

Мощность электроплитки подразумеваем 
постоянной. Поэтому:

,

,

откуда:,

6. 29°С

m1 = 1,4 кг с1=4200 Дж/(кг×0С) t2 = 100°С h = 0,7 m2 = 0,1 кг q = 29×106 Дж/кг	Решение h = , где Qполез = Q1 + Q2 = = cm1(t2 – t1) + L, а Qзатр = qm2. Тогда h =
t1-?

Выражаем t₁:   t₁ = t₂ –

t₁ =
100 –  100 – 71 = 29 (°С).

7.  563
г.

m1 = 0,5кг l = 3,4×105   Дж/кг t1 = 0°С с = 4200 Дж/(кг×0С) L = 2,3×106 Дж/кг t2 = 100°С	Решение Q1 = Q2 + Q3, lm1 = Lm2 + cm2(t2 – t1), m2 = , m2 =
m – ?

                                                                              
= 0,063 (кг) = 63
г

       В итоге:   m = m₁ + m₂ = 500 +63 = 563 (г).

8.    65 г

m1 = 0,4 кг m2 = 0,2 кг l = 3,4×105 Дж/кг t1 = 0°С c =4200Дж/(кг×0С) t2 = 100°С L = 2,3×106 Дж/кг q = 20°С C = 1000 Дж/0С	Решение Q1 + Q2 + Q3 = Q4 + Q5, lm2 + c(m1 + m2)(0 – t1) + + C(q – t1) = = Lm3 + cm3(t2 – q),             m3 =  0,065 (кг).
m3 – ?

9.    27,1 кг.

C = 1000 Дж/0С m1 = 5 кг c1=4200 Дж/(кг×0С) t1 = 20°С t2 = –40°С c2=2100 Дж/(кг×0С) l = 3,4×105 Дж/кг q = –2°С	Решение Q1 + Q2 + Q3 + Q4 + Q5 = Q6, Q2  + Q4 = C(t1 – q) – теплота, отданная калориметром; Q1 + Q3 + Q5 = c1m1(t1 – 0) + lm1 + c2m1(0 – q) – теплота, отданная водой; Q6  = c2m2(q – t2) – теплота, принятая льдом.
m2 – ?

Тогда m₂
= .

m₂  =
 27,1 (кг).

10. 340
г льда и 60 г пара.

с1 = 920Дж/(кг×0С) m1 = 0,2 кг t1 = t2 = –20°С c2=2100 Дж/(кг×0С) t3 = 100°С L = 2,3×106 Дж/кг l = 3,4×105 Дж/кг c3=4200 Дж/(кг×0С) q = 20°С m =  0,4 кг	Решение Q1 + Q2 + Q3 + Q4 + Q5 = = Q6 + Q7. Q2, Q3, Q4 – теплоты, полученные льдом;      Q1, Q5 – теплоты, полученные калориметром; Q6, Q7 – теплоты, отданные паром. c1m1(q – t1) + c2m2(0 – t2) + lm2 +  c3m2(q – 0) = = L(m – m2) + c3(m – m2)(100 – q), Масса льда:
m2 – ?  m3 – ?

m₂ =

     m₂ =
 0,34 (кг)

     Масса пара: m₃ = m – m₂ = 0,4 кг – 0,34 кг = 0,06 кг.

11. Смесь, состоящая из 1,4 кг льда и 3,6
кг воды при температуре 0⁰С.

m1 = 3 кг t1 = 20°С c1= 4200 Дж/(кг×0С) m2 = 2 кг t2 = –10°С c2= 2100 Дж/(кг×0С) l = 3,4×105 Дж/кг	Решение 1. Q1 = c1m1(t1 – 0) = 4200×3×20 = 252000 (Дж) – может отдать вода, остывая от 20°С  до 0°С. 2. Q2 = c2m2(0 – t2) = 2100×2×10 = 42000 (Дж) – нужно льду, чтобы нагреться от –10°С до 0°С. 3. Q3 = lm2 = 340000×2 = 680000 (Дж) – нужно льду, чтобы полностью расплавиться. 4. Q1 – Q2 < Q3 – значит, у воды не хватит      энергии, чтобы расплавить весь лёд.
m¢1 – ? m¢2 – ? q – ?

    Вывод: лёд растает не весь, и
в калориметре будет находиться смесь воды со льдом при температуре 0°С.

   Сколько растает льда?

lm¢ = Q₁
– Q₂ Þ m¢ =  (кг)

 Тогда останется  льда: m¢₂ = m₂ – m¢ = 2 кг – 0,6
кг = 1,4 кг.

Масса воды: m¢₁ = m₁
+ m¢ = 3
кг + 0,6 кг  =
3,6 кг

12. 0,2
кг льда и 1,7 кг воды при температуре 0⁰С.

m1 = 1 кг m2 = 0,8 кг t1 = t2 = 0°С l = 3,4×105 Дж/кг c = 4200 Дж/(кг×0С) m3 = 0,1 кг t3 = 100°С L = 2,3×106 Дж/кг

Решение 1. Q1 = lm1 = 340000×1 = 340000 (Дж) – нужно льду, чтобы полностью растаять при 00С. 2. Q2 = Lm3 = 2300000×0,1 = 230000 (Дж) – может отдать пар, конденсируясь при 1000С  в воду. 3. Q3 = cm3(t3 – t1) = 4200×0,1×100 = 42000 (Дж) – может отдать пар, остывая от 1000С до 00С.         4.  Q2 + Q3 = 230000 + 42000 = 272000 (Дж) < Q1.  Поэтому лёд растает не весь, пар весь сконденсируется, а образовавшаяся из него вода остынет до 0°С.

q – ? m¢1 ­– ? m¢2 – ?

  Сколько льда растает?

lm¢ = Q₂ + Q₃ Þ m¢ =  (кг).

В калориметре останется льда: m¢₁
= m₁
– m¢ = 1 кг – 0,8
кг = 0,2 кг .

Масса воды: m¢₂ =
m₂
+ m¢ +  m₃ = (0,8 + 0,8 + 0,1) кг  = 1,7 (кг)

Полученная смесь находится при температуре 0°С.

13. Смесь воды (750
г) и льда (750 г) при 0⁰С.

m1 = 0,6 кг c1= 4200 Дж/(кг×0С) t1 = 5°С m2 = 0,3 кг t2 = 10°С m3 = 0,6 кг t3 = –600С с2= 2100 Дж/(кг×0С) l = 3,4×105 Дж/кг

Решение 1. Q1 = c1m1(t1 – 0) = 4200×0,6×5 = 12600 (Дж) – выделят 600 г воды, остывая от 5°С до 0°С. 2. Q2 = c1m2(t2 – 0) = 4200×0,3×10 = 12600 (Дж) – выделят 300 г воды, остывая от 10°С до 0°С. Q1 + Q2 = 25200 Дж. 3. Q3 = c2m3(0 – t3) = 2100×0,6×60 = 75600 (Дж) – нужно льду, чтобы нагреться от -60°С до 0°С. Q3 > Q1 + Q2 Þ вся вода остынет до 0°С, а лёд ещё при этом не нагреется до 0°С. DQ = Q3 – (Q1 + Q2) = 75600 – 25200 = 50400 (Дж). Нагреваясь до 0°С, лед «приморозит» к себе часть воды m¢:

q – ? mводы – ? mльда – ?

lm¢ = DQ Þ
m¢ =  =  (кг).

Итак, в калориметре будет находиться
смесь воды со льдом при температуре 0°С:

m_воды = m₁ + m₂ – m¢ = 0,6 + 0,3 – 0,15 = 0,75 (кг),

m_льда = m₃ + m¢ =
0,6 + 0,15 = 0,75 (кг)

14. 2,4
кг воды при температуре 36⁰С.

m1 = 0,4 кг c1 = 380 Дж/(кг×0С) m2 = 2 кг c2= 2100 Дж/(кг×0С) t1 = t2 =  –10°С l = 3,4×105 Дж/кг m3 = 0,4 кг t3 = 110°С с3= 2100 Дж/(кг×0С) L = 2,3×106 Дж/кг c4= 4200 Дж/(кг×0С)	Решение 1. Q1 = c1m1(0 – t1) = 380×0,4×10 = 1520 (Дж) – нужно получить медному сосуду, чтобы нагреться от -10°С до 0°С. 2. Q2 = c2m2(0 – t1) = 2100×2×10 = 42000 (Дж) – нужно получить льду, чтобы он нагрелся от      –10°С до 0°С. 3. Q3 = lm2 = 340000×2 = 680000 (Дж) – нужно получить льду, чтобы растаять и стать водой при 0°С. Q1 + Q2 + Q3 = 723520 (Дж) – нужно получить сосуду и льду, чтобы в сосуде при 0°С была вода. 4. Q4 = c3m3(t3 – 100) = 2100×0,4×10 = 8400 (Дж) – может отдать пар, остывая от 110°С до 100°С. 5. Q5  = Lm3 = 2300000×0,4 = 920000 (Дж) – может отдать пар, конденсируясь в воду при 1000С.
q – ? m – ?

Q₄ + Q₅ = 8400 + 920000 = 928400 (Дж) – может отдать пар, превращаясь в пар с
температурой 100°С;

DQ = (Q₄ + Q₅) – (Q₁ + Q₂ + Q₃) = 928400 – 723520 = 204880 (Дж) –
столько энергии останется у пара, когда он станет водой при 100⁰С, 
(лед при этом превратится в воду при 0°С).

Проверим, хватит ли этой энергии,
чтобы вода, образовавшаяся из льда, нагрелась вместе с сосудом от 0°С до 100°С?

Q₆ =
(c₁m₁ + c₂m₂)(100 – 0) = (380×0,4 + 4200×2)×100 =  855200 (Дж).

Это больше, чем 204880 Дж. Значит,
вода, образовавшаяся из льда, нагреется не до 100°С. Найдем, до какой 
температуры нагреются вода и сосуд:

Q₁ + Q₂ + Q₃ + (c₁m₁
+ c₄m₂)(q – 0) = Q₄ + Q₅ + c₄m₃(100
– q),

c₁m₁q + c₄m₂q + c₄m₃q = c₄m₃×100 + 204880,

q =  36(°С).

15. 174
г.

m = 0,2 кг l = 3,4×105 Дж/кг L = 2,3×106 Дж/кг	Решение
m1  – ?

Q₁ = lm₁ – энергия,
которая выделяется при замерзании воды массой m₁.

       Q₂ = L(m – m₁) – энергия, которая необходима для превращения оставшейся воды в пар.

Q₁ = Q₂,

lm₁
= L(m – m₁)

                                                                  
m₁ = m×, откуда

m₁ =  (кг) = 0,174 кг = 174 г.

Учебное издание

Самарин Григорий Геннадьевич

Решение задач на теплообмен с использованием уравнения теплового
баланса

(методические рекомендации)

Редактор
– Г. Д. Попырина

Компьютерная
верстка – К. В. Маренин

Подписано
в печать:

Бумага
типографская

Условных
печатных листов – 2,25

Тираж
– 100 экз.

Заказ
–

Цена
договорная.

Лицей естественных наук

610006, г. Киров, ул. Возрождения, 6