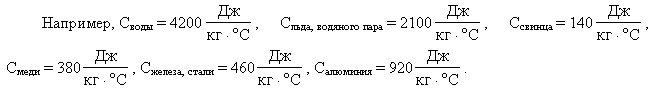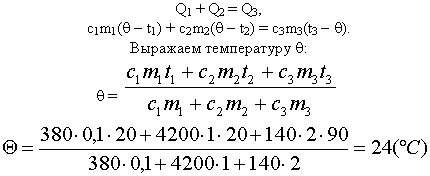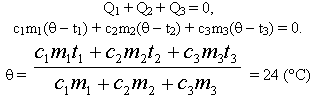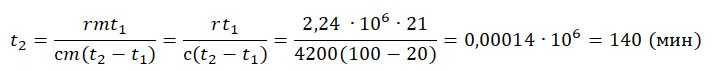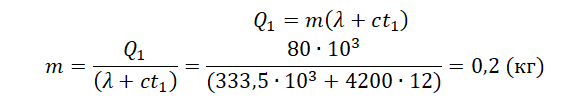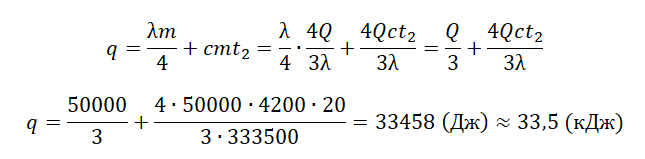Пособие рекомендовано учащимся, желающим
получить практические навыки в решении задач на
теплообмен, и может быть полезным для учителей и
абитуриентов.
При соприкосновении тел, имеющих разные
температуры, между этими телами происходит
теплообмен. С точки зрения
молекулярно-кинетической теории, это
объясняется так: молекулы более нагретого тела
имеют большую кинетическую энергию, чем молекулы
тела, менее нагретого. При “столкновениях”
молекул соприкасающихся тел происходит процесс
выравнивания их средних кинетических энергий.
Молекулы более нагретого тела теряют часть своей
кинетической энергии, при этом нагретое тело
будет остывать. Кинетическая энергия молекул
холодного тела возрастает, поэтому температура
этого тела будет увеличиваться. В конечном итоге
кинетические энергии молекул обоих тел
сравняются, и температуры тел станут
одинаковыми. На этом теплообмен прекращается.
Энергию, которую тело получает или отдаёт в
процессе теплообмена, называют количеством
теплоты (Q).
Количество теплоты, как и все другие виды
энергии, измеряется в системе СИ в Джоулях: [Q] = Дж.
(Здесь и в дальнейшем единицы измеряются в
системе СИ.)
Нагревание или охлаждение
При нагревании или охлаждении тела количество
теплоты, поглощаемое или выделяемое им,
рассчитывается по формуле:
Q = сm(t2 – t1), (1)
где m – масса тела, кг;
(t2 – t1) – разность температур
тела,° С (или К);
с – удельная теплоёмкость вещества, из
которого состоит тело,
Удельная теплоёмкость вещества – это
количество теплоты, которое нужно сообщить
одному килограмму данного вещества, чтобы
увеличить его температуру на 1° С (или это
количество теплоты, которое выделяет один
килограмм данного вещества, остывая на 1° С).
Значения удельных теплоемкостей других
веществ можно найти в справочниках, а также в
школьном учебнике или задачнике.
При нагревании тела его внутренняя энергия
увеличивается. Это требует притока энергии к
телу от других тел. Значит, оно поглощает
некоторое количество теплоты, принимая его от
других тел, участвующих в теплообмене.
При охлаждении тела его внутренняя энергия
уменьшается. Поэтому остывающее тело отдаёт
кому-либо некоторое количество теплоты.
Обычно конечную температуру, установившуюся в
результате теплообмена, обозначают греческой
буквой (тэта).
В формуле (1) произведение cm для каждого
конкретного тела есть величина постоянная. Её
называют теплоёмкостью тела и обозначают С:
C = c m.(2)
Размерность теплоемкости: Теплоемкость тела показывает,
сколько энергии нужно подвести к данному телу,
чтобы нагреть его на 1° С (или сколько энергии
выделяет это тело, остывая на 1° С).
Теплообмен между телами, имеющими одинаковые
температуры, не происходит, даже если
контактируют вещества, находящиеся в разных
агрегатных состояниях. Например, при температуре
плавления (0° С) лёд и вода могут находиться
бесконечно долго, при этом количество льда и
количество воды останутся неизменными.
Аналогично ведут себя пар и жидкость,
находящиеся при температуре кипения. Теплообмен
между ними не происходит.
Плавление или кристаллизация
Если при нагревании тела его температура
достигнет температуры плавления, то начинает
происходить процесс перехода этого вещества из
твердого состояния в жидкое. При этом идут
изменения в расположении и характере
взаимодействия молекул. Температура при
плавлении не изменяется. Это означает, что
средние кинетические энергии молекул жидкости и
твердого тела при температуре плавления
одинаковы. Однако внутренняя энергия тела при
плавлении возрастает за счет увеличения энергии
взаимодействия молекул. Количество теплоты,
поглощаемое телом при плавлении, рассчитывается
по формуле
(3)
где m – масса тела, кг;
–
удельная теплота плавления,
При кристаллизации, наоборот, внутренняя
энергия тела уменьшается на величину и эта теплота данным
телом выделяется. Она поглощается другими
телами, участвующими в теплообмене.
Удельная теплота плавления показывает,
сколько энергии нужно сообщить одному
килограмму данного вещества, взятого при
температуре плавления, чтобы полностью
превратить его при этой температуре в жидкость
(или сколько энергии выделяет 1 кг жидкости,
взятой при температуре кристаллизации, если вся
она при этой температуре полностью превратится в
твёрдое тело).
Удельную теплоту плавления любого вещества
можно найти в справочниках. Для льда же
Температура плавления у каждого вещества своя.
Её также можно найти в справочниках. Важно
подчеркнуть, что температура плавления вещества
равна температуре кристаллизации этого же
вещества. У льда tпл = 0° С.
Кипение или конденсация
При достижении жидкостью температуры кипения
начинает происходить другой фазовый переход –
кипение, при котором расстояния между молекулами
значительно увеличиваются, а силы
взаимодействия молекул уменьшаются. Вся
подводимая к жидкости теплота идет на разрыв
связей между молекулами. При конденсации пара в
жидкость, наоборот, расстояния между молекулами
значительно сокращаются, а силы взаимодействия
молекул увеличиваются. Для кипения жидкости
энергию к жидкости нужно подводить, при
конденсации пара энергия выделяется. Количество
теплоты, поглощаемое при кипении или выделяемое
при конденсации, рассчитывается по формуле:
где m – масса тела, кг; L – удельная
теплота парообразования,
Удельная теплота парообразования
показывает, сколько энергии нужно сообщить
одному килограмму жидкости, взятой при
температуре кипения, чтобы при этой температуре
полностью превратить её в пар (для конденсации:
сколько энергии выделяет один килограмм пара,
взятого при температуре конденсации, полностью
превращаясь в жидкость).
При одинаковом давлении температура кипения и
температура конденсации одного и того же
вещества одинаковы.
Температуры кипения и удельные теплоты
парообразования также можно найти в
справочниках. Для воды же они соответственно
равны: рис. 9 (при нормальном атмосферном
давлении).
Уравнение теплового баланса
Тела, участвующие в теплообмене, представляют
собой термодинамическую систему.
Термодинамическая система называется теплоизолированной,
если она не получает энергию извне и не отдаёт её;
теплообмен происходит только между телами,
входящими в эту систему. Для любой
теплоизолированной системы тел справедливо
следующее утверждение: количество теплоты,
отданное одними телами, равно количеству
теплоты, принимаемому другими телами.
Qотд. = Qполуч. (5)
Это утверждение описывает частный случай
закона сохранения и превращения энергии в
применении к процессу теплообмена. А формула (5)
является одним из видов уравнения теплового
баланса.
При решении задач с помощью данного вида
уравнения теплового баланса в формуле (1) в
качестве t2 следует брать большую
температуру, а в качестве t1 – меньшую.
Тогда разность (t2 – t1) будет
положительна и всё произведение cm(t2–t1)
также будет положительным. Все теплоты, отданные
и полученные, будут положительными.
Уравнение теплового баланса можно записать и в
таком виде:
Q1+ Q2+…+ Qn= 0, (6)
где n – количество тел системы.
Алгебраическая сумма всех количеств теплоты
(поглощенных и выделенных) в теплоизолированной
системе равна нулю.
Q1, Q2, …, Qn – это теплоты,
поглощаемые или выделяемые участниками
теплообмена. Очевидно, что в этом случае какие-то
теплоты должны быть положительны, а какие-то –
отрицательны. При записи уравнения теплового
баланса в виде (6) всегда t2 – конечная
температура, а t1 – начальная.
Если тело нагревается, то разность (t2 – t1)
положительна и все произведение cm(t2 – t1)
положительно. То есть Q > 0 тогда, когда теплота к
данному телу подводится.
А если t2 < t1 (тело остывает), то
разность (t2 – t1) отрицательна, то есть
Q < 0. В этом случае тело энергию выделяет.
Если при фазовом переходе энергия к телу
подводится (плавление, кипение), то Q > 0; если
тело выделяет энергию (кристаллизация,
конденсация), то Q < 0.
В принципе уравнения (5) и (6) равносильны.
Результат решения задачи не зависит от того,
каким видом уравнения пользуемся. Выбор способа
решения – за читателем.
Применим уравнение теплового баланса для
решения ряда задач (здесь приводим лишь одну
задачу, остальные материалы можно найти по
адресу http:// kirov-festival.nm.ru).
Задача 1
В медном калориметре массой 100 г находится 1 кг
воды при температуре 20° С. В воду опускают
свинцовую деталь массой 2 кг, имеющую температуру
90° С. До какой температуры нагреется вода? (В этой
и последующих задачах потерями теплоты в
калориметре пренебречь.)
Решение
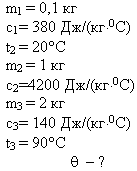 |
Проведём анализ:
Вода и калориметр При опускании в воду с температурой 20° С |
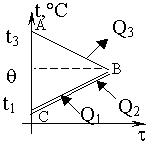 |
Изменение температур тел с течением времени удобно изображать на графике зависимости t(t ). Отрезок АВ соответствует |
| Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q1 и Q2, которую они поглощают. |
|
| Решим задачу с использованием уравнения теплового баланса в виде (5): |
Решим задачу с использованием уравнения
теплового баланса в виде (6):
Ответ: Вода нагреется до 24° С.
Предлагаю читателю самостоятельно сделать
проверку размерности.
Напомним, остальной материал (полноценную
версию пособия) можно найти по адресу http:// kirov-festival.nm.ru.
Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.
Что такое теплообмен и при каких условиях он происходит
Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.
Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.
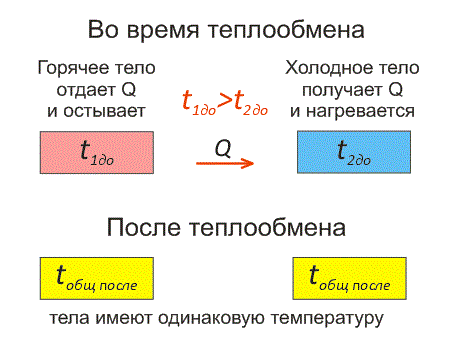
Рассмотрим два тела, имеющие различные температуры (рис. 1).
Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.
Рис.1. Два тела во время теплообмена и после
На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.
Когда температуры тел выравниваются, теплообмен прекращается.
Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.
Когда температура тел выравняется, теплообмен прекратится.
Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.
Уравнение теплового баланса и сохранение тепловой энергии
Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».
А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».
Эти факты отражены на рисунке 2.
Рис. 2. Полученное количество теплоты имеет знак «+», а отданное Q – знак «-»
Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.
Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.
Уравнение теплового баланса
Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.
Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:
[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]
(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.
(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.
В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.
Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.
В некоторых учебниках применяют сокращения:
[large Q_{1} + Q_{2} = 0 ]
Примечание: Складывая два числа мы получим ноль, когда эти числа будут:
- равными по модулю и
- имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).
Если несколько тел участвуют в процессе теплообмена
Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:
[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]
При этом:
- Q для каждого нагреваемого тела будет обладать знаком «+»,
- Q для каждого охлаждаемого тела — знаком «-».
Пример расчетов для теплообмена между холодным и горячим телом
К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.
Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
Решение:
В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.
Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.
1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:
[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]
2). Теперь запишем формулу для каждого количества теплоты:
[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]
[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]
Примечания:
- (large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
- Массу воды переводим в килограммы;
- Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
- Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;
3). Подставим выражения для каждого Q в уравнение баланса:
[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]
4). Для удобства, заменим символы числами:
[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]
Проведем упрощение:
[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]
Раскрыв скобки и решив это уравнение, получим ответ:
[large t_{text{общ}} = 58,33 ]
Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.
Задача для самостоятельного решения:
В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.
Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:
- (large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
- (large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
- (large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;
А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.
Выводы
- Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
- Когда тела будут иметь равную температуру, теплообмен прекратится;
- Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
- А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
- Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
- Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
- В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
- В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.
Фазовые переходы — это термодинамические процессы, приводящие к изменению агрегатного состояния вещества.
Плавление и отвердевание
ОпределениеПлавление — переход вещества из твердого состояния в жидкое.
Для расчета количества теплоты, необходимого для процесса плавления, следует применять формулу:
Q=λm
m — масса вещества, λ (Дж/кг) — удельная теплота плавления.
Плавление каждого вещества происходит при определенной температуре, которую называют температурой плавления. Все проводимое тепло идет на разрушение кристаллической решетки, при этом увеличивается потенциальная энергия молекул. Кинетическая энергия остается без изменения и температура в процессе плавления не изменяется.
Удельная теплота плавления показывает, какое количество теплоты необходимо сообщить 1 кг данного вещества, чтобы перевести его из твердого состояния в жидкое при условии, что оно уже нагрето до температуры плавления. В процессе отвердевания 1 кг данной жидкости, охлажденной до температуры отвердевания, выделится такое же количество теплоты.
Внимание! Удельная теплота плавления — табличная величина.
ОпределениеОтвердевание, или кристаллизация — переход состояния из жидкого состояния в твердое (это процесс, обратный плавлению).
Отвердевание происходит при той же температуре, что и плавление. В процессе отвердевания температура также не изменяется. Количество теплоты, выделяемое в процессе отвердевания:
Q=−λm
Парообразование и конденсация
ОпределениеПарообразование, или кипение — переход вещества из жидкого состояния в газообразное.
Количество теплоты, необходимое для процесса кипения, вычисляют по формуле:
Q=rm
m — масса вещества, r (Дж/кг) — удельная теплота парообразования.
Парообразование происходит при определенной температуре, которую называют температурой кипения. В отличие от испарения, процесс парообразования идет со всего объема жидкости. Несмотря на то, что к кипящему веществу подводят тепло, температура не изменяется. Все затраты энергии идут на увеличение промежутком между молекулами. Температура кипения зависит от рода вещества и внешнего атмосферного давления.
Удельная теплота парообразования показывает, какое количество теплоты необходимо затратить, чтобы перевести в пар 1 кг жидкости, нагретой до температуры кипения. Такое же количество теплоты выделится в процессе конденсации 1 кг пара, охлажденного до температуры конденсации.
Внимание! Удельная теплота парообразования — табличная величина.
ОпределениеКонденсация — процесс, обратный кипению. Это переход вещества из газообразного состояния в жидкое.
Конденсация происходит при температуре кипения, которая также не изменяется во время всего процесса. Количество теплоты, выделяемое в процессе конденсации:
Q=−rm
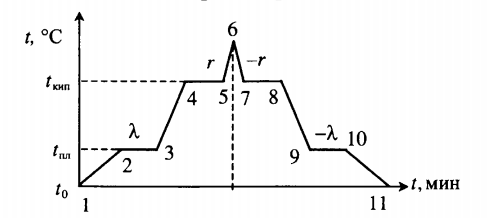
Тепловые процессы при нагревании и охлаждении
Все фазовые переходы, а также процессы нагревания и остывания вещества можно отобразить графически. Посмотрите на график фазовых переходов вещества:
Он показывает зависимость температуры вещества от времени в процессе его нагревания и остывания. Опишем процессы, отображаемые на графике, в таблице.
| Процесс | Что происходит | Количество выделенной теплоты |
| 1–2 | Нагревание твердого тела |
Q=cтm(tпл−t0) ст — удельная теплоемкость вещества в твердом состоянии. |
| 2–3 | Плавление при температуре плавления (tпл) |
Q=λm |
| 3–4 | Нагревание жидкости |
Q=cжm(tкип−tпл) сж — удельная теплоемкость вещества в жидком состоянии. |
| 4–5 | Кипение при температуре кипения (tкип) |
Q=rm |
| 5–6 | Нагревание пара |
Q=cпm(t−tкип) сп — удельная теплоемкость вещества в газообразном состоянии. |
| 6–7 | Охлаждение пара |
Q=cпm(tкип−t) |
| 7–8 | Кипение при температуре кипения (tкип) |
Q=−rm |
| 8–9 | Охлаждение жидкости |
Q=cжm(tпд−tкип) |
| 9–10 | Отвердевание при температуре плавления (tпл) |
Q=−λm |
| 10–11 | Охлаждение твердого тела |
Q=cтm(t0−tпл) |
Внимание! На участках 2–3 и 9–10 вещество частично находится в жидком и твердом состояниях, а на 4–5 и 7–8 — в жидком и газообразном.
Частные случаи тепловых процессов
| Что происходит | График | Формула количества теплоты |
| Полностью растопили лед, имеющий отрицательную температуру. | 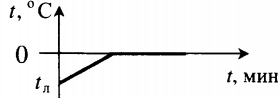 |
Q=cлm(tпл−tл)+λm cл — удельная теплоемкость льда, tл — начальная температура льда. |
| Лед, взятый при отрицательной температуре, превратили в воду при комнатной температуре. | 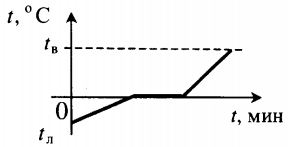 |
Q=cлm(tпл−tл)+λm+cвm(tв−tпл) cв — удельная теплоемкость воды. |
| Взяли лед при температуре 0 оС и полностью испарили. | 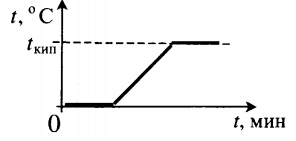 |
Q=λm+cвm(tкип−tпл)+rm |
| Взяли воду при комнатной температуре и половину превратили в пар. | 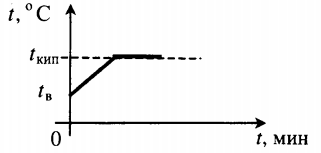 |
Q=cвm(tкип−tв)+rm2 |
Подсказки к задачам
| Единицы измерения | Температуру можно оставлять в градусах Цельсия, так как изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах. |
| Кипяток | Вода, которая при нормальном атмосферном давлении имеет температуру в 100 оС. |
| Объем воды 5 л | m = 5 кг, так как:
m=ρV=103· Внимание! Равенство V (л) = m (кг) справедливо только для воды. |
Пример №1. Какое количество теплоты нужно сообщить льду массой 2 кг, находящемуся при температуре –10 оС, чтобы превратить его в воду и нагреть ее до температуры +30 оС?
Можно выделить три тепловых процесса:
- Нагревание льда до температуры плавления.
- Плавление льда.
- Нагревание воды до указанной температуры.
Поэтому количество теплоты будет равно сумме количеств теплоты для каждого из этих процессов:
Q=Q1+Q2+Q3
Q=cлm(0−t1)+λm+cвm(t2−0)
Удельные теплоемкости и удельную теплоту плавления смотрим в таблицах:
- Удельная теплоемкость льда = 2050 Дж/(кг∙К).
- Удельная теплоемкость воды = 4200 Дж/(кг∙К).
- Удельная теплота плавления льда = 333,5∙103 Дж/кг.
Отсюда:
Q=2050·2(0−(−10))+333,5·103·2+4220·2·30=961200 (дж)=961,2 (кДж)
Уравнение теплового баланса
Суммарное количество теплоты, которое выделяется в теплоизолированной системе равно количеству теплоты (суммарному), которое в этой системе поглощается.
Математически уравнение теплового баланса с учетом знаков количества теплоты записывается так:
Qотд=−Qпол
Отданное количество теплоты меньше нуля (Qотд < 0), а полученное количество теплоты положительно (Qполуч > 0).
Подсказки к задачам на уравнение теплового баланса
| Теплообмен происходит в калориметре | Потерями энергии можно пренебречь. |
| Жидкость нагревают в некотором сосуде | Начальные и конечные температуры жидкости и сосуда совпадают. |
| В жидкость опускают термометр | Через некоторое время он покажет конечную температуру жидкости и термометра. |
| Мокрый снег | Содержит воду и лед при 0 оС. Учтите, что лед плавится, если он находится при температуре 0 оС и получает энергию от более нагретого тела. Вода кристаллизируется при температуре 0 оС, если она отдает энергию более холодному телу. Если лед и вода находятся при температуре 0 оС, то никаких агрегатных переходов между ними не происходит. |
Частные случаи теплообмена
| В воду комнатной температуры бросили ком снега, содержащий некоторое количество воды, после чего установилась некоторая положительная температура. | 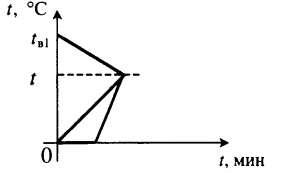
Уравнение теплового баланса: Q1+Q2+Q3=0 cвmв1(t−tв1)+cвmв2(t−0)+λmл+cвmл(t−0)=0 |
| Для получения некоторой положительной температуры воды используют горячую воду и лед, имеющий отрицательную температуру. | 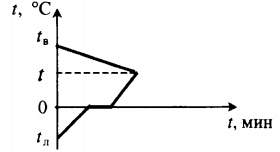
Уравнение теплового баланса: Q1+Q2=0 cвmв(t−tв)+cлmл(0−tл)+λmл+cвmл(t−0)=0 |
| В воду комнатной температуры бросают раскаленное твердое тело, в результате часть воды испаряется. | 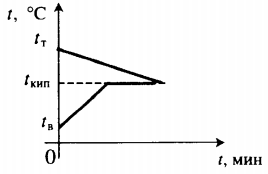
Уравнение теплового баланса: Q1+Q2=0 cтmт(100−tт)+cвmв(100−tв)+rmп=0 |
| Воду комнатной температуры нагревают до кипения, вводя пар при t = 100 оС. | 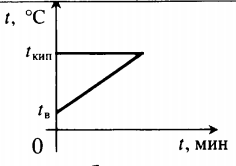
Уравнение теплового баланса: Q1+Q2=0 −rmп+cвmв(100−tв)=0 |
| Лед, имеющий температуру плавления, нагревают до положительной температуры, вводя пар при t = 100 оС. | 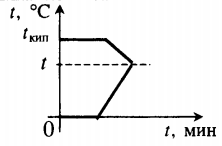
Уравнение теплового баланса: Q1+Q2=0 −rmп+cвmп(t−tкип)+λmл+cвmл(t−tпл)=0 |
Пример №2. В кастрюлю, где находится вода объемом 2 л при температуре 25 оС, долили 3 л кипятка. Какая температура воды установилась?
2 л = 2 кг
3 л = 3 кг
Количество теплоты, отданное кипятком, равно количеству теплоты, принятому более прохладной водой. Поэтому:
cm1(t−t0)=−cm2(t−tкип)
Или:
m1(t−t0)=−m2(t−tкип)
m1t+m2t=m1t0+m2tкип
(m1+m2)t=m1t0+m2tкип
t=m1t0+m2tкипm1+m2
t=2·25+3·1002+3=3505=70 (°C)
Взаимные превращения механической и внутренней энергии
Если в тексте задачи указан процент одного вида энергии, перешедший в другой, то он указывается в виде десятичной дроби перед этой энергией, которой тело обладало вначале.
Частные случаи закона сохранения энергии
| При неупругом ударе о стенку пуля нагрелась |
mv22=cmΔt |
| Тело падает с некоторой высоты и в момент падения нагревается |
mgh=cmΔt |
| В результате того, что пуля пробивает стену, ее скорость уменьшается, 50% выделившейся при этом энергии идет на нагревание пули |
0,5(mv202−mv22)=cmΔt |
| Летящая пуля при ударе о стенку расплавилась. Начальная температура пули меньше температуры плавления |
mv22=cmΔt+λm |
| Капля воды, падая с некоторой высоты, в момент удара испарилась. Температура капли у поверхности земли меньше температуры кипения. На нагрев пошло 60% выделившейся механической энергии |
0,6mgh=cmΔt+rm |
| Вследствие сгорания топлива ракета поднялась на некоторую высоту |
qmтоп=mрgh |
| Вследствие сгорания топлива снаряд приобрел некоторую скорость, и на это было затрачено 25% энергии |
0,25qmтопmсv22 |
Пример №3. Свинцовая дробинка, летящая со скоростью 100 м/с, попадает в доску и входит в нее. 52% кинетической энергии дробинки идет на ее нагревание. На сколько градусов нагрелась дробинка? Удельная теплоемкость свинца 130 Дж/(кг∙К).
Запишем закон сохранения энергии для этого случая:
0,52mv22=cmΔt
Δt=0,52v22c=0,52·10022·130=20 (К)
Примеры КПД
| Устройство | Полезная энергия (работа), затраченная энергия (полная работа) | КПД |
| Электронагреватель, электроплитка, электрочайник, кипятильник. |
Qполезн=cmΔT Иногда: Qполезн=cmΔT+rm Wзатр=Pt (произведение мощности на время) |
η=cmΔTPt100% |
| Газовая горелка, паровая турбина, спиртовка, плавильная печь. |
Qполезн=cmΔT Qзатр=qmтоп |
η=cmΔTqmтоп100% |
| Двигатель автомобиля, самолета. |
Aполезн=Nt=Nsv Qзатр=qmтоп |
η=cmΔTvqmтоп100 |
| Ружье с пороховым зарядом, пушка |
Eполезн=mv22 Qзатр=qmпор |
η=mv22qmпор100 |
Внимание! Если в задаче указано время, в течение которого происходит один тепловой процесс, а спрашивают о времени протекания другого, то считайте, что мощность нагревателя или холодильника постоянна:
Q1t1=Q2t2
Пример №4. Для нагревания на электроплитке некоторого количества воды от 20 до 100 оС потребовалась 21 минута. Сколько времени после этого необходимо для полного испарения воды? Удельная теплоемкость воды 4200 Дж (кг∙К), удельная теплота парообразования 2,24 МДж/кг.
Будем считать, что мощность электроплитки постоянна. Поэтому:
Q1t1=Q2t2
Количество теплоты, сообщенное воде при нагревании:
Q1=сm(t2−t1)
Количество теплоты, которое нужно сообщить, чтобы вода полностью испарилась:
Q1=rm
Отсюда:
сm(t2−t1)t1=rmt2
Задание EF17544
Кусок льда, имеющий температуру 0°С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 12°С, требуется количество теплоты 80 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 60 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь.
Ответ:
а) 0°С
б) 4°С
в) 6°С
г) 9°С
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать уравнение теплового баланса для первого случая.
Решение
Запишем исходные данные:
• Начальная температура льда: t0 = 0 oC.
• Конечная температура воды в первом случае: t1 = 12 oC.
• Количество теплоты, выделенное электронагревателем в первом случае: Q1 = 80 кДж.
• Количество теплоты, выделенное электронагревателем во втором случае: Q2 = 60 кДж.
Составим уравнение теплового баланса для первого случая:
Q1=λm+cmt1
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Найдем массу льда из уравнения теплового баланса для первого случая. Учтем что:
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).
• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).
Отсюда:
Чтобы расплавить кусок льда массой 0,5 кг, нужно затратить следующее количество теплоты:
Лед не расплавится весь, так как ему будет сообщено лишь 60 кДж теплоты. Поэтому в калориметре температура будет равна 0 оС.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18791
Внимательно прочитайте текст задания и выберите верный ответ из списка
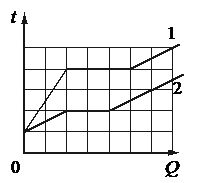
Используя данные графиков, выберите из предложенного перечня два верных утверждения и укажите их номера.
Ответ:
а) Температура плавления первого тела в 1,5 раза больше, чем второго.
б) Тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
в) Удельная теплоёмкость второго тела в твёрдом агрегатном состоянии
в 3 раза больше, чем первого.
г) Оба тела имеют одинаковую удельную теплоту плавления.
д) Тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Алгоритм решения
- Проанализировать каждое из утверждений.
- Проверить истинность утверждений с помощью графика.
- Выбрать и записать верные утверждения.
Решение
Проверим первое утверждение, согласно которому, температура плавления первого тела в 1,5 раза больше, чем второго.
Если это было бы так, то количество клеток до горизонтального участка графика 1 относилось к количеству клеток до горизонтального участка графика 2 как 3 к 2. Но мы видим, что до 1 графика 4 клетки, до 1 — 2. Следовательно, температура плавления первого тела в 2 раза больше, чем второго.
Первое утверждение неверно.
Проверим второе утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков совпадали бы. Только в таком случае температура тел увеличивалась на одну и ту же температуру при получении одного и того же количества теплоты. Но мы видим, что это не так.
Второе утверждение неверно.
Проверим третье утверждение, согласно которому удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого.
Если это было бы так, то первое тело при сообщении телам одинакового количества теплоты нагревалось бы втрое быстрее второго. И это действительно так, потому что температура второго во время нагревания в твердом состоянии увеличилась только на 1 клетку, в то время как температура первого тела — на 2 клетки.
Третье утверждение верно.
Проверим четвертое утверждение, согласно которому оба тела имеют одинаковую удельную теплоту плавления.
Если это было бы так, то протяженность горизонтальных участков обоих графиков была бы одинаковой. Но это не так. Протяженность этого участка для тела 1 составляет 3 клетки, для тела 2 — 2 клетки.
Четвертое утверждение верно.
Проверим пятое утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков были параллельными. Только при таком условии при повышении температуры на одно и то же количество градусов тела бы получли одинаковое количество теплоты. И это действительно так.
Пятое утверждение верно.
Вывод: верным утверждения «в» и «д».
Ответ: вд
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22685
В сосуде лежит кусок льда. Температура льда t1 = 0 °C. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20 °C? Тепловыми потерями на нагрев сосуда пренебречь.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать уравнение теплового баланса.
3.Выполнить решение в общем виде.
4.Определить и вычислить искомую величину.
Решение
Запишем исходные данные:
• Начальная температура льда: t1 = 0 oC.
• Конечная температура воды: t2 = 20 oC.
• Количество теплоты, переданное льду изначально: Q = 50 кДж.
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).
• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).
50 кДж = 50000 Дж
333,5 кДж = 333500 Дж
Составим уравнение теплового баланса:
Qобщ=Q+q
где q — количество теплоты, необходимое для того, чтобы окончательно растопить лед и нагреть воду:
q=Q2+Q3
Мы знаем, что изначально было растоплено 3/4 льда. Поэтому:
Q=3λm4
Отсюда масса льда равна:
m=4Q3λ
На растопку оставшегося льда уйдет следующее количество теплоты:
Q2=λm4
На нагревание воды уйдет следующее количество теплоты:
Q3=cmt2
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Отсюда:
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13k
В этой статье тема «найти тепловое равновесие» будет кратко изложена. В состоянии теплового равновесия передача тепла между двумя веществами, находящимися в контакте, отсутствует.
Из нулевого закона термодинамики мы получаем ясное представление о тепловом равновесии. Тепловое равновесие – это состояние между двумя объектами, при котором тепло не передается и объекты контактируют друг с другом. Температура для двух объектов остается одинаковой для условия теплового равновесия.
Очень интересной концепцией, связанной с температурой, является термин тепловое равновесие. Два вещества находятся в состоянии теплового равновесия, если в замкнутой системе температура объектов повышается или снижается до тех пор, пока они не достигнут состояния равновесия, несмотря на то, что между двумя веществами не происходит передачи энергии. Так же, как и когда вещества не находятся в контакте, они также находятся в состоянии теплового равновесия, если, находясь в контакте, тем не менее обмен энергией между двумя веществами не происходит.
Кредит изображения – Википедия
Примеры теплового равновесия:
Некоторые примеры теплового равновесия обсуждаются ниже.
- Измерение температуры тела человека термометром хороший пример теплового равновесия. При исследовании температуры с помощью термометра температура набирается термометром и через определенное время, когда температура тела и термометра становится одинаковой, теплопередача между телом и термометром прекращается, что означает, что состояние достигает равновесного состояния.
- Внезапно сунуть руку в кубик льда — еще один хороший пример теплового равновесия. Когда рука помещается в кубик льда, в это время температура между кубиком и рукой начинает снижаться. передавать тепло и когда температура между рукой и кубиком льда станет одинаковой, теплопередача будет остановлена, что означает, что состояние достигает состояния равновесия.
- Плавление кубика масла также является примером теплового равновесия. Когда кубик масла помещается в естественную в это время температуру между кубиком и атмосферой, попытайтесь достичь той же температуры, таким образом, начнется передача тепла, и когда температура между атмосферой и кубиком масла станет одинаковой, теплопередача прекратится. , означает, что состояние достигает состояния равновесия.
Как найти тепловое равновесие?
Тепловое равновесие – это состояние, при котором теплообмен двух веществ прекращается, когда их температуры достигают одной и той же точки. Тепловое равновесие определяется по этой формуле
Где,
Q = полная энергия удельной материи тела, выраженная в джоулях.
m = масса конкретного вещества тела, выраженная в граммах.
Ce = Удельная теплоемкость удельной материи тела, которая выражается в джоулях на кельвин на килограмм
Δt = температура конкретного вещества тела, выраженная в градусах Кельвина.
Если заданы значения массы вещества и удельной теплоемкости, температуры, то легко подставляя значения в …уравнение (1), мы можем определить величину теплового равновесия.
Теперь с помощью численной задачи обсуждается тепловое равновесие,
Проблема:
Чтобы 40 граммов воды нагрелись до 45 градусов по Цельсию. Теперь определите значение энергии, при котором вода остается в состоянии теплового равновесия.
Решение:-
В задаче приведены данные,
Масса воды (м) = 40 грамм
Удельная теплоемкость воды Ce = 4.17 Дж на грамм-градус Цельсия
Температура Δt = 45 градусов по Цельсию
Мы знаем, что формула теплового равновесия такова:
Q = м х Сe х Δt
Где,
Q = Полная энергия удельной материи тела
m = масса конкретного вещества тела
Ce= Удельная теплоемкость удельного вещества тела
Δt = температура конкретного вещества тела
Теперь мы помещаем значения в уравнение,
Q = 40 х 4.17 х 45
Q = 7506 Дж.
Чтобы 40 граммов воды нагрелись до 45 градусов по Цельсию. Значение энергии, при котором вода остается на тепловое равновесие состояние 7506 Дж.
Когда найти тепловое равновесие?
Когда два тела соприкасаются, тепло (энергия) передается от одного к другому, пока они не достигнут одинаковой температуры (находятся в тепловом равновесии). Когда объекты имеют одинаковую температуру, теплопередача отсутствует.
Формула для расчета теплового равновесия:
Тепло – это поток энергии от более высокой температуры к более низкой температуре. Когда эти температуры уравновешиваются, тепло перестает течь, тогда говорят, что система (или набор систем) находится в тепловом равновесии.
Формула теплового равновесия:
Q = м х Сe х Δt
Где,
Q = полная энергия удельной материи тела, выраженная в джоулях.
m = масса конкретного вещества тела, выраженная в граммах.
Ce= удельная теплоемкость удельного вещества тела, выраженная в джоулях на кельвин на килограмм.
Δt = температура конкретного вещества тела, выраженная в градусах Кельвина.
Как найти конечную температуру в тепловом равновесии?
С помощью числовых значений конечная температура в тепловом равновесии описана ниже,
Кусок железа массой 220 грамм. Температура куска железа составляет 310 градусов по Цельсию. Предположим, что кусок железа опущен на сосуд, наполненный водой. Вес воды 1.2 кг, температура 22 градуса по Цельсию.
Определить конечную температуру теплового равновесия воды.
Решение:-
Пусть конечная температура в тепловом равновесии для воды = Т градусов по Цельсию.
Теперь изменение температуры,
Δт = Токончательный – Тначальный
Изменение тепла,
Q = м х Сe х Δt
Итак, изменение теплоты куска железа равно
ΔQжелезо = 220/1000 х 450 х (Т – 310) Дж
ΔQжелезо = 99 (Т – 310) Дж
Итак, изменение теплоты воды равно
ΔQводы = 1.20 х 4200 х (Т – 22) Дж
ΔQводы = 5040 (Т – 22) Дж
Используя закон сохранения энергии, мы можем написать,
ΔQжелезо+ ΔQводы = 0
Помещая полученные значения,
99 (Т – 310) + 5040 (Т – 22) = 0
99 Тл – 30690 + 5040Т – 110880 = 0
5138 Т = 141570
Т = 141570/5138
Т = 27.5 градусов по Цельсию.
Кусок железа массой 220 грамм. Температура куска железа составляет 310 градусов по Цельсию. Предположим, что кусок железа опущен на сосуд, наполненный водой. Вес воды 1.2 кг, температура 22 градуса по Цельсию.
Конечная температура в тепловом равновесии для воды составляет 27.5 градусов по Цельсию.
Проблема: 1
Сколько энергии потребуется для повышения температуры 55 граммов воды на 40 градусов по Цельсию?
Решение:-
Данные данные,
Масса воды (м) = 40 грамм
Удельная теплоемкость воды Ce = 4.17 Дж на грамм-градус Цельсия
Температура ΔT = 55 градусов по Цельсию
Мы знаем, что формула теплового равновесия такова:
Q = м х Сe х ΔТ
Где,
Q = Полная энергия удельной материи тела
m = масса конкретного вещества тела
Ce = Удельная теплоемкость удельного вещества тела
Delta; t = Температура конкретного вещества тела
Q = 40 х 4.17 х 55
Q = 9174 Дж.
Для повышения температуры 9174 граммов воды на 55 градусов по Цельсию требуется энергия 40 Дж.
Проблема: 2
Рамеш, друг Ратана, увлекается коллекционированием камней. Пока Рамеш собирает камни, он всегда бросает их в контейнер. Контейнер изготовлен из металлического алюминия. Вес контейнера 15.2 грамма. Естественно, температура контейнера составляет около 36 градусов по Цельсию. Теперь Рамешу в алюминиевую тару наливают холодную воду. Температура воды будет 22 градуса по Цельсию, а вес воды 32 грамма.
Определите точную температуру, при которой температура алюминиевого сосуда и температура холодной воды будут одинаковыми.
Решение: –
Мы знаем, что формула теплового равновесия такова:
Q = м х Сe х ΔТ
Где,
Q = Полная энергия удельной материи тела
m = масса конкретного вещества тела
Ce = Удельная теплоемкость удельного вещества тела
Delta; t = (Конечная температура – Начальная температура) удельного вещества тела
Для алюминия,
QA = мA * СeA * ΔtA ………….. уравнение (1)
Данные данные,
mA = 15.2 грамма
CeA = 0.215 калории на грамм-градус Цельсия
ΔtA = (Тf – ТiA) градус Цельсия = (Tf – 36) градусов по Цельсию
Для воды,
QW = мW * СeW * ΔtW ………….. уравнение (1)
Данные данные,
mW = 32 грамм
CeW = 1 калории на грамм-градус Цельсия
ΔtW = (Тf – ТiW) градус Цельсия = (Tf – 22) градусов по Цельсию
Теперь из ………….. уравнения (1) и ………….. уравнения (2) мы можем написать,
QA = мA * СeA * ΔtA знак равно QW = (-) мW * СeW * ΔtW
Подставляя значение из уравнения (1) и уравнения (2),
15.2 х (0.215) х (Тf – 36) = (-) 32 х 1 х (Тf – 22)
(Поместите значение для CeW = 1 калории на грамм-градус Цельсия
3.268 х (Тf – 36) = -32 (Тf – 22)
3.268 Tf – 117.648 = -32 Тлf + 704
3.268 Tf + 32 тf = 704 + 117.648
Tf = 704 + 117.648/35.268
Tf = 23.2 градуса по Цельсию
Рамеш, друг Ратана, увлекается коллекционированием камней. Пока Рамеш собирает камни, он всегда бросает их в контейнер. Контейнер изготовлен из металлического алюминия. Вес контейнера 15.2 грамма. Естественно, температура контейнера составляет около 36 градусов по Цельсию. Теперь Рамешу в алюминиевую тару наливают холодную воду. Температура воды будет 22 градуса по Цельсию, а вес воды 32 грамма.
Точная температура, при которой температура алюминиевого контейнера и температура холодной воды будут одинаковыми, составляет 23.2 градуса по Цельсию.
Проблема: 3
Неустановленный металл хранится в лаборатории. Вес неуказанного металла 6 грамм. Теперь к неуказанному металлу добавлена энергия 248.2 Дж. Температура неуказанного металла повышается до 116 градусов по Цельсию.
Теперь определите количество удельной теплоемкости для неуказанного металла.
Решение:-
Данные данные,
Масса неуказанного металла (м) = 6 грамм
Нужно рассчитать,
Удельная теплоемкость для неуказанного металла Ce знак равно Джоуль на грамм-градус Цельсия
Температура Delta; t = 116 градуса по Цельсию
Общая энергия неуказанного металла (Q) = 248.2 Дж.
Мы знаем, что формула теплового равновесия такова:
Q = м х Сe х ΔТ
Ce = Q/мDelta; t
Где,
Q = Полная энергия удельной материи тела
m = масса конкретного вещества тела
Ce= Удельная теплоемкость удельного вещества тела
Delta; t = Температура конкретного вещества тела
Ce = 248.2 / 6Delta; t
Ce= 248.2/6 х 116
Ce = 0.356 Дж на грамм-градус Цельсия.
Неустановленный металл хранится в лаборатории. Вес неуказанного металла 6 грамм. Теперь к неуказанному металлу добавлена энергия 248.2 Дж. Температура неуказанного металла повышается до 116 градусов по Цельсию. Количество удельной теплоты для неуказанного металла составляет 0.356 Дж на грамм-градус Цельсия.
Вывод:
Две физические системы находятся в тепловом равновесии, если между ними нет чистого потока тепловой энергии, когда они соединены путем, проницаемым для тепла.
Содержание:
- Изменение внутренней энергии
- Внутренняя энергия тела
- Теплообмен
- Виды теплообмена
- Изменение внутренней энергии при нагревании и охлаждении
- Уравнение теплового баланса при теплообмене
- Подсчет теплоты, выделяемой при сжигании топлива. К. П. Д. нагревателя
- Изменение внутренней энергии при выполнении механической работы
- Закон сохранения и превращения энергии в механике
- Закон сохранения и превращения энергии в механических и тепловых процессах
- Первое начало термодинамики
- Применение первого начала термодинамики к изопроцессам в идеальном газе
- Адиабатный процесс
- Понятие о строении солнца и звезд
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе Q = ΔU · A
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Изменение внутренней энергии
Внутренняя энергия тела – это полная энергия всех молекул, которые его составляют. Внутренняя энергия идеального газа пропорциональна его температуре.
Чтобы изменить внутреннюю энергию вещества, надо сообщить ему некоторое количество тепла или совершить работу.
Внутренняя энергия тела
Под внутренней энергией тела подразумевается сумма кинетической и потенциальной энергий всех частиц тела и энергии ядер его атомов. Возникает вопрос: какая же энергия не входит во внутреннюю энергию тела?
Пусть для примера таким телом является наша Земля. Известно, что Земля притягивается к Солнцу и движется по орбите вокруг него, т. е. обладает по отношению к Солнцу как потенциальной, так и кинетической энергией. Эта энергия не входит во внутреннюю энергию Земли, так как она связана с телом, находящимся вне Земли. Таким образом, во внутреннюю энергию тела не входит кинетическая и потенциальная энергия этого тела относительно всех тех тел, которые находятся вне его. Аналогично во внутреннюю энергию системы тел не входит кинетическая и потенциальная энергия этой системы относительно тех тел, которые не входят в эту систему.
Не менее важным является вопрос о том, как вычислять внутреннюю энергию тела или системы тел. Оказывается, что только для идеального газа имеется соответствующая формула . Во всех других случаях вычислять внутреннюю энергию мы не умеем. Однако для решения практических вопросов существенную роль играет не сама внутренняя энергия, а ее изменение, т. е. разность между ее значениями в начале и в конце того или иного процесса. А для этого не нужно знать числового значения всей внутренней энергии. Это относится не только к внутренней энергии. Примером сказанного может служить и разность температур, которая и по термодинамической шкале и по шкале Цельсия одинакова, т. е. не зависит от числового значения самой температуры, если ее единица не меняется.
Поскольку в молекулярной физике рассматриваются только такие явления, при которых молекулы не изменяются, то можно считать, что в этих явлениях изменяются только молекулярно-кинетическая и молекулярно-потенциальная энергии. Это упрощение значительно облегчает многие расчеты.
На основании закона сохранения энергии можно утверждать, что изменение внутренней энергии тела всегда связано с его взаимодействием с другими телами и с окружающей средой. В некоторых случаях, узнав, какое количество энергии теряют или получают при взаимодействии эти тела и окружающая среда, определяют изменение внутренней энергии тела. В других случаях, наоборот, по изменению внутренней энергии тела определяют, сколько энергии получила окружающая среда и другие взаимодействующие тела.
Одним из важнейших видов обмена энергией между телами и окружающей средой является теплообмен.
Теплообмен
Стоящий на столе горячий чайник через некоторое время остывает. Солнечные лучи летом заметно нагревают поверхность Земли. Металлическая ручка сковороды, стоящей на газовой плите, сильно нагревается. Все это примеры теплообмена. Обмен внутренней энергией между телами и окружающей средой или между частями тела без совершения механической работы называется теплообменом.
Обмен энергией при теплообмене обусловлен множеством актов отдельных взаимодействий между молекулами, иначе говоря, множеством микропроцессов. Например, остывание горячей воды в воздухе объясняется обменом энергией между молекулами воды и воздуха при их столкновениях. При этом нагревание воздуха и остывание воды обусловлено тем, что при большинстве таких столкновений молекулы воды теряют энергию, а молекулы воздуха приобретают ее. Однако при отдельных столкновениях молекулы воздуха могут терять энергию, а молекулы воды — приобретать, так как у некоторых молекул величина энергии может значительно отличаться от ее среднего значения (§3.4). Такие случаи будут происходить тем чаще, чем ближе станут температуры воды и воздуха. А при равенстве их температур случаи увеличения и уменьшения энергии молекул воздуха при столкновениях с молекулами воды будут равновероятны и никакой передачи энергии от воды к воздуху или обратно в целом происходить не будет.
Таким образом, при теплообмене большинство актов молекулярного взаимодействия способствует передаче энергии от тела с большей температурой к телу с меньшей температурой и ведет к выравниванию температур этих тел.
В силу исторических условий изменение внутренней энергии тела при теплообмене часто называют переданным или полученным количеством теплоты 






Подчеркнем, что количество теплоты 
Виды теплообмена
Теплообмен в природе осуществляется с помощью теплопроводности, конвекции и излучения (лучепоглощения и лучеиспускания).
Механизм теплопроводности фактически объяснен в предыдущем параграфе. Приведем еще одни пример. При нагревании конца металлического стержня его молекулы начинают двигаться быстрее, т. е. внутренняя энергия этого конца возрастает. Так как на другом конце стержня молекулы движутся медленнее, то внутри стержня с помощью хаотического движения атомов и электронов происходит передача внутренней энергии от горячего к холодному концу. Передача внутренней энергии от одних частей вещества к другим, обусловленная хаотическим движением молекул и других частиц вещества, называется теплопроводностью.
Среди различных видов вещества наилучшей теплопроводностью обладают металлы. Это объясняется тем, что в них находятся свободные электроны, Отметим еще, что теплопроводность вещества в твердом состоянии больше, чей в жидком, а в жидком больше, чей в газообразном. (Объясните, почему.)
Рассмотрим сущность конвекции. Чтобы показать плохую теплопроводность воды, обычно сосуд с водой нагревают сверху. При этом вверху вода может закипеть, а внизу останется холодной. Однако если сосуд нагревать снизу, то вода нагревается равномерно во всем объеме. Объясняется это тем, что вода при нагревании расширяется и ее плотность уменьшается. Если нагретая вода находится внизу, то верхние, более плотные слои воды под действием силы тяжести опускаются и вытесняют теплую воду вверх. Такое перемешивание воды будет происходить до тех пор, пока вся вода не закипит. Теплообмен, который происходит при перемешивании неравномерно нагретых слоев жидкости или газа под действием силы тяжести, называется конвекцией. Нетрудно сообразить, что в космическом корабле при состоянии невесомости конвекция отсутствует. (Подумайте, почему морозильная камера в холодильниках укрепляется вверху, а не внизу.)
Может показаться, что конвекцию нельзя причислять к теплообмену, так как она связана с работой силы тяжести. Однако при конвекции увеличение внутренней энергии жидкости или газа происходит только за счет подводимого извне тепла, а действие силы тяжести сводится только к ускорению равномерного прогрева жидкости или газа. Дополнительного вклада во внутреннюю энергию жидкости или газа действие силы тяжести при конвекции не дает. Поэтому конвекцию относят к теплообмену.
Теплообмен между Солнцем и Землей осуществляется посредством электромагнитного излучения. Электромагнитное излучение создается’ движением электрических зарядов и резко возрастает при повышении температуры. Излучение тела, которое определяется только его температурой, называется тепловым излучением.
Процесс излучения происходит за счет внутренней энергии тела. Когда излучение поглощается каким-либо другим телом, то внутренняя энергия тела увеличивается за счет энергии поглощенного излучения. Таким образом, посредством излучения происходит передача энергии от более нагретых тел к менее нагретым. Этот вид теплообмена происходит и при отсутствии вещества между телами.
Изменение внутренней энергии при нагревании и охлаждении
Выясним, как можно вычислять изменение внутренней энергии при теплообмене. Чтобы возможно точнее это сделать, нужно свести к минимуму неучтенные потери теплоты при теплообмене. Поэтому при научных исследованиях теплообмен осуществляют в калориметре (рис. 6.1), применение которого позволяет достаточно точно определять теплоту 
Калориметр состоит из двух сосудов: внешнего и внутреннего. Внутренний сосуд делается из хорошего проводника тепла (латуни, меди), так как его температура должна быть такой же, как у налитой в него жидкости. Наружный сосуд предохраняет внутренний сосуд от потерь тепла путем конвекции и излучения. Поэтому его обычно окрашивают белой краской или делают из блестящей жести. Чтобы предохранить внутренний сосуд от потерь тепла путем теплопроводности, его ставят на деревянные подставки (у дерева плохая теплопроводность). Во внутренний сосуд помещают мешалку (из такого же материала, как сосуд) и термометр.
Теплообмен осуществляют следующим образом. С помощью весов определяют массу внутреннего сосуда калориметра и мешалки, а затем и массу налитой в него жидкости, например воды. После этого измеряют массу тела, нагревают его до известной температуры и, заметив начальную температуру жидкости, опускают нагретое тело в калориметр. Измерив конечную температуру жидкости, можно подсчитать, сколько теплоты отдало тело в процессе теплообмена.
С помощью таких опытов легко установить, что изменение внутренней энергии какого-либо тела прямо пропорционально его массе т и изменению температуры тела 
здесь с — коэффициент пропорциональности. Поскольку изменение внутренней энергии при теплообмене оценивается количеством теплоты 
Начальную температуру тела обычно обозначают 



Опыты показывают, что 
Величина с, характеризующая зависимость изменения внутренней энергии тела при нагревании или охлаждении от рода вещества и от внешних условий, называется удельной теплоемкостью вещества. Удельная теплоемкость вещества измеряется количеством теплоты, необходимым для нагревания единицы массы вещества на единицу температуры:
Выведем единицу удельной теплоемкости в СИ:
В СИ за единицу удельной теплоемкости принимается удельная теплоемкость такого вещества, для которого при нагревании массы в 1 кг на 1 К затрачивается 1 Дж энергии. При небольших изменениях температуры удельную теплоемкость можно считать постоянной. Для решения задач ее берут из таблиц.
Следует иметь в виду, что при определении количества теплоты, необходимой для нагревания или выделенной при охлаждении тела, иногда пользуются теплоемкостью тела С — величиной, измеряемой количеством теплоты, необходимым для нагревания тела на единицу температуры. Следовательно,
Пользоваться при расчетах теплоемкостью всего тела особенно удобно, когда отдельные части тела сделаны из разного вещества. В СИ за единицу теплоемкости тела принимается 1 Дж/К. (Покажите это с помощью формулы (6.3).)
Отметим еще, что удельная теплоемкость газа зависит от характера процесса, при котором происходит его нагревание. Например, удельная теплоемкость газа при постоянном давлении 

Уравнение теплового баланса при теплообмене
Вспомним, что при отсутствии механической работы изменение внутренней энергии тела оценивают количеством теплоты 
Теплообмен происходит до тех пор, пока температуры тел не сравняются. Общую температуру, которая получается после окончания теплообмена, обозначают 
Для примера составим уравнение теплового баланса, которое используется при определении удельной теплоемкости вещества с помощью калориметра. Приближенно можно считать, что в этом случае в теплообмене участвуют три тела: калориметр, жидкость и тело, удельную теплоемкость вещества которого определяют. Это тело предварительно нагревают до известной температуры 





Поскольку
имеем
или
Подставляя в правую часть последней формулы числовые значения величин, полученные из опыта, вычисляют удельную теплоемкость вещества тела.
Подсчет теплоты, выделяемой при сжигании топлива. К. П. Д. нагревателя
Внутренняя энергия тела частично может освобождаться, когда с веществом тела происходит химическая реакция. Особенно много теплоты выделяется при реакции горения. Вещества, которые используют для получения теплоты, называют топливом. Энергию, выделяемую при сгорании топлива, широко используют на производстве, на транспорте и в быту. Топливо бывает твердое, жидкое и газообразное.
Опыт показывает, что количество теплоты 
Теплота 

Величина 
Найдем единицу удельной теплоты сгорания 
Формула (6.4) удобна для вычисления теплоты, выделяемой при сжигании твердого и жидкого топлива. Расход газообразного топлива удобнее выражать не массой, а объемом сгоревшего газа. Поскольку давление газа в газопроводе повышено, газовые счетчики устраиваются так, что они показывают объем израсходованного газа, приведенный к нормальным условиям — 


Здесь 
(Покажите, что в СИ 
Отметим, что потребность в топливе часто выражают в тоннах условного топлива, удельная теплота сгорания которого принята равной 29,3 .106 Дж/кг.
Топливо сжигают в печах, топках, форсунках и т. д., которые условно называют нагревателями. Тип устройства для сжигания топлива в основном определяется видом топлива и назначением выделенной теплоты. Полностью использовать теплоту, выделяющуюся в нагревателях, не удается, так как часть теплоты уносится с продуктами сгорания и рассеивается в окружающей среде.
Величина 

Отметим, что величина 

Изменение внутренней энергии при выполнении механической работы
Опыт Джоуля. Внутренняя энергия может изменяться не только при теплообмене, но и при выполнении механической работы. Например, при пилке дров происходит нагревание пилы. При сверлении механической детали сверло и деталь сильно нагреваются. Резец токарного станка при обработке деталей становится горячим. Такого рода примеров можно привести очень много. Все они показывают, что когда совершается механическая работа А по преодолению трения или разрушению материала, то происходит нагревание тел, т. е. увеличение их внутренней энергии, аналогичное тому, какое происходит при получении этими телами некоторого количества теплоты 
Если с помощью механической работы можно получить неограниченное количество теплоты, то возникает вопрос: существует ли при этом между механической работой и теплотой определенное количественное соотношение? Иначе говоря, всегда ли за счет одинакового количества работы получается одно и то же количество теплоты? Для ответа на этот вопрос английский ученый Д. Джоуль выполнил серию опытов, которые дали утвердительный ответ. Свой первый опыт он произвел в 1843 г.
На рис. 6.2 изображена схема одного из опытов Джоуля. Установка состояла из калориметра с ртутью.
Через калориметр проходила ось, заканчивавшаяся валиком с ручкой. На валик наматывалась нить, к концам которой были прикреплены равные грузы массой т каждый. Рядом с грузами укреплялись линейки, с помощью которых измеряли перемещение грузов. Для усиления трения при движении грузов внутри калориметра делались выступы, а к оси прикреплялись лопасти.
Перед началом опыта с помощью ручки грузы поднимали в верхнее положение и измеряли температуру ртути. Затем ручка освобождалась, и при движении вниз грузы приводили во вращение лопасти внутри калориметра. При этом, вследствие большого трения между лопастями и ртутью, в калориметре выделялось тепло за счет работы, совершаемой при движении грузов на некотором пути h. Поскольку трение в других частях установки было ничтожно малым, можно считать, что в этом опыте увеличение внутренней энергии калориметра равно уменьшению механической энергии грузов в процессе их движения. В то время закон сохранения энергии еще не был твердо установлен, но Джоуль считал, что количество теплоты 

Такого рода опытами Джоулю удалось доказать, что количество теплоты, выделенное при трении, прямо пропорционально произведенной работе.
По современным данным, для нагревания 1 кг воды от 292,5 К до 293,5 К, т. е. на 1 К, требуется 4186,8 Дж энергии. Это означает, что удельная теплоемкость воды
Отметим, что до опытов Джоуля с помощью теплообмена можно было находить только относительные удельные теплоемкости, т. е. узнавать, во сколько раз удельная теплоемкость одного вещества больше удельной теплоемкости другого. При этом удельная теплоемкость воды условно принималась за единицу. Количество теплоты, нужное для нагревания 1 кг воды на 1°С, было названо килокалорией (ккал). Удельная теплоемкость воды выражалась следующим образом:
Таким образом, на основании опытов Джоуля имеем
Из этого соотношения вытекает связь между килокалорией и джоулем:
В XVIII в. для объяснения тепловых явлений пользовались теорией теплорода. Ученые предполагали, что существует особый невесомый вид материи — теплород, количество которого в природе неизменно. Считалось,’ что при охлаждении тела теплород перетекает из тела в окружающую среду, а при нагревании тела в него перетекает теплород из других тел.
Одним из первых выступил против теории теплорода М. В. Ломоносов (1711— 1765 гг.), который объяснял тепловые явления движением невидимых частиц тела. В 1798 г. англичанин Б. Румфорд показал, что при сверлении пушечных стволов теплота может быть получена в неограниченном количестве (за счет механической работы). Эти исследования Румфорда доказали несостоятельность теории теплорода. Не менее важными для опровержения теории теплорода были и исследования французского ученого С. Карно, который создал теорию работы тепловых машин.
Закон сохранения и превращения энергии в механике
Назовем процессы, при которых не происходит превращения механического движения в другие формы движения материи, чисто механическими. Система, в которой происходят чисто механические процессы, называется консервативной. Эта система является идеализированной, так как в ней отсутствуют силы трения и другие сопротивления, приводящие к рассеянию механической энергии, т. е. к ее превращению в другие формы энергии. В консервативной системе может происходить только превращение кинетической энергии в потенциальную и обратно. Работа сил, действующих на тело в консервативной системе, не зависит от формы пути, а определяется только начальным и конечным положением тела. Напомним, что примером такого рода сил является сила тяжести. Из сказанного следует, что в консервативной системе работа силы на замкнутом пути равна нулю.
Для такой системы справедлив закон сохранения энергии в следующей форме: в замкнутой консервативной системе сумма кинетической и потенциальной энергий всех тел, составляющих систему, есть величина постоянная. Если обозначить эту сумму Е, то при отсутствии внешних воздействий на консервативную систему
Например, при свободном падении тела сумма его кинетической и потенциальной энергий остается постоянной.
Вспомним, что единственной мерой передачи механической энергии от одного тела к другому является работа А. Поэтому, если механическая энергия консервативной системы в каком-либо состоянии равна

Напомним еще, что в более широком смысле механическая работа А при любых явлениях природы служит единственной мерой передачи и превращения механического движения в другие формы движения материи и обратно.
Закон сохранения и превращения энергии в механических и тепловых процессах
Было объяснено, что механическая энергия сохраняется только при отсутствии трения’ и других сопротивлений. Действие сил трения ведет к уменьшению механической энергии. Действительно, после выключения двигателя автомобиль постепенно теряет кинетическую энергию и останавливается; скатившись с горы, санки постепенно теряют скорость и т. д. Нетрудно сообразить, что бесследное исчезновение энергии в такого рода случаях является лишь кажущимся: при этом всегда происходит выделение некоторого количества теплоты. Таким образом, при трении и вообще при любом сопротивлении движению происходит превращение механической энергии во внутреннюю энергию.
Как известно, мерой уменьшения механической энергии в подобного рода случаях является работа А, а мерой увеличения внутренней энергии — полученная теплота 

Это означает, что сумма механической и внутренней энергий всех тел, составляющих замкнутую систему, есть величина постоянная. Иначе говоря, суммарное изменение механической и внутренней энергий всех тел замкнутой системы в любом процессе, найденное по выполненной работе и переданной теплоте, равно нулю.
Изучение явлений природы показало, что изменение энергии тела происходит только при выполнении работы и при теплообмене. Следовательно, работа и количество теплоты — единственно возможные формы обмена энергией между телами. Таким образом, переданное телу количество теплоты 
Немецкий врач Р. Майер в 1842 г. обратил внимание на взаимную превращаемость всех форм движения материи друг в друга и пытался распространить принцип сохранения энергии на все явления природы. Однако научно обосновал этот принцип в 1847 г. немецкий ученый Г. Гельмгольц.
Сформулируем теперь закон сохранения и превращения энергии: энергия замкнутой системы никогда не исчезает и не создается из ничего. При всех явлениях внутри системы она только превращается из одного вида в другой или передается от одного тела к другому, не изменяясь количественно.
Закон сохранения энергии является всеобщим законом природы, на котором базируется все современное естествознание. С его помощью проверяются новые теории и оцениваются результаты новых экспериментов. Нарушение этого закона в каких-либо явлениях природы привело бы к полной перестройке всех естественных наук и к изменению нашего миропонимания.
Первое начало термодинамики
Весьма важным способом изучения тепловых процессов служит термодинамический метод. Сущность этого метода заключается в следующем. При выполнении экспериментов измеряют числовые значения макроскопических величин, характеризующих изучаемый процесс. Их часто называют термодинамическими параметрами (§ 5.1). По результатам таких экспериментов находят закономерную связь между параметрами, а затем производят математический анализ этой связи на основе всеобщих законов природы, в справедливости которых нет никаких сомнений. Всеобщие законы природы, на основе которых проводят такой анализ, называют началами термодинамики.
Чтобы успешно проводить анализ связей между параметрами, математические выражения начал термодинамики должны иметь специфический, удобный для такого анализа вид. Поскольку все выводы термодинамики делают на основе экспериментов и незыблемых законов природы, они всегда оказываются верными. Термодинамический метод изучения природы позволяет предсказать ход многих явлений, но не дает наглядной модели, объясняющей физический смысл происходящих явлений. Этот недостаток термодинамического метода восполняет молекулярно-кинетическая теория, которая объясняет многие явления с помощью таких моделей. Таким образом, оба эти важнейших метода исследования явлений дополняют друг друга и совместно помогают нам глубоко осмыслить происходящие процессы.
Первым всеобщим законом природы, на основе которого строится термодинамика, является закон сохранения энергии. Его называют первым началом термодинамики и формулируют следующим образом: подведенное к системе количество теплоты 

Отметим, что система, к которой применима формула (6.9), может состоять из одного тела. Напомним еще, что работа А в (6.9) численно равна энергии, переданной системой окружающим телам в форме механического движения.
Применение первого начала термодинамики к изопроцессам в идеальном газе
Выясним, какой вид принимает формула (6.9) для различных изопроцессов в идеальном газе. Мы уже знаем, что при изохорическом процессе работа газа А равна нулю. Следовательно, формула (6.9) для этого процесса принимает вид
Это означает, что при изохорическом процессе все подведенное к газу количество теплоты идет на увеличение его внутренней энергии.
Для изобарического процесса формула первого начала термодинамики имеет вид (6.9):
Действительно, в этом случае 

При изотермическом процессе температура газа не изменяется. Поэтому на основании формул (5.22)—(5.24) можно утверждать, что в этом случае внутренняя энергия газа остается постоянной, т. е. 
Это означает, что при изотермическом процессе все подведенное к газу количество теплоты идет на выполнение газом работы.
Анализ формулы (6.9) показывает, что с газом может происходить еще один важный процесс, при котором 
Адиабатный процесс
Процесс в какой-либо системе, который происходит без обмена теплом с окружающей средой, называется адиабатным. Так как при таком процессе 
Это означает, что при адиабатном процессе система может выполнять работу над внешними телами только за счет своей внутренней энергии. Наоборот, когда при адиабатном процессе внешние тела совершают работу над системой, то ее внутренняя энергия увеличивается.
Если газ при адиабатном расширении совершает работу над окружающей средой, то его внутренняя энергия уменьшается. Следовательно, в этом случае газ должен охлаждаться. (Подумайте, охладится ли газ, если он будет адиабат-но расширяться в вакуум.) Очевидно, что при адиабатном сжатии газ должен нагреваться. График адиабатного процесса в координатах р и V изображен на рис.6.3.
Он называется адиабатой. Для сравнения на рис. 6.3 изображена одна из изотерм для этой же массы идеального газа. С помощью формулы (4.9): 


В реальных условиях адиабатный процесс осуществить невозможно, так как в природе не существуют идеальные тепловые изоляторы. Однако при хорошей тепловой изоляции процесс в газе может быть близок к адиабатному, особенно если он протекает в течение короткого времени, так как при этом заметного обмена теплотой между газом и окружающей средой не успеет произойти. Поэтому любой газ при быстром сжатии нагревается, а при быстром расширении охлаждается.
Это можно показать на следующем опыте. Возьмем стеклянную бутыль с узким горлом и нальем в нее немного воды. Заткнем бутыль резиновой пробкой, в которой имеется трубка, соединенная с нагнетающим насосом, и будем накачивать в бутыль воздух. При этом вода в бутыли исчезает. Следовательно, температура воздуха в бутыли повысилась. При достаточно большом давлении пробка вылетает и в бутыли появляется туман, что свидетельствует об охлаждении воздуха при расширении.
При быстром несильном сжатии газ может нагреваться очень сильно. Если при этом в газе находятся пары бензина или других горючих веществ, то они воспламеняются. Это явление используют в двигателях Дизеля для зажигания горючей смеси.
Понятие о строении солнца и звезд
Солнце является типичной звездой и представляет собой гигантский газовый шар. По своим физическим характеристикам Солнце — средняя звезда с массой около 2 . 1030 кг и радиусом 7 . 108 м.
Солнце состоит в основном из водорода (~70% по массе) и гелия (~29%). (Водорода по числу атомов в 10 раз больше, чем остальных элементов.) Масса Солнца в 330 ООО раз больше массы Земли, и огромное гравитационное притяжение сильно сжимает эти газы. Вычислив объем солнечного шара, можно подсчитать, что средняя плотность солнечного вещества составляет 1,4 . 103 кг/м3, т. е. больше плотности воды. По направлению к центру давление вышележащих слоев растет и плотность газа увеличивается, достигая в центре Солнца около 1,5 . 105 кг/м3, что более чем в 10 раз превышает плотность свинца.
Солнце излучает в мировое пространство ежесекундно огромное количество энергии. Источником этой энергии являются термоядерные реакции, которые протекают в его недрах. Температура в центре Солнца достигает 13 . 106 К и постепенно уменьшается по мере удаления от центра.
Передача энергии из недр Солнца осуществляется главным образом излучением. Излучение внутренних слоев поглощается вышележащими слоями, которые в свою очередь посредством излучения передают энергию следующим слоям, и так далее, до слоя, излучение которого прорывается, наконец, наружу, в космическое пространство.
Слой, в котором образуется видимое излучение Солнца, называемый фотосферой, мы наблюдаем как солнечный диск. Толщина фотосферы составляет несколько сотен километров, давление — порядка 0,1 атм. Температура внутренних слоев фотосферы около 6000 К и уменьшается до 4500 К в ее внешнем слое. Фотосфера составляет нижний слой атмосферы Солнца. Над ней расположена хромосфера, а самую наружную разреженную часть атмосферы называют короной (рис. 6.4).
Газ в хромосфере и короне очень сильно разрежен: в верхних слоях хромосферы содержится только около 1015 атомов/м3, а в короне — еще на порядок меньше (сравните с атмосферой Земли: 
Теряя энергию на излучение в мировое пространство, газ в фотосфере быстро охлаждается, и в слое, лежащем под фотосферой, происходит вертикальное перемешивание — конвекция. При наблюдении в телескоп видно, что фотосфера состоит из множества гранул — небольших облаков более горячего газа, которые поднимаются из глубины, вытесняя остывший газ, и через несколько минут распадаются, заменяясь новыми. Иногда образуются устойчивые восходящие потоки горячих газов, которые называют факелами. Они видны в виде более ярких областей. Время от времени в фотосфере появляются темные пятна, представляющие собой более холодные области. Кстати, по движению этих пятен было обнаружено вращение Солнца.
Под действием мощных конвективных движений в солнечном веществе возникают механические колебания и образуются волны, похожие на звуковые. По мере распространения этих волн в верхние слои атмосферы, где газ сильно разрежен, амплитуда (размах) колебаний частиц газа увеличивается до нескольких километров и сильно увеличиваются скорости колебательного движения частиц. Однако такие колебания не могут долго сохранять правильный характер, и волнообразные движения протяженных областей газа разбиваются на отдельные мелкие беспорядочно движущиеся массы газа. В результате за счет механической энергии волн сильно возрастает средняя энергия хаотического движения частиц газа, и температура увеличивается в хромосфере до десятков тысяч Кельвинов, а в короне — до 106 К *).
*) См, замечание о кинетической температуре в § 3.10.
Вследствие очень низкой плотности вещества яркость короны в миллион раз меньше, чем фотосферы, и не превышает яркости Луны. Корону удобно наблюдать во время полного солнечного затмения, когда Луна закрывает от нас яркий диск фотосферы. Корона имеет лучистую структуру, причем длина лучей может более чем в десять раз превышать радиус фотосферы.
Кинетическая энергия частиц газа в короне- так велика, что многие из них преодолевают притяжение Солнца и улетают в межпланетное пространство. Поток этих частиц, движущихся со скоростью в сотни км/с, называют солнечным ветром. Заметим, что солнечный ветер, а также давление света вызывают образование «хвоста кометы», который всегда направлен в сторону от Солнца.
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно – кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома