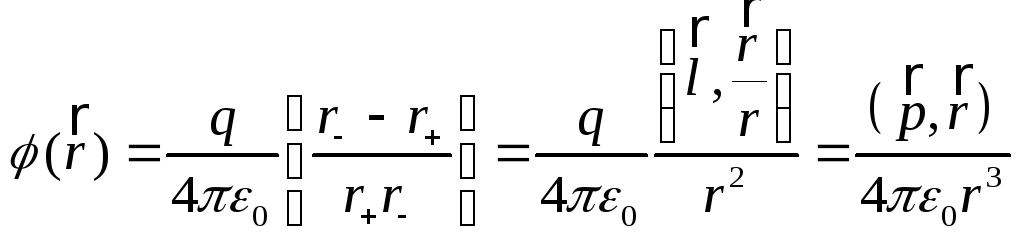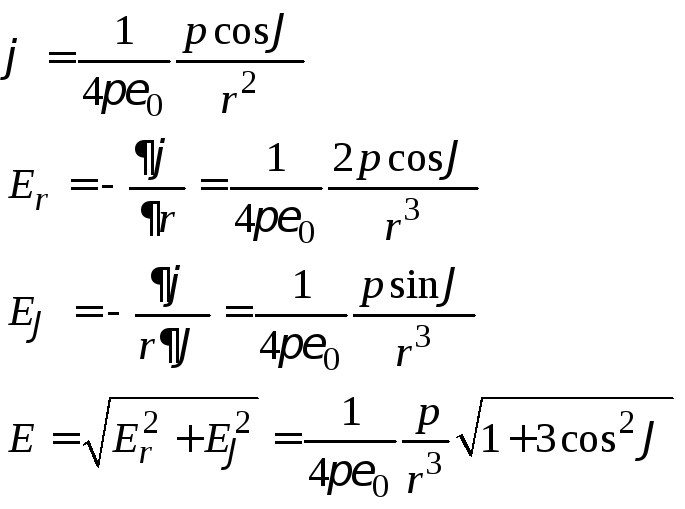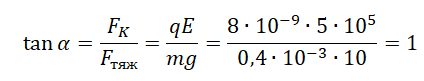Понятие электрического потенциала является одним из важных основ теории электростатики и электродинамики. Понимание его сущности является необходимым условием для дальнейшего изучения этих разделов физики.
Содержание
- 1 Что такое электрический потенциал
- 2 Свойства потенциала
- 3 Разность потенциалов
- 4 Эквипотенциальные поверхности
Что такое электрический потенциал
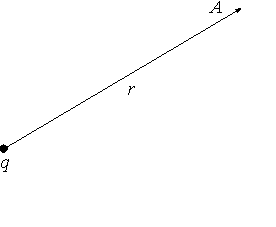
Пусть в поле, создаваемым неподвижным зарядом Q, помещён единичный заряд q, на который действует сила Кулона F=k*Qq/r.
Здесь и далее k=((1/4)*π* ε0* ε), где ε0 — электрическая постоянная (8,85*10-12 Ф/м), а ε – диэлектрическая постоянная среды.
Внесённый заряд под действием этой силы может перемещаться, а сила при этом совершит определенную работу. Это означает, что система из двух зарядов обладает потенциальной энергией, зависящей от величины обоих зарядов и расстояния между ними, причём величина этой потенциальной энергии не зависит от величины заряда q. Здесь и вводится определение электрического потенциала – он равен отношению потенциальной энергии поля к величине заряда:
φ=W/q,
где W – потенциальная энергия поля, создаваемого системой зарядов, а потенциал является энергетической характеристикой поля. Чтобы переместить заряд q в электрическом поле на какое-то расстояние, надо затратить определённую работу на преодоление кулоновских сил. Потенциал точки равен работе, которую надо затратить для перемещения единичного заряда из этой точки в бесконечность. При этом надо отметить, что:
- эта работа будет равна убыли потенциальной энергии заряда (A=W2-W1);
- работа не зависит от траектории перемещения заряда.
В системе СИ единицей измерения потенциала является один Вольт (в русскоязычной литературе обозначается буквой В, в зарубежной – V). 1 В=1Дж/1 Кл, то есть, можно говорить о потенциале точки в 1 вольт, если для перемещения заряда в 1 Кл в бесконечность потребуется совершить работу в 1 Джоуль. Название выбрано в честь итальянского физика Алессандро Вольта, внесшего значительный вклад в развитие электротехники.
Чтобы наглядно представить, что такое потенциал, его можно сравнить с температурой двух тел или температурой, замеренной в разных точках пространства. Температура служит мерой нагрева объектов, а потенциал – мерой электрической заряженности. Говорят, что одно тело нагрето более другого, также можно сказать, что одно тело заряжено более, а другое – менее. Эти тела обладают разным потенциалом.
Значение потенциала зависит от выбора системы координат, поэтому требуется какой-то уровень, который надо принять за ноль. При измерении температуры за базовую границу можно принять, например, температуру тающего льда. Для потенциала за нулевой уровень обычно принимают потенциал бесконечно удаленной точки, но для решения некоторых задач за нулем можно считать, например, потенциал земли или потенциал одной из обкладок конденсатора.
Свойства потенциала
Среди важных свойств потенциала надо отметить следующие:
- если поле создается несколькими зарядами, то потенциал в конкретной точке будет равен алгебраической (с учетом знака заряда) сумме потенциалов, создаваемых каждым из зарядов φ=φ1+φ2+φ3+φ4+φ5+…+φn;
- если расстояния от зарядов таковы, что сами заряды можно считать точечными, то суммарный потенциал считается по формуле φ=k*(q1/r1+q2/r2+q3/r3+…+qn/rn), где r – расстояние от соответствующего заряда то рассматриваемой точки.
Если поле образовано электрическим диполем (двумя связанными зарядами противоположного знака), то потенциал в любой точке, находящейся на расстоянии r от диполя будет равен φ=k*p*cosά/r2, где:
- p – электрическое плечо диполя, равное q*l, где l – расстояние между зарядами;
- r – расстояние до диполя;
- ά – угол между плечом диполя и радиус-вектором r.
Если точка лежит на оси диполя, то cosά=1 и φ=k*p/r2.
Разность потенциалов
Если две точки обладают определённым потенциалом, и если они не равны, то говорят о том, что между двумя точками существует разность потенциалов. Разность потенциалов возникает между точками:
- потенциал которых определяется зарядами разных знаков;
- точкой с потенциалом от заряда любого знака и точкой с нулевым потенциалом;
- точками, имеющими потенциал равного знака, но отличающимися по модулю.
То есть, разность потенциалов не зависит от выбора системы координат. Можно провести аналогию с бассейнами с водой, расположенными на разной высоте относительно нулевой отметки (например, уровня моря).
Вода каждого бассейна имеет определенную потенциальную энергию, но если соединить два любых бассейна трубкой, то в каждой из них возникнет поток воды, расход которой определяется не только размерами трубки, но и разностью потенциальных энергий в гравитационном поле Земли (то есть, разностью высот). Абсолютное значение потенциальных энергий значения в данном случае не имеет.
Точно так же, если соединить проводником две точки с разным потенциалом, по нему потечёт электрический ток, определяемый не только сопротивлением проводника, но и разностью потенциалов (но не их абсолютным значением). Продолжая аналогию с водой, можно сказать, что вода в верхнем бассейне скоро закончится, и если не найдется той силы, которая переместит воду обратно наверх (например, насоса), то и поток очень быстро прекратится.
Так и в электрической цепи – чтобы поддерживать разность потенциалов на определенном уровне, потребуется сила, переносящая заряды (точнее, носители зарядов) к точке с наибольшим потенциалом. Такая сила называется электродвижущей силой и сокращенно обозначается ЭДС. ЭДС может носить различную природу – электрохимическую, электромагнитную и т.п.
На практике имеет значение в основном разность потенциалов между начальной и конечной точками траектории движения носителей зарядов. В этом случае эту разность называют напряжением, и оно в СИ также измеряется в вольтах. О напряжении в 1 Вольт можно говорить, если поле совершает работу в 1 Джоуль при перемещении заряда в 1 Кулон из одной точки в другую, то есть 1В=1Дж/1Кл, и Дж/Кл также может являться единицей измерения разности потенциалов.
Эквипотенциальные поверхности
Если потенциал нескольких точек одинаков, и эти точки образуют поверхность, то такая поверхность называется эквипотенциальной. Таким свойством обладает, например, сфера, описанная вокруг электрического заряда, ведь электрическое поле убывает с расстоянием одинаково во все стороны.
Все точки этой поверхности имеют одинаковую потенциальную энергию, поэтому при перемещении заряда по такой сфере работа затрачиваться не будет. Эквипотенциальные поверхности систем из нескольких зарядов имеют более сложную форму, но у них есть одно интересное свойство – они никогда не пересекаются. Силовые линии электрического поля всегда перпендикулярны поверхностям с одинаковым потенциалом в каждой их точке. Если эквипотенциальную поверхность рассечь плоскостью, получится линия равных потенциалов. Она имеет те же свойства, что и эквипотенциальная поверхность. На практике равный потенциал имеют, например, точки на поверхности проводника, помещенного в электростатическое поле.
Разобравшись с понятием потенциала и разности потенциалов, можно приступать к дальнейшему изучению электрических явлений. Но не ранее, потому что без понимания базовых принципов и понятий углубить знания не получится.
Рассмотрим
вычисление потенциала поля, созданного
некоторыми заряженными телами.
Рис.3.
Расположение точки наблюдения А по
отношению к точечному источнику поля
q
1.
Пример
Точечный
заряд.
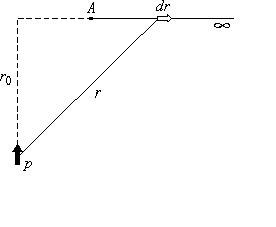
Используя соотношения (1) и (4) и совмещая
точку 1 с точкой наблюдения А
(рис.3), а точку 2 удаляя на бесконечность,
получим
(7)
Замечание.
До сих пор использовалось понятие
векторного поля – поля векторов
(каждой точке пространства ставится в
соответствие вектор).
Представление о потенциале
как
функции точки пространства позволяет
ввести понятие скалярного поля – поля
чисел
(каждой точке пространства ставится в
соответствие, с точностью до произвольной
аддитивной постоянной, число
).
Поэтому в дальнейшем кроме понятий
электростатическое поле и поле
,
будем использовать понятие поля.
2.Пример. Найдем потенциал бесконечной однородно заряженной с линейной плотностью нити.
Наша задача найти
как функцию
.
К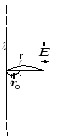
уже было показано для бесконечно длинной
нити:.
Выберем где-нибудь
точку из которой мы стартуем, к примеру
в точке
,
то
.
Договоримся, что
в точке старта потенциал равен нулю:
,
тогда
.
Это при такой
нормировке. Если в такой задаче нормировать
,
то получим,то
есть все потенциалы во всех точках
бесконечно большие. Кому нужна такая
нормировка? Если Вас интересует какой-то
конкретный пространственный диапазон,
то нормировать надо где-то вблизи этой
области, тогда все потенциалами будут
конечными приятными числами. От
бесконечной нити нельзя уйти на
бесконечность, по этой же причине не
следует ожидать хорошего результата
откак суммы потенциалов точечных фрагментов
нити, каждый из которых нормирован
условием.
3.Пример. Потенциал поля точечного диполя (первый способ).
И
мы рассматриваем точечный диполь и
точку наблюдения достаточно далеко от
этой нашей гантельки.
Давайте искать
потенциал этой точки наблюдения.
Во первых, принцип
суперпозиции.
Во-вторых, как
известно
.
Учтя, что
есть проекция вектора
на
и то, что расстояние до диполя очень
велико, то
Потенциал поля точечного диполя (второй способ).
Используем готовую
формулу для напряженности поля:
.
Вот такое выражение мы с вами в свое
время вывели. Обопремся на него.
Д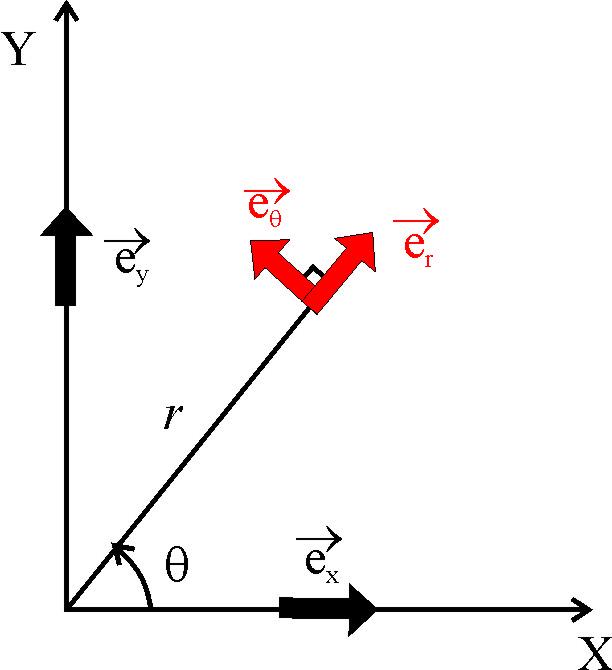
выберем такое направление, чтобы нам
было удобно вычислять этот интеграл,
так как поле потенциальное, то результат
не будет зависеть от вида траектории.
Ориентация диполя, направление движения
и векторпоказаны
на рисунке. С учетом некоторых соотношений
(5) примет вид:
Определение
вектора
точечного
диполя из
в
полярной системе координат.
Оператор
запишется в полярной системе координат
так:
Ортыкоординатных
осей декартовой и полярной систем
координат (см.рис.)
4.Пример
См. Иродов задача
3.38. (часть2)
Показать, что
потенциал диполя с электрическим
моментом может быть представлен как,
где–радиус
вектор. Найти с помощью этого выражения
модуль напряженности электрического
поля диполя как функциюи
.
–
это уже показали выше, отсюда, раскрывая
скалярное произведение и продифференцировав
формулу для потенциала, мы получим
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Работа в электрическом поле.
Так как сила, действующая в электрическом поле на точечный заряд Q Равна
(6.1)
То при перемещении заряда Q на расстояние Эта сила совершает работу:
(6.2)
При перемещении заряда из точки 1 в точку 2 по траектории работа равна:

Потенциальность кулоновского поля.
Поле, созданное кулоновскими зарядами, потенциально. Поле сил называется потенциальным, если при перемещении в этом поле работа зависит лишь от начального и конечного положения точек (тела) пути и не зависит от формы пути — траектории. Вторым эквивалентным определением потенциальности поля является условие равенства нулю работы при перемещении в нем по любому замкнутому контуру.
Вся математическая часть учения о потенциале была разработана в рамках теории тяготения, а понятие о потенциале возникло в работах Ж. Л. Лагранжа (1736-1813) в 1777г. Выражение “потенциал” было введено в науку в 1828 г. Дж. Грином и независимо К. Ф. Гауссом (1775-1855). Большой вклад в теорию потенциала был внесен П. С. Лапласом (1749-1827) и С. Д. Пуассоном (1781-1840).
На основании принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.
Из сказанного следует, что , тогда условие потенциальности электрического поля
(6.4)
(6.4) – интегральная формулировка потенциальности электрического поля.
Дифференциальная формулировка потенциальности поля.
Если воспользоваться формулой Стокса
, то из (6.4) следует дифференциальная формулировка потенциальности поля:
(6.5)
Непосредственной проверкой можно убедиться, что
. (6.6)
Тогда сопоставляя (6.6) и (6.5) можно записать:
, (6.7)
где — некоторая скалярная функция, которая называется потенциалом. Знак «-» выбран для того, чтобы вектор напряженности Е был направлен в сторону убывания
. Скалярная функция
называется скалярным потенциалом электрического поля.
Если напряженность поля можно измерить экспериментально, то потенциал не имеет определенного числового значения и бессмысленно говорить об экспериментальном определении его значения. Потенциал определен с точностью до некоторого постоянного значения.
Для того, чтобы не было неоднозначности, используют процедуру нормировки потенциала. При решении пространственных задач за ноль принимают потенциал бесконечно удаленной точки. А при решении задач, связанных с изучением электрических полей вблизи поверхности Земли, за ноль принимают потенциал Земли.
Выражение работы через потенциал.
Если заряд перемещается между точками (1) и (2), то

Если сопоставить (6.8) и (6.3), то 

Таким образом, с помощью (6.9) можно вычислить разность потенциалов между двумя точками поля.
Потенциал поля точечного заряда.
Будем нормировать потенциал на нуль в бесконечности. Считая, что в формуле (6.9) точка (2) находится в бесконечности, полагаем и получаем выражение для потенциала в точке (1):

Воспользовавшись выражением для напряженности поля точечного заряда получим:

Соотношение (6.11) определяет потенциал поля, создаваемого точечным зарядом.
Потенциал поля системы точечных зарядов.
Если имеется система из точечных зарядов, то потенциал поля в некоторой точке А равен
. (6.12)
В случае, когда заряд распределен непрерывно с объемной плотностью =
, потенциал в некоторой точке (x, y, z) поля:
(6.13)
— расстояние от точечного заряда
находящегося в точке
до точки
где вычисляется потенциал.
Если заряд распределен по поверхности, то потенциал определяется формулой, (6.14)
где R –расстояние между элементом площадки DS и точкой, где
Вычисляется потенциал.
Бесконечность потенциала поля точечного заряда.
Из (6.14) следует, что при потенциал
. Это связано с тем, что точечный заряд формально имеет бесконечную объемную плотность, поскольку его объем равен нулю. Именно бесконечная объемная плотность заряда и обуславливает обращение в бесконечность потенциала.
При непрерывном распределении заряда с конечной плотностью потенциал нигде не обращается в бесконечность, т. е. потенциал функция конечная.
Конечность потенциала при непрерывном распределении заряда с конечной плотностью.
При непрерывном распределении заряда с конечной плотностью потенциал нигде не обращается в бесконечность. В этом можно убедиться при вычислении потенциала по формуле (6.13). Причем точку (X,Y,Z) за начало координат (X=Y=Z=0) и будем вести расчет в сферической системе координат. Элемент объема в ней выражается формулой , где
. Тогда [см. (6.13)]
.
Следовательно, Если Конечно, то и потенциал
конечен, Что и требовалось доказать.
Непрерывность потенциала.
Производная от потенциала по декартовой координате дает соответствующую компоненту напряженности электрического поля. Ясно, что напряженность не может быть бесконечной, значит, производные по координатам от потенциала должны быть конечными. А это означает, что потенциал является непрерывной функцией. Таким образом, потенциал является непрерывной и конечной функцией с конечными производными по координатам. Эти условия важны при решении дифференциальных уравнений для
.
Теорема Ирншоу.
Эта теорема утверждает, что не существует такой конфигурации неподвижных зарядов, которая была бы устойчивой, если нет других сил, кроме сил кулоновского взаимодействия между зарядами системы. Устойчивые конфигурации неподвижных зарядов могут существовать лишь тогда, когда кроме сил электрического взаимодействия между ними имеются некоторые посторонние силы, удерживающие заряды в положении равновесия.
Доказательство теоремы Ирншоу следует из теоремы Гаусса. Допустим, что равновесие устойчиво. Тогда при смещении любого из зарядов системы из его положения равновесия в любом направлении на него должна действовать сила, стремящаяся возвратить заряд в прежнее положение. А это означает, что напряженность поля, создаваемого вблизи каждого из покоящихся зарядов всеми другими зарядами, направлена вдоль радиусов, исходящих из точки нахождения этого заряда. Поток напряженности этого поля сквозь замкнутую поверхность вокруг заряда отличен от нуля, поскольку напряженность направлена вдоль радиусов в одном направлении (вблизи положительного заряда – к заряду, вблизи отрицательного – от заряда). По теореме Гаусса поток сквозь замкнутую поверхность создается зарядом, находящимся в ограничиваемом ею объеме. Это противоречит исходному предположению о том, что он создается зарядами, находящимися вне объема. Тем самым отвергается допущение об устойчивости конфигурации неподвижных зарядов, и теорема Ирншоу доказана.
Устойчивые конфигурации неподвижных зарядов могут существовать лишь тогда, когда кроме сил взаимодействия между ними имеются какие-то посторонние силы, удерживающие заряды в положениях равновесия. Устойчивые состояния движущихся зарядов возможны, как, например, движение двух разноименных зарядов по эллипсам вокруг центра масс (если, конечно, пренебречь излучением).
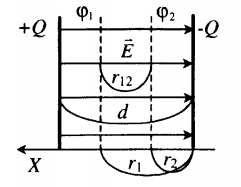
Однородное электрическое поле сосредоточено между разноименно заряженными пластинами (обкладками конденсатора).
Характеристики однородного электростатического поля
| Силовые линии | Начинаются на положительно заряженной пластине, а заканчиваются на отрицательно заряженной. Силовые линии параллельны друг другу, т. е. поле однородно. |
| Напряженность |
−E |
| Потенциал |
φ=Er |
| Разность потенциалов |
φ1−φ2=Er12 |
| Напряжение между пластинами |
U=Ed d — расстояние между заряженными пластинами. |
| Эквипотенциальные поверхности | Плоскости, параллельные заряженным пластинам. |
| Закон Кулона |
FK=qE=qUd |
| Ускорение силы Кулона (следует из второго закона Ньютона) |
a=FKm=qEm=qUmd |
Подсказки к решению задач:
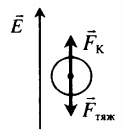 |
Равновесие заряженного тела в электростатическом поле:
Fтяж=FK Сила тяжести равна произведению массы заряженного тела на ускорение свободного падения: Fтяж=mg Сила Кулона равна: FK=qE=qUd |
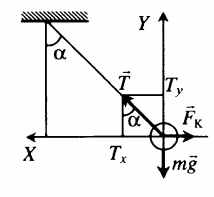 |
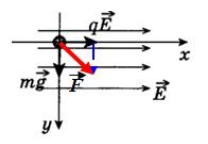
Отклонение от вертикали нити с заряженным телом в горизонтальном электростатическом поле.
Второй закон Ньютона в векторной форме: −FK+m−g+−T=m−a Проекции на оси: OX:Tsinα−FK=0 OY:Tcosα−mg=0 Отсюда сила Кулона равна: FK=mgtanα FK=qE=qUd |
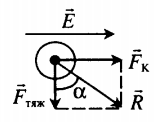 |
Направление траектории полого шарика массой m и зарядом q, который движется в горизонтальном электрическом поле напряженностью −E. Важно! Направление траектории совпадает с направлением равнодействующей силы. Равнодействующая силы находится по второму закону Ньютона: −R=−FK+m−g Из рисунка видно, что: tanα=FKFтяж=qEmg |
Пример №1. Полый шарик массой m = 0,4 г с зарядом q = 8 нКл движется в горизонтальном однородном электрическом поле, напряженность которого E = 500 кВ/м. Какой угол α образует с вертикалью траектория шарика, если его начальная скорость равна нулю?
0,4 г = 0,4∙10–3 кг
8 нКл = 8∙10–9 Кл
500 кВ/м = 5∙105 В/м
При движении в электрическом поле на заряженную частицу действует сила тяжести:
−Fтяж=m−g
На нее также действует сила Кулона со стороны электрического поля:
−FK=q−E
В инерциальной система отсчета, связанной с Землей, в соответствии со вторым законом Ньютона:
−FK+m−g=m−a
При движении из состояния покоя с постоянным ускорением тело движется по прямой в направлении вектора ускорения, т. е. в направлении равнодействующей приложенных сил. Прямая, вдоль которой направлен вектор ускорения, образует угол с вертикалью, равный:
Тангенс, равный единице, соответствует углу, равному 45 градусам.
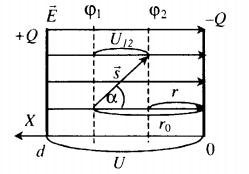
Работа однородного электрического поля
Из курса механики вспомним, что работа определяется произведением силы, действующей на тело, на его перемещение и косинус угла между векторами силы и этого перемещения:
A=Fscosα
Эту же формулу можно использовать для нахождения работы однородного электрического поля. В качестве силы в данном случае выступает сила Кулона:
FK=qE=qUd
А произведение перемещения на косинус угла между силой и перемещением в этом случае равно разности начального и конечного положения заряда:
scosα=r0−r
Отсюда работа однородного электрического поля равна:
Формулы работы электрического поля
A=±qE(r0−r)=±qUd(r0−r)
или
A=FKscosα=±qEscosα=±qUdscosα
- E (В/м или Н/Кл) — модуль напряженности электрического поля;
- U (В) — разность потенциалов (напряжение) между пластинами;
- d (м) — расстояние между пластинами;
- ±q — заряд, переносимый полем;
- s (м) — модуль перемещения заряда;
- α — угол между силой Кулона и перемещением;
- r0 (м) — начальное положение заряда;
- r (м) — конечное положение заряда.
Работу также можно выразить через разность потенциалов:
A=±q(φ1−φ2)=±qU12
- φ1 — начальный потенциал;
- φ2 — конечный потенциал;
- U12 — напряжение между начальным и конечным положением заряда.
Внимание! Работа электростатического поля не зависит от вида траектории.
Работа и изменение кинетической энергии:
A=mv22−mv202=ΔEk
Работа и изменение потенциальной энергии:
A=−(qEr−qEr0)=−ΔWp
Пример №2. В точке А потенциал электрического поля равен 200 В. Потенциал в точке В равен 100В. Какую работу совершают силы электростатического поля при перемещении заряда 5 мКл из точки А в точку В?
5 мКл = 5∙10–3 Кл
A=±q(φ1−φ2)=5·10−3(200−100)=0,5 (Дж)
Задание EF17633
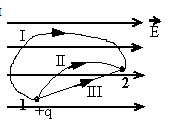
Ответ:
а) максимальна в случае перемещения по траектории I
б) не совершается в случае перемещения по траектории II
в) минимальна в случае перемещения по траектории III
г) одинакова при перемещении по всем траекториям
Алгоритм решения
- Установить, от чего зависит работа электростатического поля, затрачиваемая на перемещение в нем заряженной частицы.
- Определить, какую работу совершает поле при движении заряда по каждой из траекторий.
Решение
Кулоновская сила — это потенциальная сила. Поэтому работа, которую она совершает, не зависит от вида траектории. Учитываться будет только перемещение, равное кратчайшему расстоянию между точками 1 и 2. Следовательно, работа будет одинаковой при перемещении положительного заряда по всем траекториям.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18815
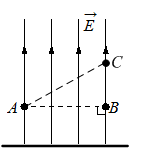
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
Ответ:
1) Пластина имеет отрицательный заряд.
2) Потенциал электростатического поля в точке В ниже, чем в точке С.
3) Работа электростатического поля по перемещению пробного точечного отрицательного заряда из точки А и в точку В равна нулю.
4) Если в точку А поместить пробный точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз.
5) Напряжённость поля в точке А меньше, чем в точке С.
Алгоритм решения
1.Проанализировать каждое из утверждений.
2.Установить, какие из утверждений являются истинными.
3.Записать номера верных утверждений.
Решение
Согласно утверждению 1, пластина имеет отрицательный заряд. Известно, что векторы напряженности поля, создаваемого отрицательным зарядом, направляются в сторону этого заряда. Но мы видим, что векторы направляются от заряда. Следовательно, пластина заряжена положительно, а утверждение 1 неверно.
Согласно утверждению 2, потенциал электростатического поля в точке В ниже, чем в точке С. Известно, что потенциал зависит от расстояния до отрицательно пластины. Поскольку в нашем случае пластина заряжена положительно, с увеличением расстояния от нее потенциал уменьшается. Поэтому потенциал в точке С меньше потенциала в точке В, а утверждение 2 неверно.
Согласно утверждению 3, работа электростатического поля по перемещению пробного точечного отрицательного заряда из точки А и в точку В равна нулю. Работа определяется формулой:
A=FKscosα=±qEscosα
Видно, что работа зависит от перемещения относительно заряженной пластины. Но точки А и В находятся от пластины на одинаковом расстоянии. Следовательно, перемещение относительно нее равно 0. Поэтому работа по перемещению заряда тоже будет нулевой, и утверждение 3 верно.
Согласно утверждению 4, если в точку А поместить пробный точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз. Это действительно так. Мы выяснили, что пластина заряжена положительно. Следовательно, отрицательный заряд будет притягиваться к ней, и утверждение 4 верно.
Согласно утверждению 5, напряжённость поля в точке А меньше, чем в точке С. Это не так, потому что речь идет об однородном поле. Напряженность однородного поля одинакова во всех точках, и утверждение 5 неверно.
Верные утверждения: 3 и 4.
Ответ: 34
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.6k
Конечное значение – потенциал
Cтраница 1
Конечные значения потенциалов определятся энергией, которую израсходуют внешние силы на перемещение последнего единичного заряда с шарика В на шарик А.
[1]
При любом конечном значении потенциала электрода скорость обоих указанных процессов ( / 0 и / в) не может быть равной нулю.
[2]
В приводимых выше работах [5, 6, 8, 9] нами неоднократно отмечалось влияние кинетики установления потенциала на его величину и было показано, что конечное значение потенциала в ряде систем зависит от способа предварительной обработки электродов. Кроме того, нами [10-12] была найдена зависимость между скоростью установления потенциала и изменением его каталитических свойств.
[3]
В отсутствие поля два пучка различной длины волны приводят к взаимному погашению при интегрировании на больших расстояниях; функции FO ( х) и FI ( х) влияют на Т только в областях с конечным значением потенциала взаимодействия, и основное их влияние сосредоточено вблизи классических точек остановки.
[4]
Потенциал скоростей при исследовании собственных колебаний сферической полости удобно выразить в виде ( 8 17), причем следует положить Вто0, поскольку пт ( 0) – со, а в центре сферы должно получиться конечное значение потенциала. Для расчета собственных частот сферического слоя необходимо учитывать второй член.
[5]
Для постоянных напряжений характерно то, что они вызываю. На конечные значения потенциалов постоянные напряжения если и влияют, то весьма незначительно.
[6]
Если скорость раз-вертки потенциала точно измерена и воспроизводимо задается, то конечное значение потенциала может быть вычислено по времени развертки. Екон, от погрешности / задания линейности развертки потенциала и погрешности лентопротяжного механизма. Обычно имеется возможность оценки двух последних погрешностей путем записи зависимости постоянной составляющей тока на активной нагрузке от налагаемого на нее напряжения развертки.
[7]
Однако иногда для увязки статики и динамики сушильного процесса представляет интерес и аналитическое определение конечного значения сушильного потенциала.
[8]
Следовательно, при любом значении потенциала ( кроме равновесного) протекают два противоположных по смыслу процесса, но с различной скоростью. Строго говоря, скорость ни того, ни другого не может стать равной нулкГпри любом конечном значении потенциала.
[9]
Следовательно, при любом значении потенциала ( кроме равновесного) протекают два противоположных по смыслу процесса, но с различной скоростью. Строго говоря, скорость ни того, ни другого не может стать равной нулю при любом конечном значении потенциала.
[10]
Следовательно, при любом значении потенциала ( кроме равновесного) протекают два противоположных по смыслу процесса, но с различной скоростью. Строго говоря, скорость ни того, ни другого не может стать равной нулю при любом конечном значении потенциала.
[11]
При электрометрических измерениях окислительного потенциала критерием достижения им равновесного значения считается неизменяемость потенциала во времени. При этом, как неоднократно указывалось ранее [17, 20], измерение должно производиться с двумя электродами, что позволяет прийти к конечному значению потенциала с двух противоположных сторон. Для этого можно применять катодно и анодно поляризованные электроды.
[12]
На самом деле, если считать, что в растворе совершенно отсутствует одна из форм окислительно-восстановительной пары, потенциал согласно уравнению Нернста должен быть равен или – оо, что невозможно. С другой стороны, как было сказано выше, растворитель ( в данном случае вода) способен окисляться и восстанавливаться, в результате при весьма большом или малом начальном значении потенциала системы приходят в равновесие и возникает концентрация отсутствовавшей сопряженной формы окислительно-восстановительной пары, при которой раствор приобретает некоторое конечное значение потенциала. Этот потенциал невозможно вычислить, но можно экспериментально измерить. По этой причине при вычислении кривых титрования редоксиметрии обычно не приводят значение потенциала для точки, соответствующей моменту, когда в исследуемый раствор еще не прибавлен титрант.
[13]
Однако в противоположность методу Ритца величина / в уравнении ( 2), используя значение из ( 6), для данного случая будет всегда меньше истинного минимального значения / при правильном решении, если только последнее не было выражено как конечная сумма Фт. Отличный метод вывода решения уравнения Лапласа, соответствующий вполне определенной физической проблеме течения, заключается в графическом интегрировании уравнения. При этом способе решение последнего представляется геометрической сетью эквипотенциальных линий и линий тока, соответствующих физической задаче. Эта сеть получается в результате следования определенным правилам и при повторении дает последовательно более близкое приближение к форме сети, определяемой точным решением. Отдельные детали этого метода могут быть самого разнообразного порядка. Они могут базироваться на принципе соответственного преобразования первоначально произвольной сети, которая показывала бы режим на контурах, соответствующий заранее принятым граничным условиям, или же на принципе дальнейшего развития элементов сети, первоначально выбранных так, чтобы удовлетворить полностью или частично граничным условиям внутри интересующей области, согласно правилам, соответствующим дифе-ренциальному уравнению, которое необходимо решить. Главной особенностью совершенно иной схемы является графическое построение функций Грина для рассматриваемой области и последующий подсчет конечного значения потенциала графическим или численным интегрированием согласно уравнению ( 1), гл.
[14]
Страницы:
1