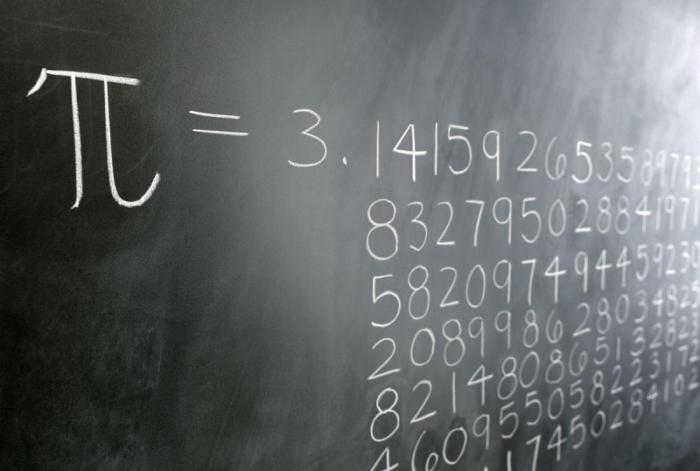Как найти конец бесконечности

Ответы

Бесконечность является абстрактным понятием, используемым, чтобы описать или обозначить нечто бесконечное или безграничное. Это понятие важно для математики, астрофизики, физики, философии, логики и искусства.

Вот несколько удивительных фактов об этом комплексном понятии, которые способны взорвать мозг лбого человека, не очень близко знакомого с математикой.

Символ бесконечности

У бесконечности есть свой собственный специальный символ: ∞. Символ, или лемниската, был введен священнослужителем и математиком Джоном Уоллисом в 1655 году. Слово «лемниската» происходит от латинского слова lemniscus, что означает «лента».

Уоллис, возможно, основал символ бесконечности на римской цифре 1000, рядом с которой римляне раньше указывали «бесчисленный», в дополнение к числу. Также возможно, что символ основан на омеге (Ω или ω), последней букве греческого алфавита.

Интересный факт заклчается в том, что понятие бесконечности появилось и использовалось задолго до того, как Уоллис наградил его символом, который мы используем по сей день.

В четвертом веке до нашей эры джайнистский математический текст под названием Сурья-праджнапти-сутра разделял все числа на три категории, каждая из которых, в свою очередь, разделялась на три подкатегории. В этих категориях были указаны перечислимые, неперечислимые и бесконечные числа.

Апория Зенона

Зенон Элейский, родившийся приблизительно в пятом веке до н. э., был известен парадоксами, или апориями, включающими и понятие бесконечности.

Из всех парадоксов Зенона самым известным является «Ахиллес и Черепаха». В апории черепаха бросает вызов греческому герою Ахиллесу, приглашая его на гонку. Черепаха утверждает, что выиграет гонку, если Ахиллес даст ей преимущество в тысячу шагов. Согласно парадоксу, за то время, что Ахиллес пробежит все расстояние, черепаха сделает в ту же сторону еще сто шагов. Пока Ахиллес пробежит еще сто шагов, черепаха успеет сделать еще десять и так далее по убывающей.

В более простом изложении парадокс рассматривается так: попробуйте пересечь комнату, если каждый следующий шаг в половину меньше предыдущего. Хоть каждый шаг и приближает вас к краю комнаты, вы никогда на самом деле не доберетесь до него, или доберетесь, но на это потребуется бесконечное количество шагов.

Согласно одной из современных трактовок, этот парадокс основан на ложном представлении о бесконечной делимости времени и пространства.

Число пи – пример бесконечности

Отличным примером бесконечности является число пи. Математики используют для числа пи символ, потому что невозможно записать все число целиком. Пи состоит из бесконечного количества чисел. Оно часто округляется до 3,14 или даже 3,14159, но неважно, сколько цифр записано после запятой, ведь невозможно добраться до конца числа.

Теорема о бесконечных обезьянах

Еще один способ думать о бесконечности – рассмотреть теорему о бесконечных обезьянах. Согласно теореме, если дать обезьяне печатную машинку и бесконечное количество времени, в конечном счете у обезьяны получится напечатать «Гамлета» или любое другое произведение.

В то время как многие люди воспринимают теорему как демонстрацию веры в то, что нет ничего невозможного, математики рассматривают ее как доказательство невозможности определенного события.

Фракталы и бесконечность

Фрактал – это абстрактный математический объект, используемый в математике и искусстве, чаще всего он моделирует природные явления. Фрактал записывается как математическое уравнение. Рассматривая фрактал, можно заметить его сложную структуру на любом масштабе. Другими словами, фрактал бесконечно увеличиваем.

Снежинка Коха является интересным примером фрактала. Снежинка выглядит как равносторонний треугольник, образующий замкнутую кривую бесконечной длины. Увеличивая кривую, на ней можно увидеть все новые и новые детали. Процесс увеличения кривой может продолжаться бесконечное количество раз. Несмотря на то что у снежинки Коха есть ограниченная область, она ограниченна бесконечно длинной линией.

Бесконечность разных размеров

Бесконечность безгранична, на все же она поддается измерению, пусть и сравнительному. Положительные числа (больше 0) и отрицательные числа (меньше 0) могут похвастать бесконечными наборами чисел равных размеров. А что происходит, если объединить оба набора? Получится вдвое большой набор. Или еще пример – все четные числа (их бесконечное количество). И все равно это всего лишь половина бесконечного количества всех целых чисел. Другой пример, просто прибавьте единицу к бесконечности. Поучится число на 1 больше бесконечности.

Космология и бесконечность

Космологи изучают Вселенную, неудивительно, что понятие бесконечности играет для них важную роль. Есть ли границы у Вселенной или она бесконечна?

Этот вопрос до сих пор остается без ответа. Наша Вселенная расширяется, но куда? И где предел этого расширения? Даже если у физической Вселенной и существуют границы, у нас все еще есть теория мультивселенной, которая рассматривает существование бесконечного количества Вселенных, в которых могут быть отличные от нашей законы физики.

Деление на ноль

Деления на ноль не существует. Оно невозможно, по крайней мере, в обычной математике. В привычной нам математике единицу, поделенную на ноль, невозможно определить. Это ошибка. Однако так бывает не всегда. В расширенной теории комплексных чисел деление единицы на ноль не вызывает неминуемого коллапса и определяется некоторой формой бесконечности. Другими словами, математика бывает разной, и не вся она ограничивается правилами из учебников.

Нашли нарушение? Пожаловаться на содержание

А вы много знаете о числах? ПРАВДА или ВЫМЫСЕЛ, что знаменитое в математике число Пи равно 3,14 и ещё 31 триллион знаков после запятой?

Узнать ответ и проверить себя вы сможете в конце статьи.

Что мы понимаем под бесконечностью

Если спросить, что есть бесконечного в нашем мире, то большинство из вас вспомнит именно про вселенную. Некоторые, однако, назовут и счёт. Далее пойдут версии про пространство, воображение, фантазию и даже вариации отпечатков пальцев у людей или полос у зебры. Также, некоторые ошибочно предполагают, что существует бесконечное число авто номеров или, например, штрихкодов, о которых мы говорили в предыдущих статьях.

Но что такое бесконечность с научной точки зрения?

Бесконечность-это категория мышления человека. Она характеризует неисчерпаемые и безграничные явления или предметы. В общем всё, у чего нет конца. Как например бесконечна вселенная (предположительно) и, следовательно, количество атомов во вселенной. Об этом вы, кстати, можете почитать в нашей статье «Есть ли конец у вселенной?».

Сюда же относится бесконечное множество совершенных чисел.

Факториал простым языком. Есть ли последнее число у комбинаций?

Представьте, что перед вами лежат две разноцветные карточки: красная и зеленая. И у вас задача разложить их максимальное число раз в последовательности, которая не повторяется. Недолго думая, вы выдаёте два очевидных варианта: красная-зеленая и зелёная-красная. Количество таких вариантов для какого-то числа и называют факториал. В данном случае факториал числа 2 равен 2-ум.

Например, для трёх цветов уже будет возможно 6 вариантов такой раскладки. А для четырёх-24. Интерес в том, что чем больше число, тем более невероятный у него факториал. Так, всего у 12-ти разноцветных карточек есть более 479 млн неповторяемых вариаций! А 20 таких цветных карт будут иметь 2 квинтиллиона комбинаций (это число из 19 знаков)!

Говоря о количестве комбинаций партий на шахматной доске, мы условно подразумеваем бесконечность. Однако число это вовсе не бесконечно, просто оно является немыслимо большим.

Вернёмся к счёту

С бесконечностью, кажется, разобрались. Осталось понять, до какого момента продолжается счёт?

Большинство из нас знает только первые 4-5 названий чисел, где каждый раз прибавляется по три нуля (в 1000 раз больше предыдущего). Это один, тысяча, миллион, биллион (или как принято его у нас называть-миллиард) и триллион.

Перечислять все числа мы не будем. Но охватим некоторые из последующих. Так, число с 60-ю нулями называется новемдециллион, с 99ю-дуотригинтиллион. А со 123мя-квадрагинтиллион.

Кстати, число состоящее из единицы со ста нулями носит название гугол (googol). И да, одноименная знаменитая поисковая система названа именно в честь этого числа.

Максимально известное сегодня «последнее число»

Счёт действительно не имеет конца. Но максимальное известное значение сегодня мы всё-таки определить в силах.

Это происходит потому, что даже современные мощные машины и специальная техника не в состоянии высчитать такие огромные значения. На расчет бесконечности ей элементарно не хватило бы памяти!

Итак, название максимально известного рассчитанного числа равно 10 в степени 3003 и называется миллеиллион. Есть числа и намного больше этого (например мириада, Скьюза, стасплекс), но они уже считаются внесистемными. Конечные расчеты настолько длинные, что их условно приравнивают к бесконечности.

А теперь вернёмся с вами к нашему вопросу. ПРАВДА или ВЫМЫСЕЛ, что знаменитое в математике число Пи равно 3,14 и ещё 31 триллион знаков после запятой?

ВЫМЫСЕЛ

На самом деле число Пи имеет бесконечное количество знаков после запятой. Однако современной технике пока под силу рассчитать это число только до ≈ 31 триллиона знаков.

А до какого числа сможете сосчитать вы?