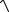Как найти коническую передачу

Как найти коническую передачу

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

Скачиваний:

521

Добавлен:

17.03.2015

Размер:

526.36 Кб

Скачать

Лекция 7 КОНИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ

П л а н л е к ц и и

1. Общие сведения.

2. Особенности геометрии зубьев и колес.

3. Усилия в зацеплении.

4. Условие работоспособности по контактной и изгибной прочности.

1. Общие сведения

Конические зубчатые передачи предназначены для передачи механической энергии между валами с пересекающимися осями под углом (рис. 7.1).

Наибольшее распространение имеют ортогональные ( = 90º) передачи. Конические передачи могут быть прямозубые (рис 7.2) и с круговыми зубьями.

Рис. 7.1

Рис. 7.2

1

Разновидностью конических передач являются гипоидные передачи, у которых оси вращения колес не пересекаются, а перекрещиваются.

Достоинства конических передач – возможность передачи механической энергии между валами с пересекающимися валами.

Недостатки конических передач:

меньшая нагрузочная способность. По опытным данным, она меньше нагрузочной способности передач цилиндрическими колесами до 20 %. Пересечение валов затрудняет расположение опор. Одно из конических колес (как правило, шестерню) располагают консольно, при этом увеличивается неравномерность распределения нагрузки по длине зуба, что приводит к снижению нагрузочной способности;

необходимость регулирования зацепления в передаче; большая сложность изготовления;

большие нагрузки на опоры из-за значительных осевых нагрузок.

2. Особенности геометрии зубьев и колес

Линии пересечения боковых поверхностей зубьев с делительной конической поверхностью называют линией зубьев.

Взависимости от формы линии зуба различают конические передачи

спрямыми зубьями (рис. 7.3, а), у которых линии зубьев проходят через вершину делительного конуса, с тангенциальными (рис. 7.3, б) и с круговыми зубьями (рис. 7.3, в).

Конические колеса с круговыми зубьями характеризуют наклоном зуба

всреднем сечении по ширине зубчатого венца. Угол наклона m – острый угол между касательной в данной точке к линии зуба и образующей делительного конуса.

Передачи с прямыми зубьями имеют начальный линейный контакт

взацеплении, передачи с круговыми зубьями – точечный.

Рис. 7.3

2

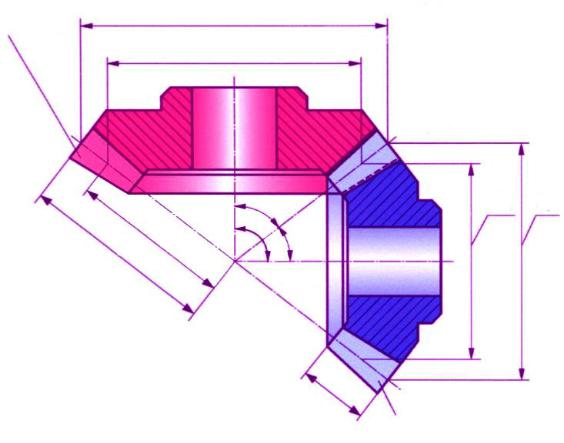
Угол наклона для передач с прямым зубом составляет m = 0º, для передач с круговым зубом принимают m = 35º. Наличие наклона зуба повышает плавность работы, контактную прочность и прочность на изгиб, но увеличивает нагрузки на опоры и валы.

Конические колеса с круговыми зубьями обладают большой несущей способностью, работают с меньшим шумом по сравнению с прямозубыми.

Для повышения износостойкости и сопротивления зубьев заеданию смещение исходного контура выравнивают удельные скольжения в граничных точках зацепления. Шестерню и колесо выполняют с одинаковыми значениями смещений, но с разными знаками: шестерню – с положительным смещением, а колесо – с отрицательным.

Основные геометрические параметры зацепления конического коле-

са приведены на рис. 7.4. Это углы делительного конуса 1 и 2; внешнее конусное расстояние Re – длина отрезка образующей делительного конуса от его вершины до внешнего торца; Rm – среднее конусное расстояние; b – ширина венца зубчатого колеса, ограниченного двумя дополнительными конусами – внешним и внутренним.

Пересечение делительных конусов с дополнительными конусами определяют диаметры делительных окружностей конического зубчатого колеса. Различают внешний de и средний dm делительные диаметры.

δ2

dm1

de1

Re

δ1

Rm

b

ШЕСТЕРНЯ

Рис. 7.4

3

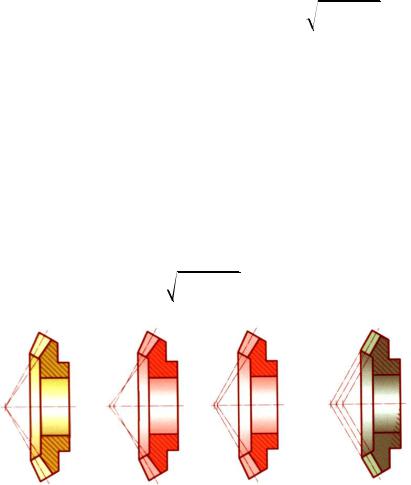
Передаточное число (мгновенное передаточное отношение) конической передачи вычисляют по формуле

i

de2

dm2

tg δ

2

1

Z2

,

de1

dm1

tgδ1

Z1

где de1, de2, dm1, dm2 и 1, 2 – соответственно внешние, средние делительные диаметры и углы делительных конусов шестерни и колеса; Z1 и Z2 – число зубьев шестерни и колеса.

Для конической прямозубой передачи рекомендуют значение i до 3,15; при колесах с круговыми зубьями – до 6,3.

Осевая форма зуба. Зубья конических колес в зависимости от изменения размеров их нормальных сечений по длине выполняют трех осевых форм (рис. 7.5):

осевая форма I – нормально понижающиеся зубья (рис. 7.5, а). Вершины делительного конуса и конуса впадин совпадают, высота ножки зуба пропорциональна конусному расстоянию. Применяют для прямых зубьев,

а также ограниченно для круговых при m 2 мм и 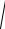Z12 Z22 = 20–50;

осевая форма II – нормально сужающиеся зубья (рис. 7.5, б). Вершина конуса впадин расположена так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу пропорциональна конусному расстоянию. Эта форма обеспечивает оптимальную прочность на изгиб во всех сечениях, позволяет одним инструментом обрабатывать сразу обе поверхности зубьев колеса, что повышает производительность при нарезании зубчатых колес. Является основной для колес с круговыми зубьями. Применяют в массовом производстве;

осевая форма III – равновысокие зубья (рис. 7.5, в). Образующие конусов делительного, впадин и вершин параллельны. Высота зубьев постоянна по всей длине. Применяют для неортогональных передач с межосевым углом

40º и круговыми зубьями при Z12 Z22 60.

Рис. 7.5

4

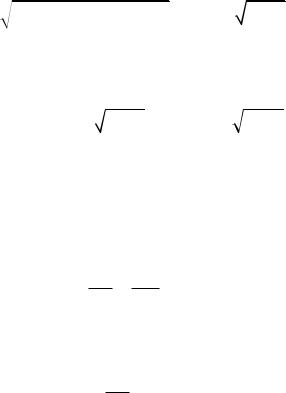
Основные геометрические соотношения. В конических зубчатых колесах с осевыми формами I и II высота зуба, а следовательно, и модуль зацепления увеличиваются от внутреннего к внешнему дополнительному конусу (рис. 7.5, а, б). Для удобства измерения размеры конических колес принято определять по внешнему торцу зуба.

Максимальный модуль зубьев – внешний окружной модуль mte получают на внешнем торце колеса.

Ниже приведены основные геометрические соотношения для конических зубчатых передач (рис. 7.4).

Внешние делительные диаметры шестерни и колеса:

de1 = mteZ1, de2 = mteZ2.

Внешнее конусное расстояние

Re (0,5de1)2 (0,5de2 )2 0,5de1 1 i2 .

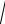
Ширина зубчатого венца: b = KbeRe. Для большинства конических передач коэффициент ширины зубчатого венца Kbe = 0,285. Тогда

b = 0,285 0,5de1 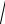1 i2 = 0,143de1 1 i2 .

Среднее конусное расстояние

Rm = Re – 0,5d = Re – 0,5 0,285Re = 0,857Re.

Из условия подобия (рис. 7.4) следует

de1 dm1 . Re Rm

Тогда средний делительный диаметр шестерни

dm1 de1 Rm 0,857de1.

Re

Модуль окружной в среднем сечении mtm = 0,857mte.

Модуль нормальный в среднем сечении для кругового зуба ( m = 35º)

mn = mtm cos m ≈ 0,702mte.

Углы делительных конусов

tg 1 =

Z1

1

,

2 = 90º – 1.

Z2

i

5

Для конических зубчатых колес с прямыми зубьями в качестве расчетного принимают внешний окружной модуль mte, для конических зубчатых колес с круговыми зубьями средний нормальный модуль mn в середине зубчатого венца.

Одной и той же зуборезной головкой можно нарезать конические колеса с модулями, изменяющимися в некотором непрерывном диапазоне. Поэтому допускается использовать нестандартные значения модуля.

Эквивалентное колесо. Для прямозубой передачи профили зубьев конического колеса на среднем дополнительном конусе близки к профилям зубьев цилиндрического прямозубого колеса с делительным эквивалентным диаметром dv.

Дополнив развертку среднего дополнительного конуса на плоскость до полной окружности, получим эквивалентное цилиндрическое колесо с числом зубьев Zv и делительным диаметром

dv = mnZv.

Рассмотрим связь между делительными эквивалентным диаметром dv и средним dm:

dv =

dm

mnZ

.

cosδ

cosδ

Из равенства mnZv

=

mnZ

следует

зависимость для определения

cos δ

эквивалентного числа зубьев

Zv =

Z

,

cos δ

т. е. фактическое коническое прямозубое колесо с числом зубьев Z в прочностных расчетах можно заменить цилиндрическим с эквивалентным числом

зубьев Zv.

Для передачи с круговыми зубьями профили зубьев конического колеса в нормальном сечении близки к профилям зубьев эквивалентного цилиндрического прямозубого колеса. Эквивалентное число зубьев Zvn получают двойным приведением – конического колеса к цилиндрическому и кругового зуба к прямому зубу:

Z

Zvn = cos δ cos3βm .

6

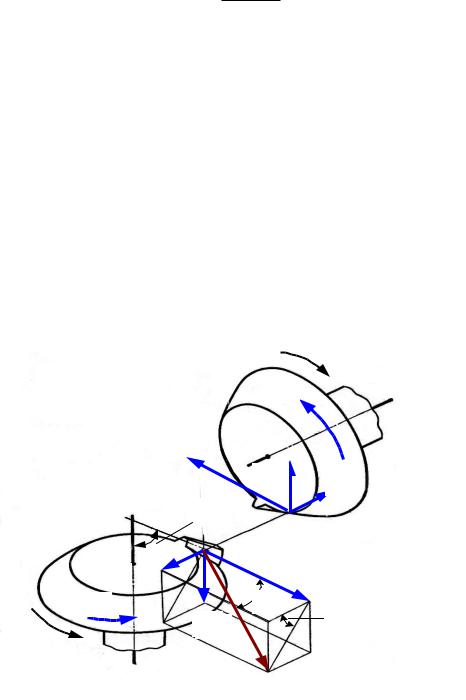
3.Усилия в зацеплении

Вконической передаче местом приложения силы Fn (рис. 7.6), действующей перпендикулярно поверхности зуба, считают сечение на середине ширины зубчатого венца.

Силу Fn раскладывают на составляющие: Ft, Fr и Fa. Окружная сила Ft1 на шестерне

Ft1 = 2T1 103 , dm1

где T1 – вращающий момент, Н м; dm1 – средний делительный диаметр, мм.

В прямозубой передаче для определения составляющих запишем промежуточное выражение (αw = 20º угол зацепления)

R = Fttg αw.

Радиальная сила на шестерне

Fr1 = Rcos 1 = Fttg αw cos 1.

Осевая сила на шестерне

Fa1 = Rsin 1 = Fttg αw sin 1.

ω2

Т2

Ft2

Fr2

Fa2

1

Fr1

Ft1

αw

Т1

1

Fa1

ω1

Fn

Рис. 7.6

7

Силы на колесе (рис. 7.6):

Fr2 = Fa1, Fa2 = Fr1.

Впередаче с круговым зубом во избежание заклинивания зубьев при значительных зазорах в подшипниках необходимо обеспечить направление

осевой силы Fa1 на ведущей шестерне к основанию делительного конуса. Для этого направление вращения ведущей шестерни (если смотреть со стороны вершины делительного конуса) и направление наклона зубьев должны совпадать. Шестерня вращается против часовой стрелки, т. е. влево, и зуб шестерни левый.

Впередаче с круговым зубом при соблюдении этого условия: радиальная сила на шестерне

Fr1 =

Ft (tg αw cosδ1 sinβm sin δ1)

;

cosβm

oсевая сила на шестерне

Fa1 =

Ft (tg αw sin δ1 sinβm cosδ1)

.

cosβm

Такие же знаки в формулах будут при вращении по часовой стрелкe ведущей шестерни с правым зубом.

Силы на колесе:

Fr2 = Fa1, Fa2 = Fr1.

4.Условие работоспособности по контактной

иизгибной прочности

Прочностной расчет конической передачи основан на допущении, что несущая способность зубьев конического колеса такая же, как у эквивалентного цилиндрического с той же длиной b зуба и профилем, соответствующим среднему дополнительному конусу (среднему сечению зуба). Прочность зубьев определяется зависимостями

где H – контактное напряжение; F – напряжение изгиба; [ ]H и [ ]F – соответствующие допускаемые напряжения.

Для проверочного расчета вывод формулы в параметрах эквивалентной цилиндрической прямозубой передачи по среднему дополнительному конусу (см. рис. 7.4) имеет вид

8

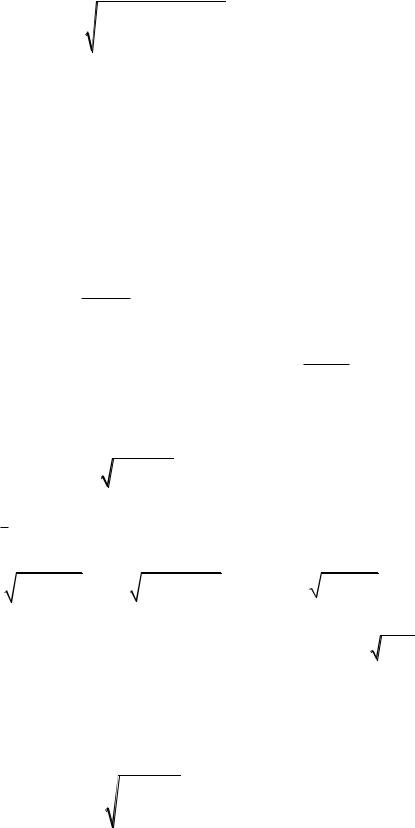
H = ZмZHZ

KH Ft (iv 1)

1

,

(7.1)

bdv1

iv

H

где iv – передаточное число эквивалентной

цилиндрической

передачи;

Н – коэффициент, учитывающий влияние на несущую способность передачи вида конических колес.

Передаточное число эквивалентной цилиндрической передачи

i

dv2

dm2

cos δ1

i cos δ1

.

v

dv1

cos δ2

dm1

cos δ2

Учитывая, что cos 1 = sin 2, a tg 2 = i, получим

iv i sin δ2 i2. cos δ2

Диаметр эквивалентной цилиндрической шестерни

Заменяя функцию косинуса функцией тангенса:

cos δ1

1

1 tg2δ

1

и имея в виду, что tg δ1 1i , а dm1 0,857de1 , запишем

dv1 dm1 . cos δ1

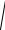
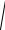
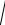
dv1 dm1cosδ1 dm1 1 tg2δ1 dm1 (i2 1) / i2 0,857de1 i2 1/ i.

2T 103

Ft1

, b 0,143de1

1 i

2

Подставив в формулу (7.1) значения iv, dv1,

1

,

0,857de1

с учетом условия прочности σH σH и рекомендуемых числовых значений Zм,

ZH и Z , получим формулу для проверочного расчета стальных конических

зубчатых передач

σH 6,7 104

KH T1

σ

.

(7.2)

d 3 i

H

H

e1

Для прямозубых конических передач H 0,85. Для передач с круговыми зубьями значения H зависят от твердости зубчатых колес пары и передаточного числа ( H 1).

9

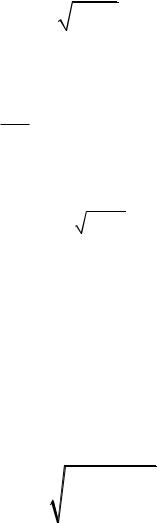
Коэффициент нагрузки для конических передач

KH KαKHβKHv.

Значения коэффициента Kα назначают так же, как и для цилиндрических зубчатых передач.

Коэффициент KH учитывает неравномерность распределения нагрузки по длине контактных линий.

В конических передачах шестерню располагают консольно, при этом вследствие меньшей жесткости консольного вала и деформаций опор повышена неравномерность распределения нагрузки по длине контактных линий в зацеплении. По этой причине конические колеса по сравнению с цилиндрическими работают с бóльшим шумом. С целью повышения жесткости опор валы устанавливают на конических роликовых подшипниках.

Для конических колес с прямыми зубьями

KHβ KH0 β ;

с круговыми зубьями, при условии KHβ 1, 2,

K Hβ 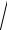K H0 β ,

где KH0 β коэффициент, выбираемый по таблицам или графикам для цилиндрических зубчатых передач в зависимости от значения коэффициента

относительной ширины ψbd b , твердости зубчатых колес и расположе- de1

ния передачи относительно опор. Для конических передач

ψbd 0,166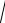i2 1.

Значение коэффициента KHv внутренней динамической нагрузки для передач с круговыми зубьями принимают таким же, как и для цилиндрических косозубых передач. Для конических прямозубых передач KHv назначают так же, как для цилиндрических прямозубых, но с условным понижением степени точности на единицу (например, для фактической степени точности 7 значение KHv принимают по степени точности 8).

Решив зависимость (7.2) относительно de, получим формулу проектировочного расчета для внешнего делительного диаметра шестерни стальных конических зубчатых передач

de1 1650

KH T1

3

.

i σ 2

H

H

10

Соседние файлы в папке Конспекты лекций

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #

Источник
Параметры и обозначения Числовые значения шестерни
ведущей шестерни ведомой
(колеса) Число зубьев, Z Z Модуль,мм me Межосевой угол ∑o Ширина зубчатого венца α Внешний торцевой исходный контур ГОСТ 13754-81 ha c pf Число зубьев эквивалентного плоского колеса zc – Внешнее конусное расстояние Re Re = 0.5 me zc Ширина зубчатого венца b ≤ 0.3 Re; b ≤ 10 me Среднее конусное расстояние Re = 0.5 b Средний окружной модуль mm =me Rm / Re Внутренний окружной модуль m1 =me (Re – b)/ Re Cредний делительный диаметр d =mm z Угол делительного конуса tan(β1) = sin(∑) / (z2 / z1 + cos(∑));
β2 = ∑ – β1 Передаточное число эквивалентной конической передачи Число зубьев эквивалентной конической шестерни Внешняя высота головки зуба hae = ha me Внешняя высота ножки зуба hfe1 = hae + c me Внешняя высота зуба he = hae + hfe Внешняя окружная толщина зуба se = 0.5 π me Угол ножки зуба tan(Θf) =hfe / Re Угол головки зуба Θa = Θf Угол конуса верши δa = δ + Θa Угол конуса впадин δf = δ – Θf Внешний делительный диаметр de = me z Внешний диаметр вершин зубьев dae = de + 2 hae cos(δ) Расстояние от вершины до плоскости внешней окружности вершин зубьев B = Re cos(δ) – hae sin(δ) Внешняя постоянная хорда зуба sce = se cos2(α) Высота до внешней постоянной хорды зуба hce = hae – 0.25 se sin(2α) Половина внешней угловой толщины зуба ψe = se cos(δ) / de Внешняя делительная толщина зуба по хорде se = de sin(ψe ) / cos(δ) Высота до внешней делительной хорды hae = hae + 0.25 se ψe
Источник

Прямозубые конические передачи вы­полняют с осевой формой I с пропорцио­нально
понижающимися зубьями (рис. 28) и постоянным радиальным зазором по ши­рине
зубчатого венца.

При обработке зубчатых колес зубострогальными резцами дно впадины имеет ко­ническую
форму (рис. 29, а), а при обра­ботке парными зуборезными головками — вогнутую
(рис. 29, б).

Числа зубьев шестерни и колеса ортого­нальной
конической зубчатой передачи при исходном контуре по ГОСТ 13754—81 сле­дует
выбирать с учетом данных, приведен­ных в табл. 67.

Число зубьев цементованных ко­нических зубчатых колес рекомендуется определять по
номограмме, приведенной на рис. 30.

Термически улучшенные конические зубчатые колеса можно выполнять с тем же увеличенным числом зубьев на 10-20 %.

Модули. В качестве расчетного принят внешний окружной модуль mе. Модуль mе рекомендуется устанавливать по ГОСТ 9563-60.

Параметры исходного контура. Ко­нические передачи с прямыми зубьями общего назначения при mе выше 1мм должны выполняться в соответствии с ис­ходным контуром по ГОСТ 13754—81 со следующими параметрами:

а = 20°; ha* = 1; с* = 0,2 и pf*
= 0,3.

Исходный контур для прямозубых ко­нических колес см. на рис. 1.

Выбор коэффициентов смещения и ко­эффициентов изменения расчетной толщины зуба
исходного контура.

1. При u > 1 шестерню рекомендуется выполнять с положительным смешением (х1)
по табл. 68, а колесо с равным ему по величине отрицательным смещением (х2
= -х1)

Для передач, у которых u и z1 от­личаются от указанных в табл. 68, коэффи­циенты
смещения принимают с округлени­ем в большую сторону.

2. При u≥ 2,5 зубчатые колеса рекомен­дуется выполнять не только со смещением,
устанавливаемым по п. 1, но и с различной толщиной зуба исходного контура:
увеличенной по сравнению с расчетной (πme/2), у исходного
контура шестерни и соответственно уменьшенной у исходного контура колеса.

Осевая форма зуба I

Осевая форма зуба I

Рис. 28. Осевая форма зуба I:

1 — делительный конус; 2 — конус впадин

Форма впадины

Форма впадины

Рис. 29. Форма впадины:

а — при обработке зубострогальными резцами; б — при
обработке парными зуборезными головками

Коэффициент изменения расчетной толщины зуба исходного контура xτ1,
положительный для шестерни и равный ему по величине, но обратный по знаку хτ2
для колеса, рекомендуется вычислять по формуле

хτ1 = 0,03 + 0,008(u — 2,5)

67. Минимальное допустимое число зубьев ортогональной
конической передачи с прямыми зубьями

Число зубьев шестерни z1

Наименьшее число зубьев сопряженного колеса z2

Число зубьев шестерни z1

Наименьшее число зубьев сопряженного колеса z2

12

30

15

19

13

26

16

18

14

20

17

17

68. Коэффициенты смещения для ортогональных конических
зубчатых передач с прямыми зубьями при исходном контуре по ГОСТ 13754—81

Число зубьев шестерни z1

Значения коэффициента смещения х1 при
передаточном числе передачи u

1

1,12

1,25

1,4

1,6

1,8

2,0

2,5

3,15

4,0

5,0

6,3 и выше

12

—

—

—

—

—

—

—

0,50

0,53

0,56

0,57

0,58

13

—

—

—

—

—

—

0,44

0,48

0,52

0,54

0,55

0,56

14

—

—

—

0,27

0,34

0,38

0,42

0,47

0,50

0,52

0,53

0,54

15

—

—

0,18

0,25

0,31

0,36

0,40

0,45

0,48

0,50

0,51

0,52

16

—

0,10

0,17

0,24

0,30

0,35

0,38

0,43

0,46

0,48

0,49

0,50

18

0,00

0,09

0,15

0,22

0,28

0,33

0,36

0,40

0,43

0,45

0,46

0,47

20

0,00

0,08

0,14

0,20

0,26

0,30

0,34

0,37

0,40

0,42

0,43

0,44

25

0,00

0,07

0,13

0,18

0,23

0,26

0,29

0,33

0,36

0,38

0,39

0,40

30

0,00

0,06

0,11

0,15

0,19

0,22

0,25

0,28

0,31

0,33

0,34

0,35

40

0,00

0,05

0,09

0,12

0,15

0,18

0,20

0,22

0,24

0,26

0,27

0,28

Примечание. Данные таблицы могут быть использованы также для повышающих передач при u< 1.

69. Ширины зубчатых конических венцов в зависимости от
de2 и u

рисунок

Допускается применять ширины зубчатых венцов, определяемые расчетным путем по табл. 70 и 71.

Значения без скобок являются предпочтительными.

Фактические значения могут отличаться от номинальных не более, чем на 2 % для de2
и 3 % для u

Номинальные значения внешнего делительного диаметра
колеса de2, мм

Ширина зубчатых венцов b, мм, для номинальных
передаточных чисел u

1,00

(1,12)

1,25

(1,40)

1,60

(1,80)

2,00

(2,24)

2,50

(2,80)

3,15

(3,55)

4,00

(4,50)

5,00

(5,60)

6,30

50

10

9,5

9

9

8,5

—

—

—

—

—

—

—

—

—

—

—

—

(56)

11

10,5

10

10

9,5

—

—

—

—

—

—

—

—

—

—

—

—

63

13

12

11,5

11

10,5

10

10

—

—

—

—

—

—

—

—

—

—

(71)

14

14

13

12

12

11,5

11,5

—

—

—

—

—

—

—

—

—

80

16

15

15

14

13

13

13

12

12

—

—

—

—

—

—

—

—

(90)

18

17

16

16

15

15

14

14

14

—

—

—

—

—

—

—

—

100

20

19

18

18

17

16

16

16

15

15

15

—

—

—

—

—

—

(112)

22

21

20

20

19

18

18

17

17

17

17

—

—

—

—

—

—

125

25

24

22

22

21

20

20

19

19

19

19

19

18

—

—

—

—

(140)

28

26

26

24

24

22

22

22

21

21

21

21

21

20

—

—

—

160

32

30

30

28

28

26

25

25

25

24

24

24

24

24

24

24

24

(180)

36

34

32

32

30

30

28

28

28

28

26

26

26

26

26

26

26

200

40

38

38

34

34

32

32

32

30

30

30

30

30

30

30

30

28

(225)

45

42

42

40

38

36

36

36

34

34

34

34

32

32

32

32

32

250

50

48

45

45

42

40

40

40

38

38

38

38

36

36

36

36

36

280

55

52

52

50

48

45

45

45

42

42

42

42

42

40

40

40

40

315

65

60

60

.55

52

52

50

50

48

48

48

48

45

45

45

45

45

355

70

70

65

63

60

60

55

55

55

55

55

52

52

52

52

52

52

400

80

75

75

70

70

65

63

63

60

60

60

60

60

60

60

60

60

450

90

85

80

80

75

75

70

70

70

70

65

65

65

65

65

65

65

500

100

95

90

90

85

80

80

80

75

75

75

75

75

75

75

70

70

560

ГОСТ 12289 – 76 предусматривает de2 до
1600мм

90

90

90

85

85

85

85

80

80

80

80

80

630

100

100

100

95

95

95

95

90

90

90

90

90

710

120

110

110

110

110

105

105

105

105

105

105

100

800

130

130

125

125

120

120

120

120

120

120

120

120

900

—

—

140

140

140

130

130

130

130

130

130

130

1000

—

—

160

150

150

150

150

150

150

150

140

140

70. Формулы и пример расчета конической передачи с
прямыми зубьями без смещения

Линейные размеры, мм

рисунок

Параметры и обозначения

Расчетные формулы и указания

Численные значения

Исходные данные

Число зубьев z1

z2

Задаются или выбираются в соответст­вии с расчетом
зубьев на прочность, требованием кинематики и по конст­руктивным соображениям

18

20

Внешний окружноймодуль mе

Определяют из расчета на прочность (при нарезании на
зубострогальных станках модули могут выбираться не­стандартными и дробными)

5

Межосевой угол передачи Σ

Внешний торцовый исходный контур

По конструктивным соображениям

По ГОСТ 13754-81

90°

—

Число зубьев плоского колеса zc

Внешнее конусное расстояниеRe Ширина зубчатого
венца b

Среднее конусное расстояние Rm

Средний окружной модуль mm

Средний делительный диаметр dm

формулы

26,9072

67,268

20

57,268

4,2567

77,6206

85,1340

Угол делительного конуса δ

tgδ1 = z1/z2

41°59′

δ2= 90° — δ1

48°01′

sinδ1 = cosδ2

0,66891

cosδ1= sinδ2

0,74334

Передаточное число u

u = z2/z1

при u < 2,5 не изменяется толщина зуба исходного
контура

1,1111

Внешняя высота головки зуба hae

haeпри h* = l

5

Внешняя высота ножки зуба hfе

hfe = hae + 0,2me

6

Внешняя высота зуба he

he = hae + hfe

11,0

Внешняя окружная толщина зуба se

se= 0,5πme

7,85

Угол ножки зуба θf

tgθf = hf/Re;

tgθf= 0,0893;

θf= 5°06′

Угол головки зуба θа

θa = θf

5°06′

Угол конуса вершин δа

δa1 = δ1 + θa

δa2 = δ2 + θa

47°05′

53°07′

Угол конуса впадин δf

δf1 = δ1 — θf

δaf2 = δ2
— θf

36°53′

42°55′

Внешний делительный диаметр de

de1= mez1

de2= mez2

90

100

Внешний диаметр вершин зубьев dae

dae1 = de1 + 2haecosδ1

dae2 = de2 + 2haecosδ2

97,4334

106,6891

Расстояние от вершины до плоскости внешней
окружности вершин зубьев В

B1 = 0,5de2 — haesinδ1

B2 = 0,5de1 — haesinδ2

56,6555

41,2833

Внешняя постоянная хордазуба


6,9315

Высота до внешней постоянной хорды

формула

3,7385

Половина внешней угловой толщины ψе,
рад*

формулы

0,0648 рад или 3°42’45»

0,0525 рад или 3°00’29»

Внешняя делительная толщина зуба по хорде

формулы

7,8340

7,0496

Высота до внешней делительной хорды зуба haе

<формулы

5,1272

5,1030

*1 рад =
57°17’44»

71. Формулы и пример расчета ортогональной конической
передачи с прямыми зубьями при стандартном исходном контуре со смещением

Линейные размеры, мм

Параметры и обозначения

Формулы и указания

Численные значения

Исходные данные

Число зубьев z1

z2

—

15

30

Внешний окружноймодуль mе

—

5

Внешний торцовыйисходный контур

По ГОСТ 13754-81

—

Число зубьев плоского колеса zc

Внешнее конусное расстояние Re

Ширина зубчатого венца b

Среднее конусное расстояние Rm

Средний окружной модуль mm

Внутренний окружной модуль mt

Средний делительный диаметр dm

Угол делительного конуса δ

Передаточное число u

<!формулы

33,5410

83,8525

25

71,3525

4,2546

3,5093

63,8190

127,6380

26°34′

63°26′

0,44724

0,89441

2

Коэффициент смещения у шестерни x1

Коэффициент изменения толщины зуба шестерни хτ1

Внешняя высота головки зуба hae

Внешняя высота ножки зуба hfe

Внешняя высота зуба he

Внешняя окружная толщина se

формулы

0,40

0(так как u < 2,5)

7,0000

3,0000

4,0000

8,0000

11,0000

11,0000

9,3096

6,3979

Угол ножки зуба θf

tgθf1 = hfe1 / Re

tgθf1= 0,04770

θf1 = 2°44″

tgθf2 = hfe2 / Re

tgθf1== 0,09540

θf1= 5°27′

Угол головки зуба 60

Угол конуса вершин δa

Угол конуса впадин δf

Внешний делительный диаметр de

Внешний диаметр вершин зубьев dae

Расстояние от вершины до плоскости внешней
окружности вершин зубьев В

<формулы

5°27′

2°44′

32°0Г

66° 10′

23°50′

57°59′

75,0000

150,0000

87,5217

152,6834

71,8693

34,8168

Расчет внешней постоянной хорды и высоты до нее (при
х1 ≥ 0,4)

Внешняя постоянная хорды зуба

Высота до внешней постоянной хорды

формулы

8,2206

5,6496

5,5039

1,9718

Расчет внешней делительной толщины зуба по хорде и
высоты до нее (при х1 ≤ 0,4)

Половина внешней угловой толщины зуба ψ

Внешняя делительная толщина зуба по хорде

Высота до внешней делительной хорды зуба

формулы

0,11102

0,01907

9 2986

6,3422

7,2584

3,0305

72. Дополнительный расчет

Данный расчет приводится в дополнение к табл. 71 в части расчета внешней посто­янной хорды, высоты до нее и расчета внешней делительной толщины зуба по хорде и высоты до
нее и расчета внешней де­лительной толщины зуба по хорде и высоты до нее для
более общих случаев.

Параметры и обозначения

Формулы и указания

Расчет внешней постоянной хорды зуба и высоты до
постоянной хорды*

Внешняя постоянная хорда зуба

Высота до внешней постоянной хорды зуба

формулы

Расчет внешней делительной толщины зуба по хорде и
высоты до хорды

Половина внешней угловой толщины зуба ψе,
рад

Внешняя делительная толщина зуба по хорде

Высота до внешней делительной хорды зуба

формулы

* Метод измерения рекомендуется для шестерни при любом значении х1, а для
колеса при x1 ≤ 0,4.

ГОСТ 19624—74 предусматривает расчет конической передачи с прямыми зубьями при ме­жосевом угле Σ ≠ 90°, а также при параметрах исходного контура, отличных от
установлен­ных ГОСТ 13754-81.

Номограмма определения рекомендуемого числа зубьев шестерни (a=20°; Σ=90°)

Номограмма определения рекомендуемого числа зубьев шестерни (a=20°; Σ=90°)

Рис. 30. Номограмма определения рекомендуемого числа
зубьев шестерни (a=20°; Σ=90°):

формула

Пример. Дано de1 = 300мм, u = 4.
По номограмме определяют z1 = 28

Основные параметры. Ширины зубчатых колес в зависимости от номинального внешнего делительного диаметра колеса и передаточных чисел приведены в табл. 69. Эти данные распространяются на ортого­нальные конические передачи и являются стандартными (обязательными) для редук­торов и рекомендуемыми для встроенных передач.

При отсутствии дополнительных указа­ний везде, где упоминается профиль зуба,
имеется в виду внешний торцовый про­филь.

Источник

Конические зубчатые передачи



Общие сведения о конических зубчатых передачах

Конические зубчатые колеса применяют в передачах, когда оси валов пересекаются под некоторым углом Σ. Обычно это связано с необходимостью изменить направление передаваемого вращающего момента. Наибольшее распространение получили ортогональные конические передачи, изменяющие направление вращающего момента под прямым углом (угол Σ = 90˚, см. рис. 3).

Конические передачи подразделяются не только по углу пересечения валов и осей зубчатых колес. Они бывают с прямыми и круговыми (спиралевидными) зубьями. Встречаются и конические передачи, у которых колеса выполнены с шевронными зубьями, но из-за сложности изготовления такие передачи широкого практического применения не нашли.

Прямозубые конические передачи имеют начальный линейный контакт в зацеплении, а передачи с круговыми зубьями – точечный контакт.

расчет на прочность конических зубчаных передач

Основными преимуществами зубчатых колес с круговыми зубьями являются бόльшая несущая способность, относительная бесшумность и плавность работы. Недостаток – они сложнее в изготовлении, а, следовательно, дороже.

Нарезание кругового зуба производят резцовыми головками по методу обкатки (рис. 1). Угол наклона зуба βn в середине ширины зубчатого венца выбирают, учитывая плавность зацепления. Рекомендуется принимать βn = 35˚.

Сопряженные колеса с круговым зубом имеют противоположное направление линий зубьев – правое и левое, если смотреть со стороны вершины конуса. Шестерни выполняют с правым зубом, колеса – с левым (рис. 1 ).

конические зубчатые передачи

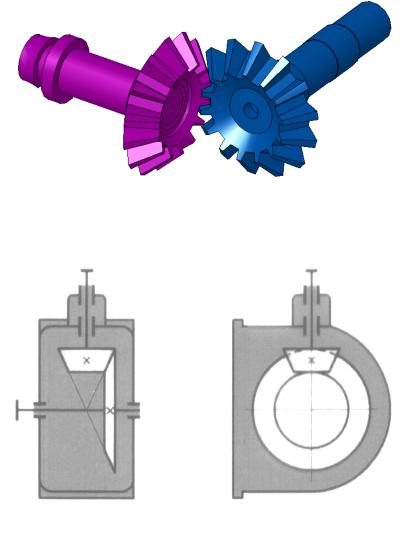
В конических передачах шестерню, как правило, располагают консольно (рис. 2), при этом вследствие меньшей жесткости консольного вала и деформаций опор увеличивается неравномерность распределения нагрузки пол длине контактных линий в зацеплении. По этой причине конические колеса по сравнению с цилиндрическими работают с большим шумом.
С целью снижения деформаций зубьев вал устанавливают на конических роликовых подшипниках, выдерживая соотношение l/l1 = 2,5 (рис. 2). Подшипники располагают в стакане для обеспечения возможности осевого перемещения узла конической шестерни при регулировании зацепления.

достоинства и недостатки конических зубчаных передач

Передаточное число конической зубчатой передачи может быть определено из соотношений:

u = n1/n2 = d1/d2 = z2/z1 = tgδ2 =1/ tgδ1.

где de1, de2 и δ1, δ2 – соответственно внешние делительные диаметры и углы делительных конусов шестерни и колеса.

Для конической прямозубой передачи рекомендуемые значения передаточного числа u = 2…3, при колесах с круговыми зубьями – до 6,3.

***

Геометрия зацепления колес

Аналогами начальных и делительных цилиндров цилиндрических зубчатых передач в конических передачах являются начальные и делительные конусы. При вращении колес начальные конусы катятся друг по другу без скольжения (рис .3). В конических передачах угловая модификация не применяется, поэтому начальные и делительные конусы всегда совпадают.

геометрия зацепления колес конических зубчаных передач

Угол Σ между осями зубчатых колес равен сумме углов делительных конусов: Σ = δ1 + δ2.

Эвольвентные зубья конического колеса профилируют на развертке дополнительного конуса, образующая которого перпендикулярна образующей делительного конуса. Дополнительные конусы можно построить для внешнего, среднего и внутреннего сечений зуба конического колеса.
Ширина b венца зубчатого колеса ограничена двумя дополнительными конусами – внешним и внутренним.

Зубья конических колес в зависимости от изменения размеров их нормальных сечений по длине выполняют трех осевых форм (рис. 4).

осевые формы колес конических зубчаных передач

Осевая форма I – нормально понижающиеся зубья.
Вершины делительного конуса и конуса впадин совпадают. Применяют для прямых зубьев, а также для круговых зубьев при m ≥ 2 мм и √(z12 + z22) = 20…100.

Осевая форма II – нормально сужающиеся зубья.
Вершина конуса впадин располагается так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу растет с увеличением расстояния от вершины. По этой форме одним инструментом можно обработать сразу обе поверхности зубьев колеса, что повышает производительность при нарезании зубчатых колес. Осевая форма II является основной для колес с круговыми зубьями. Применяют в массовом производстве.

Осевая форма III – равновысокие зубья.
Образующие конусов делительного, впадин и вершин параллельны. Высота зубьев постоянна по всей длине. Применяют для круговых зубьев при √(z12 + z22) ≥ 60 и для неортогональных передач с углом Σ < 40˚.

Далее рассмотрены зубья осевой формы I.

***

Основные геометрические соотношения конических передач

В конических зубчатых колесах высота зуба, а следовательно, и модуль зацепления увеличиваются от внутреннего 1 к внешнему 3 дополнительному конусу (см. рис. 3, 4). Для удобства измерения размеры зубчатых колес принято определять по внешнему торцу зуба, образованному внешним дополнительным конусом.

Максимальный модуль зубьев – внешний окружной модуль – получается на внешнем торце колеса. Его принимают за основной и обозначают: me – для прямозубых колес, и mte – для колес с круговыми зубьями.

Внешний окружной модуль me или mte можно не округлять до стандартного, так как одним и тем же режущим инструментом можно нарезать колес с различными значениями модуля, лежащими в некотором непрерывном интервале.

Для повышения износостойкости и сопротивления зубьев заеданию конические зубчатые колеса выполняют с высотной модификацией., выравнивающей удельные скольжения зубьев шестерни и колеса. Коэффициенты смещения режущего инструмента хe1 для прямозубой шестерни и хn1 для шестерни с круговым зубом принимают по справочным таблицам.
Коэффициенты смещения для колес соответственно равны:

хe2 = – хe1     и     хn2 = – хe1.

Для передач, у которых число зубьев z и передаточное число u отличаются от табличных значений, коэффициенты смещения хe1 и хn1 принимают с округлением в бόльшую сторону.

Основные геометрические соотношения конических зубчатых передач в соответствии с рисунком 4 приведены в таблице 1.

Таблица 1. Геометрические соотношения конических зубчатых передач.

Параметр зацепления

Геометрическое соотношение для прямозубой передачи

Геометрическое соотношение для передачи с круговыми зубьями

Внешний делительный диаметр

de1 = mez1,
de2 = mez2

de1 = mtez1,
de2 = mtez2

Внешнее конусное расстояние

Re = 0,5me√(z12 + z22) =
= 0,5 de2√(u2 + 1)/u

Re = 0,5mte√(z12 + z22) =
= 0,5 de2√(u2 + 1)/u

Ширина зубчатого венца

b = KbeRe = 0,285Re =
= 0,143de1√(u2 + 1)

b = KbeRe = 0,285Re =
= 0,143de1√(u2 + 1)

Среднее конусное расстояние

R = Re – 0,5b = 0,857Re

R = Re – 0,5b = 0,857Re

Угол делительного конуса

tg δ1 = z1/z2 = 1/u;
δ2 = 90˚ – δ1

tg δ1 = z1/z2 = 1/u;
δ2 = 90˚ – δ1

Модуль нормальный в среднем сечении

m = (me – b sin δ1)/z1 =
= 0,857me

m = [(mte – b sin δ1)/z1]cos βn =
= 0,857me

Средний делительный диаметр

d1 = mz1 = 0,857de1
d2 = mz2 = 0,857de2

d1 = mnz1/cos βn = 0,857de1
d2 = mnz2/ cos βn = 0,857de2

Высота головки зуба:
     внешняя, hae
     в среднем сечении he

hae1 = (1 + xe1)me
hae2 = (1 – xe1)me

ha1 = (1 + xn1)mn
ha2 = (1 – xn1)mn

Высота ножки зуба:
     внешняя hfe
     в среднем сечении hf

hfe1 = (1,2 – xe1)me
hfe2 = (1,2 + xe1)me

hf1 = (1,25 – xn1)mn
hf2 = (1,25 + xn1)mn

Угол ножки зуба

tg θf1 = hfe1/Re;
tg θf2 = hfe2/Re

tg θf1 = hf1/R;
tg θf2 = hf2/R

Угол головки зуба

θa1 = θf2;     θa2 = θf1

θa1 = θf2;     θa2 = θf1

Угол конуса вершин

δa1 = δ1 + θa1;
δa2 = δ2 + θa2

δa1 = δ1 + θa1;
δa2 = δ2 + θa2

Внешний диаметр вершин зубьев

dae1 = de1 + 2(1 + xe1)me cos δ1;
dae2 = de2 + 2(1 + xe1)me cos δ2

dae1 = de1 + 1,64(1 + xn1)mte cos δ1;
dae2 = de2 + 1,64(1 + xn1)mte cos δ2

***

Эквивалентное колесо

Для прямозубой передачи профили зубьев конического колеса, построенные на развертке среднего дополнительного конуса (рис. 3), близки к профилям зубьев эквивалентного цилиндрического прямозубого колеса. Дополнив развертку до полной окружности (рис. 5), получим эквивалентное цилиндрическое колесо с числом зубьев zv.

Из треугольника OCS (рис. 5) делительный диаметр эквивалентного колеса определяется из соотношений:
dve = de/cos δ = mez/cos δ = mezv, откуда эквивалентное число зубьев:

zv = z/cos δ.

где z – действительное число зубьев конического колеса.

Для передачи с круговыми зубьями профили зубьев конического колеса в нормальном сечении близки к профилю зубьев эквивалентного цилиндрического прямозубого колеса с числом зубьев zvn, полученным двойным приведением: конического колеса к цилиндрическому и кругового зуба к прямому зубу:

zvn = z/(cos δ×cos3δn).

***



Силы в коническом зацеплении

Силы в конической зубчатой передаче определяют по размерам сечения на середине ширины зубчатого венца, в котором лежит точка приложения силы Fn, действующей перпендикулярно поверхности зуба (рис. 6).
расчеты конических зубчаных передач
Силу Fn раскладывают на составляющие: окружную силу Ft, радиальную силу Fr и осевую силу Fa.

В прямозубой передаче:

Окружная сила на шестерне или колесе определяется по формулам:

Ft = 2×103Т1/d1 = 2×103Т2/d2,

где Т1 и Т2 – передаваемый крутящий момент в Нм, d1 и d2 – в мм.

Радиальная сила на шестерне:

Fr1 = tg αw cos δ1 = 0,36 F1 cos δ1.

Осевая сила на шестерне:

Fa1 = F1 tg αw sin δ1 = 0,36 F1 sin δ1.

Силы на колесе соответственно равны:

Fr2 = Fa1;        Fa2 = Fr1.

В передаче с круговыми зубьями:

В передаче с круговыми зубьями во избежание заклинивания зубьев в процессе зацепления при значительных зазорах в подшипниках необходимо осевую силу Fa1 на ведущей шестерне направить к основанию делительного конуса. Для этого направление вращения ведущей шестерни (если смотреть со стороны вершины делительного конуса) и направление наклона зубьев должны совпадать.

В передаче с круговым зубом при соблюдении этого условия окружную силу Fr определяют по формуле:

Ft = 2×103Т1/d1 = 2×103Т2/d2.

Радиальная сила на шестерне (при αw = 20˚; βn = 35˚):

Fr1 = Ft (0,44 cos δ1 – 0,7 sin δ1);

Окружная сила на шестерне (при αw = 20˚; βn = 35˚):

Fa1 = Ft (0,44 sin δ1 – 0,7 cos δ1);

Силы на колесе соответственно равны: Fr2 = Fa1;     Fa2 = Fr1.

***

Расчет конических передач на прочность

Расчет на контактную прочность

Прочностной расчет конической передачи основан на допущении, что несущая способность зубьев конического колеса такая же, как у эквивалентного цилиндрического (см. рис. 3) с той же длиной зуба b и профилем, соответствующим среднему дополнительному конусу (среднему сечению зуба). Однако практика эксплуатации показала, что при одинаковой степени нагруженности конические передачи выходят из строя быстрее, чем цилиндрические.

С учетом преобразований и условий прочности формула для проверочного расчета стальных конических зубчатых передач имеет вид:

σн = 6,7×104√(КнТ1/de13uΘн) ≤ [σ]н,

где Т1 – в Нм;    d1 – в мм.

Для прямозубых конических передач Θн = Θr = 0,85.

Для передач с круговыми зубьями значения Θн принимаются из справочных таблиц.

Коэффициент нагрузки КA для конических передач может быть определен по формуле:

Кн = КА×КНβ×КНv.

Коэффициент КA, учитывает внешнюю динамическую нагрузку. Его назначают так же, как и при расчетах цилиндрических зубчатых передач.

Коэффициент КНβ учитывает неравномерность распределения нагрузки по длине контактных линий зубьев в зацеплении.
Для колес с круговыми зубьями этот коэффициент определяется по формуле:

КНβ = √(КНβ0) при условии КНβ ≥ 1,2.

где КНβ0 – коэффициент, выбираемый по справочным таблицам в зависимости от отношения ψbd = b/d1, твердости зубчатых колес и схемы передачи.

Для большинства конических передач отношение ширины зубчатого венца (длины зуба) к внешнему конусному расстоянию Kbe = b/Re = 0,285, тогда:

ψbd = 0,166 √(u2 + 1).

Для прямозубых конических передач КНβ выбирают из справочных таблиц, при этом принимают КНβ = КНβ0.

Значение коэффициента КНv внутренней динамической нагрузки для передач с круговыми зубьями выбирают, как и для цилиндрических косозубых передач. Для конических прямозубых передач КНv выбирают также по справочным таблицам, но с понижением степени точности на единицу.

Проектировочный расчет

Решив зависимость σн = 6,7×104√(КнТ1/de13uΘн) ≤ [σ]н, относительно de1, получим формулу проектировочного расчета для стальных конических зубчатых передач:

de1 = 1650 × 3√КнТ1/u[σ]Н2 ΘН),

где de1 – внешний делительный диаметр шестерни, мм;     Т1 – в Нм,    [σ]н в Н/мм2.

***

Расчет зубьев конических передач на прочность при изгибе

Аналогично расчету цилиндрической зубчатой передачи расчетные напряжения изгиба в зубьях конических колес и условие их прочности описываются формулами:

σF1 = КFF1YFs1/bmΘF ≤ [σ]F1;
   σF2 = σF1YFs2/ YFs1 ≤ [σ]F2,

где m или mn – модуль нормальный в среднем сечении зуба конического колеса (справочная величина);
YFs – коэффициент форму зуба и концентрации напряжений эквивалентного колеса с учетом коэффициента смещения хe (хn) по zv (zvn);
ΘF – коэффициент, учитывающий влияние на несущую способность передачи вида конических колес; выбирают по рекомендациям, приведенным выше.

Коэффициент KF нагрузки для конических передач:

КF = КA×КFβ×KFv,

где КA – коэффициент, учитывающий внешнюю динамическую нагрузку, зависящий от степени равномерности нагружения ведущего и ведомого звена передачи. При задании нагрузки циклограммой моментов или типовым режимом нагружения, в которых учтены внешние динамические нагрузки, КA = 1;
KFβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий зубьев в зацеплении.

Для прямозубых конических передач КFβ = К’Fβ;

Для колес с круговыми зубьями:

КFβ = √ К’Fβ при условии КFβ ≥ 1,15,

где К’Fβ определяют по формуле КFβ = 0,18 + 0,82КНβ0.

Коэффициент КFv внутренней динамической нагрузки принимают по справочным таблицам.
Допускаемые напряжения [σ]F1, [σ]F2 определяют по рекомендациям.

***

Расчет на прочность открытых конических передач

Открытые конические передачи выполняют только с прямыми зубьями и применяют при окружных скоростях колес менее 2 м/с. Степень точности по нормам плавности и контакта – 9-я. Размеры передачи определяют из расчета на контактную прочность зубьев с последующей проверкой на изгиб.
При расчете принимают допускаемые напряжения:

[σ]Н = σНlim/[s]Н;         [σ]F = σFlim/[s]F

Коэффициенты внутренней динамической нагрузки КНv и КFv принимают по справочным таблицам.
Коэффициенты неравномерности распределения нагрузки по длине контактных линий принимают:
КНβ = КFβ = 1.

Из-за повышенного изнашивания зубьев открытых передач значение модуля зацепления рекомендуют принимать в 1,5 раза большим, чем для закрытых передач таких же размеров.

***

Планетарные зубчатые передачи



Источник

Устройство конической зубчатой передачи

Классическая схема подобных передач имеет в своём составе два вала. Один является ведущим, второй – ведомым. На каждом из них закреплены колёса, выточенные в форме конуса. Коническое зубчатое колесо обработано под заданным углом. В результате обработки получается зубчатое колесо с изменяемым диаметром от основания к вершине. Полученная фигура напоминает конус. На боковой поверхности вырезаны зубья. Итоговый угол направления вращения определяется суммой нескольких углов. Он складывается из углов обоих колёс которые изготовлены в форме конуса.

Общие сведения про конические зубчатые передачи включены в справочники по расчёту редукторов и мультипликаторов.

Закрепленное на валу колесо, с которого производится передача вращения, называется ведущим. Колесо, которому передаётся вращение, называется ведомым.

Подобные конструкции классифицируются по следующим показателям:

  • механическим;
  • геометрическим.

К механическим характеристикам относятся:

  • форма передаточного механизма;
  • форме применяемых зубьев;
  • количеству ступеней;
  • направление пересечения осей;
  • нагрузочная способность;
  • значение передаточного числа;
  • прочность при изгибе;
  • величина усилия в зацеплении;
  • передаваемая мощность.

К характеристикам, определяющим геометрическую форму применяемых колёс, шестерёнок, валов относятся значения углов и линейные размеры отдельных частей деталей.

По форме механизма передачи бывают:

  • чисто конические;
  • цилиндрические конические;
  • конические линейные.

Формы зубьев и способам зацепления устройства изготавливаются следующих видов:

  • прямоугольной формы (прямозубое);
  • зубьями на скос, которые получили название косозубые;
  • округлой формы;
  • в форме спирали с постоянным шагом;
  • эвольвентные;
  • циклоидные;

При внешнем зацеплении шестерни вращаются в противоположных направлениях. Во втором случае вращение происходит в одном направлении.

Важным параметром является показатель круговой скорости вращения. Они подразделяются:

  • с низкой скоростью (так называемые тихоходные, у которых скорость вращения не превышает 3 м/с);
  • среднескоростные (скорость которых достигает 15 м/с);
  • высокоскоростные (для них допускается превышение скорости 15 м/с).

Конструкция подобных механизмов бывает одноступенчатая и многоступенчатая. Схема передачи выполняется с преобразованием характера движения или без него. В первом случае вращательное движение сохраняется на выходе передаточного механизма. Во втором случае оно может быть преобразовано из вращательного движения в поступательное движение.

По форме касательных линий нарезанных зубьев выделяют следующие виды шестерён:

  • С зубьями, боковое ребро которых представляет прямую линию. Линия зуба у них всегда проходит через вершину делительного конуса;
  • У круговых зубьев угол наклона при обработке делается острым. Он получил название линия конуса и измеряется между касательной к выбранной точке и линией самого зуба.

Широко распространённым в таких механизмах является эвольвентное зацепление. При такой форме зацепления происходит перекатывание поверхности ведущего зуба по образующей плоскости ведомого колеса.

Серьёзным недостатком всех конических передач является большие массогабаритные характеристики. Еще одной трудностью является проблема обработки. На конусе, который получен в качестве заготовки будущей шестерёнки значительно сложнее нарезать зубья. Если в кинематической схеме нет элементов с пересекающимися осями, такие механизмы называются гипоидными.

Дальнейшее развитие получили варианты не только с прямыми, но и криволинейными зубьями: круговыми, эвольвеньными, циклоидной формы.

В некоторых устройствах применяется коническая зубчатая передача, у которой колёса имеют прямые зубьями с радиальной нарезкой или нарезкой в форме спирали. Все эти типы применяются для решения конкретных технических задач.

При проектировании расчёт основных технических характеристик, определяющих параметры редуктора, производится с использованием известных выражений. Полученные значения подтверждаются результатами проведенных экспериментов, испытаний, и эксплуатационных данных. Например, опытным путём было установлено, что нагрузочная способность любой конической передачи ниже, чем у цилиндрической. Поэтому при расчёте применяют специальный коэффициент, учитывающий это снижение.

Передаточное отношение определяет, к какому классу относится данный вид механизма. Если передаточное число конической передачи меньше единицы – конструкция понижающая (редуктор). Если этот показатель больше или равен единице – повышающая (мультипликатор).

Он рассчитывается как отношение угловых скоростей на ведомом валу по отношению к ведущему валу.

Криволинейные зубья на шестерёнках конических передач обладают более высокими нагрузочными характеристиками. Работают плавно без рывков и проскальзываний. Это снижает общие динамические нагрузки и уровень шума.

Разработанными стандартами определены величины допусков. Они имеют двенадцать ступеней точности. Каждая из степеней зависит от скорости передаваемого вращения. Разрешенные круговые скорости имеют следующие значения:

  • до 6-й степени точности включительно скорость может достигать 20 м/с;
  • для 7-й степени этот параметр не должен превышать 10 м/с;
  • 8-я степень допускает передачу на скоростях до 7 м/с;
  • у девятой и выше скорости не должны превышать 3 м/с.

РАСЧЁТ ГЕОМЕТРИИ ПЕРЕДАЧ С КРУГОВЫМИ ЗУБЬЯМИ

Расчёт выполняется в соответствии с ГОСТ 19326 – 73.

Выбирают средний угол наклона зубаи направление линии зуба. Расчётный угол наклона зуба может находиться в пределах от 0 до . Его величину выбирают с учётом величины и направления осевой силы. С увеличением возрастает плавность работы передачи, но одновременно возрастает осевая сила. Угол целесообразно назначать таким, чтобы коэффициент осевого перекрытия был не менее 1,25; при требовании максимальной плавности работы передачи рекомендуется .

Для упрощения расчётов рекомендуется придавать углу одно из значений ряда: 0; 10; 15; 20; 25; 30; 35; 40; .

Чаще всего принимают = .

Выбирают модуль.

Для передач с круговыми зубьями в качестве расчётного принимается нормальный модуль в середине ширины венца.

Для зубчатых колёс с , а также для зубчатых колёс с осевой формой зуба III принимают , для остальных зубчатых колёс .

Полученное значение модуля округляется до стандартного по ГОСТ 9563 -60. При этом модуль не должен быть менее 2 мм.

Число зубьевшестерни и колеса округляют до ближайшего целого числа. При этом должны выполняться рекомендации, приведённые в табл.2.2 .

Таблица 2.2

наименьшее наименьшее
32 при 30 при 26 при от 0 до 24 при св.15 до 22 при св.29 до
30 при 28 при св. 29 до 20 при от 0 до
30 при от 0 до 28 при 26 при св. 29 до 19 при от 0 до
18 при от 0 до
17 при от 0 до

Выбирают осевую форму зуба

Различают пропорционально понижающуюся ( I ), понижающуюся (II ) и равновысокую ( III ) осевые формы зуба. У первой – вершины делительного конуса и конуса впадин сходятся в общей точке и, следовательно, высота ножки зуба пропорциональна расстоянию от вершины конуса; у второй –вершины делительного конуса и конуса впадин смещены вдоль оси относительно друг друга на величину, обеспечивающую изменение делительной окружной толщины зуба приблизительно прямо пропорционально расстоянию от вершины делительного конуса; у третьей – образующие конуса впадин и конуса вершин зубьев параллельны образующей делительного конуса и, следовательно, высота зуба постоянна по всей его длине.

Каждая из указанных осевых форм зуба может быть применена при определённом сочетании основных параметров зубчатого колеса: среднего нормального модуля ; среднего угла наклона зуба ; числа зубьев плоского колеса ; среднего конусного расстояния (см. табл.2.3).

Осевая форма Осевая форма Осевая форма

зуба I зуба II зуба II

Таблица 2.3

Осевая форма зуба П а р а м е т р ы
. мм . мм
I от 2 до 25 от 0 до 20 – 100 от 60 до 650
II от 0,4 до 25 24 – 100 от 6 до 700
III от 2 до 25 св. 25 до св. 40 от 75 до 750

Зубья формы II имеют определённые технологические преимущества, например, их можно обрабатывать по обеим боковым сторонам одновременно одним и тем же инструментом. Поэтому эту форму следует считать основной для зубчатых колёс с круговыми зубьями.

Внешнее конусное расстояние .

Прежде, чем высчитывать внешнее конусное расстояние, проверяют соотношение между средним конусным расстоянием и шириной зубчатого венца . Для зубчатых колёс с и для зубчатых колёс с осевой формой зуба III ширина зубчатого венца не должна превышать , для остальных зубчатых колёс должно выполняться соотношение .

Выполнение соответствующего соотношения добиваются уменьшением .

Внешний окружной модуль .

Таблица 2.4

Выбор номинального диаметра зуборезной головки

Расчётный угол наклона зуба, , град Пределы среднего конусного расстояния, , мм Номиналь- ный диаметр зуборезной головки, , мм Внешняя высота зуба, , мм Ширина зубчатого венца, , мм Расчётный нормальный модуль, , мм
Осевая форма зуба I
От 0 до 15 св. 15 до 29 св. 29 до 40 36 – 58 40 – 62 40 – 55 (88,9) 10 – 20 2,0 – 3, 0
От 0 до 15 св. 15 до 29 св. 29 до 40 40 – 65 45 – 70 45 – 60 10 – 20 2,0 – 3, 0
От 0 до 15 св. 15 до 29 св. 29 до 40 50 – 80 55 – 90 55 – 75 12 – 25 2,0 – 3,5
От 0 до 15 св. 15 до 29 св. 29 до 40 60 – 100 70 – 110 70 – 90 (152,4) 15 – 30 2,5 – 3,5
От 0 до 15 св. 15 до 29 св. 29 до 40 65 – 105 72 – 110 72 – 95 16 – 32 2,5 – 4,0
От 0 до 15 св. 15 до 29 св. 29 до 40 75 – 120 85 – 135 85 – 115 (190,6) 20 – 40 2,5 – 5, 0
От 0 до 15 св. 15 до 29 св. 29 до 40 80 – 130 90 – 140 90 – 120 20 -40 2,5 – 5, 0
От 0 до 15 св. 15 до 29 св. 29 до 40 90 – 150 100 – 180 100 – 135 (228,6) 20 – 40 2,5 – 5, 0
От 0 до 15 св. 15 до 29 св. 29 до 40 100 – 160 110 – 175 110 – 175 25 – 50 2,5 – 6, 0
От 0 до 15 св. 15 до 29 св. 29 до 40 120 – 200 140 – 215 140 – 190 (304,6) 30 – 65 2,5 – 7,0

Продолжение табл.2.4

От 0 до 15 св. 15 до 29 св. 29 до 40 120 – 200 140 – 220 140 – 190 32 – 65 2,5 – 9, 0
От 0 до 15 св. 15 до 29 св. 29 до 40 160 – 250 180 – 280 180 – 240 40 – 80 3,0 – 10, 0
От 0 до 15 св. 15 до 29 св. 29 до 40 180 – 300 200 – 320 200 – 280 (457,2) 50 – 100 4,0 – 10,0
От 0 до 15 св. 15 до 29 св. 29 до 40 200 – 320 225 – 350 225 – 300 50 — 100 4,0 – 12,0
Осевая форма зуба II
От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 От 0 до 45 20 – 32 24 – 40 32 – 52 36 – 58 40 – 65 50 – 80 60 – 100 65 – 105 75 – 120 80 – 130 90 -150 100 – 160 120 – 200 120 – 200 160 – 250 180 – 300 200 – 320 50 и (50,8) (88,9) (152,4) (190,5) (228,6) (304,8) (457,2) 4 – 12 5 – 15 6 – 20 8 – 20 8 – 25 10 – 30 12 – 30 13 – 40 15 – 40 16 – 50 18 – 60 20 – 65 25 – 80 25 – 80 32 – 100 36 – 120 40 – 125 0,6 – 2,0 0,6 – 2, 0 1, 0 – 2,5 1,0 – 2, 5 1,0 – 3, 0 1,0 – 3,5 1,5 – 3,5 1,5 – 4,0 2,0 – 5,0 2,0 – 5,0 2,0 – 6,0 2,0 – 6,0 3,0 – 7,0 3,0 – 8,0 3,0 – 10,0 4,0 – 10,0 4,0 – 12,0
Осевая форма зуба III
75 – 90 68 – 90 60 – 80 (88,9) 10 – 20 2,0 – 3,0
85 – 100 75 – 100 65 – 90 10 – 20 2,0 – 3,5
105 – 125 95 – 125 80 – 110 12 – 25 2,0 – 4,0

Продолжение табл. 2.4

130 – 150 115 – 150 100 – 135 (152, 4) 15 – 30 2,0 – 4, 0
135 – 160 120 – 160 105 – 145 16 – 32 2,0 – 5, 0
160 – 190 140 – 190 125 – 170 (190, 5) 20 – 40 3,0 – 6,0
170 – 200 150 – 200 130 – 180 20 – 40 3,0 – 6,0
190 – 230 170 – 230 150 – 200 (228, 8) 25 – 50 3,0 – 6,0
210 – 250 190 – 250 160 – 225 25 – 50 3,0 – 7,0
260 – 305 230 – 305 200 – 270 (304, 8) 32 – 65 3,0 – 8,0
270 – 315 235 – 315 205 – 280 32 – 65 3,0 – 8,0
340 – 400 300 – 400 260 – 360 40 – 80 3,0 – 12,0
390 – 460 340 – 460 300 – 410 (457, 2) 50 – 100 4,0 – 12,0
420 – 500 370 – 500 330 – 450 50 – 100 4,0 – 15,0

Угол делительного конусашестерни ;

колеса .

Углы делительных конусов должны находиться в пределах .

Выбор номинального диаметра зуборезной головки для нарезания конических зубчатых колёс с круговыми зубьями рекомендуется производить по табл.2.4. При этом следует по возможности избегать применения зуборезных головок с номинальными диаметрами, заключёнными в скобки.

Выбор коэффициентов смещения и коэффициентов изменения толщины зуба исходного контура .

В передачах с при разности твёрдостей рабочих поверхностей зубьев шестерни и колеса менее 100 НВ шестерню рекомендуется выполнять с положительным смещением по табл.2.5, а колесо с равным ему по величине отрицательным смещением .

При и перепаде твёрдости зубьев шестерни и колеса, превышающем 100 НВ, передачу следует выполнять без смещения или равносмещённой с положительным смещением у шестерни, достаточным лишь для устранения подрезания зубьев.

Для передач с и , отличными от указанных в табл.2.5, коэффициенты смещения принимаются с округлением в большую сторону.

Таблица 2.5

Коэффициенты смещения для ортогональных конических зубчатых передач с круговыми зубьями при исходном контуре по ГОСТ 16202 – 70

Число зубьев шестерни Значения коэффициента смещения при передаточном числе передачи
1,0 1,12 1,25 1,40 1,60 1,80 2,0 2,5 3,15 4,0 5,0 6,3 и выше
Расчётный угол наклона зуба от 0 до
0,00 0,00 0,00 0,00 0,00 0,00 0,10 0,09 0,08 0,07 0,06 0,05 0,18 0,17 0,15 0,14 0,13 0,11 0,09 0,27 0,25 0,24 0,22 0,20 0,18 0,15 0,12 0,34 0,31 0,30 0,28 0,26 0,23 0,19 0,15 0,38 0,36 0,35 0,33 0,30 0,26 0,22 0,18 0,44 0,42 0,40 0,38 0,36 0,34 0,29 0,25 0,20 0,50 0,48 0,47 0,45 0,43 0,40 0,37 0,33 0,28 0,22 0,53 0,52 0,50 0,48 0,46 0,43 0,40 0,36 0,31 0,24 0,56 0,54 0,52 0,50 0,48 0,45 0,42 0,38 0,33 0,26 0,57 0,55 0,53 0,51 0,49 0,46 0,43 0,39 0,34 0,27 0,58 0,56 0,54 0,52 0,50 0,47 0,44 0,40 0,35 0,28
Продолжение табл. 2.5 0,07 0,06 0,06 0,05 0,05 0,04 0,03 0,14 0,14 0,13 0,12 0,11 0,10 0,08 0,05 0,21 0,20 0,20 0,19 0,18 0,16 0,14 0,12 0,08 0,26 0,25 0,24 0,23 0,22 0,21 0,18 0,15 0,12 0,33 0,32 0,30 0,29 0,28 0,27 0,24 0,20 0,18 0,14 0,37 0,36 0,34 0,32 0,31 0,30 0,26 0,23 0,20 0,16 0,40 0,39 0,37 0,35 0,34 0,33 0,29 0,25 0,22 0,18 0,43 0,42 0,40 0,38 0,37 0,36 0,33 0,28 0,25 0,20 0,45 0,44 0,42 0,40 0,39 0,38 0,35 0,30 0,26 0,20 0,47 0,45 0,43 0,41 0,40 0,39 0,36 0,31 0,27 0,21 0,48 0,46 0,43 0,42 0,41 0,39 0,36 0,32 0,27 0,22
Расчётный угол наклона зуба св. 29 до
0,00 0,00 0,00 0,00 0,00 0,06 0,05 0,05 0,04 0,03 0,03 0,12 0,11 0,10 0,09 0,08 0,07 0,05 0,18 0,17 0,16 0,15 0,13 0,11 0,09 0,07 0,23 0,22 0,21 0,19 0,17 0,15 0,11 0,09 0,27 0,26 0,25 0,24 0,22 0,20 0,17 0,15 0,11 0,32 0,30 0,29 0,27 0,26 0,24 0,22 0,19 0,16 0,11 0,38 0,37 0,35 0,33 0,31 0,30 0,27 0,26 0,21 0,18 0,14 0,41 0,39 0,37 0,35 0,33 0,32 0,30 0,28 0,24 0,21 0,16 0,44 0,41 0,39 0,37 0,35 0,34 0,32 0,29 0,25 0,22 0,17 0,45 0,42 0,40 0,38 0,36 0,35 0,32 0,29 0,25 0,22 0,17 0,45 0,43 0,41 0,38 0,37 0,35 0,33 0,30 0,26 0,23 0,18

При и зубчатые колёса рекомендуется выполнять не только со смещением по табл.2.5, но и с различной толщиной зуба исходного контура, увеличенной по сравнению с расчётной у исходного контура шестерни и соответственно уменьшенной у исходного контура колеса.

Коэффициент изменения расчётной толщины зуба исходного контура, положительный для шестерни , и равный ему по величине, но обратный по знаку для колеса рекомендуется принимать по табл.2.6.

Значения , выбранные по табл.2.6 корректируются до ближайшего значения при выбранном модуле по табл.2.7 с тем, чтобы обеспечить обработку зубчатого колеса двухсторонним методом при стандартном разводе резцов.

Таблица 2.6

Коэффициенты изменения расчётной толщины зуба исходного контура для ортогональных конических передач при исходном контуре

по ГОСТ 16202 – 70

Расчётный угол наклона зуба , град. Значения при передаточном числе передачи
От 2,5 до 4 .0 Св. 4,0 до 6,3 Св. 6,,3 до 8,0 Св. 8,0 до 10
От 0 до 15 0,04 0,06 0,08 0,10
св. 15 до 29 0,08 0,10 0,12 0,14
св. 29 до 40 0,12 0,14 0,16 0,16
св. 40 до 45 0,16 0,18 0,20 0,22

Таблица 2.7

Разводы резцов зуборезных головок по ГОСТ 11902 – 66 и соответствующие им значения коэффициентов изменения расчётной толщины зуба шестерни при средних нормальных

модулях по ГОСТ 9563 – 60

Средний нормальный модуль
1 ряд 2 ряд
2,0 2,5 3,0 4,0 5,0 6,0 8,0 2,25 2,75 3,5 4,5 5,5 7,0 9,0 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 1,3 1,4 1,6 1,8 2,0 2,2 2,6 2,8 3,2 3,6 4,0 4,6 5,2 6,0 6,5 7,0 8,0 0,030 0,119 0,072 0,024 0,024 0,156 0,060 0,239 0,143 0,148 0,047 0,036 0,120 0,071 0,150 0,371 0,095 0,04 0,05 0,06 0,07 0,07 0,08 0,04 0,05 0,06 0,07 0,10 0,08 0,09 0,06 0,04 0,07 0,09 1,4 1,6 1,8 2,0 2,2 2,6 2,8 3,2 3,6 4,0 4,6 5,2 6,0 6,5 7,0 8,0 9,0 0,14 0,14 0,14 0,14 0,20 0,14 0,14 0,14 0,14 0,18 0,20 0,20 0,15 0,12 0,14 0,16 0,17 1,6 1,8 2,0 2,2 2,6 2,8 3,2 3,6 4,0 4,6 5,2 6,0 6,5 7,0 8,0 9,0 10,0

Расчёт параметров зубчатых колёс

Некоторые параметры зубчатых колёс при разных формах зуба определяются по различным зависимостям. В дальнейшем изложении отношение применяемых зависимостей к соответствующей форме зуба будет указываться цифрами I, II, III. Если зависимость применима при всех формах зуба, цифры указываться не будут.

Высота ножки зуба в расчётном сечении, расположенном по середине ширины зубчатого венца

; .

При исходном контуре по ГОСТ 16202 – 70 ; .

Поправка вводится только при и принимается по табл. 2.7 .

Основные геометрические параметры

Построение кинематической схемы, технические характеристики, способы обработки отдельных деталей этих механизмов задаются геометрической формой отдельных элементов. Основными геометрическими параметрами, которые рассчитываются при проектировании являются:

  • углы делительных конусов (каждого колеса или шестерёнки);
  • диаметры всех элементов (обоих валов, ведущих и ведомых шестерён);
  • внешний окружной модуль шестерни;
  • расстояние от вершины конуса до его образующей (называется делительное расстояние);
  • расстояние между осей;
  • радиальный зазор применяемых подшипников;
  • делительный диаметр (он определяет величину зуба шестерёнки);
  • диаметр углублений и верхней части зубьев.

Для удобства проведения расчетов и понимания механизма зацепления вводят три вида торцовых сечений. Это сечения во внешней, внутренней и средней части каждого зуба.

Уменьшение толщины зубьев по направлению к вершине приводит к созданию надежного зацепления во время движения. Угол наклона по направлению к вершине определяет параметры, задаваемые при обработке.

Под линией зубьев понимают пересечение двух прямых. Одна образована боковой поверхностью зуба, вторая является краем делительной конической поверхности.

Для улучшения эксплуатационных характеристик — повышения износостойкости, сопротивления при контакте, уменьшение заедания и лучшей передачи коническим зубчатым колёсам энергии вращения используют метод выравнивания коэффициентов удельного скольжения.

С этой целью колесо и шестерню стараются изготовить с одинаковыми параметрами смещения, но с разными знаками. Например, для шестерни задают параметр со знаком плюс, а для колеса со знаком минус.

Основные геометрические соотношения задаются на этапе разработки всего механизма конической передачи качество передачи. Геометрические параметры рассчитываются на основании известных соотношений.

Усилия в зацеплении

Обеспечение высокой надёжности работы, точности передачи крутящего момента производится благодаря правильному расчету параметров всех сил, которые оказывают воздействие на механизм в процессе работы. Коническая зубчатая передача подвержена воздействию одновременно нескольких сил.

Суммарный результирующий вектор всех сил складывается из отдельных составляющих.

Сила, обеспечивающая нормальное зацепление зубьев называется силой нормального давления.

Она складывается из трёх составляющих. Окружной силы, осевой и радиальной.

Величина каждой из составляющих вычисляется по классическим физическим выражениям. Они приведены в справочниках по расчёту зубчатых передач. Каждое из расчетных выражений учитывает специфику соединений, размеры механизма, параметры зацепления.

Для предотвращения эффекта заклинивания зубьев во время зацепления необходимо произвести точную оценку величины силы направленной вдоль оси вала. Другая осевая сила направлена от вершины зуба, то есть конуса к центру. Направление и скорость вращения обоих типов колёс (ведущего и ведомого) определяет направление воздействия так называемых окружных сил.

Вектор сил, имеющий радиальную направленность, стремится к осям на которых вращаются колёса.

Расчет конических передач

11>

Конические зубчатые передачи применяются при необходимости передачи вращающего момента между валами, оси которых пересекаются. Угол между осями обычно равен 90°. Но возможен угол и отличный от 90°.

Конические колеса выполняются с прямыми, тангенциальными, круговыми и другими криволинейными зубьями.

По сравнению с цилиндрическими зубчатыми передачами конические имеют большую массу и габаритные размеры, дороже в изготовлении и требуют тщательной регулировки закрепления при монтаже и в процессе эксплуатации. Кроме того, в коническом зацеплении возникают осевые силы, дополнительно нагружающие подшипники. Нагрузочная способность конической прямозубой передачи приблизительно на 15 % ниже цилиндрической.

Рис. 3.4.1. Виды конических зубчатых колес с прямыми а

,

тангенциальными б

и круговыми
в
зубьями

Область применения конических колес с прямыми зубьями ограничена окружной скоростью до 3 м/с. Колеса с косыми (тангенциальными) зубьями используют редко, так как они очень чувствительны к погрешностям изготовления и монтажа и трудоемки в изготовлении. При окружных скоростях более 3 м/с в основном применяют зубчатые колеса с круговыми зубьями. Они проще в изготовлении, менее чувствительны к погрешностям изготовления и монтажа. Их зубья обладают высокой изгибной прочностью, а передачи с такими колесами – большой плавностью зацепления. Существенный недостаток передач с косыми и круговыми зубьями – возникающие в них осевые усиления, которые при изменении направления вращения колес меняются по значению и направлению.

Основные кинетические и геометрические параметры. В зависимости от размеров сечений по длине зубья конических колес выполняют трех форм (рис. 3.4.2).

Рис. 3.4.2. Формы зубьев конических колес

Осевую форму 1 применяют для конических передач с прямыми и тангенциальными (косыми) зубьями, а также для передач с круговыми зубьями при нормальном модуле , угле наклона линии зуба на среднем диаметре °и общем числе зубьев .Для этой формы характерны нормальные понижающиеся зубья и совпадения вершин делительного и внутреннего конусов.

Осевая форма 2 характеризуется равноширокими зубьями и несовпадением вершин делительного и внутреннего конусов. При такой форме ширина впадины постоянная, а толщина зуба по делительному конусу увеличивается пропорционально расстоянию от вершины. Это основная форма для колес с круговыми зубьями, так как позволяет обрабатывать одновременно обе поверхности зубьев.

Осевой форме 3 присущи равновысокие зубья, так как образующие делительного и внутреннего конусов параллельны между собой. Такую форму применяют для круговых зубьев при и средних конусных расстояниях от 75 до 750мм.

Для конических колес удобнее задавать и измерять размеры зубьев на внешнем торце. Так, в колесах с зубьями формы I задают внешний окружной модуль , значение которого может быть нестандартное. В конических колесах с зубьями формы II принято применять нормальный модуль на середине ширины зубчатого венца.

Для нарезания круговых зубьев используют немодульный инструмент, позволяющий обрабатывать зубья в некотором диапазоне модулей.

Поэтому допускается использование передач с нестандартными и даже дробными модулями.

Между модулями и существует следующая зависимость:

, (3.4.1.)

где – коэффициент относительной ширины колеса; b

– ширина зубчатого венца; – внешнее конусное расстояние; – угол наклона линии зуба.

При выборе следует помнить, что его увеличение улучшает плавность зацепления, но при этом возрастает осевое усиление зацеплении и, как следствие, увеличиваются габаритные размеры подшипниковых узлов. Для трансмиссий обычно применяют .

При ведущей шестерне конические передачи выполняют, как правило, с передаточным отношением . В передачах с круговыми зубьями предельное значение . Если шестерня ведомая, то передаточное отношение должно быть не более 3,15.

Число зубьев шестерни обычно задают в пределах Минимальное число зубьев шестерни конических передач, при котором отсутствует подрезание зубьев, определяют по формулам: для прямозубых передач с исходным контуром по ГОСТ 13754-81:

.

(3.4.2)

Для передач с круговыми зубьями при выполнении исходного контура по ГОСТ 16202-81:

, (3.4.3)

где – половина угла делительного конуса.

Для выбора в конических передачах рекомендуется: для зубчатых передач с твердостью рабочих поверхностей зубьев шестерни и колеса число зубьев шестерни определяется по графикам на рис. 3.4.3 в зависимости от внешнего делительного диаметра шестерни .

Рис.3.4.3. Графики для определения зубьев конической шестерни

а

– прямозубой;
б
– с круговыми зубьями

г

а б в

Рис. 3.4.4. Схема сил, действующих в прямозубом коническом зацеплении,

и геометрические размеры конического зацепления

Таблица 3.4.1

Условные обозначения и основные формулы геометрического расчета

параметров ортогональной конической передачи

с круговыми зубьями, изготовленными по форме 1

Параметр Обозначения и расчетные формулы
1. Число зубьев плоского колеса
2. Среднее конусное расстояние
3. Внешнее конусное расстояние
4. Ширина зубчатого венца b
5. Среднее конусное расстояние для зубьев
6. Коэффициент ширины
7. Средний нормальный модуль зубьев
8. Передаточное число u = z2 / z1
9. Угол делительного конуса Шестерня
Колесо
10. Коэффициент смещения Шестерня
Колесо
11. Коэффициент изменения толщины зубьев шестерни
12. Внешний окружной модуль при заданном
13. Высота ножки зуба в расчетном сечении, мм Шестерня
Колесо
14. Нормальная толщина зу-ба в расчетном сечении Шестерня
Колесо
15. Угол ножки зубьев Шестерня
Колесо
16. Угол головки зубьев Шестерня
Колесо
17. Увеличение высоты головки зуба при переходе от среднего сечения на внешний торец Шестерня
Колесо
18. Увеличение высоты ножки зуба при переходе от расчетного сечения на внешний торец Шестерня
Колесо
19. Высота головки зуба в расчетном сечении Шестерня
Колесо
20. Внешняя высота головки зуба Шестерня
Колесо

Окончание табл. 3.4.1

21. Внешняя высота ножки зуба Шестерня
Колесо
22. Внешняя высота зуба Шестерня
Колесо
23. Угол конуса вершин Шестерня
Колесо
24. Угол конуса впадин Шестерня
Колесо
25.Средний делительный диаметр Шестерня
Колесо
26. Внешний делительный диаметр Шестерня
Колесо
27. Внешний диаметр вершин Шестерня
Колесо
28. Расстояние от вершины до плоскости внешней окружности вершин зубьев Шестерня
Колесо
29. Коэффициент осевого перекрытия

При твердости ≤350 и ≤350 значение , определенное по графику, увеличивают в 1,6 раза; при и ≤350 – в 1,3 раза.

Подробный расчет для прямозубых конических передач приведен в ГОСТ 19624-74, а для колес с круговыми зубьями – в ГОСТ 19326-73.

Основные зависимости для определения геометрических параметров ортогональной конической передачи с круговыми зубьями, изготовленными по форме 1 и форме 2 указаны в таблицах 3.4.1. и 3.4.2.

Схема сил, действующих в прямозубом коническом зацеплении приведена на рис. 3.4.4, а, б, в

, геометрические размеры конического зацепления – на рис. 3.4.4,
г
.

Таблица 3.4.2

Основные формулы геометрического расчета параметров ортогональной

конической передачи с круговыми зубьями, изготовленными по форме 2

Параметр Обозначения и расчетные формулы
1. Число зубьев плоского колеса
2. Внешнее конусное расстояние
3. Ширина зубчатого венца b
4. Среднее конусное расстояние для зубьев R = Re — 0,5b
5. Коэффициент ширины
6. Средний угол наклона линии зубьев sinn
= (
d
0/2
R
)(1 – 0.5
b
2/
d
02)
6. Средний нормальный модуль зубьев
6. Передаточное число u = z2 / z1
7. Угол делительного конуса Шестерня
Колесо
8. Коэффициент смещения Шестерня xn1 =
2(1-1
/u
2)cos3
bn/z1
)1/2
Колесо
9. Коэффициент изменения толщины зубьев шестерни
10. Внешний окружной модуль при заданном
11. Сумма углов ножек шестерни и колеса , где ;
12. Угол ножки зубьев Шестерня
Колесо
13. Угол головки зубьев Шестерня
Колесо
14. Высота ножки зуба в расчетном сечении, мм Шестерня
Колесо
15. Увеличение высоты головки зуба при переходе от среднего сечения на внешний торец Шестерня
Колесо
16. Увеличение высоты ножки зуба при переходе от расчетного сечения на внешний торец Шестерня
Колесо
17. Уменьшение высоты головки зуба в расчетном режиме Шестерня
Колесо

Окончание табл. 3.4.2.

18. Высота головки зуба в расчетном сечении Шестерня
Колесо
19. Внешняя высота головки зуба Шестерня
Колесо
20. Внешняя высота ножки зуба Шестерня
Колесо
21. Внешняя высота зуба Шестерня
Колесо
22. Угол конуса вершин Шестерня
Колесо
23. Угол конуса впадин Шестерня
Колесо
24. Средний делительный диаметр Шестерня
Колесо
25. Внешний делительный диаметр Шестерня
Колесо
26. Внешний диаметр вершин Шестерня
Колесо
27. Расстояние от вершины до плоскости внешней окружности вершин зубьев Шестерня
Колесо
28. Коэффициент осевого перекрытия

В конических передачах >1, чтобы повысить сопротивление заеданию в зацеплении, в шестерню рекомендуется выполнять с положительным смещением ( для прямозубых передач, для передач с круглыми зубьями), а колесо – с равным ему по абсолютной величине отрицательным смещением ( или ).

Значение и определяют по таблицам ГОСТ 19624-74, ГОСТ 19326-73 или по формуле

. (3.4.4)

Для конических зацеплений с ≥2,5 применяют тангенциальную коррекцию, за счет которой увеличивается толщина зуба шестерни при соответственном уменьшении толщины зуба колеса, что приводит к выравниванию их прочности на изгиб. Коэффициент тангенциального смещения (изменения расчетной толщины зуба исходного контура)

(3.4.5)

где a, b

– постоянные коэффициенты, характеризующие инструмент:
a
= 0,03,
b
= 0,08 для прямозубых передач;
а
= 0,11,
b
= 0,01 для передач с круговыми зубьями – при
βm
=35°.

Тангенциальная коррекция не требует специального инструмента, ее выполняют разведением резцов, обрабатывающих противоположные стороны зубьев. Применение высотной коррекции в сочетании с тангенциальной позволяет одновременно уменьшить вероятность заедания зубьев и выровнять прочность зубьев шестерни и колеса.

Проектный и проверочный расчеты конических передач на контактную выносливость

По критериям эти расчеты аналогичны расчетам цилиндрических передач, отличаясь лишь уточнением некоторых коэффициентов и определением внешнего делительного диаметра колеса вместо межосевого расстояния.

Для прямозубых конических колес и колес с круговыми зубьями при βm

=35° и
=
0,285 ориентировочное значение внешнего делительного диаметра мм, можно определить по формуле

. (3.4.6)

где – расчетный вращающий момент на колесе, Н м; – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца зубчатого колеса. Для конических передач коэффициент можно определятьпо графикам (см. рис. 3.3.2) при = 0,285; u

– передаточное число, должно соответствовать одному из стандартных значений; – допустимое контактное напряжение, МПа; – коэффициент вида зубьев: для конических передач с прямым зубом
=
0,85; для передач с круговым зубом его определяют по формулам таблицы 3.4.3.

Таблица 3.4.3

Формулы для определения коэффициентов и

Коэффициент Твердость рабочих поверхностей зубьев
HB , HB HRC ,HB HRC ,НRC
=1,22+0,21u =1,13+0,13u =0,81+0,15u
=0,94+0,08u =0,85+0,043u =0,65+0,11u

Полученное значение округляют до стандартного, по которому выбирают ширину венцов колес (табл. 3.4.4).

Затем определяют внешний делительный диаметр шестерни ,и по графикам (см. рис. 3.4.3) определяют число зубьев шестерни z

1ичисло зубьев колеса
.
Полученное число зубьев округляют до целого числа в ближайшую сторону и уточняют фактическое передаточное число:
.
Отклонение расчетного значения
и
от заданного не должно превышать 4 %.

С точностью до второго знака после запятой определяют внешний окружной модуль для колес:

с прямыми зубьями

; (3.4.7)

с круговыми зубьями

. (3.4.8)

Все остальные геометрические раз­меры вычисляют по формулам, приведенным в таблицах 3.4.1 и 3.4.2..

После определения геометрических параметров колес и передачи в целом их проверяют на контактную выносли­вость по формуле

. (3.4.9)

Таблица 3.4.4

Основные параметры конических передач (по ГОСТ 12289-76)

Внешний делитель- ный диа- метр колеса Ширина венцов зубчатых колёс , мм, для номинальных передаточных чисел
1,6 (1,8) 2,0 (2,24) 2,5 (2,8) 3,15 (3,55) 4,0 (4,5) 5,0
(71) (90) (112) (140) (180) (225) (280) 10,5 11,5 11,5 – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
Примечание: Значения диаметров, данные в скобках, ограничены в применении

Параметры, входящие в эту форму­лу, определяют следующим образом: по рисунку 3.3.3; по рисунку 3.4.5; по таблице 3.3.8; по таблице 3.4.3. Коэффициент ,

учитывающий механические свойства материала шестерни и колеса, для стали равен 190 МПа. Коэффициент учитываю­щий форму сопряженных поверхнос­тей, вычисляют по формуле (3.3.14). Для колес с прямыми зубьями можно при­нимать = 2,5; с круговыми зубьями (при
β
m =35° =2,26).

Коэффициент, учитывающий сум­марную длину контактных линий:

для прямозубых конических передач

, (3.4.10)

для конических передач с круговы­ми зубьями

. (3.4.11)

Коэффициент торцевого перекры­тия зубьев вычисляют по формуле (3.3.18).

Проектный расчет конических зубча­тых передач на выносливость зубьев по напряжениям изгиба

Такой расчет вы­полняют для открытых передач, под­верженных интенсивному износу. Сначала определяют модуль при предварительно принятом числе зубьев z

1 и параметре .

Рекомендуется при со­блюдении условий: ; .

Меньшие значения целесообразно принимать для неприрабатывающихся колес, когда HB> 350 и
НВ
> 350, а также при резко переменных нагрузках.

Коэффициент ширины зубчатого венца относительно среднего диаметра шестерни можно также вычислить по формуле

. (3.4.12)

Нормальный модуль в среднем сече­нии зубчатого венца определяют из ус­ловия изгибной выносливости:

, (3.4.13)

где – допустимый коэффициент износа: =1,1…1,25 в зависимости от требуемой точнос­ти передачи.

Для колес с круговыми зубьями та­кой расчет не выполняют, так как в открытых передачах эти колеса не приме­няют.

Рис. 3.4.5. Графики для определения ориентировочных значений KHβ

и K
Fβ
для конических передач:1 – передача I

(опоры на шариковых подшипниках);

2 – передача I

(опоры на роликовых подшипниках); 3 – передача
II.
Штрихпунктирные линии соответствуют коническим передачам с круговыми зубьями. Для этих передач при HB2

< 350, а также при
HB1
< 350 и
HB2
< 350 следует принимать K
Hβ
=1

Проверочный расчет конических зуб­чатых передач на выносливость по на­пряжениям изгиба

Напряжение изгиба в зубе шестерни:

. (3.4.14)

Коэффициент , учитывающий пере­крытие зубьев, для конических передач с прямыми зубьями принимают =1, а с круговыми зубьями определяют по формуле

. (3.4.15)

Коэффициент, учитывающий на­клон линии зуба, для конических пере­дач с прямыми зубьями принимают =1, с круговыми зубьями (при βm

=35°)

. (3.4.16)

Окружная сила на среднем диамет­ре, Н:

. (3.4.17)

Коэффициент учитывает распре­деление нагрузки между зубьями. Для конических передач с прямыми зубьями принимают =1, с круговыми зубья­ми его определяют по таблице 5.18 в зависимости от степени точности изготов­ления колес и

окружной скорости, м/с:

. (3.4.18)

Коэффициент , учитывающий неравномерность распределения на­грузки по длине контактных линий, определяют по графикам (см. рис. 3.4.5), а коэффициент ,

учиты­вающий динамическую нагрузку, воз­никающую в зацеплении, – по табли­це 3.3.8.

При известном напряжении для зуба шестерни условие прочности для зуба колеса имеет вид

, (3.4.19)

где YFE2

– коэффициент, учитывающий форму зуба колеса. Его определяют по соотно- шениям, указанным табл.3.3.10 или графику (см. рис. 3.3.4) в зависимости от числа зубьев эквивалентного ко­леса и коэффициента сме­щения χ.

Силы, действующие в зацеплении кони­ческих зубчатых передач

В прямозубой конической передаче силу нормального давления Fn

можно разложить на две со­ставляющие (рис. 3.4.4,
а
):окружную
Fn
и распорную которую, всвою очередь, раскладывают на осевую
Fa
и радиальную
Fr
силы. Из рисунка 3.4.4,
б
видно,что

; (3.4.20)

,

где – окружная сила со­ответственно на шестерне и колесе (табл. 3.4.5); ,

– вращающие моменты соответственно на шестерне и колесе.

Таблица 3.4.5

Формулы для определения сил в зацеплении

Сила Ведущее зубчатое колесо Ведомое зубчатое колесо
Окружная
Осевая
Радиальная
Примечания: 1. Верхние знаки в формулах даны для случая, когда направление вращения рассматриваемого зубчатого колеса (если смотреть на него со стороны вершины конуса) совпадает с направлением наклона зубьев, как показано на рисунке 3.4.6, а нижние знаки при отсутствии оного совпадения. 2. Направление вращения по ходу часовой стрелки – правое, против хода часовой стрелки – левое. 3. Направление действия усилий Fa
и
Fr
определяют по знакам (+ или –), получаемым в результате расчета и указанным на рисунке 3.4.6.

В конических прямозубых передачах направления осевых и радиальных сил неизменные, а в конических передачах с круговыми зубьями они зависят (см. рис. 3.4.6) от направлений наклона зубьев, вращения колес и силового потока.

Направление линии зубьев следует выбирать такое, при котором большее из осевых усилий сопряжен­ных колес было бы направлено от вер­шины конуса. В противном случае в за­цеплении возможно заклинивание.

Рис. 3.4.6. Силы, действующие в зацеплении колес с круговым зубом

11>

Дата добавления: 2016-08-06; просмотров: 15884; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Узнать еще:

Достоинства и недостатки

Применение данной кинематической схемы наглядно показало наличие преимуществ.

К положительным моментам можно отнести:

  • способность изменять направление передаваемого движения;
  • широкая область применения;
  • эффективно реализована передача, преобразование, увеличение мощности вращательного движения между осями передачи расположенными под углом друг к другу;
  • достаточно широкий диапазон задания углов передачи крутящего момента от ведущего элемента к ведомому;
  • широкая вариативность при компоновке разрабатываемых зубчатых и комбинированных систем;
  • высокие нагрузочные характеристики (данные устройства способны передавать мощность величиной до 5000 кВт);
  • эксплуатация и обслуживание не вызывает трудностей;
  • удаётся получить высокий КПД.

К недостаткам специалисты причисляют:

  • нагрузочная способность ниже, чем у цилиндрических конструкций (в среднем она на 20 процентов ниже);
  • невысокая несущая способность (этот показатель ниже на 15 процентов);
  • сложность и трудоёмкость в изготовлении колёс с заданными параметрами зубьев (количеством, величиной, углом наклона);
  • повышенные требования к точности нарезания зубьев;
  • возникновение повышенных осевых и изгибных нагрузок на все валы (особенно этот эффект наблюдается между валами, расположенными консольно);
  • необходимость регулировки процесса передачи вращения;
  • обладают большей массой, чем другие зубчатые передачи;
  • высокие затраты на производство и обслуживание;
  • возникают трудно разрешимые проблемы при проектировании и изготовлении систем с изменяемым передаточным числом;
  • повышенная общая жёсткость конструкции.
Источник

Добавить комментарий