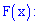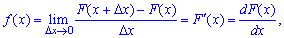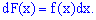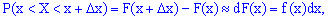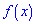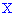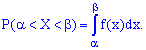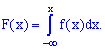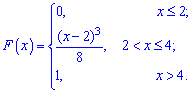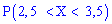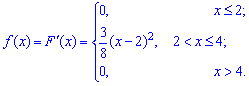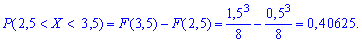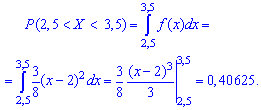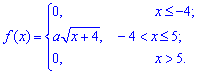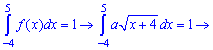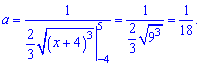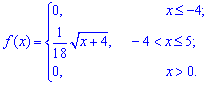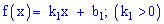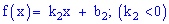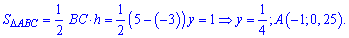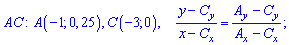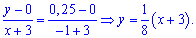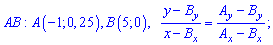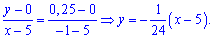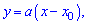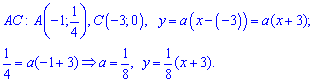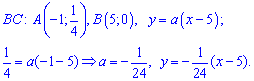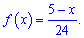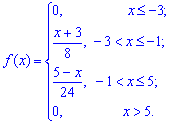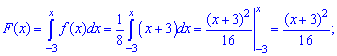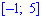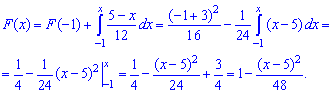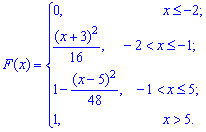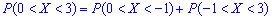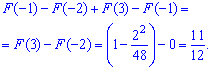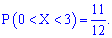Как найти константу а при плотности вероятности - Сайт, где вы сможете решить свои вопросы

Непрерывная случайная величина

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Случайная величина называется непрерывной, если ее функция
распределения

непрерывно дифференцируема. В этом случае

имеет производную, которую обозначим через

– плотность распределения вероятностей.

Плотностью распределения вероятностей непрерывной случайной
величины

называются функцию

– первую производную от функции распределения

Из этого определения следует, что функция распределения является
первообразной для плотности распределения.

Заметим, что для описания распределения вероятностей дискретной
случайной величины плотность распределения неприменима.

Вероятность того, что непрерывная случайная величина

примет значение, принадлежащее интервалу

равна определенному интегралу от плотности
распределения, взятому в пределах от

до

Зная плотность распределения

,
можно найти функцию распределения

по формуле:

Числовые характеристики непрерывной случайной величины

Математическое ожидание непрерывной случайной величины

,
возможные значения которой принадлежат всей оси

,
определяется равенством:

где

– плотность распределения случайной величины

.
Предполагается, что интеграл сходится абсолютно.

В частности, если все возможные значения принадлежат интервалу

,
то:

Все свойства математического ожидания, указанные для
дискретных случайных величин, сохраняются и для непрерывных величин.

Дисперсия непрерывной случайной величины

,
возможные значения которой принадлежат всей оси

,
определяется равенством:

или равносильным равенством:

В частности, если все возможные значения

принадлежат интервалу

,
то

или

Все свойства дисперсии, указанные для дискретных случайных
величин, сохраняются и для непрерывных случайных величин.

Среднее квадратическое отклонение
непрерывной случайной величины определяется так же, как и для дискретной
величины:

При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.

Основные законы распределения непрерывных случайных величин

Нормальный закон распределения СВ
Показательный закон распределения СВ
Равномерный закон распределения СВ

Примеры решения задач

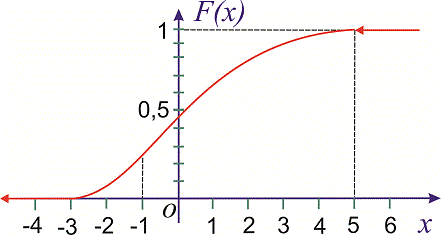
Пример 1

Дана
функция распределения F(х) непрерывной случайной величины
Х.

Найти плотность распределения вероятностей f(x), математическое ожидание M(X), дисперсию D(X) и вероятность попадания X на отрезок [a,b]. Построить графики функций F(x) и f(x).

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Плотность
распределения вероятностей:

Математическое
ожидание:

Дисперсию
можно найти по формуле:

Вероятность
попадания на отрезок:

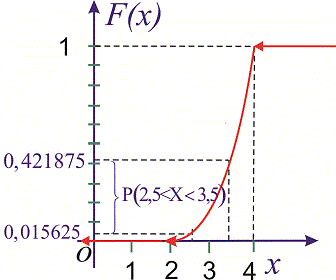
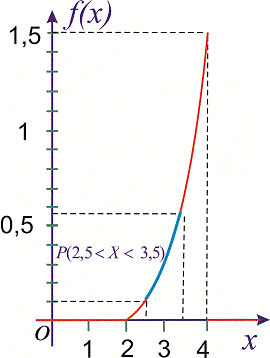
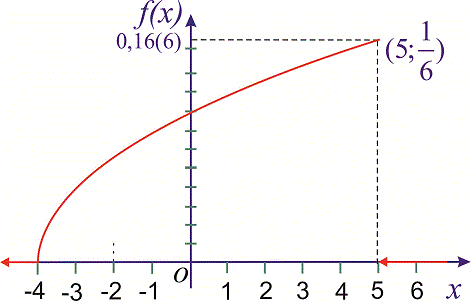
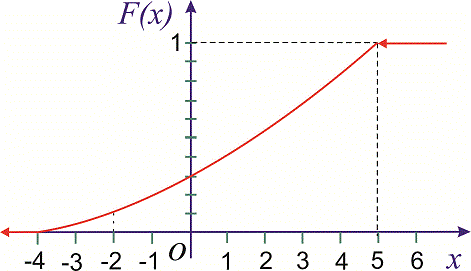
Построим графики функций F(x) и f(x).

График плотности
распределения

График функции
распределения

Пример 2

Случайная величина Х задана плотностью вероятности

Определить константу c, математическое ожидание, дисперсию, функцию распределения величины X, а также вероятность ее попадания в интервал [0;0,25].

Решение

Константу

определим,
используя свойство плотности вероятности:

В нашем случае:

Найдем математическое
ожидание:

Найдем дисперсию:

Искомая дисперсия:

Найдем функцию
распределения:

для

Искомая функция
распределения:

Вероятность попадания
в интервал

Пример 3

Плотность
распределения непрерывной случайной величины

имеет вид:

Найти:

а)
параметр

;

б)
функцию распределения

;

в)
вероятность попадания случайной величины

в интервал

г)
математическое ожидание

и дисперсию

д)
построить графики функций

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

а)
Постоянный параметр

найдем из
свойства плотности вероятности:

В нашем
случае эта формула имеет вид:

б)
Функцию распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем отметить,
что:

Остается
найти выражение для

, когда

принадлежит
интервалу

Получаем:

в)
Вероятность
попадания случайной величины

в интервал

г)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

Среднее
квадратическое отклонение равно квадратному корню из дисперсии:

д) Построим графики

График плотности вероятности f(x)

График функции распределения F(x)

Задачи контрольных и самостоятельных работ

Задача 1

НСВ на всей
числовой оси oX задана интегральной функцией:

Найти
вероятность, что в результате 2 испытаний случайная величина примет значение,
заключенное в интервале (0;4).

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 2

Дана
дифференциальная функция непрерывной СВ Х. Найти: постоянную С, интегральную
функцию F(x).

Задача 3

Случайная
величина Х задана функцией распределения F(x):

а) Найти
плотность вероятности СВ Х – f(x).

б) Построить графики
f(x), F(x).

в) Найти вероятность
попадания НСВ в интервал (0; 3).

Задача 4

Дифференциальная
функция НСВ Х задана на всей числовой оси ОХ:

Найти:

а) постоянный
параметр С=const;

б) функцию
распределения F(x);

в) вероятность
попадания в интервал -4<X<4;

г) построить
графики f(x), F(X).

Задача 5

Случайная величина
Х задана функцией распределения F(x):

а) Найти
плотность вероятности СВ Х – f(x).

б) Построить
графики f(x), F(x).

в) Найти
вероятность попадания НСВ в интервал (0;π⁄2).

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 6

НСВ X имеет
плотность вероятности (закон Коши)

а) постоянный
параметр С=const;

б) функцию
распределения F(x);

в) вероятность
попадания в интервал -1<X<1;

г) построить
графики f(x), F(X).

Задача 7

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную
функцию f(x), а при заданной дифференциальной функции f(x) найти интегральную
функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(X);

д)
вычислить вероятность попадания в интервал P(a≤x≤b);

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

Задание 8

Дана
интегральная функция распределения случайной величины X. Найти дифференциальную
функцию распределения, математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение.

Задача 9

Случайная
величина X задана интегральной функцией распределения

Найти
дифференциальную функцию, математическое ожидание и дисперсию X.

Задача 10

СВ Х
задана функцией распределения F(x). Найдите вероятность
того, что в результате испытаний НСВ Х попадет в заданный интервал (0;0,5).
Постройте график функции распределения. Найдите плотность вероятности НСВ Х и
постройте ее график. Найдите числовые
характеристики НСВ Х, если

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

● Функция
распределения и функция плотности
непрерывной случайной величины

Случайная
величина
имеет функцию распределения.
Найдите плотность вероятностислучайной величины.

Случайная
величина
имеет функцию распределения.
Найдите плотность вероятностислучайной величины.

Случайная
величина
имеет функцию распределения.
Найдите плотность вероятностислучайной величины.

Распределение
непрерывной случайной величинызадано плотностью вероятности.
Найдите плотность вероятностислучайной величины.

Случайная
величина
имеет плотность вероятности.
Найдите плотность вероятностислучайной величины.

Случайная
величина
имеет плотность вероятностиНайдите константуи вероятность.

Функция
плотности вероятности случайной
величины
имеет вид.
Найдите константуи вероятность.

Функция
плотности вероятности случайной
величины
имеет вид.
Найдите константуи вероятность.

Плотность
вероятности случайной величины
имеет вид.
Найдитеи.

● Равномерное
распределение на отрезке

Случайная
величина
равномерно распределена на отрезке.
Найдите вероятность.

Случайная
величина
равномерно распределена на отрезке.
Найдите вероятность.

Случайные
величины
независимы и равномерно распределены
на отрезке.
Найдите математическое ожидание.

Случайная
величина
имеет равномерное распределение на
отрезкеНайдите коэффициент корреляции случайных
величини

Случайная
величина
равномерно распределена на отрезке.
Найдите математическое ожидание.

Случайная
величина
равномерно распределена на отрезке.
Найдите дисперсию.

Случайная
величина
равномерно распределена на отрезке.
Найдите.

Случайная
величина
равномерно распределена на отрезке.
Найдите.

Найдите
математическое ожидание и дисперсию
произведения независимых случайных
величин
ис равномерными законами распределения:– на отрезке,– на отрезке.

Случайные
величины
инезависимые и равномерно распределены
на отрезках:– на отрезке,– на отрезке.
Найдите.

● Показательное
распределение

Случайные
величины
инезависимые и распределены по
показательному закону, причём,.
Найдите.

Случайные
величины
независимы
и распределены по показательному
закону. Найдите,
если.

Случайная
величина
распределена по показательному закону.
Найдите математическое ожидание,
если дисперсия.

Случайная
величина
распределена
по показательному закону. Найдите
математическое ожидание,
если дисперсия.

Случайная
величина
распределена по показательному закону.
Найдите вероятность,
если.

● Нормальное
распределение на прямой

Для
нормальной случайной величины
с математическим ожиданиеми дисперсиейнайдите вероятность.

Случайная
величина
имеет нормальное распределение с
параметрамии.
Найдите вероятность попаданияв интервал.

Для
нормальной случайной величины
известно, что математическое ожиданиеи вероятностьНайдите дисперсию.

Для
нормальной случайной величины
известно, что дисперсияи вероятность.
Найдите математическое ожидание.

Для
нормальной случайной величины
с математическим ожиданиеми дисперсиейнайдите вероятность.

Математические
ожидания и дисперсии независимых
нормальных случайных величин
равны 1. Найдите вероятность.

Для
нормальной случайной величины
с математическим ожиданиеми дисперсиейнайдите вероятность.

Для
независимых нормальных случайных
величин
,известны их математические ожидания
и дисперсии:,,,.
Найдите вероятность.

Независимые
нормальные случайные величины
имеют одинаковые параметры:,,.
Для случайной величинынайдите вероятность.

Для
нормальной случайной величины
с математическим ожиданиеми дисперсиейнайдите вероятность.

Случайные
величины
инезависимые и распределены по нормальному
закону, причём,.
Найдите.

Источник

Функция, интеграл которой по региону описывает вероятность события, происходящего в этом регионе График и плотность вероятности функция нормального распределения N (0, σ). Геометрическая визуализация режима , медианы и среднего произвольная функция плотности вероятности.

В теории вероятностей, функция плотности вероятности (PDF ) или плотность из непрерывная случайная величина, является функцией , значение которой в любой заданной выборке (или точке) в пространстве выборки (набор возможных значений, принимаемых случайной величиной) может интерпретироваться как обеспечение относительной вероятности того, что значение случайной величины будет равно этой выборке. Другими словами, хотя абсолютная вероятность того, что непрерывная случайная переменная примет какое-либо конкретное значение, равна 0 (поскольку существует бесконечный набор возможных значений для начала), значение PDF для двух разных выборок может использоваться для вывода, насколько более вероятно, что случайная величина будет равна одной выборке по сравнению с другой выборкой, при любом конкретном розыгрыше случайной величины.

В более точном смысле PDF используется для определения вероятности попадания случайной величины в конкретный диапазон значений, в отличие от принятия какого-либо одного значения. Эта вероятность дается интегралом PDF этой переменной в этом диапазоне, то есть она дается площадью под функцией плотности, но над горизонтальной осью и между наименьшим и наибольшим значениями диапазона. Функция плотности вероятности везде неотрицательна, и ее интеграл по всему пространству равен 1.

Термины «функция распределения вероятностей» и «функция вероятности» также иногда использовались для обозначения функции плотности вероятности. Однако такое использование не является стандартным среди специалистов по теории вероятностей и статистиков. В других источниках «функция распределения вероятностей» может использоваться, когда распределение вероятностей определяется как функция по общим наборам значений, или оно может относиться к кумулятивной функции распределения, или может быть функцией вероятности и массы (PMF), а не плотностью. Сама «функция плотности» также используется для функции массы вероятности, что ведет к дальнейшему недоразумению. Однако в целом PMF используется в контексте дискретных случайных величин (случайных величин, принимающих значения в счетном наборе), в то время как PDF используется в контексте непрерывных случайных величин.

Содержание

1 Пример
2 Абсолютно непрерывные одномерные распределения
3 Формальное определение
- 3.1 Обсуждение
4 Дополнительные сведения
5 Связь между дискретным и непрерывным распределениями
6 Семейства плотности
7 Плотности, связанные с несколькими переменными
- 7.1 Предельные плотности
- 7.2 Независимость
- 7.3 Следствие
- 7.4 Пример
8 Функция случайных величин и изменение переменных в функции плотности вероятности
- 8.1 Скаляр в скаляр
- 8.2 Вектор в вектор
- 8.3 Вектор в скаляр
9 Суммы независимых случайных величин
10 Произведения и частные независимых случайных величин
- 10.1 Пример: распределение частных
- 10.2 Пример: отношение двух стандартных норм
11 См. Также
12 Ссылки
13 Библиография
14 Внешние ссылки

Пример

Предположим, бактерии определенного вида обычно живут от 4 до 6 часов. Вероятность того, что бактерия живет ровно 5 часов, равна нулю. Многие бактерии живут приблизительно 5 часов, но нет никаких шансов, что какая-либо конкретная бактерия погибнет ровно в 5.0000000000… часов. Однако вероятность того, что бактерия погибнет в период от 5 часов до 5,01 часа, поддается количественной оценке. Предположим, ответ 0,02 (т.е. 2%). Тогда вероятность того, что бактерия погибнет в период от 5 часов до 5,001 часа, должна быть около 0,002, поскольку этот временной интервал в десять раз меньше предыдущего. Вероятность того, что бактерия погибнет в период от 5 часов до 5.0001 часа, должна быть около 0,0002 и так далее.

В этих трех примерах соотношение (вероятность смерти во время интервала) / (продолжительность интервала) приблизительно постоянное и равно 2 в час (или 2 часа). Например, вероятность смерти 0,02 в интервале 0,01 часа от 5 до 5,01 часа, а (вероятность 0,02 / 0,01 часа) = 2 часа. Это количество в 2 часа называется плотностью вероятности смерти примерно через 5 часов. Следовательно, вероятность того, что бактерия погибнет через 5 часов, может быть записана как (2 часа) dt. Это вероятность того, что бактерия погибнет в бесконечно малом временном окне около 5 часов, где dt – продолжительность этого окна. Например, вероятность того, что он живет дольше 5 часов, но меньше (5 часов + 1 наносекунда), составляет (2 часа) × (1 наносекунда) ≈ 6 × 10 (с использованием преобразования единиц измерения 3,6 × 10 наносекунд = 1 час).

Существует функция плотности вероятности f с f (5 часов) = 2 часа. интеграл от f для любого временного окна (не только бесконечно малых, но и больших окон) – это вероятность того, что бактерия погибнет в этом окне.

Абсолютно непрерывные одномерные распределения

Функция плотности вероятности чаще всего связана с абсолютно непрерывными одномерными распределениями. A случайная величина X { displaystyle X}имеет плотность f X { displaystyle f_ {X}} f_X , где е Икс { displaystyle f_ {X}} f_X – неотрицательная интегрируемая по Лебегу функция, если:

Pr [a ≤ X ≤ b] = ∫ abf X ( х) dx. { displaystyle Pr [a leq X leq b] = int _ {a} ^ {b} f_ {X} (x) , dx.} $Pr[aleq Xleq b]=int _{a}^{b}f_{X}(x),dx.$

Следовательно, если FX { displaystyle F_ {X}} $F_{X}$ – кумулятивная функция распределения для X { displaystyle X}, тогда:

FX (x) = ∫ – ∞ xf X (u) du, { displaystyle F_ {X} (x) = int _ {- infty} ^ {x} f_ {X} (u) , du,} $F_{X}(x)=int _{-infty }^{x}f_{X}(u),du,$

и (если е Икс { displaystyle f_ {X}} f_X непрерывно в x { displaystyle x})

f X (x) = ddx FX (x). { Displaystyle f_ {X} (x) = { frac {d} {dx}} F_ {X} (x).} $f_{X}(x)={frac {d}{dx}}F_{X}(x).$

Интуитивно можно представить себе f X (x) dx { displaystyle f_ {X } (x) , dx} ${displaystyle f_{X}(x),dx}$ как вероятность попадания X { displaystyle X}в бесконечно малый интервал [x, x + dx] { displaystyle [x, x + dx]}.

Формальное определение

(Это определение может быть расширено до любого распределения вероятностей с использованием теории меры определение вероятности.)

A случайная величина X { displaystyle X}со значениями в измеримое пространство (X, A) { displaystyle ({ mathcal {X}}, { mathcal {A}})}(обычно R n { displaystyle mathbb {R} ^ {n}} $mathbb {R} ^{n}$ с наборами Бореля в качестве измеримых подмножеств) имеет как распределение вероятностей меру X ∗ P на (X, A) { displaystyle ({ mathcal {X}}, { mathcal {A}})}: плотность из Икс { displaystyle X}относительно контрольной меры μ { displaystyle mu}на (X, A) { displaystyle ({ mathcal {X}}, { mathcal {A}})}– производная Радона – Никодима :

f = d X ∗ P d μ. { displaystyle f = { frac {dX _ {*} P} {d mu}}.} $f={frac {dX_{*}P}{dmu }}.$

То есть f – это любая измеримая функция со следующим свойством:

Pr [X ∈ A] = ∫ Икс – 1 A d п знак равно ∫ A fd μ { displaystyle Pr [X in A] = int _ {X ^ {- 1} A} , dP = int _ {A} f , d mu} $Pr[Xin A]=int _{X^{-1}A},dP=int _{A}f,dmu$

для любого измеримого множества A ∈ A. { displaystyle A in { mathcal {A}}.}

Обсуждение

В непрерывном одномерном случае выше эталонной мерой является мера Лебега. Функция вероятности и массы дискретной случайной величины представляет собой плотность относительно счетной меры в пространстве выборки (обычно набор целых чисел или некоторые его подмножества).

Невозможно определить плотность со ссылкой на произвольную меру (например, нельзя выбрать счетную меру в качестве эталона для непрерывной случайной величины). Более того, когда он действительно существует, плотность почти везде уникальна.

Дополнительные сведения

В отличие от вероятности функция плотности вероятности может принимать значения больше единицы; например, равномерное распределение на интервале [0, ½] имеет плотность вероятности f (x) = 2 для 0 ≤ x ≤ ½ и f (x) = 0 в другом месте.

Стандартное нормальное распределение имеет плотность вероятности

f (x) = 1 2 π e – x 2/2. { displaystyle f (x) = { frac {1} { sqrt {2 pi}}} ; e ^ {- x ^ {2} / 2}.} $f(x)={frac {1}{sqrt {2pi }}};e^{-x^{2}/2}.$

Если задана случайная величина X и его распределение допускает функцию плотности вероятности f, то ожидаемое значение X (если ожидаемое значение существует) может быть вычислено как

E ⁡ [X] = ∫ – ∞ ∞ xf (x) dx. { displaystyle operatorname {E} [X] = int _ {- infty} ^ { infty} x , f (x) , dx.} $operatorname {E} [X]=int _{-infty }^{infty }x,f(x),dx.$

Не каждое распределение вероятностей имеет функцию плотности: распределения дискретных случайных величин – нет; равно как и распределение Кантора, даже при том, что оно не имеет дискретной составляющей, т.е. не присваивает положительную вероятность какой-либо отдельной точке.

Распределение имеет функцию плотности тогда и только тогда, когда его кумулятивная функция распределения F (x) абсолютно непрерывна. В этом случае: F почти всюду дифференцируемо, и его производная может использоваться как плотность вероятности:

d d x F (x) = f (x). { displaystyle { frac {d} {dx}} F (x) = f (x).} ${frac {d}{dx}}F(x)=f(x).$

Если распределение вероятностей допускает плотность, то вероятность каждого одноточечного набора {a} равна нулю; то же самое верно для конечных и счетных множеств.

Две плотности вероятности f и g представляют одно и то же распределение вероятностей, если они различаются только на наборе Лебега нулевой меры.

в поле в статистической физике, неформальная переформулировка приведенного выше отношения между производной кумулятивной функции распределения и функцией плотности вероятности обычно используется в качестве определения функции плотности вероятности. Это альтернативное определение выглядит следующим образом:

Если dt – бесконечно малое число, вероятность того, что X входит в интервал (t, t + dt), равна f (t) dt, или:

Pr (t < X < t + d t) = f ( t) d t. {displaystyle Pr(t

Связь между дискретным и непрерывным распределениями

Можно представить определенные дискретные случайные величины, а также случайные величины, включающие как непрерывную, так и дискретную часть, с помощью обобщенного функция плотности вероятности с использованием дельта-функции Дирака. (Это невозможно с функцией плотности вероятности в смысле, определенном выше, это может быть выполнено с распределением.) Например,, рассмотрим двоичную дискретную случайную величину, имеющую распределение Радемахера, то есть принимающее -1 или 1 для значений с вероятностью 1/2 каждое. Плотность вероятности, связанная с этой переменной, равна:

е (t) = 1 2 (δ (t + 1) + δ (t – 1)). { Displaystyle f (t) = { frac {1} {2}} ( delta (t + 1) + delta (t-1)).} $f(t)={frac {1}{2}}(delta (t+1)+delta (t-1)).$

Более общие y, если дискретная переменная может принимать n различных значений среди действительных чисел, тогда соответствующая функция плотности вероятности имеет вид:

f (t) = ∑ i = 1 npi δ (t – xi), { displaystyle f (t) = sum _ {i = 1} ^ {n} p_ {i} , delta (t-x_ {i}),} $f(t)=sum _{i=1}^{n}p_{i},delta (t-x_{i}),$

где x 1…, xn { displaystyle x_ {1} ldots, x_ {n}} ${displaystyle x_{1}ldots,x_{n}}$ – дискретные значения, доступные для переменной, а p 1,…, pn { displaystyle p_ {1}, ldots, p_ {n}}– вероятности, связанные с этими значениями.

Это существенно унифицирует обработку дискретных и непрерывных распределений вероятностей. Например, приведенное выше выражение позволяет определять статистические характеристики такой дискретной переменной (такие как ее среднее, ее дисперсия и ее эксцесс ), начиная с приведены формулы для непрерывного распределения вероятности.

Семейства плотностей

Обычно функции плотности вероятности (и функции массы вероятности ) параметризуются, то есть характеризуются неопределенными параметрами . Например, нормальное распределение параметризуется в терминах среднего и дисперсии, обозначенных μ { displaystyle mu}и σ 2 { displaystyle sigma ^ {2}} $sigma ^{2}$ соответственно, что дает семейство плотностей

f (x; μ, σ 2) = 1 σ 2 π e – 1 2 (х – μ σ) 2. { displaystyle f (x; mu, sigma ^ {2}) = { frac {1} { sigma { sqrt {2 pi}}}} e ^ {- { frac {1} {2 }} left ({ frac {x- mu} { sigma}} right) ^ {2}}.} $f(x;mu,sigma ^{2})={frac {1}{sigma {sqrt {2pi }}}}e^{-{frac {1}{2}}left({frac {x-mu }{sigma }}right)^{2}}.$

Важно помнить о различии между доменом семейства плотностей и параметров семейства. Разные значения параметров описывают разные распределения разных случайных величин на одном и том же пространстве выборки (один и тот же набор всех возможных значений переменной); это пространство выборки является областью семейства случайных величин, которое описывает это семейство распределений. Данный набор параметров описывает единичное распределение внутри семейства, разделяющее функциональную форму плотности. С точки зрения данного распределения параметры являются константами, а члены функции плотности, которые содержат только параметры, но не переменные, являются частью коэффициента нормализации распределения (мультипликативный коэффициент, который гарантирует, что площадь под плотностью – вероятность того, что что-то произойдет в области – равна 1). Этот коэффициент нормализации находится за пределами ядра распределения.

Поскольку параметры являются константами, повторная параметризация плотности в терминах различных параметров, чтобы дать характеристику другой случайной переменной в семействе, означает простую замену новых значений параметров в формулу вместо старых.. Однако изменение области определения плотности вероятности сложнее и требует дополнительных усилий: см. Раздел ниже, посвященный замене переменных.

Плотности, связанные с несколькими переменными

Для непрерывных случайных величин X1,…, X n также можно определить плотность вероятности функция, связанная с множеством в целом, часто называемая совместной функцией плотности вероятности . Эта функция плотности определяется как функция n переменных, так что для любой области D в n-мерном пространстве значений переменных X 1,…, X n, вероятность того, что реализация набора переменных попадет в область D, равна

Pr (X 1,…, X n ∈ D) = ∫ D f X 1,…, X n (x 1,…, xn) dx 1 ⋯ dxn. { displaystyle Pr left (X_ {1}, ldots, X_ {n} in D right) = int _ {D} f_ {X_ {1}, ldots, X_ {n}} (x_ {1}, ldots, x_ {n}) , dx_ {1} cdots dx_ {n}.} ${displaystyle Pr left(X_{1},ldots,X_{n}in Dright)=int _{D}f_{X_{1},ldots,X_{n}}(x_{1},ldots,x_{n}),dx_{1}cdots dx_{n}.}$

Если F (x 1,…, x n) = Pr (X 1 ≤ x 1,…, X n ≤ x n) – это кумулятивная функция распределения вектора (X 1,…, X n), тогда совместная функция плотности вероятности может быть вычислена как частная производная

f (x) = ∂ n F ∂ x 1 ⋯ ∂ xn | х { displaystyle f (x) = { frac { partial ^ {n} F} { partial x_ {1} cdots partial x_ {n}}} { bigg |} _ {x}} $f(x)={frac {partial ^{n}F}{partial x_{1}cdots partial x_{n}}}{bigg |}_{x}$

Предельные плотности

Для i = 1, 2,…, n пусть f Xi(xi) будет функцией плотности вероятности, связанной только с переменной X i. Это называется функцией предельной плотности, и ее можно вывести из плотности вероятности, связанной со случайными величинами X 1,…, X n, путем интегрирования по всем значениям других n – 1 переменная:

f X i (xi) = ∫ f (x 1,…, xn) dx 1 ⋯ dxi – 1 dxi + 1 ⋯ dxn. { displaystyle f_ {X_ {i}} (x_ {i}) = int f (x_ {1}, ldots, x_ {n}) , dx_ {1} cdots dx_ {i-1} , dx_ {i + 1} cdots dx_ {n}.} $f_{X_i}(x_i) = int f(x_1,ldots,x_n), dx_1 cdots dx_{i-1},dx_{i+1}cdots dx_n.$

Независимость

Непрерывные случайные величины X 1,…, X n, допускающие плотность соединений все независимы друг от друга тогда и только тогда, когда

f X 1,…, X n (x 1,…, xn) = f X 1 (x 1) ⋯ f X n ( xn). { displaystyle f_ {X_ {1}, ldots, X_ {n}} (x_ {1}, ldots, x_ {n}) = f_ {X_ {1}} (x_ {1}) cdots f_ { X_ {n}} (x_ {n}).} ${displaystyle f_{X_{1},ldots,X_{n}}(x_{1},ldots,x_{n})=f_{X_{1}}(x_{1})cdots f_{X_{n}}(x_{n}).}$

Следствие

Если совместная функция плотности вероятности вектора из n случайных величин может быть разложена на произведение n функций одной переменной

е Икс 1,…, Икс N (Икс 1,…, xn) = f 1 (x 1) ⋯ fn (xn), { displaystyle f_ {X_ {1}, ldots, X_ {n}} (x_ {1}, ldots, x_ {n}) = f_ {1} (x_ {1}) cdots f_ {n} (x_ {n}),} ${displaystyle f_{X_{1},ldots,X_{n}}(x_{1},ldots,x_{n})=f_{1}(x_{1})cdots f_{n}(x_{n}),}$

(где каждое f i не обязательно является плотностью), то все n переменных в наборе независимы друг от друга, и функция предельной плотности вероятности каждой из них задается как

f X i (xi) = fi (xi) ∫ fi (x) dx. { displaystyle f_ {X_ {i}} (x_ {i}) = { frac {f_ {i} (x_ {i})} { int f_ {i} (x) , dx}}.} $f_{X_{i}}(x_{i})={frac {f_{i}(x_{i})}{int f_{i}(x),dx}}.$

Пример

Этот элементарный пример иллюстрирует приведенное выше определение многомерных функций плотности вероятности в простом случае функции от набора двух переменных. Назовем R → { displaystyle { vec {R}}}двумерным случайным вектором координат (X, Y): вероятность получить R → { displaystyle { vec {R}}}в четверть плоскости положительных значений x и y равно

Pr (X>0, Y>0) = ∫ 0 ∞ ∫ 0 ∞ f X, Y ( х, у) dxdy. { displaystyle Pr left (X>0, Y>0 right) = int _ {0} ^ { infty} int _ {0} ^ { infty} f_ {X, Y} (x, y) , dx , dy.} $Pr left(X>0, Y>0 right) = int _ {0} ^ { infty} int _ {0} ^ { infty} f_ {X, Y} (x, y) , dx , dy.$

Функция случайных величин и изменение переменных в функции плотности вероятности

Если функция плотности вероятности случайной величины (или вектора) X задана как f X (x), можно (но часто не обязательно; см. Ниже) вычислить функцию плотности вероятности некоторой переменной Y = g (X). Это также называется «заменой переменной» и на практике используется для генерации случайной величины произвольной формы f g (X) = f Y с использованием известного (например, равномерного) генератора случайных чисел.

Заманчиво думать, что для того, чтобы найти математическое ожидание E (g (X)), нужно сначала найти плотность вероятности f g (X) новой случайной величины Y = g (X). Однако вместо вычисления

E ⁡ (g (X)) = ∫ – ∞ ∞ yfg (X) (y) dy, { displaystyle operatorname {E} { big (} g (X) { big)} = int _ {- infty} ^ { infty} yf_ {g (X)} (y) , dy,} ${displaystyle operatorname {E} {big (}g(X){big)}=int _{-infty }^{infty }yf_{g(X)}(y),dy,}$

вместо этого можно найти

E ⁡ (g (X)) = ∫ – ∞ ∞ д (х) е х (х) дх. { displaystyle operatorname {E} { big (} g (X) { big)} = int _ {- infty} ^ { infty} g (x) f_ {X} (x) , dx.} ${displaystyle operator name {E} {big (}g(X){big)}=int _{-infty }^{infty }g(x)f_{X}(x),dx.}$

Значения двух интегралов одинаковы во всех случаях, когда и X, и g (X) фактически имеют функции плотности вероятности. Необязательно, чтобы g была однозначной функцией. В некоторых случаях последний интеграл вычисляется намного проще, чем первый. См. Закон бессознательного статистика.

От скаляра до скаляра

Пусть g: R → R { displaystyle g: { mathbb {R}} rightarrow { mathbb {R} }}быть монотонной функцией, тогда результирующая функция плотности будет

f Y (y) = f X (g – 1 (y)) | d d y (g – 1 (y)) |. { displaystyle f_ {Y} (y) = f_ {X} { big (} g ^ {- 1} (y) { big)} left | { frac {d} {dy}} { big (} g ^ {- 1} (y) { big)} right |.} ${displaystyle f_{Y}(y)=f_{X}{big (}g^{-1}(y){big)}left|{frac {d}{dy}}{big (}g^{-1}(y){big)}right|.}$

Здесь g обозначает обратную функцию.

Это следует из того факта, что вероятность, содержащаяся в дифференциальной области, должна быть инвариантным относительно замены переменных. То есть

| f Y (y) d y | = | f X (x) d x |, { displaystyle left | f_ {Y} (y) , dy right | = left | f_ {X} (x) , dx right |,} ${displaystyle left|f_{Y}(y),dyright|=left|f_{X}(x),dxright|,}$

или

f Y (y) = | д х д у | f X (x) = | d d y (x) | f X (x) = | d d y (g – 1 (y)) | f X (g – 1 (y)) = | (g – 1) ′ (y) | ⋅ е X (г – 1 (у)). { displaystyle f_ {Y} (y) = left | { frac {dx} {dy}} right | f_ {X} (x) = left | { frac {d} {dy}} (x) right | f_ {X} (x) = left | { frac {d} {dy}} { big (} g ^ {- 1} (y) { big)} right | f_ {X } { big (} g ^ {- 1} (y) { big)} = {{ big |} { big (} g ^ {- 1} { big)} ‘(y) { big |}} cdot f_ {X} { big (} g ^ {- 1} (y) { big)}.} ${displaystyle f_{Y}(y)=left|{frac {dx}{dy}}right|f_{X}(x)=left|{frac {d}{dy}}(x)right|f_{X}(x)=left|{frac {d}{dy}}{big (}g^{-1}(y){big)}right|f_{X}{big (}g^{-1}(y){big)}={{big |}{big (}g^{-1}{big)}'(y){big |}}cdot f_{X}{big (}g^{-1}(y){big)}.}$

Для функций, которые не являются монотонными, функция плотности вероятности для y равна

∑ k = 1 n (y) | d d y g k – 1 (y) | ⋅ е Икс (gk – 1 (y)), { displaystyle sum _ {k = 1} ^ {n (y)} left | { frac {d} {dy}} g_ {k} ^ {- 1} (y) right | cdot f_ {X} { big (} g_ {k} ^ {- 1} (y) { big)},} ${displaystyle sum _{k=1}^{n(y)}left|{frac {d}{dy}}g_{k}^{-1}(y)right|cdot f_{X}{big (}g_{k}^{-1}(y){big)},}$

где n (y) – количество решения по x уравнения g (x) = y { displaystyle g (x) = y}и gk – 1 (y) { displaystyle g_ {k} ^ {-1} (y)} ${displaystyle g_{k}^{-1}(y)}$ – вот эти решения.

Вектор в вектор

Вышеупомянутые формулы могут быть обобщены для переменных (которые мы снова будем называть y) в зависимости от более чем одной другой переменной. f (x 1,…, x n) должно обозначать функцию плотности вероятности переменных, от которых зависит y, и зависимость должна быть y = g (x 1,…, x n). Тогда результирующая функция плотности будет

∫ y = g (x 1,…, xn) f (x 1,…, xn) ∑ j = 1 n ∂ g ∂ xj (x 1,…, xn) 2 d V, { displaystyle int limits _ {y = g (x_ {1}, ldots, x_ {n})} { frac {f (x_ {1}, ldots, x_ {n})} { sqrt { sum _ {j = 1} ^ {n} { frac { partial g} { partial x_ {j}}} (x_ {1}, ldots, x_ {n}) ^ {2} }}} , dV,} ${displaystyle int limits _{y=g(x_{1},ldots,x_{n})}{frac {f(x_{1},ldots,x_{n})}{sqrt {sum _{j=1}^{n}{frac {partial g}{partial x_{j}}}(x_{1},ldots,x_{n})^{2}}}},dV,}$

где интеграл берется по всему (n – 1) -мерному решению уравнения с индексами, а символическое dV должно быть заменено параметризацией этого решения для конкретного вычисления; переменные x 1,…, x n в таком случае, конечно, являются функциями этой параметризации.

Это происходит из следующего, возможно, более интуитивного представления: Предположим, x – это n-мерная случайная величина с совместной плотностью f. Если y = H (x ), где H – биективная, дифференцируемая функция, то y имеет плотность g:

g (y) = f (H – 1 (y)) | det [d H – 1 (z) d z | z = y] | { Displaystyle г ( mathbf {y}) = е { Big (} H ^ {- 1} ( mathbf {y}) { Big)} left vert det left [{ frac {dH ^ {- 1} ( mathbf {z})} {d mathbf {z}}} { Bigg vert} _ { mathbf {z} = mathbf {y}} right] right vert} ${displaystyle g(mathbf {y})=f{Big (}H^{-1}(mathbf {y}){Big)}leftvert det left[{frac {dH^{-1}(mathbf {z})}{dmathbf {z} }}{Bigg vert }_{mathbf {z} =mathbf {y} }right]rightvert }$

с дифференциалом, рассматриваемым как якобиан обратной величины H (.), Вычисляемой как y.

. Например, в двумерном случае x = (x 1, x 2), предположим, что преобразование H задано как y 1 = H 1(x1, x 2), y 2 = H 2(x1, x 2) с обратными x 1 = H 1(y1, y 2), x 2 = H 2(y1, y 2). Совместное распределение для y = (y 1, y 2) имеет плотность

g (y 1, y 2) = f X 1, X 2 (H 1 – 1 (y 1, y 2), H 2 – 1 (y 1, y 2)) | ∂ H 1 – 1 ∂ y 1 ∂ H 2 – 1 ∂ y 2 – ∂ H 1 – 1 ∂ y 2 ∂ H 2 – 1 ∂ y 1 |. { displaystyle g (y_ {1}, y_ {2}) = f_ {X_ {1}, X_ {2}} { big (} H_ {1} ^ {- 1} (y_ {1}, y_ { 2}), H_ {2} ^ {- 1} (y_ {1}, y_ {2}) { big)} left vert { frac { partial H_ {1} ^ {- 1}} { partial y_ {1}}} { frac { partial H_ {2} ^ {- 1}} { partial y_ {2}}} – { frac { partial H_ {1} ^ {- 1}} { partial y_ {2}}} { frac { partial H_ {2} ^ {- 1}} { partial y_ {1}}} right vert.} ${displaystyle g(y_{1},y_{2})=f_{X_{1},X_{2}}{big (}H_{1}^{-1}(y_{1},y_{2}),H_{2}^{-1}(y_{1},y_{2}){big)}leftvert {frac {partial H_{1}^{-1}}{partial y_{1}}}{frac {partial H_{2}^{-1}}{partial y_{2}}}-{frac {partial H_{1}^{-1}}{partial y_{2}}}{frac {partial H_{2}^{-1}}{partial y_{1}}}rightvert.}$

Вектор в скаляр

Пусть V: R n → R { displaystyle V: { mathbb {R}} ^ {n} rightarrow { mathbb {R}}} ${displaystyle V:{mathbb {R} }^{n}rightarrow {mathbb {R} }}$ – дифференцируемая функция и X { displaystyle X}быть случайным вектором, принимающим значения в R n { displaystyle { mathbb {R}} ^ {n}} ${mathbb {R} }^{n}$ , f X (⋅) { displaystyle f_ {X} ( cdot)} ${displaystyle f_{X}(cdot)}$ – функция плотности вероятности от X { displaystyle X}и δ (⋅) { displaystyle delta ( cdot)}быть дельта-функцией Дирака. Можно использовать приведенные выше формулы для определения f Y (⋅) { displaystyle f_ {Y} ( cdot)} ${displaystyle f_{Y}(cdot)}$ , функции плотности вероятности Y = V (X) { displaystyle Y = V (X)}, который будет задан как

f Y (y) = ∫ R nf X (x) δ (y – V (x)) dx. { displaystyle f_ {Y} (y) = int _ {{ mathbb {R}} ^ {n}} f_ {X} ( mathbf {x}) delta { big (} yV ( mathbf { x}) { big)} , d mathbf {x}.} ${displaystyle f_{Y}(y)=int _{{mathbb {R} }^{n}}f_{X}(mathbf {x})delta {big (}y-V(mathbf {x}){big)},dmathbf {x}.}$

Этот результат приводит к Закону бессознательного статистика :

EY ⁡ [Y] = ∫ R yf Y (y) dy = ∫ R y ∫ R nf X (x) δ (y – V (x)) dxdy = ∫ R n ∫ R yf X (x) δ (y – V (x)) dydx = ∫ R n V (x) f X (x) dx = EX ⁡ [V (X)]. { displaystyle operatorname {E} _ {Y} [Y] = int _ { mathbb {R}} yf_ {Y} (y) dy = int _ { mathbb {R}} y int _ { { mathbb {R}} ^ {n}} f_ {X} ( mathbf {x}) delta { big (} yV ( mathbf {x}) { big)} , d mathbf {x } dy = int _ {{ mathbb {R}} ^ {n}} int _ { mathbb {R}} yf_ {X} ( mathbf {x}) delta { big (} yV ( mathbf {x}) { big)} , dyd mathbf {x} = int _ {{ mathbb {R}} ^ {n}} V ( mathbf {x}) f_ {X} ( mathbf {x}) d mathbf {x} = operatorname {E} _ {X} [V (X)].} ${displaystyle operatorname {E} _{Y}[Y]=int _{mathbb {R} }yf_{Y}(y)dy=int _{mathbb {R} }yint _{{mathbb {R} }^{n}}f_{X}(mathbf {x})delta {big (}y-V(mathbf {x}){big)},dmathbf {x} dy=int _{{mathbb {R} }^{n}}int _{mathbb {R} }yf_{X}(mathbf {x})delta {big (}y-V(mathbf {x}){big)},dydmathbf {x} =int _{{mathbb {R} }^{n}}V(mathbf {x})f_{X}(mathbf {x})dmathbf {x} =operatorname {E} _{X}[V(X)].}$

Доказательство:

Пусть Z { displaystyle Z}быть свернутой случайной величиной с функцией плотности вероятности p Z (z) = δ (z) { displaystyle p_ {Z} (z) = delta (z)} ${displaystyle p_{Z}(z)=delta (z)}$ (т.е. константа, равная нулю). Пусть случайный вектор X ~ { displaystyle { tilde {X}}}и преобразование H { displaystyle H}определены как

ЧАС (Z, X) знак равно [Z + V (X) X] = [YX ~] { Displaystyle H (Z, X) = { begin {bmatrix} Z + V (X) \ X end {bmatrix }} = { begin {bmatrix} Y \ { tilde {X}} end {bmatrix}}} ${displaystyle H(Z,X)={begin{bmatrix}Z+V(X)\Xend{bmatrix}}={begin{bmatrix}Y\{tilde {X}}end{bmatrix}}}$

Ясно, что H { displaystyle H}является биективное отображение, и якобиан H – 1 { displaystyle H ^ {- 1}} $H^{{-1}}$ задается следующим образом:

d H – 1 (y, x ~) dydx ~ = [ 1 – d V (x ~) dx ~ 0 n × 1 I n × n] { displaystyle { frac {dH ^ {- 1} (y, { tilde { mathbf {x}}})} {dy , d { tilde { mathbf {x}}}}} = { begin {bmatrix} 1 – { frac {dV ({ tilde { mathbf {x}}})} {d { tilde { mathbf {x}}}}} \ mathbf {0} _ {n times 1} mathbf {I} _ {n times n} end {bmatrix}}} ${displaystyle {frac {dH^{-1}(y,{tilde {mathbf {x} }})}{dy,d{tilde {mathbf {x} }}}}={begin{bmatrix}1-{frac {dV({tilde {mathbf {x} }})}{d{tilde {mathbf {x} }}}}\mathbf {0} _{ntimes 1}mathbf {I} _{ntimes n}end{bmatrix}}}$

который является верхним треугольная матрица с единицами на главной диагонали, поэтому ее определитель равен 1. Применяя теорему о замене переменной из предыдущего раздела, получаем, что

f Y, X (y, x) = f X (x) δ (y -В (Икс)) { Displaystyle F_ {Y, X} (Y, X) = F_ {X} ( mathbf {x}) delta { big (} yV ( mathbf {x}) { big) }} ${displaystyle f_{Y,X}(y,x)=f_{X}(mathbf {x})delta {big (}y-V(mathbf {x}){big)}}$

который, если его маргинализировать более чем x { displaystyle x}приводит к желаемой функции плотности вероятности.

Суммы независимых случайных величин

Функция плотности вероятности суммы двух независимых случайных величин U и V, каждая из которых имеет функцию плотности вероятности, является свертка их отдельных функций плотности:

f U + V (x) = ∫ – ∞ ∞ f U (y) f V (x – y) dy = (f U ∗ f V) ( х) { displaystyle f_ {U + V} (x) = int _ {- infty} ^ { infty} f_ {U} (y) f_ {V} (xy) , dy = left (f_ {U} * f_ {V} right) (x)} $f_{U+V}(x)=int _{-infty }^{infty }f_{U}(y)f_{V}(x-y),dy=left(f_{U}*f_{V}right)(x)$

Можно обобщить предыдущее соотношение на сумму N независимых случайных величин с плотностями U 1,…, U N:

е U 1 + ⋯ + UN (x) = (е U 1 * ⋯ * f UN) (x) { displaystyle f_ {U_ {1} + cdots + U_ {N}} (x) = left (f_ {U_ {1}} * cdots * f_ {U_ {N}} right) (x)} ${displaystyle f_{U_{1}+cdots +U_{N}}(x)=left(f_{U_{1}}*cdots *f_{U_{N}}right)(x)}$

Это можно получить из двухсторонней замены переменных с участием Y = U + V и Z = V, аналогично приведенному ниже примеру для частного независимых случайных величин.

Произведения и частные независимых случайных величин

Даны две независимые случайные величины U и V, каждая из которых имеет функцию плотности вероятности, плотность произведения Y = UV и частное Y = U / V можно вычислить заменой переменных.

Пример: частное распределение

Чтобы вычислить частное Y = U / V двух независимых случайных величин U и V, определите следующее преобразование:

Y = U / V { displaystyle Y = U / V} Y=U/V

Z = V { displaystyle Z = V} Z=V

Тогда совместная плотность p (y, z) может быть вычислена заменой переменных с U, V на Y, Z, и Y может быть получен путем маргинализации Z из плотности соединения.

Обратное преобразование:

U = YZ { displaystyle U = YZ} U=YZ

V = Z { displaystyle V = Z} V=Z

Матрица Якоби J (U, V ∣ Y, Z) { displaystyle J (U, V mid Y, Z)}этого преобразования равно

| ∂ u ∂ y ∂ u ∂ z ∂ v ∂ y ∂ v ∂ z | = | z y 0 1 | = | z |. { displaystyle { begin {vmatrix} { frac { partial u} { partial y}} { frac { partial u} { partial z}} \ { frac { partial v} { partial y}} { frac { partial v} { partial z}} end {vmatrix}} = { begin {vmatrix} z y \ 0 1 end {vmatrix}} = | z |.} ${displaystyle {begin{vmatrix}{frac {partial u}{partial y}}{frac {partial u}{partial z}}\{frac {partial v}{partial y}}{frac {partial v}{partial z}}end{vmatrix}}={begin{vmatrix}zy\01end{vmatrix}}=|z|.}$

Таким образом:

p (y, z) = p (u, v) J (u, v ∣ y, z) = p (u) p (v) J (u, v ∣ y, z) = p U (yz) p V (z) | z |. { Displaystyle п (Y, Z) знак равно п (и, v) , J (и, v середина у, г) = п (и) , р (v) , J (и, v середина у, z) = p_ {U} (yz) , p_ {V} (z) , | z |.} ${displaystyle p(y,z)=p(u,v),J(u,vmid y,z)=p(u),p(v),J(u,vmid y,z)=p_{U}(yz),p_{V}(z),|z|.}$

И распределение Y может быть вычислено путем маргинализации Z:

p (y) = ∫ – ∞ ∞ p U (yz) p V (z) | z | dz { displaystyle p (y) = int _ {- infty} ^ { infty} p_ {U} (yz) , p_ {V} (z) , | z | , dz} ${displaystyle p(y)=int _{-infty }^{infty }p_{U}(yz),p_{V}(z),|z|,dz}$

Этот метод критически требует, чтобы преобразование из U, V в Y, Z было биективным. Вышеупомянутое преобразование соответствует этому, потому что Z может быть отображено непосредственно обратно в V, и для данного V отношение U / V является монотонным. То же самое и для суммы U + V, разности U – V и произведения UV.

Точно такой же метод можно использовать для вычисления распределения других функций от нескольких независимых случайных величин.

Пример: частное двух стандартных нормалей

Для двух стандартных нормальных переменных U и V, частное можно вычислить следующим образом. Во-первых, переменные имеют следующие функции плотности:

p (u) = 1 2 π e – u 2 2 { displaystyle p (u) = { frac {1} { sqrt {2 pi}}} е ^ {- { гидроразрыва {u ^ {2}} {2}}}} ${displaystyle p(u)={frac {1}{sqrt {2pi }}}e^{-{frac {u^{2}}{2}}}}$

p (v) = 1 2 π e – v 2 2 { displaystyle p (v) = { frac {1} { sqrt {2 pi}}} e ^ {- { frac {v ^ {2}} {2}}}} ${displaystyle p(v)={frac {1}{sqrt {2pi }}}e^{-{frac {v^{2}}{2}}}}$

Преобразуем, как описано выше:

Y = U / V { displaystyle Y = U / V} Y=U/V

Z = V { displaystyle Z = V} Z=V

Это приводит к:

p (y) = ∫ – ∞ ∞ p U (yz) p V (z) | z | d z = ∫ – ∞ ∞ 1 2 π e – 1 2 y 2 z 2 1 2 π e – 1 2 z 2 | z | d z = ∫ – ∞ ∞ 1 2 π e – 1 2 (y 2 + 1) z 2 | z | dz = 2 ∫ 0 ∞ 1 2 π e – 1 2 (y 2 + 1) z 2 zdz = ∫ 0 ∞ 1 π e – (y 2 + 1) uduu = 1 2 z 2 = – 1 π (y 2 + 1) е – (Y 2 + 1) U] U знак равно 0 ∞ = 1 π (Y 2 + 1) { Displaystyle { begin {align} p (y) = int _ {- infty} ^ { infty} p_ {U} (yz) , p_ {V} (z) , | z | , dz \ [5pt] = int _ {- infty} ^ { infty} { frac {1} { sqrt {2 pi}}} e ^ {- { frac {1} {2}} y ^ {2} z ^ {2}} { frac {1} { sqrt {2 pi}}} e ^ {- { frac {1} {2}} z ^ {2}} | z | , dz \ [5pt] = int _ {- infty} ^ { infty} { frac {1} {2 pi}} e ^ {- { frac {1} {2}} (y ^ {2} +1) z ^ {2}} | z | , dz \ [ 5pt] = 2 int _ {0} ^ { infty} { frac {1} {2 pi}} e ^ {- { frac {1} {2}} (y ^ {2} +1) z ^ {2}} z , dz \ [5pt] = int _ {0} ^ { infty} { frac {1} { pi}} e ^ {- (y ^ {2} +1)u},duu={tfrac {1}{2}}z^{2}\[5pt]=left.-{frac {1}{pi (y^{2} +1)}}e^{-(y^{2}+1)u}right]_{u=0}^{infty }\[5pt]={frac {1}{pi (y^{2}+1)}}end{aligned}}} ${displaystyle {begin{aligned}p(y)=int _{-infty }^{infty }p_{U}(yz),p_{V}(z),|z|,dz\[5pt]=int _{-infty }^{infty }{frac {1}{sqrt {2pi }}}e^{-{frac {1}{2}}y^{2}z^{2}}{frac {1}{sqrt {2pi }}}e^{-{frac {1}{2}}z^{2}}|z|,dz\[5pt]=int _{-infty }^{infty }{frac {1}{2pi }}e^{-{frac {1}{2}}(y^{2}+1)z^{2}}|z|,dz\[5pt]=2int _{0}^{infty }{frac {1}{2pi }}e^{-{frac {1}{2}}(y^{2}+1)z^{2}}z,dz\[5pt]=int _{0}^{infty }{frac {1}{pi }}e^{-(y^{2}+1)u},duu={tfrac {1}{2}}z^{2}\[5pt]=left.-{frac {1}{pi (y^{2}+1)}}e^{-(y^{2}+1)u}right]_{u=0}^{infty }\[5pt]={frac {1}{pi (y^{2}+1)}}end{aligned}}}$

This is the density of a standard Cauchy distribution.

References

Bibliography

Pierre Simon de Laplace (1812). Analytical Theory of Probability.

The first major treatise blending calculus with probability theory, originally in French: Théorie Analytique des Probabilités.

The modern measure-theoretic foundation of probability theory; the original German version (Grundbegriffe der Wahrscheinlichkeitsrechnung) appeared in 1933.

Patrick Billingsley (1979). Вероятность и мера. New York, Toronto, London: John Wiley and Sons. ISBN 0-471-00710-2.
David Stirzaker (2003). Elementary Probability. ISBN 0-521-42028-8.

Chapters 7 to 9 are about continuous variables.

External links

Источник

Эта статья ведущий раздел не адекватно подвести итог ключевые моменты его содержания. Пожалуйста, подумайте о расширении интереса до предоставить доступный обзор обо всех важных аспектах статьи. (Март 2014 г.)

Концепция нормализующая константа возникает в теория вероятности и множество других областей математика. Нормализующая константа используется для сведения любой функции вероятности к функции плотности вероятности с полной вероятностью, равной единице.

Определение

В теория вероятности, а нормализующая константа – константа, на которую необходимо умножить всюду неотрицательную функцию, чтобы площадь под ее графиком была равна 1, например, чтобы сделать ее функция плотности вероятности или функция массы вероятности.^[1]^[2]

Примеры

Если мы начнем с простого Функция Гаусса

$p (x) = e ^ {{- x ^ {2} / 2}}, x in (- infty, infty)$

у нас есть соответствующие Гауссов интеграл

$int _ {{- infty}} ^ { infty} p (x) , dx = int _ {{- infty}} ^ { infty} e ^ {{- x ^ {2} / 2 }} , dx = { sqrt {2 pi ,}},$

Теперь, если мы воспользуемся последним обратная стоимость в качестве нормализующей константы для первого, определяя функцию так как

$varphi (x) = { frac {1} {{ sqrt {2 pi ,}}}} p (x) = { frac {1} {{ sqrt {2 pi ,}}} } e ^ {{- x ^ {2} / 2}}$

так что это интеграл единица

$int _ {{- infty}} ^ { infty} varphi (x) , dx = int _ {{- infty}} ^ { infty} { frac {1} {{ sqrt { 2 pi ,}}}} e ^ {{- x ^ {2} / 2}} , dx = 1$

тогда функция – функция плотности вероятности.^[3] Это плотность эталона нормальное распределение. (Стандарт, в данном случае означает ожидаемое значение равно 0 и отклонение равно 1.)

И постоянный ${ frac {1} {{ sqrt {2 pi ,}}}}$ это нормализующая константа функции р (х) .

Так же,

$sum _ {{n = 0}} ^ { infty} { frac { lambda ^ {n}} {n!}} = e ^ { lambda},$

и следовательно

$f (n) = { frac { lambda ^ {n} e ^ {{- lambda}}} {n!}}$

является функцией массы вероятности на множестве всех неотрицательных целых чисел.^[4] Это функция массы вероятности распределение Пуассона с математическим ожиданием λ.

Обратите внимание, что если функция плотности вероятности является функцией различных параметров, то это также будет ее нормирующая константа. Параметризованная нормирующая постоянная для Распределение Больцмана играет центральную роль в статистическая механика. В этом контексте нормализующая константа называется функция распределения.

Теорема Байеса

Теорема Байеса говорит, что мера апостериорной вероятности пропорциональна произведению меры априорной вероятности и функция правдоподобия. Пропорционально подразумевает, что нужно умножить или разделить на нормирующую константу, чтобы присвоить меру 1 всему пространству, то есть получить вероятностную меру. В простом дискретном случае имеем

$P (H_ {0} | D) = { frac {P (D | H_ {0}) P (H_ {0})} {P (D)}}$

где P (H₀) – априорная вероятность того, что гипотеза верна; P (D | H₀) это условная возможность данных при условии, что гипотеза верна, но учитывая, что данные известны, это вероятность гипотезы (или ее параметров) с учетом данных; P (H₀| D) – апостериорная вероятность того, что гипотеза верна с учетом данных. P (D) должно быть вероятностью получения данных, но само по себе его сложно вычислить, поэтому альтернативный способ описать эту взаимосвязь как один из пропорциональных:

$P (H_ {0} | D) propto P (D | H_ {0}) P (H_ {0}).$

Поскольку P (H | D) является вероятностью, сумма по всем возможным (взаимоисключающим) гипотезам должна быть 1, что приводит к выводу, что

$П (H_ {0} | D) = { гидроразрыва {P (D | H_ {0}) P (H_ {0})} { displaystyle sum _ {i} P (D | H_ {i}) P (Здравствуй})}}.$

В этом случае взаимный ценности

$P (D) = sum _ {i} P (D | H_ {i}) P (H_ {i}) ;$

это нормализующая константа.^[5] Его можно расширить от счетного числа гипотез до несчетного числа, заменив сумму интегралом.

Невозможно использовать

В Полиномы Лежандра характеризуются ортогональность относительно равномерной меры на интервале [- 1, 1] и того факта, что они нормализованный так что их значение в 1 равно 1. Константа, на которую умножают многочлен, чтобы его значение в 1 было 1, является нормирующей константой.

Ортонормированный функции нормализованы так, что

$langle f_ {i}, , f_ {j} rangle = , delta _ {{i, j}}$

относительно некоторого внутреннего продукта <ж, г>.

Константа 1 /√2 используется для установления гиперболические функции cosh и sinh от длин соседней и противоположной сторон гиперболический треугольник.

Смотрите также

Нормализация (статистика)

Заметки

^ Непрерывное распространение в Университете Алабамы.
^ Феллер, 1968, стр. 22.
^ Феллер, 1968, стр. 174.
^ Феллер, 1968, стр. 156.
^ Феллер, 1968, стр. 124.

использованная литература

Непрерывное распространение на факультете математических наук: Университет Алабамы в Хантсвилле
Феллер, Уильям (1968). Введение в теорию вероятностей и ее приложения (том I). Джон Вили и сыновья. ISBN 0-471-25708-7.

Источник

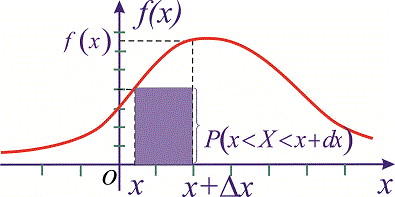
Для непрерывных случайных величин наряду с законом распределения вероятностей рассматривают плотность вероятностей, которую обозначают так .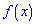

Плотностью вероятностей случайной величины 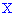называют первую производную от интегральной функции распределения вероятностей

откуда дифференциал

Поскольку прирост определяют зависимости

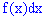
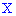
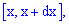
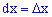
куплена плотности вероятностей на прирост случайной величины соответствует вероятность того, что случайная величина содержаться в промежутке где .

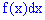
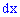
Геометрически на графике плотности вероятностей соответствует площадь прямоугольника с основанием и высотой

Свойства плотности вероятностей

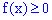
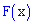
1. Плотность вероятностей принимает положительные значения . Это свойство следует из определения первой производной от функции распределения , которая в свою очередь является неубывающей функцией.

2. Условие нормирования случайной величины

3.Вероятность попадания случайной величины в промежуток 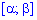определяется зависимостью

4. Функция распределения вероятностей непрерывной случайной величины определяется через плотность распределения вероятностей интегрированием

—————————————

Рассмотрим задачи для закрепления материала на практике.

Пример 1. Закон распределения случайной величины 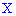заданы функцией

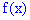
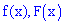
Найти плотность распределения вероятностей и построить графики обеих функций . Вычислить вероятность того, что случайная величина принадлежит промежутку

Решение. Вычисляем функцию плотности вероятностей

Графики функций 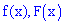изображены на рисунках

Вероятность события 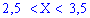вычислим по формуле

Согласно приведенной выше формулы получим

На этом задача решена.

——————————————–

Пример 2. По заданной функцией плотности распределения вероятностей

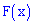
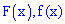
установить параметры и функцию распределения вероятностей . Построить графики функций.

Решение. Значение постоянной определяем из условия нормировки

При найденном значении плотность вероятностей будет иметь вид

Функция распределения вероятностей определяется интегрированием:

Записываем общий вид функции ,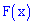

Графики функций распределения вероятностей и ее плотности показаны на рисунках ниже

—————————————

Пример 3. Случайная величина 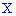имеет закон распределения вероятностей в виде треугольника

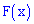
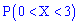
Записать выражения для плотности вероятностей и функции распределения вероятностей, построить график и вычислить .

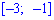
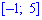
Решение. На промежутках и плотность вероятностей меняется по линейному закону вида

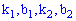
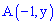
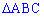
для первого и второго участки соответственно. Для нахождения неизвестных констант установим ординаты вершины треугольника . Используем условие нормирования, согласно которому площадь треугольника равна единице:

При известных координатах всех вершин находим уравнение прямых

Есть другой способ нахождения уравнения прямых, предусматривающий отыскания по одной константе на уравнение. Если известна точка пересечения прямой с осью ординат 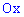, то уравнение прямой которая через эту точку проходит следующее

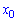
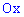
где – ордината пересечения с осью . Подстановкой второй точки прямой находят неизвестную константу . Для заданных точек получим

Со временем второй метод для Вас станет проще и практичнее в использовании. Плотность вероятностей примет значение

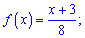
а ее функция примет вид

Функцию распределения вероятностей 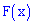находим интегрированием:

а) на промежутке :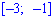

2) на промежутке

Следовательно, функция распределения вероятностей такая

Ее график приведен ниже

Вычисляем вероятность события 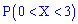согласно формуле

или

Следовательно, вероятность равна

————————-

Хорошо проанализируйте приведенные примеры – это поможет научиться быстро находить плотность распределения вероятностей и выполнять построение графика. Будьте внимательны при интегрировании и выбирайте удобную для вычислений методику.

Источник

Непрерывная случайная величина

Краткая теория

Числовые характеристики непрерывной случайной величины

Примеры решения задач

Пример 1

Пример 2

Пример 3

Задачи контрольных и самостоятельных работ

Содержание

Пример

Абсолютно непрерывные одномерные распределения

Формальное определение

Обсуждение

Дополнительные сведения

Связь между дискретным и непрерывным распределениями

Семейства плотностей

Плотности, связанные с несколькими переменными

Предельные плотности

Независимость

Следствие

Пример

Функция случайных величин и изменение переменных в функции плотности вероятности

От скаляра до скаляра

Вектор в вектор

Вектор в скаляр

Суммы независимых случайных величин

Произведения и частные независимых случайных величин

Пример: частное распределение

Пример: частное двух стандартных нормалей

See also

References

Bibliography

External links

Определение

Примеры

Теорема Байеса

Невозможно использовать

Смотрите также

Заметки

использованная литература

Вам также может понравиться

Как найти блоггеров тик ток

Узкие плечи широкие бедра у мужчин как исправить

Как найти номер карты перекресток

Добавить комментарий Отменить ответ