Как найти константу равновесия через энергию гиббса

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Понятие химического равновесия

Признаки химического равновесия

Принцип Ле Шателье

Влияние температуры на химическое равновесие

Влияние давления на химическое равновесие

Влияние концентрации на химическое равновесие

Константа химического равновесия

Примеры решения задач

Задачи для самостоятельного решения

Понятие химического равновесия

Равновесным считается состояние системы, которое остается неизменным, причем это состояние не обусловлено действием каких-либо внешних сил. Состояние системы реагирующих веществ, при котором скорость прямой реакции становится равной скорости обратной реакции, называется химическим равновесием. Такое равновесие называется еще подвижным или динамическим равновесием.

Признаки химического равновесия

1. Состояние системы остается неизменным во времени при сохранении внешних условий.
2. Равновесие является динамическим, то есть обусловлено протеканием прямой и обратной реакции с одинаковыми скоростями.
3. Любое внешнее воздействие вызывает изменение в равновесии системы; если внешнее воздействие снимается, то система снова возвращается в исходное состояние.
4. К состоянию равновесия можно подойти с двух сторон – как со стороны исходных веществ, так и со стороны продуктов реакции.
5. В состоянии равновесия энергия Гиббса достигает своего минимального значения.

Принцип Ле Шателье

Влияние изменения внешних условий на положение равновесия определяется принципом Ле Шателье (принципом подвижного равновесия): 

Если на систему, находящуюся в состоянии равновесия, производить какое–либо внешнее воздействие, то в системе усилится то из направлений процесса, которое ослабляет эффект этого воздействия, и положение равновесия сместится в том же направлении.

Принцип Ле Шателье применим не только к химическим процессам, но и к физическим, таким как кипение, кристаллизация, растворение и т. д.

Рассмотрим влияние различных факторов на химическое равновесие на примере реакции окисления NO:

2NO_(г) + O_2(г) → 2NO_2(г); ΔH^о₂₉₈ = — 113,4 кДж/моль.

Влияние температуры на химическое равновесие

При повышении температуры равновесие сдвигается в сторону эндотермической реакции, при понижении температуры – в сторону экзотермической реакции.

Степень смещения равновесия определяется абсолютной величиной теплового эффекта: чем больше по абсолютной величине энтальпия реакции ΔH, тем значительнее влияние температуры на состояние равновесия.

В рассматриваемой реакции синтеза оксида азота (IV) повышение температуры сместит равновесие в сторону исходных веществ.

Влияние давления на химическое равновесие

Сжатие смещает равновесие в направлении процесса, который сопровождается уменьшением объема газообразных веществ, а понижение давления сдвигает равновесие в противоположную сторону.

В рассматриваемом примере в левой части уравнения находится три объема, а в правой – два. Так как увеличение давления благоприятствует процессу, протекающему с уменьшением объема, то при повышении давления равновесие сместится вправо, т.е. в сторону продукта реакции – NO₂. Уменьшение давления сместит равновесие в обратную сторону. Следует обратить внимание на то, что, если в уравнении обратимой реакции число молекул газообразных веществ в правой и левой частях равны, то изменение давления не оказывает влияния на положение равновесия.

Влияние концентрации на химическое равновесие

Для рассматриваемой реакции введение в равновесную систему дополнительных количеств NO или O₂ вызывает смещение равновесия в том направлении, при котором концентрация этих веществ уменьшается, следовательно, происходит сдвиг равновесия в сторону образования NO₂. Увеличение концентрации NO₂ смещает равновесие в сторону исходных веществ.

Катализатор одинаково ускоряет как прямую, так и обратную реакции и поэтому не влияет на смещение химического равновесия.

При введении в равновесную систему (при Р = const) инертного газа концентрации реагентов (парциальные давления) уменьшаются. Поскольку рассматриваемый процесс окисления NO идет с уменьшением объема, то при добавлении инертного газа равновесие сместится в сторону исходных веществ.

Константа химического равновесия

Для химической реакции:

2NO_(г) + O_2(г) → 2NO_2(г)

константа химической реакции К_с есть отношение:

             К_с = [NO₂]²/([NO]² · [O₂])               (1)

В этом уравнении в квадратных скобках – концентрации реагирующих веществ, которые устанавливаются при химическом равновесии, т.е. равновесные концентрации веществ.

Константа химического равновесия связана с изменением энергии Гиббса уравнением:

ΔG_T^о = – RTlnK                      (2)

Примеры решения задач

Задача 1. При некоторой температуре равновесные концентрации в системе 2CO _(г) + O_{2 (г)}→2CO_{2 (г)} составляли: [CO] = 0,2 моль/л, [O₂] = 0,32 моль/л, [CO₂] = 0,16 моль/л. Определите константу равновесия при этой температуре и исходные концентрации CO и O₂, если исходная смесь не содержала СО₂.

Решение.

2CO_(г) + O_2(г) →2CO_2(г)

Вещество	CO	O2	CO2
Сисходн, моль/л	0,36	0,40	0
Спрореагир,моль/л	0,16	0,08	0,16
Сравн, моль/л	0,2	0,32	0,16

Во второй строке под С_{прореагир} понимается концентрация прореагировавших исходных веществ и концентрация образующегося CO₂, причем, С_исходн= С_{прореагир} + С_равн.

Задача 2. Используя справочные данные, рассчитайте константу равновесия процесса

3 H_{2 (г)} + N_{2 (г)} →2 NH_{3 (г)} при 298 К.

Решение.

ΔG₂₉₈^о = 2·(- 16,71) кДж = -33,42·10³ Дж.

ΔG_T^о = — RTlnK.

lnK = 33,42·10³/(8,314× 298) = 13,489. K = 7,21× 10⁵.

Задача 3. Определите равновесную концентрацию HI в системе

H_2(г) + I_2(г)  →2HI_(г),

если при некоторой температуре константа равновесия равна 4, а исходные концентрации H₂ , I₂ и HI равны, соответственно, 1, 2 и 0 моль/л.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л H_2.

Вещество	H2	I2	HI
сисходн., моль/л	1	2	0
спрореагир., моль/л	x	x	2x
cравн., моль/л	1-x	2-x	2x

Тогда,  К = (2х)²/((1-х)(2-х))

Решая это уравнение, получаем x = 0,67.

Значит, равновесная концентрация HI равна 2× 0,67 = 1,34 моль/л.

Задача 4. Используя справочные данные, определите температуру, при которой константа равновесия процесса: H_2(г) + HCOH_(г) →CH₃OH_(г) становится равной 1. Принять, что ΔН^о_Т » ΔН^о₂₉₈, а ΔS^о_T » ΔS^о₂₉₈.

Решение.

Если К = 1, то ΔG^о_T = — RTlnK = 0;

ΔG^о_T = ΔН^о₂₉₈ — ТΔ S^о₂₉₈ .

ΔН^о₂₉₈ = -202 – (- 115,9) = -86,1 кДж = — 86,1× 10³ Дж;

ΔS^о₂₉₈ = 239,7 – 218,7 – 130,52 = -109,52 Дж/К;

0 = — 86100 — Т·(-109,52) 

Т = 786,15К

Задача 5. Для реакции SO_2(Г) + Cl_2(Г)  →SO₂Cl_2(Г) при некоторой температуре константа равновесия равна 4. Определите равновесную концентрацию SO₂Cl₂, если исходные концентрации SO₂, Cl₂ и SO₂Cl₂ равны 2, 2 и 1 моль/л соответственно.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л SO_2.

SO_2(г) + Cl_2(г) →SO₂Cl_2(г)

Вещество	SO2	Cl2	SO2Cl2
cисходн., моль/л	2	2	1
cпрореагир., моль/л	x	x	х
cравн., моль/л	2-x	2-x	x + 1

Тогда получаем:

(х + 1)/(2 — х)² = 4

Решая это уравнение, находим: x₁ = 3 и x₂ = 1,25. Но x₁ = 3 не удовлетворяет условию задачи.

Следовательно, [SO₂Cl₂] = 1,25 + 1 = 2,25 моль/л.

Задачи для самостоятельного решения

1. В какой из приведенных реакций повышение давления сместит равновесие вправо? Ответ обоснуйте.

1) 2 NH_{3 (г)} → 3H_{2 (г)} + N_{2 (г)}

2) ZnCO_{3 (к)} → ZnO_(к) + CO_{2 (г)}

3) 2HBr _(г) → H_{2 (г)} + Br_{2 (ж)}

4) CO_2 (г) + C _{(графит)}  →2CO _(г)

Так как увеличение давления благоприятствует процессу, протекающему с уменьшением количества газообразных веществ, то равновесие сместится вправо в реакции 3.

2. При некоторой температуре равновесные концентрации в системе:

2HBr _(г)  →H_{2 (г)} + Br_{2 (г)}

составляли: [HBr] = 0,3 моль/л, [H₂] = 0,6 моль/л, [Br₂] = 0,6 моль/л. Определите константу равновесия и исходную концентрацию HBr.

3. Для реакции H_2(г) + S_(г)  →H₂S_(г) при некоторой температуре константа равновесия равна 2. Определите равновесные концентрации H₂ и S, если исходные концентрации H₂, S и H₂S равны, соответственно, 2, 3 и 0 моль/л.

4. Используя справочные данные, вычислите температуру, при которой константа равновесия процесса

CO_2(г) + C_{(графит)}  →2CO_(г)

становится равной 1. Примите, что ΔН^о_Т≈ΔН^о₂₉₈, а ΔS^о_T≈ΔS^о₂₉₈

5. Используя справочные данные, рассчитайте константу равновесия процесса:

С₂Н_4(г)  →С₂Н_2(г) + Н_2(г) при 298 К

6. Для реакции 2С₃Н_8(г) → н-С₅Н_12(г)+СН_4(г) при температуре 1000 К константа равновесия равна 4. Определите равновесную концентрацию н-пентана, если исходная концентрация пропана равна 5 моль/л.

7. При температуре 500 К константа равновесия процесса:

СО_2(г) + 3Н_2(г)  → СН₃ОН_(г) + Н₂О_(г)

равна 3,4·10^-5. Вычислите Δ G^о₅₀₀.

8. При температуре 800 К константа равновесия процесса н-С₆Н_14(г)+  2С₃Н_6(г)+Н_2(г) равна 8,71. Определите ΔG^о_f,800(С₃Н_6(г)), если ΔG^о_f,800(н-С₆Н_14(г)) = 305,77 кДж/моль.

9. Для реакции СО_(г) + Cl_2(г)  →СO₂Cl_2(г) при некоторой температуре равновесная концентрация СO₂Cl_2(г) равна 1,2 моль/л. Определите константу равновесия данного процесса, если исходные концентрации СО_(г) и Cl_2(г) равны соответственно 2,0 и 1,8 моль/л.

10. При некоторой температуре равновесные концентрации в системе 2SО_2(г) + О_2(г)  →2SO_3(г) составляли: [SО₂ ]=0,10 моль/л, [О₂]=0,16 моль/л, [SО₃]=0,08 моль/л. Вычислите константу равновесия и исходные концентрации SО₂ и О₂.

К=4,0; исходная концентрация SО2 составляет 0,18 моль/л; исходная концентрация О2 составляет 0,20 моль/л.

Для вычисления
энергии Гиббса реакции используется
уравнение Гиббса-Гельмгольца в виде

. (11.66)

Разделим переменные
в уравнении (11.66) и проинтегрируем
полученное выражение в интервале от
298,15 К до Т,
в результате получим:

; (11.67)

;

,

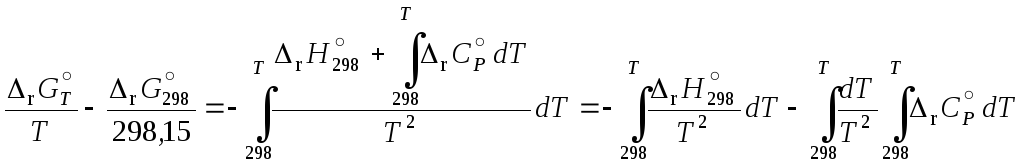
. (11.68)

Учтем, что

,

; (11.69)

,

. (11.70)

Подставим выражения
(11.69) и (11.70) в уравнение (11.68):

. (11.71)

Значения Δа,
Δb,
Δc
и Δc‘
не зависят от температуры, поэтому после
интегрирования получаем

.

Выражения, стоящие
при Δа,
Δb,
Δc
и Δc‘,
зависят только от температуры, обозначаются
M₀,
M₁,
M₂
и M_–2
соответственно и могут быть вычислены
заранее, что и сделали Темкин и Шварцман.
Значения этих коэффициентов при различных
температурах приводятся в справочниках
физико-химических величин (напр., табл.
45, стр. 92). Окончательное выражение для
расчетов имеет вид:

. (11.72)

11.12. Вычисление стандартной энергии Гиббса и константы равновесия химической реакции с помощью функции приведенной энергии Гиббса

Стандартной
приведенной энергией Гиббса (стандартным
приведенным термодинамическим
потенциалом) называется функция

или
, (11.73)

где

– стандартное значение энергии Гиббса
при температуре T;

и

– стандартные значения энтальпии при
0 и 298,15 К соответственно.

Из соотношения

следует, что при
Т
= 0 К

.

Числовые значения
стандартных энергий Гиббса и энтальпии
при 0 К неизвестны, поэтому на практике
обычно используют разности

,

которые могут быть
определены экспериментальным или
расчетным путем. Для газов значения
приведенной энергии Гиббса вычисляются
на основе молекулярных данных методом
статистической термодинамики. Для
кристаллических веществ расчет этих
величин основан на использовании данных
по теплоемкости от самых низких температур
(порядка 4 – 5 К) до заданной температуры
T.
Стандартный приведенный термодинамический
потенциал рассчитывается по уравнению

, (11.74)

где

,

.

Вычисленные
значения приведенной энергии Гиббса
приводятся в справочниках (напр., табл.
50, стр. 102 – 107).

Связь между
стандартной энергией Гиббса реакции и
изменением приведенного термодинамического
потенциала реагентов определяется
следующим выражением:

,

, (11.74)

где

– стандартная энтальпия реакции при 0
К, равная

.

Стандартные
энтальпии образования веществ при 0 К
также приводятся в справочниках (обычно
в тех же таблицах, что и приведенные
стандартные энергии Гиббса).

С учетом того, что

,

получаем выражение
для расчета стандартной константы
равновесия

,

. (11.75)

11.13. Расчет константы равновесия методом комбинирования реакций

В данном методе
используются свойства функций состояния
– их изменение не зависит от промежуточных
стадий (реакций), а определяется только
конечным и начальным состоянием системы.
Следовательно, для нахождения неизвестной
стандартной энергии Гиббса данной
реакции можно комбинировать другие
реакции с известными стандартными
энергиями Гиббса так, чтобы в сумме
получалась исследуемая реакция.

Разберем пример.
Требуется найти константу равновесия
реакции

(I),

.

Экспериментальным
путем определить константу равновесия
данной реакции трудно, поскольку давление
кислорода над оксидом никеля при
невысоких температурах очень мало. С
другой стороны, известны стандартные
энергии Гиббса (и константы равновесия)
следующих реакций:

(II),

;

(III),

.

Суммируя реакции
(II)
и (III),
получим реакцию (I).
Поэтому

, (11.76)

или

,

,

. (11.77)

Термодинамические
константы равновесия реакций приводятся
в справочниках (напр., табл. 41, стр. 63-65).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как определить константу равновесия

Константа равновесия характеризует смещение обратимой химической реакции в сторону образования продуктов реакции или исходных веществ. Вычислить константу равновесия можно различными способами, в зависимости от условий задачи.

Вам понадобится

• – ручка;
• – бумага для записей;
• – калькулятор.

Инструкция

Константу равновесия можно выразить через равновесные концентрации участников реакции – то есть концентрации веществ в момент, когда скорость прямой реакции равна скорости обратной. Пусть дана обратимая реакция веществ А и В в определенных условиях с образованием вещества С: nА+mB ↔ zС, где n, m, z – коэффициенты в уравнении реакций. Константу равновесия можно выразить: Kc = [C]^z/ ([A]^n*[B]^m), где [C], [A], [B] – равновесные концентрации веществ..

В первом типе задач требуется определить константу равновесия из равновесных концентраций веществ. Равновесные концентрации могут быть не заданы прямо. При их решении сначала запишите уравнение реакции, расставьте коэффициенты.

Пример: монооксид азота при определенных условиях реагирует с кислородом c образованием NO2. Даны начальные концентрации веществ NO и O2 – 18 моль/л и 10 моль/л. Известно, что прореагировало 60% О2. Требуется найти константу равновесия реакции.

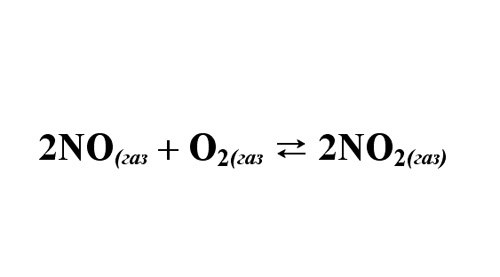
Запишите уравнение реакции, расставьте коэффициенты. Обратите внимание, в каком соотношении реагируют вещества. Вычислите концентрацию O2, вступившего в реакцию: 10моль*0,6 = 6 моль/л. Из уравнения реакции найдите концентрацию прореагировавшего NO – 12 моль/л. И концентрацию NO2 – 12 моль/л.

Определите количество не вступившего в реакцию NO: 18-12 = 6 моль. И непрореагировавшего кислорода: 10-6 = 4 моль. Вычислите константу равновесия: Кc = 12^2/(6^2*4) = 1.

Если в условии задачи указаны константы скорости прямой и обратной реакции, найдите константу равновесия из соотношения: K = k1/k2, где k1, k2 – константы скорости прямой и обратной химических реакций.

При изотермическом процессе и изобарном процессе константу равновесия можно найти из уравнения стандартного изменения энергии Гиббса: ΔGр-и = -RT*lnKc = -8,31T*2,3lgKc, где R – универсальная газовая постоянная, равная 8,31; T – температура реакции, К; lnKc – натуральный логарифм константы равновесия. Для удобства его переводят в десятичный lgKc умножением на коэффициент 2,3.

Определить изменение стандартной энергии Гиббса реакции, вы можете из уравнения для изотермического изобарного процесса: ΔG = ΔH – T ΔS, где T – температура реакции, К; ΔH – энтальпия, кДж/моль; ΔS – энтропия, Дж/(моль-град). Значение энтальпии и энтропии для 1 моля основных химических соединений при температуре 25оС даны в справочной литературе. Если температура реакции отличается от 25оС, значения энтальпии и энтропии должны быть приведены в условии задачи.

Также величину ΔG реакции при 25оС вы можете найти, сложив потенциалы образования ΔGобр каждого из продуктов реакции и вычтя из суммы ΔGобр исходных веществ. Значения потенциалов образования 25оС для 1 моля различных веществ приведены в справочных таблицах.

Обратите внимание

В случае, если участники реакции находятся в разных агрегатных состояниях, в формулу для определения константы равновесия входят концентрации веществ, находящихся в более подвижном (газ или жидкость) состоянии.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Energy can take many forms, including kinetic energy produced by an object’s movement, potential energy produced by an object’s position, heat energy transferred from one object to another due to a temperature difference, radiant energy associated with sunlight, the electrical energy produced in galvanic cells, the chemical energy stored in chemical substances, and so on. All of these different types of energy may be transformed from one form to the other.

For example, as water in a dam reservoir falls, its potential energy is turned into kinetic energy, and if the falling water is utilized to power turbines, the kinetic energy of the water is converted into electrical energy. However, if the water collides with rocks near the dam’s base. The kinetic energy of the object is transformed into thermal energy. 

As a result, the various kinds of energy are quantitatively tied to one another. Thermodynamics is the study of such quantitative relationships between various kinds of energy. Energy shifts occur as a result of physical and chemical processes. The study of energy transitions in these processes is the main focus of thermodynamics.

Thermodynamics is the branch of science that studies the many kinds of energy, their quantitative connections, and the energy changes that occur in physical and chemical processes. 

Gibbs Energy

J.W. Gibbs was an American theoretician. He introduced a new thermodynamic function called Gibbs energy denoted as G. The second law of thermodynamics states that ΔS_total = (ΔS_system + ΔS_Surrounding) must be positive for all spontaneous processes. To assess the spontaneity of a process, two entropy changes, ΔS_System and ΔS_Surrounding must be determined. As a result, it is more straightforward to describe the criteria of spontaneity in terms of the system’s thermodynamic features alone, without respect for the surroundings and this problem was solved by Gibbs.

Gibbs energy (G) is defined as,

G = H – TS

where:

• S is the entropy of the system,
• H is Enthalpy, and
• T is the Temperature.

G is also a state function because, H, T, and S are state functions. 

The change in Gibbs Energy (ΔG) on the initial and final state of the system and not on the path connecting the two states. The change in Gibbs energy at constant temperature and pressure is defined as:

ΔG = ΔH – T ΔS

where:

• ΔS is the change in entropy of the system and
• ΔH is the change in Enthalpy.

Gibbs Energy and Spontaneity

The total entropy change can be written as,

ΔS_total = ΔS_system + ΔS_surrounding = ΔS + ΔS_surr

According to the second law of thermodynamics, ΔS_total > 0 at constant temperature and pressure for the process to be spontaneous. If ΔH is the enthalpy change accompanying the reaction, that is the enthalpy change of the system then the change in enthalpy of the surroundings is (-ΔH)

Therefore,

ΔS_surr = -ΔH / T

Hence the total entropy is given by,

ΔS_total = ΔS – ΔH / T   

This equation shows that ΔS_total is expressed in terms of the properties of the system only.

Rearranging the equation we get,

-T ΔS_total = -T ΔS + ΔH

or

-T ΔStotal = ΔH -T ΔS 

Combining the above two equations, we get,

ΔG = -T ΔS_total    

This equation indicates that ΔG and ΔS_total have opposite signs because T is always positive. Thus, for a spontaneous process carried out at a constant temperature and pressure ΔS_total  > 0 and hence ΔG < 0.

Gibbs energy of a system decreases in a spontaneous change that takes place at constant temperature and pressure. On contrary, for a non-spontaneous reaction ΔS_total and hence ΔG > 0.

Gibbs energy of a system increases in a non-spontaneous change that takes place at constant temperature and pressure. The end of the spontaneous process is an equilibrium that corresponds to a minimum in G. Hence the change in Gibbs energy is:

• ΔG < 0, the process is spontaneous.
• ΔG > 0, the process is non-spontaneous.
• ΔG = 0, the process is at equilibrium.

Factor affecting the Spontaneity

Consider the equation,

ΔG = ΔH – T ΔS

The value ΔG determines whether a physical or chemical change will occur spontaneously. The equations ΔH and ΔS correspond to the values of the system alone. The equation states that two elements influence the spontaneity of reactions

• ΔH is the amount of heat transmitted at constant pressure and temperature, and
• ΔS is the rise or reduction in molecular disorder.

The spontaneous process is favoured by a decrease in enthalpy (-ΔH) and increase in entropy (ΔS) On the other hand non-spontaneous reaction is favoured by an increase in enthalpy (+ΔH) and decrease in entropy (-ΔS). The term temperature in the equation is an important component in determining the relative relevance of the enthalpy and entropy contributions to ΔG. If ΔH and ΔS in the equation are both positive or both negative, the sign of ΔG and hence the spontaneity of the reaction, depends on temperature. 

ΔH	ΔS	ΔG	Spontaneity of reaction
Negative (exothermic)	Positive	Negative	Reactions are spontaneous at all temperatures.
Negative (exothermic)	Negative	Negative or Positive	Reactions become spontaneous at low temperatures when |T. ΔS| < |ΔH|.
Positive (endothermic)	Positive	Negative or Positive	Reactions become spontaneous at low temperatures when T.ΔS < ΔH.
Positive (endothermic)	Negative	Positive	Reactions are non-spontaneous at all temperatures.

Temperature of Equilibrium

At equilibrium, i.e., ΔG = 0, the process is neither spontaneous nor non-spontaneous because it is balanced between spontaneous and non-spontaneous behavior. (+ΔH)

So, 

ΔG = ΔH – T ΔS = 0

Hence,

ΔH = TΔS or T = ΔH / ΔS

T is the temperature at which the transition from spontaneous to non-spontaneous behavior happens. T is calculated on the assumption that ΔH and ΔS are temperature independent. In reality, ΔH and ΔS change with temperature. However, for modest temperature changes, the variance in them will not add considerable mistakes. 

ΔG and Equilibrium constant

All of the substances (reactants and products) in a chemical reaction may not be in their normal forms. As a result of the connection, the change in Gibbs energy of a reaction is related to the change in standard Gibbs energy. 

ΔG = ΔG° + RT ln Q

where:

• ΔG° is the standard Gibbs energy change (change in Gibbs energy when all the substances are in their standard state).
• Q is the reaction quotient.

The expression of the reaction quotient is similar to that of the equilibrium constant, but there is one single difference between them, i.e., Equilibrium concentrations or partial pressures of products and reactants are included in the equilibrium constant. Whereas Q is expressed in terms of reactant beginning concentration partial pressures and product final concentrations or pressures. 

For Example, consider the below example:

aA +bB ⇢ cC + dD

For the above reaction, the reaction Quotient is given by 

or

When the values of concentration or partial pressure are other than equilibrium values. When the reaction reaches equilibrium, the concentrations and partial pressure reach their equilibrium values and at this stage, Q = K. At equilibrium, ΔG = 0 and Q = K, then the standard Gibbs energy equation becomes,

0 = ΔG° + RT ln K

Hence,

ΔG° = -RT ln K = -2.303RT log₁₀K

This equation gives the relationship between standard Gibbs energy change for the reaction and its equilibrium constant.

Sample Problems

Problem 1: Determine whether the reaction is spontaneous or non-spontaneous for the given value of ΔH and ΔS. Also, state whether they are exothermic or endothermic.

• ΔH = – 40 kJ and ΔS = +135 JK^-1 at 300K
• ΔH = – 60 kJ and ΔS = -160 JK^-1 at 400K

Solution:

• ΔG = ΔH – T ΔS

 ΔH = – 40 kJ,  ΔS = +135 J K^-1 = 0.135 kJ K^-1 and T = 300K

 ΔG = -40 (kJ) – 0.135(kJ K^-1) × 300(K)

= 80.5 kJ

Because ΔG is negative, the reaction is spontaneous. The negative ΔH value indicates that the reaction is exothermic.

• ΔG = ΔH – T ΔS

ΔH = – 60 kJ,  ΔS = – 160 J K^-1 = – 0.160 kJ K^-1 and T = 400K

 ΔG = -60 (kJ) – 0.160(kJ K^-1) × 400(K)

 = -60 kJ + 64 kJ = 4kJ

The reaction is non-spontaneous because ΔG is positive and exothermic as ΔH is negative.

Problem 2: For a certain reaction ΔH = -25kJ and ΔS = -40J K^-1. At what temperature will it change from spontaneous to non-spontaneous.

Solution;

T = ΔH / ΔS

 ΔH = – 25 kJ,  ΔS = -40 J K^-1  = 0.04 kJ K-1 

Hence, T = -25(kJ) / -0.04 kJ K^-1  = 625K

Because both ΔH and ΔS are negative, the reaction will occur spontaneously at lower temperatures. As a result, the reaction will be spontaneous below 625K and non-spontaneous beyond 625K.

At 625K, the transition from spontaneous to non-spontaneous occurs.

Problem 3: Determine  ΔS_total and decide whether the following reaction is spontaneous at 298K.

ΔH° = -24.8 kJ, ΔS° = 15 J K^-1

Solution: 

The heat evolved in the reaction is 24.8 kJ. The same quantity of heat is absorbed by the surroundings. 

Hence, Entropy change of the surrounding will be,

ΔS_surr = ΔH° / T

= – [(-24.8 (kJ)) / 298 (K)]

= + 83.2 J K^-1

ΔS_total = ΔS_System + ΔS_Surr 

ΔS_Sys = ΔS° = 15 J K^-1

 = 15(J K^-1) + 83.2 (J K^-1)

= 98.2 J K^-1

As ΔS_total is positive, the reaction is spontaneous at 298 K.

Problem 4: Determine whether the reaction,

N₂​O₄ ​(g)⟶2NO₂​ (g)

is spontaneous at 298 K from the following data.

Δ_fH° (N₂O₄) = 9.16 kJ mol^-1, Δ_fH° (NO₂) = 33.2 kJ mol^-1

Solution: 

ΔH=∑Δf​H°(products)−∑Δf​H°(reactants

= 2 × Δ_fH° (NO₂) – Δ_fH° (N₂O₄)

= 2(mol) × 33.2(kJ mol^-1) -1(mol) × 9.16(kJ mol^-1)

= +57.24 kJ

ΔG° = ΔH° – TΔS°

57.24(kJ) – 298(K) × 175.8 × 10^-3 (kJ K^-1)

= +4.85 kJ.

Because ΔG° is positive, the reaction is non-spontaneous at 298 K. 

The temperature at which the reaction changes from spontaneous to non-spontaneous is given by,

T = ΔH° / ΔS°

= 57.24(kJ) / 0.1758(kJ K^-1)

= 325.6 K

Because ΔH° and ΔS° are both positive, the reaction will be spontaneous at high temperature.

The reaction will be spontaneous above 325.6 K.

Problem 5: Determine K_p for the reaction,

2SO₂​(g) + O₂​(g) ⟶ 2SO_3​(g)

is 7.1 × 10²⁴ at 298 K. Calculate ΔG° for the reaction (R = 8.314 JK^-1 mol^-1).

Solution:

ΔG° = -2.303RT log₁₀ K_p

K_p = 7.1 × 10²⁴ 

R = 8.314 JK^-1 mol^-1

T = 298K

Hence,

  ΔG°  = -2.303 × 8.314 × 10^-3 (kJ K^-1 mol^-1) ×  log₁₀ (7.1 ×  10²⁴)

          = -141.8 kJ mol^-1

Problem statement 6: Calculate K_p for the reaction at 513 K,

2NOCl (g) ⟶ 2NO(g) + Cl₂​(g)

with ΔG° = 17.38 kJ mol^-1.

Solution:

ΔG° = -2.303 RT log₁₀ K_p

ΔG° = 17.38 kJ mol^-1

R = 8.314 J K^-1 mol^-1

T = 513K

Hence,

log₁₀ k_p = – ΔG° / 2.303 RT

             = – (17380(J mol^-1) / 2.303 × 8.314 ( J K^-1 mol^-1) × 513(K))

             = -1.769

Hence, K_p = antilog(-1.769)

                = 0.017