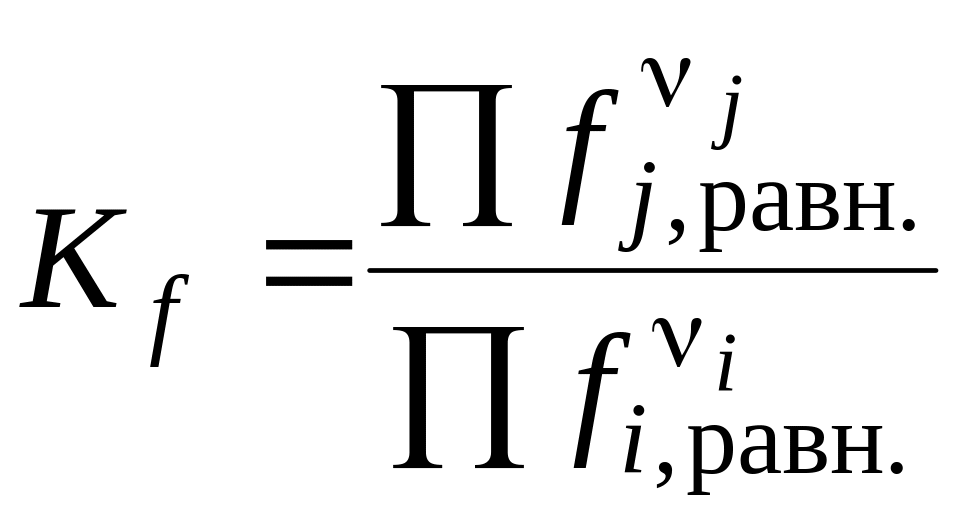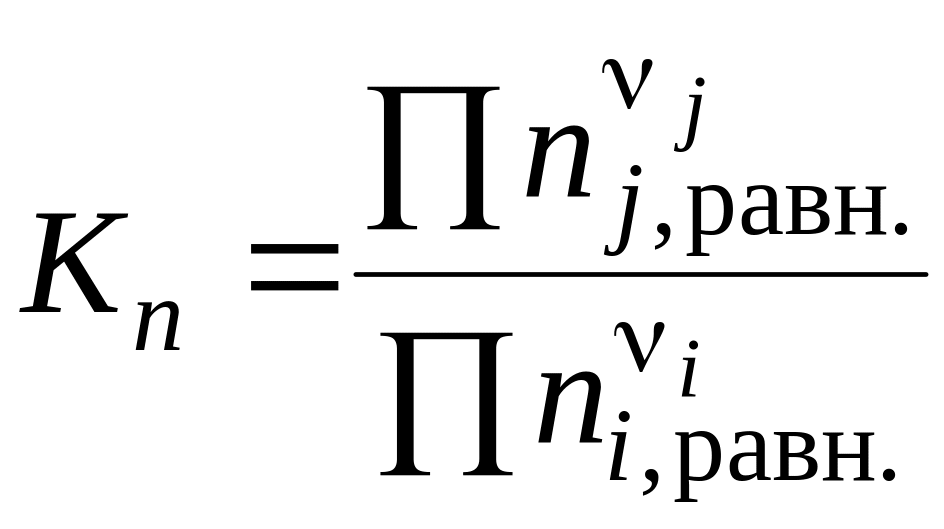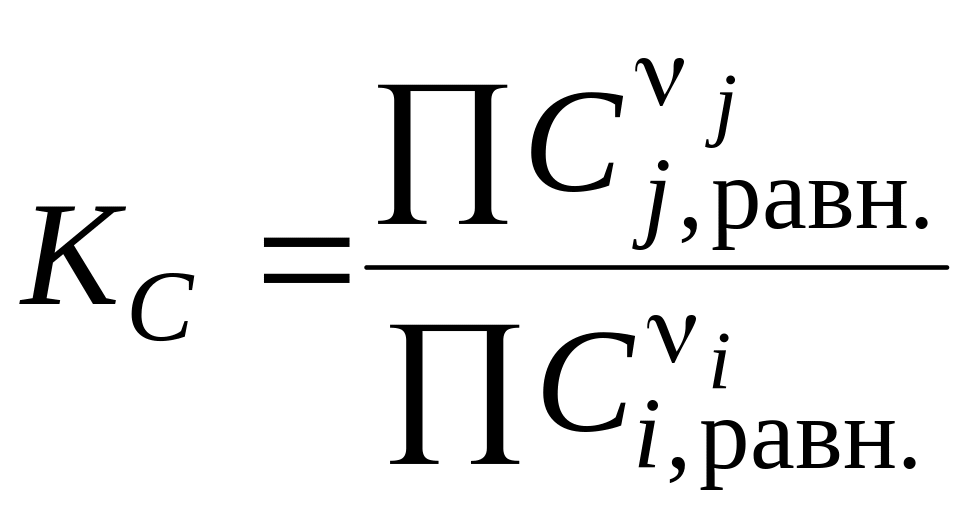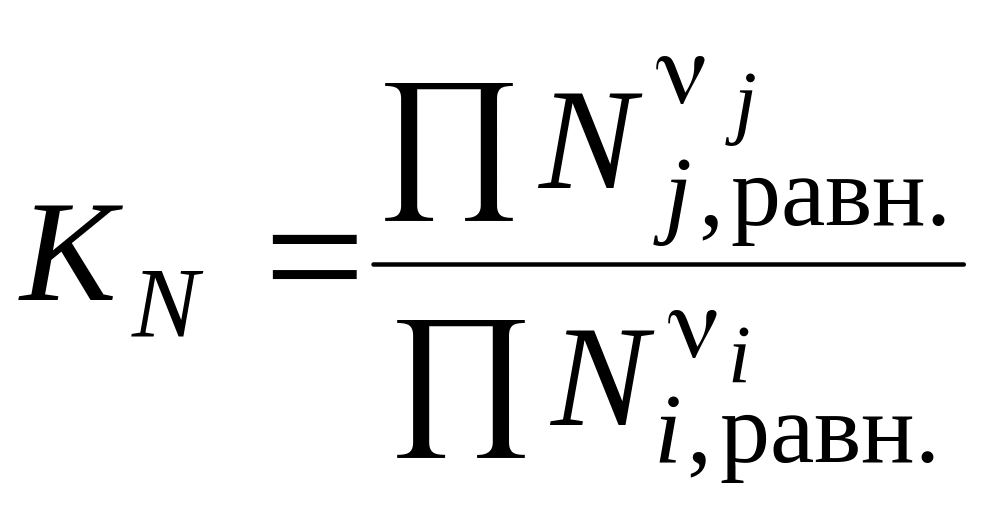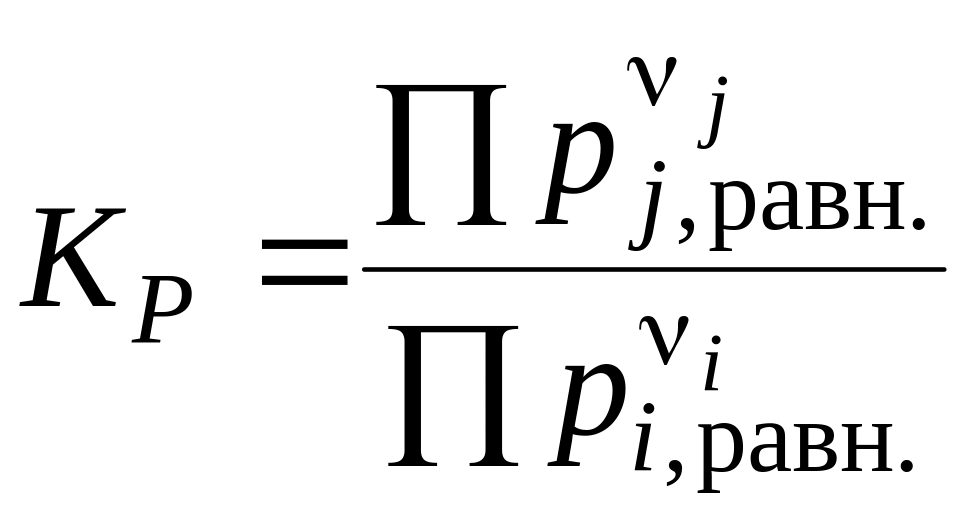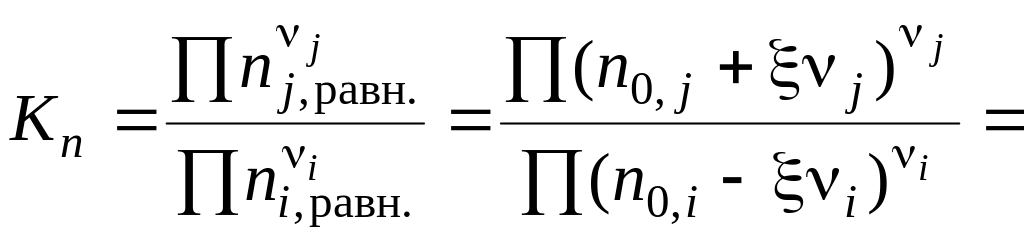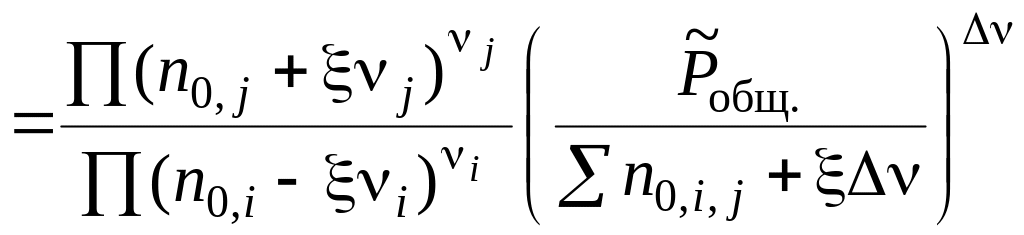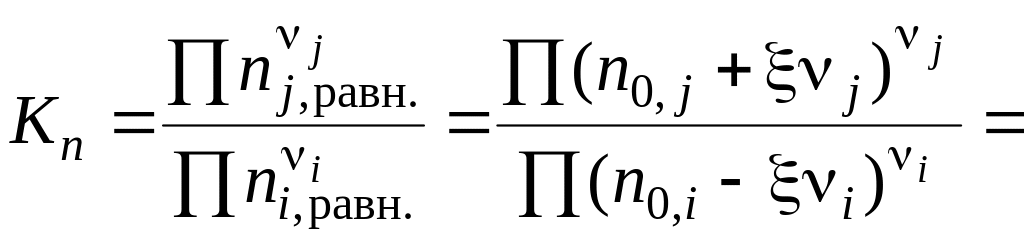Как найти константу равновесия в термодинамике - Сайт, где вы сможете решить свои вопросы

У этого термина существуют и другие значения, см. Константа.

Конста́нта равнове́сия — величина, определяющая для данной химической реакции соотношение между термодинамическими активностями (либо, в зависимости от условий протекания реакции, парциальными давлениями, концентрациями или фугитивностями) исходных веществ и продуктов в состоянии химического равновесия (в соответствии с законом действующих масс). Зная константу равновесия реакции, можно рассчитать равновесный состав реагирующей смеси, предельный выход продуктов, определить направление протекания реакции.

Способы выражения константы равновесия[править | править код]

Для реакции в смеси идеальных газов константа равновесия может быть выражена через равновесные парциальные давления компонентов $p_{i}$ по формуле^[1]:

${displaystyle K_{p}=prod p_{i}^{{nu }_{i}},}$

где $nu _{i}$ — стехиометрический коэффициент (для исходных веществ принимается отрицательным, для продуктов — положительным). ${displaystyle K_{p}}$ не зависит от общего давления, от исходных количеств веществ или от того, какие участники реакции были взяты в качестве исходных, но зависит от температуры^[2].

Например, для реакции окисления монооксида углерода:

${displaystyle mathrm {2CO} +mathrm {O} _{2}=mathrm {2CO} _{2}}$

константа равновесия может быть рассчитана по уравнению:

${displaystyle K_{p}={frac {p_{mathrm {CO} _{2}}^{2}}{p_{mathrm {CO} }^{2}cdot p_{mathrm {O} _{2}}}}}$

Если реакция протекает в идеальном растворе и концентрация компонентов выражена через молярность $c_{i}$ , константа равновесия принимает вид:

${displaystyle K_{c}=prod c_{i}^{{nu }_{i}}.}$

Для реакций в смеси реальных газов или в реальном растворе вместо парциального давления и концентрации используют соответственно фугитивность $f_{i}$ и активность $a_{i}$ :

${displaystyle K_{f}=prod f_{i}^{{nu }_{i}}}$

${displaystyle K_{a}=prod a_{i}^{{nu }_{i}}}$

В некоторых случаях (в зависимости от способа выражения) константа равновесия может являться функцией не только температуры, но и давления. Так, для реакции в смеси идеальных газов парциальное давление компонента может быть выражено по закону Дальтона через суммарное давление и мольную долю компонента ( $p_{i}=Pcdot x_{i}$ ), тогда легко показать^[2], что:

${displaystyle K_{p}=K_{x}P^{Delta n},}$

где — изменение числа молей веществ в ходе реакции. Видно, что ${displaystyle K_{x}}$ зависит от давления. Если число молей продуктов реакции равно числу молей исходных веществ (), то $K_{p}=K_{x}$ .

Часто вместо самой константы равновесия ${displaystyle K_{p}}$ используют показатель константы равновесия ${displaystyle mathrm {p} K_{mathrm {p} }}$ , который определяется как отрицательный десятичный логарифм константы ${displaystyle K_{p}}$ :

${displaystyle mathrm {p} K_{mathrm {p} }=-lg left(K_{mathrm {p} }right).}$

Стандартная константа равновесия[править | править код]

Стандартная константа равновесия реакции в смеси идеальных газов (когда начальные парциальные давления участников реакции равны их значениям в стандартном состоянии ${displaystyle p_{i}^{0}=0{,}1013}$ МПа или 1 атм) может быть рассчитана по выражению:

${displaystyle K^{0}=prod ({tilde {p_{i}}})^{v_{i}},}$

где ${tilde {p_{i}}}$ — относительные парциальные давления компонентов, ${tilde {p_{i}}}=p_{i}/p_{i}^{0}$ .

Стандартная константа равновесия — безразмерная величина. Она связана с ${displaystyle K_{p}}$ соотношением:

${displaystyle K_{p}=K^{0}(p_{i}^{0})^{Delta n}.}$

Видно, что если $p_{i}^{0}$ выражены в атмосферах, то $(p_{i}^{0})^{{Delta n}}=1$ и ${displaystyle K_{p}=K^{0}}$ .

Для реакции в смеси реальных газов в стандартном начальном состоянии парциальные фугитивности газов принимаются равными их парциальным давлениям ${displaystyle f_{i}^{0}=p_{i}^{0}=0{,}1013}$ МПа или 1 атм. K_f связана с $K_{0}$ соотношением:

${displaystyle K_{f}=K^{0}(gamma _{i}p_{i}^{0})^{Delta n},}$

где ${displaystyle gamma _{i}}$ — коэффициент фугитивности -го реального газа в смеси.

Константа равновесия реакций в гетерогенных системах[править | править код]

Для гетерогенной химической реакции, например, между компонентами реального газа и реального раствора, константа равновесия в общем случае может быть выражена уравнением:

${displaystyle K_{fa}=~prod (f_{i}^{nu _{i}}a_{k}^{nu _{k}}),}$

где $f_{i}$ — фугитивность компонентов газовой фазы, а $a_{k}$ — активность компонентов конденсированной фазы.

Если конденсированные фазы (твёрдые или жидкие) представляют собой практически чистые вещества, их активности постоянны и могут быть включены в константу равновесия (то есть в левую часть выражения выше). Условно можно принять их равными единице и, таким образом, исключить из выражения.

Например, для реакции твёрдофазного восстановления оксида железа:

${displaystyle mathrm {FeO} mathrm {(sol)} +mathrm {CO} mathrm {(gas)} =mathrm {Fe} mathrm {(sol)} +mathrm {CO} _{2}mathrm {(gas)} }$

константа равновесия (при условии, что газовая фаза идеальна) имеет вид:

${displaystyle K_{p}={frac {p_{mathrm {CO} _{2}}}{p_{mathrm {CO} }}}}$

Термодинамическое описание равновесия[править | править код]

Наряду с обозначением для соотношения активностей веществ в произвольный момент реакции («коэффициент реакции»)

${displaystyle Q_{r}={frac {left{C_{t}right}^{sigma }left{D_{t}right}^{tau }}{left{A_{t}right}^{alpha }left{B_{t}right}^{beta }}}={frac {prod a_{j(t)}^{nu _{j}}}{prod a_{i(t)}^{nu _{i}}}}=prod a_{n(t)}^{nu _{n}}}$

(обозначения для приведённой ниже реакции; последнее равенство написано в обозначении, что стехиометрические коэффициент берутся со знаком «+» для продуктов и со знаком «−» для исходных веществ)

в химической термодинамике используется обозначение ${displaystyle K_{mathrm {eq} }}$ для такого же по форме соотношения между равновесными активностями веществ

${displaystyle K_{mathrm {eq} }={frac {[C]^{sigma }[D]^{tau }}{[A]^{alpha }[B]^{beta }}}={frac {prod a_{j(t=infty )}^{nu _{j}}}{prod a_{i(t=infty )}^{nu _{i}}}}=prod a_{n(t=infty )}^{nu _{n}}}$

(то есть соотношения активностей в момент t=infty

, в момент равновесия). Далее приведено термодинамическое описание химического равновесия и описана связь ${displaystyle K_{mathrm {eq} }}$

со стандартной энергией Гиббса процесса.

В системе, где протекает химическая реакция

{displaystyle alpha A+beta Brightleftharpoons sigma C+tau D}

равновесие может быть описано условием

${displaystyle left({frac {dG}{dxi }}right)_{T,p}=0,}$

где есть химическая переменная

или, то же самое условие равновесия может быть записано с использованием химических потенциалов как

${displaystyle alpha mu _{A}+beta mu _{B}=sigma mu _{C}+tau mu _{D},}$

где химические потенциалы

${displaystyle mu _{A}=mu _{A}^{ominus }+RTln{A},}$

здесь {A} — строго говоря, активность реагента A; при допущениях об идеальных газах можно заменить их на давления, для реальных газов можно заменить на фугитивности, при допущении о том, что раствор подчиняется закону Генри, можно заменить на мольные доли, и при допущении, что раствор подчиняется закону Рауля — на парциальные давления; для системы в равновесии может быть заменена на равновесную молярную концентрацию или на равновесную активность.

Выражение для энергии Гиббса принимает вид

${displaystyle dG=Vdp-SdT+sum _{i=1}^{k}mu _{i}dN_{i},}$

а так как ${displaystyle dN_{i}=nu _{i}dxi }$ , можно записать выражение для производной изобарного потенциала по химической переменной в виде

${displaystyle left({frac {dG}{dxi }}right)_{T,p}=sum _{i=1}^{k}mu _{i}nu _{i}=Delta _{r}G_{T,p}=sigma mu _{C}+tau mu _{D}-alpha mu _{A}-beta mu _{B}=(sigma mu _{C}^{0}+tau mu _{D}^{0})-(alpha mu _{A}^{0}+beta mu _{B}^{0})+(sigma RTln{C}+tau RTln{D})-(alpha RTln{A}+beta RTln{B})=}$

${displaystyle =sum _{i=1}^{k}mu _{i}^{0}nu _{i}+RTln {frac {{C}^{sigma }{D}^{tau }}{{A}^{alpha }{B}^{beta }}}=Delta _{r}G^{0}+RTln Q_{r}.}$

При равновесии (иначе говоря, при условии что время )

${displaystyle Q_{r}=K_{mathrm {eq} }.}$

Записав теперь условие равновесия ${displaystyle Delta _{r}G=0=Delta _{r}G^{0}+RTln K_{mathrm {eq} }}$ найдём связь ${displaystyle K_{mathrm {eq} }}$ со стандартной энергией Гиббса^[3]:

${displaystyle Delta _{r}G^{0}=-RTln K_{mathrm {eq} }.}$

Равновесный состав смеси и направление реакции[править | править код]

Упомянутый выше «коэффициент реакции» (другие обозначения, встречающиеся в литературе — Omega или — «произведение реакции»)

$Q_{r}=prod a_{{n(t)}}^{{nu _{n}}}$

отражает соотношение текущих активностей всех участников реакции и может быть использован для определения направления реакции в момент, для которого известен ^[4]

Если в момент

коэффициент Q>K

, то текущие активности продуктов больше равновесных, и значит они должны уменьшиться к тому моменту, когда установится равновесие, то есть в данный момент протекает обратная реакция;

Если

, то равновесное состояние достигнуто и скорости прямой и обратной реакций равны;

Если

, то $v_{{1}}>v_{{-1}}$

С использованием величины $Q_{r}$ записывается уравнение изотермы химической реакции^[1] (изотермы Вант-Гоффа)

${displaystyle Delta G_{p,T}=RTln Q_{r}-RTln K_{mathrm {eq} }=RTln {frac {Q_{r}}{K_{mathrm {eq} }}}=sum nu _{i}mu _{i},}$

где — стехиометрические коэффициенты (для продуктов — со знаком «+», для исходных веществ — со знаком «−»; так же, как и в выражениях для и ), а — химические потенциалы,

а стандартная энергия Гиббса и стандартная константа суть

${displaystyle Delta G_{p,,T}^{0}=-RTln K_{mathrm {eq} }^{0}=sum nu _{i}mu _{i}^{0},}$

где ${displaystyle mu ^{0}}$ — стандартные химические потенциалы

Уравнение изотермы показывает, как величина связана с изменением свободной энергии реакции:

при

для прямой реакции

, то есть $sum nu _{{j}}mu _{{j}}$

для продуктов прямой реакции больше, чем для исходных веществ — это означает, что прямая реакция запрещена (значит, не запрещена обратная);

при

для прямой реакции

, то есть реакция достигла равновесного состояния;

при

для прямой реакции

, то есть эта самопроизвольное протекание этой реакции разрешено

Величина ${displaystyle K_{mathrm {eq} }}$ по определению имеет смысл только для состояния равновесия, то есть для состояния с ${frac {v_{{1}}}{v_{{-1}}}}=1$ и $Delta G_{r}=0$ . Величина ${displaystyle K_{mathrm {eq} }}$ ничего не говорит о скоростях реакций, но она описывает состав системы в состоянии равновесия.

Если

, то в системе преобладают продукты (прямой) реакции.

Если

, то в системе преобладают исходные вещества (продукты обратной реакции)^[5].

Стандартные состояния[править | править код]

Стандартная энергия Гиббса реакции в газовой смеси — энергия Гиббса реакции при стандартных парциальных давлениях всех компонентов, равных 0,1013 МПа (1 атм).

Стандартная энергия Гиббса реакции в растворе — энергия Гиббса при стандартном состоянии раствора, за которое принимают гипотетический раствор со свойствами предельно разбавленного раствора, но с концентрацией всех реагентов, равной единице.

Для чистого вещества и жидкости стандартная энергия Гиббса совпадает с энергией Гиббса образования этих веществ.

Величина стандартной энергии Гиббса реакции может быть использована для приближенной оценки термодинамической возможности протекания реакции в данном направлении, если начальные условия не сильно отличаются от стандартных. Кроме того, сравнивая величины стандартной энергии Гиббса нескольких реакций, можно выбрать наиболее предпочтительные, для которых $Delta G_{T}^{0}$ имеет наибольшую по модулю отрицательную величину.

Кинетическое описание[править | править код]

Для обратимой химической реакции константа равновесия ${displaystyle K_{mathrm {eq} }}$ может быть выражена через константы скорости прямых и обратных реакций.
Рассмотрим элементарную обратимую химическую реакцию первого порядка

{displaystyle mathrm {A} rightleftarrows mathrm {B} }

По определению, равновесие задаётся условием $v_{{1}}=v_{{-1}}$ , то есть равенством скоростей прямой и обратной реакций.

В соответствии с законом действующих масс

${displaystyle v=k{prod }{a_{j}}^{n_{j}},}$

где — константа скорости соответствующей реакции, а ${a_{j}}^{{n_{j}}}$ — равновесные активности реагентов этой реакции, возведённые в степени, равные их стехиометрическим коэффициентам

можно записать условие равновесия в виде

${displaystyle 1={frac {v_{1}}{v_{-1}}}={frac {k_{1}{prod }{a_{A}}^{n_{A}}}{k_{-1}{prod }{a_{B}}^{n_{B}}}}.}$

То есть

${displaystyle 1={frac {k_{1}}{k_{-1}}}cdot {frac {prod {a_{A}}^{n_{A}}}{prod {a_{B}}^{n_{B}}}}={frac {k_{1}}{k_{-1}}}cdot left(K_{mathrm {eq} }right)^{-1}}$

(см. термодинамическое описание константы равновесия), что возможно только если

${displaystyle K_{mathrm {eq} }={frac {k_{1}}{k_{-1}}}}$

Это важное соотношение даёт одну из «точек соприкосновения» химической кинетики и химической термодинамики^[4]^[6].

Множественные равновесия[править | править код]

В случае, когда в системе устанавливается сразу несколько равновесий (то есть одновременного или последовательного протекает нескольких процессов), каждый из них может быть охарактеризован своей константой равновесия, из которых можно выразить общую константу равновесия для всей совокупности процессов. Можно рассмотреть такую ситуацию на примере ступенчатой диссоциации двухосновной кислоты ${displaystyle mathrm {H} _{2}mathrm {A} }$ . Водный раствор её будет содержать частицы (сольватированные) ${displaystyle mathrm {H} ^{+}}$ , ${displaystyle mathrm {H} _{2}mathrm {A} }$ , ${displaystyle mathrm {HA} ^{-}}$ и ${displaystyle mathrm {A} ^{2-}}$ . Процесс диссоциации протекает в две ступени:

${displaystyle mathrm {H} _{2}mathrm {A} rightleftharpoons mathrm {HA} ^{-}+mathrm {H} ^{+}:K_{1}={frac {[mathrm {HA} ^{-}][mathrm {H} ^{+}]}{[mathrm {H} _{2}mathrm {A} ]}}}$

${displaystyle mathrm {HA} ^{-}rightleftharpoons mathrm {A} ^{2-}+mathrm {H} ^{+}:K_{2}={frac {[mathrm {A} ^{2-}][mathrm {H} ^{+}]}{[mathrm {HA} ^{-}]}}}$

K_1 и $K_{2}$ — константы первой и второй ступеней диссоциации соответственно. Из них можно выразить «полную» константу равновесия, для процесса полной диссоциации^[5]:

${displaystyle mathrm {H} _{2}mathrm {A} rightleftharpoons mathrm {A} ^{2-}+2mathrm {H} ^{+}:K_{1+2}={frac {[mathrm {A} ^{2-}][mathrm {H} ^{+}]^{2}}{[mathrm {H} _{2}mathrm {A} ]}}=K_{1}K_{2}}$

Другой пример множественного равновесия — анализ системы осадок/растворимое комплексное соединение.

Допустим, имеется равновесие

${displaystyle mathrm {AgI} _{2}^{-}mathrm {(aq)} rightleftharpoons mathrm {AgI} mathrm {(solid)} +mathrm {I} ^{-}mathrm {(aq)} }$

Реакцию можно представить в виде двух последовательных равновесий — равновесия разложения комплексного иона на составляющие его ионы, которое характеризуется «константой нестойкости» (величина, обратная «константе устойчивости» beta ):

${displaystyle mathrm {AgI} _{2}^{-}mathrm {(aq)} rightleftharpoons mathrm {Ag} ^{+}mathrm {(aq)} +2mathrm {I} ^{-}mathrm {(aq)} :K_{1}={frac {alpha _{mathrm {Ag} ^{+}}alpha _{mathrm {I} ^{-}}^{2}}{alpha _{mathrm {AgI} _{2}^{-}}}}=beta ^{-1}}$

и равновесия перехода ионов из объёма растворителя в кристаллическую решётку

${displaystyle mathrm {Ag} ^{+}mathrm {(aq)} +mathrm {I} ^{-}mathrm {(aq)} rightleftharpoons mathrm {AgI} mathrm {(solid)} :K_{2}={frac {alpha _{mathrm {AgI} }}{alpha _{mathrm {Ag} ^{+}}alpha _{mathrm {I} ^{-}}}}}$

с учётом того, что для твёрдых веществ активность принимается равной 1, а в разбавленных растворах активности могут быть заменены на молярные концентрации, получаем

${displaystyle K_{2}={frac {alpha _{mathrm {AgI} }}{alpha _{mathrm {Ag} ^{+}}alpha _{mathrm {I} ^{-}}}}={frac {1}{[mathrm {Ag} ^{+}][mathrm {I} ^{-}]}}={frac {1}{K_{mathrm {sp} }}},}$

где ${displaystyle K_{mathrm {sp} }}$ — произведение растворимости

Тогда суммарное равновесие будет описываться константой

${displaystyle mathrm {AgI} _{2}^{-}mathrm {(aq)} rightleftharpoons mathrm {AgI} mathrm {(solid)} +mathrm {I} ^{-}mathrm {(aq)} :K={frac {alpha _{mathrm {AgI} }alpha _{mathrm {I} ^{-}}}{alpha _{mathrm {AgI} _{2}^{-}}}}=K_{1}cdot K_{2}={frac {1}{beta cdot K_{mathrm {sp} }}}}$

И значение этой константы будет условием преобладания в равновесной смеси комплексного соединения или твёрдой соли: как и выше, если , то в равновесной смеси большая часть ионов связана в комплексное соединение, если , то в равновесном состоянии в системе большая часть ионов связана в кристаллической фазе.^[4]

Зависимость константы равновесия от температуры[править | править код]

Зависимость константы равновесия реакции от температуры может быть описана уравнением изобары химической реакции (изобары Вант-Гоффа):

${displaystyle dln K_{p}={frac {Delta H}{RT^{2}}}dT}$

и изохоры химической реакции (изохоры Вант-Гоффа):

${displaystyle dln K_{c}={frac {Delta U}{RT^{2}}}dT}$

Здесь Delta H и Delta U — тепловой эффект реакции, протекающей, соответственно, при постоянном давлении или при постоянном объёме. Если (тепловой эффект положителен, реакция эндотермическая), то температурный коэффициент константы равновесия ${frac {dln K_{p}}{dT}}$ тоже положителен, то есть с ростом температуры константа равновесия эндотермической реакции увеличивается, равновесие сдвигается вправо (что вполне согласуется с принципом Ле Шателье).

Методы расчета константы равновесия[править | править код]

Расчётные методы определения константы равновесия реакции обычно сводятся к вычислению тем или иным способом стандартного изменения энергии Гиббса в ходе реакции ( ${displaystyle Delta G^{0}}$ ), а затем использованию формулы:

${displaystyle Delta G^{0}=-RTln K^{0}}$

, где

— универсальная газовая постоянная.

При этом следует помнить, что энергия Гиббса — функция состояния системы, то есть она не зависит от пути процесса, от механизма реакции, а определяется лишь
начальным и конечным состояниями системы. Следовательно, если непосредственное определение или расчёт ${displaystyle Delta G^{0}}$ для некоторой реакции по каким-либо причинам затруднены, можно подобрать такие промежуточные реакции, для которых ${displaystyle Delta G^{0}}$ известно или может быть легко определено, и суммирование которых даст рассматриваемую реакцию (см. Закон Гесса). В частности, в качестве таких промежуточных реакций часто используют реакции образования соединений из элементов.

Энтропийный расчёт изменения энергии Гиббса и константы равновесия реакции[править | править код]

Энтропийный метод расчёта Delta G реакции является одним из самых распространённых и удобных^[2]. Он основан на соотношении:

${displaystyle Delta G_{T}=Delta H_{T}-TDelta S_{T}}$

или, соответственно, для стандартного изменения энергии Гиббса:

${displaystyle Delta G_{T}^{0}=Delta H_{T}^{0}-TDelta S_{T}^{0}}$

Здесь $Delta H^{0}$ при постоянных давлении и температуре равно тепловому эффекту реакции, методы расчёта и экспериментального определения которого известны — см., например, уравнение Кирхгофа:

$Delta H_{T}^{0}=Delta H_{{298}}^{0}+int _{{298}}^{T}Delta C_{p}dT$

Необходимо получить изменение энтропии в ходе реакции. Эта задача может быть решена несколькими способами, например:

По термическим данным — с опорой на тепловую теорему Нернста и с использованием сведений о температурной зависимости теплоёмкости участников реакции. Например, для веществ, при нормальных условиях находящихся в твёрдом состоянии:

${displaystyle S_{298}=S_{0}+int _{0}^{T}{frac {C_{pmathrm {(sol)} }}{T}}dT,}$

где $S_{0}=0$ (постулат Планка) и тогда, соответственно,

${displaystyle S_{298}=int _{0}^{T}{frac {C_{pmathrm {(sol)} }}{T}}dT}$

(здесь индекс sol — от англ. solid, «твердый»). При некоторой заданной температуре

${displaystyle S_{T}^{0}=S_{298}^{0}+int _{298}^{T}{frac {C_{pmathrm {(sol)} }}{T}}dT}$

Для жидких или газообразных при нормальной температуре веществ, или, в более общем случае, для веществ, в интервале температур от 0 (или 298) и до

претерпевающих фазовый переход, следует учитывать изменение энтропии, связанное с этим фазовым переходом.

Для идеальных газов — методами квантовой статистики.
Различными эмпирическими и полуэмпирическими методами, для этого часто достаточно небольшого объёма исходных данных. Например, для твёрдых неорганических веществ оценить энтропию можно по формуле^[7]:

${displaystyle S_{298}^{0}=Aln M+B}$

где

— табличные константы, зависящие от типа рассматриваемого соединения,

— молекулярная масса.

Итак, если известны $Delta H_{{298}}^{0}$ , $Delta S_{{298}}^{0}$ и температурные зависимости теплоёмкости, $Delta G_{T}^{0}$ может быть рассчитано по формуле:

$Delta G_{T}^{0}=Delta H_{{298}}^{0}-TDelta S_{{298}}^{0}+int _{{298}}^{T}Delta C_{p}dT-Tint _{{298}}^{T}Delta C_{p}{frac {dT}{T}}$

Несколько упрощённый вариант этой формулы получают, считая сумму теплоёмкостей веществ не зависящей от температуры и равной сумме теплоёмкостей при 298 K:

${displaystyle Delta G_{T}^{0}=Delta H_{298}^{0}-TDelta S_{298}^{0}+Delta C_{p~298}(T-298)-TDelta C_{p~298}ln {frac {T}{298}}}$

И ещё более упрощённый расчёт проводят, приравнивая сумму теплоёмкостей к нулю:

$Delta G_{T}^{0}=Delta H_{{298}}^{0}-TDelta S_{{298}}^{0}$

Переход от $Delta G_{T}^{0}$ к константе равновесия осуществляется по приведённой выше формуле.

Расчёт константы равновесия методами статистической термодинамики[править | править код]

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016)

Экспериментальное определение константы равновесия[править | править код]

Этот раздел статьи ещё не написан.

Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016)

См. также[править | править код]

Константа диссоциации
Константа автопротолиза
Константа гидролиза
Константа устойчивости
Константа Михаэлиса
Энергия Гиббса

Примечания[править | править код]

↑ ¹ ² Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим.-технол. спец. вузов / Под ред. А. Г. Стромберга. — 2-е изд. — М.: Высш. шк., 1988. — 496 с.
↑ ¹ ² ³ Патров Б. В., Сладков И. Б. Физическая химия. Ч. 1 : учеб. пособие. — СПб.: Изд-во Политехн. ун-та, 2009. — 127 с. — ISBN 978-5-7422-2206-4.
↑ Эткинс П. Физическая химия в 2 т., том 1. — М.: Мир, 1980. — 580 с.
↑ ¹ ² ³ Жмурко Г. П., Казаков Е. Ф., Кузнецова В. Н., Яценко А. В. Общая химия. — М.: Академия, 2012. — ISBN 978-5-7695-9188-4. — 512 с.
↑ ¹ ² Неорганическая химия в 3 т. /Под редакцией Третьякова Ю. Д. — Том 1: Физико-химические основы неорганической химии. — М.: Академия, 2004. — 240 с.
↑ Эткинс П. Физическая химия в 2 т., том 2. — М.: Мир, 1980. — 584 с.
↑ Физическая химия. Теоретическое и практическое руководство. Учеб. пособие для вузов / Под ред. акад. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987. — 880 с.

Литература[править | править код]

Киреев В. А. Методы практических расчётов в термодинамике химических реакций. — 2-е изд. — М., 1975.
Жоров Ю. М. Термодинамика химических процессов. — М., 1985.

Источник

3. 1. Расчет термодинамических и практических констант равновесия

Термодинамическая
константа равновесия может быть выражена
как через активности веществ, участвующих
в реакции, K_a,
так и через фугитивности K_f:

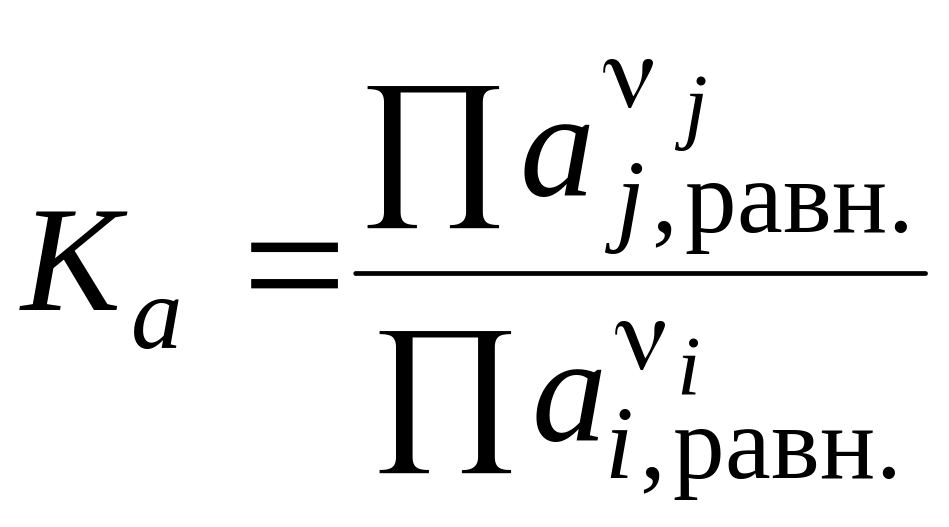
Термодинамические
константы равновесия являются
безразмерными величинами.

Константа
равновесия

может быть рассчитана по частному
уравнению изотермы химической реакции:

если
известно значение изменения стандартной
энергии Гиббса при данной температуре.
Тогда термодинамическая константа
равновесия

рассчитывается как экспонента:

Термодинамическая
константа равновесия зависит от природы
реагирующих веществ и температуры, но
не зависит от давления, поскольку
изменение стандартной энергии Гиббса
не зависит от давления по определению.

Величина
константы равновесия может принимать
значения от нуля до бесконечности:

Пример
7:
Рассчитаем термодинамическую константу
равновесия реакции синтеза метанола
при
температурах 298 и 1000 К и давлении 101,013
кПа.

Решение:
Рассчитаем изменение стандартной
энергии Гиббса при температуре 298 К,
используя рассчитанные в примерах 1 и
3 значения

и

:

=
– 90,47∙10³
– 298( – 218,83) = = – 25258,66 Дж

По частному
уравнению изотермы химической реакции

Для
расчета константы равновесия при 1000 К
воспользуемся рассчитанным в примере
5 значением стандартной энергии Гиббса
при температуре 1000 К для реакции синтеза
метанола

.

По частному
уравнению изотермы химической реакции

Если
химическая реакция протекает при
давлениях меньше ≤ 50 атм), то константа
равновесия, выраженная через приведенные
давления (
)

,
равна термодинамической константе
равновесия K_aи
является безразмерной величиной

Кроме
термодинамических констант равновесие
могут характеризовать практические
константы равновесия. Практические
константы равновесия могут быть
рассчитаны, если при равновесии определить
количества или концентрации веществ,
участвующих в реакции тем или иным
методом химического или физико-химического
анализа. Они могут быть выражены

– через
числа молей веществ n_i_,_j
в равновесии:

;

– через
молярные концентрации веществ C_i_,_j
в равновесии:

;

– через
мольные доли веществ N_i_,_j
в равновесии:

;

– через
парциальные давления веществ P_i_,_j
в равновесии:

В отличие от
термодинамических констант равновесия,
практические константы являются
размерными величинами.

Между
термодинамическими и практическими
константами равновесия существует
определенная математическая связь.
Например, константа

,
которая является термодинамической
константой равновесия при давлениях
меньше 50 атм., связана с практической
константой равновесия, выраженной через
моли K_n,
следующим
соотношением

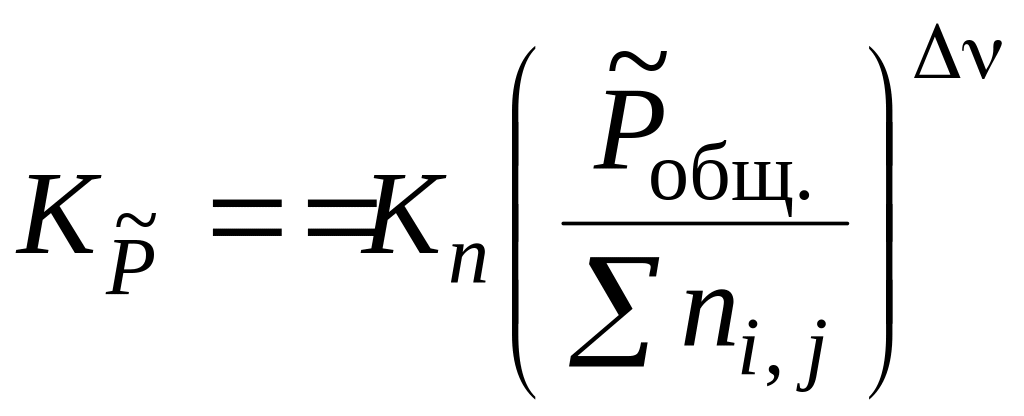
2. Расчет глубины и степени превращения исходных веществ, выхода продукта и равновесного состава.

Для
расчета равновесного состава была
введена универсальная величина –
химическая переменная или глубина
превращения ξ (кси), равная отношению
изменения количества вещества данного
реагента или продукта реакции к его
стехиометрическому коэффициенту в
уравнении химической реакции:

где знак “+”
используется для продуктов реакции, а
знак “ – “ для исходных веществ.

Равновесное
количество вещества для каждого участника
реакции выразим через глубину превращения:

Подставив
полученное выражение в уравнение,
связывающее термодинамическую K_a
=

и практическую K_n
константы равновесия, получим

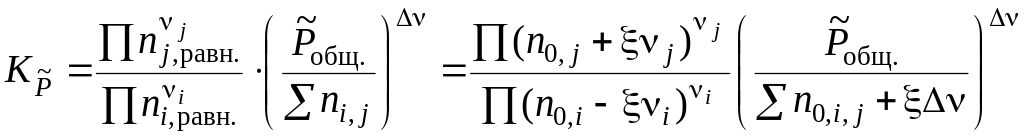
Решив
это уравнение относительно химической
переменной ξ, можно рассчитать: равновесные
количества вещества каждого участника
реакции, равновесные концентрации
реагентов, степень превращения исходных
веществ и выход продуктов реакции.

Пример
8:
Определим равновесную глубину превращения
ξ в реакции 2CO
+ S₂
= 2COS
при температуре
500 К и давлении 101,013 кПа., при
условии, что исходные вещества взяты в
стехиометрических количествах.
Термодинамическая
константа равновесия

=
3,56·10¹¹

Решение:
Выразим равновесный состав через
химическую переменную ξ
и найдем область допустимых значений
(ОДЗ) ξ из условия, число молей вещества
всегда положительная величина:

2CO

+ S₂
=

2COS

исх.
состав

n
,
моль

равн.
состав

n
,
моль

2–2
ξ

1–
ξ

2
ξ

ОДЗ ξ:
2–2ξ > 0
1–ξ > 0	=> 0 < ξ < 1
2ξ > 0

Выразим
практическую константу K_n
через глубину превращения ξ:

Выразим
сумму молей газообразных веществ в
равновесии через глубину превращения
ξ:

Найдем разность
стехиометрических коэффициентов в
уравнении реакции:

Подставим
K_n,

и

в
уравнение, связывающее термодинамическую
константу

с практической константой K_n

=

=

Полученное
кубическое уравнение

решаем
точно, отбирая корни в соответствии с
областью допустимых значений ξ, или
приближенно (методом подбора или
графически), что для практических
расчетов вполне допустимо. Используя
метод приближенных вычислений, получим,
что при

= 3,56·10¹¹

= 0,9998.

Пример
9:
Определим равновесную глубину превращения
ξ в реакции 2CO
+ S₂
= 2COS
при температуре
500 К и давлении 101,013 кПа., при
условии, что исходный состав содержал
0,2 моля СО и 2 моля газообразной серы.
Термодинамическая
константа равновесия

=
3,56·10¹¹

Решение:
Выразим равновесный состав через
химическую переменную ξ и найдем
область допустимых значений (ОДЗ) ξ:

2CO

+ S₂
=

2COS

исх.
состав

n
,
моль

0,2

равн.
состав

n
,
моль

0,2–2
ξ

2–
ξ

2
ξ

ОДЗ ξ:
0,2–2 ξ > 0
2– ξ > 0	=> 0 < ξ < 0,1
2 ξ > 0

Выразим
практическую константу K_n
через глубину превращения ξ:

Выразим
сумму молей газообразных веществ в
равновесии через глубину превращения
ξ:

Найдем разность
стехиометрических коэффициентов в
уравнении реакции:

Подставим
K_n,

в
уравнение, связывающее термодинамическую
константу

с практической константой K_n

=

=

Полученное
кубическое уравнение

решаем
приближенно и получаем, что при

= 3,56·10¹¹
ξ = 0,0999997.

Пример
10:
Определим степень превращения исходных
веществ в реакции 2CO
+ S₂
= 2COS
при условиях примеров 8 и 9.

Решение:

Степень
превращения X_i
– это отношение количества прореагировавшего
вещества к его начальному количеству:

X_i
=

При
условии примера 8

=
0,9998

Х

= 99,98 %

Х

=99,98
%

При
условии примера 9

=
0,0999997

Х
000
= 50,00 %

Х
00
= 5,00 %

Пример
11:
Определим состав равновесной смеси в
% (мол.) для реакции 2CO
+ S₂
= 2COS
при условиях примеров 8 и 9.

Решение:

Мольная доля
вещества в смеси равна:

или в %
(мол):

100

При
условии примера 8

=
0,9998

(мол.)

При
условии примера 9

=
0,0999997

(мол.)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Понятие химического равновесия

Признаки химического равновесия

Принцип Ле Шателье

Влияние температуры на химическое равновесие

Влияние давления на химическое равновесие

Влияние концентрации на химическое равновесие

Константа химического равновесия

Примеры решения задач

Задачи для самостоятельного решения

Понятие химического равновесия

Равновесным считается состояние системы, которое остается неизменным, причем это состояние не обусловлено действием каких-либо внешних сил. Состояние системы реагирующих веществ, при котором скорость прямой реакции становится равной скорости обратной реакции, называется химическим равновесием. Такое равновесие называется еще подвижным или динамическим равновесием.

Признаки химического равновесия

Состояние системы остается неизменным во времени при сохранении внешних условий.
Равновесие является динамическим, то есть обусловлено протеканием прямой и обратной реакции с одинаковыми скоростями.
Любое внешнее воздействие вызывает изменение в равновесии системы; если внешнее воздействие снимается, то система снова возвращается в исходное состояние.
К состоянию равновесия можно подойти с двух сторон – как со стороны исходных веществ, так и со стороны продуктов реакции.
В состоянии равновесия энергия Гиббса достигает своего минимального значения.

Принцип Ле Шателье

Влияние изменения внешних условий на положение равновесия определяется принципом Ле Шателье (принципом подвижного равновесия):

Если на систему, находящуюся в состоянии равновесия, производить какое–либо внешнее воздействие, то в системе усилится то из направлений процесса, которое ослабляет эффект этого воздействия, и положение равновесия сместится в том же направлении.

Принцип Ле Шателье применим не только к химическим процессам, но и к физическим, таким как кипение, кристаллизация, растворение и т. д.

Рассмотрим влияние различных факторов на химическое равновесие на примере реакции окисления NO:

2NO_(г) + O_2(г) → 2NO_2(г); ΔH^о₂₉₈ = — 113,4 кДж/моль.

Влияние температуры на химическое равновесие

При повышении температуры равновесие сдвигается в сторону эндотермической реакции, при понижении температуры – в сторону экзотермической реакции.

Степень смещения равновесия определяется абсолютной величиной теплового эффекта: чем больше по абсолютной величине энтальпия реакции ΔH, тем значительнее влияние температуры на состояние равновесия.

В рассматриваемой реакции синтеза оксида азота (IV) повышение температуры сместит равновесие в сторону исходных веществ.

Влияние давления на химическое равновесие

Сжатие смещает равновесие в направлении процесса, который сопровождается уменьшением объема газообразных веществ, а понижение давления сдвигает равновесие в противоположную сторону.

В рассматриваемом примере в левой части уравнения находится три объема, а в правой – два. Так как увеличение давления благоприятствует процессу, протекающему с уменьшением объема, то при повышении давления равновесие сместится вправо, т.е. в сторону продукта реакции – NO₂. Уменьшение давления сместит равновесие в обратную сторону. Следует обратить внимание на то, что, если в уравнении обратимой реакции число молекул газообразных веществ в правой и левой частях равны, то изменение давления не оказывает влияния на положение равновесия.

Влияние концентрации на химическое равновесие

Для рассматриваемой реакции введение в равновесную систему дополнительных количеств NO или O₂ вызывает смещение равновесия в том направлении, при котором концентрация этих веществ уменьшается, следовательно, происходит сдвиг равновесия в сторону образования NO₂. Увеличение концентрации NO₂ смещает равновесие в сторону исходных веществ.

Катализатор одинаково ускоряет как прямую, так и обратную реакции и поэтому не влияет на смещение химического равновесия.

При введении в равновесную систему (при Р = const) инертного газа концентрации реагентов (парциальные давления) уменьшаются. Поскольку рассматриваемый процесс окисления NO идет с уменьшением объема, то при добавлении инертного газа равновесие сместится в сторону исходных веществ.

Константа химического равновесия

Для химической реакции:

2NO_(г) + O_2(г) → 2NO_2(г)

константа химической реакции К_с есть отношение:

К_с = [NO₂]²/([NO]² · [O₂]) (1)

В этом уравнении в квадратных скобках – концентрации реагирующих веществ, которые устанавливаются при химическом равновесии, т.е. равновесные концентрации веществ.

Константа химического равновесия связана с изменением энергии Гиббса уравнением:

ΔG_T^о = – RTlnK (2)

Примеры решения задач

Задача 1. При некоторой температуре равновесные концентрации в системе 2CO_(г) + O_{2 (г)}→2CO_{2 (г)}составляли: [CO] = 0,2 моль/л, [O₂] = 0,32 моль/л, [CO₂] = 0,16 моль/л. Определите константу равновесия при этой температуре и исходные концентрации CO и O₂, если исходная смесь не содержала СО₂.

Решение.

2CO_(г) + O_2(г) →2CO_2(г)

Вещество	CO	O₂	CO₂
С_исходн, моль/л	0,36	0,40	0
С_{прореагир,}моль/л	0,16	0,08	0,16
С_равн, моль/л	0,2	0,32	0,16

Во второй строке под С_{прореагир}понимается концентрация прореагировавших исходных веществ и концентрация образующегося CO₂, причем, С_исходн= С_{прореагир}+ С_равн.

Задача 2. Используя справочные данные, рассчитайте константу равновесия процесса

3 H_{2 (г)} + N_{2 (г)} →2 NH_{3 (г)} при 298 К.

Решение.

ΔG₂₉₈^о = 2·(- 16,71) кДж = -33,42·10³ Дж.

ΔG_T^о = — RTlnK.

lnK = 33,42·10³/(8,314× 298) = 13,489. K = 7,21× 10⁵.

Задача 3. Определите равновесную концентрацию HI в системе

H_2(г) + I_2(г) →2HI_(г),

если при некоторой температуре константа равновесия равна 4, а исходные концентрации H₂, I₂ и HI равны, соответственно, 1, 2 и 0 моль/л.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л H_2.

Вещество	H₂	I₂	HI
с_{исходн.}, моль/л	1	2	0
с_{прореагир.}, моль/л	x	x	2x
c_равн., моль/л	1-x	2-x	2x

Тогда, К = (2х)²/((1-х)(2-х))

Решая это уравнение, получаем x = 0,67.

Значит, равновесная концентрация HI равна 2× 0,67 = 1,34 моль/л.

Задача 4. Используя справочные данные, определите температуру, при которой константа равновесия процесса: H_2(г) + HCOH_(г) →CH₃OH_(г) становится равной 1. Принять, что ΔН^о_Т » ΔН^о₂₉₈, а ΔS^о_T » ΔS^о₂₉₈.

Решение.

Если К = 1, то ΔG^о_T = — RTlnK = 0;

ΔG^о_T = ΔН^о₂₉₈ — ТΔ S^о₂₉₈ .

ΔН^о₂₉₈ = -202 – (- 115,9) = -86,1 кДж = — 86,1× 10³ Дж;

ΔS^о₂₉₈ = 239,7 – 218,7 – 130,52 = -109,52 Дж/К;

0 = — 86100 — Т·(-109,52)

Т = 786,15К

Задача 5. Для реакции SO_2(Г) + Cl_2(Г) →SO₂Cl_2(Г) при некоторой температуре константа равновесия равна 4. Определите равновесную концентрацию SO₂Cl₂, если исходные концентрации SO₂, Cl₂ и SO₂Cl₂ равны 2, 2 и 1 моль/л соответственно.

Решение. Пусть к некоторому моменту времени прореагировало x моль/л SO_2.

SO_2(г) + Cl_2(г) →SO₂Cl_2(г)

Вещество	SO₂	Cl₂	SO₂Cl₂
c_{исходн.}, моль/л	2	2	1
c_{прореагир.}, моль/л	x	x	х
c_равн., моль/л	2-x	2-x	x + 1

Тогда получаем:

(х + 1)/(2 — х)² = 4

Решая это уравнение, находим: x₁ = 3 и x₂ = 1,25. Но x₁ = 3 не удовлетворяет условию задачи.

Следовательно, [SO₂Cl₂] = 1,25 + 1 = 2,25 моль/л.

Задачи для самостоятельного решения

1. В какой из приведенных реакций повышение давления сместит равновесие вправо? Ответ обоснуйте.

1) 2 NH_{3 (г)} → 3H_{2 (г)} + N_{2 (г)}

2) ZnCO_{3 (к)} → ZnO_(к) + CO_{2 (г)}

3) 2HBr_(г) → H_{2 (г)} + Br_{2 (ж)}

4) CO_2 (г) + C_{(графит)} →2CO_(г)

Так как увеличение давления благоприятствует процессу, протекающему с уменьшением количества
газообразных веществ, то равновесие сместится вправо в реакции 3.

2. При некоторой температуре равновесные концентрации в системе:

2HBr_(г) →H_{2 (г)} + Br_{2 (г)}

составляли: [HBr] = 0,3 моль/л, [H₂] = 0,6 моль/л, [Br₂] = 0,6 моль/л. Определите константу равновесия и исходную концентрацию HBr.

3. Для реакции H_2(г) + S_(г) →H₂S_(г) при некоторой температуре константа равновесия равна 2. Определите равновесные концентрации H₂ и S, если исходные концентрации H₂, S и H₂S равны, соответственно, 2, 3 и 0 моль/л.

4. Используя справочные данные, вычислите температуру, при которой константа равновесия процесса

CO_2(г) + C_{(графит)} →2CO_(г)

становится равной 1. Примите, что ΔН^о_Т≈ΔН^о₂₉₈, а ΔS^о_T≈ΔS^о₂₉₈

5. Используя справочные данные, рассчитайте константу равновесия процесса:

С₂Н_4(г) →С₂Н_2(г) + Н_2(г) при 298 К

6. Для реакции 2С₃Н_8(г) → н-С₅Н_12(г)+СН_4(г) при температуре 1000 К константа равновесия равна 4. Определите равновесную концентрацию н-пентана, если исходная концентрация пропана равна 5 моль/л.

7. При температуре 500 К константа равновесия процесса:

СО_2(г) + 3Н_2(г) → СН₃ОН_(г) + Н₂О_(г)

равна 3,4·10^-5. Вычислите Δ G^о₅₀₀.

8. При температуре 800 К константа равновесия процесса н-С₆Н_14(г)+ 2С₃Н_6(г)+Н_2(г) равна 8,71. Определите ΔG^о_f,800(С₃Н_6(г)), если ΔG^о_f,800(н-С₆Н_14(г)) = 305,77 кДж/моль.

9. Для реакции СО_(г) + Cl_2(г) →СO₂Cl_2(г) при некоторой температуре равновесная концентрация СO₂Cl_2(г) равна 1,2 моль/л. Определите константу равновесия данного процесса, если исходные концентрации СО_(г) и Cl_2(г) равны соответственно 2,0 и 1,8 моль/л.

10. При некоторой температуре равновесные концентрации в системе 2SО_2(г) + О_2(г) →2SO_3(г) составляли: [SО₂ ]=0,10 моль/л, [О₂]=0,16 моль/л, [SО₃]=0,08 моль/л. Вычислите константу равновесия и исходные концентрации SО₂ и О₂.

К=4,0; исходная концентрация SО₂ составляет 0,18 моль/л;
исходная концентрация О₂ составляет 0,20 моль/л.

Источник

Константа равновесия

1 Способы выражения константы равновесия
- 1.1 Стандартная константа равновесия
- 1.2 Константа равновесия реакций в гетерогенных системах
2 Константа равновесия и изменение энергии Гиббса
3 Зависимость константы равновесия от температуры
4 Константа равновесия и константа скорости реакции
5 Методы расчета константы равновесия
- 5.1 Энтропийный расчёт изменения энергии Гиббса и константы равновесия реакции
- 5.2 Расчёт константы равновесия методами статистической термодинамики
- 5.3 Экспериментальное определение константы равновесия

Примечания
Литература

1. Способы выражения константы равновесия

Для реакции в смеси идеальных газов константа равновесия может быть выражена через равновесные парциальные давления компонентов pi по формуле[1]:

где νi — стехиометрический коэффициент (для исходных веществ принимается отрицательным, для продуктов — положительным). Kp не зависит от общего давления, от исходных количеств веществ или от того, какие участники реакции были взяты в качестве исходных, но зависит от температуры [2].

Например, для реакции окисления монооксида углерода:

2CO + O2 = 2CO2

константа равновесия может быть рассчитана по уравнению:

Если реакция протекает в идеальном растворе и концентрация компонентов выражена через молярность ci, константа равновесия принимает вид:

Для реакций в смеси реальных газов или в реальном растворе вместо парциального давления и концентрации используют соответственно фугитивность fi и активность ai:

В некоторых случаях (в зависимости от способа выражения) константа равновесия может являться функцией не только температуры, но и давления. Так, для реакции в смеси идеальных газов парциальное давление компонента может быть выражено по закону Дальтона через суммарное давление и мольную долю компонента (), тогда легко показать[2], что:

где Δn — изменение числа молей веществ в ходе реакции. Видно, что Kx зависит от давления. Если число молей продуктов реакции равно числу молей исходных веществ (Δn = 0), то Kp = Kx.

1.1. Стандартная константа равновесия

Стандартная константа равновесия реакции в смеси идеальных газов (когда начальные парциальные давления участников реакции равны их значениям в стандартном состоянии = 0,1013 МПА или 1 атм) может быть рассчитана по выражению:

где — относительные парциальные давления компонентов, .

Стандартная константа равновесия — безразмерная величина. Она связана с Kp соотношением:

Видно, что если выражены в атмосферах, то и .

Для реакции в смеси реальных газов в стандартном начальном состоянии парциальные фугитивности газов принимаются равными их парциальным давлениям = 0,1013 МПА или 1 атм. Kf связана с K0 соотношением:

где γi — коэффициент фугитивности i-го реального газа в смеси.

1.2. Константа равновесия реакций в гетерогенных системах

где fi — фугитивность компонентов газовой фазы, а ak — активность компонентов конденсированной фазы.

Например, для реакции твёрдофазного восстановления оксида железа:

FeOт + COг = Feт + CO2г

константа равновесия (при условии, что газовая фаза идеальна) имеет вид:

2. Константа равновесия и изменение энергии Гиббса

Для реакции, протекающей в изобарно-изотермических условиях, в некотором неравновесном исходном состоянии энергии Гиббса или химические потенциалы реагирующих веществ и продуктов реакции в общем случае не одинаковы, их разность (ΔGT) может быть рассчитана по уравнению:

где — отношение парциальных давлений участников реакции в исходном состоянии в степенях, равных их стехиометрическим коэффициентам; R — универсальная газовая постоянная.

Это уравнение называют уравнением изотермы химической реакции. Оно позволяет рассчитать изменение энергии Гиббса при протекании процесса и определить направление протекания реакции:

при π < Kp ΔG< 0 — реакция идёт в прямом направлении, слева направо;при π = Kp ΔG = 0 — реакция достигла равновесного состояния;при π >Kp ΔG > 0 — реакция идёт в обратном направлении.

Стандартная константа равновесия связана со стандартной энергией Гиббса реакции соотношением:

Стандартная энергия Гиббса реакции в газовой смеси — энергия Гиббса реакции при стандартных парциальных давлениях всех компонентов, равных 0,1013 МПа (1 атм).

Кроме того, сравнивая величины стандартной энергии Гиббса нескольких реакций, можно выбрать наиболее предпочтительные, для которых имеет наибольшую по модулю отрицательную величину.

3. Зависимость константы равновесия от температуры

и изохоры химической реакции (изохоры Вант-Гоффа):

Здесь ΔH и ΔU — тепловой эффект реакции, протекающей, соответственно, при постоянном давлении или при постоянном объёме.

Если ΔH > 0 (тепловой эффект положителен, реакция эндотермическая), то температурный коэффициент константы равновесия тоже положителен, то есть с ростом температуры константа равновесия эндотермической реакции увеличивается, равновесие сдвигается вправо (что вполне согласуется с принципом Ле Шателье).

4. Константа равновесия и константа скорости реакции

Для обратимой химической реакции константа равновесия может быть выражена через константы скорости прямых и обратных реакций, исходя из того факта, что в состоянии равновесия скорости прямой и обратной реакций равны. Например, для элементарной обратимой химической реакции первого порядка

легко показать[2], что:

где k1 — константа скорости прямой реакции, а k2 — обратной. Это важное соотношение даёт одну из «точек соприкосновения» химической кинетики и химической термодинамики.

5. Методы расчета константы равновесия

Расчётные методы определения константы равновесия реакции обычно сводятся к вычислению тем или иным способом стандартного изменения энергии Гиббса в ходе реакции (ΔG0), а затем использованию формулы:

Следовательно, если непосредственное определение или расчёт ΔG0 для некоторой реакции по каким-либо причинам затруднены, можно подобрать такие промежуточные реакции, для которых ΔG0 известно или может быть легко определено, и суммирование которых даст рассматриваемую реакцию (см. Закон Гесса).

В частности, в качестве таких промежуточных реакций часто используют реакции образования соединений из элементов.

5.1. Энтропийный расчёт изменения энергии Гиббса и константы равновесия реакции

Энтропийный метод расчёта ΔG реакции является одним из самых распространённых и удобных[2]. Он основан на соотношении:

или, соответственно, для стандартного изменения энергии Гиббса:

Здесь ΔH0 при постоянных давлении и температуре равно тепловому эффекту реакции, методы расчёта и экспериментального определения которого известны — см., например, уравнение Кирхгофа:

По термическим данным — с опорой на тепловую теорему Нернста и с использованием сведений о температурной зависимости теплоёмкости участников реакции. Например, для веществ, при нормальных условиях находящихся в твёрдом состоянии:

где S0 = 0 (постулат Планка) и тогда, соответственно,.(здесь индекс sol — от англ. solid). При некоторой заданной температуре T:Для жидких или газообразных при нормальной температуре веществ, или, в более общем случае, для веществ, в интервале температур от 0 (или 298) и до T претерпевающих фазовый переход, следует учитывать изменение энтропии, связанное с этим фазовым переходом.

Для идеальных газов — методами квантовой статистики.
Различными эмпирическими и полуэмпирическими методами, для этого часто достаточно небольшого объёма исходных данных. Например, для твёрдых неорганических веществ оценить энтропию можно по формуле[3]:

где A и B — табличные константы, зависящие от типа рассматриваемого соединения, M — молекулярная масса.

Итак, если извеcтны , и температурные зависимости теплоёмкости, может быть рассчитано по формуле:

И еще более упрощённый расчёт проводят, приравнивая сумму теплоёмкостей к нулю:

Переход от к константе равновесия осуществляется по приведённой выше формуле.

Примечания

Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим.-технол. спец. вузов / Под ред. А. Г. Стромберга. — 2-е изд. — М.: Высш. шк., 1988. — 496 с.
↑ 1234Патров Б. В., Сладков И. Б.

Физическая химия. Ч. 1 : учеб. пособие. — СПб.: Изд-во Политехн. ун-та, 2009. — 127 с. — ISBN 978-5-7422-2206-4
Физическая химия. Теоретическое и практическое руководство. Учеб. пособие для вузов / Под ред. акад. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987.
— 880 с.

Литература

Киреев В.А. Методы практических расчётов в термодинамике химических реакций. — 2-е изд. — М., 1975.
Жоров Ю.М. Термодинамика химических процессов. — М., 1985.

скачать
Данный реферат составлен на основе статьи из русской Википедии. Синхронизация выполнена 16.07.

11 17:18:59
Похожие рефераты: Профиль равновесия, Теория прерывистого равновесия, Принцип детального равновесия, Теорема Лагранжа об устойчивости равновесия, Константа, Константа Фейгенбаума, Константа Хайтина, Константа (программирование), Космологическая константа.

Категории: Физические величины, Физическая химия.

Текст доступен по лицензии Creative Commons Attribution-ShareA.

Химическое равновесие: константа химического равновесия и способы ее выражения

В 1885 году французским физиком и химиком Ле Шателье был выведен, а в 1887 году немецким физиком Брауном обоснован закон химического равновесия и константа химического равновесия, а также изучена их зависимость от влияния различных внешних факторов.

Суть химического равновесия

Равновесие — это динамическое состояние, означающее, что вещи всегда движутся. Продукты разлагаются на реактивы, а реактивы объединяются в продукты. Вещи движутся, но концентрации остаются неизменными. Реакция записывается с двойной стрелкой вместо знака равенства, чтобы показать, что она обратима.

Классические закономерности

Еще в прошлом веке химиками были открыты определенные закономерности, которые предусматривают вероятность изменения направления реакции в одной и той же емкости. Знания о том, как протекают химические реакции, невероятно важны, как для лабораторных исследований, так и промышленного производства.

При этом большое значение имеет возможность контролировать все эти явления. Человеку свойственно вмешиваться во многие природные процессы, в особенности это касается обратимых, чтобы потом использовать их себе на благо.

От знаний о химических реакциях будет больше пользы, если в совершенстве владеть рычагами управления ими.

Закон действующих масс в химии использую химики, чтобы правильно рассчитывать скорости протекания реакций.

Он дает четкое представление о том, что ни один химический процесс не будет доведен до конца в случае, если он будет проходить в системе закрытого типа.

Молекулы образующихся веществ находятся в постоянном и беспорядочном движении, и может вскоре возникнуть обратная реакция, при которой будут восстанавливаться молекулы исходного материала.

В промышленности чаще всего используют открытые системы. Сосуды, аппараты и другие емкости, где проходят химические реакции, остаются незапертыми.

Это необходимо для того, чтобы во время этих процессов можно было извлечь нужный продукт и избавиться от бесполезных продуктов реакции.

Например, уголь сжигается в открытых топках, цемент производится в печах открытого типа, домны функционируют при постоянной подаче воздуха, а аммиак синтезируется при непрерывном удалении самого аммиака.

Обратимые и необратимые химические реакции

Исходя из названия, можно дать соответствующие определения: необратимыми считаются реакции, доводимые до конца, не изменяющие своего направления и протекающие по заданной траектории вне зависимости от перепадов давления и температурных колебаний.

Их отличительной особенностью является то, что некоторые продукты могут покидать сферу реакции. Таким образом, например, можно получить газ (CaCO3 = CaO + CO2), осадок (Cu(NO3)2 + H2S = CuS + 2HNO3) или другие соединения.

Реакция также будет считаться необратимой, если во время процесса выделяется большое количество тепловой энергии, например: 4P + 5O2 = 2P2O5 + Q.

Практически все реакции, которые происходят в природе, являются обратимыми.

Независимо от таких внешних условий, как давление и температура, практически все процессы могут протекать одновременно в разных направлениях.

Как гласит закон действующих масс в химии, количество поглощенной теплоты будет равно количеству выделенной, это значит, что если одна реакция была экзотермической, то вторая (обратная) буде эндотермической.

Химическое равновесие: константа химического равновесия

Реакции — это «глаголы» химии — деятельность, которую изучают химики. Многие реакции переходят к их завершению, а затем останавливаются, а это означает, что реагенты полностью преобразуются в продукты, не имея возможности вернуться в исходное состояние.

В некоторых случаях реакция действительно необратима, например, когда сжигание изменяет как физические, так и химические свойства вещества.

Однако существует множество других обстоятельств, в которых обратная реакция является не только возможной, но и непрерывной, так как продукты первой реакции становятся реагентами во второй.

Динамическое состояние, в котором концентрации реагентов и продуктов остаются постоянными, называется равновесием. Можно предсказать поведение веществ с помощью определенных законов, которые применяются в отраслях, стремящихся снизить издержки производства конкретных химических веществ.

Для понимания процессов, которые сохраняют или потенциально угрожают здоровью людей, также полезным является понятие химического равновесия.

Константа химического равновесия представляет собой значение фактора реакции, которое зависит от ионной силы и температуры, и не зависит от концентраций реагентов и продуктов в растворе.

Вычисление константы равновесия

Эта величина является безразмерной, то есть не имеющей определенного количества единиц. Хотя расчет обычно записывается для двух реагентов и двух продуктов, он работает для любого количества участников реакции.

Расчет и интерпретация константы равновесия зависят от того, связана ли химическая реакция с однородным или гетерогенным равновесием. Это значит, что все вступающие в реакцию компоненты могут быть чистыми жидкостями или газами.

Для реакций, которые достигают гетерогенного равновесия, присутствует, как правило, не одна фаза, а как минимум две. Например, жидкости и газы или твердые вещества и жидкости.

Значение константы равновесия

Для любой заданной температуры для константы равновесия существует только одно значение, которое изменяется только в том случае, если температура, при которой происходит реакция, изменяется в ту или иную сторону.

Можно сделать некоторые прогнозы относительно химической реакции, исходя из того, является ли постоянная равновесия большой или малой. Если значение очень велико, то равновесие благоприятствует реакции вправо и получается больше продуктов, чем было реагентов.

Реакцию в этом случае можно назвать «полной» или «количественной».

Если значение константы равновесия невелико, то оно благоприятствует реакции влево, где количество реагентов было больше, чем образовавшихся продуктов.

Если это значение стремится к нулю, можно считать, что реакция не возникает.

Если же значения константы равновесия для прямой и обратной реакции почти одинаковы, то количество реагентов и продуктов будет тоже почти одинаковым. Этот тип реакции считается обратимым.

Рассмотрим конкретную обратимую реакцию

Возьмем таких два химических элемента, как йод и водород, которые при смешивании дают новое вещество — иодоводород.

H2+I2 =2HI

За v1 примем скорость прямой реакции, за v2 — скорость обратной реакции, k — константа равновесия. Используя закон действия масс, получаем следующее выражение:

v1 = k1 * c(H2) * c(I2),

v2 = k2 * c2(HI).

При смешивании молекул йода (I2) и водорода (H2) начинается их взаимодействие.

На начальном этапе концентрация этих элементов максимальная, а вот к концу реакции максимальной будет концентрация нового соединения — иодоводорода (HI). Соответственно, разными будут и скорости реакций.

В самом начале они будут максимальными. Со временем наступает момент, когда эти значения будут равными, он и является состоянием, которое называется химическим равновесием.

Выражение константы химического равновесия, как правило, обозначают с применением квадратных скобок: [H2], [I2], [HI]. Так как при состоянии равновесия скорости равны, то:

k1[H2][I2] = k2[HI]2,

так получаем уравнение константы химического равновесия:

k1/k2 = [HI]2/[H2][I2] = K.

Принцип Ле Шателье-Брауна

Существует следующая закономерность: если на систему, которая находится в равновесии, произвести определенное воздействие (изменить условия химического равновесия путем изменения температуры или давления, например), то баланс будет смещаться, чтобы частично противодействовать эффекту изменения. В дополнение к химии этот принцип также применим в несколько разных формах к областям фармакологии и экономики.

Константа химического равновесия и способы ее выражения

Равновесное выражение может быть выражено в терминах концентрации продуктов и реагентов. Только химические вещества в водной и газообразной фазах включены в равновесную формулу, поскольку концентрации жидкостей и твердых веществ не изменяются.

Какие факторы влияют на химическое равновесие? Если в нем участвует чистая жидкость или твердое вещество, считается, что оно имеет К= 1, и соответственно перестает браться в расчет, за исключением высококонцентрированных растворов.

Например, чистая вода имеет активность 1.

Другим примером является твердый углерод, который может образовываться реакцией двух молекул монооксида карбона с образованием углекислого газа и углерода.

Факторы, которые могут повлиять на равновесие, включают в себя добавление реагента или продукта (изменение концентрации влияет на баланс). Добавление реагента может привести к равновесию справа в химическом уравнении, где появляется больше форм продукта.

Добавление продукта может привести к равновесию слева, так как больше становится форм реагентов.

Равновесие возникает, когда реакция, проходящая в обоих направлениях, имеет неизменное соотношение продуктов и реагентов.

В целом, химическое равновесие статично, так как количественное соотношение продуктов и реагентов постоянны.

Однако более пристальный взгляд показывает, что равновесие на самом деле является очень динамичным процессом, так как реакция движется в обоих направлениях в равном темпе.

Динамическое равновесие является примером функции устойчивого состояния. Для системы в устойчивом состоянии наблюдаемое в настоящее время поведение продолжается и в будущем. Поэтому, как только реакция достигнет равновесия, отношение концентраций продукта и реагента останется таким же, хотя реакция продолжается.

Как просто рассказать о сложном?

Такие понятия, как химическое равновесие и константа химического равновесия, являются достаточно сложными для понимания. Возьмем пример из жизни. Вы когда-нибудь застревали на мосту между двумя городами и обращали внимание на то, что движение в другом направлении плавное и размеренное, в то время как вы безнадежно застряли в пробке? Это нехорошо.

Что, если бы машины размеренно и с одинаковой скоростью двигались с обеих сторон? Оставалось бы количество автомобилей в обоих городах постоянным? Когда скорость въезда и выезда в оба города одинакова, а количество автомобилей в каждом городе стабильно с течением времени, это означает, что весь процесс находится в динамическом равновесии.

Источник

Способы выражения константы равновесия[править | править код]

Стандартная константа равновесия[править | править код]

Константа равновесия реакций в гетерогенных системах[править | править код]

Термодинамическое описание равновесия[править | править код]

Равновесный состав смеси и направление реакции[править | править код]

Стандартные состояния[править | править код]

Кинетическое описание[править | править код]

Множественные равновесия[править | править код]

Зависимость константы равновесия от температуры[править | править код]

Методы расчета константы равновесия[править | править код]

Энтропийный расчёт изменения энергии Гиббса и константы равновесия реакции[править | править код]

Расчёт константы равновесия методами статистической термодинамики[править | править код]

Экспериментальное определение константы равновесия[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

3. 1. Расчет термодинамических и практических констант равновесия

2. Расчет глубины и степени превращения исходных веществ, выхода продукта и равновесного состава.

Понятие химического равновесия

Признаки химического равновесия

Принцип Ле Шателье

Влияние температуры на химическое равновесие

Влияние давления на химическое равновесие

Влияние концентрации на химическое равновесие

Константа химического равновесия

Примеры решения задач

Задачи для самостоятельного решения

Константа равновесия

1. Способы выражения константы равновесия

1.1. Стандартная константа равновесия

1.2. Константа равновесия реакций в гетерогенных системах

2. Константа равновесия и изменение энергии Гиббса

3. Зависимость константы равновесия от температуры

4. Константа равновесия и константа скорости реакции

5. Методы расчета константы равновесия

5.1. Энтропийный расчёт изменения энергии Гиббса и константы равновесия реакции

Примечания

Литература

Химическое равновесие: константа химического равновесия и способы ее выражения

Суть химического равновесия

Классические закономерности

Обратимые и необратимые химические реакции

Химическое равновесие: константа химического равновесия

Вычисление константы равновесия

Значение константы равновесия

Рассмотрим конкретную обратимую реакцию

Принцип Ле Шателье-Брауна

Константа химического равновесия и способы ее выражения

Как просто рассказать о сложном?

Вам также может понравиться

Как найти записанный разговор в телефоне андроид

Как найти радиус шара описанного около конуса

Как найти в файле числа строки c

Добавить комментарий Отменить ответ