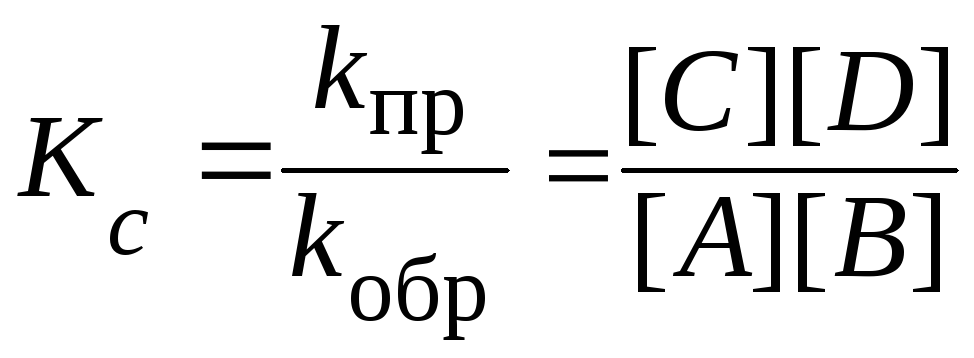Как найти константу скорости обратной реакции

Лекция по теме«Химическое равновесие»

Учебные
вопросы

1. Состояние равновесия

2. Константа
   равновесия

3. Расчет
   равновесных концентраций

4. Смещение
   химического равновесия. Принцип Ле
   Шателье

1. Состояние равновесия

Реакции,
протекающие при одних и тех же условиях
одновременно в противоположных
направлениях, называются обратимыми.

Рассмотрим
обратимую реакцию, которая протекает
в закрытой системе

A
+ B

C
+ D

Скорость
прямой реакции описывается уравнением:

_пр

= k
_пр

[A]
[B],

где
_пр
–
скорость прямой реакции;

k
_пр
–
константа скорости прямой реакции.

С
течением времени концентрации реагентов
А
и В
уменьшаются, скорость реакции падает
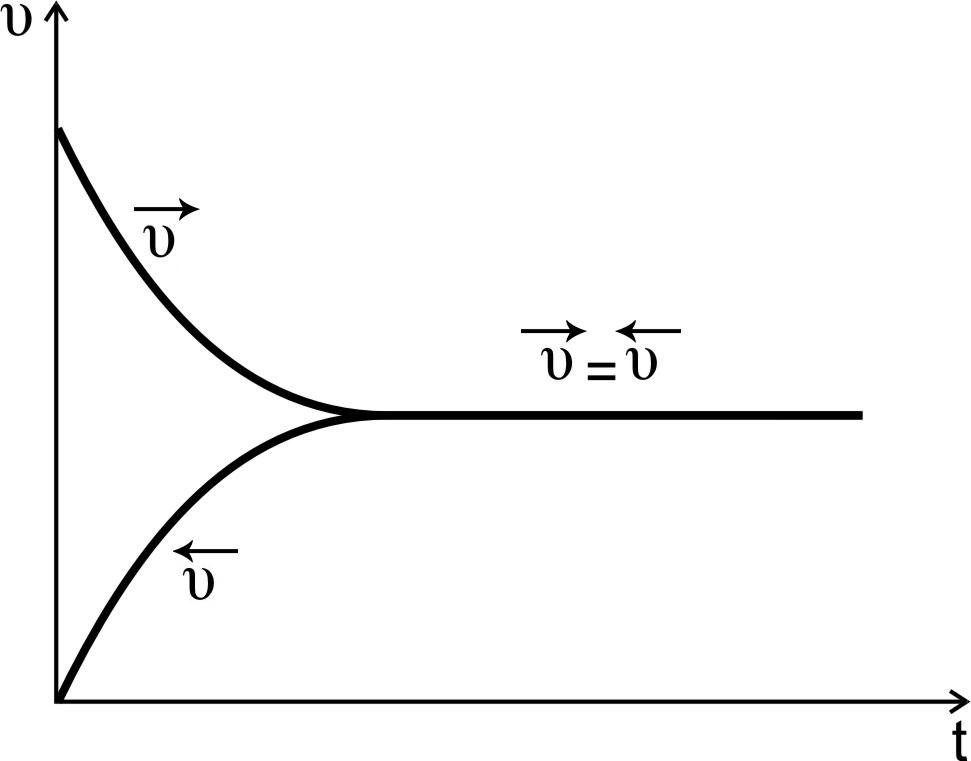
(рис.1, кривая

_пр).

Реакция
между А
и В
приводит к образованию веществ C
и D,
молекулы которых при столкновениях
могут вновь дать вещества А
и В.

Скорость
обратной реакции описывается уравнением:

_обр
= k
_обр
[С] [D],

где

_обр
–
скорость обратной реакции;

k
_обр
–
константа скорости обратной реакции.

По
мере того как концентрации веществ C
и D
возрастают, скорость обратной реакции
растет (рис.1, кривая

_обр).

Рис.1. Изменение скоростей
прямой и обратной реакций во времени

Через
некоторое время скорости
прямой и обратной реакций становятся
равными:

_пр
=
_обр

Такое
состояние системы называется состоянием
равновесия.

В
состоянии равновесия концентрации всех
его участников перестают меняться во
времени.
Такие
концентрации называются
равновесными.

Химическое
равновесие
– это
динамическое равновесие. Неизменность
концентраций веществ, присутствующих
в закрытой системе, есть следствие
непрерывно идущих химических процессов.
Скорости прямой и обратной реакции не
равны нулю, а нулю равна наблюдаемая
скорость процесса.

Равенство
скоростей прямой и обратной реакций –
это кинетическое условие химического
равновесия.

2. Константа равновесия

При
равенстве скоростей прямой и обратной
реакции

_пр
=

_обр

справедливо
равенство

k
_пр[A]
[B]
= k
_обр
[С]
[D],

где
[A],
[B],
[С],
[D]
– равновесные концентрации веществ.

Поскольку
константы скоростей не зависят от
концентраций, равенство можно записать
иначе:

Отношение
констант скоростей прямой и обратной
реакций ( k_пр/k_обр)
называют константой химического
равновесия:

Истинное
химическое равновесие может устанавливаться
только в том случае, если равновесны
все элементарные стадии механизма
реакции. Сколь бы сложны ни были механизмы
прямой и обратной реакций, но в состоянии
равновесия они должны обеспечить
стехиометрический переход исходных
веществ в продукты реакции и обратно.
Это значит, что алгебраическая сумма
всех стадий процесса равна стехиометрическому
уравнению реакции, т.е. стехиометрические
коэффициенты представляют собой сумму
молекулярностей всех стадий механизма.

Для
сложной реакции

aA
+ bB

cC
+ dD

Кс =

Для
одной и той же температуры отношение
произведения равновесных концентраций
продуктов реакции в степенях, равных
стехиометрическим коэффициентам, к
произведению равновесных концентраций
исходных веществ в степенях, равных
стехиометрическим коэффициентам,
представляет постоянную величину.

Это
вторая формулировка закона действующих
масс.

В
выражение константы равновесия
гетерогенной реакции входят только
концентрации веществ, находящихся в
жидкой или газообразной фазе, так как
концентрации твердых веществ остаются,
как правило, постоянными.

Например,
выражение для константы равновесия
следующей реакции

СО₂
(г)
+ С(тв)


2СО(г)

записывается
так:

К_с
=
.

Уравнение
константы равновесия показывает, что
в условиях равновесия концентрации
всех веществ, участвующих в реакции,
связаны между собой. Численное значение
константы равновесия определяет, каким
должно быть соотношение концентраций
всех реагирующих веществ при равновесии.

Изменение
концентрации любого из этих веществ
влечет за собой изменения концентраций
всех остальных веществ. В итоге
устанавливаются новые концентрации,
но соотношение между ними вновь отвечает
константе равновесия.

Величина
константы равновесия зависит от
природы
реагирующих веществ и температуры.

Константа
равновесия, выраженная через молярные
концентрации реагирующих веществ (Кс)
и константа равновесия, выраженная
через равновесные парциальные давления
(Кр)
(см. «Основы химической термодинамики»),
связаны между собой соотношениями:

Кр

= Кс
RT
^,
Kc
=
Кр

/ (RT)
^
,

где

– изменение числа газообразных молей в
реакции.

Стандартное
изменение энергии Гиббса равно

G_Т
= – RT
ln
Kp,

а
также

G_Т

= 
H
– T

S.

После
приравнивания правых частей уравнений:

–
RT
ln
Kp
= 
H
– T

S

или

ln
K
р
= – 
H
/ (RT)
+ 
S/R
.

Уравнение
не только устанавливает вид зависимости
константы от температуры, но и показывает,
что константа определяется природой
реагирующих веществ.

Константа
равновесия не зависит от концентраций
(как и константа скорости реакции),
механизма реакции, энергии активации,
от присутствия катализаторов.
Смена механизма, например, при введении
катализатора, не влияет на численное
значение константы равновесия, но,
конечно, меняет скорость достижения
равновесного состояния.

Соседние файлы в папке Кинетика_лекции

• #
• #
• #
• #

Обратимые и необратимые химические реакции. Понятие о химическом равновесии. Решение задач

На уроке будет рассмотрена тема «Обратимые и необратимые химические реакции. Химическое равновесие», будут рассматриваться факторы, влияющие на смещение химического равновесия. Вы познакомитесь с принципом Ле Шателье. Вводится понятие обратимых и необратимых реакций.

I. Понятие прямой и обратной реакции

II. Константа равновесия

III. Обратимые и необратимые химические реакции

IV. Факторы, влияющие на смещение равновесия

Если из­ме­нить внеш­ние усло­вия, то со­сто­я­ние хи­ми­че­ско­го рав­но­ве­сия на­ру­шит­ся. Сме­ще­ние рав­но­ве­сия в за­ви­си­мо­сти от из­ме­не­ния внеш­них усло­вий в общем виде опре­де­ля­ет­ся 

Прин­ци­пом Ле Ша­те­лье: если на си­сте­му, на­хо­дя­щу­ю­ся в рав­но­ве­сии, ока­зы­ва­ют воз­дей­ствие извне путем из­ме­не­ния ка­ко­го-ли­бо из усло­вий, опре­де­ля­ю­щих по­ло­же­ние рав­но­ве­сия, то оно сме­ща­ет­ся в на­прав­ле­нии того про­цес­са, про­те­ка­ние ко­то­ро­го ослаб­ля­ет эф­фект про­из­ве­дён­но­го воз­дей­ствия.

Так, по­вы­ше­ние тем­пе­ра­ту­ры вы­зы­ва­ет сме­ще­ние рав­но­ве­сия в на­прав­ле­нии того из про­цес­сов, те­че­ние ко­то­ро­го со­про­вож­да­ет­ся по­гло­ще­ни­ем тепла, а по­ни­же­ние тем­пе­ра­ту­ры дей­ству­ет в про­ти­во­по­лож­ном на­прав­ле­нии.

Рав­но­ве­сие сме­ща­ет­ся впра­во, если по­вы­си­лись рав­но­вес­ные кон­цен­тра­ции про­дук­тов пря­мой ре­ак­ции. Если по­вы­ша­ют­ся рав­но­вес­ные кон­цен­тра­ции ис­ход­ных ве­ществ пря­мой ре­ак­ции, то рав­но­ве­сие сме­ща­ет­ся влево. Какие фак­то­ры можно из­ме­нять, чтобы сме­стить рав­но­ве­сие? Это

· Тем­пе­ра­ту­ра

· Дав­ле­ние

· Кон­цен­тра­ции ве­ществ

До­бав­ле­ние ка­та­ли­за­то­ра и из­ме­не­ние пло­ща­ди ре­ак­ци­он­ной по­верх­но­сти ге­те­ро­ген­ных ре­ак­ций не ока­зы­ва­ют вли­я­ние на сме­ще­ние хи­ми­че­ско­го рав­но­ве­сия.

Рассмотрим влияние фак­то­ров на смещение химического равновесия более де­таль­но.

1. Влияние тем­пе­ра­ту­ры

Ре­ак­ция син­те­за ам­ми­а­ка от­но­сит­ся к эк­зо­тер­ми­че­ским ре­ак­ци­ям. При про­хож­де­нии пря­мой ре­ак­ции теп­ло­та вы­де­ля­ет­ся, а при про­хож­де­нии об­рат­ной – по­гло­ща­ет­ся.

Правило: Если уве­ли­чить тем­пе­ра­ту­ру, то, со­глас­но пра­ви­лу Ле Ша­те­лье, рав­но­ве­сие сме­стит­ся в таком на­прав­ле­нии, чтобы умень­шить это воз­дей­ствие.

В дан­ном слу­чае влево, так как теп­ло­та по­гло­ща­ет­ся. Ре­ак­ция син­те­за ам­ми­а­ка про­во­дит­ся при тем­пе­ра­ту­ре около 500

Если ре­ак­ция эн­до­тер­ми­че­ская, то по­вы­ше­ние тем­пе­ра­ту­ры при­ве­дет к сме­ще­нию рав­но­ве­сия впра­во.

2. Из­ме­не­ние кон­цен­тра­ции ве­ществ

Правило:При уве­ли­че­нии кон­цен­тра­ции ка­ко­го-ли­бо из ве­ществ, участ­ву­ю­щих в рав­но­вес­ной ре­ак­ции, рав­но­ве­сие ре­ак­ции сме­стит­ся в сто­ро­ну его рас­хо­до­ва­ния, а со­от­вет­ствен­но, при умень­ше­нии кон­цен­тра­ции ка­ко­го-ли­бо из ве­ществ – в сто­ро­ну ре­ак­ции его об­ра­зо­ва­ния.

На­при­мер, при уве­ли­че­нии кон­цен­тра­ции азота в ре­ак­ции син­те­за ам­ми­а­ка, рав­но­ве­сие сме­стит­ся впра­во, т. е. в сто­ро­ну рас­хо­до­ва­ния азота. Если же в этой ре­ак­ции уда­лять из ре­ак­ци­он­ной смеси ам­ми­ак, то рав­но­ве­сие сме­стит­ся в сто­ро­ну его об­ра­зо­ва­ния. Сде­лать это можно, на­при­мер, при рас­тво­ре­нии ам­ми­а­ка в воде.

3. Из­ме­не­ние дав­ле­ния

Правило:Из­ме­не­ние дав­ле­ния может ока­зы­вать вли­я­ние толь­ко на ре­ак­ции с уча­сти­ем га­зо­об­раз­ных ве­ществ. При увеличении давления химическое равновесие смещается в сторону уменьшения объемов веществ. 

Если в ре­ак­ции син­те­за ам­ми­а­ка уве­ли­чить дав­ле­ние, рав­но­ве­сие сме­стит­ся в сто­ро­ну умень­ше­ния числа моль газа. Если слева число моль газа боль­ше, чем спра­ва, рав­но­ве­сие сме­стит­ся в сто­ро­ну об­ра­зо­ва­ния ам­ми­а­ка.

Если число моль газа оди­на­ко­во и слева и спра­ва, на­при­мер, в ре­ак­ции по­лу­че­ния ок­си­да азота (II),

N₂ +O₂      (3)

то из­ме­не­ние дав­ле­ния не будет ока­зы­вать вли­я­ние на по­ло­же­ние хи­ми­че­ско­го рав­но­ве­сия в таких ре­ак­ци­ях. Изу­че­ние хи­ми­че­ско­го рав­но­ве­сия имеет боль­шое зна­че­ние, как для тео­ре­ти­че­ских ис­сле­до­ва­ний, так и для ре­ше­ния прак­ти­че­ских задач. Опре­де­ляя по­ло­же­ние рав­но­ве­сия для раз­лич­ных тем­пе­ра­тур и дав­ле­ний, можно вы­брать наи­бо­лее бла­го­при­ят­ные усло­вия про­ве­де­ния хи­ми­че­ско­го про­цес­са. Окон­ча­тель­ный выбор усло­вий тре­бу­ет учета вли­я­ния их и на ско­рость про­цес­са.

Видео “Химическое равновесие в растворах”

V. Примеры решения задач

Задача №1. Во сколько раз изменится скорость прямой и обратной реакции в системе: 2SO₂(г) + O₂(г) = 2SO₃(г), если объем газовой смеси уменьшить в три раза? В какую сторону сместится равновесие системы?

Решение. Обозначим концентрации реагирующих веществ: [SO₂]= a, [О₂] = b, [SO₃] = с.Согласно закону действия масс скорости v прямой и обратной реакции до изменения объема:

v_пр = Ка²b

    v_обр = К₁с²

После уменьшения объема гомогенной системы в три раза концентрация каждого из реагирующих веществ увеличится в три раза: [SO₂] = 3а, [О₂] = 3b; [SO₃] = 3с. При новых концентрациях скорости v’ прямой и обратной реакции:

v’_пр = К(3а)²(3b) = 27Ка²b

v’_обр = К₁(3с)² = 9К₁с²

Отсюда:

Следовательно, скорость прямой реакции увеличилась в 27 раз, а обратной – только в девять раз. Равновесие системы сместилось в сторону образования SO₃.

Задача №2. Вычислите, во сколько раз увеличится скорость реакции, протекающей в газовой фазе, при повышении температуры от 30 до 70^оС, если температурный коэффициент реакции равен 2.

Решение. Зависимость скорости химической реакции от температуры определяется эмпирическим правилом Вант-Гоффа по формуле:

Следовательно, скорость реакции νТ₂ при температуре 70^оС больше скорости реакции νТ₁при температуре 30^оС в 16 раз.

Задача № 3. Константа равновесия гомогенной системы: СО(г) + Н₂О(г) = СО₂(г) + Н₂(г)

при 850^оС равна 1. Вычислите концентрации всех веществ при равновесии, если исходные концентрации: [СО]_исх =3 моль/л, [Н₂О]_исх = 2 моль/л.

Решение. При равновесии скорости прямой и обратной реакций равны, а отношение констант этих скоростей постоянно и называется константой равновесия данной системы:

v_{пр =} К₁ [СО][Н₂О]

v_обр = К₂[СО₂][Н₂]

В условии задачи даны исходные концентрации, тогда как в выражение К_р входят только равновесные концентрации всех веществ системы. Предположим, что к моменту равновесия концентрации [СО₂]_р = х моль/л. Согласно уравнению системы число молей образовавшегося водорода при этом будет также х моль/л. По столько же молей (х моль/л) СО и Н₂О расходуется для образования по х молей СО₂ и Н₂. Следовательно, равновесные концентрации всех четырех веществ:

[СО₂]_р = [Н₂]_р = х моль/л; 

[СО]_р = (3 – х) моль/л;

[Н₂О]_р = (2 – х) моль/л.

Зная константу равновесия, находим значение х, а затем исходные концентрации всех веществ:

Таким образом, искомые равновесные концентрации:

[СО₂]_р = 1,2 моль/л;

[Н₂]_р= 1,2 моль/л;

[СО]_р = 3 – 1,2 = 1,8 моль/л;

[Н₂О]_р = 2 – 1,2 = 0,8 моль/л.

Задача № 4. При некоторой температуре равновесные концентрации в системе 2CO _(г) + O_{2 (г)} ↔ 2CO_2(г) составляли: [CO] = 0,2 моль/л, [O₂] = 0,32 моль/л, [CO₂] = 0,16 моль/л. Определить константу равновесия при этой температуре и исходные концентрации CO и O₂, если исходная смесь не содержала СО₂.

Решение:

1). Так как в условии задачи  даны равновесные концентрации, то константа равновесия равна 2:

2). Если исходная смесь не содержала СО₂, то на момент химического равновесия в системе образовалось 0,16 моль СО₂.

По УХР: 2CO_(г) + O_2(г) ↔ 2CO_2(г)

На образование 0,16 моль СО₂ затрачено:

υ_{прореагировавшее}(СО)=υ(CO₂)=0,16 моль

υ_{прореагировавшее}(О₂)=1/2υ(CO₂)=0,08 моль

Следовательно,

υ_{исходное} = υ_{прореагировавшее} + υ_{равновесное}

υ_{исходное} (СО)=0,16 +0,2 = 0,36 моль

υ_{исходное} (O₂)=0,08 +0,32 = 0,4 моль

Вещество	CO	O2	CO2
Сисходная	0,36	0,4	0
Спрореагировавшая	0,16	0,08	0,16
Сравновесная	0,2	0,32	0,16

Задача № 5. Определить равновесную концентрацию HI в системе H_2(г) + I_2(г) ↔ 2HI_(г), если при некоторой температуре константа равновесия равна 4, а исходные концентрации H₂ , I₂ и HI равны, соответственно, 1, 2 и 0 моль/л.

Решение. Пусть к некоторому моменту времени образовалось x моль/л  HI 

Вещество	H2	I2	HI
сисходн., моль/л	1	2	0
спрореагир., моль/л	х/2	х/2	x
cравн., моль/л	1-x/2	2-x/2	x

Тогда,

Решая это уравнение, получаем, что равновесная концентрация HI равна 1,33 моль/л.

Задача №6. Эндотермическая реакция разложения пентахлорида фосфора протекает по уравнению: PCl₅(г) = РСl₃(г) + Сl(г); ΔН = + 92,59 кДж. Как надо изменить: а) температуру; б) давление; в) концентрацию, чтобы сместить равновесие в сторону прямой реакции – разложения PCl₅?

Решение. Смещением или сдвигом химического равновесия называют изменение равновесных концентраций реагирующих веществ в результате изменения одного из условий реакции. Направление, в котором сместилось равновесно, определяется по принципу Ле Шателье: а) так как реакция разложения PCl₅ эндотермическая (ΔН > 0) то для смещения равновесия в сторону прямой реакции нужно повысить температуру; б) так как в данной системе разложение РСl₅ ведет к увеличению объема (из одной молекулы газа образуются две газообразные молекулы), то для смещения равновесия в сторону прямой реакции надо уменьшить давление; в) смещения равновесия в указанном направлении можно достигнуть как увеличением концентрации РСl₅, так и уменьшением концентрации РСl₃ или Сl₂.

VI. Решите задачи

Задача №1. Исходные концентрации СO и O₂ в обратимой реакции 2CO(г) + O₂(г)↔ 2CO₂(г) равны соответственно 6  и 4 моль/л. Вычислите константу равновесия, если концентрацияCO₂ в момент равновесия равна 2 моль/л.

Задача №2. Реакция протекает по уравнению 2SO₂(г) + O₂(г) = 2SO₃(г) + Q

Укажите, куда сместится равновесие, если

а) увеличить давление

б) повысить температуру

в) увеличить концентрацию кислорода

г) введение катализатора?

ЦОРы

Видео:“Химическое равновесие в растворах”

Химическое равновесие – состояние химической системы, при котором скорость прямой реакции равна скорости обратной.

В большом количестве заданий, которые мне довелось увидеть, я ни один раз видел, как коверкают это определение. Например, в заданиях верно-неверно
предлагают похожий вариант, однако говорят о “равенстве концентраций исходных веществ и продуктов” – это грубая ошибка. Химическое равновесие –
равенство скоростей.

Принцип Ле Шателье

В 1884 году французским химиком Анри Ле Шателье был предложен принцип, согласно которому, если на систему, находящуюся в состоянии
равновесия, оказать внешнее воздействие (изменить температуру, давление, концентрацию), то система будет стремиться компенсировать
внешнее воздействие.

Это принцип обоснован термодинамически и доказан. Однако в такой абстрактной формулировке его сложно применить для решения конкретных
задач по химическому равновесию. В этой статье я покажу конкретные примеры и обозначу алгоритм действия, чтобы вы могли успешно
справляться с заданиями.

Влияние изменения концентрации на химическое равновесие

При увеличении концентрации какого-либо компонента химической реакции, система будет стремиться восстановить равновесие:
равновесие будет смещаться в сторону расходования добавленного компонента.

Объясню проще: если вы увеличиваете концентрацию вещества, которое находится в левой части, равновесие сместится в правую сторону.
Если добавляете вещество из левой части (продуктов реакции) – смещается в сторону исходных веществ. Посмотрите на пример ниже.

Если мы попытаемся удалить какое-либо вещество из системы (уменьшить его концентрацию), то система будет стремиться заполнить “пустое”
место, которые мы создали. Наглядно демонстрирую на примере:

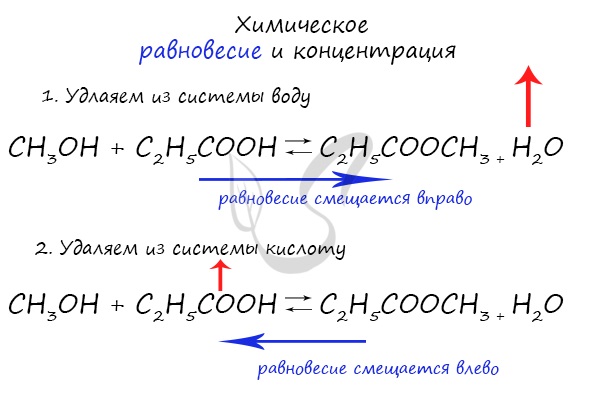
Можно подвести итог полученным знаниям таким образом: “Куда добавляем – оттуда смещается, откуда берем – туда смещается”. Воспользуйтесь
этой или придумайте свое правило для запоминания этой закономерности 😉

Изменения давления и химическое равновесие

Если речь в задании идет об изменении давления, то первое, что нужно сделать, это посчитать количество газов в уравнении слева и справа.
Твердые вещества и жидкости считать не нужно. Например:

CO_2(г) + С_(тв) ⇄ 2CO_(г) – Q

В приведенном уравнении количество молекул газа в левой части – 1, в правой – 2.

Запомните правило: “При увеличении давления равновесие смещается в сторону меньших газов, при уменьшении давления – в сторону больших газов”.
Для нашей системы правило действует таким образом:

В случае, если слева и справа количество молекул газа одинаково, например, в реакции:

H_2(г) + I_2(г) ⇄ 2HI_(г) – Q

Слева – 2 газа, и справа – 2. В такой реакции увеличение или уменьшение давления не повлияет на химическое равновесие.

Изменение температуры и химическое равновесие

Если в задании увеличивают или уменьшают температуру, то первое, что вы должны оценить: экзотермическая это реакция или
эндотермическая.

Следуйте следующему правилу: “При увеличении температуры равновесие смещается в сторону эндотермической реакции, при
уменьшении – в сторону экзотермической реакции”. У любой обратимой реакции есть экзо- и эндотермические части:

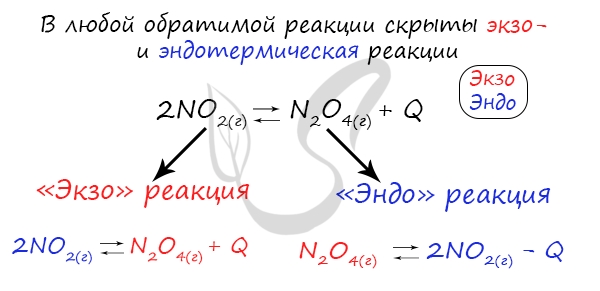
Поэтому данное правило универсально и применимо для всех реакций. Для примера разберем следующие задачи:

Чтобы не осталось белых пятен, возьмем экзотермическую реакцию и повторим с ней подобный эксперимент.

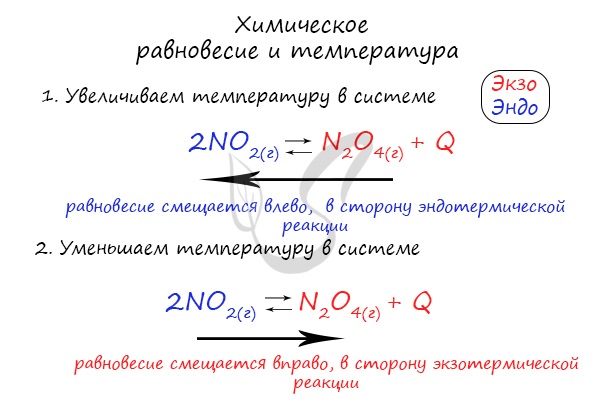
Катализатор и ингибитор

Действие катализатора и ингибитора соответственно касается только ускорения и замедления химической реакции. Они никоим образом не влияют на равновесие.

Константа равновесия

Константой равновесия называют отношения скоростей прямой и обратной реакции. Для реакции типа aA + bB = cC + dD константа
равновесия будет записана следующим образом:

Решим задачу. Дана реакция: 2NO + Cl₂ ⇄ 2NOCl . Вычислите константу равновесия, если равновесные концентрации
веществ для данной реакции: c(NO) = 1.8 моль/л , c(Cl₂) = 1.2 моль/л , c(NOCl) = 0.8 моль/л.

Константу равновесия для данной задачи можно представить в виде 1.64 * 10^-1.