Методы определения
порядка реакции.
I. Метод подстановки.
Основным условием в данном методе
является независимость константы
скорости от времени протекания реакции:
k![]() .
.
Пусть при изучении скорости протекания
реакции мы имеем следующие данные убыли
концентрации исходного вещества:
|
|
0 |
5 10 |
10 |
15 |
|
c |
c |
c |
c |
c |
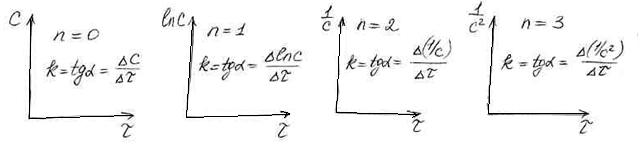
Экспериментальные данные подставляются
в одно из известных кинетических
уравнений и критерием правильности
выбранного уравнения является постоянство
константы скорости во времени.
n=0 k=![]()
n=1 k=![]()
n=2 k=![]()
n=3 k=![]()
Методом подстановки можно определить
порядок реакции, если он имеет целочисленное
значение.
II. Графический метод.
Здесь также основным условием является
независимость константы скорости от
времени протекания реакции: k![]() .
.
Зависимость концентрации от времени
для реакций различных порядков может
быть выражена прямой линией, если выбрать
соответствующую систему координат.
Уравнение прямой выглядит следующим
образом: y=ax+в,
где в – это постоянная, равная тангенсу
угла наклона этот прямой: в=tg![]() .
.
Например, n=1 (реакция
первого порядка)
k =![]() ;
;
k![]() =
=
lnc![]() –
–
lnc;
lnc = lnc![]() -k
-k![]() .
.
Это уравнение будет уравнением прямой
в координатах lnc(![]() ),
),
когда k не будет
зависеть от
![]() .
.
Из графика легко определяется константа
скорости реакции:
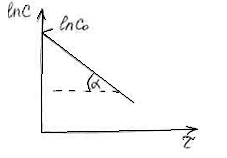
tg![]() =k=
=k=![]()
Таким образом, смотря в каких координатах
зависимости концентрации от времени
мы получим прямую, такой порядок имеет
химическая реакция.
III. Метод половинного
превращения.
Этот метод основан на том, что время
полупревращения для реакций различного
порядка по-разному зависит от начальной
концентрации реагентов:
![]() .
.
n=0:
![]() .
.
Для реакций нулевого порядка время
полупревращения прямо пропорционально
начальной концентрации реагента.
n=1:
![]() ;
;
![]()
. Для реакций первого порядка время
полупревращения не зависит от начальной
концентрации реагента.
n=2:
![]() .
.
Для реакций второго порядка время
полупревращения обратно пропорционально
начальной концентрации реагента.
n=3:
![]() .
.
Для реакций третьего порядка время
полупревращения обратно пропорционально
квадрату начальной концентрации
реагента.
В общем случае время полупревращения
равно:
n![]() 1
1
![]() (1)
(1)
;
![]()
(2)
Прологарифмируем уравнения (1) и (2) и
получим:
![]()
Таким образом, строя зависимость
![]()
от lnc![]() ,
,
по тангенсу угла наклона можно определить
порядок реакции.
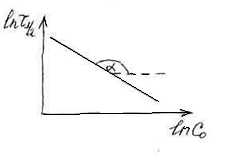
tg![]()
IV.
Метод Вант-Гоффа.
Этот метод позволяет определить дробный
порядок реакции.
Метод Вант-Гоффа заключается в следующем.
Проводится два опыта, в которых начальные
концентрации вещества, по которому
определяется порядок реакции, равны c![]()
и c![]()
(концентрации других веществ во много
раз больше). Тогда скорости реакции в
первом и втором опытах будут равны:
![]() ;
;![]() ;
;
n – порядок реакции.
![]() ;
;![]()
Поделим эти уравнения и получим:
n=![]()
Для решения этого уравнения необходимо
найти значения скоростей в момент
времени
![]()
и
![]()
![]() .
.
Скорости определяют графически из
наклона касательной в точке соответствующей
кинетической кривой.

![]()
![]()
V. Метод избытков
Оствальда (метод понижения порядка
реакции).
С помощью этого метода определяется
частный порядок по одному или нескольким
веществам вследствие понижения общего
порядка, т.к. взят избыток одного из
реагентов. Частный порядок определяется
четырьмя выше перечисленными методами.
Например, процесс инверсии сахарозы в
водном растворе представим следующим
образом:
C![]()
избыток
![]()
Порядок этой реакции должен быть вторым,
но избыток реагента – воды приводит к
тому, что ее концентрацию можно принять
равной единице (С![]() .
.
![]()
Экспериментально
определенный порядок этой реакции –
первый (![]() .
.
Рассмотрим реакцию
![]() +B
+B![]() P
P
![]()
![]()
Сначала в избытке возьмем вещество А.
Тогда скорость реакции будет пропорциональна
только концентрации вещества В, поэтому
можно определить порядок по веществу
В (![]() ).
).
Затем в избытке возьмем вещество В.
Тогда скорость реакции будет пропорциональна
только концентрации вещества А, поэтому
можно определить порядок по веществу
А (![]() .
.
А+![]()
общий
порядок будет равен сумме порядков
![]()
n![]()
по
отдельным компонентам (![]()
Пример.
Приведем пример определения порядка
реакции превращения цианата аммония в
карбамид (мочевину) NH![]() CNO
CNO![]()
по времени полупревращения
![]() ,
,
который в зависимости от исходной
начальной концентрации изменяется
следующим образом:
C![]() ,
,
моль/л 0,05 0,10 0,20
![]() ,
,
ч 37,03 19,15 9,45
Рассчитаем константу скорости реакции
для первого порядка, используя время
полупревращения.
 ;
;
![]() =
=![]()
n=1
![]()
![]()
Реакция не первого порядка, т.к. константа
скорости монотонно возрастает.
Рассчитаем константу скорости реакции
второго порядка.
k=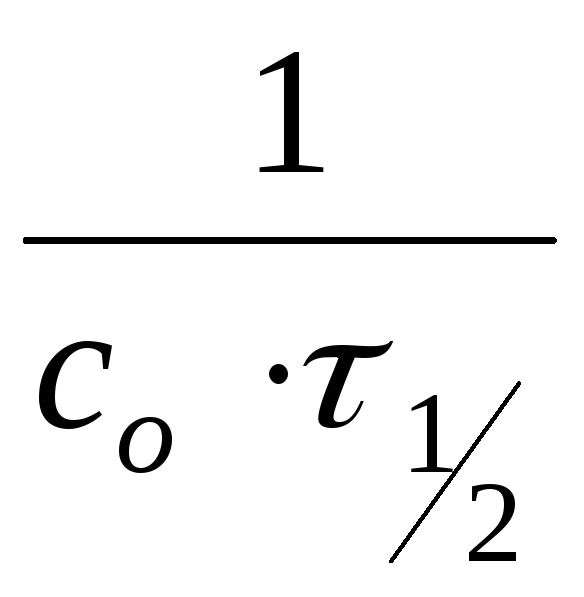 ;
;
k![]() =
=![]()
![]()
n=2 k![]()
![]()
k![]()
![]()
Так как константа скорости почти
постоянна, можно считать,
что это реакция второго порядка.
Кинетика сложных химических реакций.
Сложными называются реакции,
состоящие из нескольких простых.
Все многообразие сложных реакций
можно свести к различным комбинациям
простых (элементарных) реакций.
Суммарное кинетическое
уравнение таких реакций обычно содержит
несколько констант скоростей.
Типичными сложными реакциями
являются обратимые, параллельные,
последовательные и сопряженные
реакции.
1. А+В![]() С
С
обратимые
2. А![]()
![]()
параллельные
3. А![]()
последовательные
4. А![]()
сопряженные, т.е. одна
реакция не идет без другой
А![]()
1. Кинетика обратимых реакций.
Обратимыми называются реакции,
которые протекают одновременно в двух
противоположных направлениях. Наиболее
простой тип обратимых реакций – это
обратимые реакции первого порядка:
А![]() В
В
Обозначим, начальная концентрация
исходного вещества А: C![]() ;
;
концентрация продукта В в момент времени
![]() ;
;
концентрация исходного вещества А в
момент времени
![]() ,
,
т.к. в реакции данного типа исчезновение
определенного количества молекул
вещества А вызывает образование точного
такого же количества молекул вещества
В.
Воспользуемся постулатами химической
кинетики:
I постулат – если
протекает одновременно несколько
реакций, то каждая из них независима от
остальных.
Концентрация продукта В изменяется как
за счет прямого, так и обратного процесса.
Поэтому dx=dx![]() +dx
+dx![]() ,
,
где
dx![]() –
–
изменение концентрации вещества В в
результате прямой реакции;
dx![]() –
–
изменение концентрации вещества В в
результате обратной реакции.
Напишем кинетические уравнения прямой
и обратной реакции, используя концентрацию
продукта В:
![]()
![]()
Скорость суммарной реакции равна:
![]()
Разделим переменные, проинтегрируем
это выражение и получим:
![]()
(*)
При равновесии, когда скорость прямой
и обратной реакции равны (![]() ,
,
dx/![]() ,
,
тогда
![]() ,
,
где
![]() –
–
концентрация продукта В при равновесии.
Тогда уравнение (*) запишется в виде:
![]()
(**)
Совместно решая уравнения (*) и (**),
получим:
k![]() =
=![]()
Таким образом, для расчета скорости
обратимой реакции необходимо знать
исходные и равновесные концентрации
реагентов.
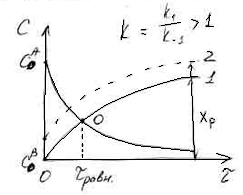
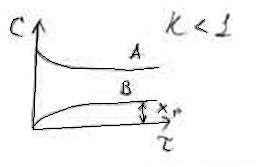
Кинетические кривые для обратимых
процессов.
Рассмотрим кинетические кривые для
обратимой реакции первого порядка.
 1.c
1.c![]()
2.c![]()
В отсутствии обратимой реакции
концентрация исходного вещества А по
мере увеличения времени реакции
становится равной нулю. В случае обратимой
химической реакции концентрация вещества
А снижается, но не достигает нуля.
Концентрация продукта В в начале реакции
равна нулю (кривая 1), а затем увеличивается.
В точке О кривые пересекаются и СА=СВ,
т.е.
![]() С
С
= СА – СВ = 0. Это означает, что
скорость обратимой реакции равна нулю
(![]() ).
).
Время, соответствующее точке О, является
временем достижения равновесия обратимой
химической реакции.
Если начальная концентрация продукта
В не равна нулю, то достижение химического
равновесия обратимой реакции произойдет
быстрее, на что указывает точка пересечения
кривой 2 и кривой убыли исходного вещества
А.
2. Кинетика
параллельных реакций.
Реакции называются параллельными,
если исходные вещества одновременно
реагируют в нескольких направлениях.
Примером односторонних параллельных
реакций является реакция разложения
бертолетовой соли, протекающая при не
очень интенсивном нагревании в двух
направлениях:
6KClO![]()
Если параллельно протекают две
мономолекулярные реакции:
![]()
x=y+z
Обозначим: С0А =а – начальная
концентрация исходного компонента А;
х – количество прореагировавшего
вещества А, независимо от того, в какой
продукт оно превратилось; у – количество
вещества, превратившегося в первый
продукт реакции В; z – во
второй продукт реакции С.
Для каждой реакции можно записать:
![]()
![]()
Полная скорость превращения исходного
вещества равна сумме двух скоростей:
![]()
После интегрирования получим:
![]()
Для констант равновесия параллельных
реакций первого порядка можно записать
следующие выражения:
k![]()
k![]()
В параллельных реакциях первого порядка
отношение количества прореагировавшего
вещества в каждой из реакции в любой
момент времени постоянно и равно
отношению констант скоростей этих
реакций:
![]()

При изучении параллельных реакций
определяют сумму констант скоростей
по убыли вещества, а по отношению
концентраций образовавшихся веществ
– отношение констант скоростей. После
этого находят величины констант
скоростей отдельных реакций.
Кинетические кривые для параллельных
реакций практически такие же, как
для обратимых реакций.
Соседние файлы в папке Лекции по ФХ 2 семестр
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Курс
Меня зовут Кузьмин Владимир Александрович.
Я репетитор по Химии
![[[pictureof]]](https://dist-tutor.info/s3/dist-tutor/user/2/ava/thumbnails/RgocnqRS3C4j3ys.jpg)
Вам нужны консультации по Химии по Skype?
Если да, подайте заявку. Стоимость договорная.
Чтобы закрыть это окно, нажмите “Нет”.
Реакции первого порядка
Реакции первого порядка – это реакции, в которых показатель степени в уравнении зависимости скорости от концентрации, в которую возводится концентрация, равен единице.
Все реакции радиоактивного распада являются реакциями первого порядка. Также можно привести в пример реакции изомеризации, распада некоторых молекул в газовой фазе: N2O5, CH3-O-CH3 и т.д.
Выражение для мгновенной скорости реакции по какому-либо из реагентов записывается в виде:

, где v – мгновенная скорость, dc – бесконечно малое изменение молярной концентрации, dt – бесконечно малый промежуток времени.
Напомним, что знак минус перед правой частью уравнения ставиться для того, чтобы скорость была положительной величиной (изменение концентрации реагента – величина отрицательная, так как концентрация реагентов во время протекания реакции уменьшается).
По закону действующих масс – закону Гульберга-Вааге, скорость реакции прямо пропорциональная концентрации. Для реакций первого порядка (порядок – показатель степени в которую возводится концентрация) математическое выражение этого закона принимает вид:

, где k – константа скорости.
Приравняем правые части приведенных выше уравнений друг к другу:


Для того чтобы понять сколько вещества вступит в реакцию за определенный интервал времени, нам необходимо решить данное дифференциальное уравнение, т.е. найти его первообразную.
Запишем выражение для вычисления определённого интеграла, чтобы в дальнейшем не решать задачу Коши (решение дифференциального уравнения, удовлетворяющего начальным условиям, для нас это исходная концентрация и исходное время). Хотя, можно поступить иначе и вычислить неопределенный интеграл данного уравнения, а затем через начальные условия определить константу интегрирования (т.е. решить задачу Коши).

Для нахождения интеграла, напомним, что:

, где С – постоянная интегрирования
Результат интегрирования следующий:



Отсюда найдем уравнение для нахождения концентрации регента в момент времени t:

Если изменить порядок действий, то легко прийти к уравнению для нахождения константы реакции первого порядка:

Выведем уравнение для нахождения константы реакции первого порядка через период полупревращения.
Период полупревращения – время, которое необходимо для превращения половины исходного количества вещества.
Т.е. к моменту времени t молярная концентрация вещества будет равна ½ её исходного значения:

Для решения расчётных задач можно использовать формулу:

Из формулы видно, что время полупревращения для реакций первого порядка не зависит от количества, или концентрации исходного вещества.


Это уравнение есть ни что иное как линейная зависимость ln(c) от t .
Построим график этой зависимости.

Отсюда, константа скорости реакции первого порядка численно равна тангенсу угла наклона прямой к оси t.

Определим размерность константы реакции первого порядка. Для этого в уравнение:

подставим размерности скорости и молярной концентрации:

Отсюда размерность константы реакции первого порядка.

Химическая кинетика
| Напечатано:: | Гость |
| Дата: | суббота, 20 мая 2023, 17:13 |
Описание
Законы химической термодинамики позволяют определить направление и предел протекания возможного при данных условиях химического процесса, а также его энергетический эффект. Однако термодинамика не может ответить на вопросы о том, как осуществляется данный процесс и с какой скоростью. Эти вопросы – механизм и скорость химической реакции – и являются предметом химической кинетики.
Оглавление
- 1. Скорость химической реакции
- 1.1. Кинетическое уравнение химической реакции. Порядок реакции
- 1.2. Реакции нулевого порядка
- 1.3. Реакции первого порядка
- 1.4. Реакции второго порядка
- 1.5. Методы определения порядка реакции
1. Скорость химической реакции
Дадим определение основному понятию химической кинетики – скорости химической реакции:
Скорость химической реакции есть число элементарных актов химической реакции, происходящих в единицу времени в единице объема (для гомогенных реакций) или на единице поверхности (для гетерогенных реакций).
Скорость химической реакции есть изменение концентрации реагирующих веществ в единицу времени.
Первое определение является наиболее строгим; из него следует, что скорость химической реакции можно также выражать как изменение во времени любого параметра состояния системы, зависящего от числа частиц какого-либо реагирующего вещества, отнесенное к единице объема или поверхности – электропроводности, оптической плотности, диэлектрической проницаемости и т.д. и т.п. Однако наиболее часто в химии рассматривается зависимость концентрации реагентов от времени. В случае односторонних (необратимых) химических реакций (здесь и далее рассматриваются только односторонние реакции) очевидно, что концентрации исходных веществ во времени постоянно уменьшаются (ΔСисх < 0), а концентрации продуктов реакции увеличиваются (ΔСпрод > 0). Скорость реакции считается положительной, поэтому математически определение средней скорости реакции в интервале времени Δt записывается следующим образом:
(II.1)
В различных интервалах времени средняя скорость химической реакции имеет разные значения; истинная (мгновенная) скорость реакции определяется как производная от концентрации по времени:
(II.2)
Графическое изображение зависимости концентрации реагентов от времени есть кинетическая кривая (рисунок 2.1).
Рис. 2.1 Кинетические кривые для исходных веществ (А) и продуктов реакции (В).
Истинную скорость реакции можно определить графически, проведя касательную к кинетической кривой (рис. 2.2); истинная скорость реакции в данный момент времени равна по абсолютной величине тангенсу угла наклона касательной:
Рис. 2.2 Графическое определение Vист.
(II.3)
Необходимо отметить, что в том случае, если стехиометрические коэффициенты в уравнении химической реакции неодинаковы, величина скорости реакции будет зависеть от того, изменение концентрации какого реагента определялось. Очевидно, что в реакции
2Н2 + О2 → 2Н2О
концентрации водорода, кислорода и воды изменяются в различной степени:
ΔС(Н2) = ΔС(Н2О) = 2 ΔС(О2).
Скорость химической реакции зависит от множества факторов: природы реагирующих веществ, их концентрации, температуры, природы растворителя и т.д.
Одной из задач, стоящих перед химической кинетикой, является определение состава реакционной смеси (т.е. концентраций всех реагентов) в любой момент времени, для чего необходимо знать зависимость скорости реакции от концентраций. В общем случае, чем больше концентрации реагирующих веществ, тем больше скорость химической реакции. В основе химической кинетики лежит т. н. основной постулат химической кинетики:
Скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ, взятых в некоторых степенях.
Т. е. для реакции
аА + bВ + dD + … → еЕ + …
можно записать
(II.4)
Коэффициент пропорциональности k есть константа скорости химической реакции. Константа скорости численно равна скорости реакции при концентрациях всех реагирующих веществ, равных 1 моль/л.
Зависимость скорости реакции от концентраций реагирующих веществ определяется экспериментально и называется кинетическим уравнением химической реакции. Очевидно, что для того, чтобы записать кинетическое уравнение, необходимо экспериментально определить величину константы скорости и показателей степени при концентрациях реагирующих веществ. Показатель степени при концентрации каждого из реагирующих веществ в кинетическом уравнении химической реакции (в уравнении (II.4) соответственно x, y и z) есть частный порядок реакции по данному компоненту. Сумма показателей степени в кинетическом уравнении химической реакции (x + y + z) представляет собой общий порядок реакции. Следует подчеркнуть, что порядок реакции определяется только из экспериментальных данных и не связан со стехиометрическими коэффициентами при реагентах в уравнении реакции. Стехиометрическое уравнение реакции представляет собой уравнение материального баланса и никоим образом не может определять характера протекания этой реакции во времени.
В химической кинетике принято классифицировать реакции по величине общего порядка реакции. Рассмотрим зависимость концентрации реагирующих веществ от времени для необратимых (односторонних) реакций нулевого, первого и второго порядков.
1.1. Кинетическое уравнение химической реакции. Порядок реакции
Одной из задач, стоящих перед химической кинетикой, является определение состава реакционной смеси (т.е. концентраций всех реагентов) в любой момент времени, для чего необходимо знать зависимость скорости реакции от концентраций. В общем случае, чем больше концентрации реагирующих веществ, тем больше скорость химической реакции. В основе химической кинетики лежит т. н. основной постулат химической кинетики:
Скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ, взятых в некоторых степенях.
Т. е. для реакции
аА + bВ + dD + … → еЕ + …
можно записать
(II.4)
Коэффициент пропорциональности k есть константа скорости химической реакции. Константа скорости численно равна скорости реакции при концентрациях всех реагирующих веществ, равных 1 моль/л.
Зависимость скорости реакции от концентраций реагирующих веществ определяется экспериментально и называется кинетическим уравнением химической реакции. Очевидно, что для того, чтобы записать кинетическое уравнение, необходимо экспериментально определить величину константы скорости и показателей степени при концентрациях реагирующих веществ. Показатель степени при концентрации каждого из реагирующих веществ в кинетическом уравнении химической реакции (в уравнении (II.4) соответственно x, y и z) есть частный порядок реакции по данному компоненту. Сумма показателей степени в кинетическом уравнении химической реакции (x + y + z) представляет собой общий порядок реакции. Следует подчеркнуть, что порядок реакции определяется только из экспериментальных данных и не связан со стехиометрическими коэффициентами при реагентах в уравнении реакции. Стехиометрическое уравнение реакции представляет собой уравнение материального баланса и никоим образом не может определять характера протекания этой реакции во времени.
В химической кинетике принято классифицировать реакции по величине общего порядка реакции. Рассмотрим зависимость концентрации реагирующих веществ от времени для необратимых (односторонних) реакций нулевого, первого и второго порядков.
1.2. Реакции нулевого порядка
Для реакций нулевого порядка кинетическое уравнение имеет следующий вид:
(II.5)
Скорость реакции нулевого порядка постоянна во времени и не зависит от концентраций реагирующих веществ; это характерно для многих гетерогенных (идущих на поверхности раздела фаз) реакций в том случае, когда скорость диффузии реагентов к поверхности меньше скорости их химического превращения.
1.3. Реакции первого порядка
Рассмотрим зависимость от времени концентрации исходного вещества А для случая реакции первого порядка А → В. Реакции первого порядка характеризуются кинетическим уравнением вида (II.6). Подставим в него выражение (II.2):
(II.6)
(II.7)
После интегрирования выражения (II.7) получаем:
(II.8)
Константу интегрирования g определим из начальных условий: в момент времени t = 0 концентрация С равна начальной концентрации Со. Отсюда следует, что g = ln Со. Получаем:
(II.9)
Рис. 2.3 Зависимость логарифма концентрации от времени для реакций первого порядка.
Т.о., логарифм концентрации для реакции первого порядка линейно зависит от времени (рис. 2.3) и константа скорости численно равна тангенсу угла наклона прямой к оси времени.
(II.10)
Из уравнения (II.9) легко получить выражение для константы скорости односторонней реакции первого порядка:
(II.11)
Еще одной кинетической характеристикой реакции является период полупревращения t1/2 – время, за которое концентрация исходного вещества уменьшается вдвое по сравнению с исходной. Выразим t1/2 для реакции первого порядка, учитывая, что С = ½Со:
(II.12)
Отсюда
(II.13)
Как видно из полученного выражения, период полупревращения реакции первого порядка не зависит от начальной концентрации исходного вещества.
1.4. Реакции второго порядка
Для реакций второго порядка кинетическое уравнение имеет следующий вид:
(II.14)
либо
(II.15)
Рассмотрим простейший случай, когда кинетическое уравнение имеет вид (II.14) или, что то же самое, в уравнении вида (II.15) концентрации исходных веществ одинаковы; уравнение (II.14) в этом случае можно переписать следующим образом:
(II.16)
После разделения переменных и интегрирования получаем:
(II.17)
Постоянную интегрирования g, как и в предыдущем случае, определим из начальных условий. Получим:
(II.18)
Таким образом, для реакций второго порядка, имеющих кинетическое уравнение вида (II.14), характерна линейная зависимость обратной концентрации от времени (рис. 2.4) и константа скорости равна тангенсу угла наклона прямой к оси времени:
(II.19)
(II.20)
Рис. 2.4 Зависимость обратной концентрации от времени для реакций второго порядка.
Если начальные концентрации реагирующих веществ Cо,А и Cо,В различны, то константу скорости реакции находят интегрированием уравнения (II.21), в котором CА и CВ – концентрации реагирующих веществ в момент времени t от начала реакции:
(II.21)
В этом случае для константы скорости получаем выражение
(II.22)
Порядок химической реакции есть формально-кинетическое понятие, физический смысл которого для элементарных (одностадийных) реакций заключается в следующем: порядок реакции равен числу одновременно изменяющихся концентраций. В случае элементарных реакций порядок реакции может быть равен сумме коэффициентов в стехиометрическом уравнении реакции; однако в общем случае порядок реакции определяется только из экспериментальных данных и зависит от условий проведения реакции. Рассмотрим в качестве примера элементарную реакцию гидролиза этилового эфира уксусной кислоты (этилацетата), кинетика которой изучается в лабораторном практикуме по физической химии:
СН3СООС2Н5 + Н2О → СН3СООН + С2Н5ОН
Если проводить эту реакцию при близких концентрациях этилацетата и воды, то общий порядок реакции равен двум и кинетическое уравнение имеет следующий вид:
(II.23)
При проведении этой же реакции в условиях большого избытка одного из реагентов (воды или этилацетата) концентрация вещества, находящегося в избытке, практически не изменяется и может быть включена в константу скорости; кинетическое уравнение для двух возможных случаев принимает следующий вид:
1) Избыток воды:
(II.24)
(II.25)
2) Избыток этилацетата:
(II.26)
(II.27)
В этих случаях мы имеем дело с так назывемой реакцией псевдопервого порядка. Проведение реакции при большом избытке одного из исходных веществ используется для определения частных порядков реакции.
1.5. Методы определения порядка реакции
Проведение реакции в условиях, когда концентрация одного из реагентов много меньше концентрации другого (других) и скорость реакции зависит от концентрации только этого реагента, используется для определения частных порядков реакции – это т.н. метод избыточных концентраций или метод изолирования Оствальда. Порядок реакции по данному веществу определяется одним из перечисленных ниже методов.
Графический метод заключается в построении графика зависимости концентрации реагента от времени в различных координатах. Для различных частных порядков эти зависимости имеют следующий вид:
|
Порядок реакции |
Зависимость концентрации от времени |
|
1 |
|
|
2 |
|
|
3 |
|
Если построить графики этих зависимостей на основании опытных данных, то лишь одна из них будет являться прямой линией. Если, например, график, построенный по опытным данным, оказался прямолинейным к координатах lnC = f(t), то частный порядок реакции по данному веществу равен единице.
Метод подбора кинетического уравнения заключается в подстановке экспериментальных данных изучения зависимости концентрации вещества от времени в кинетические уравнения различных порядков. Подставляя в приведённые в таблице уравнения значения концентрации реагента в разные моменты времени, вычисляют значения константы скорости. Частный порядок реакции по данному веществу равен порядку того кинетического уравнения, для которого величина константы скорости остаётся постоянной во времени.
|
Порядок реакции |
Выражение для константы скорости |
|
1 |
|
|
2 |
|
|
3 |
|
Метод определения времени полупревращения заключается в определении t1/2 для нескольких начальных концентраций. Как видно из приведённых в таблице уравнений, для реакции первого порядка время полупревращения не зависит от Co, для реакции второго порядка – обратно пропорционально Co, и для реакции третьего порядка – обратно пропорционально квадрату начальной концентрации.
|
Порядок реакции |
Выражение для периода полупревращения |
|
1 |
|
|
2 |
|
|
3 |
|
По характеру зависимости t1/2 от Co нетрудно сделать вывод о порядке реакции по данному веществу. Данный метод, в отличие от описанных выше, применим и для определения дробных порядков.
Реакции первого порядка – это реакции, в которых показатель степени в уравнении зависимости скорости от концентрации, в которую возводится концентрация, равен единице.
Все реакции радиоактивного распада являются реакциями первого порядка. Также можно привести в пример реакции изомеризации, распада некоторых молекул в газовой фазе: N2O5, CH3-O-CH3 и т.д.
Выражение для мгновенной скорости реакции по какому-либо из реагентов записывается в виде:
Напомним, что знак минус перед правой частью уравнения ставиться для того, чтобы скорость была положительной величиной (изменение концентрации реагента – величина отрицательная, так как концентрация реагентов во время протекания реакции уменьшается).
По закону действующих масс – закону Гульберга-Вааге, скорость реакции прямо пропорциональная концентрации. Для реакций первого порядка (порядок – показатель степени в которую возводится концентрация) математическое выражение этого закона принимает вид:
Приравняем правые части приведенных выше уравнений друг к другу:
Разнесем переменные:
Для того чтобы понять сколько вещества вступит в реакцию за определенный интервал времени, нам необходимо решить данное дифференциальное уравнение, т.е. найти его первообразную.
Запишем выражение для вычисления определённого интеграла, чтобы в дальнейшем не решать задачу Коши (решение дифференциального уравнения, удовлетворяющего начальным условиям, для нас это исходная концентрация и исходное время). Хотя, можно поступить иначе и вычислить неопределенный интеграл данного уравнения, а затем через начальные условия определить константу интегрирования (т.е. решить задачу Коши).
Для нахождения интеграла, напомним, что:
Результат интегрирования следующий:
Запишем уравнение иначе:
Потенцируем уравнение:
Отсюда найдем уравнение для нахождения концентрации регента в момент времени t:
Если изменить порядок действий, то легко прийти к уравнению для нахождения константы реакции первого порядка:
Выведем уравнение для нахождения константы реакции первого порядка через период полупревращения.
Период полупревращения – время, которое необходимо для превращения половины исходного количества вещества.
Т.е. к моменту времени t молярная концентрация вещества будет равна ½ её исходного значения:
Для решения расчётных задач можно использовать формулу:
Из формулы видно, что время полупревращения для реакций первого порядка не зависит от количества, или концентрации исходного вещества.
Приведем уравнение
к виду
Это уравнение есть ни что иное как линейная зависимость ln(c) от t .
Построим график этой зависимости.
Отсюда, константа скорости реакции первого порядка численно равна тангенсу угла наклона прямой к оси t.
Определим размерность константы реакции первого порядка. Для этого в уравнение:
подставим размерности скорости и молярной концентрации:
Отсюда размерность константы реакции первого порядка.
