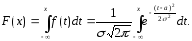Как найти константы функции распределения - Сайт, где вы сможете решить свои вопросы

Непрерывная случайная величина

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Случайная величина называется непрерывной, если ее функция
распределения

непрерывно дифференцируема. В этом случае

имеет производную, которую обозначим через

– плотность распределения вероятностей.

Плотностью распределения вероятностей непрерывной случайной
величины

называются функцию

– первую производную от функции распределения

Из этого определения следует, что функция распределения является
первообразной для плотности распределения.

Заметим, что для описания распределения вероятностей дискретной
случайной величины плотность распределения неприменима.

Вероятность того, что непрерывная случайная величина

примет значение, принадлежащее интервалу

равна определенному интегралу от плотности
распределения, взятому в пределах от

до

Зная плотность распределения

,
можно найти функцию распределения

по формуле:

Числовые характеристики непрерывной случайной величины

Математическое ожидание непрерывной случайной величины

,
возможные значения которой принадлежат всей оси

,
определяется равенством:

где

– плотность распределения случайной величины

.
Предполагается, что интеграл сходится абсолютно.

В частности, если все возможные значения принадлежат интервалу

,
то:

Все свойства математического ожидания, указанные для
дискретных случайных величин, сохраняются и для непрерывных величин.

Дисперсия непрерывной случайной величины

,
возможные значения которой принадлежат всей оси

,
определяется равенством:

или равносильным равенством:

В частности, если все возможные значения

принадлежат интервалу

,
то

или

Все свойства дисперсии, указанные для дискретных случайных
величин, сохраняются и для непрерывных случайных величин.

Среднее квадратическое отклонение
непрерывной случайной величины определяется так же, как и для дискретной
величины:

При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.

Основные законы распределения непрерывных случайных величин

Нормальный закон распределения СВ
Показательный закон распределения СВ
Равномерный закон распределения СВ

Примеры решения задач

Пример 1

Дана
функция распределения F(х) непрерывной случайной величины
Х.

Найти плотность распределения вероятностей f(x), математическое ожидание M(X), дисперсию D(X) и вероятность попадания X на отрезок [a,b]. Построить графики функций F(x) и f(x).

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Плотность
распределения вероятностей:

Математическое
ожидание:

Дисперсию
можно найти по формуле:

Вероятность
попадания на отрезок:

Построим графики функций F(x) и f(x).

График плотности
распределения

График функции
распределения

Пример 2

Случайная величина Х задана плотностью вероятности

Определить константу c, математическое ожидание, дисперсию, функцию распределения величины X, а также вероятность ее попадания в интервал [0;0,25].

Решение

Константу

определим,
используя свойство плотности вероятности:

В нашем случае:

Найдем математическое
ожидание:

Найдем дисперсию:

Искомая дисперсия:

Найдем функцию
распределения:

для

Искомая функция
распределения:

Вероятность попадания
в интервал

Пример 3

Плотность
распределения непрерывной случайной величины

имеет вид:

Найти:

а)
параметр

;

б)
функцию распределения

;

в)
вероятность попадания случайной величины

в интервал

г)
математическое ожидание

и дисперсию

д)
построить графики функций

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

а)
Постоянный параметр

найдем из
свойства плотности вероятности:

В нашем
случае эта формула имеет вид:

б)
Функцию распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем отметить,
что:

Остается
найти выражение для

, когда

принадлежит
интервалу

Получаем:

в)
Вероятность
попадания случайной величины

в интервал

г)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

Среднее
квадратическое отклонение равно квадратному корню из дисперсии:

д) Построим графики

График плотности вероятности f(x)

График функции распределения F(x)

Задачи контрольных и самостоятельных работ

Задача 1

НСВ на всей
числовой оси oX задана интегральной функцией:

Найти
вероятность, что в результате 2 испытаний случайная величина примет значение,
заключенное в интервале (0;4).

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 2

Дана
дифференциальная функция непрерывной СВ Х. Найти: постоянную С, интегральную
функцию F(x).

Задача 3

Случайная
величина Х задана функцией распределения F(x):

а) Найти
плотность вероятности СВ Х – f(x).

б) Построить графики
f(x), F(x).

в) Найти вероятность
попадания НСВ в интервал (0; 3).

Задача 4

Дифференциальная
функция НСВ Х задана на всей числовой оси ОХ:

Найти:

а) постоянный
параметр С=const;

б) функцию
распределения F(x);

в) вероятность
попадания в интервал -4<X<4;

г) построить
графики f(x), F(X).

Задача 5

Случайная величина
Х задана функцией распределения F(x):

а) Найти
плотность вероятности СВ Х – f(x).

б) Построить
графики f(x), F(x).

в) Найти
вероятность попадания НСВ в интервал (0;π⁄2).

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 6

НСВ X имеет
плотность вероятности (закон Коши)

а) постоянный
параметр С=const;

б) функцию
распределения F(x);

в) вероятность
попадания в интервал -1<X<1;

г) построить
графики f(x), F(X).

Задача 7

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную
функцию f(x), а при заданной дифференциальной функции f(x) найти интегральную
функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(X);

д)
вычислить вероятность попадания в интервал P(a≤x≤b);

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

Задание 8

Дана
интегральная функция распределения случайной величины X. Найти дифференциальную
функцию распределения, математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение.

Задача 9

Случайная
величина X задана интегральной функцией распределения

Найти
дифференциальную функцию, математическое ожидание и дисперсию X.

Задача 10

СВ Х
задана функцией распределения F(x). Найдите вероятность
того, что в результате испытаний НСВ Х попадет в заданный интервал (0;0,5).
Постройте график функции распределения. Найдите плотность вероятности НСВ Х и
постройте ее график. Найдите числовые
характеристики НСВ Х, если

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Лекция
7.

Функция
распределения и плотность распределения
непрерывной случайной величины, их
взаимосвязь и свойства.

Определение
и свойства функции распределения
сохраняются и для непрерывной случайной
величины, для которой функцию распределения
можно считать одним из видов задания
закона распределения. Но для непрерывной
случайной величины вероятность каждого
отдельного ее значения равна 0. Это
следует из свойства 4 функции распределения:
р(Х
= а)
= F(a)
– F(a)
= 0. Поэтому для такой случайной величины
имеет смысл говорить только о вероятности
ее попадания в некоторый интервал.

Вторым
способом задания закона распределения
непрерывной случайной величины является
так называемая плотность распределения
(плотность вероятности, дифференциальная
функция).

Определение.
Функция
f(x),
называемая плотностью
распределения непрерывной
случайной величины, определяется по
формуле:

f
(x)
= F′(x),

то
есть является производной функции
распределения.

Свойства
плотности распределения.

f(x)
≥ 0, так как функция распределения
является неубывающей.
,
что следует из определения плотности
распределения.
Вероятность
попадания случайной величины в интервал
(а,
b)
определяется формулой

Действительно,
(условие
нормировки). Его справедливость следует
из того, что

а
так
как

при

Таким
образом, график плотности распределения
представляет собой кривую, расположенную
выше оси Ох,
причем эта ось является ее горизонтальной
асимптотой при

(последнее справедливо только для
случайных величин, множеством возможных
значений которых является все множество
действительных чисел). Площадь
криволинейной трапеции, ограниченной
графиком этой функции, равна единице.

Замечание.
Если
все возможные значения непрерывной
случайной величины сосредоточе-ны на
интервале [a,
b],
то все интегралы вычисляются в этих
пределах, а вне интервала [a,
b]

f(x)
≡ 0.

Пример
1. Плотность распределения непрерывной
случайной величины задана формулой

Найти:
а) значение константы С;
б) вид функции распределения; в) p(-1
< x
< 1).

Решение.
а) значение константы С
найдем
из свойства 4:

откуда
.

б)

в)

Пример
2. Функция распределения непрерывной
случайной величины имеет вид:

Найти
плотность распределения.

Решение.

Числовые
характеристики непрерывных случайных
величин.

Математическим
ожиданием
непрерывной случайной величины называют
интеграл

Дисперсией
непрерывной случайной величины называют
математическое ожидание квадрата ее
отклонения

Среднее
квадратическое отклонение
непрерывной случайной величины
определяется равенством

Замечание.
Можно доказать, что свойства математического
ожидания и дисперсии дискретной случайной
величины сохраняются для непрерывных
величин.

Равномерный
закон распределения.

Определение.
Закон
распределения непрерывной случайной
величины называется равномерным,
если на интервале, которому принадлежат
все возможные значения случайной
величины, плотность распределения
сохраняет постоянное значение (
f(x)
= const
при a
≤ x
≤ b,
f(x)
= 0 при x
< a,
x
> b.

Найдем
значение, которое принимает f(x)
при

Из условия нормировки следует, что

откуда
.

Вероятность
попадания равномерно распределенной
случайной величины на интервал

равна при этом

Вид
функции распределения для нормального
закона:

Пример.
Автобусы некоторого маршрута идут с
интервалом 5 минут. Найти вероятность
того, что пришедшему на остановку
пассажиру придется ожидать автобуса
не более 2 минут.

Решение.
Время ожидания является случайной
величиной, равномерно распределенной
в интервале [0, 5]. Тогда

Нормальный
закон распределения

Определение.
Непрерывная
случайная величина называется
распределенной по нормальному
закону,
если ее плотность распределения имеет
вид:

Замечание.
Таким
образом, нормальное распределение
определяется двумя параметрами: а
и σ.

График
плотности нормального распределения
называют нормальной
кривой (кривой Гаусса).
Выясним, какой вид имеет эта кривая, для
чего исследуем функцию f(x).

Область
определения этой функции: (-∞, +∞).
f(x)
> 0 при любом х
(следовательно, весь график расположен
выше оси Ох).
то
есть ось Ох
служит горизонтальной асимптотой
графика при
при
х
= а;

при x
> a,

при x
< a.
Следовательно,

– точка максимума.
F(x
– a)
= f(a
– x),
то есть график симметричен относительно
прямой х
= а.
при
,
то есть точки

являются точками перегиба.

Примерный
вид кривой Гаусса изображен на рис.1.

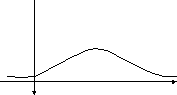
Рис.1.

Найдем
вид функции распределения для нормального
закона:

Перед
нами так называемый «неберущийся»
интеграл, который невозможно выразить
через элементарные функции. Поэтому
для вычисления значений F(x)
приходится пользоваться таблицами. Они
составлены для случая, когда а
= 0, а σ
= 1.

Определение.
Нормальное
распределение с параметрами а
= 0, σ
= 1
называется нормированным,
а его функция распределения

функцией
Лапласа.

Замечание.
Функцию
распределения для произвольных параметров
можно выразить через функцию Лапласа,
если сделать замену:
,
тогда
.

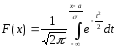
Найдем
вероятность попадания нормально
распределенной случайной величины на
заданный интервал:

Пример.
Случайная величина Х
имеет нормальное распределение с
параметрами а
= 3, σ = 2. Найти вероятность того, что она
примет значение из интервала (4, 8).

Решение.

Правило
«трех сигм».

Найдем
вероятность того, что нормально
распределенная случайная величина
примет значение из интервала (а
– 3σ,
а + 3σ):

Следовательно,
вероятность того, что значение случайной
величины окажется вне
этого интервала, равна 0,0027, то есть
составляет 0,27% и может считаться
пренебрежимо малой. Таким образом, на
практике можно считать, что все
возможные значения нормально распределенной
случайной величины лежат в интервале
(а
– 3σ,
а + 3σ).

Полученный
результат позволяет сформулировать
правило
«трех сигм»:
если
случайная величина распределена
нормально, то модуль ее отклонения от
х = а не превосходит 3σ.

Показательное
распределение.

Определение.
Показательным
(экспоненциальным) называют
распределение вероятностей непрерывной
случайной величины Х,
которое описывается плотностью

В
отличие от нормального распределения,
показательный закон определяется только
одним параметром λ.
В этом его преимущество, так как обычно
параметры распределения заранее не
известны и их приходится оценивать
приближенно. Понятно, что оценить один
параметр проще, чем несколько.

Найдем
функцию распределения показательного
закона:

Следовательно,

Теперь
можно найти вероятность попадания
показательно распределенной случайной
величины в интервал (а,
b):

Значения
функции е^-х
можно найти из таблиц.

Функция
надежности.

Пусть
элемент
(то
есть некоторое устройство) начинает
работать в момент времени t₀
= 0
и должен проработать в течение периода
времени t.
Обозначим за Т
непрерывную случайную величину – время
безотказной работы элемента, тогда
функция F(t)
= p(T
< t)
определяет вероятность отказа за время
t.
Следовательно, вероятность безотказной
работы за это же время равна

R(t)
= p(T
> t)
= 1 – F(t).

Эта
функция называется функцией
надежности.

Показательный
закон надежности.

Часто
длительность безотказной работы элемента
имеет показательное распределение, то
есть

F(t)
= 1 – e^–^λt
.

Следовательно,
функция надежности в этом случае имеет
вид:

R(t)
= 1 – F(t)
= 1 – (1 – e^-λt)
= e^-λt
.

Определение.
Показательным
законом надежности
называют функцию надежности, определяемую
равенством

R(t)
= e^–^λt
, где λ
–
интенсивность отказов.

Пример.
Пусть время безотказной работы элемента
распределено по показательному закону
с плотностью распределения f(t)
= 0,1 e^–^0,1^t
при
t
≥ 0. Найти вероятность того, что элемент
проработает безотказно в течение 10
часов.

Решение.
Так как λ
= 0,1, R(10)
= e^-0,1^·¹⁰
= e^-1
= 0,368.

Соседние файлы в папке Лекции 2 курс

Источник

СВ имеет абсолютно непрерывную функцию распределения:[math]begin{cases}
0,&text{ $xleqslant a$;}\
0.2sqrt{x},&text{ $a<x leqslant b$;}\
1,&text{ $x>b$.}
end{cases}[/math]

Найти [math]a,b,D(7-2xi)[/math] и [math]P(1.48<3xi+1leqslant 3.43)[/math]
Из функции распределения можно найти плотность [math]F'(x)=f(x)=begin{cases}
frac{0.1}{sqrt{x}},&text{ $ b leqslant x leqslant a$;}\
0 ,&text{ $xnotin [a,b]$;}
end{cases}[/math]

И [math]M[xi]=intlimits_{a}^{b}frac{0.1x}{sqrt{x}}dx=0.1frac{2}{3}x^{frac{3}{2}} |_a^b[/math]
[math]M[xi^2]=intlimits_{a}^{b}frac{0.1x^2}{sqrt{x}}dx=…[/math]
Получается уже есть все, чтобы найти дисперсию и нужную вероятность. Но что делать с a,b? Как их искать?

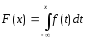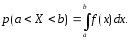
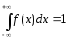
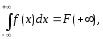
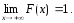
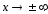
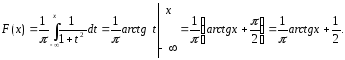
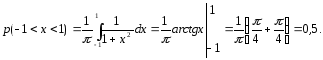
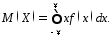
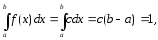
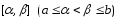
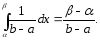
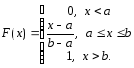
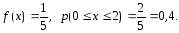
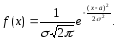
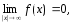
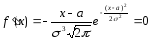
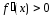
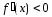
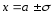Источник

Непрерывная случайная величина

Краткая теория

Числовые характеристики непрерывной случайной величины

Примеры решения задач

Пример 1

Пример 2

Пример 3

Задачи контрольных и самостоятельных работ

Вам также может понравиться

Как найти силу натяжения в стропах

Как найти расстояние между точками пересечения прямых

Как найти похоронку на погибшего вов

Добавить комментарий Отменить ответ