Как найти контрактную кривую

From Wikipedia, the free encyclopedia

Blue curve of Pareto efficient points, at points of tangency of indifference curves in an Edgeworth box. If the initial allocations of the two goods are at a point not on this locus, then the two people can trade to a point on the efficient locus within the lens formed by the indifference curves that they were originally on. The set of all these efficient points that could be traded to is the contract curve.
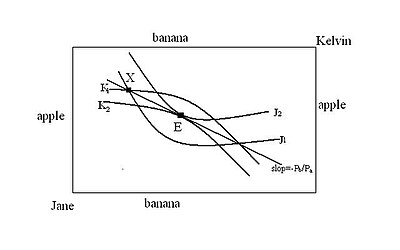
In the graph below, the initial endowments of the two people are at point X, on Kelvin’s indifference curve K₁ and Jane’s indifference curve J₁. From there they could agree to a mutually beneficial trade to anywhere in the lens formed by these indifference curves. But the only points from which no mutually beneficial trade exists are the points of tangency between the two people’s indifference curves, such as point E. The contract curve is the set of these indifference curve tangencies within the lens—it is a curve that slopes upward to the right and goes through point E.

In microeconomics, the contract curve or Pareto set^[1] is the set of points representing final allocations of two goods between two people that could occur as a result of mutually beneficial trading between those people given their initial allocations of the goods. All the points on this locus are Pareto efficient allocations, meaning that from any one of these points there is no reallocation that could make one of the people more satisfied with his or her allocation without making the other person less satisfied. The contract curve is the subset of the Pareto efficient points that could be reached by trading from the people’s initial holdings of the two goods. It is drawn in the Edgeworth box diagram shown here, in which each person’s allocation is measured vertically for one good and horizontally for the other good from that person’s origin (point of zero allocation of both goods); one person’s origin is the lower left corner of the Edgeworth box, and the other person’s origin is the upper right corner of the box. The people’s initial endowments (starting allocations of the two goods) are represented by a point in the diagram; the two people will trade goods with each other until no further mutually beneficial trades are possible. The set of points that it is conceptually possible for them to stop at are the points on the contract curve.

However, most authors^[2]^[3]^[4]^[5]^[6]^[7]^[8]^[9] identify the contract curve as the entire Pareto efficient locus from one origin to the other.

Any Walrasian equilibrium lies on the contract curve. As with all points that are Pareto efficient, each point on the contract curve is a point of tangency between an indifference curve of one person and an indifference curve of the other person. Thus, on the contract curve the marginal rate of substitution is the same for both people.

Example[edit]

Assume the existence of an economy with two agents, Octavio and Abby, who consume two goods X and Y of which there are fixed supplies, as illustrated in the above Edgeworth box diagram. Further, assume an initial distribution (endowment) of the goods between Octavio and Abby and let each have normally structured (convex) preferences represented by indifference curves that are convex toward the people’s respective origins. If the initial allocation is not at a point of tangency between an indifference curve of Octavio and one of Abby, then that initial allocation must be at a point where an indifference curve of Octavio crosses one of Abby. These two indifference curves form a lens shape, with the initial allocation at one of the two corners of the lens. Octavio and Abby will choose to make mutually beneficial trades — that is, they will trade to a point that is on a better (farther from the origin) indifference curve for both. Such a point will be in the interior of the lens, and the rate at which one good will be traded for the other will be between the marginal rate of substitution of Octavio and that of Abby. Since the trades will always provide each person with more of one good and less of the other, trading results in movement upward and to the left, or downward and to the right, in the diagram.

The two people will continue to trade so long as each one’s marginal rate of substitution (the absolute value of the slope of the person’s indifference curve at that point) differs from that of the other person at the current allocation (in which case there will be a mutually acceptable trading ratio of one good for the other, between the different marginal rates of substitution). At a point where Octavio’s marginal rate of substitution equals Abby’s marginal rate of substitution, no more mutually beneficial exchange is possible. This point is called a Pareto efficient equilibrium. In the Edgeworth box, it is a point at which Octavio’s indifference curve is tangent to Abby’s indifference curve, and it is inside the lens formed by their initial allocations.

Thus the contract curve, the set of points Octavio and Abby could end up at, is the section of the Pareto efficient locus that is in the interior of the lens formed by the initial allocations. The analysis cannot say which particular point along the contract curve they will end up at — this depends on the two people’s bargaining skills.

Mathematical explanation[edit]

In the case of two goods and two individuals, the contract curve can be found as follows. Here $x_{{2}}^{{1}}$ refers to the final amount of good 2 allocated to person 1, etc., $u^{1}$ and $u^{2}$ refer to the final levels of utility experienced by person 1 and person 2 respectively, $u_{{0}}^{{2}}$ refers to the level of utility that person 2 would receive from the initial allocation without trading at all, and $omega _{{1}}^{{tot}}$ and $omega _{{2}}^{{tot}}$ refer to the fixed total quantities available of goods 1 and 2 respectively.

$max _{{x_{{1}}^{{1}},x_{{2}}^{{1}},x_{{1}}^{{2}},x_{{2}}^{{2}}}}u^{1}(x_{{1}}^{{1}},x_{{2}}^{{1}})$

subject to:

$x_{{1}}^{{1}}+x_{{1}}^{{2}}leq omega _{{1}}^{{tot}}$

$x_{{2}}^{{1}}+x_{{2}}^{{2}}leq omega _{{2}}^{{tot}}$

$u^{2}(x_{{1}}^{{2}},x_{{2}}^{{2}})geq u_{{0}}^{{2}}$

This optimization problem states that the goods are to be allocated between the two people in such a way that no more than the available amount of each good is allocated to the two people combined, and the first person’s utility is to be as high as possible while making the second person’s utility no lower than at the initial allocation (so the second person would not refuse to trade from the initial allocation to the point found); this formulation of the problem finds a Pareto efficient point on the lens, as far as possible from person 1’s origin. This is the point that would be achieved if person 1 had all the bargaining power. (In fact, in order to create at least a slight incentive for person 2 to agree to trade to the identified point, the point would have to be slightly inside the lens.)

In order to trace out the entire contract curve, the above optimization problem can be modified as follows. Maximize a weighted average of the utilities of persons 1 and 2, with weights b and 1 – b, subject to the constraints that the allocations of each good not exceed its supply and subject to the constraints that both people’s utilities be at least as great as their utilities at the initial endowments:

$max _{{x_{{1}}^{{1}},x_{{2}}^{{1}},x_{{1}}^{{2}},x_{{2}}^{{2}}}}bcdot u^{1}(x_{{1}}^{{1}},x_{{2}}^{{1}})+(1-b)cdot u^{2}(x_{{1}}^{{2}},x_{{2}}^{{2}})$

subject to:

$x_{{1}}^{{1}}+x_{{1}}^{{2}}leq omega _{{1}}^{{tot}}$

$x_{{2}}^{{1}}+x_{{2}}^{{2}}leq omega _{{2}}^{{tot}}$

$u^{1}(x_{{1}}^{{1}},x_{{2}}^{{1}})geq u_{{0}}^{{1}}$

$u^{2}(x_{{1}}^{{2}},x_{{2}}^{{2}})geq u_{{0}}^{{2}}$

where $u^{1}$ is the utility that person 1 would experience in the absence of trading away from the initial endowment. By varying the weighting parameter b, one can trace out the entire contract curve: If b = 1 the problem is the same as the previous problem, and it identifies an efficient point at one edge of the lens formed by the indifference curves of the initial endowment; if b = 0 all the weight is on person 2’s utility instead of person 1’s, and so the optimization identifies the efficient point on the other edge of the lens. As b varies smoothly between these two extremes, all the in-between points on the contract curve are traced out.

Note that the above optimizations are not ones that the two people would actually engage in, either explicitly or implicitly. Instead, these optimizations are simply a way for the economist to identify points on the contract curve.

References[edit]

^ Varian, Hal R. (2010). Intermediate microeconomics : a modern approach (8 ed.). New York: W.W. Norton & Co. ISBN 978-0-393-93424-3. OCLC 317920200.
^ Varian, Hal R. Microeconomic analysis, third edition, 1992, page 324.
^ Nicholson, Walter. Snyder, Christopher. “Intermediate Microeconomics and Its Application”, eleventh edition, 2010, page 362.
^ Pindyke, Robert S. Rubinfeld, Daniel L. “Microeconomics”, ninth edition, 2018, page 620.
^ Jehle, Geoffrey L. Reny, Philip J. “Advanced Microeconomic Theory”, third edition, 2011, page 197.
^ Perloff Jeffrey M. “Microeconomics, Theory and Applications with Calculus”, fifth edition, page 338.
^ Browning,Edgar K. Zupan, Mark, A. “Microeconomics, Theory and Applications”, twelfth edition, 2015, page 148.
^ Kreps, David M. “A Course in Microeconomic Theory”, 1990, page 156.
^ Serrano, Roberto. Feldman, Alan M. “A Short Course in Intermediate Microeconomics with Calculus”, 2013, page 271.

Mas-Colell, Andreu; Whinston, Michael D.; & Green, Jerry (1995). Microeconomic Theory. New York: Oxford University Press. ISBN 0-19-510268-1

Источник

Рассмотрим
экономику, в которой имеется два
участника, которые могут обмениваться
двумя благами. Суммарное количество
первого блага обозначим a,
суммарное количество второго блага –
b.
Пусть первоначально первый участник
имел набор благ
,
а второй –.
Могут ли при этом участники улучшить
своё нынешнее положение, обмениваясь
между собой благами, т.е. вступать в
коалиции? Будем считать, что заданы
функции полезности:– для первого участника и– для второго. Будем также считать, что
издержки на получение информации,
заключение контрактов и поиск партнёров
(трансакционные издержки) равны нулю.

Для ответа на этот
вопрос Эджворт предложил свою модель
– Ящик
Эджворта.

Рисунок 1

Изобразим карту
кривых безразличия для каждого из
участников (см. рис. 1). Можно ли улучшить
положение первого участника, не ухудшая
при этом положение второго.

В пределе мы получим
точку A
на кривой безразличия
,
в которой эта кривая касается кривой
безразличия первого участника. Рассуждая
аналогично, можно улучшить положение
второго участника, не ухудшая при этом
положение первого. Лучшее решение будет
находиться в точкеB,
где кривая
касается кривой.
Таким образом, мы получим множество
точек, в которых кривая безразличия
первого участника касается кривой
безразличия второго участника. Это
множество точек лежит на кривой,
которая называетсяконтрактной
кривой.

Рассмотрим
контрактную кривую с точки зрения
эффективности по Парето. На рис. 1., при
переходе от точки M
к точке A,
первый участник улучшает своё положение,
а положение второго остаётся неизменным;
при переходе от точки M
к точке B,
положение второго участника улучшается,
а положение первого остаётся неизменным.
Таким образом, получается, что положение
A
предпочтительнее положения B,
а положение B,
в свою очередь, предпочтительнее
положения M.

При переходе от A
к B
полезность одного из участников
увеличивается, а полезность другого
уменьшается. Такие решения называются
Парето-несопоставимыми.

Множество решений,
которые являются Парето-предпочтительными
по сравнению с решениями, не входящими
в данное множество, называют множеством
Парето-эффективных решений.
Таким образом, контрактная кривая
является множеством решений, эффективных
по Парето.

Пример.
Вернёмся к вопросу об улучшении условий
каждого участника при обмене.

Рисунок 2

Очевидно, что
первый участник согласится на обмен,
при котором его кривая безразличия
сдвинется вверх и вправо (Рис.2), а второй
участник, согласится на обмен, при
котором его кривая безразличия сдвинется
вниз и влево. Таким образом, множество
эффективных обменов будет лежать на
контрактной кривой между точками
и.
Этот участок объединяет множество
решений, которые могут принимать
участники в ходе переговоров (торга).
Именно поэтому, это множество называетсяпереговорным.

Найдём условие,
которым удовлетворяют элементы
переговорного множества. Условие
Парето-эффективности означает, что
игроки решают одну из двух задач. Либо
первый игрок максимизирует свою
полезность,
при
условии, что полезность второго игрока
сохраняет своё стационарное значение,
т.е.(задача 1), либо второй игрок максимизирует
свою полезностьпри
условии, что.

Какая именно из
двух задач будет решаться, зависит от
того, кто из игроков обладает большей
властью или, другими словами, имеет
преимущество в переговорной силе. Если
такое преимущество имеет первый игрок,
то будет решаться задача 1, если таким
преимуществом обладает второй игрок,
то решаться будет соответственно задача
2. Очевидно, что

Решим задачу 1,
т.е.

Имеем задачу
нахождения условного экстремума для
функции
.
Для её решения используем функцию
Лагранжа.

Найдём частные
производные и приравняем их к нулю.

Отсюда получаем
условие первого порядка (необходимое
условие экстремума, касающиеся первых
производных)

Исключая параметрполучим уравнение:

(3.7)

В уравнении (3.7)
предельные полезности продуктов обмена
для первого игрока

Предельная норма
замещения продукта x
продуктом y
для первого игрока будет в этом случае
равна:

(3.8)

аким образом, из условия первого
порядка следует уравнение:

Следовательно,
все точки на контрактной кривой
удовлетворяют уравнению (3.8).
К уравнению (3.8)
нужно добавить условия индивидуальной
рациональности:

(3.9)

Решение задачи
максимизации полезности вторым игроком
(задача 2) будет аналогичным.

Если оба продукта
x
и y
являются
нормальными товарами, то можно показать,
что в некоторой точке переговорного
множества будет выполняться и условие
второго порядка. Следовательно,
контрактная кривая описывается уравнением
(3.8).
Переговорное множество удовлетворяет
уравнению (3.8)
и системе неравенств (3.9).

Пример.
Два туземных племени живут охотой и
рыболовством. Для того, чтобы природные
ресурсы не истощались, правительство
установило общие квоты на отлов рыбы и
отстрел дичи: рыбы – не более 100 тонн в
год; дичи – не более 400 тонн в год.

Первоначально
первое племя добывало 60 тонн рыбы и 20
тонн дичи, а второе племя добывало 40
тонн рыбы и 20 тонн дичи.

Предположим, что
каждое из племён имеет собственную
функцию полезности:

Вожди обоих племён
собрались и решили заключить соглашение
об охоте и рыболовстве, выполнение
которого должно увеличить полезность
каждого племени. Требуется найти
множество контрактов, улучшающих
положение каждого племени, т.е. необходимо
найти контрактную кривую.

Решение.
Изобразим ящик Эджворта (см. рис.3.)

Рисунок 3

(_*)

Найдём уравнение
контрактной кривой, для чего обратимся
к функции (3.8).
Найдём предельные нормы замещения:

(_**)

одставляя в уравнение (3.8), получим

(***)

Уравнение (_***)
– уравнение контрактной кривой.

Для того, чтобы на
контрактной кривой определить переговорное
множество, нужно найти полезности
каждого племени в точке угрозы:

Найдём полезность
каждого племени в точках на контрактной
кривой:

Получаем условия
индивидуальной рациональности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Синяя кривая эффективных точек Парето в точках касания кривые безразличия в Коробка Эджворта. Если первоначальное распределение двух товаров находится в точке, отличной от этого локуса, то два человека могут торговать до точки на эффективном локусе в пределах линзы, образованной кривыми безразличия, на которых они изначально находились. Набор всех этих эффективных точек, до которых можно было бы торговать, и есть кривая контракта.
На приведенном ниже графике начальные способности двух людей находятся в точке X на кривой безразличия Кельвина K.₁ и кривая безразличия Джейн J₁. Оттуда они могли согласиться на взаимовыгодную торговлю в любую точку линзы, образованной этими кривыми безразличия. Но единственные точки, из которых не существует взаимовыгодной торговли, – это точки соприкосновения между кривыми безразличия двух людей, например точка E. Кривая контракта – это совокупность этих касаний кривых безразличия внутри линзы – это кривая, идущая вверх. вправо и проходит через точку E.

В микроэкономика, то кривая контракта – это набор точек, представляющих окончательное распределение двух товаров между двумя людьми, которое могло произойти в результате взаимовыгодной торговли между этими людьми с учетом их первоначального распределения товаров. Все точки этого локуса Парето эффективный распределения, что означает, что из любого из этих пунктов нет перераспределения, которое могло бы сделать одного из людей более удовлетворенным его или ее распределением, но не сделало бы другого менее удовлетворенным. Контрактная кривая – это подмножество точек, эффективных по Парето, которые могут быть достигнуты при торговле из первоначальных запасов людей двумя товарами. Он нарисован в Коробка Эджворта приведенная здесь диаграмма, на которой распределение каждого человека измеряется по вертикали для одного товара и по горизонтали для другого товара из источника этого лица (точка нулевого распределения для обоих товаров); происхождение одного человека – это нижний левый угол прямоугольника Эджворта, а происхождение другого человека – верхний правый угол поля. Первоначальные запасы людей (начальные распределения двух благ) представлены точкой на диаграмме; двое людей будут торговать друг с другом товарами до тех пор, пока взаимовыгодные сделки не прекратятся. Набор точек, в которых они теоретически могут остановиться, – это точки на кривой контракта. Однако некоторые авторы^[1] определить контрактную кривую как весь эффективный по Парето локус от одного источника к другому.

Любой Вальрасовское равновесие лежит на кривой контракта. Как и все Парето эффективный каждая точка на кривой контракта является точкой соприкосновения между кривой безразличия одного человека и кривой безразличия другого человека. Таким образом, на контрактной кривой предельная ставка замещения одинаково для обоих людей.

Пример

Предположим, что существует экономика с двумя агентами, Октавио и Эбби, которые потребляют два товара X и Y, из которых есть фиксированные запасы, как показано на приведенной выше диаграмме Эджворта. Далее, предположим начальное распределение (снабжение) товаров между Октавио и Эбби, и пусть каждый имеет нормально структурированные (выпуклые) предпочтения, представленные кривые безразличия которые являются выпуклыми по отношению к соответствующему происхождению людей. Если первоначальное распределение не находится в точке соприкосновения между кривой безразличия Октавио и кривой безразличия Эбби, тогда это первоначальное распределение должно быть в точке, где кривая безразличия Октавио пересекает кривую безразличия Октавио. Эти две кривые безразличия образуют форму линзы с начальным расположением в одном из двух углов линзы. Октавио и Эбби предпочтут совершать взаимовыгодные сделки – то есть они будут торговать до точки, которая находится на лучшей (более удаленной от начала) кривой безразличия для обоих. Такая точка будет внутри линзы, и скорость обмена одного товара на другой будет находиться между предельной скоростью замещения Октавио и Эбби. Поскольку сделки всегда предоставляют каждому человеку больше одного товара и меньше другого, торговля приводит к движению вверх и влево или вниз и вправо на диаграмме.

Эти два человека будут продолжать торговать, пока каждый предельная ставка замещения (абсолютное значение наклона кривой безразличия человека в этой точке) отличается от значения наклона кривой безразличия другого человека при текущем распределении (в этом случае будет взаимоприемлемое соотношение обмена одного товара на другой между разными маржинальными скорости замещения). В тот момент, когда предельная норма замещения Октавио равна предельной норме замещения Эбби, взаимовыгодный обмен невозможен. Эта точка называется Парето эффективный равновесие. В поле Эджворта это точка, в которой кривая безразличия Октавио касается кривой безразличия Эбби, и находится внутри линзы, образованной их начальными выделениями.

Таким образом, кривая контракта, набор точек, в которых могли бы закончить Октавио и Эбби, является частью эффективного по Парето локуса, который находится внутри линзы, образованной начальным распределением. Анализ не может сказать, в какой конкретной точке контрактной кривой они окажутся – это зависит от навыков ведения переговоров между двумя людьми.

Математическое объяснение

В случае двух товаров и двух людей кривую контракта можно найти следующим образом. Здесь $х _ {{2}} ^ {{1}}$ относится к окончательному количеству товара 2, выделенному лицу 1 и т. д., $и ^ {1}$ и $и ^ {2}$ относятся к конечным уровням полезности, испытываемой человеком 1 и человеком 2 соответственно, $u _ {{0}} ^ {{2}}$ относится к уровню полезности, которую человек 2 получил бы от первоначального распределения без торговли вообще, и $omega _ {{1}} ^ {{tot}}$ и $omega _ {{2}} ^ {{tot}}$ относятся к фиксированному общему количеству товаров 1 и 2 соответственно.

$max _ {{x _ {{1}} ^ {{1}}, x _ {{2}} ^ {{1}}, x _ {{1}} ^ {{2}}, x _ {{2}} ^ {{2}}}} u ^ {1} (x _ {{1}} ^ {{1}}, x _ {{2}} ^ {{1}})$

при условии:

$x _ {{1}} ^ {{1}} + x _ {{1}} ^ {{2}} leq omega _ {{1}} ^ {{tot}}$

$x _ {{2}} ^ {{1}} + x _ {{2}} ^ {{2}} leq omega _ {{2}} ^ {{tot}}$

$u ^ {2} (x _ {{1}} ^ {{2}}, x _ {{2}} ^ {{2}}) geq u _ {{0}} ^ {{2}}$

Эта задача оптимизации гласит, что товары должны быть распределены между двумя людьми таким образом, чтобы не более доступного количества каждого товара распределялось между двумя людьми вместе, а полезность первого лица должна быть как можно выше, пока сделать полезность второго человека не ниже, чем при первоначальном распределении (чтобы второе лицо не отказывалось торговать от первоначального распределения до найденной точки); эта формулировка задачи находит на линзе точку, эффективную по Парето, как можно дальше от места происхождения человека 1. Это тот момент, который был бы достигнут, если бы у человека 1 была вся сила на переговорах. (Фактически, чтобы создать хотя бы легкий стимул для человека 2 согласиться торговать до определенной точки, точка должна быть немного внутри линзы.)

Чтобы проследить всю кривую контракта, указанная выше задача оптимизации может быть изменена следующим образом. Максимизируйте средневзвешенное значение полезности лиц 1 и 2 с помощью весов б и 1 – б, при условии, что распределение каждого товара не превышает его предложения, и при условии, что полезность обоих людей должна быть не меньше, чем их полезности при начальных запасах:

$max _ {{x _ {{1}} ^ {{1}}, x _ {{2}} ^ {{1}}, x _ {{1}} ^ {{2}}, x _ {{2}} ^ {{2}}}} b cdot u ^ {1} (x _ {{1}} ^ {1}}, x _ {{2}} ^ {{1}}) + (1-b) cdot u ^ {2} (x _ {{1}} ^ {{2}}, x _ {{2}} ^ {{2}})$

при условии:

$x _ {{1}} ^ {{1}} + x _ {{1}} ^ {{2}} leq omega _ {{1}} ^ {{tot}}$

$x _ {{2}} ^ {{1}} + x _ {{2}} ^ {{2}} leq omega _ {{2}} ^ {{tot}}$

$u ^ {1} (x _ {{1}} ^ {{1}}, x _ {{2}} ^ {{1}}) geq u _ {{0}} ^ {{1}}$

$u ^ {2} (x _ {{1}} ^ {{2}}, x _ {{2}} ^ {{2}}) geq u _ {{0}} ^ {{2}}$

куда $и ^ {1}$ это полезность, которую человек 1 испытал бы, если бы не торговал за пределами первоначального капитала. Изменяя весовой параметр б, можно проследить всю кривую контракта: Если б = 1 проблема такая же, как и в предыдущей задаче, и она определяет эффективную точку на одном краю линзы, образованную кривыми безразличия начального запаса; если б = 0 весь вес приходится на полезность человека 2, а не человека 1, поэтому оптимизация определяет эффективную точку на другом крае линзы. В качестве б плавно меняется между этими двумя крайностями, все промежуточные точки на кривой контракта прослеживаются.

Обратите внимание, что вышеупомянутые оптимизации не являются теми, в которых эти два человека фактически участвовали бы, явно или неявно. Вместо этого эти оптимизации – просто способ для экономиста определить точки на кривой контракта.

Смотрите также

Экономика благосостояния
Список тем по экономике

Рекомендации

^ Вариан, Хэл Р. Микроэкономический анализ, третье издание, 1992 г., стр. 324.

Мас-Колелл, Андреу; Whinston, Michael D .; И Грин, Джерри (1995). Микроэкономическая теория. Нью-Йорк: Издательство Оксфордского университета. ISBN 0-19-510268-1

Источник

Ф. Эджворту принадлежат такие понятия как кривая безразличия , контрактная кривая и ядро экономики . Специалистам в области математической экономики хорошо известен так называемый ящик Эджворта , с помощью которого можно моделировать процесс чистого обмена товарами между двумя участниками. По сути дела, этот анализ опирается на понятие парето-оптимального решения, которое Ф. Эджвортом в случае двух критериев использовалось до того, как его в общем виде ввел В. Парето. [c.170]

Все приведенные здесь точки будут эффективными по Парето, ибо при любом дальнейшем перераспределении благ ни один из потребителей не сможет улучшить свое положение, не причиняя вреда другому. При этом следует иметь в виду, что движение по направлению к контрактной кривой представляет собой увеличение суммарного благосостояния, а движение вдоль контрактной кривой изменяет распределение суммарного благосостояния между участниками обмена. [c.285]

Множество этих точек составляет контрактную кривую — на рис. 3 это линия, соединяющая точки ОА и ОВ. Поскольку каждое размещение на этой кривой парето-эффективно, при перемещении по контрактной кривой увеличение полезности одного индивида достигается только за счет уменьшения полезности другого. Поэтому контрактную кривую называют также конкурентной. [c.256]

Заметим, что контрактная кривая является аналогом кривой возможных полезностей, только в первом случае на осях откладываются количества благ, а во втором — уровни полезности индивидов, получаемые от наборов благ. Если предположить, что уровень полезности измерим количественно, мы сможем построить рис. 1 по данным об уровнях полезности на контрактной кривой на рис. 3. [c.256]

Обсуждая условия сделки, Андрей и Борис могут найти парето-эффективное состояние, если выберут точку на участке АС, принадлежащем контрактной кривой. Но какую именно точку они должны будут выбрать, определить невозможно. Все точки на участке АС представляют собой состояния, после достижения [c.257]

Участок АС контрактной кривой, называется ядром, экономики обмена Вспомните, что контрактная кривая называется также конкурентной кривой [c.258]

Обратите внимание, точка равновесия у принадлежит контрактной кривой СС. Так как кривые предложения строятся по точкам касания кривых безразличия индивида с бюджетными линиями, в точке у общей бюджетной линии будут с двух сторон касаться сразу две кривые безразличия — Андрея и Бориса. [c.268]

Кривые UA и UB в точке е пересекаются, следовательно, при таких ценах парето-эффективность не достигается. Это означает, что равновесие при монополизации рынка какого-либо блага устанавливается за пределами контрактной кривой. В нашем случае [c.458]

Аналогичный результат мы получили бы, если бы записали выражение не для У,, а для У2. Контрактная кривая также представляла бы диагональ квадрата (уравнение Х2 — У2). [c.721]

Заказанная комбинация благ не будет эффективной, так как не лежит на контрактной кривой. Уравнение контрактной кривой Хг – Yl (X2 – У2) предполагает, что количество единиц блага X в распоряжении любого из индивидов должно быть равно находящегося в его же распоряжении количеству единиц блага У. [c.722]

Таким образом обеспечивается общее экономическое равновесие. Одновременно заказанные комбинации благ находятся на контрактной кривой. [c.722]

Двусторонняя монополия предполагает, что следует обговаривать и цены, и количества. Для обеих сторон выгодно, естественно, оперировать на контрактной кривой, которая здесь соответствует объемам, максимизирующим величину общей прибыли, а не вне ее [8]. Но это только устанавливает объемы, вовлекаемые в обмен. Условия торговли еще должны быть определены. Допускается любая цена, обеспечивающая положительные прибыли для обеих сторон. Можно ожидать длительных переговоров. Предположительно торг будет продолжаться, пока одна из сторон не осознает, что предельная частная чистая прибыль равна нулю. Хотя такой торг с точки зрения обеих сторон (и социально) непродуктивен, он образует источник частных доходов. Поскольку одновременно это ведет к сокращению общей прибыли, возникает стимул по возможности устранить данные потери. [c.38]

Объяснение того, зачем нужно неопределенное число участников, заключается в следующем. При двусторонней монополии сделка будет неопределенной — точка равновесия может быть в любом месте контрактной кривой.28 Показано, что если до- [c.310]

Участок АС контрактной кривой называется ядром экономики обмена [c.101]

Вспомните, что контрактная кривая называется также конкурентной кривой [c.101]

КОНТРАКТНАЯ КРИВАЯ [ ontra t urve] (иногда —договорная кривая, кривая сделок) — геометрическое место оптимальных точек на графике двусторонней монополии (см. Рынок), который называется Эджуорта диаграммой. К.к. показывает точки касания кривых безразличия продавца и покупателя, и собственно сделки происходят вдоль нее, поскольку именно в этих точках изменение условий сделок является обоюдно невыгодным. Подробнее см. Эджуорта диаграмма. [c.152]

Этого нельзя сказать о точках вне контрактной кривой. Например, точка G не является парето-эффек-тивным размещением, так как из нее индивиды могут переместиться в другую точку (например, в точку D), увеличив полезность каждого. [c.256]

Поскольку все точки касания кривых безразличия принадлежат контрактной кривой, точка у тоже ей принадлежит. Таким образом, в точке конкурентного равновесия достигается парето-эффективностъ в обмене. Формально это условие можно записать как [c.269]

Возьмем знакомую нам экономику обмена при наличии цен. По-прежнему в ней два блага (X и У), два индивида (А и В). Пусть А — покупатель товара X, а В — продавец. Как известно, в соответствии с первой теоремой экономики благосостояния, конкурентные цены обеспечивают рыночное равновесие, которое является парето-эффективным. Это означает, что оно устанавливается на контрактной кривой в точке пересечения (точка е на рис. 1) кривых предложения (offer urves) O A и ОСВ. Бюджетная линия ар показывает соотношение конкурентных равновесных цен (Р I -Ру). [c.457]

Отсюда получаем У, – Х,У,/Х2 => У, – Х,(210 – У1)/(210 – X,) => 210 У, –Х,У,”” 210 X, – X1Y1 = X, У, — уравнение контрактной кривой (на рис. 16 — диагональ квадрата, представляющего коробку Эджуорта). [c.721]

Контрактная кривая ( ontra t urve) — множество эффективных сделок меж-ДУ двумя субъектами, при которых невозможно достичь увеличения выгоды для одного из участников без уменьшения выгоды для другого. В частности, для двусторонней монополии контрактная кривая — множество таких комбинаций объем—цена , что увеличение прибыли продавца возможно лишь за счет уменьшения прибыли покупателя, и наоборот [c.735]

Контрактная кривая ( ontra t urve) — множество эффективных сделок между двумя субъектами, при которых невозможно достичь увеличения выгоды для одного из участников без уменьшения выгоды для другого. В частности, для двусторонней монополии контрактная кри- [c.261]

Множество всех таких точек касания образует линию ОхОу, аналогичную контрактной кривой. Во всех точках линии OXOY предельные нормы замены для обоих продуктов равны. [c.102]

Источник

Контрактная кривая

Cтраница 1

Контрактная кривая ( contract curve) – множество эффективных сделок меж – ДУ двумя субъектами, при которых невозможно достичь увеличения выгоды для одного из участников без уменьшения выгоды для другого.
[1]

Контрактная кривая ( contract curve) – множество эффективных сделок между двумя субъектами, при которых невозможно достичь увеличения выгоды для одного из участников без уменьшения выгоды для другого.
[2]

Заметим, что контрактная кривая является аналогом кривой возможных полезностей, только в первом случае на осях откладываются количества благ, а во втором – уровни полезности индивидов, получаемые от наборов благ.
[3]

Множество этих точек составляет контрактную кривую – на рис. 3 это линия, соединяющая точки ОА и ОВ. Поскольку каждое размещение на этой кривой парето-эффективно, при перемещении по контрактной кривой увеличение полезности одного индивида достигается только за счет уменьшения полезности другого. Поэтому контрактную кривую называют также конкурентной.
[4]

Заказанная комбинация благ не будет эффективной, так как не лежит на контрактной кривой. Уравнение контрактной кривой Хг – Yl ( X2 – У2) предполагает, что количество единиц блага X в распоряжении любого из индивидов должно быть равно находящегося в его же распоряжении количеству единиц блага У.
[6]

Найдем координаты точек, в которых кривые безразличия индивидов 1 и 2, проходящие через точку изначального размещения благ, пересекают контрактную кривую.
[9]

Заказанная комбинация благ не будет эффективной, так как не лежит на контрактной кривой. Уравнение контрактной кривой Хг – Yl ( X2 – У2) предполагает, что количество единиц блага X в распоряжении любого из индивидов должно быть равно находящегося в его же распоряжении количеству единиц блага У.
[10]

Таким образом обеспечивается общее экономическое равновесие. Одновременно заказанные комбинации благ находятся на контрактной кривой.
[11]

Эти точки предпочтительне всех остальных потому, что в любой из других точек один из участии ков обмена может улучшить свое положение, не ухудшая положени другого. Из точки Q, не лежащей на контрактной кривой, можно и кривой 2 переместиться в точку на кривой ССс выигрышем для Ро бинзона и без потерь для Пятницы.
[12]

Все приведенные здесь точки будут эффективными по Парето, ибо при любом дальнейшем перераспределении благ ни один из потребителей не сможет улучшить свое положение, не причиняя вреда другому. При этом следует иметь в виду, что движение по направлению к контрактной кривой представляет собой увеличение суммарного благосостояния, а движение вдоль контрактной кривой изменяет распределение суммарного благосостояния между участниками обмена.
[15]

Страницы:

Источник

Example[edit]

Mathematical explanation[edit]

See also[edit]

References[edit]

Пример

Математическое объяснение

Смотрите также

Рекомендации

Контрактная кривая

Добавить комментарий Отменить ответ

Example[edit]

Mathematical explanation[edit]

See also[edit]

References[edit]

Пример

Математическое объяснение

Смотрите также

Рекомендации

Контрактная кривая

Вам также может понравиться

Вылетает браузер как исправить

Как найти пациента в больнице москвы

Как составить резюме попроще

Добавить комментарий Отменить ответ