Простой расчет контрольной суммы
Время на прочтение
12 мин
Количество просмотров 197K
При передачи данных по линиям связи, используется контрольная сумма, рассчитанная по некоторому алгоритму. Алгоритм часто сложный, конечно, он обоснован математически, но очень уж неудобен при дефиците ресурсов, например при программировании микроконтроллеров.
Чтобы упростить алгоритм, без потери качества, нужно немного «битовой магии», что интересная тема сама по себе.
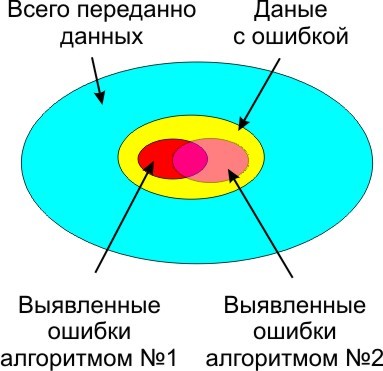
Без контрольной суммы, передавать данные опасно, так как помехи присутствуют везде и всегда, весь вопрос только в их вероятности возникновения и вызываемых ими побочных эффектах. В зависимости от условий и выбирается алгоритм выявления ошибок и количество данных в контрольной сумме. Сложнее алгоритм, и больше контрольная сумма, меньше не распознанных ошибок.
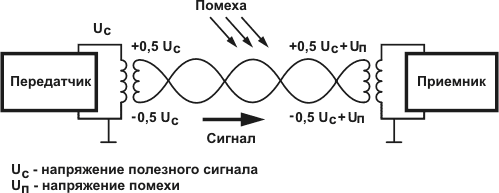
Причина помех на физическом уровне, при передаче данных.
Вот пример самого типичного алгоритма для микроконтроллера, ставшего, фактически, промышленным стандартом с 1979 года.
Расчет контрольной суммы для протокола Modbus
void crc_calculating(unsigned char puchMsg, unsigned short usDataLen) /*##Расчёт контрольной суммы##*/
{
{
unsigned char uchCRCHi = 0xFF ; /* Инициализация последнего байта CRC */
unsigned char uchCRCLo = 0xFF ; /* Инициализация первого байта CRC */
unsigned uIndex ; /* will index into CRC lookup table */
while (usDataLen--) /* pass through message buffer */
{
uIndex = uchCRCHi ^ *puchMsg++ ; /* Расчёт CRC */
uchCRCLo = uchCRCLo ^ auchCRCHi[uIndex] ;
uchCRCHi = auchCRCLo[uIndex] ;
}
return (uchCRCHi << 8 | uchCRCLo) ;
/* Table of CRC values for high–order byte */
static unsigned char auchCRCHi[] = {
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01,
0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40
};
/* Table of CRC values for low–order byte */
static char auchCRCLo[] = {
0x00, 0xC0, 0xC1, 0x01, 0xC3, 0x03, 0x02, 0xC2, 0xC6, 0x06, 0x07, 0xC7, 0x05, 0xC5, 0xC4,
0x04, 0xCC, 0x0C, 0x0D, 0xCD, 0x0F, 0xCF, 0xCE, 0x0E, 0x0A, 0xCA, 0xCB, 0x0B, 0xC9, 0x09,
0x08, 0xC8, 0xD8, 0x18, 0x19, 0xD9, 0x1B, 0xDB, 0xDA, 0x1A, 0x1E, 0xDE, 0xDF, 0x1F, 0xDD,
0x1D, 0x1C, 0xDC, 0x14, 0xD4, 0xD5, 0x15, 0xD7, 0x17, 0x16, 0xD6, 0xD2, 0x12, 0x13, 0xD3,
0x11, 0xD1, 0xD0, 0x10, 0xF0, 0x30, 0x31, 0xF1, 0x33, 0xF3, 0xF2, 0x32, 0x36, 0xF6, 0xF7,
0x37, 0xF5, 0x35, 0x34, 0xF4, 0x3C, 0xFC, 0xFD, 0x3D, 0xFF, 0x3F, 0x3E, 0xFE, 0xFA, 0x3A,
0x3B, 0xFB, 0x39, 0xF9, 0xF8, 0x38, 0x28, 0xE8, 0xE9, 0x29, 0xEB, 0x2B, 0x2A, 0xEA, 0xEE,
0x2E, 0x2F, 0xEF, 0x2D, 0xED, 0xEC, 0x2C, 0xE4, 0x24, 0x25, 0xE5, 0x27, 0xE7, 0xE6, 0x26,
0x22, 0xE2, 0xE3, 0x23, 0xE1, 0x21, 0x20, 0xE0, 0xA0, 0x60, 0x61, 0xA1, 0x63, 0xA3, 0xA2,
0x62, 0x66, 0xA6, 0xA7, 0x67, 0xA5, 0x65, 0x64, 0xA4, 0x6C, 0xAC, 0xAD, 0x6D, 0xAF, 0x6F,
0x6E, 0xAE, 0xAA, 0x6A, 0x6B, 0xAB, 0x69, 0xA9, 0xA8, 0x68, 0x78, 0xB8, 0xB9, 0x79, 0xBB,
0x7B, 0x7A, 0xBA, 0xBE, 0x7E, 0x7F, 0xBF, 0x7D, 0xBD, 0xBC, 0x7C, 0xB4, 0x74, 0x75, 0xB5,
0x77, 0xB7, 0xB6, 0x76, 0x72, 0xB2, 0xB3, 0x73, 0xB1, 0x71, 0x70, 0xB0, 0x50, 0x90, 0x91,
0x51, 0x93, 0x53, 0x52, 0x92, 0x96, 0x56, 0x57, 0x97, 0x55, 0x95, 0x94, 0x54, 0x9C, 0x5C,
0x5D, 0x9D, 0x5F, 0x9F, 0x9E, 0x5E, 0x5A, 0x9A, 0x9B, 0x5B, 0x99, 0x59, 0x58, 0x98, 0x88,
0x48, 0x49, 0x89, 0x4B, 0x8B, 0x8A, 0x4A, 0x4E, 0x8E, 0x8F, 0x4F, 0x8D, 0x4D, 0x4C, 0x8C,
0x44, 0x84, 0x85, 0x45, 0x87, 0x47, 0x46, 0x86, 0x82, 0x42, 0x43, 0x83, 0x41, 0x81, 0x80,
0x40
};
}
}
Не слабый такой код, есть вариант без таблицы, но более медленный (необходима побитовая обработка данных), в любом случае способный вынести мозг как программисту, так и микроконтроллеру. Не во всякий микроконтроллер алгоритм с таблицей влезет вообще.
Давайте разберем алгоритмы, которые вообще могут подтвердить целостность данных невысокой ценой.
Бит четности (1-битная контрольная сумма)
На первом месте простой бит четности. При необходимости формируется аппаратно, принцип простейший, и подробно расписан в википедии. Недостаток только один, пропускает двойные ошибки (и вообще четное число ошибок), когда четность всех бит не меняется. Можно использовать для сбора статистики о наличии ошибок в потоке передаваемых данных, но целостность данных не гарантирует, хотя и снижает вероятность пропущенной ошибки на 50% (зависит, конечно, от типа помех на линии, в данном случае подразумевается что число четных и нечетных сбоев равновероятно).
Для включения бита четности, часто и код никакой не нужен, просто указываем что UART должен задействовать бит четности. Типично, просто указываем:
включение бита четности на микроконтроллере
void setup(){
Serial.begin(9600,SERIAL_8N1); // по умолчанию, бит четности выключен;
Serial1.begin(38400,SERIAL_8E1); // бит четности включен
Serial.println("Hello Computer");
Serial1.println("Hello Serial 1");
}
Часто разработчики забывают даже, что UART имеет на борту возможность проверки бита четности. Кроме целостности передаваемых данных, это позволяет избежать устойчивого срыва синхронизации (например при передаче данных по радиоканалу), когда полезные данные могу случайно имитировать старт и стоп биты, а вместо данных на выходе буфера старт и стоп биты в случайном порядке.
8-битная контрольная сумма
Если контроля четности мало (а этого обычно мало), добавляется дополнительная контрольная сумма. Рассчитать контрольную сумму, можно как сумму ранее переданных байт, просто и логично
Естественно биты переполнения не учитываем, результат укладываем в выделенные под контрольную сумму 8 бит. Можно пропустить ошибку, если при случайном сбое один байт увеличится на некоторое значение, а другой байт уменьшится на то же значение. Контрольная сумма не изменится. Проведем эксперимент по передаче данных. Исходные данные такие:
- Блок данных 8 байт.
- Заполненность псевдослучайными данными Random($FF+1)
- Случайным образом меняем 1 бит в блоке данных операцией XOR со специально подготовленным байтом, у которого один единичный бит на случайной позиции.
- Повторяем предыдущий пункт 10 раз, при этом может получится от 0 до 10 сбойных бит (2 ошибки могут накладываться друг на друга восстанавливая данные), вариант с 0 сбойных бит игнорируем в дальнейшем как бесполезный для нас.
Передаем виртуальную телеграмму N раз. Идеальная контрольная сумма выявит ошибку по количеству доступной ей информации о сообщении, больше информации, выше вероятность выявления сбойной телеграммы. Вероятность пропустить ошибку, для 1 бита контрольной суммы:
.
Для 8 бит:
,
на 256 отправленных телеграмм с ошибкой, одна пройдет проверку контрольной суммы. Смотрим статистику от виртуальной передачи данных, с помощью простой тестовой программы:
Статистика
1: 144 (тут и далее — вероятность прохождения ошибки)
1: 143
1: 144
1: 145
1: 144
1: 142
1: 143
1: 143
1: 142
1: 140
Общее число ошибок 69892 из 10 млн. итераций, или 1: 143.078
Или условный КПД=55%, от возможностей «идеальной» контрольной суммы. Такова плата за простоту алгоритма и скорость обработки данных. В целом, для многих применений, алгоритм работоспособен. Используется одна операция сложения и одна переменная 8-битовая. Нет возможности не корректной реализации. Поэтому алгоритм и применяется в контроллерах ADAMS, ICP, в составе протокола DCON (там дополнительно может быть включен бит четности, символы только ASCI, что так же способствует повышению надежности передачи данных и итоговая надежность несколько выше, так как часть ошибок выявляется по другим, дополнительным признакам, не связанных с контрольной суммой).
Не смотря на вероятность прохождения ошибки 1:143, вероятность обнаружения ошибки лучше, чем 1:256 невозможна теоретически. Потери в качестве работы есть, но не всегда это существенно. Если нужна надежность выше, нужно использовать контрольную сумму с большим числом бит. Или, иначе говоря, простая контрольная сумма, недостаточно эффективно использует примерно 0.75 бита из 8 имеющихся бит информации в контрольной сумме.
Для сравнения применим, вместо суммы, побитовое сложение XOR. Стало существенно хуже, вероятность обнаружения ошибки 1:67 или 26% от теоретического предела. Упрощенно, это можно объяснить тем, что XOR меняет при возникновении ошибке еще меньше бит в контрольной сумме, ниже отклик на единичный битовый сбой, и повторной ошибке более вероятно вернуть контрольную сумму в исходное состояние.
Так же можно утверждать, что контрольная сумма по XOR представляет из себя 8 независимых контрольных сумм из 1 бита. Вероятность того, что ошибка придется на один из 8 бит равна 1:8, вероятность двойного сбоя 1:64, что мы и наблюдаем, теоретическая величина совпала с экспериментальными данными.
Нам же нужен такой алгоритм, чтобы заменял при единичной ошибке максимальное количество бит в контрольной сумме. Но мы, в общей сложности, ограниченны сложностью алгоритма, и ресурсами в нашем распоряжении. Не во всех микроконтроллерах есть аппаратный блок расчета CRC. Но, практически везде, есть блок умножения. Рассчитаем контрольную сумму как произведение последовательности байт, на некоторую «магическую» константу:
CRC=CRC + byte*211
Константа должна быть простой, и быть достаточно большой, для изменения большего числа бит после каждой операции, 211 вполне подходит, проверяем:
Статистика
1: 185
1: 186
1: 185
1: 185
1: 193
1: 188
1: 187
1: 194
1: 190
1: 200
Всего 72% от теоретического предела, небольшое улучшение перед простой суммой. Алгоритм в таком виде не имеет смысла. В данном случае теряется важная информация из отбрасываемых старших 8..16 бит, а их необходимо учитывать. Проще всего, смешать функцией XOR с младшими битами 1..8. Приходим к еще более интенсивной модификации контрольной суммы, желательно с минимальным затратами ресурсов. Добавляем фокус из криптографических алгоритмов
CRC=CRC + byte*211
CRC= CRC XOR (CRC SHR 8); // "миксер" битовый, далее его применяем везде
CRC=CRC AND $FF; //или просто возвращаем результат как 8, а не 16 бит
- Промежуточная CRC для первого действия 16-битная (после вычислений обрезается до 8 бит) и в дальнейшем работаем как с 8-битной, если у нас 8-битный микроконтроллер это ускорит обработку данных.
- Возвращаем старшие биты и перемешиваем с младшими.
Проверяем:
Статистика
1: 237
1: 234
1: 241
1: 234
1: 227
1: 238
1: 235
1: 233
1: 231
1: 236
Результат 91% от теоретического предела. Вполне годится для применения.
Если в микроконтроллере нет блока умножения, можно имитировать умножение операций сложения, смещения и XOR. Суть процесса такая же, модифицированный ошибкой бит, равномерно «распределяется» по остальным битам контрольной суммы.
CRC := (CRC shl 3) + byte;
CRC := (CRC shl 3) + byte;
CRC:=(CRC XOR (CRC SHR 8)) ; // как и в предыдущем алгоритме
Результат:
Статистика
1: 255
1: 257
1: 255
1: 255
1: 254
1: 255
1: 250
1: 254
1: 256
1: 254
На удивление хороший результат. Среднее значение 254,5 или 99% от теоретического предела, операций немного больше, но все они простые и не используется умножение.
Если для внутреннего хранения промежуточных значений контрольной суммы отдать 16 бит переменную (но передавать по линии связи будем только младшие 8 бит), что не проблема даже для самого слабого микроконтроллера, получим некоторое улучшение работы алгоритма. В целом экономить 8 бит нет особого смысла, и 8-битовая промежуточная переменная использовалась ранее просто для упрощения понимания работы алгоритма.
Статистика
1: 260
1: 250
1: 252
1: 258
1: 261
1: 255
1: 254
1: 261
1: 264
1: 262
Что соответствует 100.6% от теоретического предела, вполне хороший результат для такого простого алгоритма из одной строчки:
CRC:=CRC + byte*44111; // все переменные 16-битные
Используется полноценное 16-битное умножение. Опять же не обошлось без магического числа 44111 (выбрано из общих соображений без перебора всего подмножества чисел). Более точно, константу имеет смысл подбирать, только определившись с предполагаемым типом ошибок в линии передачи данных.
Столь высокий результат объясняется тем, что 2 цикла умножения подряд, полностью перемешивают биты, что нам и требовалось. Исключением, похоже, является последний байт телеграммы, особенно его старшие биты, они не полностью замешиваются в контрольную сумму, но и вероятность того, что ошибка придется на них невелика, примерно 4%. Эта особенность практически ни как не проявляется статистически, по крайней мере на моем наборе тестовых данных и ошибке ограниченной 10 сбойными битами. Для исключения этой особенности можно делать N+1 итераций, добавив виртуальный байт в дополнение к имеющимся в тестовом блоке данных (но это усложнение алгоритма).
Вариант без умножения с аналогичным результатом. Переменная CRC 16-битная, данные 8-битные, результат работы алгоритма — младшие 8 бит найденной контрольной суммы:
CRC := (CRC shl 2) + CRC + byte;
CRC := (CRC shl 2) + CRC + byte;
CRC:=(CRC XOR (CRC SHR 8));
Результат 100.6% от теоретического предела.
Вариант без умножения более простой, оставлен самый минимум функций, всего 3 математических операции:
CRC:=byte + CRC;
CRC:=CRC xor (CRC shr 2);
Результат 86% от теоретического предела.
В этом случае потери старших бит нет, они возвращаются в младшую часть переменной через функцию XOR (битовый миксер).
Небольшое улучшение в некоторых случаях дает так же:
- Двойной проход по обрабатываемым данным. Но ценой усложнения алгоритма (внешний цикл нужно указать), ценой удвоения времени обработки данных.
- Обработка дополнительного, виртуального байта в конце обрабатываемых данных, усложнения алгоритма и времени работы алгоритма практически нет.
- Использование переменной для хранения контрольной суммы большей по разрядности, чем итоговая контрольная сумма и перемешивание младших бит со старшими.
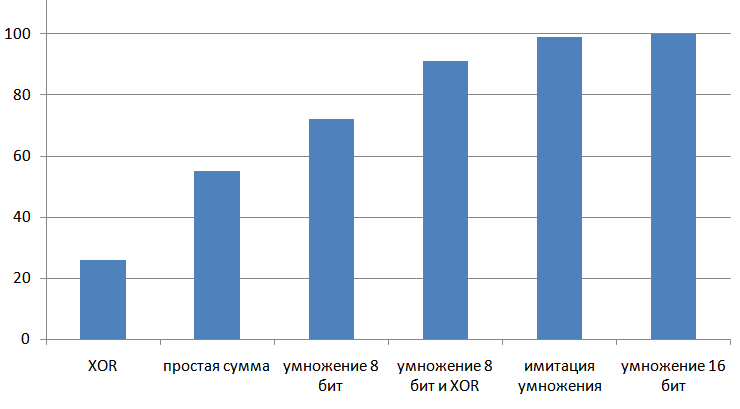
Результат работы рассмотренных алгоритмов, от простых и слабых, к сложным и качественным:
16-битная контрольная сумма
Далее, предположим что нам мало 8 бит для формирования контрольной суммы.
Следующий вариант 16 бит, и теоретическая вероятность ошибки переданных данных 1:65536, что намного лучше. Надежность растет по экспоненте. Но, как побочный эффект, растет количество вспомогательных данных, на примере нашей телеграммы, к 8 байтам полезной информации добавляется 2 байта контрольной суммы.
Простые алгоритмы суммы и XOR, применительно к 16-битной и последующим CRC не рассматриваем вообще, они практически не улучают качество работы, по сравнению с 8-битным вариантов.
Модифицируем алгоритм для обработки контрольной суммы разрядностью 16 бит, надо отметить, что тут так же есть магическое число 8 и 44111, значительное и необоснованное их изменение ухудшает работу алгоритма в разы.
CRC:=CRC + byte16*44111; //все данные 16-битные
CRC:=CRC XOR (CRC SHR 8);
Результат:
Статистика
1: 43478
1: 76923
1: 83333
1: 50000
1: 83333
1: 100000
1: 90909
1: 47619
1: 50000
1: 90909
Что соответствует 109% от теоретического предела. Присутствует ошибка измерений, но это простительно для 10 млн. итераций. Так же сказывается алгоритм создания, и вообще тип ошибок. Для более точного анализа, в любом случае нужно подстраивать условия под ошибки в конкретной линии передачи данных.
Дополнительно отмечу, что можно использовать 32-битные промежуточные переменные для накопления результата, а итоговую контрольную сумму использовать как младшие 16 бит. Во многих случаях, при любой разрядности контрольной суммы, так несколько улучшается качество работы алгоритма.
32-битная контрольная сумма
Перейдем к варианту 32-битной контрольной суммы. Появляется проблема со временем отводимым для анализа статистических данных, так как число переданных телеграмм уже сравнимо с 2^32. Алгоритм такой же, магические числа меняются в сторону увеличения
CRC:=CRC+byte32*$990C9AB5;
CRC:=CRC XOR (CRC SHR 16);
За 10 млн. итераций ошибка не обнаружена. Чтобы ускорить сбор статистики обрезал CRC до 24 бит:
CRC = CRC AND $FFFFFF;
Результат, из 10 млн. итераций ошибка обнаружена 3 раза
Статистика
1: 1000000
1: no
1: no
1: no
1: 1000000
1: no
1: 1000000
1: no
1: no
1: no
Вполне хороший результат и в целом близок к теоретическому пределу для 24 бит контрольной суммы (1:16777216). Тут надо отметить что функция контроля целостности данных равномерно распределена по всем битам CRC, и вполне возможно их отбрасывание с любой стороны, если есть ограничение на размер передаваемой CRC.
Для полноценных 32 бит, достаточно долго ждать результата, ошибок просто нет, за приемлемое время ожидания.
Вариант без умножения:
CRC := (CRC shl 5) + CRC + byte;
CRC := (CRC shl 5) + CRC;
CRC:=CRC xor (CRC shr 16);
Сбоя для полноценной контрольной суммы дождаться не получилось. Контрольная сумма урезанная до 24 бит показывает примерно такие же результаты, 8 ошибок на 100 млн. итераций. Промежуточная переменная CRC 64-битная.
64-битная контрольная сумма
Ну и напоследок 64-битная контрольная сумма, максимальная контрольная сумма, которая имеет смысл при передачи данных на нижнем уровне:
CRC:=CRC+byte64*$5FB7D03C81AE5243;
CRC:=CRC XOR (CRC SHR 8); // магическое число 1..20
Дождаться ошибки передачи данных, до конца существования вселенной, наверное не получится 🙂
Метод аналогичный тому, какой применили для CRC32 показал аналогичные результаты. Больше бит оставляем, выше надежность в полном соответствии с теоретическим пределом. Проверял на младших 20 и 24 битах, этого кажется вполне достаточным, для оценки качества работы алгоритма.
Так же можно применить для 128-битных чисел (и еще больших), главное подобрать корректно 128-битные магические константы. Но это уже явно не для микроконтроллеров, такие числа и компилятор не поддерживает.
Комментарии
В целом метод умножения похож на генерацию псевдослучайной последовательности, только с учетом полезных данных участвующих в процессе.
Рекомендую к использованию в микроконтроллерах, или для проверки целостности любых переданных данных. Вполне рабочий метод, уже как есть, не смотря на простоту алгоритма.
Мой проект по исследованию CRC на гитхаб.
Далее интересно было бы оптимизировать алгоритм на более реальных данных (не псевдослучайные числа по стандартному алгоритму), подобрать более подходящие магические числа под ряд задач и начальных условий, думаю можно еще выиграть доли процента по качеству работы алгоритма. Оптимизировать алгоритм по скорости, читаемости кода (простоте алгоритма), качеству работы. В идеале получить и протестировать образцы кода для всех типов микроконтроллеров, для этого как-раз и нужны примеры с использованием умножения 8, 16, 32 битных данных, и без умножения вообще.
В интернете существует большое количество вариантов расчёта контрольной суммы CRC. Но что же собственно такое контрольная сумма и почему она рассчитывается именно так? Давайте разберёмся. А заодно напишем программу, которая будет рассчитывать CRC с заданными параметрами.
1Теория, лежащая в основе расчёта CRC
Для начала давайте немного разберёмся в теории. Итак, что же такое CRC? Если кратко, это одна из разновидностей подсчёта контрольной суммы. Контрольная сумма – это метод проверки целостности принятой информации на стороне приёмника при передаче по каналам связи. Например, одна из простейших проверок – использование бита чётности. Это когда суммируются все биты передаваемого сообщения, и если сумма оказывается чётной, то в конец сообщения добавляется 0, если нечётной – то 1. При приёме также подсчитывается сумма битов сообщения, и сравнивается с принятым битом чётности. Если они отличаются, значит при передаче возникли ошибки, и передаваемая информация была искажена.
Но такой способ определения наличия ошибок – очень неинформативный и срабатывает не всегда, т.к. при искажении нескольких битов сообщения, чётность суммы может не измениться. Поэтому существует множество более «продвинутых» проверок, в том числе CRC.
По сути, CRC – это не сумма, а результат деления некого объёма информации (информационного сообщения) на константу, а точнее – остаток от деления сообщения на константу. Тем не менее, CRC исторически также называют «контрольная сумма». В значение CRC вносит вклад каждый бит сообщения. То есть, если хотя бы один бит исходного сообщения изменится при передаче, контрольная сумма тоже изменится, причём существенно. Это большой плюс такой проверки, так как он позволяет однозначно определить, исказилось исходное сообщение при передаче или нет.
Что такое исходное сообщение – понятно. Это непрерывная последовательность битов произвольной длины.
Что за константа, на которую мы должны делить исходное сообщение? Это некоторое число также любой длины, но обычно используются числа, кратные 1 байту – 8, 16 или 32 бита. Просто так легче считать, ведь компьютеры работают именно с байтами, а не с битами.
Константу-делитель обычно записывают в виде полинома (многочлена) вот таким образом: x8 + x2 + x1 + x0. Здесь степень числа “x” означает позицию бита-единицы в числе, начиная с нулевой, а старший разряд указывает на степень полинома и отбрасывается при интерпретации числа. То есть записанное ранее число – это не что иное как 100000111 в двоичной системе счисления.
Обычно при записи многочлена старший разряд подразумевается, но не пишется. То есть вышеуказанный многочлен можно было бы записать в двоичной системе как (1)00000111. В скобках я указал подразумеваемый старший разряд числа. Поэтому говорят, что многочлен равен 7 в десятичной системе счисления (111b = 7d).
Вот ещё пример: (x16 +) x15 + x2 + x0 = (1)1000000000000101 = 0x8005 = 32773.
Обычно используются некие стандартные многочлены для разных типов CRC. Вот некоторые из них:
| Алгоритм CRC | Образующий многочлен |
|---|---|
| CRC-16 | 0x8005 |
| CRC-16-CCITT | 0x1021 |
| CRC-16-DNP | 0x3D65 |
| CRC-32-IEEE 802.3 | 0x04C11DB7 |
| CRC-32C | 0x1EDC6F41 |
| CRC-32K | 0x741B8CD7 |
В посвящённой расчёту CRC статье на Википедии есть большая таблица образующих полиномов.
Так как же считать контрольную сумму? Существует базовый метод – деление сообщения на полином «в лоб» – и его модификации в целях уменьшения количества вычислений и, соответственно, ускорения расчёта CRC. Для начала мы рассмотрим именно базовый метод.
В общем виде деление числа на многочлен выполняется по такому алгоритму. Алгоритм вычисления контрольной суммы CRC:
- Создаётся массив (регистр), заполненный нулями, равный по длине разрядности (степени) полинома.
- Исходное сообщение дополняется нулями в младших разрядах, в количестве, равном числу разрядов полинома.
- В младший разряд регистра заносится один старший бит сообщения, а из старшего разряда регистра выдвигается один бит.
- Если выдвинутый бит равен “1”, то производится инверсия битов (операция XOR, исключающее ИЛИ) в тех разрядах регистра, которые соответствуют единицам в полиноме.
- Если в сообщении ещё есть биты, переходим к шагу 3).
- Когда все биты сообщения поступили в регистр и были обработаны этим алгоритмом, в регистре остаётся остаток от деления, который и является контрольной суммой CRC.
Назовём этот метод расчёта CRC метод побитового сдвига или простой метод.
Рисунок иллюстрирует деление исходной последовательности битов на число (1)00000111, или многочлен x8 + x2 + x1 + x0.
Кстати, проверить правильность расчёта CRC очень просто. В пункте (2) описанного алгоритма мы должны вместо дополнения исходного сообщения нулями дополнить его битами рассчитанной контрольной суммы, а остальное оставить как есть. Теперь остаток от деления дополненного сообщения на полином должен равняться нулю – это и есть признак верно рассчитанной контрольной суммы. Отличный от нуля остаток свидетельствует об ошибке.
Осталась ещё пара моментов, о которых стоит сказать. Как вы могли заметить, сообщение можно разделить на любое число. Как его выбрать? Существует ряд стандартных полиномов, которые используются при вычислении CRC. Например, для CRC32 это может быть число 0x04C11DB7, а для CRC16 это может быть 0x8005.
Кроме того, в регистр в начале вычислений можно записать не нули, а какое-то другое число. (И это рекомендуется делать: так повышается надёжность определения начала передачи сообщения, если, например, сообщение имеет в начале нулевые биты).
Также при расчётах непосредственно перед выдачей финальную контрольную сумму CRC можно поделить на какое-то другое число.
И последнее. Байты сообщения при записи в регистр могут помещаться как старшим битом «вперёд», так и наоборот, младшим. И результирующая CRC также может выдаваться, начиная со старшего бита или с младшего.
Изменение порядка битов в байте на обратный назовём «обращение», «реверс» или «отзеркаливание» байта.
Итого имеются 6 параметров, которые влияют на значение контрольной суммы:
- порядок CRC;
- образующий многочлен (его иногда называют «генераторный полином», переводя с английского буквально);
- начальное содержимое регистра;
- значение, с которым производится финальное XOR;
- реверс байтов информационного сообщения;
- реверс байтов CRC перед финальным XOR.
2Расчёт контрольной суммы CRC методом побитового сдвига
На основании всего вышеизложенного, давайте напишем функцию на языке Visual Basic .NET, которая будет рассчитывать контрольную сумму CRC, принимая ряд параметров, которые я описал выше, и возвращая значение CRC в виде 32-разрядного беззнакового числа.
Код расчёта CRC методом побитового сдвига на языке VB.NET
''' <summary>
''' Возвращает контрольную сумму типа CRC, рассчитанную методом побитового сдвига.
''' </summary>
''' <param name="bytes">Входная последовательность байтов (исходное сообщение).</param>
''' <param name="poly">Образующий многочлен разрядности <paramref name="width">width</paramref>.</param>
''' <param name="width">Порядок CRC в битах, 8/16/32.</param>
Public Shared Function GetCrc_Simple(ByVal bytes As Byte(), ByVal poly As UInteger, Optional ByVal width As Integer = 32, Optional ByVal initReg As UInteger = &HFFFFFFFFUI, Optional ByVal finalXor As UInteger = &HFFFFFFFFUI, Optional ByVal reverseBytes As Boolean = True, Optional ByVal reverseCrc As Boolean = True) As UInteger
Dim widthInBytes As Integer = width 8
'Дополняем сообщение width нулями (расчёт в байтах):
ReDim Preserve bytes(bytes.Length - 1 + widthInBytes)
'Создаём очередь битов из сообщения:
Dim msgFifo As New Queue(Of Boolean)(bytes.Count * 8 - 1)
For Each b As Byte In bytes
Dim ba As New BitArray({b})
If reverseBytes Then
For i As Integer = 0 To 7
msgFifo.Enqueue(ba(i))
Next
Else
For i As Integer = 7 To 0 Step -1
msgFifo.Enqueue(ba(i))
Next
End If
Next
'Создаём очередь из битов начального заполнения регистра:
Dim initBytes As Byte() = BitConverter.GetBytes(initReg)
Dim initBytesReversed As IEnumerable(Of Byte) = (From b As Byte In initBytes Take widthInBytes).Reverse
Dim initFifo As New Queue(Of Boolean)(width - 1)
For Each b As Byte In initBytesReversed
Dim ba As New BitArray({b})
If Not reverseBytes Then
For i As Integer = 0 To 7
initFifo.Enqueue(ba(i))
Next
Else
For i As Integer = 7 To 0 Step -1
initFifo.Enqueue(ba(i))
Next
End If
Next
'Сдвиг и XOR:
Dim register As UInteger = 0 'заполняем width-разрядный регистр нулями.
Do While msgFifo.Count > 0
Dim poppedBit As Integer = CInt(register >> (width - 1)) And 1 'определить перед сдвигом регистра.
Dim shiftedBit As Byte = Convert.ToByte(msgFifo.Dequeue)
If initFifo.Count > 0 Then
Dim b As Byte = Convert.ToByte(initFifo.Dequeue)
shiftedBit = shiftedBit Xor b
End If
register = register << 1
register = register Or shiftedBit
If poppedBit = 1 Then
register = register Xor poly
End If
Loop
'Финальные преобразования:
Dim crc As UInteger = register 'Регистр содержит остаток от деления - контрольную сумму.
If reverseCrc Then
crc = reflect(crc, width)
End If
crc = crc Xor finalXor
crc = crc And (&HFFFFFFFFUI >> (32 - width)) 'маскируем младшие разряды.
Return crc
End Function
''' <summary>
''' Обращает заданное число младших битов переданного числа.
''' </summary>
''' <param name="inpValue">Число, которое требуется «отзеркалить».</param>
''' <param name="bitsToReflect">Сколько младших битов обратить, 0..32.</param>
''' <returns></returns>
''' <remarks>Например: reflect(&H3E23, 3) == &H3E26.</remarks>
Private Shared Function reflect(ByVal inpValue As UInteger, Optional ByVal bitsToReflect As Integer = 32) As UInteger
Dim t As UInteger = inpValue
Dim reflected As UInteger = inpValue
For i As Integer = 0 To bitsToReflect - 1
Dim bm As UInteger = bitMask(bitsToReflect - 1 - i)
If (t And 1) = 1 Then
reflected = reflected Or bm
Else
reflected = reflected And Not bm
End If
t >>= 1
Next
Return reflected
End Function
''' <summary>
''' Возвращает наибольший разряд числа.
''' </summary>
''' <param name="number">Число, разрядность которого следует определить.</param>
''' <returns></returns>
Private Shared Function bitMask(ByVal number As Integer) As UInteger
Dim res As UInteger = (1UI << number)
Return res
End Function
Как вы могли заметить, в данной реализации расчёта CRC используется LINQ, так что соответствующая ссылка должна быть добавлена в проект.
Предлагаемая программа плохо масштабируема. То есть она работает хорошо при вычислении контрольной суммы CRC для коротких сообщений, длиной до нескольких десятков килобайтов. Я писал её с целью только продемонстрировать работу простого алгоритма, и не занимался оптимизацией. При расчёте CRC для длинного сообщения, размером десятки или сотни мегабайтов, программа будет сильно загружать процессор и память, т.к. всё сообщение целиком загружается в очередь. Этому способствует метод преобразования числа в битовую последовательность, используя Queue(Of Boolean). Для работы с такими большими сообщениями желательно реализовать промежуточный буфер, который будет передавать сообщение в программу небольшими порциями.
Зато у этой программы есть одно преимущество: она может быть использована для расчёта CRC любого порядка, не обязательно 8, 16 или 32. Это может быть CRC5 или CRC49. Только для чисел больше 32-х разрядов нужно изменить соответствующим образом входные параметры – допустим, poly передавать не как UInteger, а как ULong, или передавать его в виде битового массива (тогда теоретически порядок CRC вообще будет неограничен).
3Расчёт контрольной суммы CRC табличным методом
Для сокращения числа вычислений из предыдущего метода – метода побитового сдвига – придуманы некоторые оптимизации.
В частности, сдвигают не по одному биту за раз, а сразу по несколько. Наибольшую популярность снискали варианты, в которых сообщение сдвигается на число битов, кратное числу битов в байте: 8, 16 или 32, т.к. с байтами легче работать (не нужны дополнительные преобразования). При этом идея алгоритма осталась та же: сдвиг и исключающее ИЛИ с содержимым регистра.
Кроме того, оказывается, что часть расчётов можно провести заранее и записать в массив – таблицу, из которой по мере необходимости будет браться нужное число. Такой метод расчёта назвали табличный метод расчёта CRC.
Я не буду здесь вдаваться в теорию, она довольно сложна и много раз описана в других статьях. В частности, очень хорошее и подробное описание бинарной арифметики, лежащей в основе расчёта CRC, и описание табличного метода, даётся в статье Ross N. Williams: “A Painless Guide to CRC Error Detection Algorithms”. Рекомендую к прочтению обязательно! Оригинальный текст – в приложении к статье, а русский перевод легко найти в интернете.
Ну что же, пришло время для самой программы. Она будет несколько длиннее предыдущей. По сути, это реализация алгоритма из указанной статьи в стиле объектно-ориентированного программирования. Опять же будем писать программу на моём любимом языке программирования VB.NET. Я назвал этот класс RocksoftCrcModel, по названию компании, в которой работал автор указанной статьи.
Код расчёта CRC табличным методом на языке VB.NET
''' <summary>
''' Реализует алгоритм расчёта CRC методом Rocksoft^tm Model CRC.
''' </summary>
Public Class RocksoftCrcModel
#Region "PROPS AND FIELDS"
''' <summary>
''' Таблица предвычисленных значений для расчёта контрольной суммы.
''' </summary>
Public ReadOnly CrcLookupTable(255) As UInteger
''' <summary>
''' Порядок CRC, в битах (строго 8, 16 или 32).
''' Изменение этого свойства ведёт к пересчёту таблицы.
''' </summary>
Public Property CrcWidth As Integer
Get
Return _CrcWidth
End Get
Set(value As Integer)
If _CrcWidth <> value Then
_CrcWidth = value
_TopBit = getBitMask(_CrcWidth - 1)
_WidMask = (((1UI << (_CrcWidth - 1)) - 1UI) << 1) Or 1UI
generateLookupTable()
End If
End Set
End Property
Private _CrcWidth As Integer = 32
''' <summary>
''' Образующий многочлен.
''' Изменение этого свойства ведёт к пересчёту таблицы.
''' </summary>
Public Property Polynom As UInteger
Get
Return _Polynom
End Get
Set(value As UInteger)
If _Polynom <> value Then
_Polynom = value
generateLookupTable()
End If
End Set
End Property
Private _Polynom As UInteger = &H4C11DB7
''' <summary>
''' Обращать ли байты сообщения?
''' Изменение этого свойства ведёт к пересчёту таблицы.
''' </summary>
Public Property ReflectIn As Boolean
Get
Return _ReflectIn
End Get
Set(value As Boolean)
If _ReflectIn <> value Then
_ReflectIn = value
generateLookupTable()
End If
End Set
End Property
Private _ReflectIn As Boolean = True
''' <summary>
''' Начальное содержимое регистра.
''' </summary>
Public Property InitRegister As UInteger
Get
Return _InitRegister
End Get
Set(value As UInteger)
If _InitRegister <> value Then
_InitRegister = value
End If
End Set
End Property
Private _InitRegister As UInteger = &HFFFFFFFFUI
''' <summary>
''' Обращать выходное значение CRC?
''' </summary>
Public Property ReflectOut As Boolean
Get
Return _ReflectOut
End Get
Set(value As Boolean)
If _ReflectOut <> value Then
_ReflectOut = value
End If
End Set
End Property
Private _ReflectOut As Boolean = True
''' <summary>
''' Значение, с которым XOR-ится выходное значение CRC.
''' </summary>
Public Property XorOut As UInteger
Get
Return _XorOut
End Get
Set(value As UInteger)
If _XorOut <> value Then
_XorOut = value
End If
End Set
End Property
Private _XorOut As UInteger = &HFFFFFFFFUI
#End Region '/PROPS AND FIELDS
#Region "READ-ONLY PROPS"
''' <summary>
''' Возвращает старший разряд полинома.
''' </summary>
ReadOnly Property TopBit As UInteger
Get
Return _TopBit
End Get
End Property
Private _TopBit As UInteger = getBitMask(CrcWidth - 1)
''' <summary>
''' Возвращает длинное слово со значением (2^width)-1.
''' </summary>
Private ReadOnly Property WidMask As UInteger
Get
Return _WidMask
End Get
End Property
Private _WidMask As UInteger = (((1UI << (CrcWidth - 1)) - 1UI) << 1) Or 1UI
#End Region '/READ-ONLY PROPS
#Region "CTOR"
''' <summary>
''' Конструктор, инициализированный параметрами по умолчанию для алгоритма CRC32.
''' </summary>
Public Sub New()
generateLookupTable()
End Sub
''' <summary>
''' Инициализирует новый экземпляр параметрической модели CRC с настраиваемыми параметрами.
''' </summary>
''' <param name="width">Разрядность контрольной суммы в битах.</param>
''' <param name="poly">Полином.</param>
''' <param name="initReg">начальное содержимое регистра.</param>
''' <param name="isReflectIn">Обращать ли входящие байты сообщения?</param>
''' <param name="isReflectOut">Обратить ли CRC перед финальным XOR.</param>
''' <param name="xorOut">Конечное значение XOR.</param>
Public Sub New(ByVal width As Integer, ByVal poly As UInteger, Optional ByVal initReg As UInteger = &HFFFFFFFFUI, Optional ByVal isReflectIn As Boolean = True, Optional ByVal isReflectOut As Boolean = True, Optional ByVal xorOut As UInteger = &HFFFFFFFFUI)
Me.CrcWidth = width
Me.Polynom = poly
Me.InitRegister = initReg
Me.ReflectIn = isReflectIn
Me.ReflectOut = isReflectOut
Me.XorOut = xorOut
generateLookupTable()
End Sub
#End Region '/CTOR
#Region "ВЫЧИСЛЕНИЕ CRC"
''' <summary>
''' Вычисляет значение контрольной суммы переданного сообщения.
''' </summary>
''' <param name="message">Исходное сообщение, для которого нужно посчитать контрольную сумму.</param>
Public Function ComputeCrc(ByRef message As Byte()) As UInteger
Dim registerContent As UInteger = InitRegister 'Содержимое регистра в процессе пересчёта CRC.
For Each b As Byte In message
registerContent = getNextRegisterContent(registerContent, b)
Next
Dim finalCrc As UInteger = getFinalCrc(registerContent)
Return finalCrc
End Function
''' <summary>
''' Вычисляет значение контрольной суммы переданного сообщения и возвращает его в виде массива байтов.
''' </summary>
''' <param name="message">Исходное сообщение, для которого нужно посчитать контрольную сумму.</param>
Public Function ComputeCrcAsBytes(ByRef message As Byte()) As Byte()
Dim crc As UInteger = ComputeCrc(message)
Dim crcBytes As Byte() = BitConverter.GetBytes(crc)
Dim crcBytesOrdered(crcBytes.Length - 1) As Byte
For i As Integer = 0 To crcBytes.Length - 1
crcBytesOrdered(i) = crcBytes(crcBytes.Length - 1 - i)
Next
Return crcBytesOrdered
End Function
''' <summary>
''' Обрабатывает один байт сообщения (0..255).
''' </summary>
''' <param name="prevRegContent">Содержимое регистра на предыдущем шаге.</param>
''' <param name="value">Значение очередного байта из сообщения.</param>
Private Function getNextRegisterContent(ByVal prevRegContent As UInteger, ByVal value As Byte) As UInteger
Dim uValue As UInteger = value
If ReflectIn Then
uValue = reflect(uValue, 8)
End If
Dim reg As UInteger = prevRegContent
reg = reg Xor (uValue << (CrcWidth - 8))
For i As Integer = 0 To 7
If (reg And TopBit) = TopBit Then
reg = (reg << 1) Xor Polynom
Else
reg <<= 1
End If
reg = reg And WidMask()
Next
Return reg
End Function
''' <summary>
''' Возвращает значение CRC для обработанного сообщения.
''' </summary>
''' <param name="regContent">Значение регистра до финального обращения и XORа.</param>
Private Function getFinalCrc(ByVal regContent As UInteger) As UInteger
If ReflectOut Then
Dim res As UInteger = XorOut Xor reflect(regContent, CrcWidth)
Return res
Else
Dim res As UInteger = XorOut Xor regContent
Return res
End If
End Function
#End Region '/ВЫЧИСЛЕНИЕ CRC
#Region "РАСЧЁТ ТАБЛИЦЫ"
''' <summary>
''' Вычисляет таблицу предвычисленных значений для расчёта контрольной суммы.
''' </summary>
Private Sub generateLookupTable()
For i As Integer = 0 To 255
CrcLookupTable(i) = generateTableItem(i)
Next
End Sub
''' <summary>
''' Рассчитывает один байт таблицы значений для расчёта контрольной суммы
''' по алгоритму Rocksoft^tm Model CRC Algorithm.
''' </summary>
''' <param name="index">Индекс записи в таблице, 0..255.</param>
Private Function generateTableItem(ByVal index As Integer) As UInteger
Dim inbyte As UInteger = CUInt(index)
If ReflectIn Then
inbyte = reflect(inbyte, 8)
End If
Dim reg As UInteger = inbyte << (CrcWidth - 8)
For i As Integer = 0 To 7
If (reg And TopBit) = TopBit Then
reg = (reg << 1) Xor Polynom
Else
reg <<= 1
End If
Next
If ReflectIn Then
reg = reflect(reg, CrcWidth)
End If
Dim res As UInteger = reg And WidMask
Return res
End Function
#End Region '/РАСЧЁТ ТАБЛИЦЫ
#Region "ВСПОМОГАТЕЛЬНЫЕ"
''' <summary>
''' Возвращает наибольший разряд числа.
''' </summary>
''' <param name="number">Число, разрядность которого следует определить, степень двойки.</param>
Private Function getBitMask(ByVal number As Integer) As UInteger
Dim res As UInteger = 1UI << number
Return res
End Function
''' <summary>
''' Обращает заданное число младших битов переданного числа.
''' </summary>
''' <param name="value">Число, которое требуется обратить («отзеркалить»).</param>
''' <param name="bitsToReflect">Сколько младших битов числа обратить, 0..32.</param>
''' <remarks>Например: reflect(0x3E23, 3) == 0x3E26.</remarks>
Private Function reflect(ByVal value As UInteger, Optional ByVal bitsToReflect As Integer = 32) As UInteger
Dim t As UInteger = value
Dim reflected As UInteger = value
For i As Integer = 0 To bitsToReflect - 1
Dim bm As UInteger = getBitMask(bitsToReflect - 1 - i)
If (t And 1) = 1 Then
reflected = reflected Or bm
Else
reflected = reflected And Not bm
End If
t >>= 1
Next
Return reflected
End Function
#End Region '/ВСПОМОГАТЕЛЬНЫЕ
End Class
Этот код полностью готов к использованию, можно брать и применять. Пользоваться данной программой так:
- создать экземпляр класса RocksoftCrcModel(), передав в конструктор параметры модели CRC;
- для расчёта контрольной суммы, вызвать метод данного объекта ComputeCrc() или ComputeCrcAsBytes(), передав в качестве параметра информационное сообщение, для которого необходимо посчитать контрольную сумму;
- если меняются параметры модели CRC, таблица автоматически пересчитывается, и новый экземпляр класса можно не создавать.
Приведу пример использования данного класса для алгоритма CRC16. В качестве сообщения message будем использовать массив байтов, который представляет собой строку “123456789” в коде ASCII, которая используется во многих онлайн-калькуляторах CRC:
Dim crcModel As New RocksoftCrcModel(16, &H8005, 0, True, True, 0)
Dim message as Byte() = {&H31, &H32, &H33, &H34, &H35, &H36, &H37, &H38, &H39}
Dim crc As UInteger = crcModel.ComputeCrc(message)
Данная реализация расчёта CRC была проверена мною путём сличения со многими онлайн-калькуляторами CRC (назовём это «слабой» проверкой, именно такое определение дано в вышеуказанной статье, когда проверка осуществляется на основании сравнения рассчитанной контрольной суммы с эталонной, при одинаковых исходных параметрах и сообщении).
Для любителей C# перепишем данный класс таким образом:
Код расчёта CRC табличным методом на языке C# (разворачивается)
using System;
namespace CRC
{
/// <summary>Реализует алгоритм расчёта CRC методом Rocksoft^tm Model CRC.</summary>
public class RocksoftCrcModel
{
/// <summary>Таблица предвычисленных значений для расчёта контрольной суммы.</summary>
public readonly uint[] CrcLookupTable;
private int _CrcWidth;
private uint _Polynom;
private bool _ReflectIn;
private uint _InitRegister;
private bool _ReflectOut;
private uint _XorOut;
private uint _TopBit;
private uint _WidMask;
/// <summary>
/// Порядок CRC, в битах (8/16/32).
/// Изменение этого свойства ведёт к пересчёту таблицы.
/// </summary>
public int CrcWidth
{
get
{
return this._CrcWidth;
}
set
{
if (this._CrcWidth == value)
return;
this._CrcWidth = value;
this._TopBit = this.getBitMask(checked (this._CrcWidth - 1));
this._WidMask = (uint) ((int) checked (unchecked ((uint) (1 << checked (this._CrcWidth - 1))) - 1U) << 1 | 1);
this.generateLookupTable();
}
}
/// <summary>
/// Образующий многочлен.
/// Изменение этого свойства ведёт к пересчёту таблицы.
/// </summary>
public uint Polynom
{
get
{
return this._Polynom;
}
set
{
if ((int) this._Polynom == (int) value)
return;
this._Polynom = value;
this.generateLookupTable();
}
}
/// <summary>
/// Обращать байты сообщения?
/// Изменение этого свойства ведёт к пересчёту таблицы.
/// </summary>
public bool ReflectIn
{
get
{
return this._ReflectIn;
}
set
{
if (this._ReflectIn == value)
return;
this._ReflectIn = value;
this.generateLookupTable();
}
}
/// <summary>Начальное содержимое регистра.</summary>
public uint InitRegister
{
get
{
return this._InitRegister;
}
set
{
if ((int) this._InitRegister == (int) value)
return;
this._InitRegister = value;
}
}
/// <summary>Обращать выходное значение CRC?</summary>
public bool ReflectOut
{
get
{
return this._ReflectOut;
}
set
{
if (this._ReflectOut == value)
return;
this._ReflectOut = value;
}
}
/// <summary>Значение, с которым XOR-ится выходное значение CRC.</summary>
public uint XorOut
{
get
{
return this._XorOut;
}
set
{
if ((int) this._XorOut == (int) value)
return;
this._XorOut = value;
}
}
/// <summary>Возвращает старший разряд полинома.</summary>
public uint TopBit
{
get
{
return this._TopBit;
}
}
/// <summary>Возвращает длинное слово со значением (2^width)-1.</summary>
/// <returns></returns>
/// <remarks></remarks>
private uint WidMask
{
get
{
return this._WidMask;
}
}
/// <summary>
/// Конструктор, инициализированный параметрами по умолчанию для алгоритма CRC32.
/// </summary>
public RocksoftCrcModel()
{
base..ctor();
this.CrcLookupTable = new uint[256];
this._CrcWidth = 32;
this._Polynom = 79764919U;
this._ReflectIn = true;
this._InitRegister = uint.MaxValue;
this._ReflectOut = true;
this._XorOut = uint.MaxValue;
this._TopBit = this.getBitMask(checked (this.CrcWidth - 1));
this._WidMask = (uint) ((int) checked (unchecked ((uint) (1 << checked (this.CrcWidth - 1))) - 1U) << 1 | 1);
this.generateLookupTable();
}
/// <summary>
/// Инициализирует новый экземпляр параметрической модели CRC с настраиваемыми параметрами.
/// </summary>
/// <param name="width">Разрядность контрольной суммы в битах.</param>
/// <param name="poly">Полином.</param>
/// <param name="initReg">начальное содержимое регистра.</param>
/// <param name="isReflectIn">Обращать ли входящие байты сообщения?</param>
/// <param name="isReflectOut">Обратить ли CRC перед финальным XOR.</param>
/// <param name="xorOut">Конечное значение XOR.</param>
public RocksoftCrcModel(int width, uint poly, uint initReg = 4294967295, bool isReflectIn = true, bool isReflectOut = true, uint xorOut = 4294967295)
{
base..ctor();
this.CrcLookupTable = new uint[256];
this._CrcWidth = 32;
this._Polynom = 79764919U;
this._ReflectIn = true;
this._InitRegister = uint.MaxValue;
this._ReflectOut = true;
this._XorOut = uint.MaxValue;
this._TopBit = this.getBitMask(checked (this.CrcWidth - 1));
this._WidMask = (uint) ((int) checked (unchecked ((uint) (1 << checked (this.CrcWidth - 1))) - 1U) << 1 | 1);
this.CrcWidth = width;
this.Polynom = poly;
this.InitRegister = initReg;
this.ReflectIn = isReflectIn;
this.ReflectOut = isReflectOut;
this.XorOut = xorOut;
this.generateLookupTable();
}
/// <summary>Вычисляет значение контрольной суммы переданного сообщения.</summary>
/// <param name="message">Исходное сообщение, для которого нужно посчитать контрольную сумму.</param>
/// <returns></returns>
public uint ComputeCrc(ref byte[] message)
{
uint num1 = this.InitRegister;
byte[] numArray = message;
int index = 0;
while (index < numArray.Length)
{
byte num2 = numArray[index];
num1 = this.getNextRegisterContent(num1, num2);
checked { ++index; }
}
return this.getFinalCrc(num1);
}
/// <summary>
/// Вычисляет значение контрольной суммы переданного сообщения и возвращает его в виде массива байтов.
/// </summary>
/// <param name="message">Исходное сообщение, для которого нужно посчитать контрольную сумму.</param>
/// <returns></returns>
public byte[] ComputeCrcAsBytes(byte[] message)
{
byte[] bytes = BitConverter.GetBytes(this.ComputeCrc(ref message));
byte[] numArray = new byte[checked (bytes.Length - 1 + 1)];
int num1 = 0;
int num2 = checked (bytes.Length - 1);
int index = num1;
while (index <= num2)
{
numArray[index] = bytes[checked (bytes.Length - 1 - index)];
checked { ++index; }
}
return numArray;
}
/// <summary>Обрабатывает один байт сообщения (0..255).</summary>
/// <param name="prevRegContent">Содержимое регистра на предыдущем шаге.</param>
/// <param name="value">Значение очередного байта из сообщения.</param>
private uint getNextRegisterContent(uint prevRegContent, byte value)
{
uint num1 = (uint) value;
if (this.ReflectIn)
num1 = this.reflect(num1, 8);
uint num2 = prevRegContent ^ num1 << checked (this.CrcWidth - 8);
int num3 = 0;
do
{
num2 = (((int) num2 & (int) this.TopBit) != (int) this.TopBit ? num2 << 1 : num2 << 1 ^ this.Polynom) & this.WidMask;
checked { ++num3; }
}
while (num3 <= 7);
return num2;
}
/// <summary>Возвращает значение CRC для обработанного сообщения.</summary>
/// <param name="regContent">Значение регистра до финального обращения и XORа.</param>
/// <returns></returns>
private uint getFinalCrc(uint regContent)
{
if (this.ReflectOut)
return this.XorOut ^ this.reflect(regContent, this.CrcWidth);
return this.XorOut ^ regContent;
}
/// <summary>Вычисляет таблицу предвычисленных значений для расчёта контрольной суммы.</summary>
private void generateLookupTable()
{
int index = 0;
do
{
this.CrcLookupTable[index] = this.generateTableItem(index);
checked { ++index; }
}
while (index <= (int) byte.MaxValue);
}
/// <summary>
/// Рассчитывает один байт таблицы значений для расчёта контрольной суммы
/// по алгоритму Rocksoft^tm Model CRC Algorithm.
/// </summary>
/// <param name="index">Индекс записи в таблице, 0..255.</param>
private uint generateTableItem(int index)
{
uint num1 = checked ((uint) index);
if (this.ReflectIn)
num1 = this.reflect(num1, 8);
uint num2 = num1 << checked (this.CrcWidth - 8);
int num3 = 0;
do
{
if (((int) num2 & (int) this.TopBit) == (int) this.TopBit)
num2 = num2 << 1 ^ this.Polynom;
else
num2 <<= 1;
checked { ++num3; }
}
while (num3 <= 7);
if (this.ReflectIn)
num2 = this.reflect(num2, this.CrcWidth);
return num2 & this.WidMask;
}
/// <summary>Возвращает наибольший разряд числа.</summary>
/// <param name="number">Число, разрядность которого следует определить, степень двойки.</param>
/// <returns></returns>
private uint getBitMask(int number)
{
return (uint) (1 << number);
}
/// <summary>Обращает заданное число младших битов переданного числа.</summary>
/// <param name="value">Число, которое требуется обратить ("отзеркалить").</param>
/// <param name="bitsToReflect">Сколько младших битов числа обратить, 0..32.</param>
/// <returns></returns>
/// <remarks>Например: reflect(0x3E23, 3) == 0x3E26.</remarks>
private uint reflect(uint value, int bitsToReflect = 32)
{
uint num1 = value;
uint num2 = value;
int num3 = 0;
int num4 = checked (bitsToReflect - 1);
int num5 = num3;
while (num5 <= num4)
{
uint bitMask = this.getBitMask(checked (bitsToReflect - 1 - num5));
if (((long) num1 & 1L) == 1L)
num2 |= bitMask;
else
num2 &= ~bitMask;
num1 >>= 1;
checked { ++num5; }
}
return num2;
}
}
}
Данная программа на C# не тестировалась мной, в отличие от предыдущей, написанной на VB.NET. Этот код получен через декомпиляцию предыдущего. Если в нём обнаружатся какие-то ошибки, то пишите в комментариях или мне на почту, исправлю.
Прикладываю к статье полностью рабочий и готовый к использованию файл RocksoftCrcModel.vb с реализацией расчёта контрольной суммы CRC, который мы тут рассмотрели, а также RocksoftCrcModel.cs на C#.
Полную и самую последнюю версию кода можно скачать с репозитория на GitHub.
4«Взлом» контрольной суммы CRC32 и CRC16
Кратко затронем вопрос «взлома» CRC32. И прежде всего давайте определимся с понятием «взлом» применительно к данному вопросу.
Если задача определения контрольной суммы некоторого массива данных – прямая задача, то «взлом» – это обратная задача, а именно: подгонка контрольной суммы под определённый массив данных.
Допустим, вы имеете файл и рассчитали его контрольную сумму. Вам нужно изменить в нём произвольное число байтов, сохранив при этом контрольную сумму. Сделать это совсем не сложно.
Для начала нужно посчитать обычным образом контрольную сумму CRC32, CRC16 или любую другую, какая вам нужна, для этого изменённого файла. Пусть это будет C1. Теперь нужно добавить такое же число нулевых байтов в конец файла, которое содержится в контрольной сумме (для CRC32 – 4 байта, для CRC16 – 2 байта, и т.д.). Можно простым перебором подобрать такое число C2, которое мы и запишем в эти нулевые байты. Ведь понятно, что полный диапазон всех допустимых значений CRC32 укладывается в 232 ~ 4,295 млрд. То есть за 4 с небольшим миллиарда итераций расчёта контрольной суммы с начальным содержимым регистра, равным С1, мы брутфорсом («в лоб», методом грубой силы) подберём нужное значение. При современных вычислительных мощностях это не составит проблемы. А уж «взломать» с помощью перебора CRC16 вообще дело нескольких секунд.
Можно ли разместить нулевые байты в середине или начале файла? Можно. К операции XOR применим сочетательный закон: a XOR (b XOR c) = (a XOR b) XOR c, поэтому можно с успехом разбить файл на 3 части: до вставки, после вставки, и сама вставка. Посчитать CRC для первых двух частей (C1 и C2 на иллюстрации), объединить их операцией XOR, заполнить этим числом начальное содержимое регистра, а затем «сбрутфорсить» CRC оставшейся третьей части X.
+-----------------+-----+---------+ | c1 | x | c2 | +-----------------+-----+---------+
Есть более интеллектуальный и изящный способ подогнать CRC под нужное значение. Суть его в том, что вместо последовательного перебора всех подряд значений мы «прокручиваем назад» несколько раз (по числу байтов или битов контрольной суммы) наш табличный алгоритм или алгоритм побитового сдвига до тех пор, пока CRC не будет желаемой. На эту тему есть подробные и качественные материалы в сети.
Таким образом, напрашивается вывод: контрольная сумма типа CRC хорошо подходит для проверки целостности данных при случайных искажениях информации в канале передачи данных, но совершенно не подходит для защиты от намеренного взлома.
5Программа для расчёта контрольной суммы по алгоритмам CRC32, CRC16 и CRC8
На основе приведённого алгоритма была написана программа – калькулятор для расчёта контрольных сумм по алгоритмам CRC32, CRC16 и CRC8. Внешний вид окна приведён на рисунке. Программа работает под ОС Windows и требует .NET версии 3.5.
Программа позволяет рассчитывать CRC массива байтов (введённого в поле «Сообщение») или указанного файла. Все рассмотренные выше параметры контрольной суммы настраиваются через интерфейс программы.
Ну и напоследок выкладываю ссылки на архив, в архиве лежат: программа «Калькулятор CRC», оригинальная статья “A Painless Guide to CRC Error Detection Algorithms”, класс RocksoftCrcModel() на Visual Basic.NET и на C#.
Итак, подведём итоги. В этой статье мы:
– узнали, что такое контрольная сумма CRC и какие бывают её виды;
– научились считать CRC методом побитового сдвига и табличным методом;
– узнали алгоритмы «взлома» CRC и сделали вывод об области применимости контрольной суммы типа CRC.
Скачать программу «Калькулятор контрольной суммы CRC»
2023.05. Добавил версию 1.2 калькулятора. Пароль на архив – soltaurus.
При скачивании ISO образов и архивов больших размеров всегда есть вероятность получить «битый» файл. Во времена Dial-UP такое было сплошь и рядом. И хотя сейчас такое случается намного реже, чтобы убедиться, что перед вами «оригинальный» файл придумали контрольные суммы, которые вычисляются на основе содержимого и позволяют заметить несоответствие даже одного байта.
То есть, если вы измените один байт в проверяемом файле, то и контрольная сумма такого файла так же изменится.
Для чего нужны контрольные суммы
У контрольных сумм две задачи:
- Убедиться, что файл скачался корректно.
- Убедиться, что файл не был изменен злоумышленниками.
Зная контрольную сумму оригинала, можно проверить является ли ваша копия подлинной.
Как вычислить контрольную сумму он-лайн
Контрольную сумму можно проверить он-лайн. Но я не буду рекомендовать этот способ, так как если размер вашего файла несколько ГигаБайт, то это займет много времени и всегда есть вероятность ошибки при передаче файла. Кроме того делиться своими файлами со сторонними сервисами не правильно.
Как узнать контрольную сумму файла в Windows
Разумнее вычислить контрольную сумму локально на своем компьютере. Это быстро и конфиденциально. В этой статье я опишу несколько способов получения контрольных сумм, как с помощью сторонних программ, так и непосредственно с помощью самой операционной системы Виндовс.
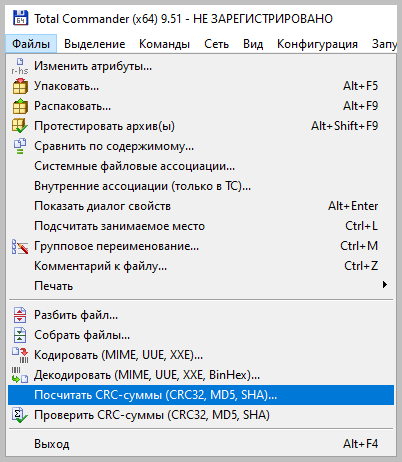
Файловый менеджер Total Commander
Total Commander — это популярный файловый менеджер, работающий на платформах Microsoft Windows и Android. В нем есть встроенная функция вычисления контрольных сумм.
После чего вы можете выбрать один из алгоритмом вычисления контрольных сумм.
По-умолчанию Total Commander создает файл с именем проверяемого и с расширением по имени выбранного алгоритма расчета контрольной суммы.
Файловый архиватор 7-Zip
7-Zip — свободный, бесплатный файловый архиватор с высокой степенью сжатия данных. Он поддерживает несколько алгоритмов сжатия и множество форматов данных, включая собственный формат 7z c высокоэффективным алгоритмом сжатия LZMA.
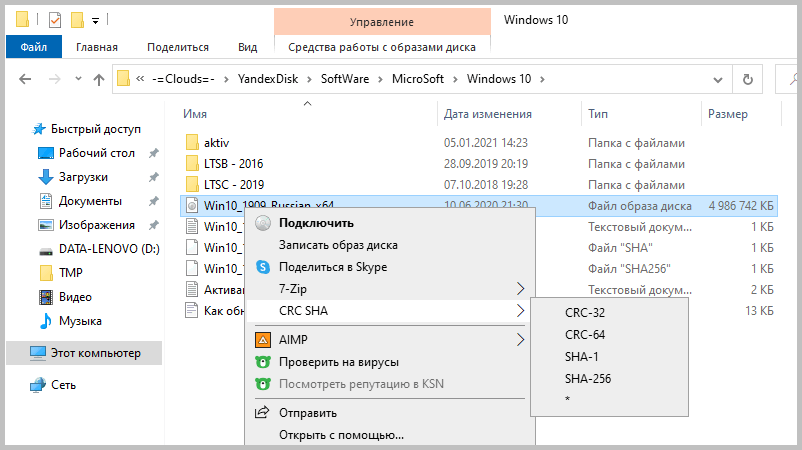
Этот архиватор имеет встроенную функцию вычисления контрольных сумм. Запустить ее можно прямо из контекстного меню Windows:
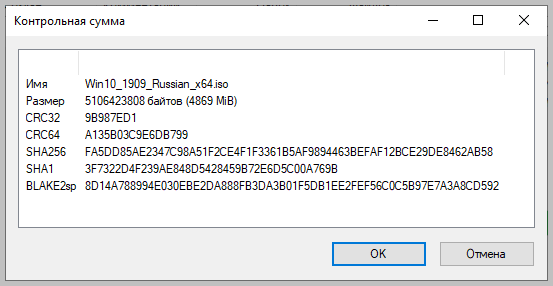
Если выбрать «звездочку», то программа подсчитает сразу несколько контрольных сумм:
Полученные данные можно выделить и скопировать в текстовый документ.
Как подсчитать контрольную сумму файла из консоли Windows
Чтобы посчитать контрольную сумму совсем не обязательно устанавливать специальные программы. И если вы не пользуетесь упомянутыми выше, то можете рассчитать контрольную сумму прямо из командной строки операционной системы.
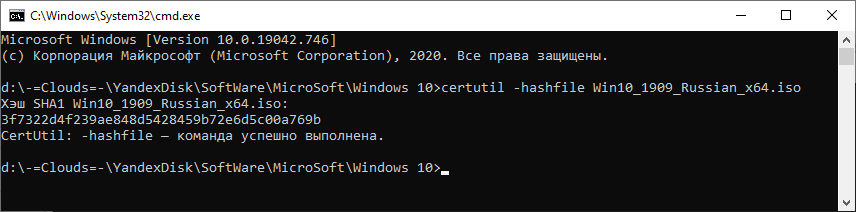
Например, чтобы посчитать контрольную сумму SHA1 с помощью утилиты CertUtil нужно запустить командную строку Windows 10, 8 или Windows 7 и ввести следующую команду:
certutil -hashfile путь_к_файлу алгоритм
Вот пример ее работы через несколько минут:
Считаем контрольную сумму в PowerShell
PowerShell — это средство автоматизации от Microsoft, с интерфейсом командной строки и языка сценариев, работает и включена в состав Windows 8 и новее.
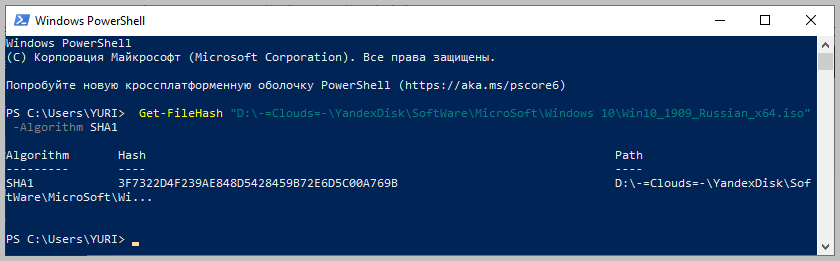
Чтобы вычислить контрольную сумму файла необходимо выполнить команду Get-FileHash указав через пробел имя файла и алгоритм вычисления контрольной суммы:
Get-FileHash "Disk:Full Path to fileFile Name.Extension" -Algorithm SHA1
Обратите внимание, что полный путь и имя файла лучше заключить в двойные кавычки.
По-умолчанию, если не указать тип контрольной суммы, то будет посчитана SHA-256.
Для алгоритмов вычисления контрольной суммы в Windows PowerShell поддерживаются следующие значения:
- SHA1
- SHA256 (по умолчанию)
- SHA384
- SHA512
- MD5
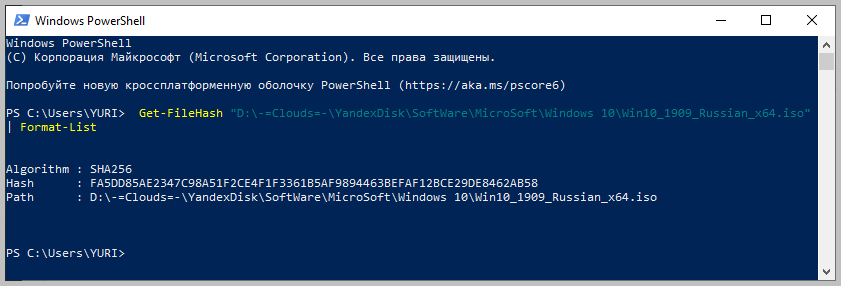
Для оформления вывода в виде списка можно использовать параметр | Format-List. Например:
Get-FileHash "Disk:Full Path to fileFile Name.Extension" | Format-List
Тогда результат работы будет выглядеть так:
Подробнее об использовании команды Get-FileHash можно прочитать на официальном сайте Microsoft — https://docs.microsoft.com/ru-ru/powershell/module/microsoft.powershell.utility/get-filehash
Какой алгоритм вычисления контрольных сумм самый правильный
MD5, SHA-1, SHA-256 и прочие – это разные алгоритмы хеш-функции. Хэши являются результатом работы криптографических алгоритмов, и представляют собой строку символов. Часто эти строки имеют фиксированную длину, независимо от размера входных данных.
MD5 самый быстрый, считается устаревшим, а SHA-256 имеет наименьшую вероятность коллизии, когда два разных файла имеют одинаковую контрольную сумму.
Для проверки целостности файла вам следует использовать тот, который предоставляет издатель. Если у вас на выбор есть несколько контрольных сумм, то лучше выбрать в следующей последовательности MD5, SHA-1, SHA-256, последний вариант является более предпочтительным.
Выводы
Если вы сомневаетесь в целостности скаченных файлов из интернета, особенно когда это касается оригинальных образов операционных систем, то проверьте их контрольную сумму. Сделать это можно как с помощью уже имеющихся у вас программ, так и воспользовавшись встроенными средствами операционной системы Windows.

22 апреля 2017
В интернете существует большое количество вариантов расчёта контрольной суммы CRC. Но что же собственно такое контрольная сумма и почему она рассчитывается именно так? Давайте разбираться.

Инструкция
Для начала давайте немного разберёмся в теории. Итак, что же такое CRC? Если кратко, это одна из разновидностей подсчёта контрольной суммы. Контрольная сумма – это метод проверки целостности принятой информации на стороне приёмника при передаче по каналам связи. Например, одна из простейших проверок – использование бита чётности. Это когда суммируются все биты передаваемого сообщения, и если сумма оказывается чётной, то в конец сообщения добавляется 0, если нечётной – то 1. При приёме также подсчитывается сумма битов сообщения, и сравнивается с принятым битом чётности. Если они отличаются, значит при передаче возникли ошибки, и передаваемая информация была искажена.
Но такой способ определения наличия ошибок – очень неинформативный и срабатывает не всегда, т.к. при искажении нескольких битов сообщения, чётность суммы может не измениться. Поэтому существует множество более “продвинутых” проверок, в том числе CRC.
По сути, CRC – это не сумма, а результат деления некого объёма информации (информационного сообщения) на константу, а точнее – остаток от деления сообщения на константу. Тем не менее, CRC исторически также называют “контрольная сумма”. В значение CRC вносит вклад каждый бит сообщения. То есть, если хотя бы один бит исходного сообщения изменится при передаче, контрольная сумма тоже изменится, причём существенно. Это большой плюс такой проверки, так как он позволяет однозначно определить, исказилось исходное сообщение при передаче или нет.
Прежде чем приступать к вычислению CRC, понадобится ещё немного теории.
Что такое исходное сообщение должно быть понятно. Это непрерывная последовательность битов произвольной длины.
Что за константа, на которую мы должны делить исходное сообщение? Это некоторое число также любой длины, но обычно используются числа, кратные 1 байту – 8, 16 и 32 бита. Просто так легче считать, ведь компьютеры работают именно с байтами, а не с битами.
Константу-делитель обычно записывают в виде полинома (многочлена) вот таким образом: x^8 + x^2 + x^1 + x^0. Здесь степень числа “x” означает позицию бита-единицы в числе, начиная с нулевой, а старший разряд указывает на степень полинома и отбрасывается при интерпретации числа. То есть записанное ранее число – это не что иное как (1)00000111 в двоичной системе счисления, или 7 в десятичной. В скобках я указал подразумеваемый старший разряд числа.
Вот ещё пример: x^16 + x^15 + x^2 + x^0 = (1)1000000000000101″ = 0x8005 = 32773.
Обычно используются некие стандартные многочлены для разных типов CRC.
Так как же считать контрольную сумму? Существует базовый метод – деление сообщения на полином “в лоб” – и его модификации в целях уменьшения количества вычислений и, соответственно, ускорения расчёта CRC. Мы рассмотрим именно базовый метод.
В общем виде, деление числа на многочлен выполняется по такому алгоритму:
1) создаётся массив (регистр), заполненный нулями, равный по длине разрядности полинома;
2) исходное сообщение дополняется нулями в младших разрядах, в количестве, равном числу разрядов полинома;
3) в младший разряд регистра заносится один старший бит сообщения, а из старшего разряда регистра выдвигается один бит;
4) если выдвинутый бит равен “1”, то производится инверсия битов (операция XOR, исключающее ИЛИ) в тех разрядах регистра, которые соответствуют единицам в полиноме;
5) если в сообщении ещё есть биты, переходим к шагу 3);
6) когда все биты сообщения поступили в регистр и были обработаны этим алгоритмом, в регистре остаётся остаток от деления, который и является контрольной суммой CRC.
Рисунок иллюстрирует деление исходной последовательности битов на число (1)00000111, или многочлен x^8 + x^2 + x^1 + x^0.
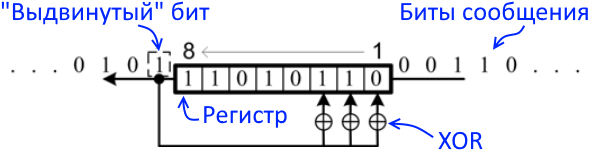
Осталась ещё пара дополнительных штрихов. Как вы могли заметить, сообщение можно разделить на любое число. Как его выбрать? Существует ряд стандартных полиномов, которые используются при вычислении CRC. Например, для CRC32 это может быть число 0x04C11DB7, а для CRC16 это может быть 0x8005.
Кроме того, в регистр в начале вычислений можно записать не нули, а какое-то другое число.
Также при расчётах непосредственно перед выдачей финальную контрольную сумму CRC могут делить на какое-то другое число.
И последнее. Байты сообщения при записи в регистр могут помещаться как старшим битом “вперёд”, так и наоборот, младшим.
На основании всего вышеизложенного, давайте напишем функцию на языке Basic .NET, которая будет рассчитывать контрольную сумму CRC, принимая ряд параметров, которые я описал выше, и возвращая значение CRC в виде 32-разрядного беззнакового числа.
Public Shared Function GetCrc(ByVal bytes As Byte(), ByVal poly As UInteger, Optional ByVal width As Integer = 32, Optional ByVal initReg As UInteger = &HFFFFFFFFUI, Optional ByVal finalXor As UInteger = &HFFFFFFFFUI, Optional ByVal reverseBytes As Boolean = True, Optional ByVal reverseCrc As Boolean = True) As UInteger
Dim widthInBytes As Integer = width 8
‘Дополняем сообщение width нулями (расчёт в байтах):
ReDim Preserve bytes(bytes.Length – 1 + widthInBytes)
‘Создаём очередь битов из сообщения:
Dim msgFifo As New Queue(Of Boolean)(bytes.Count * 8 – 1)
For Each b As Byte In bytes
Dim ba As New BitArray({b})
If reverseBytes Then
For i As Integer = 0 To 7
msgFifo.Enqueue(ba(i))
Next
Else
For i As Integer = 7 To 0 Step -1
msgFifo.Enqueue(ba(i))
Next
End If
Next
‘Создаём очередь из битов начального заполнения регистра:
Dim initBytes As Byte() = BitConverter.GetBytes(initReg)
Dim initBytesReversed As IEnumerable(Of Byte) = (From b As Byte In initBytes Take widthInBytes).Reverse
Dim initFifo As New Queue(Of Boolean)(width – 1)
For Each b As Byte In initBytesReversed
Dim ba As New BitArray({b})
If Not reverseBytes Then
For i As Integer = 0 To 7
initFifo.Enqueue(ba(i))
Next
Else
For i As Integer = 7 To 0 Step -1
initFifo.Enqueue(ba(i))
Next
End If
Next
‘Сдвиг и XOR:
Dim register As UInteger = 0 ‘заполняем width-разрядный регистр нулями.
Do While msgFifo.Count > 0
Dim poppedBit As Integer = CInt(register >> (width – 1)) And 1 ‘определить перед сдвигом регистра.
Dim shiftedBit As Byte = Convert.ToByte(msgFifo.Dequeue)
If initFifo.Count > 0 Then
Dim b As Byte = Convert.ToByte(initFifo.Dequeue)
shiftedBit = shiftedBit Xor b
End If
register = register << 1
register = register Or shiftedBit
If poppedBit = 1 Then
register = register Xor poly
End If
Loop
‘Финальные преобразования:
Dim crc As UInteger = register ‘Регистр содержит остаток от деления == контрольную сумму.
If reverseCrc Then
crc = reflect(crc, width)
End If
crc = crc Xor finalXor
crc = crc And (&HFFFFFFFFUI >> (32 – width)) ‘маскируем младшие разряды.
Return crc
End Function
Полезный совет
Предлагаемая программа плохо масштабируема. То есть она работает хорошо при вычислении контрольной суммы CRC для коротких сообщений, длиной до нескольких десятков килобайтов. При расчёте CRC для длинного сообщения, размером десятки или сотни мегабайтов, программа будет сильно загружать процессор и память, т.к. всё сообщение целиком загружается в массив. Для работы с такими большими сообщениями нужно реализовать промежуточный буфер, который будет передавать сообщение в программу небольшими порциями.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Во время передачи информации от одного устройства к другому могут возникать различные ошибки (помехи в радио-эфире, электромагнитные наводки в проводах), приводящие к повреждению данных. Достаточно повредить один бит, и число может сильно измениться! Например передавали число 123, которое выглядит как 0b01111011, и неправильно передали один бит. Приёмник получил число 0b01011011, что уже является числом 91! Если речь идёт о дистанционном управлении каким-то устройством, то даже один “битый” бит в посылке может привести к серьёзной аварии. Как приёмнику понять, что принятые данные повреждены?
Контрольная сумма
Самый простой вариант – контрольная сумма. Перед отправкой данных передатчик суммирует все байты и отправляет их например последними в посылке. Благодаря такой штуке как переполнение переменной, даже в один байт можно бесконечно суммировать данные и получить в итоге конкретное число, олицетворяющее все передаваемые данные. Например, передаём набор байтов 201, 125, 47, 94, 10, 185. Их суммой будет число 662, если брать ячейку int, или 150, если это byte. Осталось отправить контрольную сумму последним байтом (или двумя, если передаём int число)! Приёмник получает посылку, в свою очередь суммирует все байты кроме последнего (или двух последних, если контрольная сумма 16-битная), а затем сравнивает это значение с полученной контрольной суммой. Если отличается хоть на 1 – данные повреждены. Причём повреждёнными при передаче могут быть как сами данные, так и контрольная сумма: в любом случае они не совпадут, а это означает, что передача произошла с ошибкой. Давайте рассмотрим пример “передачи и приёма” структуры, где будет использоваться конструкция, позволяющая разбивать любые данные на байтовый поток. Три таких конструкции мы рассмотрели в уроке про указатели и ссылки. Структуру используем для удобства упаковки и использования данных. Универсальная для любого типа данных функция расчёта хеш-суммы может выглядеть так:
byte getHash(byte* data, int length) {
byte hash = 0;
int i = 0;
while (length--) {
hash += *(data + i);
i++;
}
return hash;
}
И возвращать байт суммы. Создадим и заполним структуру данными и прогоним через эту функцию. В последний байт структуры запишем контрольную сумму:
// структура данных посылки
struct MyData {
byte channel;
int val_i;
float val_f;
byte hash; // байт контрольной суммы
};
void setup() {
Serial.begin(9600);
// создаём и заполняем дату
MyData data;
data.channel = 16;
data.val_i = 12345;
data.val_f = 3.1415;
data.hash = 0;
// расчёт суммы
byte thisHash = getHash((byte*)&data, sizeof(data));
// пакуем в посылку
data.hash = thisHash;
// выведем для отладки
Serial.println(thisHash); // выдаст 102
}
Теперь можно передать структуру приёмнику! Пример “синтетический”, так как кому и каким способом передавать данные мы не рассматриваем. Хотя, можно отправить по Serial, например с одной Ардуины на другую, как в уроке по парсингу Serial:
Serial.write((byte*)&data, sizeof(data));
Далее на приёмнике примем данные:
// структура данных посылки
struct MyData {
byte channel;
int val_i;
float val_f;
byte hash; // байт контрольной суммы
};
MyData rxData;
void setup() {
Serial.begin(9600);
}
void loop() {
if (Serial.readBytes((byte*)&rxData, sizeof(rxData))) {
// приняли данные
}
}
Теперь нужно убедиться в том, что данные верны. Для этого прогоним их через ту же суммирующую функцию, но без учёта последнего байта, так как он сам является суммой:
byte thisHash = getHash((byte*)&rxData, sizeof(rxData) - 1);
Если значение совпадёт с переданным rxData.hash – данные верны! Дополним предыдущий код:
void loop() {
if (Serial.readBytes((byte*)&rxData, sizeof(rxData))) { // читаем дату
byte thisHash = getHash((byte*)&rxData, sizeof(rxData) - 1); // считаем сумму
if (thisHash == rxData.hash) {
// данные верны
} else {
// данные повреждены
}
}
}
И по условию можем выполнять какие-то действия, например применить полученные данные к устройству или проигнорировать их. Достоинства контрольной суммы:
- Быстрое и простое вычисление на любой платформе
- Возможность сделать 8 и 16 бит без особых вмешательств в код (это ваше домашнее задание)
Недостатки контрольной суммы:
- Низкая надёжность по сравнению с другими алгоритмами
Низкая надёжность заключается в том, что контрольная сумма не учитывает порядок байтов в посылке, то есть не является уникальным “отпечатком” всех данных. Например, данные повредились так, что из вот такого пакета
data.channel = 16; data.val_i = 12345; data.val_f = 3.1415;
Превратились в такой:
data.channel = 15; data.val_i = 12346; data.val_f = 3.1415;
Но контрольная сумма всё равно будет 102! Также контрольная сумма фактически игнорирует нули, то есть любой набор данных со всеми нулями и условно одной единичкой будет обрабатываться одинаково (например 0, 0, 0, 1, 0, 0 и 0, 1, 0, 0, 0, 0), что также снижает надёжность. Поэтому рассмотрим более хитрый алгоритм, который называется CRC.
CRC
CRC (cyclic redundancy code) – циклический избыточный код. Алгоритм тоже выдаёт некое “число” при прохождении через него потока байтов, но учитывает все предыдущие данные при расчёте. Как работает данный алгоритм мы рассматривать не будем, об этом можно почитать на Википедии или здесь. Рассмотрим реализацию CRC 8 бит по стандарту Dallas, он используется в датчиках этой фирмы (например DS18b20 и домофонные ключи iButton). Данная реализация должна работать на всех платформах, так как это чисто C++ без привязки к архитектуре (компилятор сам разберётся):
byte crc8(byte *buffer, byte size) {
byte crc = 0;
for (byte i = 0; i < size; i++) {
byte data = buffer[i];
for (int j = 8; j > 0; j--) {
crc = ((crc ^ data) & 1) ? (crc >> 1) ^ 0x8C : (crc >> 1);
data >>= 1;
}
}
return crc;
}
Данная функция применяется точно так же, как предыдущая getHash(), просто “скармливаем” ей данные в байтовом представлении и всё! Но есть пара моментов:
- При расчёте CRC перед отправкой нужно исключить байт самого CRC (последний), даже если он нулевой. То есть в примерах выше:
byte thisHash = crc8((byte*)&data, sizeof(data) - 1); - При расчёте CRC на стороне приёмника можно прогнать все данные полностью, вместе с байтом CRC. В этом случае функция вернёт
0, если данные верны! Это очень удобно использовать.
Финальный пример. Передатчик:
// структура данных посылки
struct MyData {
byte channel;
int val_i;
float val_f;
byte crc; // байт crc
};
void setup() {
Serial.begin(9600);
// создаём и заполняем дату
MyData data;
data.channel = 16;
data.val_i = 12345;
data.val_f = 3.1415;
// расчёт CRC (без последнего байта)
byte crc = crc8((byte*)&data, sizeof(data) - 1);
// пакуем в посылку
data.crc = crc;
}
void loop() {
// отправляем
Serial.write((byte*)&data, sizeof(data));
delay(1000);
}
byte crc8(byte *buffer, byte size) {
byte crc = 0;
for (byte i = 0; i < size; i++) {
byte data = buffer[i];
for (int j = 8; j > 0; j--) {
crc = ((crc ^ data) & 1) ? (crc >> 1) ^ 0x8C : (crc >> 1);
data >>= 1;
}
}
return crc;
}
Приёмник:
// структура данных посылки
struct MyData {
byte channel;
int val_i;
float val_f;
byte crc; // байт crc
};
MyData rxData;
void setup() {
Serial.begin(9600);
}
void loop() {
if (Serial.readBytes((byte*)&rxData, sizeof(rxData))) { // читаем дату
byte crc = crc8((byte*)&rxData, sizeof(rxData)); // считаем crc посылки полностью
if (crc == 0) {
// данные верны
} else {
// данные повреждены
}
}
}
byte crc8(byte *buffer, byte size) {
byte crc = 0;
for (byte i = 0; i < size; i++) {
byte data = buffer[i];
for (int j = 8; j > 0; j--) {
crc = ((crc ^ data) & 1) ? (crc >> 1) ^ 0x8C : (crc >> 1);
data >>= 1;
}
}
return crc;
}
Также коллега поделился реализацией данного алгоритма на ассемблере для AVR, она работает чуть быстрее и весит чуть легче, что может быть критично например для ATtiny:
byte crc8_asm(byte *buffer, byte size) {
byte crc = 0;
for (byte i = 0; i < size; i++) {
byte data = buffer[i];
// резкий алгоритм для AVR
uint8_t counter;
uint8_t buffer;
asm volatile (
"EOR %[crc_out], %[data_in] nt"
"LDI %[counter], 8 nt"
"LDI %[buffer], 0x8C nt"
"_loop_start_%=: nt"
"LSR %[crc_out] nt"
"BRCC _loop_end_%= nt"
"EOR %[crc_out], %[buffer] nt"
"_loop_end_%=: nt"
"DEC %[counter] nt"
"BRNE _loop_start_%="
: [crc_out]"=r" (crc), [counter]"=d" (counter), [buffer]"=d" (buffer)
: [crc_in]"0" (crc), [data_in]"r" (data)
);
}
return crc;
}
Функция используется точно так же, как предыдущая.
Полезные страницы
- Набор GyverKIT – большой стартовый набор Arduino моей разработки, продаётся в России
- Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с AliExpress у проверенных продавцов
- Подборка библиотек для Arduino, самых интересных и полезных, официальных и не очень
- Полная документация по языку Ардуино, все встроенные функции и макросы, все доступные типы данных
- Сборник полезных алгоритмов для написания скетчей: структура кода, таймеры, фильтры, парсинг данных
- Видео уроки по программированию Arduino с канала “Заметки Ардуинщика” – одни из самых подробных в рунете
- Поддержать автора за работу над уроками
- Обратная связь – сообщить об ошибке в уроке или предложить дополнение по тексту ([email protected])