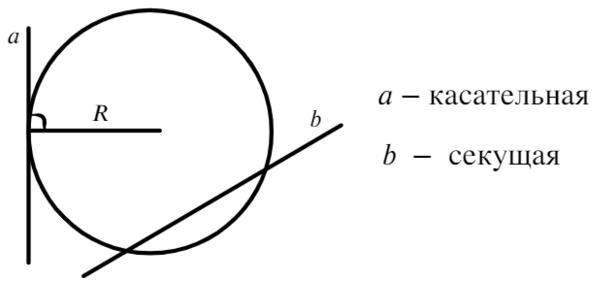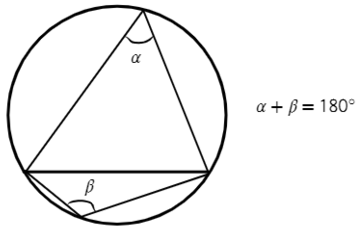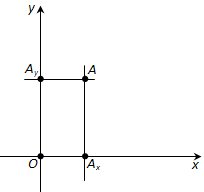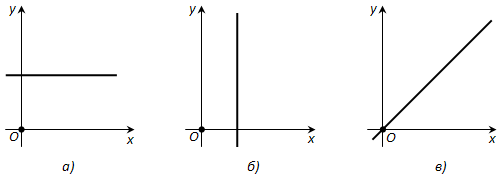Как найти контрольную точку в геометрии

Причины нарушения

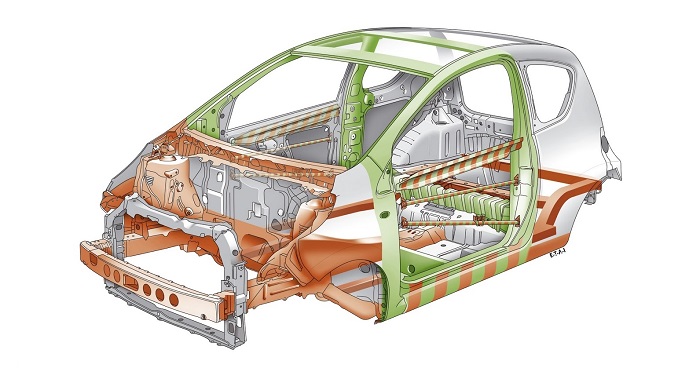
Правильное расстояние между всеми конкретными технологическими отверстиями на кузове автомобиля называется геометрией кузова. Расстояние определяется заводом-изготовителем. Его неизменность обеспечивает оптимальную работу всех узлов и агрегатов автомобиля, установленных на кузове. Места проверки:

1. Диагональ дверных проемов.
2. Расстояние между опорными точками кузова, к которым крепятся двигатель и ходовая.
3. Диагональ между лонжеронами и стаканами.
4. Диагональ капота, багажного отделения.
5. Расстояние между контрольной точкой на крыше и передним бампером.

Любое повреждение транспортного средства, годовая эксплуатация приводят к нарушению геометрии кузова. Расстояния изменяются, деформируя размер колесной базы, смещая внутренние детали.

Геометрия нарушается в следующих случаях:

1. Авария. Иногда достаточно задеть бампером забор.
2. Частая езда по ухабам, переезд ж/д путей на высокой скорости.
3. Заводские недоработки — недостаточно жестко прикрученные болты.

В двух последних случаях 70 % нагрузки берет на себя подвеска автомобиля, автомобилист же сталкивается с такой проблемой, как растянутые пружины и сломанные амортизаторы. Кузовная геометрия в этом случае изменяется постепенно.

После ДТП на кузов приходится 100 % нагрузки, геометрия изменяется моментально, необходимо проводить диагностику на стапеле в СТО или нивелиром (можно в гараже).

Первые признаки нарушения

Больше половины водителей не проводят регулярные замеры между технологическими отверстиями даже самостоятельно после кузовного ремонта. Приобретая автомобиль на вторичном рынке, для проверки необходимо ехать на специализированное СТО, часто информация о заводских размерах конкретной марки недоступна. Осмотр платный, однако экономия средств может вылиться в крупный ремонт уже через несколько месяцев. Признаки, что геометрия кузова нарушена:

1. Тяжело закрываются двери в салон, крышка капота, багажник.

В автомобилях ВАЗ багажник может плохо закрываться не по причине нарушенной геометрии, а при неисправностях с замками. Это характерная и знакомая многим поломка ВАЗ.

1. Проседание деталей в 80 % связано с деформацией стоек, а не с поломками в крепежах.
2. На скорости более 80 км/ч автомобиль «кидает» из стороны в сторону, появляется вибрация кузова. При осмотре комплектующих все агрегаты работают исправно, вибрация кузова отсутствует.
3. Частые поломки в ходовой части — признак деформации стаканов и лонжеронов.

Порванная подушка двигателя — первый признак нарушенной конструкции, даже если не было ДТП.

Что значат контрольные точки геометрии кузова

Чтобы получить представление о рассматриваемой характеристике, следует, прежде всего, разобраться с таким понятием как контрольные точки, которые необходимы для правильного проведения измерений.

Большая часть контрольных точек автомобиля являются технологическими отверстиями в элементах его кузова. В принципе, контрольными точками могут выступать все стационарные элементы на структурных кузовных деталях. Например, можно проводить замеры расстояний между симметричными углами кузова.

Необходимо, чтобы контрольные точки находились в горизонтальной или вертикальной плоскостях. Место их нахождения у разных моделей машин может отличаться (обычно, это указывается в руководстве по ремонту авто, где также приведено расстояние между конкретными контрольными точками).

При проверке геометрии кузова размеры учитываются между центрами или краями контрольных отверстий.

Как правило, это расстояние между центрами стационарных отверстий, которые находятся на противоположных участках кузова машины. В случае, когда такие отверстия имеют достаточно большой диаметр, нужно измерять расстояние между их краями.

Что такое геометрия кузова автомобиля

Что входит в понятие геометрии кузова машины? Как и с помощью каких приспособлений проводятся измерения этой геометрии? Рассматриваемое в нашей статье понятие можно охарактеризовать как установленную производителем систему расположения контрольных точек кузова друг относительно друга. Другими словами, геометрия кузова определяет точное расположение кузовных деталей, обеспечивающее слаженную работу узлов и агрегатов, закрепленных на кузове. Расположение таких деталей может определяться по размерам диагоналей проемов дверей, подкапотной части и багажника.

Наиболее важные контрольные размеры геометрии кузова показывают удаленность элементов, выполняющих несущую функцию по отношению к узлам подвески (расстояние между лонжеронами, стаканами и другими кузовными деталями, к которым крепится подвеска).

Таким образом, можно сделать вывод, что геометрия кузова влияет на колесную базу машины, размер колес и другие характеристики, являющиеся важной составляющей комфортной и безопасной езды. В связи с этим необходимо внимательно относиться к этому параметру. Какие факторы приводят к нарушению геометрии кузова?

К таким последствиям могут привести:

• дефекты дорожного покрытия;
• препятствия на дорогах;
• ДТП и последствия стихийных бедствий.

Факторы, которые приводят к нарушению геометрии кузова, могут оказывать различное по силе воздействие, что влияет на степень изменения расстояний между контрольными точками.

К примеру, все неровности дорожного покрытия и нагрузку, возникающую при случайном наезде на препятствия, в основном принимает на себя ходовая часть машины, но при этом и кузов может получать незаметные, на первый взгляд, деформации, которые накапливаются со временем.

Зачем проводить проверку геометрии кузова автомобиля

Диагностика геометрии кузова входит в число основных проверок, которые эксперты рекомендуют проводить перед тем, как купить машину с пробегом. Это позволит потенциальному покупателю выяснить, попадал ли автомобиль в ДТП, в каких условиях он эксплуатировался и насколько качественно выполнялся его ремонт.

В некоторых случаях измерение расстояний между контрольными точками осуществляется для проверки качества рихтовки и ремонта кузова. Не всегда владелец авто, которое было отремонтировано после ДТП, уделяет должное внимание проверке качества выполненных работ. На первый взгляд, все может выглядеть достаточно хорошо, но не всегда можно восстановить кузов после аварии методом простой рихтовки и вытягивания вмятин. В некоторых случаях необходимо проводить замену отдельных кузовных элементов, осуществлять «холодное» или «горячее» вытягивание деталей. Некачественное восстановление геометрии кузова может в будущем привести к серьезным неприятностям.

Автовладельцы, которые ответственно относятся к состоянию своего авто, стараются регулярно проверять правильность геометрии кузова. Можно встретить рекомендации специалистов относительно ежегодного проведения измерения расстояний между контрольными точками. Более того, некоторые автосервисы предлагают своим клиентам проверять геометрию кузова каждые полгода. Если учитывать состояние отечественных автомагистралей, то такие рекомендации можно считать вполне резонными.

Некоторые автовладельцы, даже не уточняя, сколько стоит геометрия кузова, утверждают, что это бессмысленные расходы. Таким водителям следует знать о существовании ряда признаков, при которых следует поскорее провести такую диагностику. Чем скорее они обратятся в автосервис, тем меньше нужно будет заплатить за устранение дефектов.

1. Первым признаком нарушения геометрии кузова авто является плохое закрывание капота, багажника или дверей. Если причиной затрудненного закрывания дверок не являются просевшие петли, значит, имеет место деформация стоек или других кузовных элементов.
2. Второй признак значительной деформации кузова будет куда более опасным. Он связан с нестабильным поведением машины на высоких скоростях. Она может «рыскать» в разные стороны, вибрировать в движении или автомобиль будет сильно тянуть в одну сторону. Если причина такого поведения авто не заключается в неисправной подвеске, значит, присутствует серьезная проблема с лонжеронами, стаканами или другими несущими элементами.

Правила измерения геометрии кузова авто

1. Для правильного проведения замеров расстояний между контрольными точками нужно установить машину на ровной поверхности и проверить давление в колесах (оно должно быть одинаковым). Некоторые измерительные линейки имеют встроенный уровень, позволяющий осуществлять измерения параллельно плоскости авто (параллельное положение линей часто является необходимым условием, чтобы точно сравнить полученные данные с точными данными относительно расстояния между контрольными точками). Следует отметить, что некоторые руководства по ремонту могут содержать сведения по расстояниям, выраженные в значениях шкалы измерительной линейки, а в другой документации могут приводиться фактические расстояния между контрольными точками (это, как правило, совершенно разные данные).Чтобы провести измерение расстояний в шкале линейки, измерительный прибор нужно в обязательном порядке располагать параллельно кузову. В противном случае показания будут некорректными. Чтобы удовлетворить требование параллельности, указатели измерительной линейки нужно выдвинуть на разную длину. В таком случае показания по шкале линейки будут отличаться от тех, которые можно получить с помощью рулетки (фактические показатели расстояния между контрольными точками). Если же указатели линейки при проведении измерений выдвинуты на одинаковое расстояние, то значение на ее шкале будет таким же, как и фактическое расстояние от одной точки до другой.
2. Замеры следует проводить между фиксированным точкам кузова (технологические отверстия, крепежные разъемы, болты и т.д.).
3. Каждый замер нужно проверить с использованием 2-х вспомогательных контрольных точек.Предпочтительнее проводить измерение расстояний между наиболее удаленными контрольными точками. При таких замерах картина смещения конструкционных элементов кузова будет более достоверной.
4. Иногда проведение замеров между аналогичными контрольными точками, которые расположены с противоположных сторон кузова, позволяет получить более объективную информацию относительно наличия деформаций, чем замеры по диагонали. Диагональные измерения необходимо дополнять замерами по длине кузова.
5. Проверка расстояний между контрольными точками приемлет суммарный допуск, не превышающий 3 мм (именно такая погрешность длительное время была допустимой для автопроизводителей). Современные технологии дают возможность выпускать кузова автомобилей с нулевой погрешностью.

Как проверяют геометрию кузова автомобиля

Мнение о том, что отсутствие отклонений в показателях развала схождения колес машины может служить подтверждением правильной геометрии кузова, является ошибочным. Диагностика кузова – это отдельная процедура, для которой необходимы специальные стенды и стапели.

С помощью таких устройств по контрольным точкам можно проверить соответствие размеров и диагоналей подкапотной части, багажника, дверных проемов, а также расстояние между лонжеронами, усилителями, несущими деталями кузова и т.д.

Существуют три варианта проверки геометрии кузова:

• Проведение замеров расстояний между контрольными точками. Этот вид диагностики позволяет быстро проверить правильность геометрии как перед началом ремонтных работ, так и в процессе их выполнения. Выполняют такие замеры с помощью обычной рулетки или специальной линейки.
• В ходе сравнительных измерений проводится анализ соответствия расстояний между симметричными точками, расположенными на противоположных сторонах кузова. Это вид проверки отличается универсальностью и простотой проведения диагностики кузовных повреждений. Как правило, специалисты сравнивают длину диагоналей между симметричными точками кузова. В этом случае можно сравнить данные замеров на поврежденной и целой стороне автомобиля.
• При трехмерном измерении производится определение пространственное расположения контрольных точек по отношению к базовым плоскостям кузова. Для такой диагностики необходимо иметь специальное оборудование.

В ходе проведения замеров специалист может установить степень основных повреждений, определить наличие второстепенных дефектов и наметить план восстановительных работ.

Для измерения геометрии кузова применяют мерные линейки или используют стационарное оборудование, стапель, который позволяет выполнить проверку расстояний между контрольными точками по специальным меткам или по электронным маячкам.

Для этого машину с помощью цепей фиксируют на платформе и на определенные точки кузова навешивают измерительные датчики. Достаточно часто мастера сталкиваются с ситуацией, когда контрольные точки спрятаны под обшивкой панелей кузова, под бамперами, под защитными элементами, поэтому приходится проводить частичную разборку кузова, чтобы обеспечить доступ к скрытым местам.

Чтобы провести в отношении геометрии кузова восстановление исходных параметров, в автосервисе проводят рихтовочные работы. Это достаточно сложная и многоэтапная работа, которая должна выполняться квалифицированными мастера, которые имеют соответствующее образование, опыт и хорошо чувствуют металл.

Гаражные специалисты могут рассказывать, что без проблем восстановят ваш автомобиль после аварии с помощью специальной сертифицированной линейки. Но доверять таким заверениям не стоит. Без такого оборудования, как стапель, геометрию кузова после серьезной аварии в полной мере восстановить не получится. Машины, отремонтированные в кустарных условиях, как правило, имеют отклонения в геометрии кузова.

На СТО

Проверка геометрии на специализированной автостанции становится неизбежной, если после диагностики колес на развал и схождение слесарь говорит, что отрегулировать посадку уже невозможно и необходимо проверить кузов на точное соотношение расстояний.

Первичная диагностика на СТО проводится с помощью нивелира. Прибор показывает, как отклонились колеса от заданного размера. Эта процедура лишь определяет, есть ли нарушение геометрии в принципе или нет.

Дальнейшая диагностика проводится на стенде. Автомобиль закрепляется на стапеле, предварительно с машины снимаются вся навесная облицовка: бампера, обвесы. В редких случаях необходим демонтаж агрегатов ходовой.

Дальнейшее диагностирование проводится электронными датчиками. Слесарь устанавливает их на контрольные точки, а устройства посылают трехмерный сигнал своего местонахождения на монитор.

Если СТО не имеет современного оборудования, мастер может использовать линейку для измерения геометрии кузова. Но это кустарный метод, дающий отклонение в размерах ± 5 мм.

На стапеле по контрольным точкам проводят следующие замеры:

• проем багажника;
• моторный отсек;
• передние, задние лонжероны;
• проем переднего, заднего стекла;
• проем всех дверей авто;
• срезы передней, средней, задней части автомобиля.

Каркас выправляют с помощью гидравлического оборудования и вакуумных присосок. После серьезной аварии кузов выравнивают растяжкой только при условии, что металл сохранил свои свойства.

Если в СТО предложат компьютерную проверку геометрии с помощью диодной указки, то разбирать авто на составляющие не потребуется — достаточно поставить машину на стенд. Программа проведет замеры и наложит их на шаблон модели. Буквально 10 минут диагностики, и распечатка кузова со всеми проблемами готова. Допустимая норма отклонений ± 5 мм.

В домашних условиях

Проверка кузова автомобиля в гараже необходима, если водитель замечает сложности с управлением без видимых причин. Для этого понадобится:

• линейка геометрическая, рулетка;
• масштабная рейка;
• циркуль;
• штангенциркуль.

Необходимые расстояния между контрольными точками находят в техдокументации на авто. Можно воспользоваться подсказками в интернете. Необходимо брать официальные сайты производителя. Японские бренды размещают техдокументацию на свои модели в свободном доступе, европейские комплектации придется поискать. Что проверять самостоятельно:

1. Визуально проверить, насколько плотно и равномерно закрываются двери, багажник и капот. Посмотреть расстояние от крышки, проема двери до кузова.
2. Загнать авто на яму, снизу проверить межосевое расстояние, используя рулетку.
3. Расстояние между колесами на оси поперечное.
4. Найти по инструкции все контрольные точки (технические отверстия, болты).
5. Снять элементы обшивки, если они мешают провести замеры и перекрывают доступ.
6. Начинать замер от центральной части основания кузова или рамы.
7. Проверить диагонали между точками в моторном отсеке.
8. Провести замер по контрольным отверстиям и болтам между направляющими рамы, от них к крепежам силового блока.
9. Каждый замер проверять дополнительными измерениями.
10. Проверить диагональ крыши.

Расхождения на 0,5 см указывают на среднюю степень изменения геометрии, более 1 см — на значительные отклонения в расстоянии.

Проверка геометрии кузова рулеткой

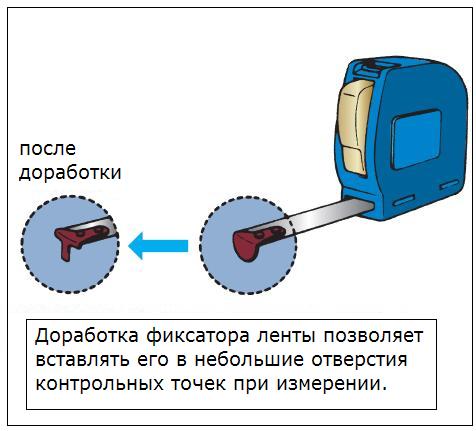
Рулет­ка исполь­зу­ет­ся, когда нет пре­пят­ствий меж­ду изме­ря­е­мы­ми точ­ка­ми. При изме­ре­нии рулет­кой нуж­но, что­бы лен­та не была изо­гну­та. Смот­реть на шка­лу нуж­но толь­ко под углом 90 гра­ду­сов и каж­дый раз с оди­на­ко­во­го места, что­бы не оши­бить­ся в зна­че­нии. Нуж­но, что­бы фик­са­тор лен­ты не имел излиш­не­го люф­та.  Лен­та рулет­ки долж­на лежать ров­но меж­ду точ­ка­ми, что­бы изме­ре­ние было кор­рект­ным. Для удоб­ства рабо­ты с неболь­ши­ми отвер­сти­я­ми, фик­са­тор лен­ты мож­но дора­бо­тать (см. рисунок).

Линейка для измерения геометрии кузова автомобиля

Рас­клад­ная изме­ри­тель­ная линей­ка явля­ет­ся наи­бо­лее часто при­ме­ня­е­мым устрой­ством для про­вер­ки гео­мет­рии кузова.

Изме­ри­тель­ная линей­ка спо­соб­на мерить рас­сто­я­ние меж­ду дву­мя точ­ка­ми. Каж­дое рас­сто­я­ние долж­но про­ве­рять­ся дву­мя допол­ни­тель­ны­ми кон­троль­ны­ми точками.

Совре­мен­ная линей­ка для изме­ре­ния гео­мет­рии кузо­ва явля­ет­ся теле­ско­пи­че­ским устрой­ством с регу­ли­ру­е­мы­ми по высо­те ука­за­те­ля­ми. Даже при рас­кла­ды­ва­нии на пол­ную дли­ну, она не даёт погреш­но­сти. В зави­си­мо­сти от типа исполь­зу­е­мой линей­ки может потре­бо­вать­ся допол­ни­тель­ный замер меж­ду ука­за­те­ля­ми. К допол­ни­тель­ным аксес­су­а­рам отно­сят­ся насад­ки и рас­ши­ре­ния для плот­но­го раз­ме­ще­ния в отверстиях.

Линей­ка поз­во­ля­ет про­из­во­дить изме­ре­ния при нали­чии пре­пят­ствий меж­ду изме­ря­е­мы­ми точками.

Все авто­мо­би­ли сим­мет­рич­ны отно­си­тель­но вооб­ра­жа­е­мой цен­траль­ной плос­ко­сти, рас­по­ло­жен­ной вдоль цен­тра маши­ны. Одна­ко, быва­ет несколь­ко точек на неко­то­рых авто, кото­рые, по раз­ным при­чи­нам, не сим­мет­рич­ны, но они не дела­ют всю маши­ну асси­мет­рич­ной. Без сим­мет­рии авто­мо­биль было бы очень слож­но изго­то­вить, да и продать.

Важ­но, что­бы ука­за­те­ли были плот­но встав­ле­ны в отверстия.

Как было упо­мя­ну­то ранее, если ука­за­те­ли были выстав­ле­ны на раз­ную высо­ту, то зна­че­ние на шка­ле линей­ки может отли­чать­ся от фак­ти­че­ско­го рас­сто­я­ния меж­ду изме­ря­е­мы­ми точ­ка­ми. Для кор­рект­но­го зна­че­ния нуж­но допол­ни­тель­но мерить рас­сто­я­ние меж­ду ука­за­те­ля­ми рулеткой.

Линей­ка и ука­за­те­ли долж­ны быть ров­ны­ми. Ука­за­те­ли долж­ны рас­по­ла­гать­ся на 90 гра­ду­сов отно­си­тель­но линей­ки и не иметь люфта.

Важ­но, что­бы при изме­ре­нии дли­на ука­за­те­лей была выстав­ле­на на оди­на­ко­вом расстоянии.

Если не тре­бу­ет­ся полу­чить точ­ные зна­че­ния, а про­из­во­дит­ся срав­не­ние одной сто­ро­ны с дру­гой, то линей­ка не обя­за­тель­но долж­на рас­по­ла­гать­ся парал­лель­но плос­ко­сти маши­ны. Мож­но срав­ни­вать рас­сто­я­ния с про­ти­во­по­лож­ной частью, а так­же с подоб­ны­ми точ­ка­ми тако­го же цело­го авто.

Ука­за­те­ли не нуж­но надав­ли­вать при изме­ре­нии, что­бы они не гну­лись и пока­за­ния не иска­жа­лись. Дан­ную линей­ку мож­но изго­то­вить само­му (см. ста­тью).

В допол­не­ние к диа­го­наль­ным изме­ре­ни­ям необ­хо­ди­мо делать заме­ры дли­ны и шири­ны. Это даст более точ­ное пред­став­ле­ние о пра­виль­но­сти рас­по­ло­же­ния кон­троль­ных точек. Диа­го­наль­ные изме­ре­ния могут сов­па­дать, даже если есть сме­ще­ние обе­их сторон.

Измерение днища кузова

На дни­ще про­из­во­дят­ся как диа­го­наль­ные изме­ре­ния, так и про­вер­ка на скру­чи­ва­ние и сме­ще­ние отно­си­тель­но цен­траль­ной линии.

Скру­чи­ва­ние или сме­ще­ние отно­си­тель­но цен­тра мож­но про­ве­рить на цен­траль­ной сек­ции кузова.

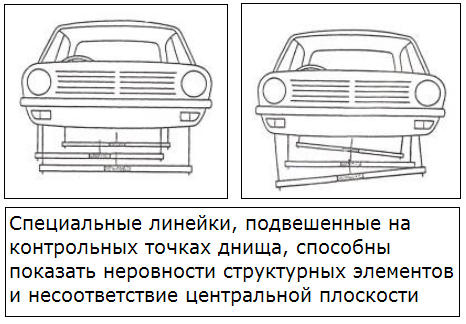
Для такой про­вер­ки суще­ству­ет метод под­ве­ши­ва­ния цен­три­ру­ю­щих лине­ек в кон­троль­ные отвер­стия на дни­ще. Места, на кото­рые под­ве­ши­ва­ют­ся линей­ки, не долж­ны быть дефор­ми­ро­ва­ны. Под­ве­ши­ва­ет­ся несколь­ко лине­ек вдоль сило­вых эле­мен­тов дни­ща. Если они парал­лель­ны, то скру­чи­ва­ния нет, если не парал­лель­ны, то скру­чи­ва­ние при­сут­ству­ет. Центр лине­ек так­же дол­жен сов­па­дать, ина­че суще­ству­ет сме­ще­ние отно­си­тель­но цен­траль­ной плоскости.

Сравнительное измерение геометрии кузова автомобиля

Самый быст­рый метод изме­ре­ния повре­ждён­ной части кузо­ва – срав­ни­тель­ное изме­ре­ние. Для этих целей хоро­шо под­хо­дит спе­ци­аль­ный цир­куль, но так­же мож­но исполь­зо­вать и изме­ри­тель­ную линей­ку. Если, к при­ме­ру, делать заме­ры про­стран­ства под капо­том, то одна часть цир­ку­ля встав­ля­ет­ся в одно из бол­то­вых отвер­стий, рас­по­ло­жен­ных у лобо­во­го стек­ла, а дру­гая ста­вить­ся к любо­му месту, кото­рое нуж­но срав­нить с про­ти­во­по­лож­ной сто­ро­ной. Далее цир­куль фик­си­ру­ет­ся спе­ци­аль­ным меха­низ­мом и пере­став­ля­ет­ся на такие же точ­ки с про­ти­во­по­лож­но­го места. Таким обра­зом мож­но быст­ро про­ве­рить несколь­ко сим­мет­рич­ных точек и понять куда про­изо­шло сме­ще­ние струк­тур­ных эле­мен­тов. Подоб­ным обра­зом цир­ку­лем мож­но изме­рять любую часть маши­ны. Такое срав­не­ние мож­но делать мно­же­ство раз в про­цес­се ремон­та для контроля.

Цир­куль для срав­ни­тель­но­го изме­ре­ния гео­мет­рии кузова

Цир­куль для срав­ни­тель­но­го изме­ре­ния гео­мет­рии кузо­ва напо­ми­на­ет по кон­струк­ции обыч­ный цир­куль. Два ука­за­те­ля соеди­не­ны вме­сте и не име­ют какой-либо шка­лы. Для срав­ни­тель­но­го заме­ра необ­хо­ди­мо каж­дый из ука­за­те­лей поме­стить в отвер­стие кон­троль­ных точек, рас­сто­я­ние меж­ду кото­ры­ми необ­хо­ди­мо про­ве­рить. Далее ука­за­те­ли фик­си­ру­ют­ся спе­ци­аль­ным фик­са­то­ром, вхо­дя­щим в кон­струк­цию устрой­ства, и цир­куль пере­став­ля­ет­ся на точ­ки, рас­по­ло­жен­ные с про­ти­во­по­лож­ной части, для срав­не­ния. При необ­хо­ди­мо­сти мож­но заме­рить рас­сто­я­ние меж­ду ука­за­те­ля­ми при помо­щи рулет­ки. Такой цир­куль хорош тем, что мож­но очень быст­ро сде­лать срав­не­ние двух сто­рон авто­мо­би­ля для опре­де­ле­ния сте­пе­ни несо­от­вет­ствия. Им мож­но срав­ни­вать самые труд­но­до­ступ­ные места. Такой инстру­мент неслож­но изго­то­вить самому.

Можно ли провести диагностику геометрии кузова в домашних условиях

Если восстановление геометрии кузова в автосервисе вам не подходит, то при необходимости (к примеру, если стали появляться проблемы с управляемостью авто без видимых причин) такую процедуру можно выполнить самостоятельно в гараже. Для измерения понадобятся следующие приспособления:

• раскладная измерительная линейка;
• рулетка без дополнительных люфтов;
• масштабная рейка;
• циркуль;
• штангенциркуль.

Определить точное расположение контрольных точек можно с помощью технической документации для вашего автомобиля. Если под рукой таких документов нет, можно посмотреть в интернете. Рекомендуем пользоваться официальными сайтами от производителя вашей модели. На японские машины найти техдокументацию легче (она есть в свободном доступе), чем на европейские модели.

Как проверяется геометрия кузова своими руками:

1. На глаз посмотреть, если двери автомобиля, багажная крышка и капот закрываются неплотно. Проверить расстояние проемов дверей.
2. С помощью рулетки измерить расстояние между осями. Для этого машину нужно поставить на яму.
3. Измерить поперечное расстояние между колесными осями.
4. Определить, где находятся контрольные точки с помощью техдокументации.
5. При возникновении проблем с доступом к контрольным точкам необходимо снять обшивку.
6. Замер начинается от центральной части кузова.
7. Измерить расстояние по диагонали между контрольными точками моторного отсека.
8. Измерить расстояние между контрольными точками, болтами, направляющими рамы и контрольным точкам на силовом блоке.
9. После каждого замера проводить дополнительные измерения, чтобы удостовериться в корректности данных.
10. Проверить крышу по диагонали.

Расхождения на 0,5 см указывают на среднюю степень изменения геометрии, более 1 см — на значительные отклонения в расстоянии.

• Измерение геометрии кузова рулеткойПри использовании рулетки необходимо руководствоваться несколькими правилами: отсутствие препятствий для проведения замеров между контрольными точками; измеряемые значения на шкале нужно смотреть под углом в 90 градусов и с одного и того же места (это важно для получения максимально корректных данных); фиксатор ленты рулетки должен быть без дополнительных люфтов.

Трёхмерная электронная диагностика геометрии кузова

Диагностика геометрии кузова в трехмерном виде включает в себя данные о длине, ширине и высоте частей кузова. Такое измерение происходит с помощью специальных трехмерных систем.

Принцип работы измерительной системы: данные поступают от воображаемых частей кузова, которые дают представление о расстоянии между его плоскостями.

Трехмерная система измеряет и использует полученные воображаемые плоскости для создания полной картины о состоянии автомобиля.

Основные измерения: от центральной плоскости измеряется ширина, от нулевой плоскости — длина, а от основной плоскости (параллельно днищу) — высота.

1. Центральная плоскостьЦентральная линия (или плоскость) разделяет авто на две одинаковые половины (разделять нужно вдоль). Некоторые автомобили имеют метки, помогающие определить центр машины. Обычно их можно найти на верхней или нижней металлической части кузова. Такой меткой можно воспользоваться при наличии специальной линейки или рулетки. Это позволит сэкономить время при замерах. Симметрия будет проявляться в расстояниях между центром и определенной точкой с правой или левой сторон. Расстояния должны быть одинаковы. В большинстве случаев автомобили имеют лишь несколько асимметричных точек, а в остальном они полностью симметричны. Части кузова должны быть зеркальны друг другу.
2. Измерение днища кузоваНа основной плоскости кузова проводятся два вида измерений: замеры расстояния до контрольных точек по диагонали, а также диагностика на наличие скручивания или смешения по центральной плоскости.

   Наличие/отсутствие скручивания и смещения проверяется по центральной плоскости кузова.

   Проведение такого рода проверки происходит на днище за счет подвешивания в контрольные отверстия центрирующих линеек. Места для подвешивания линеек должны быть без изгибов и деформаций. Вдоль силовых элементов днища крепятся центрирующие линейки. Если присутствует скручивание, значит, линейки не будут расположены параллельно. Совпадать должен и центр измерительных устройств, в противном случае можно говорить о наличии смещения по центральной плоскости.

К чему может привести эксплуатация автомобиля, у которого нарушена геометрия кузова

Ранее мы отмечали, что правильные параметры геометрии кузова являются важным фактором обеспечения безопасности водителя и пассажиров. Угол наклона колес и их расположение задаются относительно несущих кузовных элементов. Другими словами, нарушенная геометрия кузова не позволит нормально отрегулировать развал-схождение. При небольшом изменении расстояний между контрольными точками специалист сможет выставить нужное положение колес, но это будет временная мера.

Нарушение геометрии способствует постепенной деформации днища автомобиля. Изменения происходят между сварными соединениями, и в длинномерных кузовных деталях могут формироваться складки. Все эти изменения снижают характеристики безопасности кузовной конструкции.

Конструкторы рассчитывают геометрию кузова автомобилей таким образом, чтобы в случае лобового столкновения мотор проваливался под днище. При нарушенной геометрии кузова двигатель в результате удара может влететь в салон авто, что на 25% увеличивает риск смерти водителя и на 50% — пассажиров.

Гаражные рихтовщики, восстанавливая дефекты кузова авто, выполняют простую рихтовку кузовных деталей и подтяжку крепежных болтов. Для проверки расстояний между контрольными точками чаще всего используется обычная рулетка. Если деформация кузова вызвана длительным сроком службы машины, следует проверить все соединения, включая сварные швы.

Для восстановления кузова после аварии необходимо специальное оборудование. Даже, если точность измерений будет очень высокой, то для восстановления параметров кузова нужно не выравнивать деформированные кузовные детали, а заменить их новыми. Если выявлена деформация несущей ямы, то кузов нужно вытягивать на специальном стенде.

Возможные последствия

Правильные геометрические параметры автомобиля — это безопасность водителя и пассажиров. Относительно положения силовых элементов кузова задается угол расположения каждого из колес автомобиля. При нарушении геометрии измерительная система развала-схождения никогда не будет соответствовать норме. Если кузов «повело» относительно мало, мастер настроит положение колес, но ненадолго.

Изменения геометрии приводят к тому, что постепенно деформируется днище, в промежутках между точками сварки в длинномерных элементах кузова появляются складки, характеристики безопасности конструкции заметно снижаются.

При лобовом столкновении двигатель должен провалиться под днище. Если размеры кузова нарушены, мотор влетит в салон, риск смертельного исхода для водителя и пассажира увеличивается на 50 %.

Как восстановить геометрию

Восстановление геометрии в гараже сводится к рихтовке кузовных элементов и подтяжке всех болтов, если авто не стало участником аварии. Рулеткой проверяются замеры между технологическими отверстиями. Если геометрия нарушена незначительно из-за долгой эксплуатации, рекомендуется проверить все крепежи кузова и сварочные швы.

Основательно восстановить кузов после ДТП самостоятельно, без специального оборудования, практически невозможно. Даже если с точностью до миллиметра провести замеры, выровнять кузовные элементы часто нельзя, необходимо менять их на новые. При деформации рамы потребуется устанавливать авто на стенд и проводить вытяжку.

[spoiler title=»Источники»]

• https://InfoKuzov.ru/kuzov/kontrolnye-tochki
• https://rad-star.ru/pressroom/articles/geometriya-kuzova/
• https://kuzov.info/geometriya-kuzova-avtomobilya-podrobn/
• https://avto-sovet.ru/kuzov/kontrolnye-tochki-kuzova.html

[/spoiler]

Контрольные точки геометрии кузова — главный параметр, который позволяет проверить целостность транспортного средства. По этим точкам проверяют соответствие геометрии автомобиля заводским нормам. Любое отклонение в расстоянии между точками замеров приводит к кузовному ремонту, который, в зависимости от нарушений, можно провести самостоятельно или в СТО.

Причины нарушения

Правильное расстояние между всеми конкретными технологическими отверстиями на кузове автомобиля называется геометрией кузова. Расстояние определяется заводом-изготовителем. Его неизменность обеспечивает оптимальную работу всех узлов и агрегатов автомобиля, установленных на кузове. Места проверки:

1. Диагональ дверных проемов.
2. Расстояние между опорными точками кузова, к которым крепятся двигатель и ходовая.
3. Диагональ между лонжеронами и стаканами.
4. Диагональ капота, багажного отделения.
5. Расстояние между контрольной точкой на крыше и передним бампером.

Любое повреждение транспортного средства, годовая эксплуатация приводят к нарушению геометрии кузова. Расстояния изменяются, деформируя размер колесной базы, смещая внутренние детали.

Геометрия нарушается в следующих случаях:

1. Авария. Иногда достаточно задеть бампером забор.
2. Частая езда по ухабам, переезд ж/д путей на высокой скорости.
3. Заводские недоработки — недостаточно жестко прикрученные болты.

В двух последних случаях 70 % нагрузки берет на себя подвеска автомобиля, автомобилист же сталкивается с такой проблемой, как растянутые пружины и сломанные амортизаторы. Кузовная геометрия в этом случае изменяется постепенно.

После ДТП на кузов приходится 100 % нагрузки, геометрия изменяется моментально, необходимо проводить диагностику на стапеле в СТО или нивелиром (можно в гараже).

Первые признаки нарушения

Больше половины водителей не проводят регулярные замеры между технологическими отверстиями даже самостоятельно после кузовного ремонта. Приобретая автомобиль на вторичном рынке, для проверки необходимо ехать на специализированное СТО, часто информация о заводских размерах конкретной марки недоступна. Осмотр платный, однако экономия средств может вылиться в крупный ремонт уже через несколько месяцев. Признаки, что геометрия кузова нарушена:

1. Тяжело закрываются двери в салон, крышка капота, багажник.

В автомобилях ВАЗ багажник может плохо закрываться не по причине нарушенной геометрии, а при неисправностях с замками. Это характерная и знакомая многим поломка ВАЗ.

1. Проседание деталей в 80 % связано с деформацией стоек, а не с поломками в крепежах.
2. На скорости более 80 км/ч автомобиль «кидает» из стороны в сторону, появляется вибрация кузова. При осмотре комплектующих все агрегаты работают исправно, вибрация кузова отсутствует.
3. Частые поломки в ходовой части — признак деформации стаканов и лонжеронов.

Порванная подушка двигателя — первый признак нарушенной конструкции, даже если не было ДТП.

Как проверить геометрию автомобиля

Стандартно проверка кузова должна проводится 1 раз в год, если авто не побывало в аварии. Самостоятельно можно сделать проверку геометрии, ориентируясь на ширину передней и задней колеи и на межосевое расстояние. В техсопровождении к паспорту автомобиля есть прописанные размеры. Проверка занимает меньше минуты, водитель всегда может приблизительно прикинуть возможные нарушения.

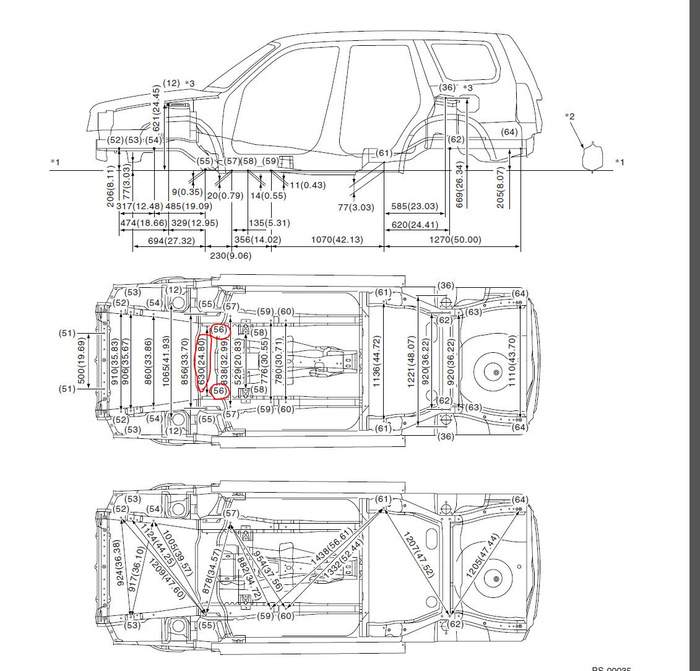
Наиболее важны для диагностики геометрии кузова расстояния (в миллиметрах) между контрольными точками. Это расстояние от места крепления агрегата (от лонжерона) до стакана. Для самостоятельного определения необходимо знать расстояния и места измерения, которые определяются изготовителем.

На СТО

Проверка геометрии на специализированной автостанции становится неизбежной, если после диагностики колес на развал и схождение слесарь говорит, что отрегулировать посадку уже невозможно и необходимо проверить кузов на точное соотношение расстояний.

Первичная диагностика на СТО проводится с помощью нивелира. Прибор показывает, как отклонились колеса от заданного размера. Эта процедура лишь определяет, есть ли нарушение геометрии в принципе или нет.

Дальнейшая диагностика проводится на стенде. Автомобиль закрепляется на стапеле, предварительно с машины снимаются вся навесная облицовка: бампера, обвесы. В редких случаях необходим демонтаж агрегатов ходовой.

Дальнейшее диагностирование проводится электронными датчиками. Слесарь устанавливает их на контрольные точки, а устройства посылают трехмерный сигнал своего местонахождения на монитор.

Если СТО не имеет современного оборудования, мастер может использовать линейку для измерения геометрии кузова. Но это кустарный метод, дающий отклонение в размерах ± 5 мм.

На стапеле по контрольным точкам проводят следующие замеры:

• проем багажника;
• моторный отсек;
• передние, задние лонжероны;
• проем переднего, заднего стекла;
• проем всех дверей авто;
• срезы передней, средней, задней части автомобиля.

Каркас выправляют с помощью гидравлического оборудования и вакуумных присосок. После серьезной аварии кузов выравнивают растяжкой только при условии, что металл сохранил свои свойства.

Если в СТО предложат компьютерную проверку геометрии с помощью диодной указки, то разбирать авто на составляющие не потребуется — достаточно поставить машину на стенд. Программа проведет замеры и наложит их на шаблон модели. Буквально 10 минут диагностики, и распечатка кузова со всеми проблемами готова. Допустимая норма отклонений ± 5 мм.

В домашних условиях

Проверка кузова автомобиля в гараже необходима, если водитель замечает сложности с управлением без видимых причин. Для этого понадобится:

• линейка геометрическая, рулетка;
• масштабная рейка;
• циркуль;
• штангенциркуль.

Необходимые расстояния между контрольными точками находят в техдокументации на авто. Можно воспользоваться подсказками в интернете. Необходимо брать официальные сайты производителя. Японские бренды размещают техдокументацию на свои модели в свободном доступе, европейские комплектации придется поискать. Что проверять самостоятельно:

1. Визуально проверить, насколько плотно и равномерно закрываются двери, багажник и капот. Посмотреть расстояние от крышки, проема двери до кузова.
2. Загнать авто на яму, снизу проверить межосевое расстояние, используя рулетку.
3. Расстояние между колесами на оси поперечное.
4. Найти по инструкции все контрольные точки (технические отверстия, болты).
5. Снять элементы обшивки, если они мешают провести замеры и перекрывают доступ.
6. Начинать замер от центральной части основания кузова или рамы.
7. Проверить диагонали между точками в моторном отсеке.
8. Провести замер по контрольным отверстиям и болтам между направляющими рамы, от них к крепежам силового блока.
9. Каждый замер проверять дополнительными измерениями.
10. Проверить диагональ крыши.

Расхождения на 0,5 см указывают на среднюю степень изменения геометрии, более 1 см — на значительные отклонения в расстоянии.

Возможные последствия

Правильные геометрические параметры автомобиля — это безопасность водителя и пассажиров. Относительно положения силовых элементов кузова задается угол расположения каждого из колес автомобиля. При нарушении геометрии измерительная система развала-схождения никогда не будет соответствовать норме. Если кузов «повело» относительно мало, мастер настроит положение колес, но ненадолго.

Изменения геометрии приводят к тому, что постепенно деформируется днище, в промежутках между точками сварки в длинномерных элементах кузова появляются складки, характеристики безопасности конструкции заметно снижаются.

При лобовом столкновении двигатель должен провалиться под днище. Если размеры кузова нарушены, мотор влетит в салон, риск смертельного исхода для водителя и пассажира увеличивается на 50 %.

Как восстановить геометрию

Восстановление геометрии в гараже сводится к рихтовке кузовных элементов и подтяжке всех болтов, если авто не стало участником аварии. Рулеткой проверяются замеры между технологическими отверстиями. Если геометрия нарушена незначительно из-за долгой эксплуатации, рекомендуется проверить все крепежи кузова и сварочные швы.

Основательно восстановить кузов после ДТП самостоятельно, без специального оборудования, практически невозможно. Даже если с точностью до миллиметра провести замеры, выровнять кузовные элементы часто нельзя, необходимо менять их на новые. При деформации рамы потребуется устанавливать авто на стенд и проводить вытяжку.

Окружность и круг

теория по математике 📈 планиметрия

Определения

Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.

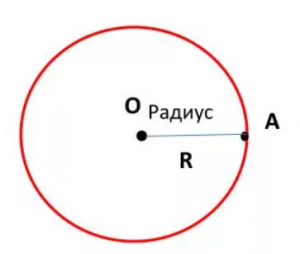
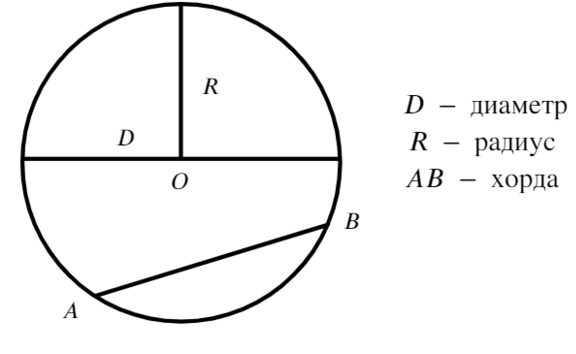
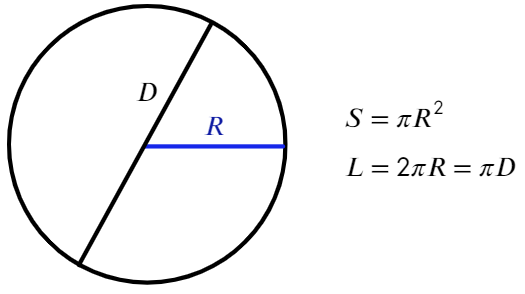
На рисунке центр окружности обозначен точкой О. Определения

Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.

Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.

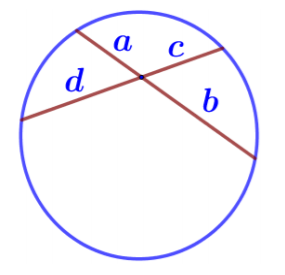
Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.

Свойство хорд

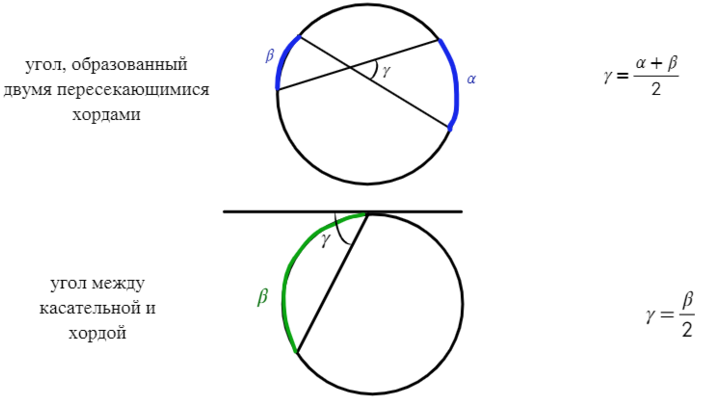
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.

Длина окружности

Длину окружности можно вычислить по формуле:

C=2πR, где π=3,14.

Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.

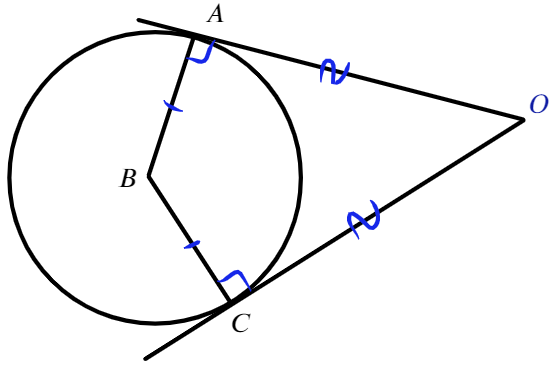
Дуга, касательная, круг, сектор, сегмент

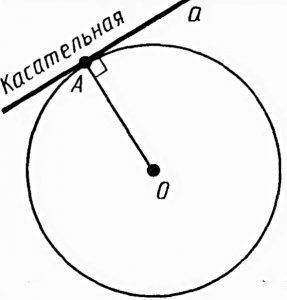
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).

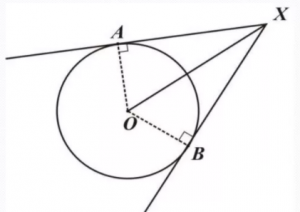
Свойства касательной

На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.

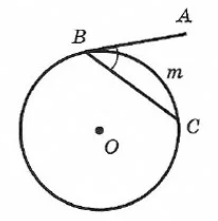
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.

Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.

Площадь круга вычисляется по формуле:

S=πR 2 , где π=3,14.

Сектор и его площадь

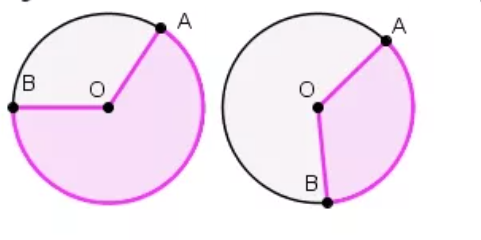
Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.

Площадь кругового сектора вычисляется по формуле:

S= π R 2 360 . . × α , где α – угол между радиусами.

Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.

Окружность. Форма и положение.

Окружность – это замкнутая плоская линия, всякая точки которой равноудалена от одной и той же точки (O), называемой центром.

Прямые (OA, OB, OС. . . ), соединяющие центр с точками окружности – это радиусы.

Бесконечная прямая (MN), прочерченная через какие-нибудь две точки окружности – секущая. а часть ее (EF), заключенная между этими точками, называется хордой.

Всякая хорда (AD), прочерченная через центр – диаметр.

Диаметр представляет наибольшую из хорд..Всякий диаметр делит окружность и круг пополам. Таким образом, всякий диаметр разделит окружность на две полуокружности, а круг на два полукруга.

Какая-нибудь часть окружности (напр. EmF ) называется дугой.

О хорде (EF), соединяющей концы дуги, говорят, что она стягивает эту дугу.

Для определения дуги иногда применяют знак È ; напр., пишут так: ÈEmF.

Часть плоскости, ограниченная окружностью, именуют кругом.

Часть круга (напр., СOB, заштрихованная на чертеже), ограниченная дугой и двумя радиусами, проведенными к концам дуги, обозначают как сектор.

Часть круга, (напр., EmF), ограниченная дугой и стягивающей ее хордой, обозначают как сегмент.

Из этого получаем:

1. Все радиусы одной окружности равны.

2. Два круга с одинаковыми радиусами будут равны.

3. Диаметр равен двум радиусам.

4. Точка, лежащая внутри круга, ближе к центру, а точка, лежащая вне круга, дальше от центра, чем точки окружности.

5. Диаметр, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.

6. Дуги, заключенные между параллельными хордами, равны.

При работе с окружностями применяют следующие теоремы:

1. Теорема. Прямая и окружность не могут иметь более двух общих точек.

Из этой теоремы получаем два логично вытекающих следствия:

Никакая часть окружности не может совместиться с прямой, потому что в противном случае окружность с прямой имела бы более двух общих точек.

Линия, никакая часть которой не может совместиться с прямой, называется кривой.

Из предыдущего следует, что окружность есть кривая линия.

2. Теорема. Через всякие три точки, не лежащие на одной прямой, можно провести окружность и только одну.

Как следствие данной теоремы получаем:

Три перпендикуляра к сторонам треугольника вписанного в окружность проведенные через их середины, пересекаются в одной точке, которая является центром окружности.

Решим задачу. Требуется найти центр предложенной окружности.

Отметим на предложенной три любые точки A, B и С , начертим через них две хорды, например, AB и СB, и из середины этих хорд укажем перпендикуляры MN и PQ. Искомый центр, будучи одинаково удален от A, B и С, должен лежать и на MN, и на PQ, следовательно, он находится на пересечении этих перпендикуляров, т.е. в точке O.

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Числовая и единичная окружность

В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.

Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.

Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:

Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.

Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.

Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:

В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.

Выглядит единичная окружность так:

Откладывание углов на единичной окружности

Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:

Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.

Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:

Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:

Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:

В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.

Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:

Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:

Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:

Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.

Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:

С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:

Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:

Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:

Например, верны следующие равенства:

15° + 3•360° = 15° + 1080° = 1095°

100° + 10•360° = 100° + 3600° = 3700°

1000° = 1000° – 2•360° = 1000° – 720° = 280°

Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5

[spoiler title=”источники:”]

http://www.calc.ru/Okruzhnost-Forma-I-Polozheniye.html

http://100urokov.ru/predmety/urok-1-edinichnaya-okruzhnost

[/spoiler]

Определение принадлежности точки кругу с центром в начале координат

Будем считать, что точка принадлежит кругу, если находится внутри его или на его окружности.

Из любой точки координатной плоскости можно провести отрезок к началу координат. Если длина этого отрезка больше радиуса круга, то точка лежит за пределами круга и, следовательно, не принадлежит ему. Если же отрезок, соединяющий точку и начало координат, меньше радиуса круга с центром в начале координат или равен ему, то точка будет принадлежать кругу.

Отрезок между любой точкой и нулевой точкой (началом координат) является гипотенузой прямоугольного треугольника, катеты которого равны значениям x и y координаты данной точки.

Таким образом задача сводится по-сути к двум действия:

1. Нахождение длины отрезка между точкой и началом координат по теореме Пифагора (квадрат длины гипотенузы равен сумме квадратов длин катетов).
2. Сравнению полученного значения с радиусом круга.

Pascal

Определение принадлежности точки кругу с центром в начале координат паскаль

Язык Си

Для gcc компилировать с ключом -lm.

Python

Определение принадлежности точки кругу с центром в начале координат Python

Уравнение окружности.

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.

Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

Теория и практика окружности

Свойство касательных.

Свойства касательных и секущих.

Площадь, сектор, длина окружности.

Задачи на окружности.

По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!

Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.

В окружности может быть проведено 3 типа отрезка:

Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).

Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).

Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).

А также две прямые снаружи от окружности:

Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.

Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.

Теперь чуть-чуть об углах и дугах:

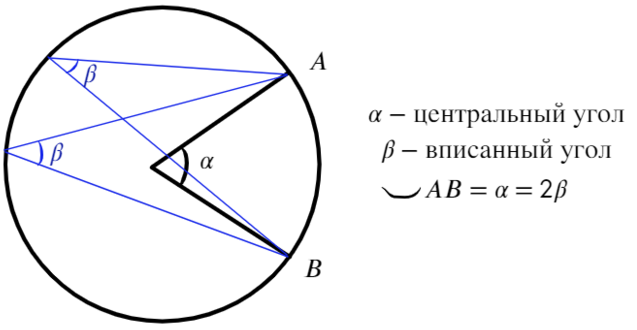
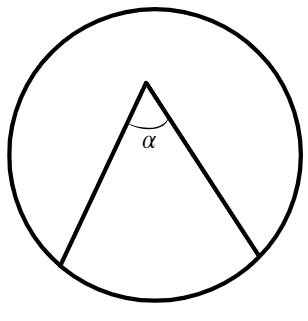
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.

Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.

Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.

Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.

А вот такой угол НЕвписанный, такой угол «никто и звать никак».

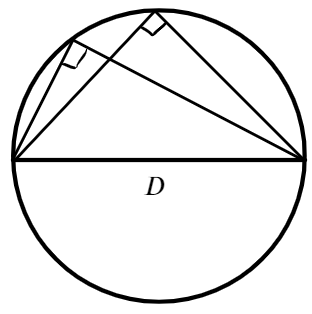
Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:

Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.

Запишем основные свойства углов в окружности:

Нашел что-то общее?

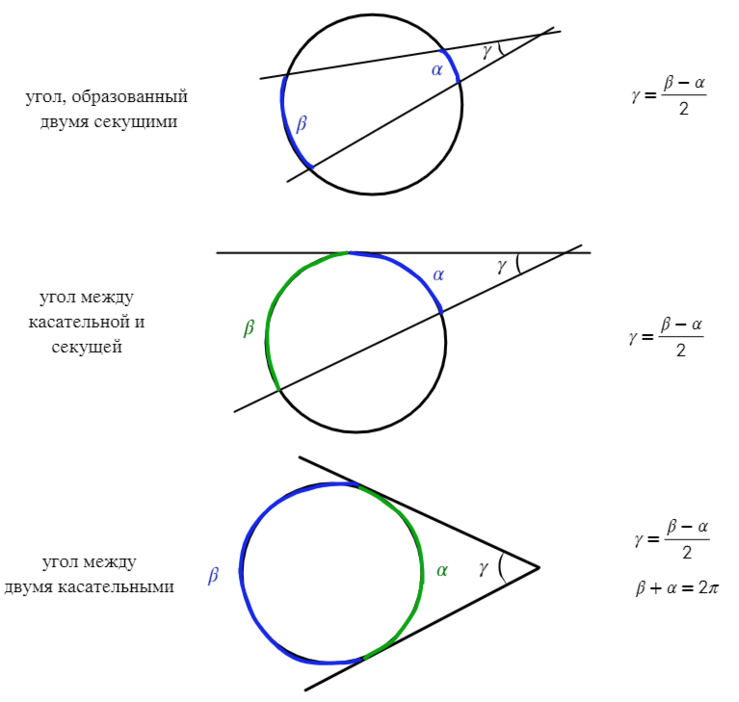
Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.

Если угол находится внутри окружности, то находим его через полусумму дуг.

Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.

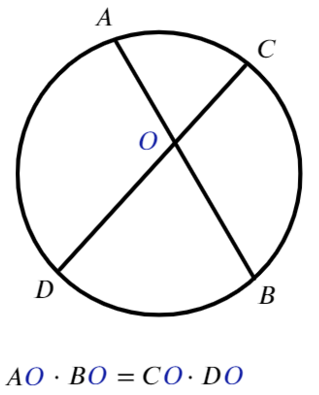
Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:

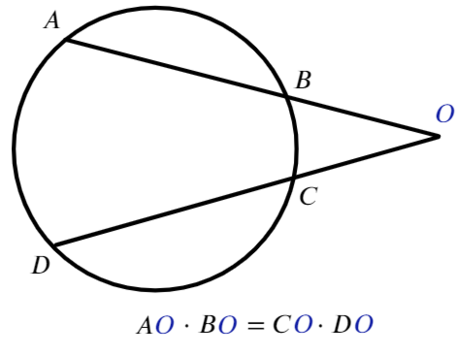
Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:

Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).

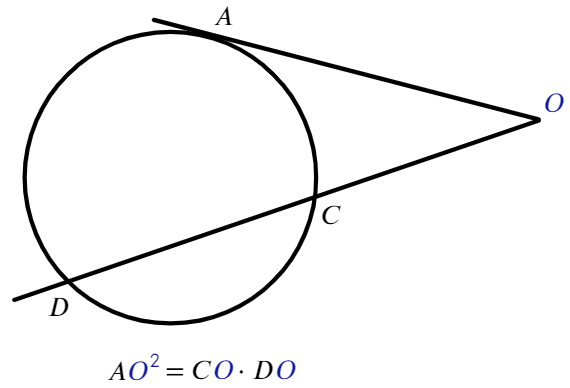
Если из точки, лежащей вне окружности, проведены касательная и секущая:

Аналогично в каждом отрезке присутствует точка, вне окружности (О).

Если теперь провести две касательные из точки O, то получим такие равные отрезки:

Касательные равны, как, сообственно, и радиусы!

Площадь и длина окружности находятся по формуле:

По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD

Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!

Страница 1 из 2

Вопрос 1. Объясните, как определяются координаты точки.
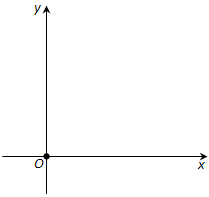
Ответ. Проведём на плоскости через точку O две взаимно перпендикулярные прямые x и y – оси координат (рис. 170). Ось x (она обычно горизонтальная) называется осью абсцисс, а ось y – осью ординат. Точкой пересечения O – началом координат – каждая из осей разбивается на две полуоси. Условимся одну из них называть положительной, отмечая её стрелкой, а другую – отрицательной.

Рис. 170

Каждой точке A плоскости мы сопоставим пару чисел – координаты точки – абсциссу (x) и ординату (y) по такому правилу.
Через точку A проведём прямую, параллельную оси ординат (рис. 171). Она пересечёт ось абсцисс x в некоторой точке A_x. Абсциссой точки A мы будем называть число x, абсолютная величина которого равна расстоянию от точки O до точки A_x. Это число будет положительным, если Ax принадлежит положительной полуоси и отрицательным, если A_xпринадлежит отрицательной полуоси. Если точка A лежит на оси ординат y, то полагаем x равным нулю.

Рис. 171

Ордината (y) точки A определяется аналогично. Через точку A проведём прямую, параллельную оси абсцисс x (см. рис. 171). Она пересечёт ось ординат y в некоторой точке A_y. Ординатой точки A мы будем называть число y, абсолютная величина которого равна расстоянию от точки O до точки A_y. Это число будет положительным, если A_y принадлежит положительной полуоси и отрицательным, если A_y принадлежит отрицательной полуоси. Если точка A лежит на оси абсцисс x, то полагаем y равным нулю.
Координаты точки будем записывать в скобках рядом с буквенным обозначением точки, например: A (x; y) (на первом месте абсцисса, на втором – ордината).

Вопрос 2. Какие знаки у координат точки, если она принадлежит первой (второй, третьей, четвёртой) четверти?
Ответ. Оси координат разбивают плоскость на четыре части – четверти: I, II, III, IV (рис. 172). В пределах одной четверти знаки обеих координат сохраняются и имеют значения.

Рис. 172

Если точка принадлежит первой четверти, то её абсцисса и ордината будут положительными.
Если точка принадлежит второй четверти, то её абсцисса будет отрицательной, а ордината будет положительной.
Если точка принадлежит третьей четверти, то её абсцисса и ордината будут отрицательными.
Если точка принадлежит четвёртой четверти, то её абсцисса будет положительной, а ордината будет отрицательной.

Вопрос 3. Чему равны абсциссы точек, лежащих на оси ординат?
Чему равны ординаты точек, лежащих на оси абсцисс?
Чему равны координаты начала координат?
Ответ. Точки оси x (оси абсцисс) имеют равные нулю ординаты (y = 0), а точки оси y (оси ординат) имеют равные нулю абсциссы (x = 0).
Если какая-либо точка лежит на оси ординат y, то абсцисса данной точки равна нулю.
Если какая-либо точка лежит на оси абсцисс x, то ордината данной точки равна нулю.
У начала координат абсцисса и ордината равны нулю.

Вопрос 4. Выведите формулы для координат середины отрезка.
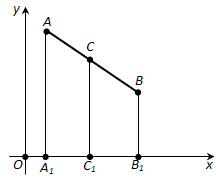
Ответ. Пусть A (x₁; y₁) и B (x₂;y₂) – две произвольные точки и C (x; y) – середина отрезка AB. Найдём координаты x, y точки C.
Рассмотрим сначала случай, когда отрезок AB не параллелен оси y, т.е. (x_1 neq x_2). Проведём через точки A, B, C прямые, параллельные оси y (рис. 173). Они пересекут ось x в точках A1 ((x_1); 0), B1 ((x_2); 0), C ((x); 0). По теореме Фалеса точка (C_1) будет серединой отрезка (A_1B_1).

Рис. 173

Так как точка (C_1) – середина отрезка (A_1B_1), то (A_1C_1 = B_1C_1), а значит, (|x – x_1| = |x – x_2|). Отсюда следует, что либо (x – x_1 = -(x – x_2)). Первое равенство невозможно, так как (x_1 neq x_2). Поэтому верно второе. А из него получается формула

(x = frac{x_1 + x_2}{2}).

Если (x_1 = x_2), т.е. отрезок AB параллелен оси y, то все три точки (A_1, B_1, C_1) имеют одну и ту же абсциссу. Значит, формула остаётся верной и в этом случае.
Ордината точки C находится аналогично. Через точки A, B, C проводятся прямые, параллельные оси x. Получается формула

(x = frac{y_1 + y_2}{2}).

Вопрос 5. Выведите формулу для расстояния между точками.
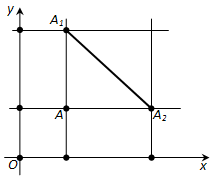
Ответ. Пусть на плоскости xy даны две точки: (A_1) с координатами (x_1, y_1) и (A_2) с координатами (x_2, y_2). Выразим расстояние между точками (A_2) и (A_2) через координаты этих точек.
Рассмотрим сначала случай, когда (x_1 neq x_2) и (y_1 neq y_2). Проведём через точки (A_1) и (A_2) прямые, параллельные осям координат, и обозначим через A точку их пересечения (рис. 174). Расстояние между точками (A) и (A_1) равно (|y_1 – y_2|), а расстояние между точками (A) и (A_2) равно (|x_1 – x_2|). Применяя к прямоугольному треугольнику (AA_1A_2) теорему Пифагора, получим:

(d^2 = (x_1 – x_2)^2+ (y_1 – y_2)^2), (*)

где d –расстояние между точками (A_1) и (A).

Рис. 174

Хотя формула (*) для расстояния между точками выведена нами в предположении (x_1 neq x_2), (y_1 neq y_2), она остаётся верной и в других случаях. Действительно, если (x_1 = x_2), (y_1 neq y_2), то d равно (|y_2 – y_2|). Тот же результат даёт и формула (*). Аналогично рассматривается случай, когда (x_1 neq x_2, y_1 = y_2). При (x_1 = x_2, y_1 = y_2) точки (A_1) и (A_2) совпадают и формула (*) даёт d = 0.

Вопрос 6. Что такое уравнение фигуры в декартовых координатах?
Ответ. Уравнением фигуры в декартовых координатах на плоскости называется уравнение с двумя неизвестными x и y, которому удовлетворяют координаты любой точки фигуры. И обратно: любые два числа, удовлетворяющие этому уравнению, являются координатами некоторой точки фигуры.

Вопрос 7. Выведите уравнение окружности.
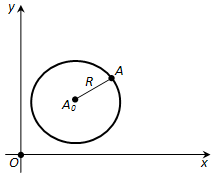
Ответ. Составим уравнение окружности с центром в точке A_O (a; b) и радиусом R (рис. 175). Возьмём произвольную точку A (x; y) на окружности. Расстояние от неё до центра A_O равен ((x – a)^2 + (y – b)^2). Таким образом, координаты x, y каждой точки A окружности удовлетворяют уравнению

((x – a)^2 + (y – b)^2 = R^2). (*)

Рис. 175

Обратно: любая точка A, координаты которой удовлетворяют уравнению (*), принадлежит окружности, так как расстояние от неё до точки A_O равно R. Отсюда следует, что уравнение (*) действительно является уравнением окружности с центром A_Oи радиусом R. Заметим, что если центром окружности является начало координат, то уравнение окружности имеет вид:

(x^2 + y^2 = R^2).

Вопрос 8. Докажите, что прямая в декартовых координатах имеет уравнение вида ax + by + c = 0.
Ответ. Докажем, что любая прямая в декартовых координатах x, y имеет уравнение вида

ax + by + c = 0, (*)

где a, b, c – некоторые числа.
Пусть h – произвольная прямая на плоскости xy. Проведём какую-нибудь прямую, перпендикулярную прямой h, и отложим на ней от точки пересечения C с прямой h равные отрезки CA₁ и CA₂(рис. 176).

Рис. 176

Пусть a₁, b₁ – координаты точки A₁ и a₂, b₂ – координаты точки A₂. Как мы знаем, любая точка A (x; y) прямой h равноудалена от точек A₁ и A₂. Поэтому координаты её удовлетворяют уравнению

((x – a_1)^2 + (y – b_1)^2 = (x – a_2)^2 + (y – b_2)^2). (**)

Обратно: если координаты x и y какой-нибудь точки удовлетворяют уравнению (**), то эта точка равноудалена от точек A₁ и A₂, а значит, принадлежит прямой h. Таким образом, уравнение (**) является уравнением прямой h. Если в этом уравнении раскрыть скобки и перенести все члены уравнения в левую его часть, то оно примет вид:

(2(a_2 – a_1)x + 2(b_2 – b_1)y + (a_1^2 + b^2_1 – a^2_2 – b^2_2) = 0.)

Обозначая (2(a_2 – a_1) = a), (2(b_2 – b_1) = b), (a^2_1 + b^2_1 – a^2_2 – b^2_2 = c), получаем уравнение (*). Утверждение доказано.

Вопрос 9. Как найти координаты точки пересечения двух прямых, если заданы уравнения этих прямых?
Ответ. Пусть заданы уравнения двух прямых:

ax + by + c = 0,

a₁x + b₁y + c₁ = 0.

Найдём координаты их точки пересечения.
Так как точка пересечения (x; y) принадлежит каждой из прямых, то её координаты удовлетворяют и первому и второму уравнению. Поэтому координаты точки пересечения являются решением системы уравнений, задающих прямые. Рассмотрим пример.
Пусть уравнениями данных прямых будут:

3x – y + 2 = 0,

5x – 2y + 1 = 0.

Решая эту систему уравнений, находим x = -3, y = -7. Точка пересечения прямых (-3; -7).

Вопрос 10. Как расположена прямая, если в её уравнении коэффициент a = 0 (b = 0; c = 0)?
Ответ. Выясним, как расположена прямая относительно осей координат, если её уравнение ax + by + c = 0 имеет тот или иной частный вид.
1. a = 0, b (neq) 0. В этом случае уравнение прямой можно переписать так:

(y = -frac{c}{b}).

Таким образом, все точки прямой имеют одну и ту же ординату ((-frac{c}{b})); следовательно, прямая параллельна оси x (рис. 177, а). В частности, если c = 0, то прямая совпадает с осью x.
2. b = 0, a (neq) 0. Этот случай рассматривается аналогично. Прямая параллельна оси y (рис. 177, б) и совпадает с ней, если c = 0.

Рис. 177

3. c = 0. Прямая проходит через начало координат, так как его координаты (0; 0) удовлетворяют уравнению прямой (рис. 177, в).