Как найти контрольные точки в графике парабола

Произвольно выбираем несколько значений

и находим значения функции –

Контрольные точки (x,
помогают
более точно построить график функции.

9 Построение графика функции

Построим графики функций

,

используя результаты исследования в
п.1-7

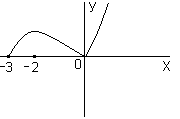
Рис.6

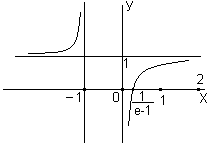
Рис.7

Замечание После того как рассмотрите построение графиков сопоставьте с результатами исследования.

10 Образцы выполнения исследования функции и построения графиков

Исследовать
поведение функции и построить график.

10.1

1 Область определения

Данная функция, существует при любом
действительном значении х, тогда

.

2 Исследование функции на четность и
нечетность

Так как область определения функции
множество четное относительно начала
координат, то найдем

:

.

Видим, что

и
,
значит функция ни четная ни нечетная,
т.е. функция общего вида.

3 Точки пересечения графика функции с
осями координат

С осью

:
полагаем

и, подставляя это значение в данную
функцию

,
находим

.
Получим точку

.

С осью

:
полагаем

,
находим

из уравнения

(*)

Корни уравнения являются делителями
свободного члена 16. Следовательно,
попробуем подставить в уравнение (*)
числа:

При

:
получаем

,
следовательно

является корнем уравнения (*). Тогда
многочлен

делится на

без остатка. Выполним деление:

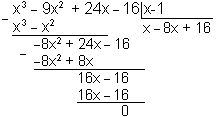
Итак,

.
Уравнение (*) принимает вид:

,
откуда

(эти значения называют нулями функции).
Таким образом, график функции пересекает
ось

в точках:

.

4 Промежутки знакопостоянства функции.
Исследование функции на концах
промежутков знакопостоянства

Промежутки знакопостоянства функции
разделяют точки разрыва и нули функции.
Для данной функции – это

.
Обратите внимание, что

кратный корень, значит в интервалах
прилегающих к этой точке функция знак
не меняет. Изобразим их на числовой
оси:

Знак функции определяется непосредственной
подстановкой любого значения

из полученных интервалов в аналитическое
выражение функции.

Если на интервале

функция
отрицательная, то ее график располагается
под осью

,
на интервалах

функция положительная, то над осью

.

Для выяснения поведения функции на
концах промежутков знакопостоянства

Найдем пределы функции при

:

;

,
таким образом, знак бесконечности
определяется знаком старшего члена

.
Это означает, что слева график функции
уходит неограниченно вниз, а справа –
неограниченно вверх.

5 Асимптоты графика функции

Т.к. функция не имеет бесконечных
разрывов, то вертикальные асимптоты
отсутствуют.

Для отыскания наклонных асимптот

,
найдем

:

,
т.к

,
то график функции наклонных асимптот
не имеет.

6 Исследование функции на монотонность.
Точки экстремума

Найдем критические точки функции.
Согласно необходимого условия экстремума:
в точках экстремума производная равна
нулю или не существует.

Найдем производную:

.

Решим уравнение

:

;

;

Производная функции обращается в нуль
в точках

и

– критические точки. Они делят область
определения на интервалы монотонности
(интервалы убывания и возрастания).

Интервалы

изобразим их на числовой оси (рис.8):

Рис.8

Поведение функции на каждом интервале
определяется знаком производной.

Для определения знака производной на
каждом интервале достаточно взять
любое значение

из этого интервала и подставить в
производную

.

На интервале

,
возьмем любое

,
например

,
и подставим в производную

.
Получили

,
следовательно функция

на интервале

возрастает.

Аналогично устанавливаем:

– на интервале

,
следовательно функция убывает;

– на интервале

,
следовательно функция возрастает.

Знаки производной

проставлены на рисунке 8 в каждом
интервале. Стрелками схематично указано
поведение функции

.

Замечаем, что при переходе через точку

производная меняет знак, с «+» на «-».
Это означает, что в точке

функция имеет максимум (на основании
достаточного условия существования
экстремума). Найдем значение

при

:

.

Значит, точка максимума

.

При переходе через точку

производная меняет знак с «-» на «+».
Это означает, что при

функция имеет минимум:

.
Точка минимума

.

7 Исследование графика функции на
выпуклость и вогнутость. Точки перегиба

Это исследование проводится с помощью
второй производной. Найдем точки,
подозрительные на перегиб, используя
необходимое условие перегиба: в точках
перегиба вторая производная либо равна
нулю, либо не существует.

Так как

,
то

и существует при любых

.
Приравняем вторую производную к нулю
и найдем корни уравнения:

.

Отсюда

– точка, подозрительная на перегиб.
Точка

делит область определения на интервалы

и

Рис.9

Определим знак второй производной на
каждом из полученных интервалов,
непосредственным способом.

На интервале

получаем

,
значит, при

график функции вогнутый (),
рисунок 8.

На интервале

получаем

,
значит, при

график функции выпуклый (),
рисунок 8.

Так как при переходе через точку

вторая производная

меняет знак, то график меняет выпуклость
на вогнутость, то есть

абсцисса точки перегиба.

.

Точка перегиба

.

8 Контрольные точки

Для более точного построения графика
найдем насколько дополнительных точек:

,
точка

9 Построение графика по полученным
результатам исследования

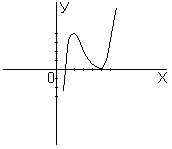
Замечание При исследовании
будем использовать только краткую
запись, так как все действия аналогичны
исследованной функции

.

10.2

1 Область определения

2 Исследование функции на четность и
нечетность

Так как область определения множество
симметричное относительно начала
отсчета, то найдем

:

.

Делаем вывод: функция нечетная. Для
дальнейшего исследования будем
использовать свойства нечетной функции
на симметричных интервалах:

– меняет знакопостоянство;

– сохраняет монотонность;

– точки максимума и минимума симметричны
относительно начала координат;

– меняет выпуклость на вогнутость;

– график функции симметричен относительно
начала координат.

3 Точки пересечения графика функции с
осями координат

С осью

:

.

Решим уравнение:

.

Получили точки:

С осью

:

.

. Получили
точку

.

4 Промежутки знакопостоянства функции.
Исследование функции на концах
промежутков знакопостоянства

Для выяснения поведения функции на
концах промежутков знакопостоянства
вычислим следующие пределы:

5 Асимптоты графика функции

5.1 Так как в точках

функция
претерпевает бесконечный разрыв, то
график функции имеет вертикальные
асимптоты :

5.2

.

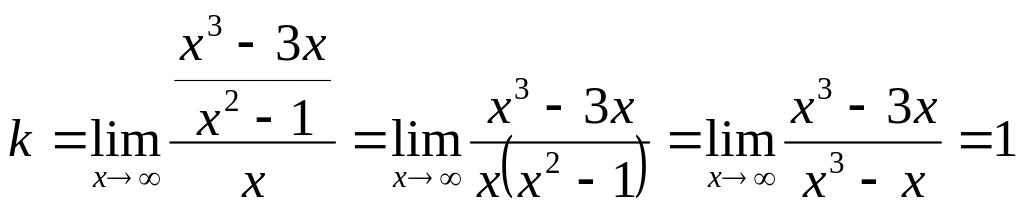
Получили

– наклонная асимптота.

6 Исследование функции на монотонность.
Экстремумы функции

Решим уравнение

:

Критические точки (по первой производной):
точек, в которых производная равна нулю
нет,

Отметим на числовой прямой критические
точки и исследуем знак производной на
каждом из полученных интервалов

Делаем вывод, что функция возрастает
на всей области определения.

Так как функция в области определения
монотонности не меняет, то точек
экстремума нет.

7 Исследование графика функции на
выпуклость и вогнутость. Точки перегиба

Найдем вторую производную функции:

.

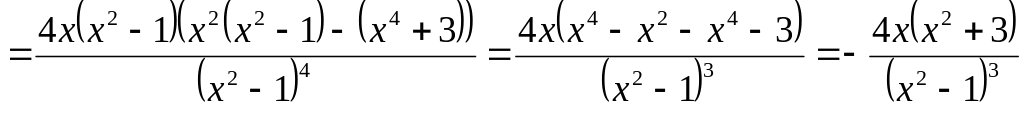
Решим уравнение

:

Критические точки (по второй производной):

Отметим на числовой прямой полученные
точки и исследуем знак второй производной

При

график функции имеет перегиб.

Точка

– точка перегиба.

9 Контрольные точки

9 Построение графика по полученным
результатам исследования

При построении графика помним, что он
симметричен относительно точки

.

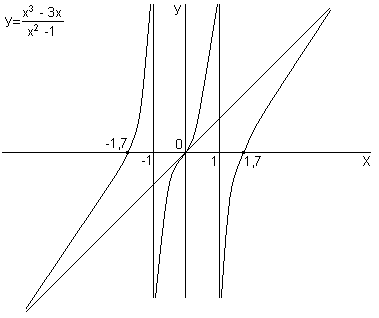
11.3

Замечаем, что функция задана в неявном
виде. Выразим y в явном
виде

.

Достаточно
исследовать и построить график функции

,
а за тем отобразить симметрично оси
OX.

1 Область определения функции

Решим методом интервалов:

.

Делаем вывод:

.
На интервалах

и

функция в дальнейшем не исследуется,
т.к. они не входят в область определения.

2 Исследование функции на четность и
нечетность

Так
как область определения множество
несимметричное относительно начала
координат, то делаем вывод, что функция
ни четная ни нечетная.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Функция вида  , где  называется квадратичной функцией. 

График квадратичной функции – парабола. 

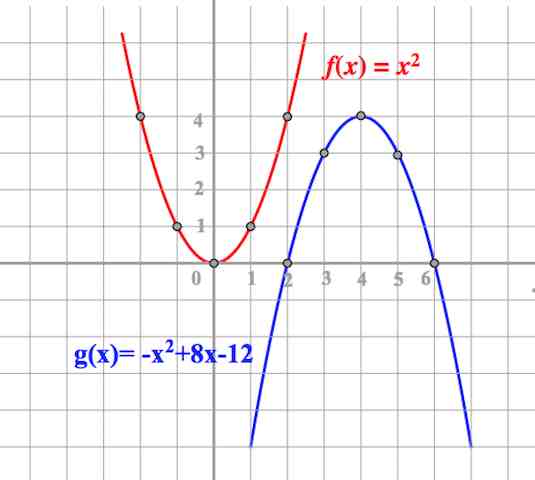
Рассмотрим случаи:

I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА 

, то есть , ,

Для построения заполняем таблицу, подставляя значения x в формулу:

Отмечаем  точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:

Нетрудно заметить, что если мы возьмем случай , , , то есть , то мы получим параболу, симметричную относительно оси (ох). Убедиться  в этом несложно, заполнив аналогичную таблицу:

II СЛУЧАЙ,  «a» ОТЛИЧНО ОТ ЕДИНИЦЫ

Что же будет, если мы будем брать , , ? Как изменится поведение параболы? При парабола   изменит форму, она “похудеет” по сравнению с параболой (не верите – заполните соответствующую таблицу – и убедитесь сами):

На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях  ордината    каждой точки умножилась на 4.  Это произойдет со всеми ключевыми точками исходной  таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.

А при парабола  «станет шире»  параболы :

Давайте подитожим:

III СЛУЧАЙ, ПОЯВЛЯЕТСЯ  «С»

 Теперь давайте введем в игру (то есть рассматриваем случай, когда ), будем рассматривать параболы вида . Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы вдоль оси вверх или вниз в зависимости от знака :

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»

Когда же парабола “оторвется” от оси и будет, наконец, “гулять” по всей координатной плоскости? Когда перестанет быть равным .

Здесь для построения параболы нам понадобится формула для вычисления вершины: ,   .

Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу , что уже нам по силам. Если  имеем дело со случаем , то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с , например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.

Например, вершина параболы :

,  . Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы ,  ведь в нашем случае.

При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:

1) парабола обязательно пройдет через точку .  Действительно, подставив в формулу x=0, получим, что . То есть ордината точки пересечения параболы  с осью (оу), это .   В нашем примере (выше), парабола пересекает ось ординат в точке , так как .

2) осью симметрии параболы является прямая , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.

3) Приравнивая к , мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение . В зависимости от дискриминанта, будем получать одну (,  ), две (, ) или нИсколько () точек пересечения с осью (ох). В предыдущем примере у нас  корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения  с осью (ох) у нас будут (так как ), хотя, в общем, это видно и без дискриминанта.

Итак, давайте выработаем

Алгоритм для построения параболы, если она задана  в виде

1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)

2) находим координаты вершины параболы по формуле ,   .

3) находим точку пересечения параболы с осью (оу) по свободному члену , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение велико… пропускаем этот пункт…)

4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу . Если , то парабола становится у’же по сравнению с , если , то парабола расширяется по сравнению с 

5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение

Пример 1

Пример  2

Замечание 1. Если же парабола изначально нам задана в виде , где – некоторые числа (например, ), то построить ее будет еще легче, потому что нам уже заданы координаты вершины . Почему?

Возьмем квадратный трехчлен и выделим в нем полный квадрат:  Посмотрите, вот мы и получили, что , . Мы с вами ранее называли   вершину параболы , то есть теперь , .

Например,  . Отмечаем на плоскости вершину параболы , понимаем, что ветви направлены вниз, парабола расширена (относительно ). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).

Замечание 2. Если парабола задана в виде, подобном этому (то есть представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае  – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.

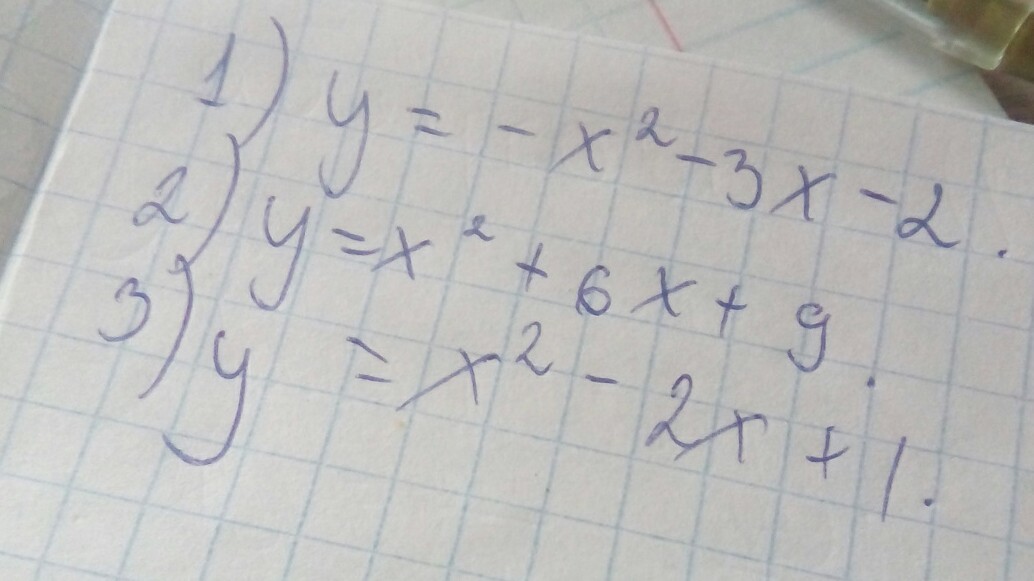
На этой странице находится вопрос Как в параболе находить контрольные точки?, относящийся к категории
Алгебра. По уровню сложности данный вопрос соответствует знаниям
учащихся 5 – 9 классов. Здесь вы найдете правильный ответ, сможете
обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С
помощью автоматического поиска на этой же странице можно найти похожие
вопросы и ответы на них в категории Алгебра. Если ответы вызывают
сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.