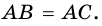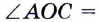Как посчитать длину окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать длину окружности
Чтобы посчитать длину окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор

Как посчитать длину окружности зная диаметр
Какая длина у окружности если
её диаметр ?
Ответ:
0
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d, где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
её радиус ?
Ответ:
0
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r, где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
её площадь ?
Ответ:
0
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅√S/π, где π ≈ 3.14
Пример
Если площадь круга равна 6 см2, то его длина примерно равна 8.68 см.
См. также
Рисование кривой или окружности
В этой статье рассмотрены кривые рисунки, круги и овалы. Сведения о рисовании линий см. в этой ссылке. Сведения о фигурах с бесплатной формой и их редактировании см. в этой статьи.
Рисование кривой
На вкладке Вставка нажмите кнопку Фигуры.
В разделе Линии щелкните элемент Кривая.
Щелкните место, где необходимо начать кривую, перетащите указатель для рисования кривой, а затем щелкните в место, где необходимо добавить кривую.
Чтобы завершить рисование фигуры, выполните одно из следующих действий:
Чтобы оставить фигуру незамкнутой, дважды щелкните в любой момент рисования.
Чтобы замкнуть фигуру, щелкните вблизи ее начальной точки.
Нарисуйте овал или круг
На вкладке Вставка нажмите кнопку Фигуры.
В разделе Основные фигуры щелкните Овал.
Щелкните в том месте, где должен начинаться овал, и перетащите его, чтобы нарисовать фигуру.
Чтобы нарисовать круг, при перетаскиваниях нажмите shift.
Вы можете изменить внешний вид круга или кривой, добавив заливу или эффект фигуры илиизменив границу.
Если вы хотите получить более сложную схему, например перекрывающиеся круги, организационную диаграмму или блок-схему, можно создать графический элемент SmartArt, а не рисовать каждую фигуру вручную.
Круги и овалы заполняются автоматически. Если вы не хотите, чтобы фигура скрывает что-то под ней, например текст или ячейки, выйдите фигуру, а затем на вкладке Формат нажмите кнопку Заливка фигуры ивыберите нет заливки.
Рисование кривой
На вкладке Вставка в группе Иллюстрации нажмите кнопку Фигуры.
В области Линиищелкните Кривая .
Щелкните место, где необходимо начать кривую, перетащите указатель для рисования кривой, а затем щелкните в место, где необходимо добавить кривую.
Чтобы завершить рисование фигуры, выполните одно из следующих действий:
Чтобы оставить фигуру незамкнутой, дважды щелкните в любой момент рисования.
Чтобы замкнуть фигуру, щелкните вблизи ее начальной точки.
Примечание: К замкнутой фигуре по умолчанию применяется заливка. Чтобы она не скрывала находящиеся под ней ячейки, выберите фигуру, а затем в разделе Средства рисования на вкладке Формат в группе Стили фигур щелкните Заливка фигуры и выберите значение Нет заливки.
Нарисуйте овал или круг
На вкладке Вставка в группе элементов Иллюстрации нажмите кнопку Фигуры.
В области Основные фигурыщелкните Овал .
Щелкните в том месте, откуда следует начать круг. Чтобы получить круг, удерживайте нажатой клавишу SHIFT при перетаскивании указателя.
Вы можете изменить внешний вид круга или кривой, добавив заливку или эффект либо настроив границы.
Если вы хотите получить более сложную схему, например перекрывающиеся круги, организационную диаграмму или блок-схему, можно создать графический элемент SmartArt, а не рисовать каждую фигуру вручную.
К кругу или овалу по умолчанию применяется заливка. Чтобы она не скрывала находящиеся под ней ячейки, выберите фигуру, а затем в разделе Средства рисования на вкладке Формат в группе Стили фигур щелкните Заливка фигуры и выберите значение Нет заливки.
Урок 3. Окружность в перспективе. Как нарисовать кружку и вазу
В этом уроке мы разберемся, как изображать объекты, в основе которых лежат окружности: чайник, вазу, бокал, кувшин, колонну, маяк. Сложность их изображения в пространстве заключается в том, что принцип равноудаленности точек окружности от центра срабатывает, только когда мы смотрим на плоскость прямо (то есть направление взгляда перпендикулярно ей). Например, мы видим круглый циферблат часов перед собой или чашку и блюдце, когда наклонились над ними. В других случаях (взгляд падает на плоскость под углом) мы видим искажение формы окружности, ее превращение в овал (эллипс).
Содержание:
Ненадолго вернемся к коробкам из прошлого урока. Только теперь рассмотрим кубическую форму. Обратите внимание, как квадраты плоскостей, уходящих вдаль, сплющиваются. Верхние и нижние грани превращаются в трапеции. И тем сильнее они сужаются по вертикальной оси, чем ближе находятся к уровню глаз (к линии горизонта).
То же самое происходит и с окружностями. Чем дальше от линии горизонта они находятся, тем больше они открываются (обратите внимание на верхние и нижние плоскости этих спилов). А на уровне глаз окружность сужается до линии. Мы видим лишь переднюю грань предмета.
Принципы рисования эллипсов:
Принцип 1. У эллипса есть две оси симметрии: большая и малая. Они перпендикулярны. Здесь будем работать с наиболее частым случаем – когда предмет расположен прямо, то есть вертикальная ось (малая) находится под углом в 90°, а горизонтальная (большая) – под углом в 180°.
Принцип 2. У эллипса 4 вершины (они лежат на пересечении с осями). Эти точки в наибольшей степени удалены от центра. Форма эллипса выглядит искаженной, если соседние с вершинами точки смещены на тот же уровень (на эллипсе справа показано красным цветом).
Принцип 3. Другая крайность – это заострение боков эллипсов. Они должны быть скругленными. В бока можно вписать окружности. И чем больше раскрыт эллипс, тем больше диаметр этой окружности относительно высоты эллипса (на примере ниже это сравнение показано бледно-голубым цветом).
Принцип 4. Центр эллипса смещен вдаль (вверх) относительно геометрического центра из-за перспективного искажения. То есть ближняя половина эллипса больше дальней. Однако обратите внимание, что это смещение очень незначительно. Разберем, почему. Начнем с квадратов, поскольку круг вписывается в эту форму. Ниже показаны кубы, справа их верхние квадратные грани в перспективе. Проведены оси красным. Сравните, насколько их ближние половины больше дальних. Разница очень небольшая. То же самое будет и для эллипсов, вписанных в них. Ошибочно преувеличивать в рисунках эту разницу между ближней и дальней половинками эллипсов.
Рисуем эллипсы
Шаг 1. Для начала проведем две перпендикулярных оси.
Шаг 2. Отметим границы произвольного эллипса симметрично по горизонтальной оси. А для вертикальной верхнюю половину (дальнюю) сделаем чуть-чуть меньше нижней.
Шаг 3. Нарисуем по этим отметкам прямоугольник, в который будем вписывать эллипс.
Шаг 4. Наметим легкие дуги в местах пересечения осей и прямоугольника.
Шаг 5. Соединим легкими линиями эти дуги, стараясь изобразить эллипс более симметрично.
Шаг 6. По обозначенному пути проведем более четкую линию. Смягчим ластиком лишнее.
Более правильно было бы при рисовании эллипса вписывать его в квадратную плоскость в перспективе, то есть в трапецию. Однако, во-первых, сложно точно построить такую трапецию, зная лишь вершины эллипса. А во-вторых, овал, вписанный в квадрат в перспективе, мало отличается от вписанного в прямоугольник по тем же самым вершинам.
Рисуем кружку
Шаг 1. Начинаем с общих пропорций предмета. Измеряем, сколько раз ширина кружки (ее верха) умещается в высоте. Можно пока не учитывать ручку, однако надо оставить для нее достаточно места на листе. Намечаем общие габариты. Находим середину предмета по ширине и проводим через нее вертикальную ось. Чтобы нарисовать ее ровно, удобно сделать 2-3 вспомогательные отметки по высоте предмета на том же расстоянии от ближнего края листа, что и первая отметка середины предмета.
Шаг 2. Найдем высоту верхнего эллипса. Для этого измерим, сколько раз она умещается в его ширине (которую мы нашли ранее). Отметим нижнюю границу эллипса от верхнего края кружки. Легкими линиями нарисуем прямоугольник по намеченным крайним точкам.
Шаг 3. Проведем горизонтальную ось и впишем эллипс в прямоугольник. Затем найдем ширину нижней части кружки, сравнив ее с шириной верха. Высоту нижнего эллипса мы найдем, измерив расстояние по вертикали от самой нижней отметки кружки до нижней отметки ее бока (до точки, через которую пройдет горизонтальная ось этого эллипса). Найденное расстояние – это половина искомой высоты. Удвоим его и отложим от самой нижней точки кружки. Здесь важно не запутаться: в данном случае ось надо провести через нижнюю точку бока кружки, а не через низ самой кружки. Иначе пропорции нарушатся. Зная высоту нижнего эллипса, проверим, соблюдается ли принцип их постепенного раскрытия по мере удаления от уровня глаз. Верхний эллипс расположен ближе к уровню наших глаз, чем нижний, поэтому должен быть уже. Найдем, сколько раз высота нижнего овала помещается в его ширине – около четырех раз. Для верхнего овала было соотношение примерно 5 к 1. Таким образом нижний овал шире, то есть раскрыт в большей степени. Принцип соблюдается.
Шаг 4. Рисуем стенки кружки, соединяя боковые вершины верхнего и нижнего эллипсов. Для большей объемности покажем толщину стенки. Нарисуем второй овал внутри верхнего. При этом учитываем, что из-за перспективного искажения толщина стенок выглядит не одинаковой. Передняя и дальняя стенки визуально сужаются сильнее боковых примерно в два раза. Отметим вершины внутреннего овала на некотором расстоянии от вершин первого овала. Делаем этот отступ чуть больше для боковых вершин. Ставим отметки симметрично относительно вертикальной и горизонтальной осей. Нарисуем новый эллипс через эти вершины.
Шаг 5. Найдем расположение ручки и ее общие пропорции, а затем схематично наметим основные отрезки, формирующие ее контур. Их наклоны определяем методом визирования (а где-то – на глаз).
Шаг 6. Уточним контур ручки, сделаем его более плавным. По необходимости подправим очертания кружки. Смягчим немного ластиком линии построения. Выделим более сильным нажимом на карандаш контуры, расположенные ближе к нам. Кружка готова!
Рисуем вазу
В этом упражнении поработаем с воображением. Придумаем свою вазу и потренируемся рисовать эллипсы.
В прошлом задании для построения кружки было достаточно нарисовать два эллипса. Две ключевые окружности (верхняя и нижняя) определяли ее форму. Диаметр кружки равномерно уменьшался от верха к низу. А, например, форма вазы из рисунка ниже зависит от четырех окружностей (причем верхняя находится на уровне глаз, поэтому превратилась в линию).
Перейдем к рисованию. И помним важный принцип: чем дальше эллипс от уровня глаз, тем более он раскрыт.
Шаг 1. Проведем вертикальную ось. От нее симметрично отложим горизонтальные оси будущих эллипсов. Длину вертикальной и горизонтальных осей, а также количество эллипсов и расстояние между ними выбирайте сами.
Шаг 2. Обозначим боковые вершины эллипсов симметрично относительно вертикальной оси. Теперь перейдем к обозначению верхних и нижних вершин. И здесь пользуемся принципом постепенного раскрытия эллипсов по мере удаления от линии горизонта. Например, здесь мы рисовали вазу, расположенную в целом ниже уровня глаз. Для первого эллипса взяли высоту, примерно в пять раз меньше ширины. Измеряли это карандашом. Для последующих эллипсов постепенно увеличивали степень раскрытия. Так высота среднего эллипса укладывается в ширине примерно четыре раза, а для самого нижнего – примерно три раза. Чем ближе друг к другу эллипсы, тем ближе они по степени раскрытия. Чем дальше – тем больше разница. Намечая вершины, нижнюю половинку (ближнюю) делаем чуть-чуть больше верхней (дальней).
Шаг 3. Через вершины легкими линиями рисуем прямоугольники. А затем вписываем в них эллипсы.
Шаг 4. Теперь самое интересное: надо соединить боковые вершины эллипсов линиями. Вам решать, какими они будут, прямыми или округлыми, вогнутыми или выпуклыми. Можно сделать пару вариантов. Постарайтесь наиболее симметрично повторить форму внешнего контура для двух половинок вазы. Чтобы проверить симметрию, пробуйте перевернуть работу вверх ногами. Взглянув на предмет по-новому, проще увидеть расхождения.
Шаг 5. Так же, как мы делали для кружки, здесь можно показать толщину стенки. Нарисуем внутри верхнего эллипса еще один поменьше, предварительно наметив его вершины. Смягчим ластиком оси и дальние половинки эллипсов. Можно чуть высветлить те эллипсы, в которых изменение формы вазы более плавное. Рисунок готов!
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
ИЗОБРАЖЕНИЕ ОКРУЖНОСТИ В ПЕРСПЕКТИВЕ.
Перспектива окружности в горизонтальной плоскости.
Множество предметов, находящихся вокруг нас, имеют формы,
очертанием которых является окружность.
Чаще всего эта окружность находится в горизонтальной плоскости: это могут быть края чашки, стоящей на столе или табуретка с круглым сидением.
Если такая окружность находится на уровне наших глаз, на линии горизонта, мы видим ее как прямую линию.
Если мы смотрим на окружность сверху, то мы видим ее без искажений, как окружность.
Во всех остальных случаях, когда окружность располагается в горизонтальной плоскости, мы видим ее как эллипс.*
То есть, как лекальную кривую, симметричную относительно двух взаимно перпендикулярных осей.
При чем, одна из этих осей ВСЕГДА строго вертикальна, а другая, соответственно, горизонтальна.
*Строго говоря, изображение окружности в перспективе не является эллипсом, так как дальняя от нас его часть чуть меньше, чем ближняя. И, соответственно, он не симметричен относительно горизонтальной оси.
Соотношение между длинами осей эллипса называют раскрытием.
Грубо говоря, чем больше эллипс похож на круг, тем более он раскрытый.
В изображении эллипсов в горизонтальной плоскости есть два основных правила:
- Чем дальше находится эллипс от линии горизонта, тем более раскрытым мы его картинка
- Дальняя часть эллипса ЧУТЬ меньше, чем ближняя.
Легко понять, почему это так , построив в перспективе окружность вписанную в квадрат.
Упражнение 1.
Постройте окружность тем же способом, с той же точкой схода, но выше линии горизонта. Выделите более толстой линией ее передний край.
ОБРАТИТЕ ВНИМАНИЕ что в рисунке окружности, лежащие в горизонтальной плоскости мы НЕ строим с помощью описанного квадрата. Так как этот даёт искажения, если точка схода для квадрата не лежит на вертикальной оси эллипса.
Мы проводим две оси эллипса и задаем степень раскрытости на глаз, но учитываем положение эллипса относительно линии горизонта и других эллипсов.
Упражнение 2.
На рисунках изображена последовательность построения цилиндра и конуса.
Нарисуйте цилиндры и конусы выше и ниже линии горизонта . Раскрытие эллипсов задаём на глаз. Окружность в квадрат не вписываем.
Перспектива окружности в вертикальной или наклонной плоскости.
С окружностями в вертикальной плоскости нам приходится иметь дело достаточно часто. Например, рисуя арки в архитектуре.
Самый простой случай — когда окружность находится в плоскости параллельной картинной. Тогда мы видим ее без искажений.
View of the Tiber with the Castel Sant’Angelo
Bernardo Bellotto1743/1744
Если окружность находится под углом к картине, для построений мы также используем описанный квадрат. Этот способ применяется как в черчение, так и в рисунке, так как на глаз нарисовать окружность в таком ракурсе очень сложно .
В этом курсе мы только знакомимся со способом построения окружности в вертикальной плоскости. Но если у вас есть желание, подробно об этом можно прочитать в учебнике Осмоловской (ст. 26) или, в упрощенном виде у Шарова и Барщ.
Перспективные зарисовки с натуры.
Мы закончили блок теории построений. Теперь начинаем работать с натуры.
На этом этапе важно осознать, что рисунок — не черчение. В рисунке мы не пользуемся линейкой, редко строим точки схода на дополнительном листе. Наша задача, зная, какие построения применялись бы для перспективного чертежа, сделать минимум из них на глаз так, чтобы в результате получилось убедительное изображение, соответствующее основным правилам перспективы.
Рисование с фотографии.
Я вас очень прошу, по крайней мере на начальном этапе не срисовывать с фотографии, даже называя это рисованием с референсов.
Рисуя с фото вы НЕ развиваете пространственное воображение и умение на плоскости изображать объем. Вы только учитесь копировать с одного листа на другой пятна тона. Это, конечно, тоже полезный навык но для хорошего рисунка его не достаточно.
Постановка натуры.
Правильная постановка натуры помогает избежать многих ошибок в рисунке и делает работу легче и приятнее.
Поэтому я очень прошу вас уделить этому внимание.
- Организуйте рабочее место так, чтобы смотреть на натуру все время с одной точки зрения. Если вы работаете в несколько сеансов, запомните, где вы стояли или сидели относительно натуры. Чтобы не оказалось так, что половина предметов на работе у вас сделана с одной точки зрения, а половина — с другой.
- Не садитесь слишком близко или слишком далеко от натуры. Между вами и натурой должно укладываться примерно два ее размера.
- В начале обучения, старайтесь ставить предметы на контрастный фон, чтобы их очертания хорошо читались.
- В начале обучения, не ставьте предметы против света или с несколькими источниками света. Старайтесь чтобы освещение было сбоку и форма предметов хорошо читалась.
- Отходите от рисунка или переворачивание его кверх ногами. Так вы увидите ошибки. Ещё можно смотреть на работу в зеркало.
Рисунок с натуры коробки или книжки.
- Задаем положение переднего вертикального ребра и определяем, под каким углом к горизонтали мы видим нижние ребра.
- Определяем пропорции.Смысл рисования с натуры в том, чтобы она была передана точно. Эту задачу не решить без соблюдения пропорций. То есть отношений разных размеров объектов друг к другу. Если вы сделаете лицо портретируемого в два раза шире, чем на самом деле, вряд ли он вас за это поблагодарит. Для измерения пропорций есть достаточно простые приемы. О них я рассказываю на этом видео.
Упражнение 4
Нарисуйте с натуры предмет с прямыми ребрами ( книжку, коробку и т. п.)
Мы НЕ рисуем с фото, мы НЕ копируем рисунок, разобранный выше.
Упражнение 5
Нарисуйте два предмета с прямыми ребрами, один из которых стоит на другом.
РИСУНОК С НАТУРЫ КРУЖКИ.
Для постановки нужно выбрать кружку простой цилиндрической формы, с ручкой. Саму кружку мы видим без сокращений, поэтому отношение высоты и ширины можно измерить, приложив карандаш непосредственно к натуре.
- Начинаем с построения цилиндра. Помним, что чем дальше эллипс от линии горизонта, тем более он раскрыт.
- Строим толщину стенок кружки.
- Строим ручку: начинаем с мест крепления ручки, обратите внимание, что они находятся на одной вертикальной оси.
- Строим ось ручки. обратите внимание, что она лежит в плоскости, проходящей через центр цилиндра.
- Строим внешнюю, внутреннюю и боковую поверхности ручки.
Упражнение 6
Нарисуйте кружку с натуры.
Упражнение 7.
Нарисуйте ту же кружку в другом ракурсе по представлению(не глядя на натуру)
[spoiler title=”источники:”]
http://4brain.ru/draw/okruzhnost-v-vperspective.php
[/spoiler]
Содержание:
Пусть в природе не существовало бы ни одного круга или треугольника, и все-таки истины, доказанные Евклидом, навсегда сохранили бы свою достоверность и очевидность.
Раньше вы знакомились с основными геометрическими фигурами, устанавливали особенности этих фигур и их взаимное расположение. Но на практике довольно часто приходится решать «обратную» задачу — по определенным особенностям находить фигуру, имеющую их. Именно таково содержание задач на построение, которые будут рассматриваться в этом разделе.
Еще в работах древнегреческих математиков описаны задачи на построение и методы их решения.
Многие из этих задач составляют классику евклидовой геометрии. Кроме практической ценности, такие задачи представляют значительный исследовательский интерес, поскольку в ходе их решения определяются новые особенности построенных фигур.
Окружность и круг:
Определение. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от данной точки, которая называется центром окружности.
Радиусом окружности называется отрезок, соединяющий центр окружности с любой точкой на окружности (или длина этого отрезка).
Хордой окружности называется отрезок, соединяющий две точки окружности.
Диаметром окружности называется хорда, проходящая через центр окружности.
Дугой окружности называется часть окружности, ограниченная двумя точками.
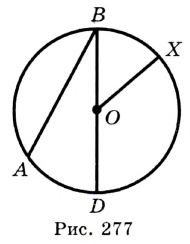
На рисунке 48 точка О — центр, отрезок ОС — радиус окружности. Радиус обозначают буквой R (или
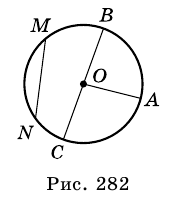
На рисунке 49 изображены: хорда ЕН, дуга КМ (обозначается: 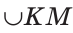
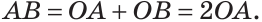
Любые две точки окружности разбивают ее на две дуги, которые дополняют друг друга до окружности. Эти дуги так и называются — дополнительными. Чтобы различать такие дуги, их иногда обозначают тремя буквами. На рисунке 49 дуги АКМ и АНМ — дополнительные.
Определение. Кругом называется часть плоскости, ограниченная окружностью.
Точки окружности также принадлежат кругу (рис. 50). Поэтому центр, радиус, хорда и диаметр у круга те же, что и у его окружности.
Часть круга, заключенная между двумя радиусами, называется сектором. Часть круга, заключенная между дугой окружности и хордой, соединяющей концы дуги, называется сегментом (рис. 51). Два радиуса разбивают круг на два сектора, хорда разбивает круг на два сегмента.
Полуокружностью называется дуга окружности, концы которой являются концами диаметра. Полукругом называется часть круга, ограниченная полуокружностью и диаметром, соединяющим концы полуокружности. На рисунке 49 дуга АКВ — полуокружность, сегмент АКВ — полукруг.
Угол, вершина которого находится в центре окружности, называется центральным углом. На рисунке 51 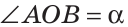
Окружности (круги) равны, если равны их радиусы.
Две окружности могут не иметь общих точек, могут пересекаться в двух точках или касаться друг друга в одной точке. Окружности разного радиуса с общим центром называются концентрическими. Часть плоскости между двумя концентрическими окружностями называется кольцом (рис. 52).
Определение окружности и круга
Окружность — это замкнутая линия на плоскости, все точки которой находятся на одинаковом расстоянии от одной точки — центра окружности.
Круг — это внутренняя часть плоскости, ограниченная окружностью.
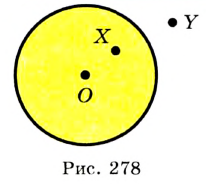
Размеры окружности и круга определяются их радиусом — отрезком, который соединяет центр с точкой на окружности (рис. 3).
В математике «окружность» и «круг» — два различных, хотя и связанных между собой, понятия. Окружность, например, является моделью обруча, а круг — моделью крышки люка.
Определение окружности и ее элементов
Пусть на плоскости отмечена точка О. Очевидно, что от точки О можно отложить бесконечное множество отрезков длиной R (рис. 162). Концы всех таких отрезков на плоскости образуют окружность — фигуру, уже известную из курса математики. Определение Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, удаленных от данной точки (центра окружности) на одинаковое расстояние. Иначе говорят, что все точки окружности равноудалены от ее центра. Определение Кругом называется часть плоскости, ограниченная окружностью и содержащая ее центр. Иначе говоря, круг состоит из всех точек плоскости, удаленных от данной точки (центра круга) на расстояние, не превышающее заданного. На рисунке 163 заштрихованная часть плоскости — круг, ограниченный окружностью с тем же центром. Центр окружности и круга является точкой круга, но не является точкой окружности.
Определение Радиусом окружности (круга) называется расстояние от центра окружности до любой ее точки. Радиусом также называется любой отрезок, соединяющий точку окружности с ее центром. На рисунке 162 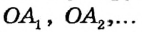
Радиус – от латинского «радиус» – луч, спица
Хорда – от греческого «хорда» — струна, тетива
Диаметр — от греческого «диа» — насквозь и «метрео» – измеряющий насквозь; другое значение этого слова — поперечник
Радиусом также называется любой отрезок, соединяющий точку окружности с ее центром. На рисунке 162 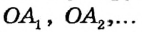
Определение:
Хордой называется отрезок, соединяющий две точки окружности.
Диаметром называется хорда, проходящая через центр окружности.
На рисунке 164 изображены две хорды окружности, одна из которых является ее диаметром. Обычно диаметр обозначают буквой d. Очевидно, что диаметр вдвое больше радиуса, то есть d = 2R.
Построение окружности выполняют с помощью циркуля.
Что такое окружность и круг
Окружность — это фигура, состоящая из всех точек плоскости, равноудален ных от данной точки. Эту точку называют центром окружности.
Отрезок, соединяющий любую точку окружности с ее центром, называют ради усом. Отрезок, соединяющий две против вольные точки окружности, — хорда окружности. Хорда, проходящая через центр окружности, — диаметр (рис. 200). Каждый диаметр окружности состоит’ из двух радиусов, поэтому его длина вдвое больше длины радиуса. Длина хорды, не проходящей через центр окружности, меньше длины диаметра, (Почему?)
Окружность на бумаге описывают < помощью циркуля. Считается, что из данного центра на плоскости можно описать только одну окружность данного радиуса (рис. 201).
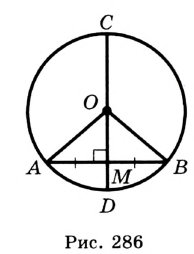
Прямая и окружность могут иметь две общие точки (рис. 202, а), одну общую точку (рис. 202, б) или не иметь ни одной (рис. 202, в)
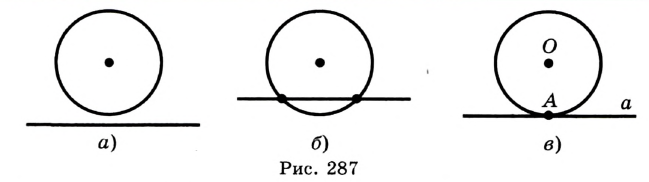
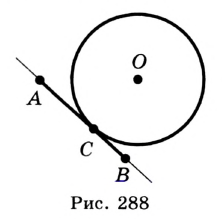
Прямая, имеющая с окружностью две общие точки, называется секущей.
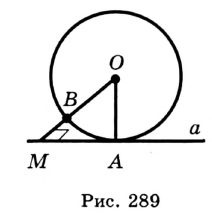
Прямая, имеющая с окружностью только одну общую точку, Напивается касательной к окружности. Их общую точку называют точкой касания. (Речь идет о фигурах одной плоскости.) Точка касания лежит на окружности, поэтому касательная удалена от центра окружности на расстояние, равное длине радиуса. Другие точки касательной лежат вне окружности, расстояния т них до центра окружности больше длины радиуса.
Отсюда следует, что касательная к окружности перпендикулярна к ее радиусу, проведенному в точку касания.
Чтобы через данную на окружности Точку К провести касательную к этой окружности, нужно провести радиус ОК, потом — прямую КМ, перпендикулярную к этому радиусу (рис. 203).
Если две разные окружности имеют дин общие точки, то говорят, что данные окружности пересекаются в этих Точках. Точки пересечения двух окружностей лежат по разные стороны от Прямой, проходящей через центры этих окружностей. На рисунке 204 показаны окружности с центрами О и Ох, пересекающиеся в точках А и В.
Если две окружности имеют только одну общую точку, говорят, что они касаются и этой точке. Касание двух окружностей может быть внешним (рис. 205) и внутренним (рис. 206). В обоих случаях точка касания и центры окружностей лежат на одной прямой.
Две окружности одной плоскости, имеющие общий центр, называют концентрическими окружностями (рис. 207).
Обычно окружности чертят, пользуясь циркулем. Но иногда удобнее это делать с помощью специальных шаблонов с вырезанными кругами разных радиусов.
Окружность делит плоскость на две части (области). Объединение окружности с ее внутренней областью называется кругом. Граница круга — окружность. Поэтому центром, радиусом, диаметром, хордой круга называют соответственно центр, радиус, диаметр, хорду данной окружности (рис. 208).
Форму окружности имеет обруч, форму круга — дно ведра, видимый диск Солнца и др. Колесо на рельсе — материальная модель окружности, касающейся прямой. На схематическом изображении подшипника (рис. 209) видны несколько касающихся окружностей.
Как вам известно из предыдущих классов, длина С окружности и площадь S круга выражаются через радиус г следующими формулами:
Строгие доказательства этих формул будут рассмотрены в старших классах.
Для любознательных:
Слово коло древнерусское. Оно одного корня со словами кольцо, кольцевать, колобок, кольчуга, колесо, колея, коловорот, околица, околыш и др. До XIX в. в русской научной литературе вместо слова окружность писали округ, кружение, окружие, циркумференция, периферия и даже периметр, а вместо круг— циркуль, обруч, колесо. Например, в «Арифметике» Л. Магницкого — первой математической книге, напечатанной в России (1703 г.), читаем: «Чрез « центр колесе линию проведи я же называется меридиана, что современном прочтении означает: «Через центр круга проведи отрезок, называемый диаметром».
Пример:
Докажите, что точки касания окружности к сторонам треугольника равноудалены от его вершины.
Решение:
Пусть окружность с центром О касается сторон угла А в точках В и С (рис. 210). Докажем, что АВ = АС.
Радиусы ОВ и ОС, проведенные в точки касания, перпендикулярны к соответствующим касательным и равны. Поэтому прямоугольные треугольники АВО и АСО равные по катету и гипотенузе. Следовательно, АВ = АС.
Пример:
Докажите, что диаметр окружности, проходящий через середину хорды, отличной от диаметра, перпендикулярен к ней.
Решение:
Пусть АВ — хорда окружности, но проходящая через центр О окружности, а КР — диаметр окружное и, проходящий через середину М хорды АВ (рис. 211). Треугольник ОАВ равнобедренный, поскольку ОА = ОВ. А медиана ОМ равнобедренного треугольника, проведения к его основанию, также являете и высотой треугольника. Поэтому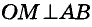
Пример:
Найдите площадь кольца, ограниченного двумя концентрическими окружностями радиусов 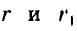
Решение:
Площадь S кольца равна разности площадей кругов радиусов 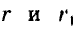
Геометрическое место точек
Чтобы решать более сложные задачи на Построение, следует знать, что такое геометрическое место точек.
Геометрическим местом точек (ГМТ) называется фигура, состоящая из всех точек, имеющих определенное свойство. Рассмотрим несколько геометрических мест точек плоскости. Окружность — это геометрическое место точек, равноудаленных от данной точки.
Круг радиуса r — геометрическое место точек, расстояния tit которых до данной точки не превышают r.
Пример №1
Найдите геометрическое место точек, равноудаленных от концов данного отрезка.
Решение:
Пусть дан отрезок АВ.
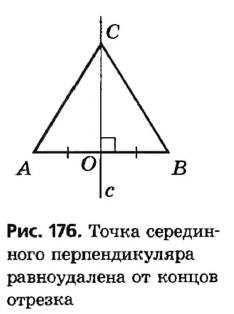
Его середина М равноудалена от А и В (рис. 215, а). Проведем прямую МК, перпендикулярную к АВ. Каждая ее точка К, отличная от М, также равноудалена от А и 4 В, поскольку А КАМ = А КВМ.
Таким образом, КА = КВ.
Если же точка Р не лежит на прямой МК, она не может быть равноудаленной от А и В (рис. 215, б).
Действительно, из допущения, что РА = РВ, следует перпендикулярность прямых РМ и АВ, так как медиана РМ равнобедренного треугольника РАВ является его высотой. Тогда сумма двух прямых углов РМВ и КМ А не равнялись бы 180°, а этого не может быть. Следовательно, вне прямой МК не существует точки, равноудаленной от А и В.
Таким образом, любая точка прямой МК равноудалена от B, а точка, не лежащая на МК, не может быть равноудаленной от А и В.
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром данного отрезка. Из этого следует, что геометрическим местом точек, равноудаленных от концов отрезка, является его серединный перпендикуляр.
Пример №2
Найдите геометрическое место точек, лежащих внутри угли и равноудаленных от его сторон.
Решение:
1) Пусть М — точка угла, равно удаленная от его сторон ОА и О Л (рис. 216). Перпендикуляры МА и MB, опущенные из М на стороны угла, равны. Поэтому 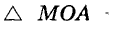
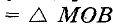
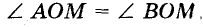
■ 2) Если М — произвольная точка биссектрисы угла АОВ, > МА и MB — перпендикуляры на ОА и ОВ (см. рис. 216), то 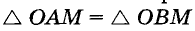
Геометрическим местом точек угла, равноудаленных от его сторон, является биссектриса этого угла.
Примечание:
Здесь имеются в виду углы меньше развернутого.
Для любознательных:
Верно ли, что геометрическим местом точек, равноудален-ных от сторон угла, является биссектриса этого угла? Нет. Когда в планиметрии говорят о геометрическом месте точек, не уточняя, о каких именно точках идет речь, то имеют в виду точки плоскости, которой принадлежит данная фигура. При таком условии геометрическим местом точек, равноудаленных от ф сторон угла, является объединение биссектрисы I данного угле g и всех точек некоего другого угла, показанного на рисунке 217,
Ведь каждая точка угла КОР также равноудалена от сторон донного угла АО В (речь идет об углах меньше развернутого).
Когда мы говорим, что геометрическим местом точек, равноудаленных от концов отрезка, является серединный перпендикуляр этого отрезка, то мы имеем в виду, что речь идет о геометрическом месте точек плоскости, на которой лежит отрезок.
А геометрическим местом точек пространства, равноудаленных от концов отрезка, является некая плоскость (мал. 218).
Подумайте, как расположена эта плоскость относительно денного отрезка.
Геометрические места точек пространства изучают в старших классах.
Пример №3
Докажите, что серединные перпендикуляры двух сторон треугольника пересекаются.
Решение:
Пусть n и m— серединные перпендикуляры сторон ВС и АВ треугольника (рис. 219). Докажем, что они не могут быть параллельны. Доказывать будем от противного. Допустим, что n || m. Тогда прямая, перпендикулярная к п, должна быть перпендикулярной и к m, то есть 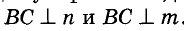
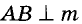
Окружность и треугольник
Окружность и треугольник могут не иметь общих точек или иметь 1, 2, 3, 4, 5, 6 общих точек (соответствующие рисунки выполните самостоятельно). Заслуживаем внимания случаи, когда окружность проходит через все три вершины треугольника или когда она касается всех и сторон треугольника. Рассмотрим такие случаи подробнее.
Описанная окружность
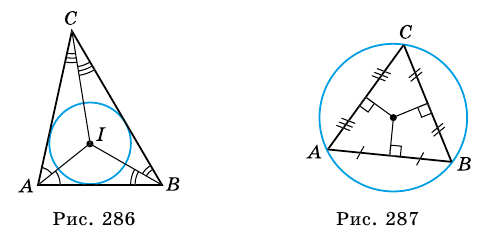
Окружность называется описанной около треугольника, если она проходит через все вершины треугольника (рис. 223).
Теорема: Около каждого треугольника можно описать только одну окружность. Ее центром является точка пересечения серединных перпендикуляров двух сторон треугольника.
Пусть ABC — произвольный треугольник (рис. 224). Найдем точку, равноудаленную от вершин А, В и С.’ Метрическое место точек, равноудаленных от А и В, — серединный перпендикуляр m отрезка АВ; геометрическое место точек, равноудаленна от В и С, — серединный перпендикуляр n отрезка ВС. Эти два серединных перпендикуляра не могут быть параллельными, они пересекаются в точке О. А она равноудалена от Н и С. Следовательно, ОА = ОВ = ОС, поэтому О — центр окружности, описанной около ABC.
Для каждого отрезка АВ существует серединный перпендикуляр, и только один, а для ВС — серединный перпендикуляр и только один. И точка их пересечения существует всегда, только одна. Таким образом, около каждого треугольника можно описать одну окружность, и только одну.
Следствия:
- Серединные перпендикуляры всех трех сторон произвольного треугольника проходят через одну и ту же точку.
- Через любые три точки, не лежащие на одной прямой, можно провести окружность, и только одну.
Из доказанной теоремы следует cnocof построения окружности, описанной около треугольника. Чтобы описать около треугольника ABC окружность, достаточно:
- построить серединные перпендикуляры двух сторон данного треугольника;
- определить точку О, в которой эти серединные перпендикуляры пересекаются;
- ) из центра О провести окружность радиуса ОА.
Центр окружности, описанной около треугольника, может лежать во внутренней или внешней области данного треугольника либо на его сторон (рис. 225).
Вписанная окружность
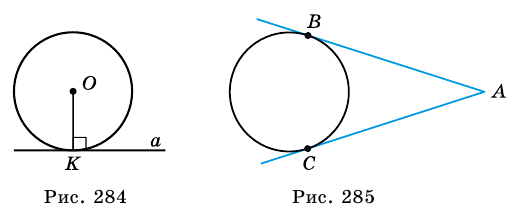
Окружность называется вписанной в треугольник если она касается всех сторон треугольника (рис. 226). Центр окружности, вписанной в треугольник, лежим’ и внутренней области этого треугольник.
Теорема: В каждый треугольник можно вписан только одну окружность. Ее центром является точка пересечения двух биссектрис треугольника.
Доказательство:
Пусть ABC — произвольный треугольник. Определим точи О, равноудаленную от всех его сторон (рис. 227). Геометрическое место точек, лежащих внутри угла А и равноудаленных второй АВ и АС, — биссектриса l угла А. Гtjметрическое место точек, равноудаленных от сторон АВ и ВС и лежащих внутри угла В, — биссектриса t угла B. Эти две биссектрисы обязательно Пересекаются (докажите это!). Точка U, в которой пересекаются биссектрисы l и t, равноудалена от всех трех сторон данного треугольника. Следовательно, точка О — центр окружности, Вписанной в треугольник АВС.
Следствие:
В каждом треугольнике все три биссектрисы пересекаются в одной точке.
Из доказанной теоремы следует способ построения окружности, вписанной в треугольник. Чтобы вписать в данный треугольник окружность, достаточно:
- провести две его биссектрисы;
- из точки их пересечения О опустить перпендикуляр OL на произвольную сторону треугольника;
- из центра О радиуса OL описать окружность. Она касается каждой стороны треугольника, следовательно, является вписанной в данный треугольник.
Для любознательных:
Теорема: Центром окружности, описанной около прямоугольного треугольника, является середина его гипотенузы.
Пусть ABC — произвольный треугольник с прямым углом С, t— серединный перпендикуляр катета АС, пересекающий гипотенузу АВ в точке О (рис. 228).
Поскольку точка О лежит на серединном перпендикуляре отрезка АС, то 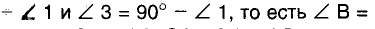
точка О—середина гипотенузы АВ, равноудаленная от всех вершин треугольника. Таким образом, окружность с центром О и радиусом ОА проходит через все вершины данного треугольника.
Диаметр окружности, описанной около прямоугольного треугольника, равен его гипотенузе.
Теорема: Из любой точки окружности ее Диаметр, не выходящий из этой точки, виден под прямым углом.
Доказательство:
Пусть АВ — произвольный диаметр окружности с центром О, а С— произвольная точка окружности, отличная от А и В (рис. 229). Покажем, что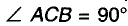
Геометрическим местом точек плоскости, из которых отрезок АВ виден под прямым углом, является окружность диаметра АВ. На самом деле этому ГМТ точки А и В не принадлежат. Подробнее об этом вы узнаете в старших классах.
Пример №4
Найдите радиус окружности, описанной около прямоугольного треугольника с гипотенузой 6 см.
Решение:
Диаметр окружности, описанной около прямоугольного треугольника, является его гипотенузой. Радиус вдвое меньше: 3 см.
Пример №5
Докажите, что диаметр окружности, вписанной в прямоугольный треугольник с катетами а и Ь и гипотенузой с, равен a + b — c.
Решение:
Пусть в 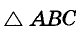
Геометрические построения
Пользуясь линейкой’ и циркулем, моле но выполнить много геометрических построений, то есть начертить геометрические фигуры. Рассмотрим сначала, как выполняются самые простые геометрические построения.
Пример №6
Постройте треугольник по данным сторонам.
Решение:
Пусть даны три отрезки а, b и с (рис. 232). Нужно построить, треугольник, стороны которого были бы равны этим отрезкам. С помощью линейки проводим произвольную прямую, обозначаем на ней произвольную точку В и циркулем откладываем на этой прямой отрезок ВС = а. Раствором циркуля, равным с описываем дугу окружности с центром В. С той же стороны от прямой СВ описываем дугу окружности радиуса b с центром С. Точку пересечения А этих дуг соединяем отрезками с С и В. Треугольник ABC — именно тот, который требовалось построить, так как его стороны ВС, АС и АВ равны данным отрезкам.
Примечание:
Если построенные дуги не пересекаются, требуемый треугольник построить невозможно. Это бывшие в том случае, когда один из данных отрезков больше суммы двух других или равен их сумме.
Пример №7
Постройте угол, равный данному углу.
Решение:
Пусть дан угол АОВ и требуется построить угол КРТ, равный 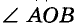
который требовалось построить. Ведь треугольники КРТ и АОВ равны (по трем сторонам), поэтому
Пример №8
Постройте биссектрису данного угла.
Решение:
Пусть АОВ — данный угол (рис. 234). Произвольным раствором циркуля опишем дугу с центром О. Пусть А и В — точки пересечения этой дуги с лучами О А и ОВ. Из центров А и В опишем дуги такими же радиусами. Если D — точка пересечения этих дуг, то луч OD — биссектриса угла АОВ.
Действительно, 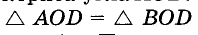
Пример №9
Разделите данный отрезок пополам.
Решение:
Пусть АВ — данный отрезок (рис. 235). Из точек А и В радиусом АВ описываем дуги. Они пересекутся в неких точках С и D.
Прямая CD точкой М разделит данный отрезок пополам.
Действительно, по трем сторонам 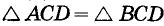
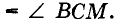
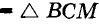
Пример №10
Через данную точку Р проведите прямую, перпендикулярную и данной прямой а.
Решение:
В зависимости от того, лежит или не лежит точка Р на прямой а, задачу можно решить, как показа но на рисунках 236 и 237. Опишите и аргументируйте эти построения самостоятельно.
Пример №11
Через точку Р, не лежащую на прямой АВ, проведите прямую, параллельную прямой АВ.
Решение:
Через точку Р и про из вольную точку А прямой АВ проводим прямую АТ (рис. 238). Строим угол ТРМ, равный углу РАВ, так, что бы эти углы стали соответственны ми при прямых РК, АВ и секущей АР. Построенная таким образом пря мая РК удовлетворяет задачу: она проходит через данную точку Р и параллельна прямой АВ, поскольку
Для любознательных:
Геометрическими построениями часто приходилось заниматься многим людям. Еще в доисторические времена мастера, изготавливающие колеса к колесницам, умели делить окружность на несколько равных частей. В наше время выполнять такие построения приходится специалистам, проектирующим или изготавливающим шестеренки, дисковые пилы (рис. 239), турбины и различные роторные механизмы. Как бы вы разделили окружность, например, на 5, 6 или 7 равных частей?
Основные чертежные инструменты — линейка и циркуль — были известны еще несколько тысячелетий назад.
Слово линейка происходит от слова линия, которое на латинском языке сначала означало «льняная нитка», «черта, проведенная ниткой, бечевкой» (производное от лат. Плит — лен). Слово циркуль тоже латинского происхождения, первоначально слово циркулюс означало «окружность, круг», а потом стало означать инструмент, с помощью которого проводят окружности.
В Древней Греции линейку и циркуль признавали единственными приборами геометрических построений. Задачу на построение считали решенной, если все построения в ней выполнялись только с помощью линейки и циркуля. Сейчас специалисты при выполнении построений пользуются угольником, транспортиром, рейсмусом, рейсшиной и другими чертежными приспособлениями.
Пример №12
Разделите данную дугу окружности на две равные части.
Решение:
Пусть дана дуга АВ окружности с центром О (рис. 240). Представим угол АОВ и проведем его биссектрису ОК. Треугольники АОК и КОВ равны, поэтому и дуги АК и КВ равны.
Пример №13
Постройте угол вдвое больше данною.
Решение:
Пусть АОВ — данный угол (рис. 241) Опишем дугу окружности с центром О Если она пересечет стороны данного угла в точках А и В, из В как из центра сделаем засечку ВС = ВА и проведем луч ОС. Угол АОС вдвое больше
Задачи на построение
С геометрическими построениями имеют дело различные специалисты. Геометрические построении выполняют чертежники, архитекторы, конструкторы, топографы, геодезисты, штурманы. Разные геометрические фигуры строят также: слесарь — на жести, столяр — на доске, портной— на ткани, садовник — на земле.
В задаче на построение требуется построить геометрическую фигуру, которая должна удовлетворять определенные условия. В геометрии построения выполняют чаще всего с помощь к линейки и циркуля. Условимся: если в задаче не сказано, какими инструментами следует выполнить построение, то имеются в виду только линейка (без делений) и циркуль.
Более сложные задачи на построение часто решают методом геометрических мест. Пусть, например, в задаче требуете!’ найти точку X, удовлетворяющую два условия. Если первое условие удовлетворяют точки фигуры К, а второе — точки фигуры Р, то X должна принадлежать каждой из этих фигур. Тс есть X — точка пересечения фигур К и Р.
Пример №14
Постройте прямоугольный треугольник по да» ному катету а и гипотенузе с (рис. 243).
Решение:
Строим прямой угол АСВ, на его стороне откладываем отрезок СВ = а. Точки С и В — две вершины треугольника, который требуется построить. Третья верши» должна лежать, во-первых, на луче СА, во-вторых, на pfti стоянии с от В, то есть на окружности радиуса с с центр В. Если эту окружность пересекает луч СА в точке А, 1 треугольник ABC — именно тот, который требовалось не строить. Ведь его угол С прямой, ВС = а, ВА = с.
Второй способ (рис. 244). Откладываем отрезок АВ = с и проводим окружность диаметра АВ — ГМТ, из которых АВ виден под прямым углом. Дальше строим полуокружность радиуса а с центром В — ГМТ, удаленных от В на расстояние а и лежащих по одну сторону от прямой АВ. Если два ГМТ пересекаются в точке С, то треугольник ABC — именно тот, который требовалось построить.
Составные части решения задачи на построение — анализ, построение, доказательство и исследование. В анализе ищут способ решения задачи, в построении выполняется само построение, в доказательстве обосновывается правильность выполненного построения, в исследовании выясняется, сколько решений имеет задача.
Пример №15
Постройте треугольник по данной стороне, прилежащему к ней углу и сумме двух других сторон (рис. 245).
Решение:
Анализ. Допустим, что требуемый треугольник ABC построен. Его сторона с и угол А = а — даны. Дан также отрезок, равный сумме сторон а и b. По данным отрезкам с и а + b и углу А между ними можно построить A ABD. Вершиной С искомого треугольника будет такая точка отрезка AD, для которой CD = СВ. Следовательно, точка С должна лежать и на серединном перпендикуляре отрезка BD.
Построение. По двум данным отрезкам и углу между ними строим 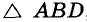
Доказательство:
В треугольнике 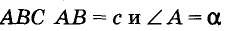
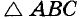
Исследование. Задача имеет решение только при условии, что а + b > с.
Примечание:
Если задача несложная и способ ее решения известен, анализ можно не описывать. А в решении не обязательно выделять анализ, построение, доказательство и исследование.
Для любознательных:
В математике чаще всего имеют дело с задачами: на вычисление, на доказательство, на построение, на преобразование и на исследование. Геометрическими задачами на построение активно интересовались античные геометры. Допуская лишь классические построения (выполняемые только линейкой и циркулем), они исследовали, какие из построений можно вы-полнить, а какие невозможно. В частности, выясняли:
- можно ли любой угол разделить на три равные части;
- можно ли построить квадрат, площадь которого была бы равна площади данного круга;
- можно ли построить ребро такого куба, объем которого был бы в 2 раза больше объема данного куба.
Много столетий выдающиеся геометры пытались решить эти задачи и не смогли. Эти три классические задачи древности получили специальные названия:
- трисекция угла,
- 2квадратура круга,
- удвоение куба.
Последнюю задачу называют еще делосской задачей, связывая ее с древнегреческой легендой. согласно которой оракул бога Аполлона согласился спасти жителей острова Делос от чумы, если кубический жертовник в делосском храме заменят на жертовник такой же формы, но вдвое большего объема. Только почти через 2000 лет ученые убедились, что ни одну из этих трех задач с помощью лишь линейки и циркуля решить невозможно.
В настоящее время специалисты, которым приходится выполнять геометрические построения, пользуются не только линейкой и циркулем. С точки зрения классических методов такие построения приближенные. Но для практических нужд точности, которую обеспечивают приближенные методы, вполне достаточно
Пример №16
Найдите центр данной окружности.
Решение:
Обозначим на данной окружности три производные точки А, В и С (рис. 246).
Представим хорды АВ, ВС и проведем их серединные перпендикуляры n и m. Точка О, в которой пересекаются прямые n и m., — центр данной окружности. Ведь ОА = ОВ = ОС.
Пример №17
Через данную точку проведите касательную к данной окружности.
Решение:
Если данная точка А лежит на окружности центра О (рис. 247, а), проводим луч ОА, потом — прямую АК, перпендикулярную к ОА. Прямая АК — касательная, которую и требовалось построить.
Если точка А лежит вне данной окружности центра О (рис. 247, б), то на диаметре ОА описываем окружность. Она пересечется с данной окружностью в двух точках К и Р. Прямые АК и АР — искомые касательные, поскольку 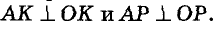
Свойство диаметра, перпендикулярного хорде
Опорная задача:
Диаметр, перпендикулярный хорде, проходит через ее середину. Докажите.
Решение
Пусть СО — диаметр окружности с центром О, АВ — хорда этой окружности, 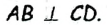
В случае, когда хорда АВ сама является диаметром, точка М совпадает с центром О и утверждение задачи очевидно. Пусть хорда АВ не является диаметром (рис. 165). Проведем радиусы OA и ОВ. Тогда в равнобедренном треугольнике АОВ высота ОМ является медианой. Итак, AM = ВМ, что и требовалось доказать.
Докажите самостоятельно еще одно утверждение (опорное): диаметр окружности, проведенной через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
Касательная к окружности
Определение и свойство касательной
Любая прямая, проходящая через точки окружности, называется секущей; ее отрезок, лежащий внутри окружности, является хордой. На рисунке 167 хорда CD — отрезок секущей b. Рассмотрим теперь прямую, имеющую с окружностью только одну общую точку.
Определение:
Касательной к окружности называется прямая, имеющая с окружностью единственную общую точку. Общая точка касательной и окружности называется точкой касания.
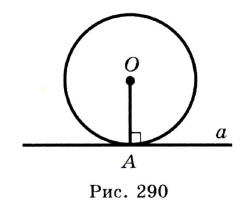
На рисунке 167 прямая а является касательной к окружности с центром О. Иначе говоря, прямая а касается окружности с центром О в точке А.
Определим взаимное расположение касательной и радиуса окружности, проведенного в точку касания.
Теорема (свойство касательной)
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Доказательство:
Пусть прямая а касается окружности с центром О в точке А (рис. 168). Докажем, что 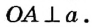
Пусть отрезок OA не является перпендикуляром к прямой а. Тогда, по теореме о существовании и единственности перпендикуляра к прямой, из точки О можно провести перпендикуляр ОB к прямой а. На луче АВ от точки В отложим отрезок ВС, равный АВ, и соединим точки О и С. Поскольку по построению отрезок ОВ — медиана и высота треугольника АОС, то этот треугольник равнобедренный с основанием АС, то есть OA = ОС. Таким образом, расстояние между точками О и С равно радиусу окружности, и, по определению радиуса, точка С должна лежать на данной окружности. Но это противоречит определению касательной, поскольку А — единственная общая точка окружности с прямой а. Из этого противоречия следует, что наше предположение неверно, то есть OA 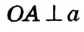
Признак касательной
Докажем теорему, обратную предыдущей.
Теорема: (признак касательной)
Если прямая проходит через точку окружности перпендикулярно радиусу, проведенному в эту точку, то она является касательной к окружности.
Доказательство:
Пусть прямая а проходит через точку А, лежащую на окружности с центром О, причем 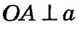
Пусть прямая а имеет с окружностью общую точку В, отличную от А (рис. 169). Тогда из определения окружности ОА = ОВ как радиусы, то есть треугольник АОВ равнобедренный с основанием АВ. По свойству углов равнобедренного треугольника 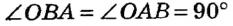
Следовательно, точка А — единственная общая точка окружности и прямой а, значит, прямая а — касательная к окружности.
Свойство отрезков касательных
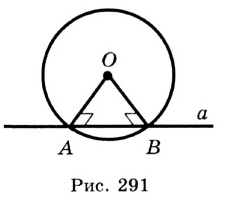
Пусть даны окружность с центром О и точка А, не принадлежащая кругу, ограниченному данной окружностью (рис. 170).
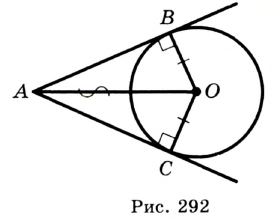
Через точку А можно провести две касательные к данной окружности. Отрезки, соединяющие данную точку А с точками касания, называют отрезками касательных, проведенных из точки А к данной окружности. На рисунке 170 АВ и АС — отрезки касательных, проведенных к окружности из точки А .
Опорная задача
Отрезки касательных, проведенных из данной точки к окружности, равны. Докажите.
Решение
Пусть АВ и АС — отрезки касательных, проведенных к окружности с центром О из точки А (рис. 170). Рассмотрим треугольники АОВ и АОС. По свойству касательной 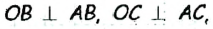
Касание двух окружностей
Определение:
Две окружности, имеющие общую точку, касаются в этой точке, если они имеют в ней общую касательную.
Общая точка двух окружностей в таком случае называется точкой касания окружностей.
Различают два вида касания окружностей: внутреннее и внешнее.
Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от общей касательной, проведенной через точку касания (рис. 171, а);
Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от общей касательной, проведенной через точку касания (рис. 171, б).
Рис. 171 Касание двух окружностей. 1. внутреннее; 2. внешнее.
По свойству касательной радиусы данных окружностей, проведенные в точку касания, перпендикулярны общей касательной. Из теоремы о существовании и единственности прямой, перпендикулярной данной, следует, что центры касающихся окружностей и точка касания окружнос тей лежат на одной прямой.
Касающиеся окружности имеют единствен ную общую точку — точку касания.
Если данные окружности имеют радиусы R и r (R > r), то расстояние между центрами окружностей равно R-r в случае внутреннего касания и R+r в случае внешнего касания.
Задачи на построение
Что такое задачи на построение?
Задачи на построение представляют собой отдельный класс геометрических задач, решение которых подчиняется определенным правилам. Цель решения этих задач — построение геометрических фигур с заданными свойствами с помощью чертежных инструментов. Если в условии задачи нет специальных примечаний, то имеются в виду построения с помощью циркуля и линейки. С помощью линейки можно провести:
- произвольную прямую;
- прямую, проходящую через данную точку;
- прямую, проходящую через две данные точки.
Заметим, что никаких других построений линейкой выполнять нельзя. В частности, с помощью линейки нельзя откладывать отрезки заданной длины.
Циркуль – от латинского “циркулус” – окружность, круг.
С помощью циркуля можно:
- провести окружность (часть окружности) произвольного или заданного радиуса с произвольным или заданным центром;
- отложить от начала данного луча отрезок заданной длины.
Кроме того, можно отмечать на плоскости точки и находить точки пересечения прямых и окружностей.
Все перечисленные операции называют элементарными построениями, а решить задачу на построение — это значит найти последовательность элементарных построений, после выполнения которых искомая фигура считается построенной, и доказать, что именно эта фигура удовлетворяет условию задачи.
Итак, решение задач на построение заключается не столько в самом построении фигуры, сколько в нахождении способа построения и доказательстве того, что полученная фигура искомая.
Основные задачи на построение
Если каждый шаг построений описывать полностью, решение некоторых задач может оказаться довольно громоздким. С целью упрощения работы выделяют несколько важнейших задач, которые считаются основными и не детализируются каждый раз при решении более сложных задач.
| Построение треугольника с данными сторонами | |
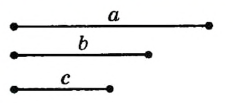 |
Пусть даны отрезки длиной а, b и с. Построим треугольник со сторонами, b и с. |
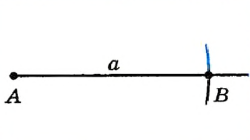 |
Проведем произвольный луч и отметим на нем точку А. Раствором циркуля, равным а, построим окружность с центром А. Пусть В — точка пересечения этой окружности с лучом. |
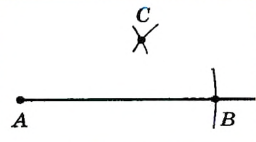 |
Раствором циркуля, равным b, опишем окружность с центром А, а раствором циркуля, равным с,— окружность с центром В. Пусть С — точка пересечения этих окружностей. |
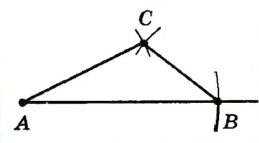 |
Проведем отрезки АС и ВС. По построению треугольник ABC имеет стороны длиной а, b и с, то есть треугольник ABC искомый1. |
1 По данным задачи можно построить четыре разных треугольника с общей стороной АВ. По третьему признаку эти треугольники равны, то есть совмещаются наложением. В таких случаях решением задачи считают любой из этих равных треугольников.
Отметим, что эта задача имеет решение при условии, что длины отрезков а, b и с удовлетворяют неравенству треугольника.
С помощью описанных операций несложно решить задачу о построении угла, равного данному неразвернутому углу А. Для этого достаточно отложить на сторонах данного угла А отрезки АВ и АС и построить треугольник, равный треугольнику ABC.
| Построение перпендикулярной прямой | |
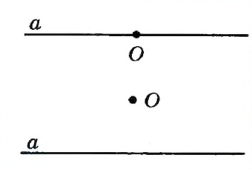 |
Пусть даны прямая а и точка О . Построим прямую, проходящую через точку О и перпендикулярную прямой а . Рассмотрим два случая |
| Точка O лежит на прямой а | |
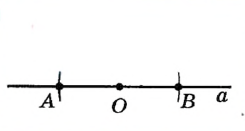 |
Построим окружность произвольного радиуса с центром О. Пусть А и B — точки пересечения этой окружности с прямой а . |
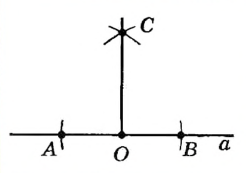 |
Построим окружности радиуса АВ с центрами А и В. Пусть С — одна из точек их пересечения. Проведем прямую через точки С и О. |
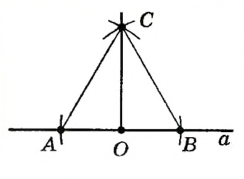 |
По построению отрезок СО — медиана равностороннего треугольника ABC , которая является также его высотой. Итак, 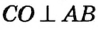 , то есть прямая СО — искомая. , то есть прямая СО — искомая. |
| Точка O не лежит на прямой а | |
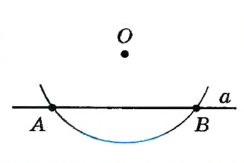 |
Построим окружность с центром О , которая пересекает прямую O, в точках А и В . |
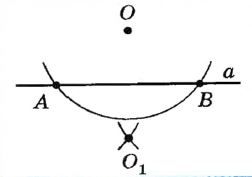 |
Построими окружности того же радиуса с центрами A и В . Пусть Ol — точка пересечения этих окружностей, причем точки О и Ol лежат по разные стороны от прямой а . |
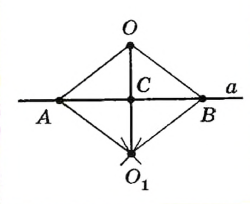 |
Проведем прямую 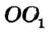 . Пусть С — точка пересечения прямых . Пусть С — точка пересечения прямых 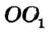 и а . По построению и а . По построению 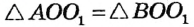 (по третьему признаку). Отсюда (по третьему признаку). Отсюда 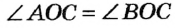 . Тогда ОС — биссектриса равнобедренного треугольника АОВ , проведенная к основанию. Она также является медианой и высотой треугольника. Следовательно, . Тогда ОС — биссектриса равнобедренного треугольника АОВ , проведенная к основанию. Она также является медианой и высотой треугольника. Следовательно, 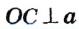 а , то есть прямая а , то есть прямая 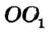 — искомая. — искомая. |
Отметим, что построенная прямая 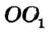
Пользуясь описанными построениями, несложно решить задачи на построение середины данного отрезка и на построение прямой, параллельной данной.
Для построения середины отрезка АВ достаточно провести две окружности радиуса АВ с центрами в точках А к В (рис. 172). Обозначив точки пересечения этих окружностей через 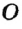
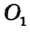
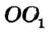
Для построения прямой, проходящей через данную точку О параллельно данной прямой а, достаточно провести через точку О прямую b, перпендикулярную а, и прямую с, перпендикулярную b (рис. 173). Тогда а || с по теореме о двух прямых, перпендикулярных третьей.
Таким образом, основными задачами на построение будем считать следующие:
- построение треугольника с данными сторонами;
- построение угла, равного данному неразвернутому углу;
- построение биссектрисы данного неразвернутого угла;
- построение прямой, проходящей через данную точку перпендикулярно данной прямой;
- построение серединного перпендикуляра к данному отрезку;
- построение середины данного отрезка;
- построение прямой, проходящей через данную точку параллельно данной прямой.
Если эти задачи применяются как вспомогательные при решение более сложных задач, соответствующие построения можно подробно не описывать.
Решение задач на построение
Решение задач на построение состоит из четырех основных этапов: анализ, построение, доказательство, исследование.
| Общая схема решения задач на построение | ||
|
1 |
Анализ |
Выполнение рисунка-эскиза искомой фигуры и установление связи между ее элементами и данными задачи. Определение плана построения искомой фигуры. |
|
2 |
Построение |
Осуществление плана, разработанного в ходе анализа. |
|
3 |
Доказательство |
Обоснование того, что построенная фигура имеет заданную форму, а размеры и расположение ее элементов удовлетворяют условию задачи. |
|
4 |
Исследование [1] |
Определение количества решений и условий существования искомой фигуры или обоснование невозможности ее построения. |
Если задача достаточно проста, то отдельные этапы ее решения можно проводить устно.
1] В некоторых задачах для исследования необходимы геометрические утверждения и соотношения, изучаемые в 8—9 классах. В этих случаях исследования мы будем проводить в сокращенном виде или вообще опускать.
Рассмотрим на конкретных примерах некоторые методы решения задач на построение.
Пример №18
Постройте треугольник по двум сторонам и медиане, проведенной к одной из них.
Решение:
Анализ
Пусть a, b, 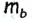
Допустим, что треугольник ABC построен (рис. 175). Если ВМ — данная медиана треугольника ABC, то в треугольнике АВМ известны длины трех сторон 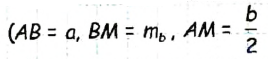
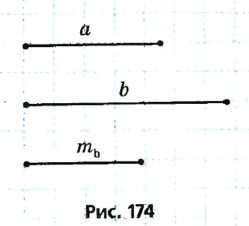
Построение
- Разделим отрезок b пополам.
- Построим треугольник АВМ со сторонами АВ = а,
- Отложим на луче AM отрезок
.
- Соединим точки В и С.
Доказательство
В треугольнике 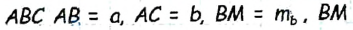
Исследование
Задача имеет решение при условии существования треугольника АВМ, то есть, если числа 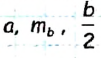
Сравним только что решенную задачу с задачей о доказательстве равенства треугольников но двум сторонам и медиане, проведенной к одной из них (п. 13.1). Решая обе эти задачи, мы использовали треугольник АВМ в котором все стороны известны по условию. Его рассмотрение помогло в задаче на доказательство получить необходимые соотношения для углов данных треугольников, а в задаче на построение — найти две вершины искомого треугольника. Треугольник АВМ называют вспомогательным а соответствующий метод решения — методом вспомогательного треугольника.
Решение задач на построение с помощью метода вспомогательной треугольника подробно рассмотрено в Приложении 2.
Геометрическое место точек
Понятие о геометрическом месте точек
До сих пор мы описывали геометрические фигуры с помощью определений и устанавливали их особенности путем доказательства свойств и признаков, относящихся к фигуре в целом. Для случаев, когда определенное свойство и соответствующий ему признак имеет каждая точка фигуры, существует еще один способ описания.
Определение:
Геометрическим местом точек (сокращенно ГМТ) на плоскости называется фигура, которая состоит из всех точек плоскости, удовлетворяющих определенному условию.
Например, по определению окружность является геометрическим местом точек, удаленных от данной точки плоскости на одинаковое расстояние.
В определении ГМТ обратим внимание на слово «всех». Оно указывает на то, что для выяснения геометрического места точек недостаточно доказать, что точки указанной фигуры удовлетворяют определенному условию (то есть установить свойство точек). Необходимо также показать, что других точек, удовлетворяющих данному условию, на плоскости нет, то есть доказать соответствующий признак: если точка удовлетворяет указанному условию, то она принадлежит данной фигуре.
Иначе говоря, доказательство того, что некоторая фигура F является геометрическим местом точек, удовлетворяющих условию Р, состоит из доказательства двух утверждений — прямого и обратного:
- если определенная точка P принадлежит фигуре F, то она удовлетворяет условию Р ;
- если определенная точка удовлетворяет условию Р, то она принадлежит фигуре F .
Основные теоремы о ГМТ
Часто геометрическим местом точек является прямая или часть прямой. Докажем две важные теоремы о ГМТ.
Теорема: (о серединном перпендикуляре)
Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов этого отрезка.
Доказательство:
Нам необходимо доказать два утверждения:
- если точка принадлежит серединному перпендикуляру к отрезку, то она равноудалена от концов этого отрезка;
- если точка равноудалена от концов отрезка, то она принадлежит серединному перпендикуляру к этому отрезку.
Докажем первое из этих утверждений. Пусть точка С лежит на прямой с, перпендикулярной отрезку АВ и проходящей через его середину — точку О (рис. 176). В треугольнике АСВ отрезок СО — медиана и высота, значит, этот треугольник равнобедренный с основанием АВ. Отсюда АС=ВС , то есть расстояния от точки С до концов отрезка АВ равны. Докажем второе утверждение. Пусть точка D равноудалена от точек А и В , то есть AD = BD (рис. 177). Тогда в равнобедренном треугольнике ADB отрезок DO — медиана, проведенная к основанию, которая является также и высотой. Таким образом, прямая DO — серединный перпендикуляр к отрезку АВ. Теорема доказана.
Теорема: (о биссектрисе угла)
Биссектриса неразвернутого угла является геометрическим местом точек, равноудаленных от сторон этого угла.
Доказательство
По аналогии с предыдущей теоремой докажем сначала, что любая точка биссектрисы равноудалена от сторон угла.
Пусть даны неразвернутый угол с вершиной А и точка D на его биссектрисе (рис. 178). Опустим из точки D перпендикуляры DB и DC на стороны данного угла. По определению, DB и DC — расстояния от точки D до сторон угла А.
Прямоугольные треугольники DBA и DCA имеют общую гипотенузу 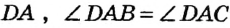
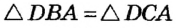
Теперь докажем, что любая точка, равноудаленная от сторон угла, принадлежит его биссектрисе. Пусть F — некоторая точка, равноудаленная от сторон угла А, то есть перпендикуляры FB и FC, опущенные из точки F на стороны данного угла, равны (рис. 179). Соединим точки F и А . Тогда прямоугольные треугольники FBA и FCA равны по гипотенузе и катету.
Отсюда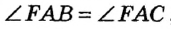
Теорема доказана.
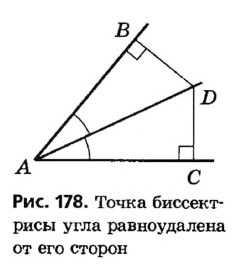
*Здесь и далее, говоря о точках, равноудаленных от сторон угла, мы имеем в виду точки, лежащие внутри угла и равноудаленные от прямых, содержащих его стороны.
Метод геометрических мест
Понятие ГМТ часто используется при решении задач на построение. Например, пусть необходимо построить точку, удовлетворяющую условиям 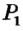
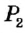
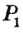
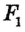
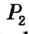
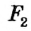
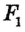
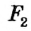
Рассуждения по такой схеме лежат в основе метода геометрических мест.
Пример №19
Постройте прямоугольный треугольник по гипотенузе и катету.
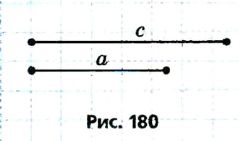
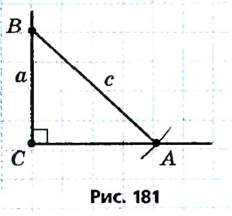
Решение:
Пусть в искомом прямоугольном треугольнике ABC гипотенуза АВ равна с, катет ВС равен а (рис. 180). Для построения треугольника воспользуемся методом геометрических мест. Для этого на стороне прямого угла С отложим катет ВС, ВС = а (рис. 181). Точка А должна принадлежать второй стороне прямого угла и быть удаленной от точки В на расстояние с, то есть А — точка пересечения окружности с центром В радиуса с со второй стороной прямого угла. Построенные точки А, В и С являются вершинами искомого прямоугольного треугольника ABC. В соответствии со следствием теоремы о сравнении сторон и углов треугольника задача имеет решение при условии а 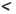
Описанная и вписанная окружности треугольника
Окружность, описанная около треугольника
Определение:
Окружность называется описанной около треугольника, если все вершины треугольника лежат на данной окружности.
В этом случае говорят, что треугольник является вписанным в данную окружность.
На рисунке 183 окружность с центром О описана около треугольника ABC.
Поскольку все вершины треугольника лежат на описанной окружности, то все они равноудалены от центра окружности. Этот факт лежит в основе доказательства теоремы об описанной окружности.
Теорема: (об окружности, описанной около треугольника)
Около любого треугольника можно описать единственную окружность. Центр этой окружности является точкой пересечения серединных перпендикуляров к сторонам треугольника.
Доказательство:
Пусть прямые а и b — серединные перпендикуляры к сторонам АВ и ВС данного треугольника ABC (рис. 184).
Сначала докажем методом от противного, что прямые а и b пересекаются. Предположим, что эти прямые не пересекаются, то есть а || b . Тогда поскольку 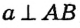
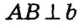
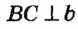
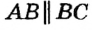
По теореме о серединном перпендикуляре точка О равноудалена от точек А и В (то есть OA = OB) и равноудалена от точек В и С (то есть ОВ = ОС). Отсюда OA = OB = ОС. Следовательно, существует окружность с центром О, проходящая через все вершины треугольника ABC.
Докажем методом от противного, что такая окружность единственна.
Допустим, что около треугольника можно описать еще одну окружность, отличную от построенной. Тогда центр этой окружности равноудален от вершин треугольника и потому совпадает с О, точкой пересечения серединных перпендикуляров к сторонам треугольника. Радиус этой окружности равен расстоянию от точки О до вершин треугольника. Значит, эта окружность совпадает с построенной.
И наконец, серединный перпендикуляр с к стороне АС содержит вое точки, равноудаленные от точек А и С. Поскольку точка О также равноудалена от точек А и С, то этот серединный перпендикуляр проходит через точку О. Теорема доказана.
Следствие:
Три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке.
Отметим, что центр описанной окружности не всегда лежит внутри треугольника; он также может лежать на одной из его сторон или вне треугольника (рис. 185).
Окружность, вписанная в треугольник
Определение:
Окружность называется вписанной в треугольник, если она касается всех его сторон.
В этом случае треугольник является описанным около данной окружности.
На рисунке 186 окружность с центром О вписана в треугольник ABC. Прямые, содержащие стороны треугольника, являются касательными к вписанной окружности, а точки касания лежат на сторонах треугольника. Радиусы вписанной окружности, проведенные в точки касания, перпендикулярны сторонам данного треугольника.
Далее в таком случае мы будем говорить, что центр вписанной окружности равноудален от сторон треугольника.
Теорема: (об окружности, вписанной в треугольник)
В любой треугольник можно вписать единственную окружность. Центр этой окружности является точкой пересечения биссектрис треугольника.
Доказательство:
Пусть AD и BE — биссектрисы данного треугольника ABC (рис. 187).
Докажем методом от противного, что эти биссектрисы пересекаются. Пусть AD и BE не пересекаются. Тогда AD || BE, а углы BAD и ABE — внутренние односторонние при параллельных прямых AD и BE и секущей АВ. Сумма этих углов должна быть равна 180°, что противоречит теореме о сумме углов треугольника.
Итак, биссектрисы AD и BE пересекаются в некоторой точке О. Тогда по теореме о биссектрисе угла точка О равноудалена от сторон АВ и АС, а также равноудалена от сторон АВ и ВС . Таким образом, три перпендикуляра, опущенные из точки О на стороны данного треугольника, равны. Следовательно, существует окружность с центром О, которая касается всех сторон треугольника ABC.
Докажем методом от противного, что эта окружность единственна.
Допустим, что в треугольник можно вписать еще одну окружность, отличную от построенной. Тогда ее центр одинаково удален от сторон треугольника и совпадает с О, точкой пересечения биссектрис треугольника. Радиус этой окружности равен расстоянию от точки О до сторон треугольника. Таким образом, эта окружность совпадает с построенной.
И наконец, биссектриса CF содержит все точки, равноудаленные от сторон СА и СВ. Поскольку точка О также равноудалена от СА и СВ, то эта биссектриса проходит через точку О. Теорема доказана.
Следствие:
Три биссектрисы треугольника пересекаются в одной точке.
Поскольку все биссектрисы треугольника лежат внутри него, то и центр вписанной окружности всегда лежит внутри треугольника.
Пример №20
В равностороннем треугольнике центры описанной и вписанной окружностей совпадают. Докажите.
Решение:
В равностороннем треугольнике ABC биссектрисы 
Верно также и обратное утверждение: если в треугольнике центры описанной и вписанной окружностей совпадают, то этот треугольник равносторонний. Попробуйте доказать это самостоятельно.
Историческая справка:
Простейшие геометрические задачи на построение:
Возникновение задан на построение было обусловлено необходимостью измерений земельных участков и строительством. Значительных успехов в решении таких задач достигли древнегреческие ученые, прежде всего Евклид и Платон, в VII – III в. до н. з. Именно со времен Платона в решении задач на построение стали выделять четыре этапа: анализ, собственно построение, доказательство и исследование.
Задачи, которые невозможно решить с помощью циркуля и линейки
Особый интерес математиков древности вызывали три классические задачи, которые не удавалось решить с помощью циркуля и линейки – о квадратуре круга, трисекции угла и удвоении куба. Задача о квадратуре круга состояла в построении квадрата, площадь которого равна площади данного круга. В задаче о трисекции угла пытались разделить данный угол на три равные части. Такую задачу несложно решить для некоторых конкретных углов, например развернутого, прямого, но не для любого угла. Задача об удвоении куба состояла в построении куба, объем которого вдвое больше объема данного куба. Невозможность решить эти задачи с помощью циркуля и линейки была доказана в XIX в.
Циркуль или линейка
Интересна историй ограничений в выборе инструментов для решения задач на построение. В X веке арабский математик Абу-ль-Вафа предложил ограничиться в геометрических построениях односторонней линейкой и циркулем постоянного раствора. В 1797 г. итальянец Лоренцо Маскерони доказал: любая задача на построение, решенная с помощью циркуля и линейки, может быть решена и с помощью одного циркуля (при этом предполагалось, что через любые две точки может быть проведена прямая). А еще раньше, в 1672 г. к такому же выводу пришел датчанин Г. Мор. Так, теорема о возможности построений только циркулем получила название «теоремы Мора – Маскерони». В 1833 г. швейцарский геометр Якоб Штейнер показал, что, при наличии на плоскости окружности с отмеченным центром, любую задачу на построение можно решить с помощью одной линейки. Задачи на построение играют особую роль в обучении геометрии, ведь они прекрасно развивают логику и абстрактное мышление. Специалисты считают задачи на построение одними из самых полезных и красивых задач геометрии.
Об аксиомах геометрии
Вы ознакомились с начальными понятиями геометрии: точкой и прямой, а также лучом, отрезком и углом. Их основные свойства — аксиомы — не доказываются, но являются фундаментом для доказательства других утверждений. Первую попытку провести логическое обоснование геометрии с помощью систематизированного перечня исходных положений (аксиом или постулатов) осуществил древнегреческий математик Евклид в своей знаменитой книге «Начала». На протяжении многих веков ученые-геометры опирались именно на евклидовы аксиомы. Но в XIX—XX вв., после создания Лобачевским неевклидовой геометрии, исследования системы геометрических аксиом вышли на качественно новый уровень. Одним из тех, кто внес заметный вклад в усовершенствование аксиоматики, был выдающийся украинский математик Алексей Васильевич Погорелов. В своей фундаментальной работе «Основания геометрии» (1983) он разработал собственную усовершенствованную систему аксиом евклидовой геометрии, которая решила проблему преодоления ряда существенных трудностей, возникших при введении понятия меры для отрезков и углов. Более того, А. В. Погорелов предложил упрощенный вариант геометрической аксиоматики, предназначенный именно для преподавания геометрии в школе. Этот вариант был положен в основу учебника «Геометрия», по которому свыше четверти века изучали и, без сомнения, будут изучать геометрию в школе. Вот как выглядит система аксиом школьного курса, предложенная А. В. Погореловым.
- Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.
- Из трех точек на прямой одна и только одна лежит между двумя другими.
- Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
- Прямая разбивает плоскость на две полуплоскости.
Каждый угол имеет градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на
- которые он разбивается любым лучом, проходящим между его сторонами.
- На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.
- От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
- Каков бы ни был треугольник, существует равный ему треугольник, в заданном расположении относительно данной полупрямой.
- Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Этой системы аксиом мы придерживаемся и в нашем учебнике с учетом принятой нами терминологии. Некоторые аксиомы были сформулированы в главе I, другие аксиомы не формулировались, но фактически использовались в рассуждениях. Отметим, что авторы не ставили цель представлять в этом учебнике абсолютно совершенную и логически завершенную систему аксиом, а сосредоточили основное внимание на практическом применении основных свойств простейших геометрических фигур при доказательстве теорем и решении задач. В дальнейшем, при изучении свойств фигур в пространстве, формулировки некоторых аксиом будут уточнены, а сама система аксиом — расширена.
Вообще же, система аксиом должна удовлетворять условиям независимости (не содержать аксиомы, которые можно вывести с помощью других аксиом), непротиворечивости (не иметь явных или скрытых противоречий) и полноты (содержать достаточное количество аксиом, чтобы доказать основные утверждения). Исследование проблем построения таких систем аксиом является содержанием одного из разделов современной геометрии.
Метод вспомогательного треугольника
Метод вспомогательного треугольника применяется при решении многих задач на построение. Используя этот метод, необходимо придерживаться следующей последовательности действий:
- предположив, что искомый треугольник построен, выполнить рисунок- эскиз и найти на нем вспомогательный треугольник, способ построения которого известен (или получить такой треугольник путем дополнительных построений);
- установить, какие вершины искомого треугольника мы получим, построив вспомогательный треугольник;
- определить на основании данных задачи последовательность построения других вершин, предположив, что вспомогательный треугольник построен;
- осуществить все намеченные построения;
- провести необходимые доказательства и исследования.
Довольно часто метод вспомогательного треугольника используют в сочетании с другими методами. Рассмотрим такие случаи на примерах.
Пример №21
Постройте прямоугольный треугольник по катету и сумме второго катета и гипотенузы.
Решение:
Пусть а и b + с — катет и сумма второго катета и гипотенузы треугольника ABC, который необходимо построить (рис. 194).
Анализ
Допустим, что треугольник ABC построен (рис. 195). Отложим на луче ВС отрезок CD длиной с и соединим точки А и D. Треугольник АВD прямоугольный с катетами а и b+с, то есть может быть построен по данным задачи и является вспомогательным. Построив его, получим вершины А и В искомого треугольника. Для построения вершины С воспользуемся одним из признаков равнобедренного треугольника. Точка С является точкой пересечения серединного перпендикуляра к стороне АD с лучом BD.
Построение
- 1. Построим прямой угол с вершиной В.
- 2. Отложим на сторонах этого угла отрезки АВ = а и ВD = b+с и соединим точки А и О. Треугольник АВD вспомогательный.
- 3. Построим перпендикуляр к отрезку АО. который проходит через его середину В. Пусть С — точка его пересечения с лучом ВD.
- 4. Соединим точки А и С.
Доказательство:
В треугольнике 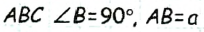
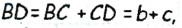
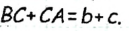
Исследование:
В соответствии с неравенством треугольника, задача имеет решение при условии a
При решении этой задачи мы использовали метод спрямления. Суть его такова: если в условии задачи на построение заданы сумма (или разность) отрезков, то на рисунке-эскизе их необходимо отложить на одной прямой от общего конца так, чтобы другие концы этих отрезков образовали заданный отрезок-сумму (разность). Благодаря такому дополнительному построению, удается получить вспомогательный треугольник.
Пример №22
Постройте треугольник по медиане и двум углам, на которые она делит угол треугольника.
Решение:
Пусть m — медиана треугольника ABC, который необходимо построить, 
Анализ
Допустим, что треугольник ABC построен (рис. 197). Применим метод удвоения медианы. Для этого на луче ВМ отложим отрезок МD, равный m, и соединим точки O и А. По первому признаку равенства треугольников 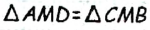
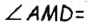
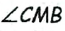
Следовательно, треугольник АВD вспомогательный, поскольку его можно построить по стороне и прилежащим к ней углам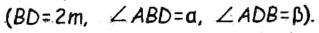
Построение (сокращенный план)
- 1. Построим треугольник АВD, в котором BD=2m
. Треугольник АВй вспомогательный.
- 2. Построим в треугольнике АВD медиану AM и на ее продолжении отложим отрезок МС, равный Am. >
- 3. Соединим точки B и С.
Доказательство
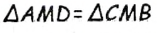
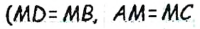
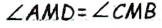
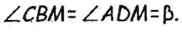
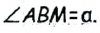
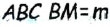
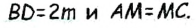
Пример №23
Постройте треугольник по стороне, медиане, проведенной к этой стороне, и высоте, опущенной на другую сторону.
Решение:
Пусть а — сторона искомого треугольника ABC, 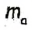
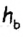
Анализ
Пусть треугольник ABC построен (рис. 199). Тогда прямоугольный треугольник ВСН можно построить по гипотенузе BC и катету ВН : на стороне прямого угла Н отложим катет BH=hb , тогда С — точка пересечения окружности с центром В радиуса а со второй стороной прямого угла.
Таким образом, мы построим вершины В и С искомого треугольника. Для построения вершины А снова используем метод геометрических мест. Поскольку основание высоты ВН принадлежит стороне АС, то точка А лежит на прямой НС. Поскольку 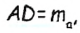
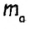
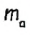
Построение
- 1. Построим прямой угол с вершиной Н.
- 2. Отложим на стороне этого угла отрезок ВН, ВН= hb.
- 3. Построим окружность с центром В радиуса а. Пусть С — точка пересечения этой окружности с другой стороной прямого угла.
- 4. Соединим точки В и С и разделим отрезок ВС пополам. Пусть точка D — его середина.
- 5. Проведем прямую СН.
- 6. Построим окружность с центром D радиуса mа. Пусть А — точка пересечения этой окружности с прямой СН.
- 7. Соединим точки А и В.
Доказательство
В треугольнике 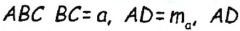
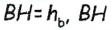
Исследование
В соответствии со следствием теоремы о сравнении сторон и углов треугольника вспомогательный треугольник существует, если hb 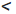
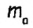
Реальная геометрия
На любой шине от автомобиля есть маркировка, указывающая на ее размеры, например, 195/55 R16 (рис. 54). Число 195 означает ширину шины в мм. В данном случае ширина шины равна 195 мм или 19,5 см.
Второе число 55 означает высоту шины или высоту ее профиля, выраженную в процентах от ее ширины. В нашем случае это 55 % от 195 мм, то есть примерно 107 мм или 10,7 см.
И наконец надпись R16 обозначает внутренний диаметр шины, выраженный в дюймах. Так как 1 дюйм 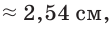
Интересно знать:
Если круг вращать около своего диаметра, получим геометрическое тело, которое вы хорошо знаете, — шар (рис. 55). Он также имеет центр, радиус, диаметр. Поверхность шара называется сферой. Сфера — это оболочка шара. Расстояние от центра шара до любой точки сферы равно радиусу шара. Диаметр шара равен двум радиусам.
Если провести плоскость, пересекающую шар, то в сечении получим круг. Когда секущая плоскость будет проходить через центр шара, радиус R полученного круга будет равен радиусу шара.
Справочный материал по окружности и кругу
18. Геометрическое место точек
- ✓ Геометрическим местом точек (ГМТ) называют множество всех точек, обладающих определенным свойством.
- ✓ Серединный перпендикуляр отрезка является геометрическим местом точек, равноудаленных от концов этого отрезка.
- ✓ Биссектриса угла является геометрическим местом точек, принадлежащих углу и равноудаленных от его сторон.
19. Окружность и круг, их элементы
- ✓ Окружностью называют геометрическое место точек, расстояния от которых до заданной точки равны данному положительному числу. Данную точку называют центром окружности.
- ✓ Любой отрезок, соединяющий точку окружности с ее центром, называют радиусом окружности.
- ✓ Отрезок, соединяющий две точки окружности, называют хордой окружности. Хорду, проходящую через центр окружности, называют диаметром.
- ✓ Диаметр окружности в два раза больше ее радиуса.
- ✓ Кругом называют геометрическое место точек, расстояния от которых до заданной точки не больше данного положительного числа. Заданную точку называют центром круга. Радиус окружности, ограничивающей круг, называют радиусом круга. Если X — произвольная точка круга с центром О и радиусом
- ✓ Окружность, ограничивающая круг, ему принадлежит.
- ✓ Хорда и диаметр круга — это хорда и диаметр окружности, ограничивающей круг.
20. Свойства окружности
- ✓ Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам.
- ✓ Диаметр окружности, который делит хорду, отличную от диаметра, пополам, перпендикулярен этой хорде.
21. Взаимное расположение прямой и окружности. Касательная к окружности
- ✓ Прямая и окружность могут не иметь общих точек, иметь две общие точки или иметь одну общую точку.
- ✓ Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности.
- ✓ Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
- ✓ Если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведенному в эту точку, то эта прямая является касательной к данной окружности.
- ✓ Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.
- ✓ Если через данную точку к окружности проведены две касательные, то отрезки касательных, соединяющие данную точку с точками касания, равны.
Описанная и вписанная окружности треугольника
Окружность называют описанной около треугольника, если она проходит через все его вершины.
На рисунке 247 изображена окружность, описанная около треугольника. В этом случае также говорят, что треугольник вписан в окружность.
- ✓ Центр описанной окружности треугольника равноудален от всех его вершин.
- ✓ Около любого треугольника можно описать окружность. Центр окружности, описанной около треугольника, — это точка пересечения серединных перпендикуляров сторон треугольника.
- ✓ Серединные перпендикуляры сторон треугольника пересекаются в одной точке.
- ✓ Окружность называют вписанной в треугольник, если она касается всех его сторон.
- ✓ На рисунке 248 изображена окружность, вписанная в треугольник. В этом случае также говорят, что треугольник описан около окружности.
- ✓ Центр вписанной окружности треугольника равноудален от всех его сторон.
- ✓ В любой треугольник можно вписать окружность. Центр окружности, вписанной в треугольник, — это точка пересечения биссектрис треугольника.
- ✓ Биссектрисы треугольника пересекаются в одной точке.
- ✓ Радиус окружности, вписанной в прямоугольный треугольник, вычисляют по формуле
где r — радиус вписанной окружности, а и b — катеты, с — гипотенуза.
Что называют окружностью
Окружностью называют геометрическую фигуру, состоящую из всех точек плоскости, равноудаленных от данной точки (рис. 282).
Эту точку называют центром окружности; отрезок, соединяющий точку окружности с ее центром, называют радиусом окружности.
На рисунке 282 точка 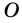
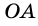
Отрезок, соединяющий две точки окружности, называют хордой. Хорду, проходящую через центр окружности, называют диаметром. На рисунке 282 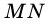
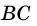
Центром, радиусом, диаметром, хордой круга называют соответственно центр, радиус, диаметр, хорду окружности, ограничивающей круг.
Свойства элементов окружности.
- Диаметр окружности вдвое больше его радиуса.
- Диаметр является наибольшей из хорд.
- Диаметр из любой точки окружности виден под прямым углом.
- Диаметр окружности, перпендикулярный хорде, делит ее пополам.
- Диаметр окружности, проходящий через середину хорды, которая не является диаметром, перпендикулярен этой хорде.
Касательной к окружности называют прямую, которая имеет с окружностью одну общую точку. Эту точку называют точкой касания.
На рисунке 284 прямая 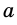
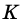
Свойство касательной. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Свойство отрезков касательных, проведенных из одной точки. Отрезки касательных, проведенных к окружности из одной точки, равны. На рисунке 285
Окружность, вписанная в треугольник
Окружность называют вписанной в треугольник, если она касается всех его сторон. При этом треугольник называют описанным около окружности (рис. 286).
В любой треугольник можно вписать окружность. Центром окружности, вписанной в треугольник, является точка пересечения биссектрис треугольника.
Окружность, описанная около треугольника
Окружность называют описанной около треугольника, если она проходит через все вершины треугольника. При этом треугольник называют вписанным в окружность (рис. 287).
Около любого треугольника можно описать окружность. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к его сторонам.
Геометрическое место точек в окружности и круге
Любое множество точек — это геометрическая фигура. Изобразить произвольную фигуру легко: все, что нарисуете, — это геометрическая фигура (рис. 272). Однако изучать фигуры, состоящие из хаотически расположенных точек, вряд ли целесообразно. Поэтому разумно выделить тот класс фигур, все точки которых обладают каким-то характерным свойством. Каждую из таких фигур называют геометрическим местом точек.
Определение. Геометрическим местом точек (ГМТ) называют множество всех точек, обладающих определенным свойством.
Образно ГМТ можно представить так: задают некоторое свойство, а потом на белой плоскости все точки, обладающие этим свойством, красят в красный цвет. Та «красная фигура», которая при этом получится, и будет ГМТ.
Например, зафиксируем две точки 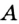
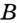
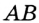
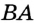
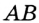
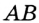
Рассмотрим перпендикулярные прямые 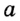
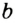
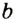
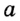
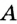
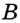
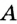
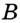
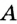
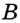
Вообще, чтобы иметь право какое-то множество точек называть ГМТ, надо доказать две взаимно обратные теоремы:
- каждая точка данного множества обладает заданным свойством;
- если точка обладает заданным свойством, то она принадлежит данному множеству.
Теорема 19.1. Серединный перпендикуляр отрезка является геометрическим местом точек, равноудаленных от концов этого отрезка.
Доказательство: По теореме 8.2 каждая точка серединного перпендикуляра обладает заданным свойством. По теореме 11.2, если точка обладает заданным свойством, то она принадлежит серединному перпендикуляру.
Теорема 19.2. Биссектриса угла является геометрическим местом точек, принадлежащих углу и равноудаленных от его сторон.
Прямая теорема. Каждая точка биссектрисы угла равноудалена от его сторон.
Доказательство: Очевидно, что вершина угла обладает доказываемым свойством.
Пусть какая-то точка 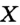
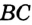
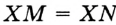
В прямоугольных треугольниках 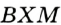
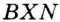
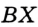
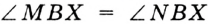
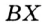
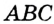
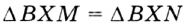

Доказательство: Очевидно, что вершина угла обладает доказываемым свойством.
Пусть какая-то точка 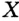
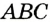
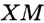
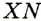
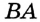
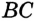
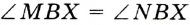
В прямоугольных треугольниках 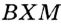
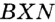
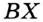
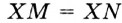
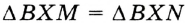
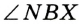
Заметим, что доказательство теоремы будет полным, если показать, что равноудаленность точки угла от его сторон исключает возможность, когда одна из точек к 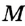
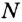
Определение. Окружностью называют геометрическое место точек, равноудаленных от заданной точки.
Заданную точку называют центром окружности. На рисунке 277 точка 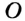
Любой отрезок, соединяющий точку окружности с ее центром, называют радиусом окружности. На рисунке 277 отрезок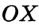
Отрезок, соединяющий две точки окружности, называют хордой окружности. На рисунке 277 отрезок 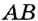
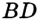
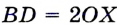
Из курса математики шестого класса вы знаете, что фигуру, ограниченную окружностью, называют кругом (рис. 278). Теперь с помощью понятия ГМТ можно дать другое
Определение. Кругом называют геометрическое место точек, расстояние от которых до заданной точки не больше данного положительного числа.
Заданную точку называют центром круга, данное число — радиусом круга. Если 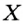
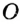
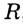
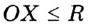
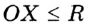
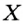
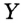
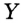
Хорда и диаметр круга — это хорда и диаметр окружности, ограничивающей круг.
Пример:
На продолжении хорды 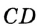
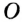
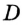
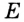
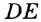
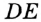
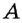
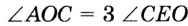
Решение:
Пусть 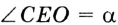
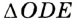
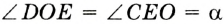
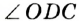
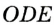
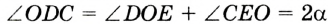
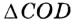
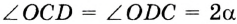
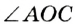
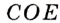
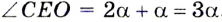
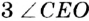
Некоторые свойства окружности. Касательная к окружности
Теорема 20.1. Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам.
Доказательство: Если хорда является диаметром, то теорема очевидна.
На рисунке 286 изображена окружность с центром 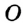
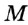
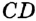
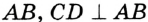
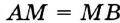
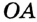
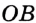
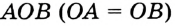
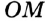
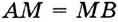
Теорема 20.2. Диаметр окружности, делящий хорду, отличную от диаметра, пополам, перпендикулярен этой хорде.
Докажите эту теорему самостоятельно. Подумайте, будет ли верным это утверждение, если хорда является диаметром.
На рисунке 287 изображены прямая и окружность, которые на рисунке 287, а не имеют общих точек, на рисунке 287, б имеют две общие точки, на рисунке 287, в — одну.
Определение. Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности.
Очевидно, что касательная к окружности имеет только одну общую точку с кругом, ограниченным этой окружностью. На рисунке 287, в прямая 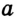
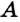
Если отрезок (луч) принадлежит касательной к окружности и имеет с этой окружностью общую точку, то говорят, что отрезок (луч) касается окружности. Например, на рисунке 288 изображен отрезок 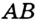
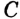
Теорема 20.3 (свойство касательной). Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Доказательство: На рисунке 289 изображена окружность с центром 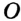
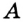
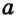
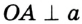
Предположим, что это не так, то есть 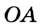
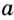
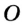
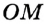
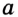
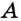
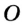
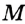
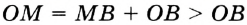
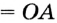
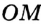
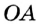
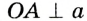
Теорема 20.4 (признак касательной к окружности). Если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведенному в эту точку, то эта прямая является касательной к данной окружности.
Доказательство: На рисунке 290 изображена окружность с центром в точке 
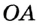
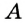
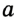
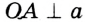
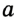
Пусть прямая 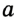
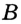
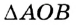
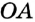
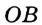
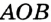
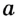
Часто при решении целого класса задач используют результат следующей задачи.
Пример:
Если из данной точки к окружности проведены две касательные, то отрезки касательных, соединяющих данную точку с точками касания, равны.
Решение:
На рисунке 292 изображена окружность с центром 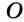
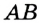
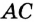
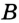
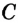
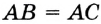
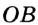
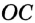
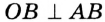
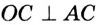
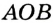
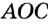
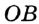
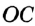
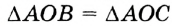
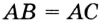
- Описанные и вписанные окружности
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
- Сравнение и измерение отрезков и углов
- Решение треугольников
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
На этой странице вы узнаете
- Где в ловце снов спрятана хорда?
- В чем отличие окружности от пиццы?
- Почему если мы хотим что-то сильно поменять, то лучше разворачивать жизнь на 180 градусов, а не на 360?
Оглянитесь вокруг: геометрические фигуры окружают нас повсюду, а в математике и вовсе встречаются почти в каждом задании. Не стали исключением и окружность и круг, которые попадают в задачки чаще, чем может показаться. Поэтому эта статья будет полезна: овладеете всеми премудростями, необходимыми для жизни и экзаменов.
Обруч и окружность
Давайте вспомним один из предметов инвентаря художественной гимнастики – обруч. Это узкое кольцо большого диаметра, внутри которого ничего нет. Обруч состоит только из “контура”, то есть из того самого кольца. Именно с помощью обруча мы приближаемся к термину “окружность”.

Окружность – это замкнутая кривая, все точки которой равноудалены от центра.
Разберем чуть подробнее, что значит фраза “равноудалены от центра”. Допустим, мы точно знаем, где центр нашего обруча, и через этот центр натянем много-много ленточек. Тогда окажется, что длина каждой ленточки от центра до обруча будет одинаковой.
То есть окружность состоит из бесконечного множества точек, которые располагаются на равном расстоянии от центра.
Элементы окружности
Радиус – это отрезок, построенный от центра окружности до любой точки на окружности.
Если вспомнить обруч с ленточками, то одна ленточка – это радиус. Радиус обозначается буквой R. В окружности можно построить множество радиусов, и все они будут равны между собой.
Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности.
Можно сразу заметить, что диаметр будет состоять из двух радиусов, которые проведены по разные стороны от центра окружности.
Диаметр обозначается буквой D и равняется двум радиусам.
D = 2R
Хорда – это отрезок, соединяющий две любые точки на окружности. При этом хорда не обязательно проходит через центр окружности.
Представим ловец снов. Когда его изготавливают, натягивают нитку от точки на ободе до точки на другом конце обода. Чтобы получился красивый узор, нитки должны быть разной длины и проходить через разные точки – не обязательно через центр.
Получается, каждая ниточка внутри ловца слов будет хордой.
Таким образом, хорда может иметь любой размер и любое направление, главное, чтобы ее начало и конец лежали на окружности.
Рассмотрим свойства хорды.
1 свойство. При пересечении двух хорд произведения их отрезков равны.
Пусть в окружности проведены хорды АВ и CD, которые пересекаются в точке О. Тогда выполняется равенство АО * ОВ = СО * OD.
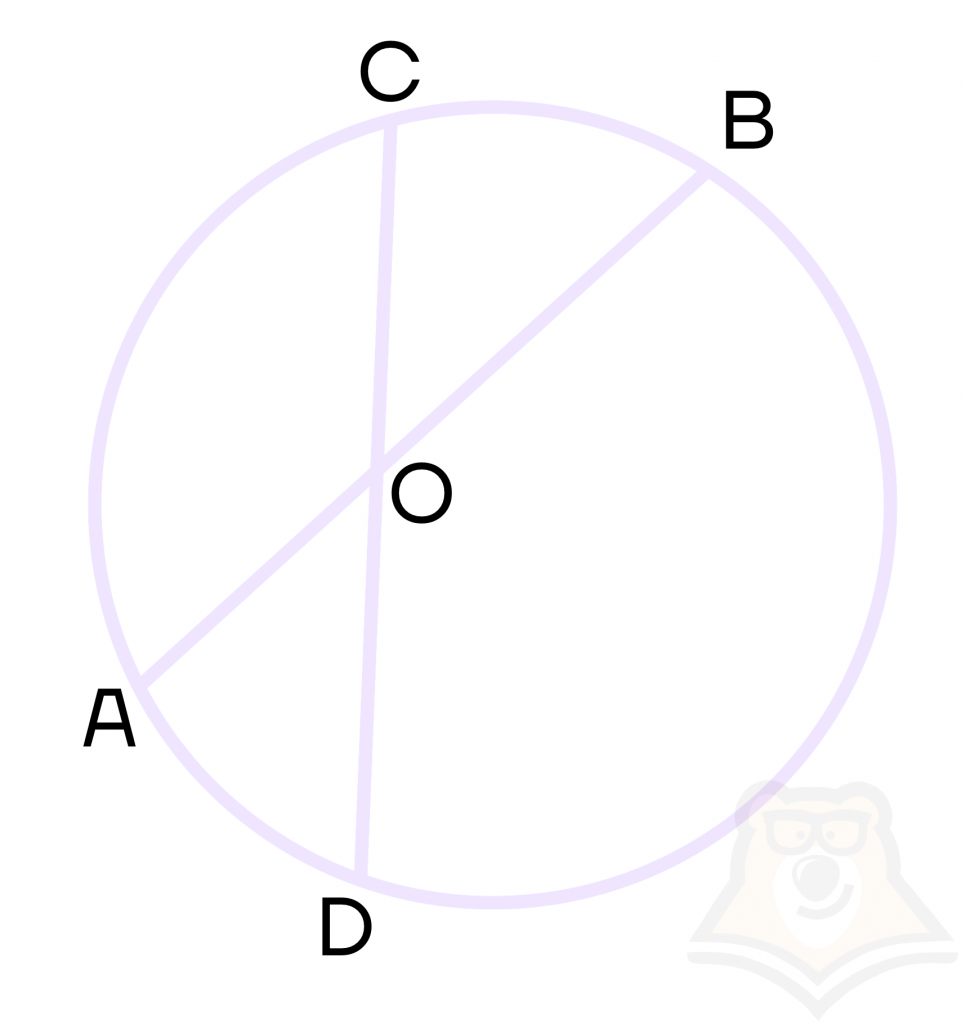
2 свойство. Равные хорды стягивают равные дуги.
3 свойство. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ей дуги пополам.
Если диаметр CD перпендикулярен хорде АВ, то АЕ = ЕВ.
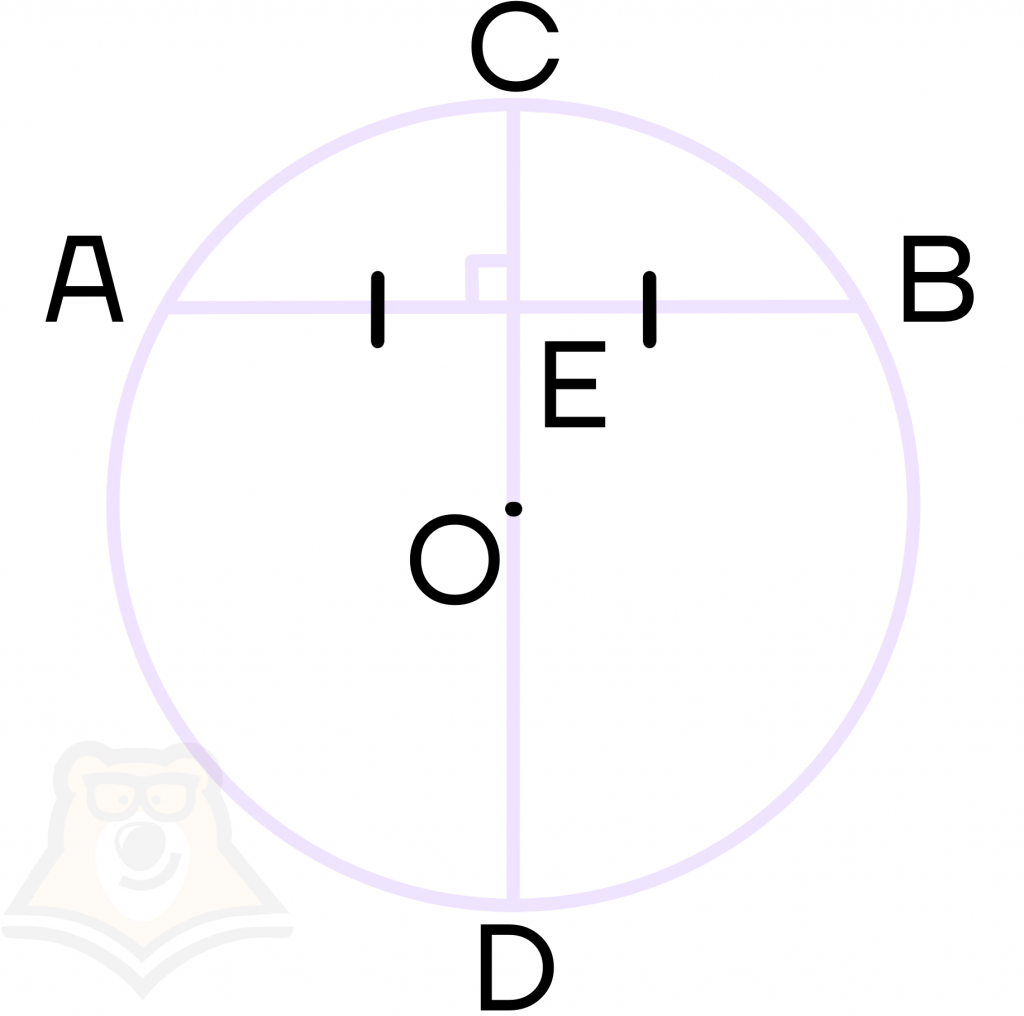
Рассмотрим, почему выполняется это свойство. Достроим треугольник АОВ, в котором АО и ОВ – радиусы. Радиусы в окружности равны, следовательно, треугольник равнобедренный.
Рассмотрим ОЕ – высота в равнобедренном треугольнике, проведенная к основанию.
Высота в равнобедренном треугольнике, проведенная к основанию, совпадает с медианой и биссектрисой, следовательно, ОЕ – медиана, а значит АЕ = ЕВ.
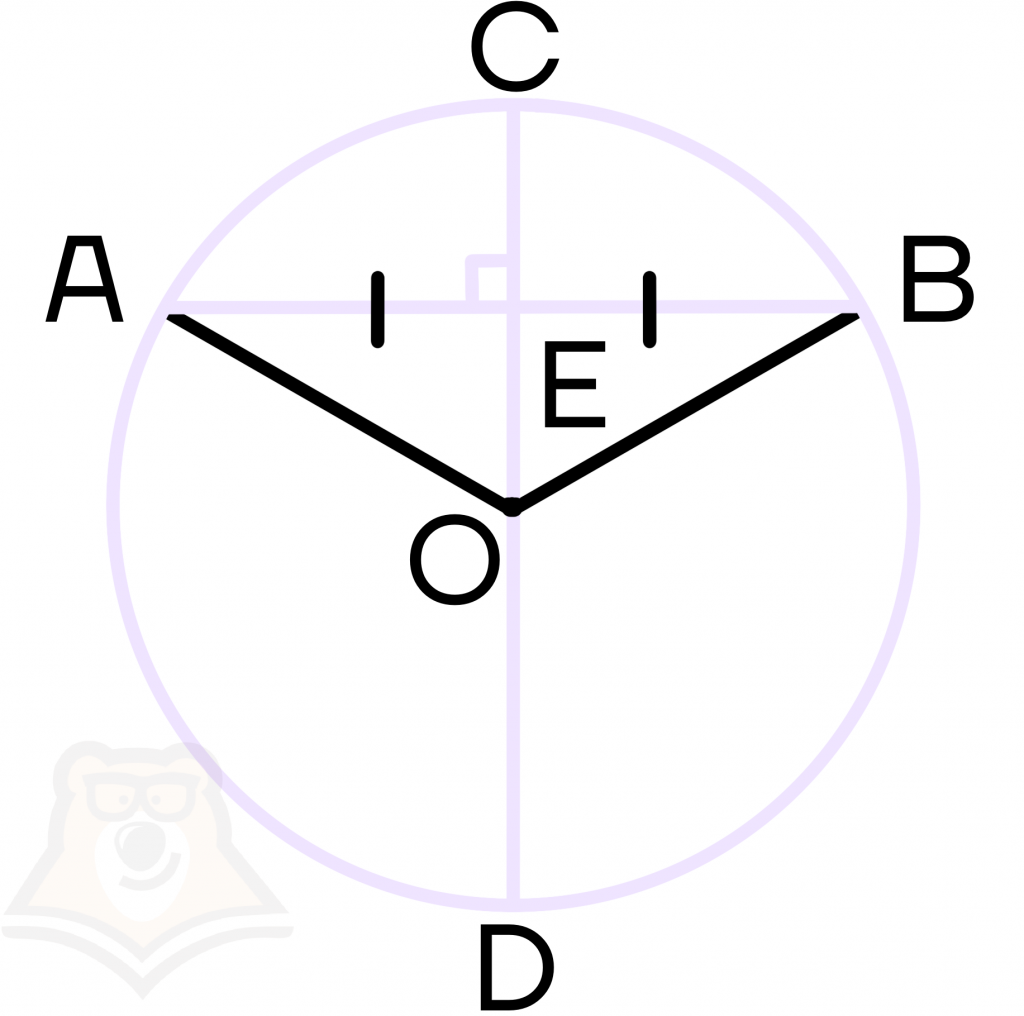
Дуга – это часть окружности, началом и концом которой являются две произвольные точки.
Допустим, из нашего обруча вырежут какую-то часть. Тогда и вырезанная часть, и оставшаяся часть будут дугами.
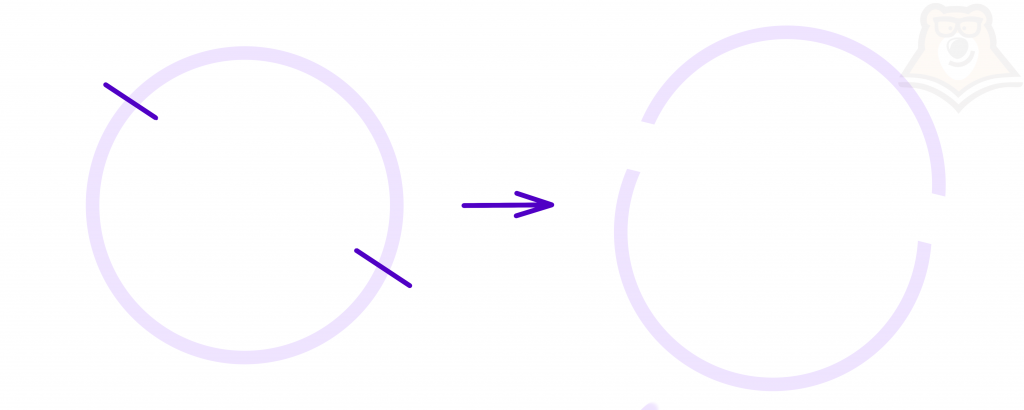
Пицца и круг
Мы рассмотрели окружность. Тут уже может возникнуть вопрос: чем круг отличается от окружности?
Представим пиццу. Она круглой формы? Да. Похожа она на обруч? Нет. И пицца, и обруч имеют форму круга. Разница в том, что обруч внутри полый, а пицца полностью состоит из теста и начинки. Иными словами, в пицце есть не только контур в виде корочки, но и все, что лежит внутри него.
Когда окружность внутри заполнена “начинкой” – это уже круг.

Круг – это геометрическая фигура, которая ограничена окружностью.
Элементы круга
Рассмотрим элементы круга.
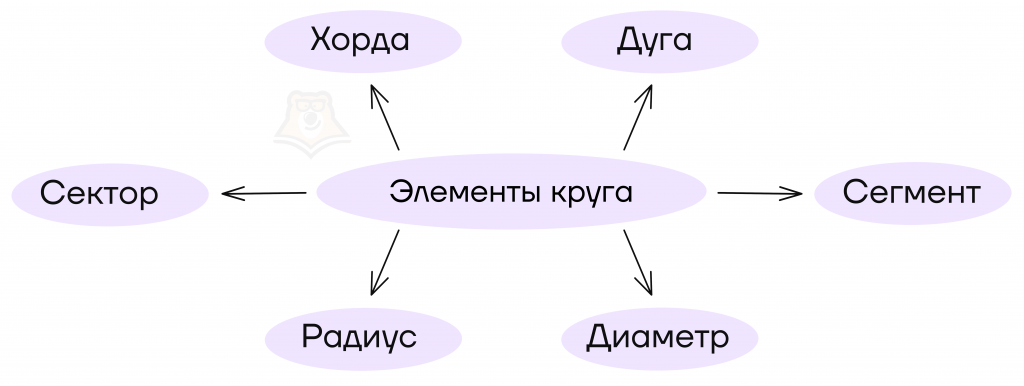
Радиус, диаметр хорды в круге имеют такие же определения, как и в окружности. Поскольку мы теперь рассматриваем не только контур, а всю фигуру, то появляются новые элементы.
Предположим, к нам в гости пришли друзья, и теперь нужно разделить пиццу между всеми. Разумеется, мы разрежем ее на несколько кусочков.

Форма кусочков пиццы очень напоминает сектор круга.
Сектор – это часть круга, которую ограничивают радиусы и дуга.
При этом два радиуса делят круг на два сектора: один больший, а другой меньший. На рисунке один из них закрашен фиолетовым, а другой белым.
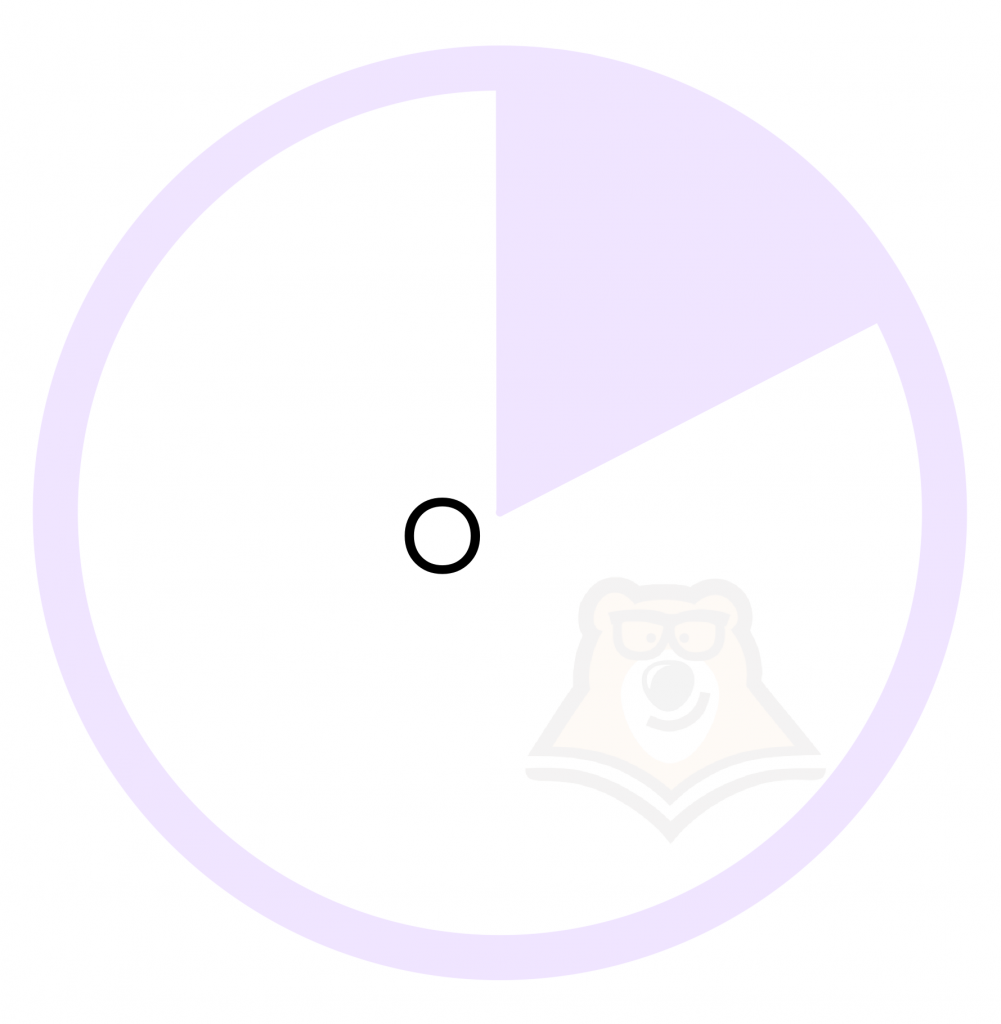
Если мы захотим отрезать только один кусочек пиццы, то и отрезанный кусочек, и оставшаяся пицца будут секторами круга.

Теперь разрежем пиццу иначе. Отрежем кусочек по прямой, не проходя через ее середину:
Таким образом, мы отрежем уже не сектор, а сегмент от пиццы.
Сегмент – это часть круга, которая ограничена хордой и дугой.
Причем одна хорда является границей для двух сегментов: и отрезанный кусочек пиццы, и оставшаяся часть будут сегментами. На рисунке ниже один сегмент закрашен фиолетовым, а другой белым.
Подведем итог:
И в окружности, и в круге можно встретить радиус, диаметр, хорду и дугу. В круге дополнительно появляются сектор и сегмент.
Формулы для окружности и круга
Мы рассмотрели окружности и круг, а также их элементы, однако ни одну задачу не получится решить без формул. Давайте рассмотрим их.
Однако перед этим необходимо ввести еще несколько терминов.
Длина окружности – это длина кривой, которая образует окружности.
Если мы с помощью сантиметровой ленты измерим длину нашего обруча, то как раз получим длину окружности.
Длина дуги – это длина части кривой, которая образует окружность.
Отличие от длины окружности только в том, что тут измеряется не вся кривая, а только ее часть.
В таблице ниже приведены основные формулы, которые могут встретиться при решении задач.
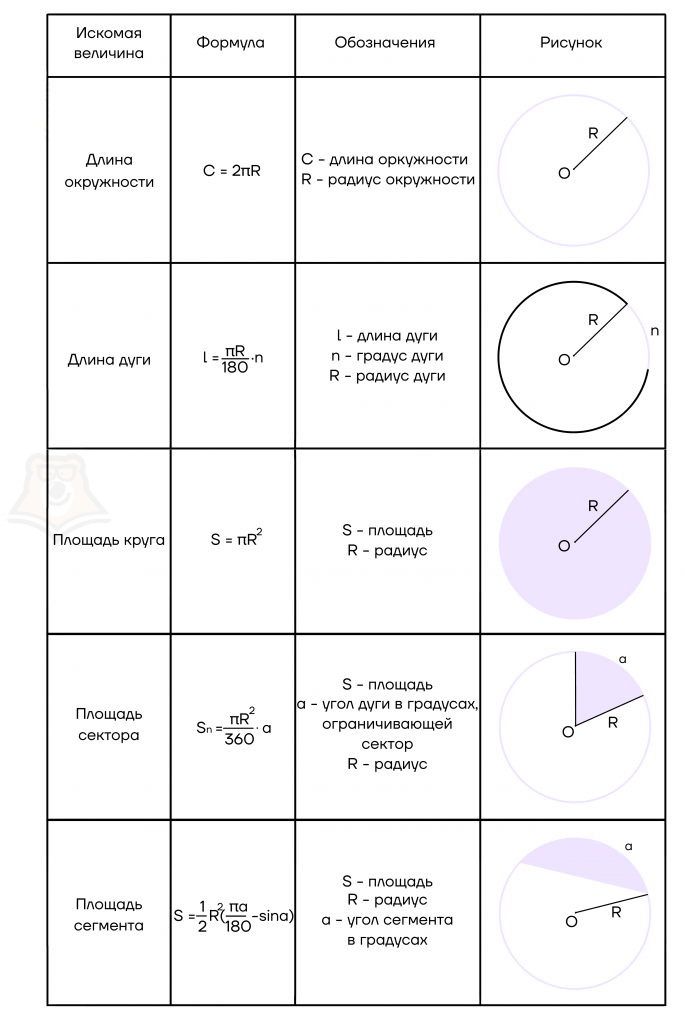
Дуга окружности
Дугу можно измерять не только в единицах измерения длины, но и в градусах. Вся дуга окружности имеет градусную меру 360(circ). Тогда половина дуги окружности будет равняться 180.
При этом дуга, равная 180(circ), называется полуокружностью. Полуокружность ограничивается двумя концами диаметра.
Думаем, хоть раз в жизни вы слышали фразу “повернуться на 180(circ) градусов” или “поменять свое мнение на 180(circ) градусов”. Это означает, что человек меняет свое мнение буквально на противоположное. Рассмотрим на примере окружности: пусть человек стоит в точке А. Ему нужно пройти по окружности ровно 180(circ).
Поскольку человеку нужно пройти полуокружность, то она ограничивается диаметром. Достроим диаметр АВ, тогда наш человек окажется в точке В, то есть на противоположной стороне окружности.
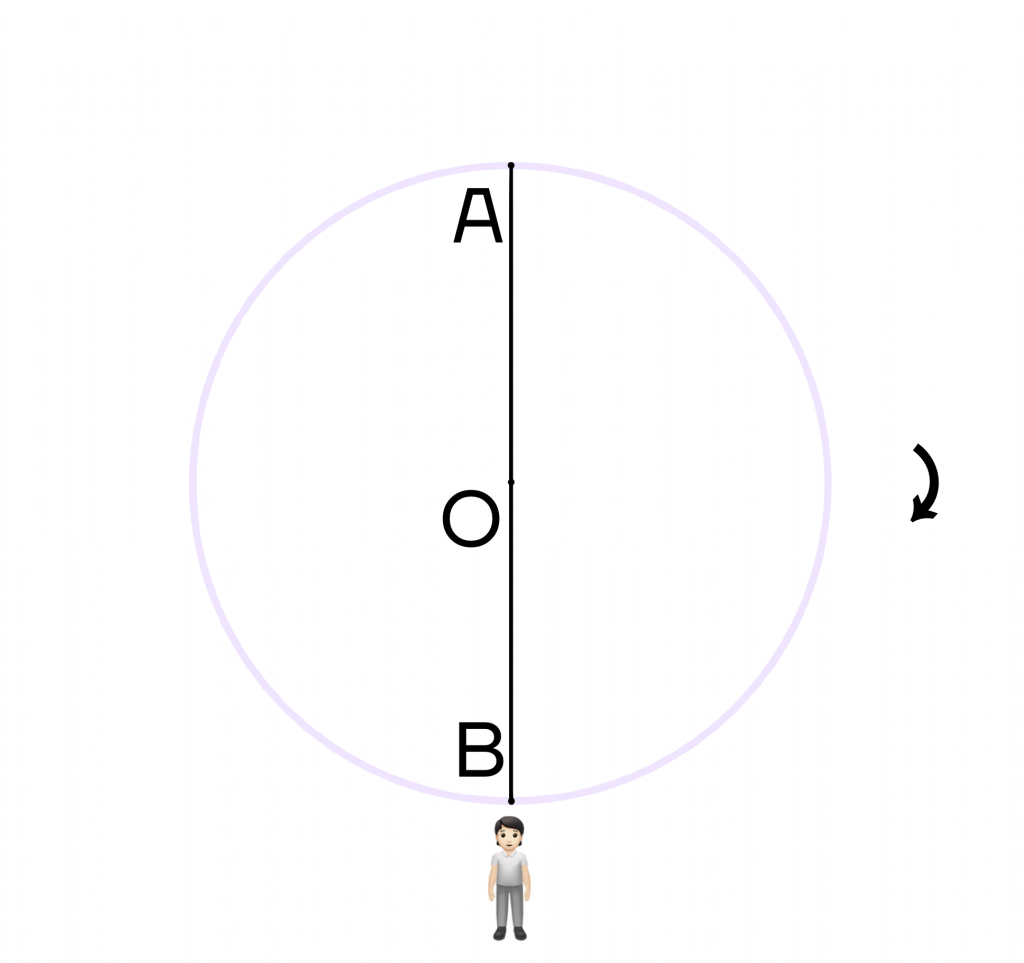
А если он дважды пройдет полуокружность, то снова окажется в точке А, то есть пройдет дугу в 2 * 180 = 360 градусов.
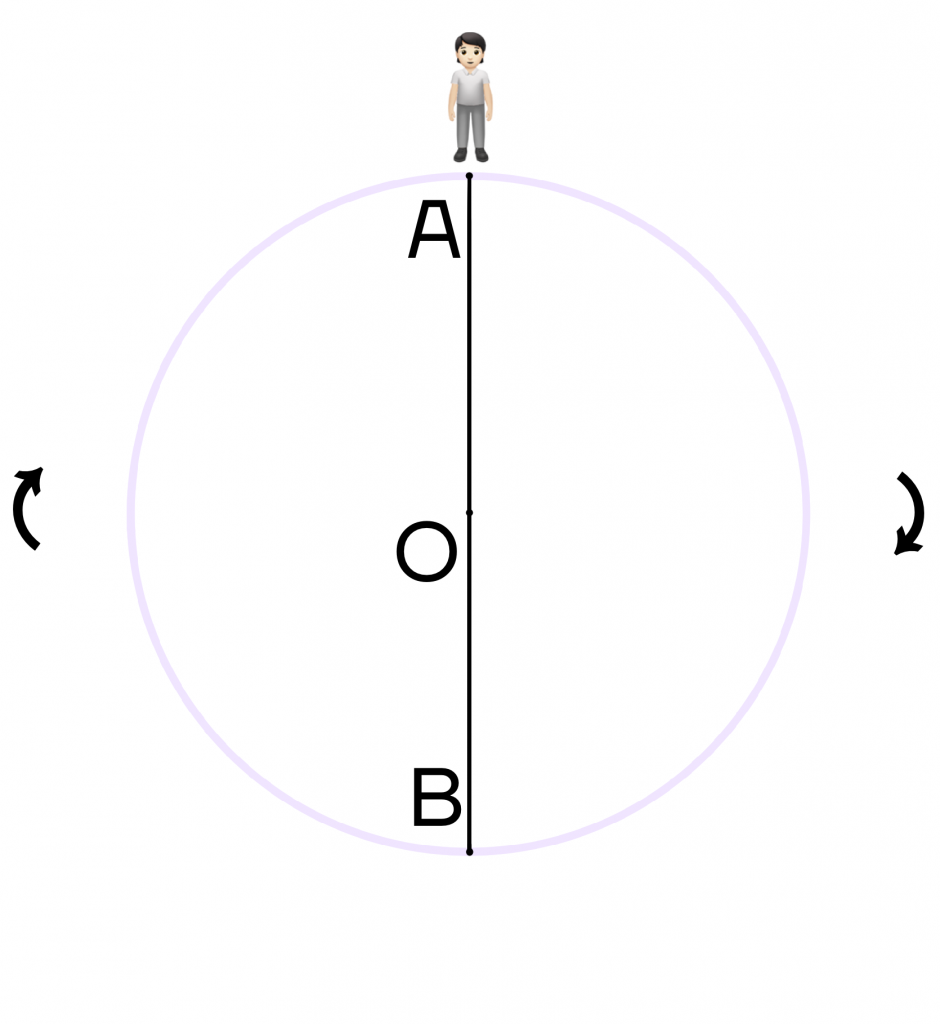
Поэтому если человек будет находиться в точке О и захочет повернуться на 180 градусов, то вместо точки А он будет смотреть на точку В. При повороте на 360 градусов, человек снова будет смотреть на точку А.
При повороте на 180 градусов, мы смотрим на что-то с совершенно противоположной стороны. А вот если повернуться на 360 градусов, то мы будем смотреть на ту же точку, на которую смотрели изначально.
Углы в окружности
Центральный угол – это угол, вершина которого лежит в центре окружности. При этом угол опирается на дугу окружности.
На рисунке угол АОВ будет центральным.
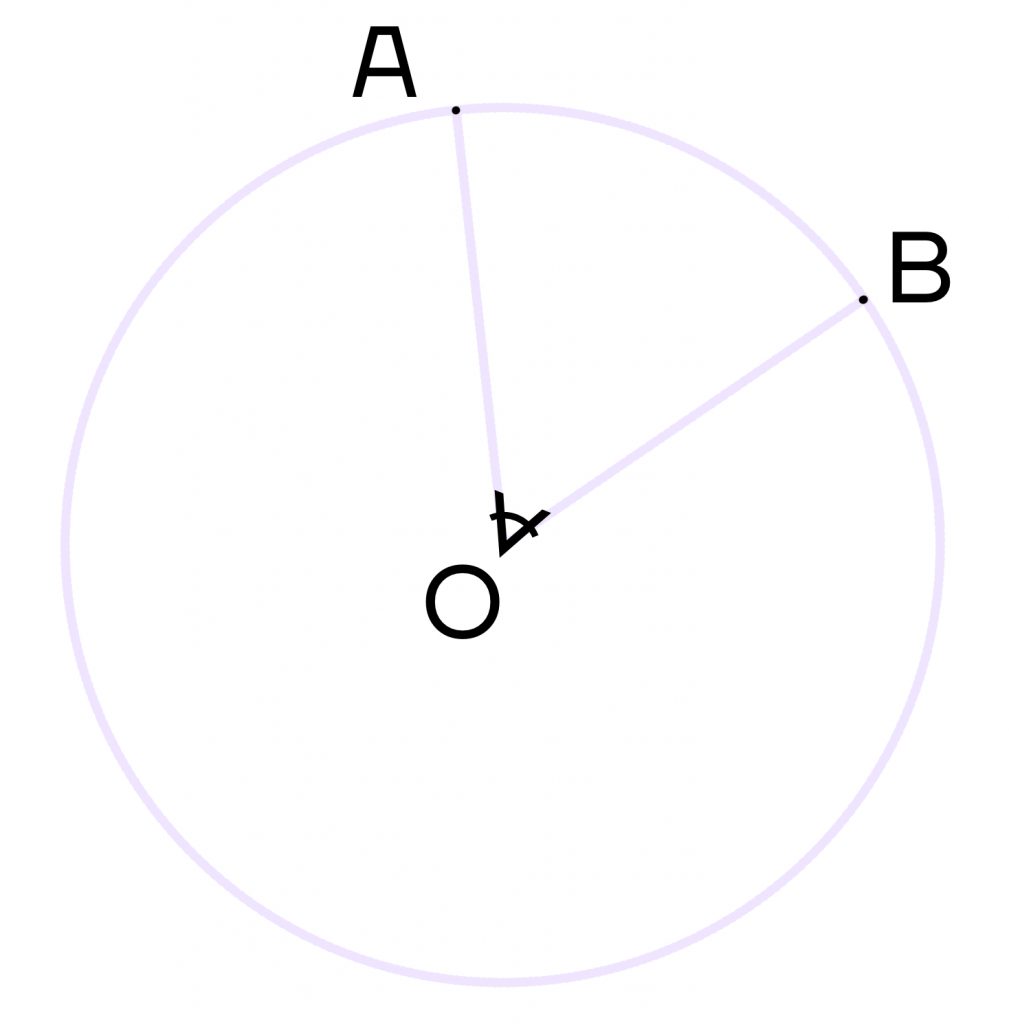
Свойство центрального угла:
- Центральный угол равен градусной мере дуги, на которую он опирается.
Например, дуга АВ равна 36(circ), тогда угол АОВ также равен 36(circ).
Вписанный угол – это угол, вершина которого лежит на окружности. Вписанный угол также должен опираться на дугу окружности.
На рисунке угол АСВ – вписанный.
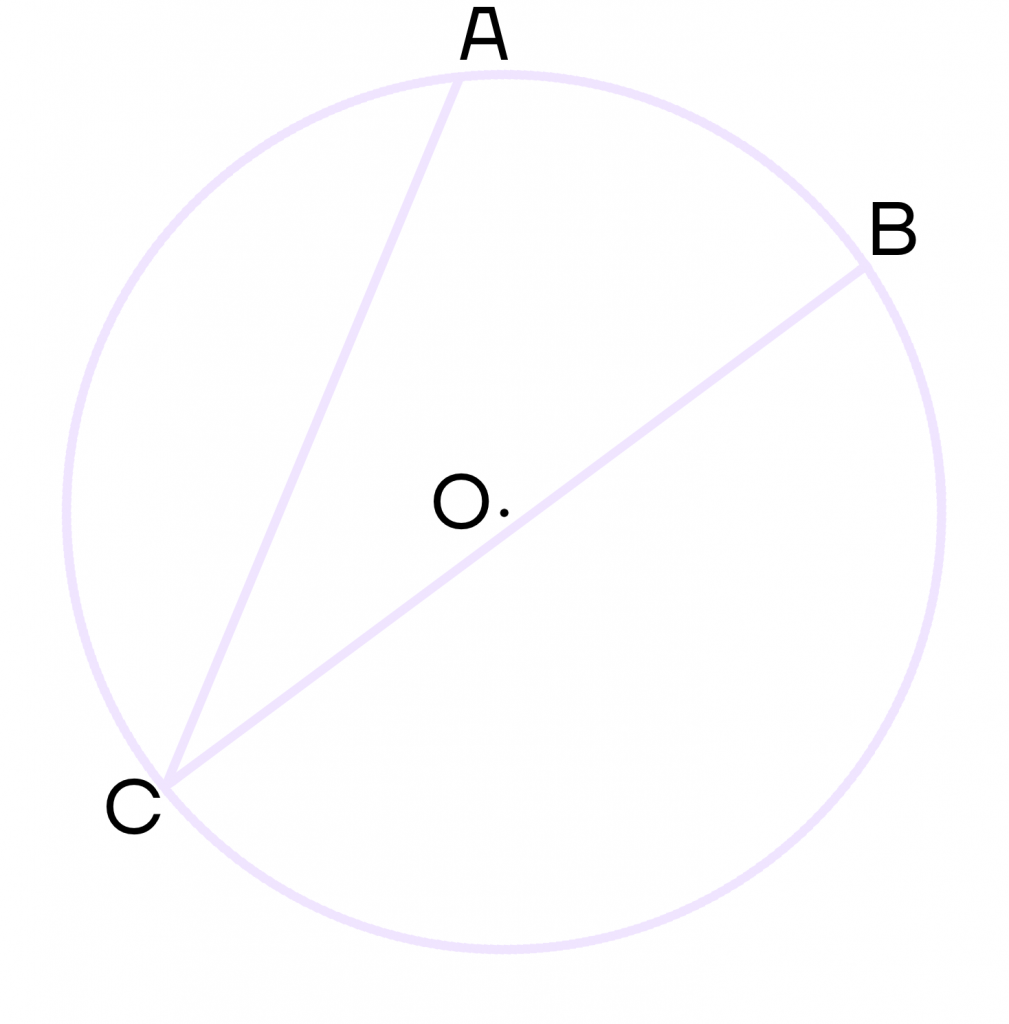
Свойства вписанного угла окружности:
- Вписанный угол равен половине градусной меры дуги, на которую он опирается.
Например, дуга АВ равна 50(circ), тогда угол АСВ равен 25(circ).
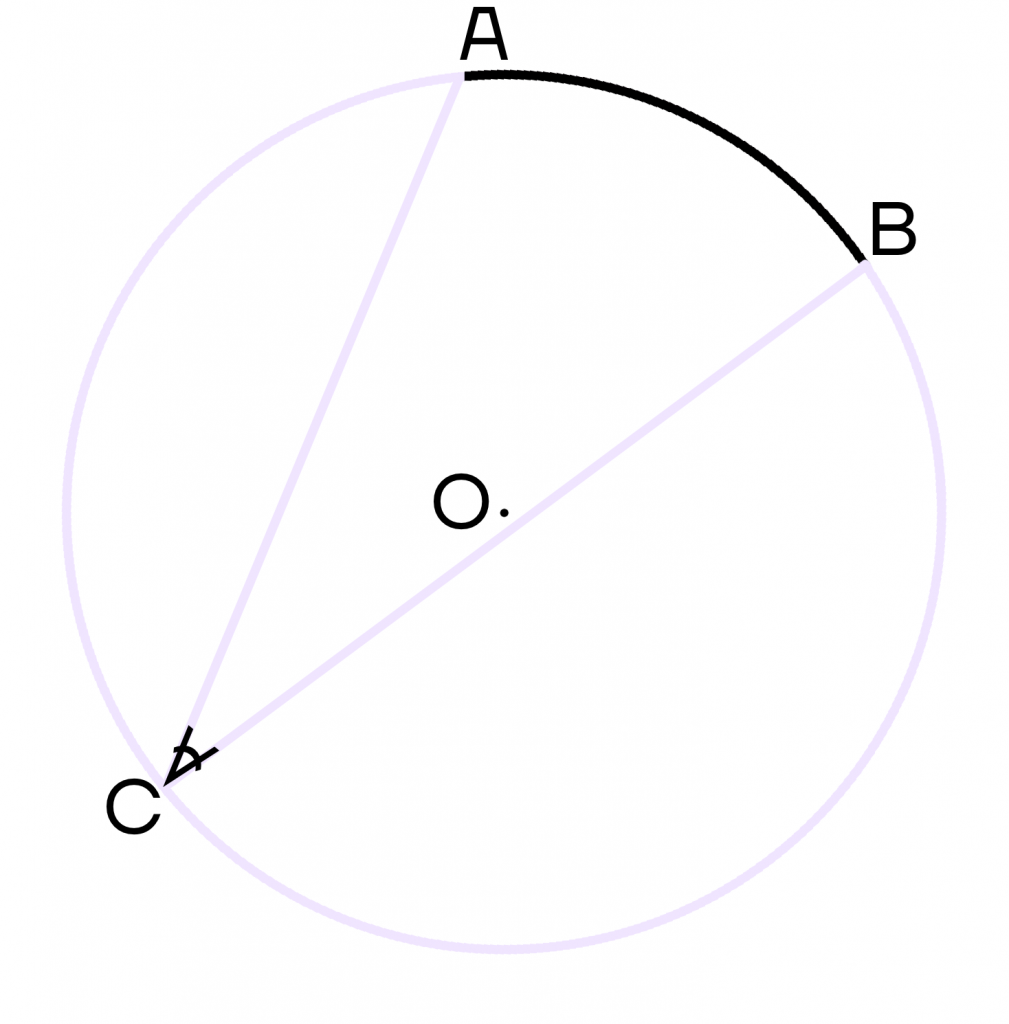
- Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Пусть углы АСВ, АЕВ и АКВ опираются на душу АВ. Тогда эти углы будут равны между собой.
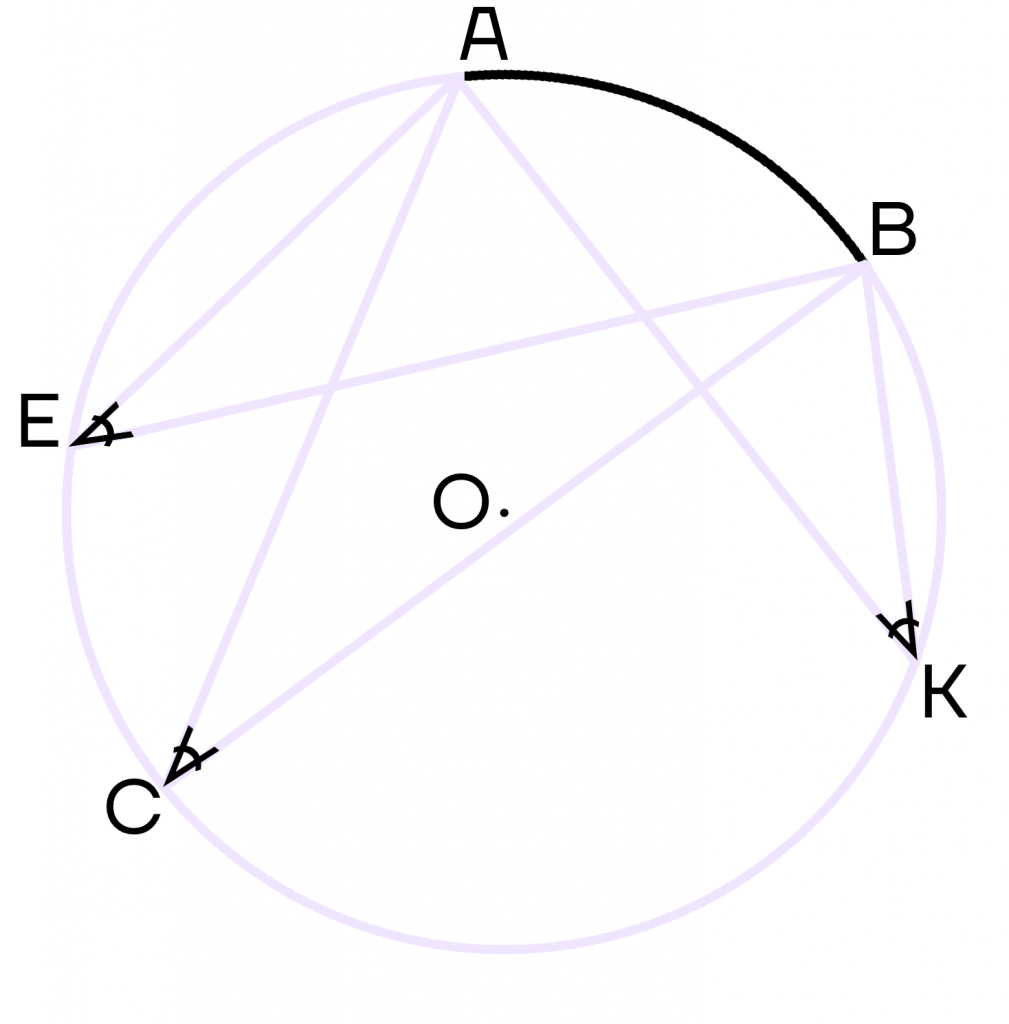
- Вписанный угол, опирающийся на диаметр, равен 90(circ).
Вспомним, что диаметр делит окружность на две полуокружности, градусные меры которых равны 180(circ). Тогда вписанный угол будет равняться 180(circ) : 2 = 90(circ).
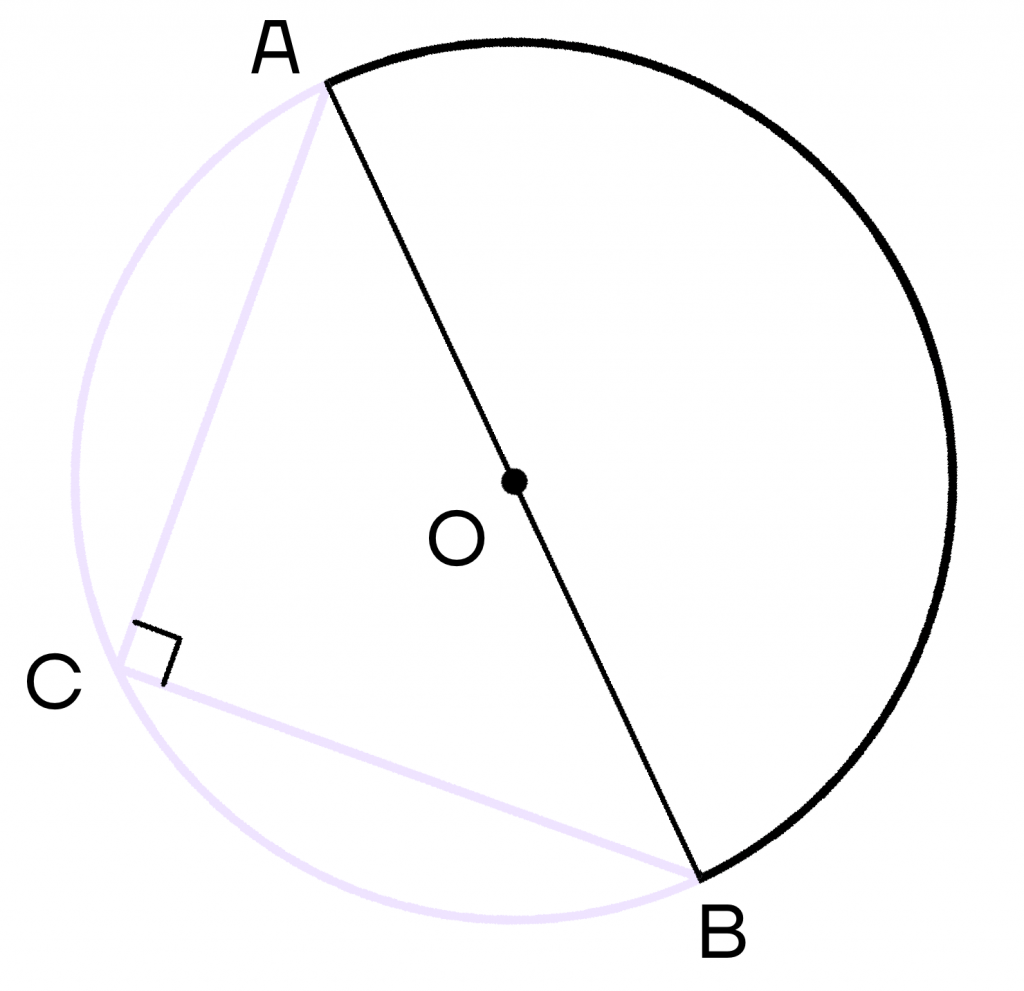
Также важно заметить, что вписанный угол равен половине центрального угла. При этом данные углы обязательно должны опираться на одну дугу.
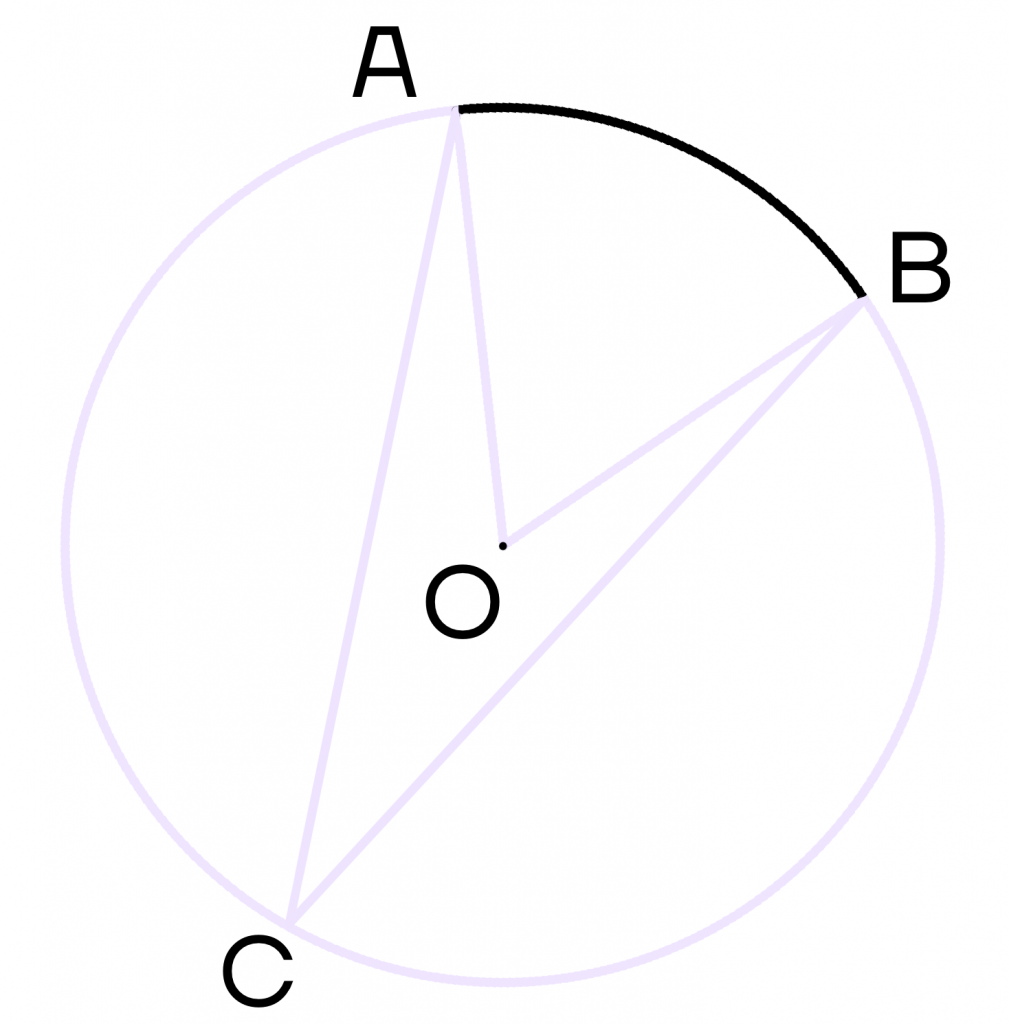
Это легко доказать, если вспомнить, что:
- центральный угол равен градусной мере дуги, на которую он опирается,
- вписанный угол равен половине градусной меры дуги, на которую он опирается.
Следовательно, (∠ACB = frac{1}{2}∠AOB).
Фактчек
- Окружность – это замкнутая кривая, все точки которой равноудалены от центра. Элементами окружности являются радиус, диаметр, хорда, дуга.
- Круг – это геометрическая фигура, которая ограничена окружностью. Помимо радиуса, диаметра и хорды, в круге может встретиться сегмент и сектор.
- Вся дуга окружности имеет величину 360 градусов. Тогда половина дуги будет равняться 180 градусам.
- В окружности встречаются центральные и вписанные углы. При этом вписанный угол равен половине дуги, на которую он опирается, а центральный угол равен градусной мере дуги, на которую он опирается. Как следствие, если центральный и вписанный углы опираются на одну дугу, то центральный угол равен двум вписанным углам.
Проверь себя
Задание 1.
Что такое окружность?
- Замкнутая кривая, все точки которой равноудалены от центра;
- Геометрическая фигура, которая ограничена замкнутой кривой, все точки которой равноудалены от центра;
- Геометрическая фигура, которая имеет круглую форму;
- Часть плоскости, ограниченная замкнутой кривой, все точки которой равноудалены от центра.
Задание 2.
Что такое диаметр окружности?
- Это отрезок, соединяющий центр окружности и любую точку на окружности;
- Это отрезок, соединяющий две произвольные точки на окружности;
- Это отрезок, соединяющий две точки на окружности и проведенный через центр окружности;
- Это половина дуги окружности.
Задание 3.
По какой формуле можно найти длину окружности?
- (l = frac{R}{180} * n)
- (C=2 pi R)
- C=2R
- (l = pi R)
Задание 4.
На окружности выделили дугу в 60 градусов. Какую часть от всей окружности занимает эта дуга?
- (frac{1}{2})
- (frac{1}{3})
- (frac{1}{6})
- (frac{1}{4})
Задание 5.
Вписанный угол равен 50 градусов. Чему равен центральный угол, опирающийся на ту же дугу?
- 200
- 50
- 100
- 150
Ответы: 1. – 1 2. – 3 3. – 2 4. – 3 5. – 3
Информация по назначению калькулятора
В евклидовой геометрии круг – это множество всех точек на плоскости на фиксированном расстоянии, называемом радиусом, от заданной точки, центра. Длина круга называется его окружностью, а любая непрерывная часть окружности называется дугой.
Окружность – это простая замкнутая кривая, которая делит плоскость на внутреннюю и внешнюю. Внутренняя часть круга называется диском. Математически круг можно понимать и несколькими другими способами. Например, это частный случай эллипса, в котором два фокуса совпадают (то есть они являются одной и той же точкой). Альтернативно, окружность можно рассматривать как коническое сечение, достигаемое, когда прямой круговой конус пересекается плоскостью, перпендикулярной оси конуса.
Число π (ПИ) равно 3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375…
Все круги обладают одинаковыми свойствами. Некоторые из них отмечены далее:
⇒ Для любого круга заключенная площадь и квадрат его радиуса находятся в фиксированной пропорции, равной математической константе π (ПИ).
⇒ Для любого круга длина окружности и радиус находятся в фиксированной пропорции, равной 2π.
⇒ Круг – это фигура с наибольшей площадью для заданной длины периметра.
⇒ Круг имеет очень симметричную форму. Каждая линия, проходящая через центр, образует линию симметрии отражения. Кроме того, существует вращательная симметрия вокруг центра для каждого угла.
⇒ Окружность с центром в начале координат радиусом 1 называется единичной окружностью.
Онлайн калькулятор поможет найти параметры круга, такие как:
- Диаметр
- Радиус
- Длина окружности
- Площадь
– равен двум радиусам или длине окружности поделенной на число π (d=r*2=P/π)
– равен половине диаметра или длине окружности поделенной на 2π (r=d/2=P/2π)
– (или периметр круга) равна диаметру умноженному на число π (P=d*π=2π*r)
– равна радиусу в квадрате умноженному на число π (S=πr2=¼πd2)
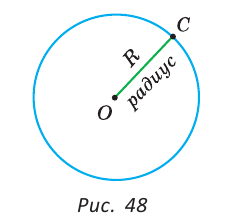
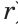
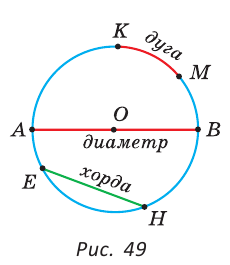
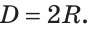
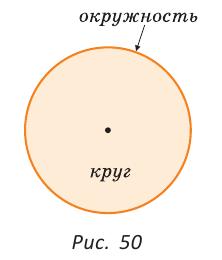
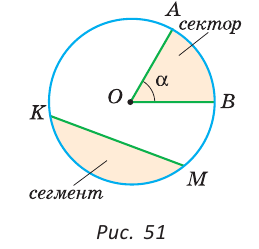
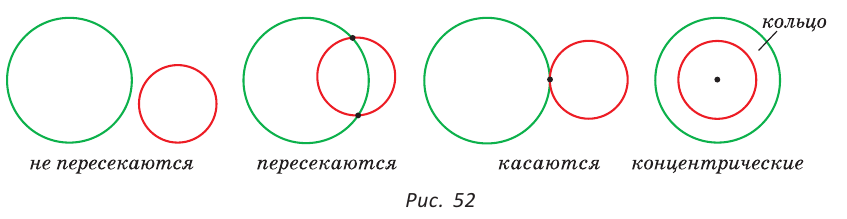
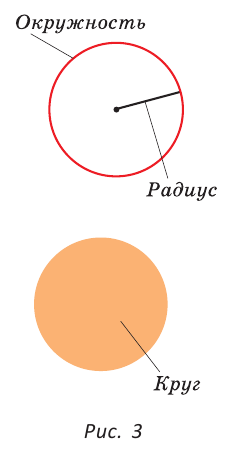

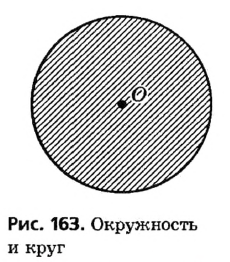
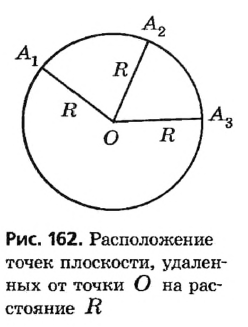
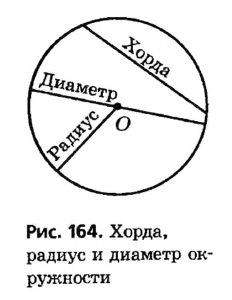
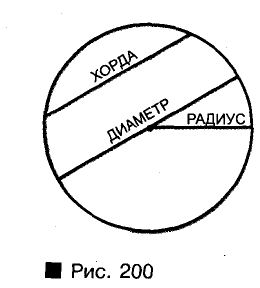
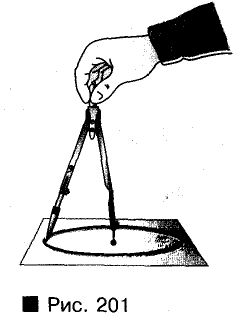
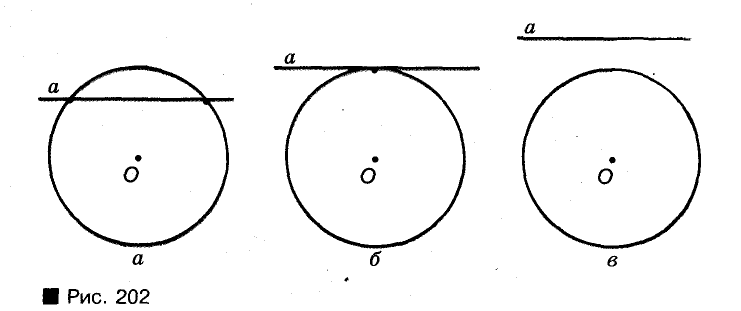
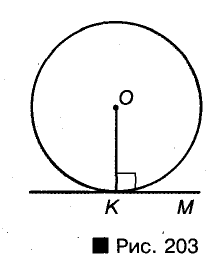
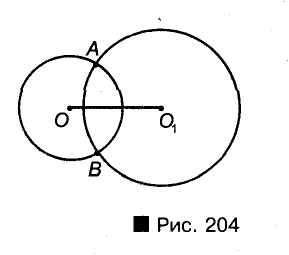
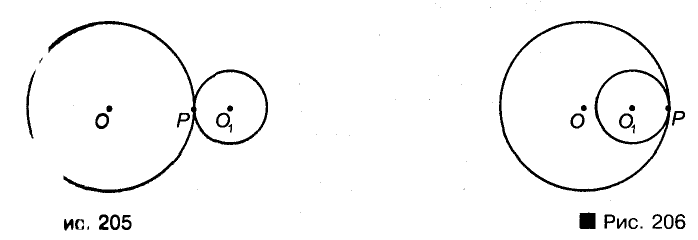
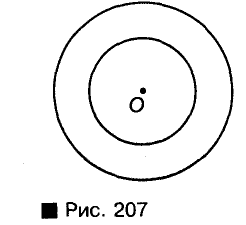
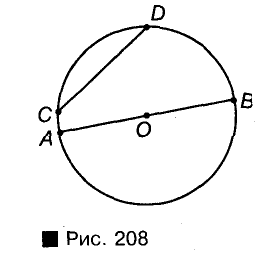
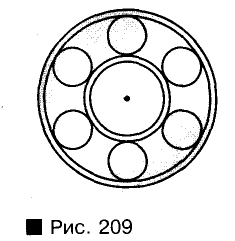
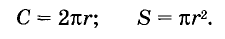
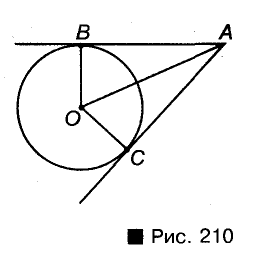
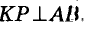
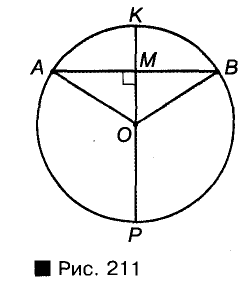
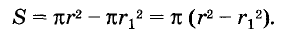
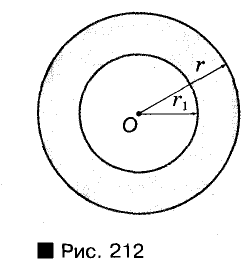
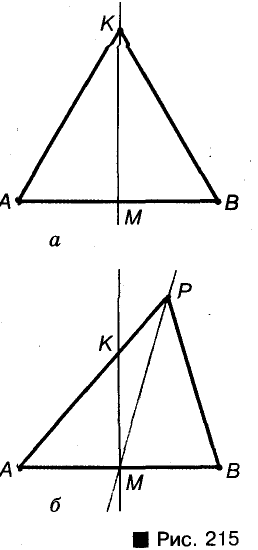
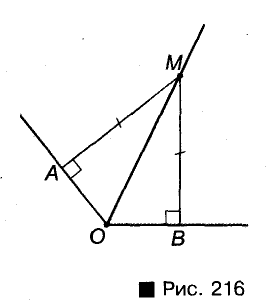
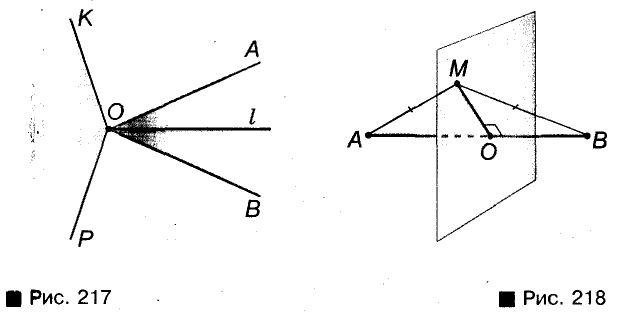
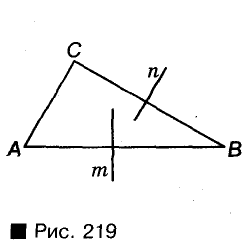
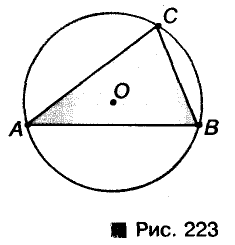

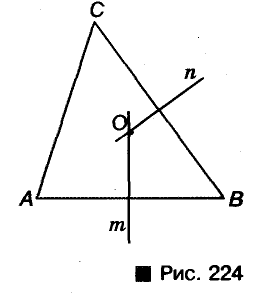
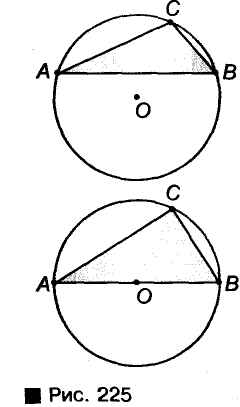
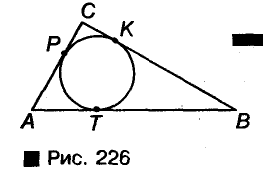

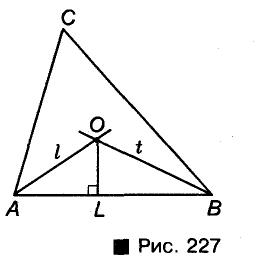
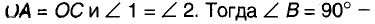
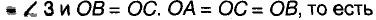
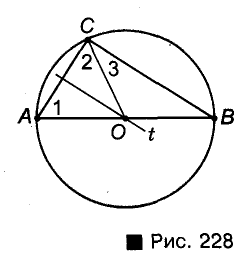
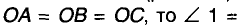
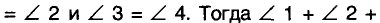
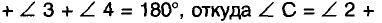
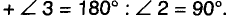
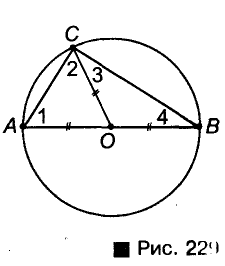
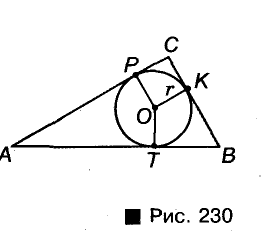
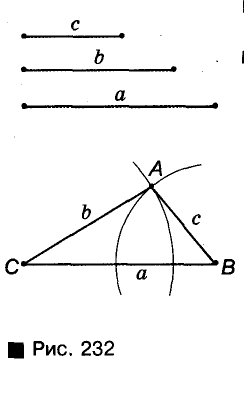
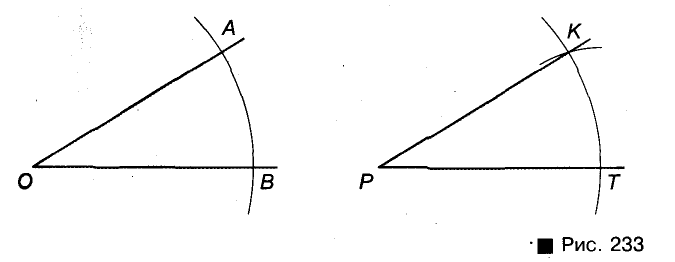
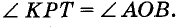
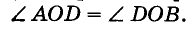
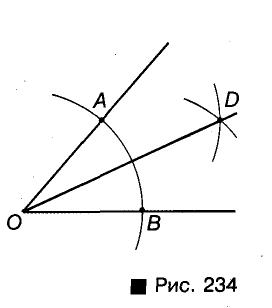
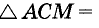
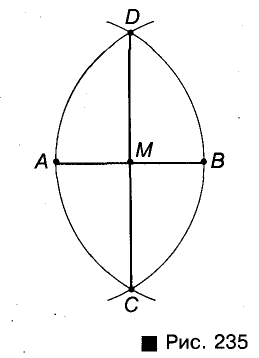
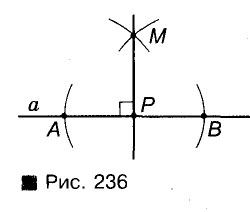
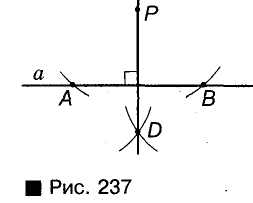
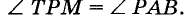
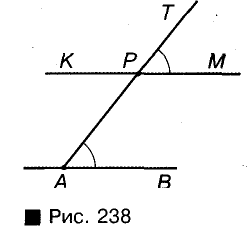
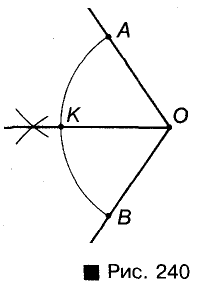
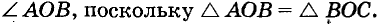
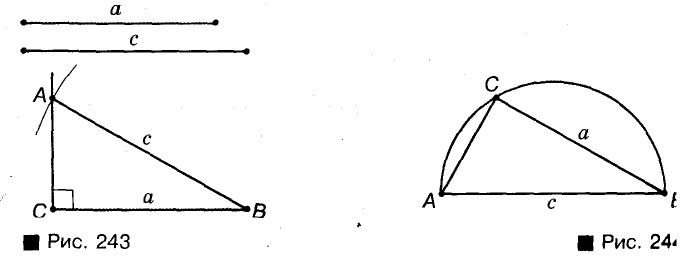
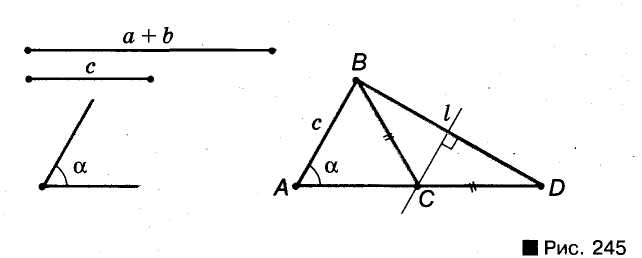
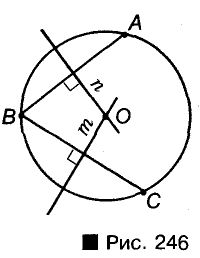
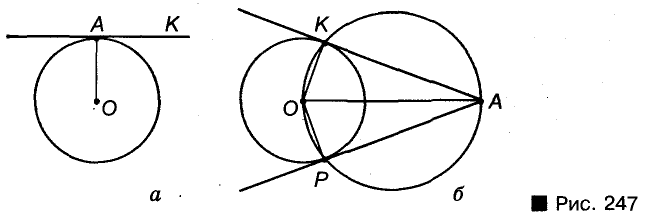
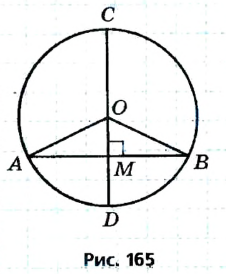
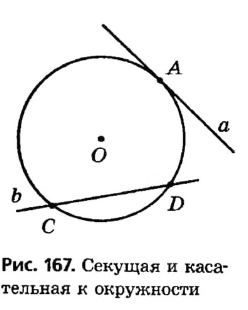
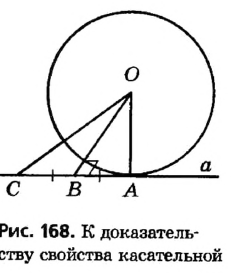
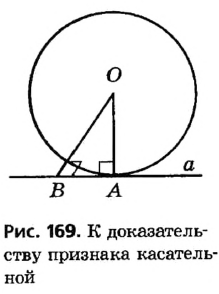
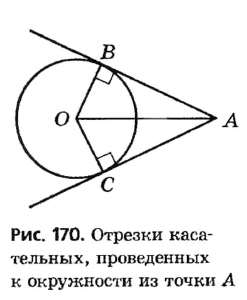
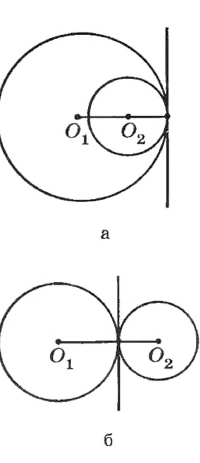
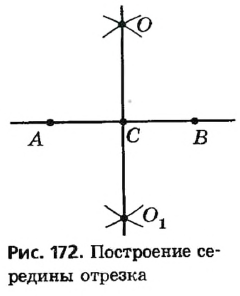
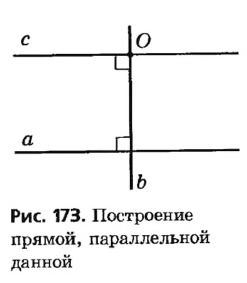
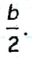
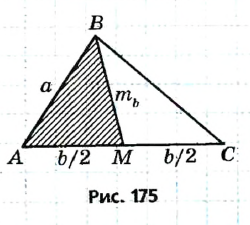
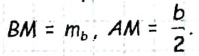
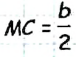 .
.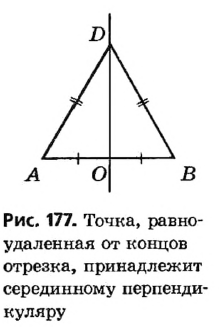
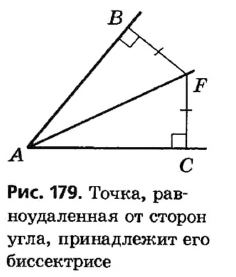
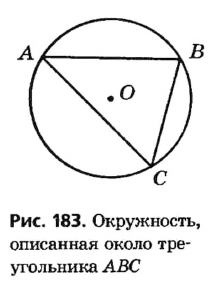
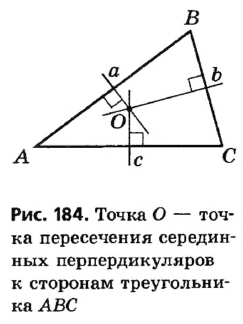
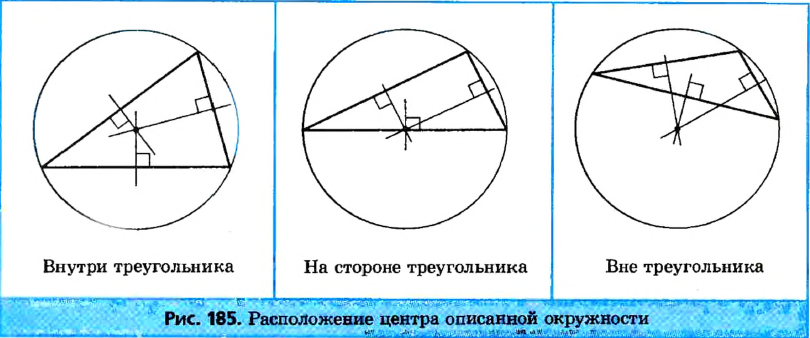
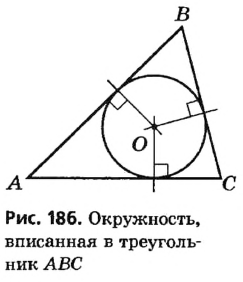
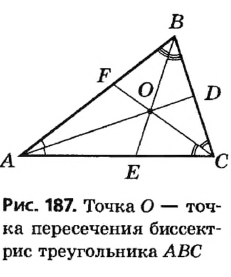
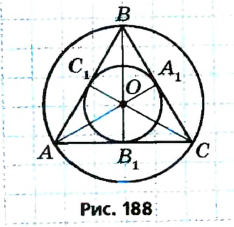
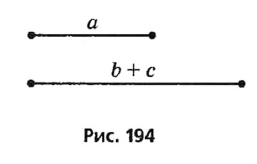
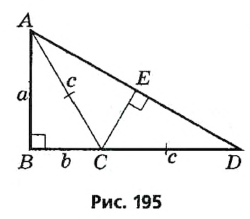
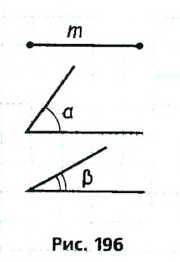
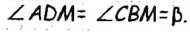
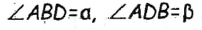 . Треугольник АВй вспомогательный.
. Треугольник АВй вспомогательный.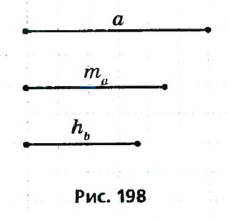
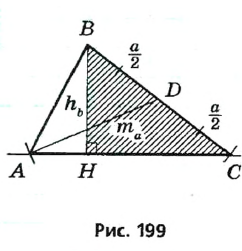
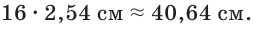
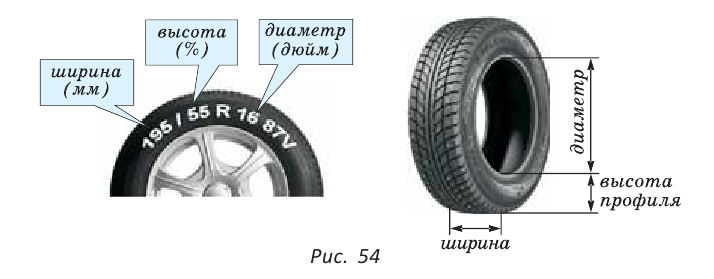
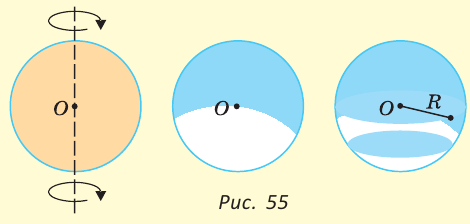
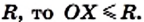
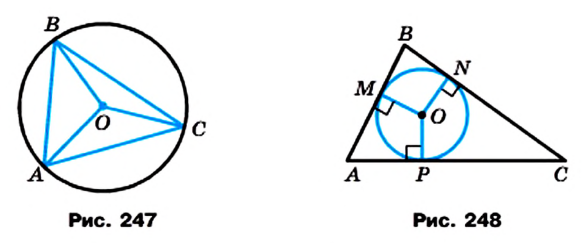
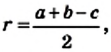 где r — радиус вписанной окружности, а и b — катеты, с — гипотенуза.
где r — радиус вписанной окружности, а и b — катеты, с — гипотенуза.