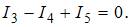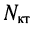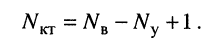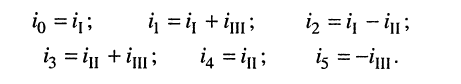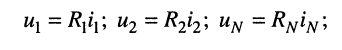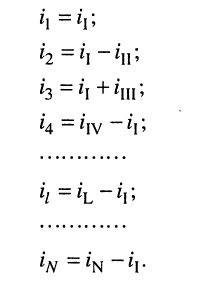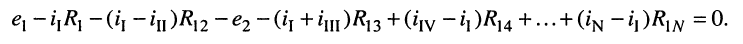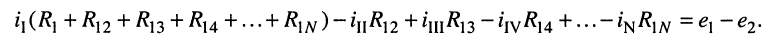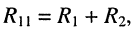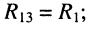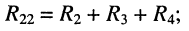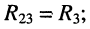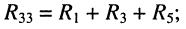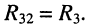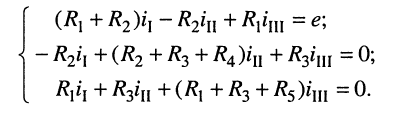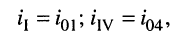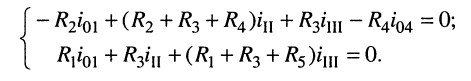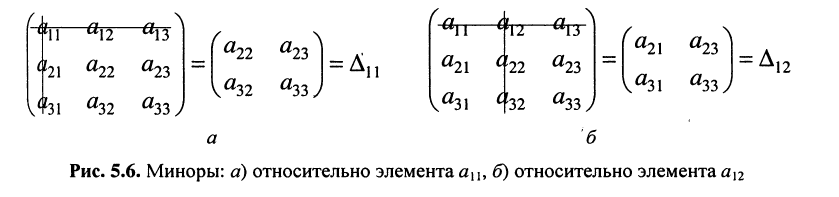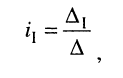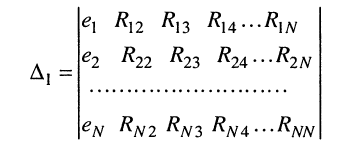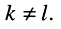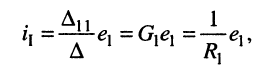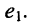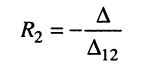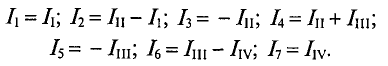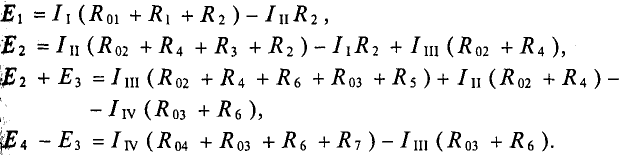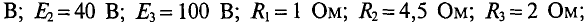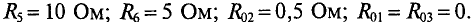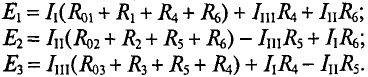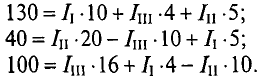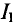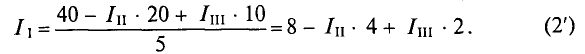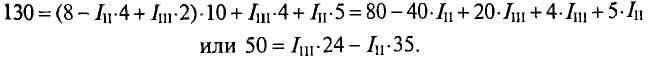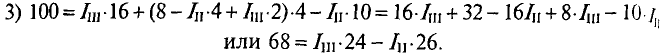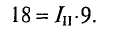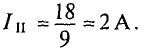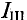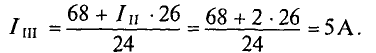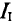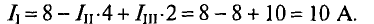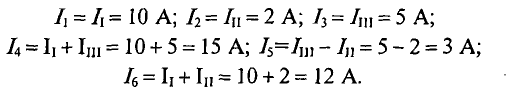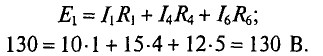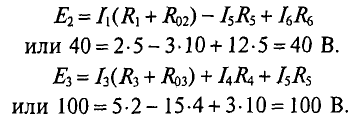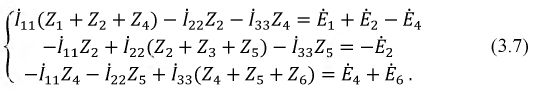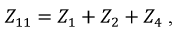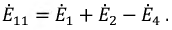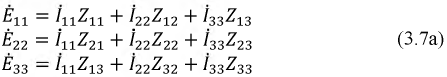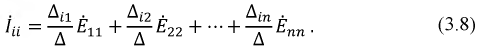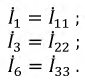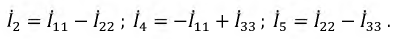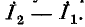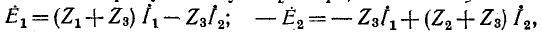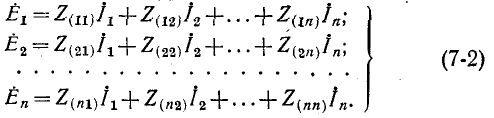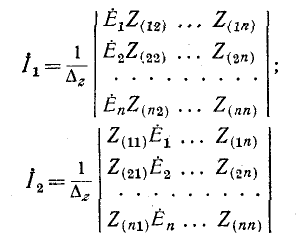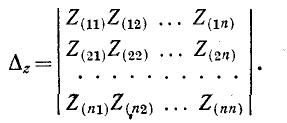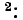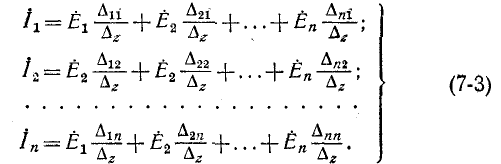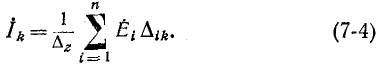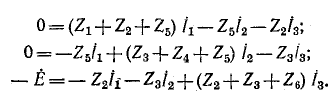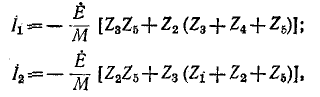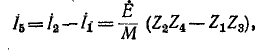Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи.
Простым языком электрическая схема это упрощенное изображение электрической цепи.
Для отображение электрических компонентов (конденсаторов, резисторов, микросхем и т. д.) в электрических схемах используются их условно графические обозначения.
Для отображения электрических соединений (дорожек, проводов, соединения между радиоэлементами) применяют простую линию соединяющие два условно графических обозначения. Причём все ненужные изгибы дорожек удаляют.
В состав электрической схемы входят: ветвь и условно графические обозначение электрических элементов так же могут входить контур и узел.
Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.
Ветви присоединённые к одной паре узлов называются параллельными.
Любой замкнутый путь, проходящий по нескольким ветвям называется контуром. На верхнем рисунке, контурами можно считать ABD; BCD; ABC.
Узел – место соединения трёх и 
- Узел A
- Узел B
- Узел C
- Узел D
Точки К и Е не являются узлами.
Контур – это замкнутый участок электрической цепи (схемы), составленный из одной или нескольких ветвей. Любой замкнутый путь, проложенный через ветви цепи и есть замкнутый контур.
На рисунке изображен замкнутый контур из сопротивлений R2, R3, R4, R5, R7, R8, R9, R10.
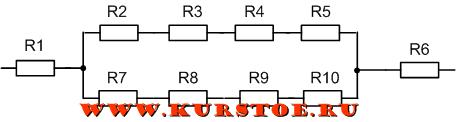
Количество контуров в схеме – 6
Это следующие контура:
R1, R2, R3
R5, R6
R1, R4, R5, R10, R9, R8, R7
R2, R3, R4, R5, R10, R9, R8, R7
R2, R3, R4, R6, R10, R9, R8, R7
R1, R4, R6, R10, R9, R8, R7
На чтение 33 мин Просмотров 14 Опубликовано 8 апреля 2023 Обновлено 8 апреля 2023
Содержание
- Что такое электрическая схема, ветвь, узел, контур.
- Тема: Основные определения и топологические параметры электрических цепей. Количество независимых контуров в представленной схеме равно
- Количество независимых контуров в представленной схеме равно
Что такое электрическая схема, ветвь, узел, контур.
Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи.
Простым языком электрическая схема это упрощенное изображение электрической цепи.
Для отображение электрических компонентов (конденсаторов, резисторов, микросхем и т. д.) в электрических схемах используются их условно графические обозначения.
Для отображения электрических соединений (дорожек, проводов, соединения между радиоэлементами) применяют простую линию соединяющие два условно графических обозначения. Причём все ненужные изгибы дорожек удаляют.
В состав электрической схемы входят: ветвь и условно графические обозначение электрических элементов так же могут входить контур и узел.
Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.
Ветви присоединённые к одной паре узлов называются параллельными.
Любой замкнутый путь, проходящий по нескольким ветвям называется контуром. На верхнем рисунке, контурами можно считать ABD; BCD; ABC.
Узел – место соединения трёх и 
Точки К и Е не являются узлами.
Источник
Тема: Основные определения и топологические параметры электрических цепей. Количество независимых контуров в представленной схеме равно



Количество независимых контуров в представленной схеме равно …
Решение:
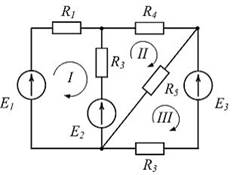
Контуром называют замкнутый путь, проходящий по ветвям и узлам цепи. Независимым является контур, в который входит хотя бы одна новая ветвь. В приведенной схеме три независимых контура: I, II, III.
Тема: Законы Кирхгофа и их применение для расчета электрических цепей
Для приведенной схемы можно составить ______ независимых уравнений по второму закону Кирхгофа.
Решение:
Количество независимых уравнений по второму закону Кирхгофа равно 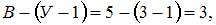
Тема: Законы Кирхгофа и их применение для расчета электрических цепей
Для одного из узлов справедливо уравнение …
Решение:
По первому закону Кирхгофа для узла b
Источник
Количество независимых контуров в представленной схеме равно
1 1)Тема: Основные определения и топологические параметры электрических цепей 1. Количество независимых контуров в представленной схеме равно Контуром называют замкнутый путь, проходящий по ветвям и узлам цепи. Независимым является контур, в который входит хотя бы одна новая ветвь. В приведенной схеме три независимых контура: I, II, III. 2. Если внутреннее сопротивление источника электрической энергии много меньше сопротивления нагрузки, то есть то такой источник характеризуется внешней характеристикой, показанной на рисунке Если то напряжение источника при изменении остается практически неизменным. Такому источнику на схемах замещения соответствует идеальный источник 1
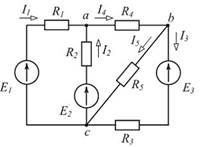
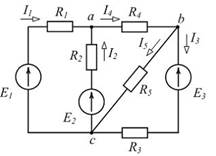
2 ЭДС с внешней характеристикой, изображенной на рисунке: 3. Количество потенциальных узлов в представленной схеме равно Узлом называют место соединения трех и более ветвей. В схеме четыре геометрических узла: c, d, e, f. Узлы dи f, имеющие одинаковые потенциалы, могут быть объединены в один потенциальный узел. Таким образом, в схеме 3 потенциальных узла: c, d, e. 4. Количество ветвей схемы, содержащих пассивные элементы, равно Пассивными элементами являются резистивные элементы находящиеся во всех пяти ветвях схемы. и 2
3 5. При заданном положительном направлении ЭДС Е положительные направления тока I и напряжения Uисточника указаны стрелками соответственно. Положительное направление тока совпадает с положительным направлением ЭДС и обозначено на приведенной схеме стрелкой 1, а положительное направление напряжения противоположно направлению ЭДС и обозначено стрелкой На рисунке приведено условное обозначение идеального источника тока. 7. На представленной схеме напряжение U на зажимах источника электрической энергии равно ЭДС Е, если Напряжение, если 3
4 8. Общее количество ветвей представленной схемы равно Ветвью называют участок электрической цепи с одним и тем же током, состоящий из одного пассивного или активного элемента, а также из нескольких последовательно соединенных элементов. В представленной схеме общее количество ветвей равно пяти. 9. Если напряжение на выводах элемента при отсутствии тока равно нулю, то это Пассивным элементом называют приемники, в которых не возникает ЭДС. Их вольтамперные характеристики проходят через начало координат при отсутствии тока напряжение на выводах этих элементов равно нулю. 10. Если внутреннее сопротивление источника электрической энергии много больше сопротивления нагрузки, то есть то такой источник характеризуется внешней характеристикой, приведенной на рисунке Если то ток источника при изменении остается практически неизменным. Такой источник называется идеальным источником тока и характеризуется следующей внешней характеристикой: 4
5 2)Тема: Закон Ома и его применение для расчета электрических цепей 1. Если при напряжении и сопротивлении ток то противо-эдс Е активного приемника равна В. По закону Ома для участка цепи с ЭДС Отсюда ЭДС 2. Если ток на участке цепи постоянного тока ЭДС сопротивление то разность потенциалов на концах этого участка равна В. По закону Ома для активного участка цепи ток Отсюда разность потенциалов 3. Если разность потенциалов на участке электрической цепи ЭДС сопротивление то ток равен А. 5
6 По закону Ома для активного участка цепи ток 4. Напряжение U на зажимах активного приемника равно По закону Ома ток где напряжение взято со знаком «+», так как его положительное направление совпадает с положительным направлением тока, а ЭДС взята со знаком «-», так как направлена против тока. Напряжение 5. На рисунке приведены зависимости тока через резисторы от напряжения на них. Сопротивление имеет резистор По закону Ома сопротивление резистора 6
7 6. На рисунке приведены зависимости тока через резисторы от напряжения на них. Наименьшим сопротивлением обладает резистор По закону Ома сопротивление Сопротивление резистора 7. Если то ток I равен А. По закону Ома для активного участка цепи ток 7
8 8. Если показания приборов двухполюсника (см. рис.) равно Ом. то входное сопротивление пассивного По закону Ома сопротивление двухполюсника 9. Проводимость g приемника с заданной вольт-амперной характеристикой (см. рис.) равна См. По закону Ома проводимость приемника 8
9 3) Тема: Законы Кирхгофа и их применение для расчета электрических цепей 1. 1 Для одного из контуров схемы справедливо уравнение Для контура уравнение по второму закону Кирхгофа имеет вид: 2. Для приведенной схемы по второму закону Кирхгофа верно составлено уравнение Для приведенной схемы по второму закону Кирхгофа верно составлено уравнение. 9
10 3. Если то ток равен А. По первому закону Кирхгофа 4. Для приведенной схемы по первому закону Кирхгофа верно составлено уравнение По первому закону Кирхгофа для узла b или 10
11 5. При известных сопротивлениях и токах напряжение источника тока можно определить из уравнения (см. рис.) на зажимах По второму закону Кирхгофа Отсюда 11
12 6. Для приведенной схемы можно составить независимых уравнений по второму закону Кирхгофа. Количество независимых уравнений по второму закону Кирхгофа равно где В-число ветвей. 7. Для приведенной схемы можно составить независимых уравнений по первому закону Кирхгофа и независимых уравнений по второму закону Кирхгофа. В приведенной схеме количество ветвей с неизвестными токами, количество узлов По первому закону Кирхгофа можно составить независимых уравнения, по второму закону Кирхгофа В-(У-1)=5-3=2. 12
13 8. Для одного из узлов справедливо уравнение По первому закону Кирхгофа для узла b 13
14 4)Тема: Анализ цепей постоянного тока с одним источником энергии 1. Если (см. рис.), то ток равен А. По формуле разброса тока ток 2. Если равно В. (см. рис.), то напряжение U на зажимах цепи, Напряжение на зажимах параллельных ветвей Ток так как сопротивления и равны. Ток Напряжение на зажимах цепи 14
15 3. В изображенной схеме и при разомкнутом выключателе В ток При замкнутом выключателе ток I будет равен А. При разомкнутом выключателе эквивалентное сопротивление цепи По закону Ома напряжение на зажимах цепи При замкнутом выключателе эквивалентное сопротивление Ток 4. Эквивалентное сопротивление цепи, показанной на рисунке, относительно точек с и d равно Резистивные элементы и и соединены параллельно. Эквивалентное сопротивление 15
16 5. Эквивалентное сопротивление цепи, показанной на рисунке, относительно точек с и b равно Так как точки а и b соединены между собой накоротко, то эквивалентное сопротивление относительно точек с и b рассчитывается для параллельного соединения сопротивлений 1 и 3 : 6. Для цепи, схема которой изображена на рисунке, верным является соотношение Если заменить участки с параллельным соединением элементов одним эквивалентным элементом, то схема примет вид 16
17 По закону Ома напряжения на участках цепи прямопропорциональны сопротивлениям этих участков, то есть По первому закону Кирхгофа Таким образом, верным является соотношение 7. Если при неизменном напряженном U замкнуть выключатель В (см. рис.), то ток I При замыкании выключателя В два из четырех одинаковых резистивных элементов окажутся закороченными. Эквивалентное сопротивление цепи уменьшится в два раза, а ток увеличится в такое же количество раз
18 Схемы рис. 1 и рис. 2 эквивалентны при равном При замене трех одинаковых ветвей, соединенных треугольником (рис. 1), тремя ветвями, соединенными звездой (рис. 2), сопротивления новых ветвей будут в три раза меньше, то есть 9. Эквивалентная проводимость цепи, показанной на рисунке, равна При параллельном соединении элементов эквивалентная проводимость
19 Эквивалентное сопротивление цепи, показанной на рисунке, равно Эквивалентное сопротивление 11. На рисунке изображены идеальные элементы схем замещения цепей переменного тока. К пассивным не относится (-ятся) элемент(-ы) К пассивным идеальным элементам схем замещения не относятся идеальные источники ЭДС (е) и тока (j). Тема: Мощность цепи постоянного тока. Баланс мощностей 1. Уравнение баланса мощностей имеет вид 19
20 Уравнение баланса мощностей имеет вид 2. Если а (см. рис.), то во внутреннем сопротивлении источника преобразуется в теплоту % его энергии. КПД источника определяется отношением мощностей приемника и источника ЭДС: Это означает, что энергии источника преобразуется в теплоту в сопротивлении 3. Пассивный двухполюсник с входным сопротивлением активному двухполюснику с параметрами этом КПД источника энергии равен подключен к (см. рис.). При 20
21 Для схемы, изображенной на рисунке, КПД определяется отношением мощностей приемника и источника ЭДС: 4. В схеме, изображенной на рисунке,. Потребляемая приемником мощность равна Вт. Мощность приемника с сопротивлением 5. При (см. рис.) вырабатываемая источником мощность равна Вт. 21
22 Мощность источника 6. Для изображенной схемы уравнение баланса мощностей имеет вид Уравнение баланса мощностей имеет вид 7. Для изображенной схемы уравнение баланса мощностей имеет вид Для изображенной схемы уравнение баланса мощностей имеет вид 22
23 8. Если (см. рис.), то показание ваттметра равно Вт. Мощность, потребляемая всей цепью, мощность одного резистивного элемента из трех, то Ваттметр измеряет есть 9. В схеме, изображенной на рисунке, ваттметра равно Вт. Показание Напряжение Мощность, измеряемая ваттметром, 23
24 5)Тема: Расчет нелинейных цепей постоянного тока 1. В точке А вольт-амперной характеристики нелинейного элемента (см. рис.) дифференциальное сопротивление равно Дифференциальное сопротивление, соответствующее точке А вольт-амперной характеристики, 2. Статические сопротивления нелинейного элемента с заданной вольт-амперной характеристикой при напряжении, равном 2 и 8 В, соответственно равны ком. Статическое сопротивление нелинейного элемента в заданной точке его характеристики равно отношению напряжения на элементе к току в нем: при при 24
25 3. Два одинаковых нелинейных элемента с заданной (см. рис.) вольт-амперной характеристикой соединены параллельно. Если напряжение на входе цепи ток в неразветвленной части цепи равен ма. то По вольт-амперной характеристике каждого из элементов при находим токи Ток в неразветвленной части цепи 4. Два одинаковых нелинейных элемента с заданной (см. рис.) вольт-амперной характеристикой соединены последовательно. Если напряжение на входе цепи то ток в цепи равен ма. Так как нелинейные элементы одинаковы, на каждый из них будет приходиться половина входного напряжения, то есть По вольт-амперной характеристике при находим ток 5. 25
26 Для нелинейной цепи задана зависимость тока от входного напряжения (см. рис.). Если то напряжение на нелинейном элементе равно В. При напряжении по вольт-амперной характеристике цепи находим ток 6. Напряжение Вольт-амперная характеристика нелинейного элемента выражается уравнением При напряжении динамическое сопротивление нелинейного элемента равно Ом. Динамическое (дифференциальное) сопротивление 7. Вольт-амперная характеристика нелинейного элемента выражается уравнением При напряжении статическое сопротивление нелинейного элемента равно Статическое сопротивление 26
27 8. Несимметричной вольт-амперной характеристикой (см. рис.) обладает Выпрямительный диод 9. В точке А вольт-амперной характеристики нелинейного элемента (см. рис.) статическое сопротивление равно Статическое сопротивление в точке А равно отношению напряжения к току в этой точке: 10. На рисунке приведены вольт-амперные характеристики четырех резистивных элементов. При увеличении напряжения статическое сопротивление увеличивается у элемента 27
28 Статическое сопротивление нелинейного элемента изменяется от точки к точке его вольт-амперной характеристики. При увеличении напряжения нелинейного элемента 3 растет. 28
29 6) Цепи однофазного синусоидального тока Тема: Электрические цепи с резистивным, индуктивным и емкостным элементами 1. При в идеальном конденсаторе угол сдвига фаз между напряжением и током равен В идеальном конденсаторе ток опережает по фазе напряжение на угол то есть 2. При и комплексное сопротивление идеального конденсатора равно Ом. Комплексное сопротивление идеального конденсатора 3. В цепях синусоидального тока реактивными не являются сопротивления элементов. В цепях синусоидального тока реактивными являются сопротивления индуктивных, емкостных и индуктивно связанных элементов. Реактивными не являются сопротивления резистивных элементов. 4. При и комплексное сопротивление идеального индуктивного элемента равно Ом. 29
30 Комплексное сопротивление ветви, содержащей только индуктивный элемент, 5. При мгновенное значение тока равно А. Мгновенное значение тока 6. На рисунке изображены зависимости полных сопротивлений z от угловой частоты. Зависимость бсоответствует элементу(-ов) Зависимость б соответствует идеальному индуктивному элементу L, у которого 30
31 7.При в идеальном индуктивном элементе угол сдвига фаз между напряжением и током равен В идеальном индуктивном элементе напряжение опережает по фазе ток на угол, то есть 8. В цепях синусоидального тока активными являются сопротивления элементов. В резистивном элементе электрическая энергия необратимо преобразуется в тепловую. По этой причине сопротивление R резистивного элемента является активным. Тема: Способы представления и параметры синусоидальных величин 1.Частота синусоидального тока равна Гц. Частота синусоидального тока равна 2. Комплексное действующее значение тока При мгновенное значение этого тока равно А. Амплитуда тока Начальная фаза тока При угловая частота Мгновенное значение тока 31
32 3.Наименьший промежуток времени, через который цикл колебаний тока повторяется, равен Через промежуток времени Т фаза тока изменяется на угол, и цикл колебаний тока повторяется снова, то есть 4. Мгновенное значение синусоидального напряжения Комплексное действующее значение этого напряжения равно В. Комплексное действующее значение напряжения 5. Производство и распределение энергии в энергосистемах Российской Федерации осуществляется на частоте равной Гц. Производство и распределение энергии в энергосистемах Российской Федерации осуществляется на частоте 6. В выражении для тока в Гц измеряется В выражении для тока в Гц измеряется частота. 7. Комплексное действующее значение напряжение Мгновенное значение этого напряжения равно Мгновенное значение напряжения 32
33 8. Период Т синусоидального тока равен с. За время фаза тока изменяется на радиан, то есть а период Тема: Сопротивления и фазовые соотношения между токами и напряжениями 1. При равный ток i по фазе от напряжения u на угол Угол сдвига фаз между напряжением и током i Ток i отстает по фазе от напряжения на угол 2. Включенные измерительные приборы (см. рис.) показали: вольтметр 120 В, амперметр 33
34 12 А, ваттметр 864 Вт. Сопротивление равно Ом. Сопротивление Полное сопротивление активное сопротивление Искомое сопротивление 3. Ток на входе цепи, показанной на рисунке, опережает по фазе напряжение при При проводимость индуктивного элемента меньше проводимости емкостного элемента, угол сдвига фаз между напряжением и током ток опережает по фазе напряжение
35 При равна Вт; реактивная мощность активная мощность двухполюсника (см. рис.) равна ВАр. Комплекс полной мощности мощность 5. реактивная мощность активная При комплексное входное сопротивление цепи (см. рис.) напряжение по фазе от тока i на угол Комплексное входное сопротивление цепи Угол сдвига фаз между напряжением и током Напряжение отстает по фазе от тока на угол
36 При равно Ом. полное сопротивление Z изображенного участка цепи Полное сопротивление Изображенной цепи не может соответствовать векторная диаграмма векторная диаграмма б, так как при 36
37 7) Тема: Трехфазные цепи. Основные понятия. Элементы трехфазных цепей 1. При ток (см. рис.) равен А. При ток 2. Потребляемая приемниками (см. рис.) активная мощность P равна Вт. Потребляемая приемниками активная мощность 3.В трехфазную сеть с линейным напряжением включены треугольником симметричные приемники с квт. Потребляемая активная мощность равна 37
38 Потребляемая симметричными приемниками активная мощность 4. При отключении фазы (см. рис.) не изменятся токи При отключении фазы изменяются: фазный ток который станет равным нулю; линейный ток станет равным току ; линейный ток станет равным току Остальные токи и не изменяются. 5.Симметричный приемник с включен треугольником в трехфазную сеть с Токи в линейных проводах будут равны А. Токи в фазах симметричного приемника Токи в линейных проводах при симметричной нагрузке 38
39 6. Векторная диаграмма цепи, показанной на рисунке, соответствует На векторной диаграмме фазные токи равны величине и отстают по фазе от соответствующих фазных напряжений на один и тот же угол нагрузка фаз симметричная активно-идуктивная. 7.В формуле для активной мощности симметричного трехфазного приемника под U и I понимают В формуле для активной мощности симметричного трехфазного приемника напряжения и тока. 8. под U и I понимают действующие значения фазных При обрыве линейного провода (см. рис.) не изменится ток.. 39
40 Ток Обрыв линейного провода не повлияет на напряжение и сопротивление, а следовательно, на величину тока 9. При ток (см. рис.) равен 3 А. Ток. На рисунке сложение комплексных действующих токов выполнено графически. Искомому току соответствует вектор длина которого равна Ток 40
41 10. В изображенной схеме сопротивления проводов сопротивлений фаз приемника. Фазное напряжение значительно меньше приемника будет равно ЭДС При при условии потенциалы нейтральных точек генератора и приемника равны между собой. Фазное напряжение приемника равно фазной ЭДС источника. 41
42 8) Тема: Свойства ферромагнитных материалов. Определения, классификация, законы магнитных цепей 1. В изображенной магнитной цепи намагничивающая обмотка с числом витков плотно навита на кольцевой сердечник из литой стали. Средняя длина сердечника При магнитной индукции магнитодвижущая сила намагничивающей обмотки При по кривой намагничивания литой стали Намагничивающая сила (МДС) катушки 42
43 2. В изображенной магнитной цепи магнитодвижущая сила намагничивающей обмотки. При магнитное сопротивление цепи По закону Ома магнитное сопротивление цепи 43
44 3. В изображенной магнитной цепи обмотка с числом витков плотно навита на кольцевой сердечник сечением из литой стали. Средняя длина сердечника При абсолютная магнитная проницаемость сердечника равна Магнитная индукция в сердечнике По кривой намагничивания литой стали напряженность магнитного поля. Абсолютная магнитная проницаемость сердечника 44
45 4. В изображенной магнитной цепи намагничивающая обмотка плотно навита на кольцевой сердечник из холоднокатаной стали марки 3411 сечением Средняя длина сердечника При магнитной индукции магнитное сопротивление сердечника При марки 3411 напряженность магнитного поля холоднокатаной стали абсолютная магнитная проницаемость Магнитное сопротивление сердечника 45
46 5. В изображенной магнитной цепи кольцевой сердечник сечением стали имеет разрез (воздушный зазор) Средняя длина из литой сердечника При магнитное напряжение на воздушном зазоре При магнитной индукции в сердечнике магнитное напряжение на воздушном зазоре 46
47 6. В изображенной магнитной цепи намагничивающая обмотка с числом витков плотно навита на кольцевой сердечник сечением из литой стали. Средняя длина сердечника Кольцо имеет разрез (воздушный зазор) При магнитодвижущая сила (МДС) катушки При поля по кривой намагничивания литой стали напряженность магнитного МДС намагничивающей обмотки 47
48 7. В изображенной магнитной цепи намагничивающая обмотка с числом витков плотно навита на кольцевой сердечник сечением из литой стали. Кольцо имеет воздушный зазор Средняя длина сердечника При ток в намагничивающей катушке При сердечнике по кривой намагничивания литой стали напряженность магнитного поля в МДС намагничивающей обмотки Ток в намагничивающей катушке 48
49 8. В изображенной магнитной цепи намагничивающая обмотка плотно навита на кольцевой сердечник сечением из горячекатаной (1512) стали. При напряженность магнитного поля Н в сердечнике равна Магнитная индукция в сердечнике По кривой намагничивания горячекатаной стали марки 1512 напряженность магнитного поля в сердечнике 9. В изображенной магнитной цепи намагничивающая обмотка с числом витков 49
50 плотно навита на кольцевой сердечник из литой стали сечением Средняя длина сердечника При магнитной индукции магнитное сопротивление сердечника При по кривой намагничивания литой стали напряженность магнитного поля Намагничивающая сила (МДС) По закону Ома для магнитной цепи магнитное сопротивление Тема: Основные понятия теории электромагнитного поля и основные магнитные величины 1. Магнитное поле, во всех точках которого векторы магнитной индукции равны по величине и параллельны, называется Магнитное поле, во всех точках которого векторы магнитной индукции величине и параллельны, называется однородным. 2. равны по При на расстоянии от оси бесконечно длинного круглого провода (см. рис.) величина напряженности магнитного поля По закону полного тока Напряженность магнитного поля 3. 50
51 Принцип непрерывности магнитного поля выражает интегральное соотношение Принцип непрерывности магнитного поля выражает интегральное соотношение. 4. Физической величиной, определяемой по силе, действующей со стороны магнитного поля на движущуюся в этом поле заряженную частицу, является Магнитная индукция B является силовой характеристикой магнитного поля. Вектор магнитной индукции определяется по силе, действующей со стороны магнитного поля на движущуюся в нем со скоростью частицу с зарядом q. 5. На рисунке изображены два провода с противоположно направленными токами I. При, интеграл равен А. По закону полного тока при противонаправленных токах 6. Сила, действующая на помещенный в однородное магнитное поле с магнитной индукцией прямолинейный проводник длиной l с током I, равна 51
52 Действующая на помещенный в однородное магнитное поле с индукцией прямолинейный проводник длиной l с током I сила совпадает с направление тока. Направление вектора 7. Сила, действующая со стороны магнитного поля на движущуюся в нем со скоростью частицу с зарядом q, равна 52
53 Действующая со стороны магнитного поля на движущуюся в нем со скоростью частицу с зарядом q сила На рисунках представлены взаимные положения векторов скорости частиц с зарядами и, магнитной индукции и силы, действующей со сторон магнитного поля на движущиеся в нем заряженные частицы. Верным является взаимное положение векторов, и на рисунке Действующая со стороны магнитного поля на движущуюся в нем заряженную частицу сила Верным является взаимное расположение векторов, и на рисунке а. 53
54 9) Тема: Магнитные цепи с постоянными магнитными потоками 1. Если в катушке с числом витков ток магнитный поток в сердечнике то магнитное сопротивление магнитопровода с зазором равно 1/Гн. Магнитное сопротивление магнитопровода с зазором 2. В воздушном зазоре кольцевого магнитопровода катушки требуется получить индукцию ток I в катушке равен А. При числе витков в катушке Так как относительная магнитная проницаемость сердечника то напряженность магнитного поля в нем По закону полного тока В намагничивающей катушке ток 54
55 3. Обмотка с числом витков намотана на ферромагнитный сердечник с заданной кривой намагничивания. Если длина средней линии магнитная индукция в сердечнике то ток I в обмотке равен A. По кривой намагничивания при находим напряженность магнитного поля По закону полного тока Отсюда ток в обмотке 4. Для анализа магнитных цепей используют вебер-амперную характеристику, выражающую графически зависимость 55
56 Для анализа магнитных цепей используют вебер-амперную характеристику, выражающую графически зависимость между магнитным потоком и магнитным напряжением участка или магнитной цепи в целом. 5. Сердечник электромагнитного устройства постоянного тока выполнен из электротехнической стали с заданной зависимостью. Если длина средней линии сердечника а площадь поперечного сечения S, то магнитное сопротивление сердечника равно Магнитное сопротивление сердечника 6. На замкнутый ферромагнитный сердечник с площадью поперечного сечения S равномерно намотана обмотка с числом витков W. Если магнитный поток в сердечнике Ф, то напряженность магнитного поля Напряженность магнитного поля в ферромагнитном сердечнике не может быть определена, так как не задана кривая 7. для материала сердечника. Если в катушке с числом витков ток магнитный поток в сердечнике то индуктивность катушки равна Гн. Индуктивность катушки 56
57 8. Между абсолютными магнитными проницаемостями в точках 1, 2 и 3 кривой намагничивания магнитопровода (см. рис.) справедливо соотношение Абсолютной магнитной проницаемостью называют отношение магнитной индукции к напряженности магнитного поля: 57
58 9. Кольцевой сердечник из электротехнической стали с заданной кривой намагничивания имеет воздушный зазор. Напряженность магнитного поля в стали Напряженность магнитного поля в зазоре равна По кривой намагничивания находим магнитную индукцию в стали Считаем, что магнитная индукция в зазоре Напряженность магнитного поля в воздушном зазоре 10. Магнитное сопротивление магнитопровода равно магнитному сопротивлению воздушного зазора. Если при неизмененной индукции увеличить длину зазора в 2 раза, то ток в обмотке 58
59 Если магнитное сопротивление магнитопровода равно магнитному сопротивлению цепи воздушного зазора, то магнитное сопротивление всей При увеличении длины зазора в 2 раза его магнитное сопротивление также увеличится в 2 раза, а увеличится в 1,5 раза. Так как то при неизменной индукции В при увеличении в 1,5 раза ток I в обмотке увеличится в 1,5 раза. 59
60 10) Тема: Магнитные цепи с переменными магнитными потоками 1. Если на обмотке идеализированной катушки с ферромагнитным сердечником напряжение то начальная фаза магнитного потока Ф равна :Магнитный поток Ф отстает по фазе от напряжения u на угол Следовательно при 2. При подключении идеализированной катушки с магнитопроводом к источнику синусоидального напряжениянесинусоидальным оказывается При синусоидальном напряжении на обмотке ток оказывается несинусоидальным. 3. Вольт-амперная характеристика обмотки с магнитопроводом изображена под номером 60
61 Вольт-амперная характеристика обмотки с магнитопроводом изображена под номером Если при неизменной амплитуде и частоте напряжения идеализированной катушки увеличить длину немагнитного зазора, то При неизменном значении напряжения ток обмотки тем больше, чем больше зазор, то есть при увеличении длины зазора ток обмотки увеличится. Значение магнитного потока идеализированной магнитной цепи не зависит от параметров магнитной цепи, в том числе и от длины зазора. 5. В идеализированной индуктивной катушке с ферромагнитным магнитопроводом при амплитуда магнитного потока не зависит от Амплитуда магнитного потока определяется только амплитудой напряжения, частотой и числом витков обмотки. 61
62 6. В изображенной на рисунке схеме замещения обмотки с магнитопроводом ЭДС от потока в магнитопроводе учитывается с помощью элемента с сопротивлением Элемент 7. учитывает ЭДС от потока в магнитопроводе. В изображенной на рисунке схеме замещения обмотки с магнитопроводом резистивный элемент учитывает Резистивный элемент 9. учитывает потери мощности в магнитопроводе. В идеализированной магнитной цепи при ЭДС самоиндукции равно В. действующее значение 62
63 Идеализированная магнитная цепь описывается уравнением ЭДС ее действующее значение 10. Если известны показания приборов а также активное сопротивление обмотки, то мощность магнитных потерь в сердечнике равна Мощность потерь в сердечнике 11. Если известны показания приборов а также масса G сердечника и активное сопротивление обмотки, то удельные потери в сердечнике равны Удельные потери в сердечнике 63
64 12. Если на обмотке идеализированной катушки с ферромагнитным сердечником напряжение то начальная фаза магнитного потока Ф равна Магнитный поток Ф отстает по фазе от напряжения u на угол Следовательно при 64
65 11) Тема: Трансформаторы 1. В трансформаторе с однородным магнитопроводом из холоднокатаной электротехнической стали марки 3411 действующее значение эквивалентного синусоидального тока При средней длине магнитопровода напряженность магнитного поля трансформатора равна По закону полного тока напряженность магнитного поля 2. Трансформация напряжений и токов при передаче энергии трансформатором сопровождается потерями энергии: магнитными в магнитопроводе и электрическими данным опыта в обмотках трансформатора. Магнитные потери определяются по Магнитные потери определяют по данным опыта холостого хода при напряжении, при котором магнитный поток в магнитопроводе равен номинальному (рабочему) потоку трансформатора. 65
66 3. На изображенной схеме приемник П присоединен к сети переменного тока через трансформатор мощностью приемника Коэффициент мощности Паспортные потери холостого хода и короткого замыкания трансформатора и. Максимальный КПД трансформатора при коэффициенте нагрузки трансформатора КПД трансформатора будет максимальным при Максимальный КПД трансформатора 4. На изображенной схеме приемник П, потребляющий активную мощность при подключен к электрической сети через однофазный трансформатор номинальной мощностью равен Коэффициент нагрузки трансформатора Коэффициент нагрузки трансформатора 66
67 5. На рисунке изображена электромагнитная схема идеализированного трансформатора. Неверно, что при синусоидальном напряжении магнитный поток Ф в сердечнике трансформатора не синусоидальный отношение напряжений и ЭДС уравнения электрического состояния обмоток имеют вид: действующие значения напряжений связаны отношением В идеализированном трансформаторе Магнитный поток в сердечнике 67
68 Следовательно, при синусоидальном напряжении магнитный поток в сердечнике идеализированного трансформатора является синусоидальным. 6. В трансформаторе величина магнитного потока сердечника Ф не зависит от Амплитуда магнитного потока в сердечнике трансформатора от площади Sпоперечного сечения сердечника. 7. не зависит На изображенной схеме приемник П, потребляющий активную мощность подключен к электрической сети через трансформатор. Если мощность потерь холостого хода и короткого замыкания трансформатора и, то при коэффициенте нагрузки КПД трансформатора равен КПД трансформатора 68
69 8. В идеализированном трансформаторе при индукции В в сердечнике трансформатора зависит от величина магнитной При постоянных значениях и магнитный поток в сердечнике магнитная индукция При величина магнитной индукции В зависит только от площади поперечного сечения магнитопровода. 9.Электрические потери в обмотках трансформатора определяют по данным опыта Электрические потери в обмотках трансформатора определяют по данным опыта короткого замыкания при. Поскольку приложенное к обмотке напряжение очень мало, то потери в магнитопроводе ничтожны, мощность это мощность электрических потерь энергии в проводах обмоток при номинальных токах. 69
70 12) Тема: Асинхронные машины 1. Для привода насоса использован трехфазный асинхронный двигатель с короткозамкнутым ротором. При частота тока в обмотке ротора равна Гц., частоте вращения ротора Частота в роторе 2. На механической характеристике режиму идеального холостого хода соответствует точка Режиму идеального холостого хода соответствует на механической характеристике точка 1, в которой 3. Асинхронная машина при работает в режиме При генератора. подключенная к трехфазной сети асинхронная машина работает в режиме 4. Асинхронная машина при работает В режиме двигателя ротор вращается в ту же сторону, что и магнитное поле с частотой 70
71 5. На рисунке изображена схема включения асинхронного двигателя с фазным ротором с двухступенчатым пусковым реостатом. Полное приведенное сопротивление пускового реостата принимают равным Пусковой момент асинхронного двигателя будет максимальным при скольжении Поэтому полное приведенное сопротивлении пускового реостата принимают равным 6. На рисунке изображена механическая характеристика асинхронного двигателя. Критическое скольжение где значения частоты вращения ротора в точках 2, 3, 4 механической характеристики. Критическое скольжение 7. Максимальный момент асинхронного двигателя не зависит от 71
72 Максимальный момент не зависит от активного сопротивления цепи ротора. 8.Регулированию частоты вращения асинхронных двигателей изменением частоты f питающего напряжения с соответствуют механические характеристики Регулированию частоты вращения асинхронных двигателей изменением частоты f питающего напряжения с характеристики на рисунке: соответствуют механические 9. В режиме идеального холостого хода скольжение S В режиме идеального холостого хода а скольжение 72
73 13) Тема: Синхронные машины 1. Зависимость момента M от угла Зависимость момента M от угла машины. называют угловой характеристикой синхронной 2. Неявнополюсному синхронному генератору соответствуют упрощенные (без учета активного падения напряжения в обмотке якоря) схема замещения и векторная диаграмма На схеме замещения неявнополюсного синхронного генератора условное положительное направление тока направлением ЭДС совпадает по направлению с условным положительным. На векторной диаграмме, соответствующей генераторному режиму работы синхронной машины, вектор ЭДС опережает по фазе вектор напряжения 3.При на угол отношение максимального момента к номинальному моменту синхронного двигателя (перегрузочная способность) равно При коэффициент перегрузочной способности синхронного двигателя 73
74 4. Активную мощность синхронных генераторов на тепловых электростанциях регулируют изменением Активную мощность генераторов на тепловых электростанциях регулируют изменением подачи пара в турбину. 5. Зависимость ЭДС якоря от тока возбуждения при номинальной частоте вращения ротора синхронного генератора и отсутствии нагрузки якоря характеристикой называется Зависимость ЭДС якоря от тока возбуждения при номинальной частоте вращения и отсутствии нагрузки называется характеристикой холостого хода. 6. Синхронные машины не работают в режиме фазовращателя Синхронные машины работают в режимах генератора, двигателя и компенсатора реактивной мощности. 7. Статорной обмотке синхронного двигателя соответствуют упрощенные схема замещения и векторная диаграмма под номерами соответственно. На схеме замещения статорной обмотки синхронного двигателя ЭДС и ток 74
75 должны быть направлены встречно (как на рисунке 2), на векторной диаграмме вектор напряжения должен опережать по фазе вектор ЭДС на угол (как на рисунке 3). 8. Максимальный момент синхронного неявнополюсного двигателя не зависит от Максимальный момент синхронного неявнополюсного двигателя зависит от момента нагрузки, присоединенной к валу двигателя. 9. При коротком замыкании на шинах электростанции необходимо Чтобы предотвратить опасный разгон турбины и генератора под воздействием момента турбины, при коротком замыкании на шинах электростанции прекращают доступ рабочей среды в турбины. 10. Электромагнитный момент неявнополюсного трехфазного синхронного двигателя М равен Н/м. Электромагнитный момент неявнополюсного трехфазного синхронного не двигателя 75
76 14) Тема: Машины постоянного тока 1.Регулирование частоты вращения изменением напряжения, подводимого к якорю, применяют для двигателей постоянного тока возбуждения. Регулирование частоты вращения изменением напряжения на якоре применяют для двигателей постоянного тока независимого возбуждения. 2. Изображенные механические характеристики соответствуют двигателю постоянного тока возбуждения при регулировании частоты вращения. Изображенные механические характеристики соответствуют двигателю постоянного тока параллельного возбуждения при полюсном регулировании частоты вращения. 3. На рисунке изображена схема машины постоянного тока. При смещении щеток 1 с геометрической нейтрали наводимая в обмотке якоря 2 ЭДС 76
77 Если сместить щетки с геометрической нейтрали, то образующие параллельные ветви проводники будут находиться в зоне действия как одного (N), так и другого (S) полюса машины. Наводимая в обмотке якоря ЭДС уменьшится. 4. Реостатное регулирование частоты вращения двигателей постоянного тока осуществляется изменением с помощью реостата суммарного сопротивления цепи якоря Реостатное регулирование частоты вращения двигателя постоянного тока осуществляют введением реостата в цепь якоря. 5. Величина начального пускового момента в первый момент после подключения двигателя постоянного тока к источнику питания не зависит от В первый момент после подключения двигателя постоянного тока к источнику питания якорь неподвижен, противо-эдс Е, электромагнитная мощность и мощность двигателя равны нулю. Величина начального пускового момента на валу зависит от и определяющего величину магнитного потока Ф. 77
78 6. Двигатель параллельного возбуждения подключен к сети с неизменным напряжением, момент нагрузки меньше номинального. После увеличения сопротивления возбуждения ток якоря, частота вращения якоря в цепи В установившемся режиме после увеличения сопротивления ток и магнитный поток Ф уменьшится. При постоянном моменте М нагрузки ток якоря увеличится. При нагрузках, меньших номинальной, уменьшение магнитного потока Ф приведет к росту частоты вращения n якоря. 7. В генераторе постоянного тока с параллельным возбуждением при снижении частоты вращения ротора n в два раза напряжение U на его зажимах в режиме холостого хода При снижении частоты вращения ротора n в два раза ток в обмотке возбуждения снизится более чем в два раза, магнитная цепь машины будет ненасыщенной. Самовозбуждение 78
79 генератора с ненасыщенной магнитной системой невозможно, поэтому напряжение U на зажимах генератора снизится до нуля. 8. Напряжение на зажимах генератора смешанного возбуждения. Если ток в обмотке ОВС то ток в обмотке ОВШ равен А. Напряжение на обмотке якоря Ток 79
80 15) Тема: Элементная база современных электронных устройств 1. Структура диодного тиристора изображена на рисунке Диодный тиристор имеет три на рисунке перехода и два вывода. Его структура изображена 2. Вывод 1 полупроводникового прибора называется На рисунке приведено условное графическое обозначение биполярного транзистора типа. Вывод 1 называется эмиттером. 3. Структура биполярного транзистора изображена на рисунке Биполярный транзистор состоит из трех областей с чередующимися типами электропроводности. Его структура изображена на рисунке 4. Полупроводниковый диод, в котором используется зависимость емкости перехода от обратного напряжения, называется Полупроводниковый диод, в котором используется зависимость емкости перехода от обратного напряжения и который предназначен для применения в качестве элемента с электрически управляемой емкостью, называется варикапом. 80
81 5. Средний слой биполярного транзистора называется Средний слой биполярного транзистора называется базой. 6. На рисунке приведено условное графическое обозначение биполярного транзистора типа. 7. Участок с отрицательным дифференциальным сопротивлением имеется в вольтамперной характеристике Участок с отрицательным дифференциальным сопротивлением имеется в вольт-амперной характеристике тиристора. 8. На рисунке изображена структура биполярного транзистора 81
82 16) Тема: Источники вторичного электрпитания 1. В мостовом однофазном выпрямителе вентили и трансформатор идеальные. При среднем значении выпрямительного напряжения максимальная величина обратного напряжения на вентилях В мостовом однофазном выпрямителе с идеальными диодами максимальная величина напряжения на вентиле 2. В мостовом однофазном выпрямителе вентили и трансформатор идеальные. При средних значениях токов в вентилях среднее значение тока в сопротивлении нагрузки В мостовом однофазном выпрямителе при средних значениях токов в вентилях среднее значение тока в сопротивлении нагрузки 82
83 3. В однополупериодном выпрямителе среднее значение напряжения При максимальное значение тока равно А. Значение тока 4. Если в однофазном выпрямителе с выводом нулевой точки вентили и трансформатор идеальные, то при среднем значении выпрямленного напряжения на нагрузке максимальная величина обратного напряжения на вентилях В однофазном выпрямителе с выводом нулевой точки максимальные значения обратных напряжений на вентилях 83
84 5. В однофазном выпрямителе с выводом нулевой точки при среднем значении напряжения сопротивлении нагрузки среднее значение тока через вентиль Среднее значение тока через вентиль 6. В однополупериодном выпрямителе среднее значение напряжения При среднее значение тока нагрузки равно А. Среднее значение тока нагрузки 84
85 7. В трехфазном выпрямителе (см. рис.) с идеальными трансформатором и вентилями отношение где среднее значение выпрямленного напряжения, действующее фазное напряжение вторичной обмотки трансформатора. В трехфазном выпрямителе с нейтральным выводом среднее значение выпрямленного напряжения где действующее фазное напряжение вторичной обмотки трансформатора. Отношение 8. В однополупериодном выпрямителе с идеальным вентилем среднее значение выпрямленного напряжения Напряжение вентиля равно В. Среднее значение выпрямленного напряжения Напряжение 85
86 9. В однополупериодном выпрямителе с идеальным трансформатором и вентилем максимальное обратное напряжение на вентиле коэффициент трансформации nтрансформатора равен При Действующее значение напряжения на вторичной обмотке трансформатора Коэффициент трансформации 10. В трехфазном мостовом выпрямителе с идеальными трансформатором и вентилями отношение где среднее значение выпрямленного напряжения, действующее фазное напряжение вторичной обмотки трансформатора. В трехфазном мостовом выпрямителе среднее значение выпрямительного напряжения где действующее значение фазного напряжения. Отношение 86
87 17) Тема: Усилители электрических сигналов 1. Если на входе усилителя действует ЭДС внутреннее сопротивление источника ЭДС входной ток то входное сопротивление усилителя равно Ом. В соответствии со вторым законом Кирхгофа Отсюда 2. На рисунке изображена структурная схема усилителя с последовательной отрицательной связью по напряжению. При коэффициенте усиления усилителя без обратной связи К = 120, коэффициенте передачи цепи обратной связи усиления усилителя с отрицательной обратной связью по напряжению коэффициент равен Коэффициент усиления усилителя с отрицательной обратной связью по напряжению 87
88 3. На рисунке изображена структурная схема усилителя с последовательной отрицательной обратной связью по напряжению. Если коэффициент усиления усилителя без обратной связи равен К, то после введения отрицательной обратной связи с коэффициентом передачи цепи обратной связи уменьшится в 1+bK 4. На рисунке приведена схема усилительного каскада с общим (-ей) На рисунке приведена схема усилительного каскада с общей базой. 88
89 5. На рисунке приведена схема усилителя. На рисунке приведена схема интегрирующего усилителя. 6. На рисунке приведена схема усилителя. На рисунке приведена схема дифференцирующего усилителя
90 В схеме усилительного каскада фаза выходного напряжения отличается от фазы входного напряжения на угол В схеме усилительного каскада с общим эмиттером выходное напряжение находится в противофазе с выходным, то есть сдвинуто по фазе на На рисунке изображены коллекторные (выходные) характеристики транзистора и линия нагрузки усилительного каскада с общим эмиттером. Точкой отсечки является точка 4 90
91 9. На рисунке приведена схема суммирующего усилителя. 10. На рисунке приведена схема усилительного каскада с общим (-ей) На рисунке приведена схема усилительного каскада с общим (-ей) эмиттером. 91
92 18) Тема: Основы цифровой электроники 1. Логический элемент, условное обозначение которого приведено на рисунке, выполняет операцию На рисунке приведено условное обозначение комбинированного логического элемента И- НЕ, реализующего операцию. 2.Логический элемент, выходной сигнал которого равен единице, если одновременно на все входы подан сигнал «1», называется элементом Логический элемент, выходной сигнал которого равен единице, если одновременно на все входы подан сигнал «1», называется элементом И. 3. К элементарным логическим операциям не относится операция логического сравнения Логические преобразования двоичных сигналов включают три элементарные логические операции: логическое сложение, логическое умножение, логическое отрицание. 4. Вход S RS-триггера, показанного на рисунке, называется установочным 92
93 входом сброса информационным синхронизирующим Вход S называется установочным (от англ. set устанавливать). 5. Регистром называют устройство, предназначенное для Регистром называют устройство, предназначенное для записи и хранения дискретного «слова» двоичного числа или другой кодовой комбинации. 6. Логический элемент, выходной сигнал которого равен единице, если хотя бы на один из входов подан сигнал «1», называется элементом ИЛИ. 7. Выходной сигнал на выходе схемы если сигналы на ее входах и соответственно равны 93
94 Приведенная схема состоит из двух логических элементов: элемента НЕ и элемента ИЛИ. На выходе элемента ИЛИ появится сигнал «0», если на оба его входа подан сигнал «0», то есть 8. Логический элемент, условное обозначение которого приведено на рисунке, выполняет операцию На рисунке приведено условное обозначение комбинированного логического элемента И- НЕ, реализующего операцию 9. Выходной сигнал на выходе схемы, если сигналы на ее входах и соответственно равны Приведенная схема состоит из двух логических элементов: элемента НЕ и элемента ИЛИ- НЕ. На выходе элемента ИЛИ-НЕ появится сигнал «1», если на оба его входа подан сигнал «0», то есть 94
95 10.Условное обозначение счетного триггера изображено на рисунке 95
Источник
Введём понятие узла. Узел – точка цепи, в которой сходится не менее трёх проводников.
Тогда разветвлённой цепью назовём цепь, имеющую один или более узлов.
Для расчёта таких цепей используются два правила Кирхгофа.
Рис. 1. Первое правило Кирхгофа
Первое правило Кирхгофа: сумма токов, входящих в узел, равна сумме токов, выходящих из узла (рис. 1). A — узел в цепи постоянного тока. Путь в цепи протекают токи —
. Тогда, исходя из первого правила Кирхгофа:
Или, обобщая:
(1)
Рис. 2. Второе правило Кирхгофа (цепь)
Второе правило Кирхгофа касается такого понятия как контур. Назовём контуром замкнутый участок цепи, содержащий любые элементы цепи. Для визуализации правила введём произвольную цепь с узлами (рис. 2). Пусть наша цепь содержит резисторы —
, конденсатор ёмкостью
и два источника ЭДС
,
с собственными внутренними сопротивлениями
и
соответственно.
Рис. 3. Второе правило Кирхгофа (Контур)
По нашей схеме нарисуем контуры (рис. 3). В цепе можно выделить 3 контура обхода: для определённости, красный, синий и зелёный.
Расставим токи для каждого из элементов, обладающих сопротивлением (рис. 4). Направление силы тока выбираем случайным образом.
Рис. 4. Второе правило Кирхгофа (Сила тока)
Тогда второе правило Кирхгофа — сумма падений напряжений на каждом из элементов контура равно сумме ЭДС в этом контуре.
Учитывая закон Ома для участка цепи:
(2)
Тогда второе правило Кирхгофа формульно:
(3)
Тогда составим второе правило Кирхгофа для контуров на рис. 3 при нескольких условиях:
- ток считать положительным при совпадении направления обхода и отрицательным при несовпадении;
- ЭДС считать положительным при направлении обхода совпадающим с генерацией тока в источнике (от плюса к минусу) и отрицательным в обратном случае.
Итак, зелёный контур:
(4)
Для синего контура:
(5)
Для красного контура:
(6)
Вывод: правила Кирхгофа (1) и (3) можно использовать для любого вида цепей, однако наибольшую пользу они приносят в случае разветвлённых цепей, в которых есть узлы. При использовании правил необходимо опираться на следующие идеи:
- ищем узлы и расписываем первое правило Кирхгофа (1) для каждого из них (часть уравнений может получится одинаковым);
- по количеству получившихся уравнений и неизвестных узнаём количество добавочных уравнений;
- определяем контур (или несколько), который будем использовать во втором правиле Кирхгофа (3);
- задаём направление обхода в контуре (произвольно);
- обозначаем токи на каждом из элементов, имеющих сопротивление (направление тока выбираем произвольно);
- записываем второе правило Кирхгофа для контура (условия выше).
Содержание:
Метод контурных токов:
Контурным током называют условный ток, протекающий внутри независимого контура.
Напомним, что контуры называются независимыми (подробнее см. разд. 2.1), если они отличаются друг от друга хотя бы одним элементом (ветвью). Направление отсчёта контурного тока выбирается произвольно и независимо от выбора направлений отсчётов контурных токов в других контурах. В отличие от метода токов ветвей, рассмотренного в лекции 4, данный метод позволяет уменьшить число уравнений, описывающих схему, до величины, равной числу
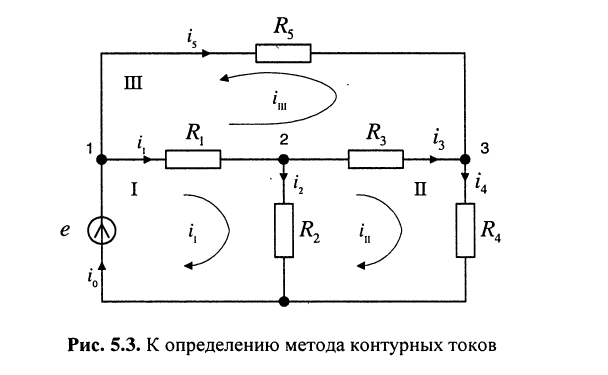
Предварительно покажем, что при известных контурных токах можно найти токи всех ветвей, а потому и напряжения на всех элементах цепи. Действительно, ток в любом элементе (ветви) определяется по первому закону Кирхгофа (ЗТК) как алгебраическая сумма контурных токов, протекающих в этом элементе. Например, при выбранных в удлинителе (рис. 5.3) направлениях отсчётов токов элементов и контурных токов имеем:
Зная токи, протекающие в элементах, можно по закону Ома определить напряжения на каждом из них.
Определение:
Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются контурные токи, называется методом контурных токов.
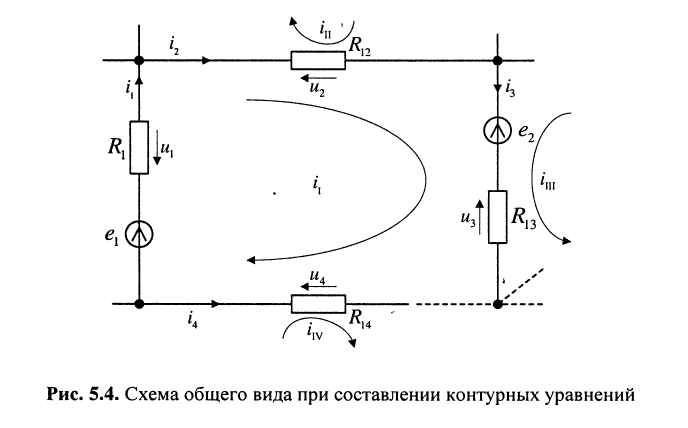
Составление контурных уравнений
При составлении системы контурных уравнений воспользуемся вторым законом Кирхгофа и будем полагать, что (рис. 5.4):
При этих условиях, выбранных независимых контурах и заданных направлениях отсчётов контурных токов запишем уравнение для первого контура (см. рис. 5.4) согласно второму закону Кирхгофа:
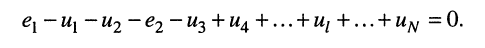
Выразим напряжения на элементах 1-го контура через токи ветвей по закону Ома:
или в общем виде:
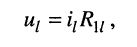
Подставим (5.6) в (5.5)
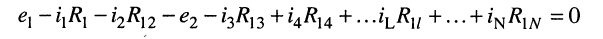
и выразим токи ветвей через контурные токи, нумерация которых осуществляется римскими цифрами и прямыми латинскими буквами. Из рис. 5.4 видно, что:
Произведём замену токов ветвей в выражении (5.7) через соотношения (5.8):
Умножим полученное уравнение на-1, раскроем скобки, приведём подобные члены и перенесём в правую часть известные значения напряжений источников; после выполнения этих действий контурное уравнение принимает вид
Подобное уравнение можно было бы составить и для любого другого контура, поэтому полученный результат позволяет сделать обобщающие выводы:
Аналогично записываются узловые уравнения для всех других контуров цепи, в результате чего образуется система контурных уравнений вида:
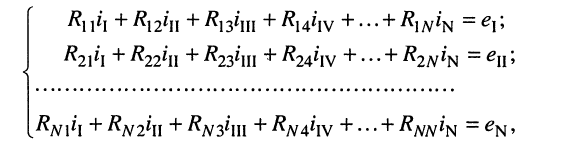
где:
Система контурных уравнений (5.9) составлена относительно неизвестных контурных токов и записана в канонической форме, а именно:
- контурные ЭДС, как свободные члены, записываются в правых частях уравнений;
- неизвестные контурные токи записываются в левых частях уравнений с последовательно возрастающими индексами;
- уравнения располагаются в соответствии с порядковыми номерами контуров.
Пример 5.2.
Записать систему контурных уравнений для удлинителя (рис. 5.3).
Решение. Предварительно найдём собственные и взаимные сопротивления трёх контуров:
I контура:
• собственное сопротивление
• взаимные сопротивления: со вторым контуром 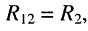
II контура:
• собственное сопротивление
• взаимные сопротивления: с первым контуром 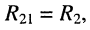
III контура:
• собственное сопротивление
• взаимные сопротивления: с первым контуром 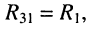
Заметим, что:
Теперь можно записать систему контурных уравнений, руководствуясь указанными ранее правилами:
Особенности составления контурных уравнений
Рассмотренные ранее цепи не содержали независимых источников тока, поэтому количество контурных уравнений согласно (5.4) равно количеству независимых контуров. Однако цепь может иметь несколько источников токов. В этом случае следует выбрать такое дерево цепи, при котором источники токов входили бы в число соединительных элементов. Тогда через каждый источник тока будет проходить ток только одного контура, который равен задающему току источника. Поэтому уменьшается как число неизвестных контурных токов, так и число контурных уравнений. Следовательно, если цепь содержит 
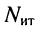
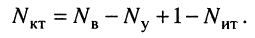
Пример 5.3.
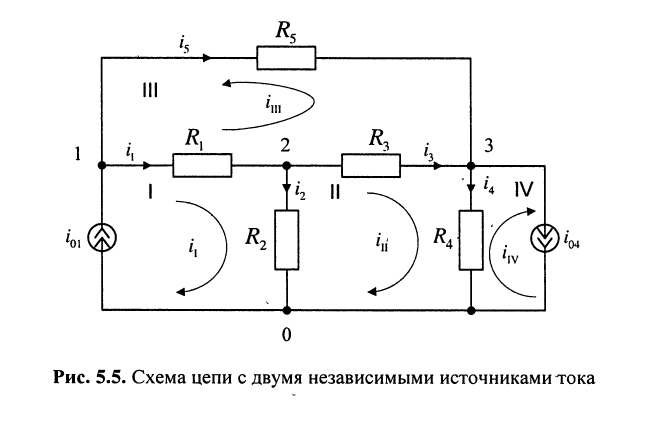
Записать систему контурных уравнений для цепи, схема которой изображена на рис. 5.5.
Решение. Цепь содержит два источника тока: в первом и четвёртом контурах, где контурные токи совпадают с токами источников:
поэтому достаточно записать только два контурных уравнения — для второго и третьего контуров.
В уравнении для третьего контура отсутствует слагаемое, содержащее ток 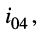
Важно:
метод контурных токов применяют в тех случаях, когда число контурных уравнений меньше числа узловых уравнений, а также при анализе колебаний в линейных электрических цепях произвольной конфигурации, содержащих все виды элементов.
Решение системы контурных (узловых) уравнений
Решение системы контурных (узловых) уравнений состоит в нахождении неизвестных контурных токов (узловых напряжений) для последующего вычислением токов и напряжений на элементах цепи. Если параметры цепи (сопротивления, проводимости, токи источников токов, ЭДС источников напряжений) заданы численно, то решение систем осуществляется с помощью специальных пакетов программ математического моделирования, например, Matlab или Matcad.
Основные понятия теории определителей
При теоретическом анализе удобнее использовать методы теории определителей, позволяющие записать решения в компактной форме. Прежде чем обращаться к этим методам, дадим основные понятия теории определителей.
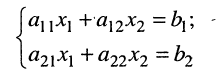
с неизвестными 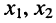
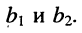
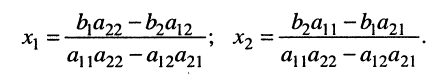
Стоящее в знаменателях полученных дробей выражение 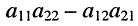
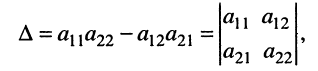
где вертикальные чёрточки являются знаком определителя. С помощью этого обозначения формулы (5.13) можно записать в виде
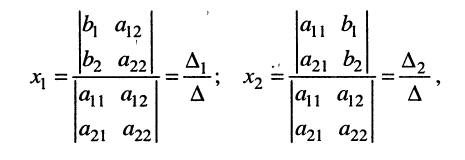
где 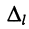
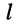
Из соотношений (5.14) следует: каждая из неизвестных 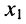
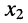
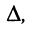
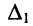
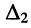
Подобным образом решается система уравнений любого порядка. Остаётся выяснить, как вычислять определители, если их порядок больше двух.
Рассмотрим вычисление определителя на примере системы третьего порядка:
решение которой приводит к дробям вида (5.12), где в знаменателе оказывается выражение
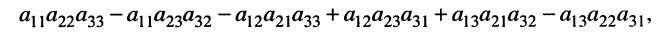
называемое определителем третьего порядка и обозначаемое
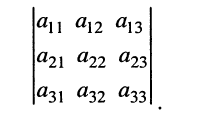
Применяя к (5.16) выражение (5.15), запишем определитель (5.16) в более удобной и наглядной форме:
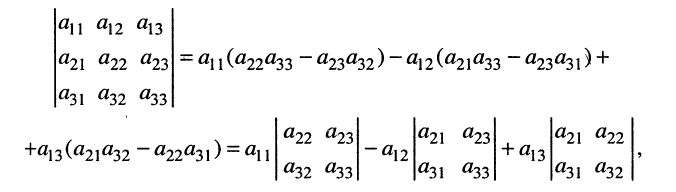
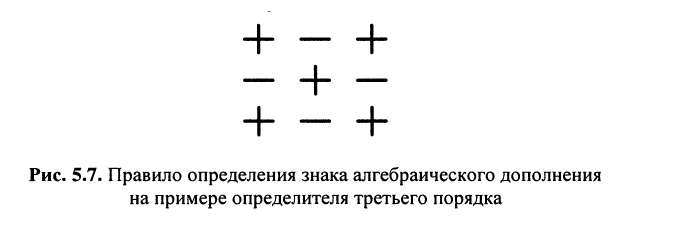
по которой можно вычислять значение определителя третьего порядка. Нетрудно видеть, что правая часть равенства состоит из суммы произведений коэффициентов (элементов) первой строки и определителей второго порядка с нужными знаками. Эти определители называются минорами и получаются из исходного определителя вычёркиванием первой строки и соответствующего данному элементу столбца. Например, минор относительно элемента 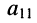
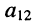
Подобные разложения можно произвести относительно элементов любой строки, предварительно записав соответствующие миноры.
Определение:
Минором 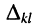
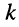
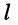
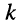
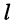
Знак минора определяется по формуле 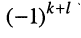
Определение:
Алгебраическим дополнением 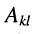
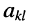
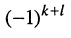
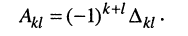
Из сказанного следует: определитель равен сумме произведений элементов какого-нибудь из рядов (строки или столбца) на алгебраические дополнения этих элементов.
При вычислении определителей больших порядков их предварительно разлагают на алгебраические дополнения. Отметим также, что подобно (5.14) для любой системы, у которой 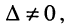
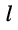
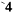
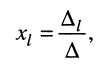
т. е. каждая 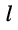
Применение теории определителей для решения контурных (узловых) уравнений
Применяя методы теории определителей к системе контурных уравнений (5.9), по формуле Крамера находим решение для первого контурного тока
где
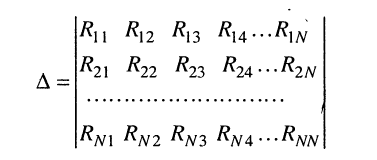
представляет собой определитель системы контурных уравнений (5.9), а
находится из определителя (5.20) при замене в нём первого столбца свободными членами. Заметим, что определитель (5.20) является симметричным относительно главной диагонали, поскольку 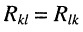
Разлагая определитель 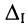
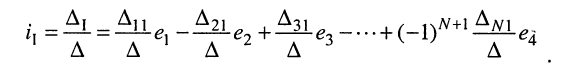
Аналогичное решение можно найти и для L-го контурного тока, разлагая определитель 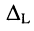
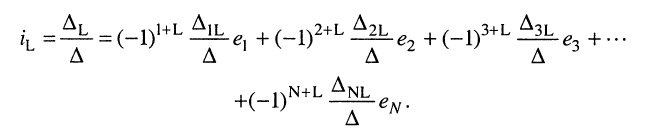
Полученное общее решение (5.22) системы контурных уравнений (5.9) показывает, что реакция в виде токов в электрической цепи представляет собой сумму реакций, вызываемых каждым из воздействий 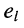
Аналогичным образом рассчитывается система узловых уравнений (5.2).
Примеры использования теории определителей
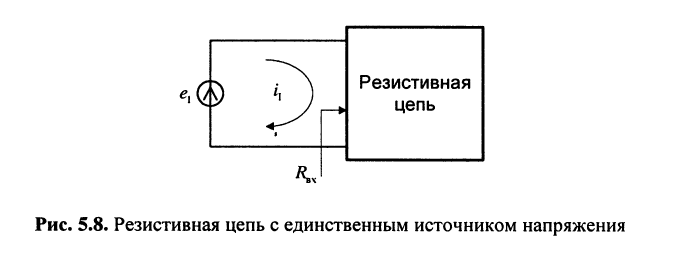
Задача 5.1.
Цепь имеет единственный источник напряжения 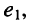
Решение. Для удобства назовём контур, замыкающийся через источник, первым. Тогда из (5.21) следует
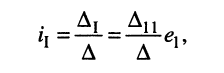
и согласно закону Ома имеем
откуда получаем соотношение
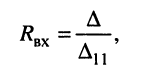
называемое входным сопротивлением двухполюсника. Оно представляет собой эквивалентное сопротивление пассивного резистивного двухполюсника.
Заметим, что в резистивном двухполюснике электрическая энергия может только рассеиваться, поэтому при выбранных на рис. 5.8 направлениях отсчёта тока и напряжения коэффициент 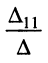
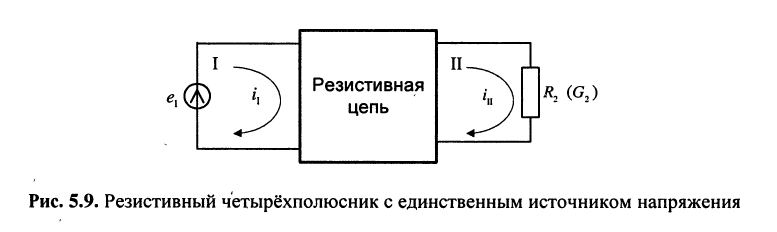
Задача 5.2.
Найти ток в заданной ветви резистивной цепи (рис. 5.9), имеющей единственный источник напряжения в
Решение. Такую цепь можно рассматривать как резистивный четырёхполюсник, в котором вновь для удобства обозначим контур, содержащий источник напряжения, первым (I), а контур, содержащий интересующую нас ветвь, вторым (II).
При выбранных направлениях отсчёта ЭДС источника 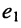
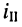
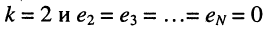
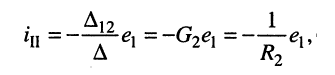
где
представляет собой собственное сопротивление второго контура и потому эквивалентное сопротивление четырёхполюсника.
Метод контурных токов
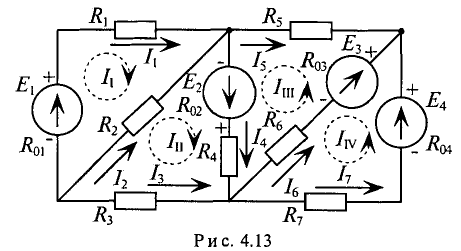
При расчете сложных цепей методом узловых и контурных уравнений (по законам Кирхгофа) необходимо решать систему из большого количества уравнений, что значительно затрудняет вычисления.
Так, для схемы рис. 4.13 необходимо составить и рассчитать систему из 7-ми уравнений
Ту же задачу можно решить, записав только 4 уравнения по второму закону Кирхгофа, если воспользоваться методом контурных токов.
Суть метода состоит в том, что в схеме выделяют т независимых контуров, в каждом из которых произвольно направлены (см. пунктирные стрелки) контурные токи 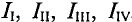
Как видно из рис. 4.13, отдельные ветви схемы входят в два смежных контура. Действительный ток в такой ветви определяется алгебраической суммой контурных токов смежных контуров.
Таким образом
Для определения контурных токов составляют т уравнений по второму закону Кирхгофа. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в данный контур (по одну сторону от знака равенства), и общее падение напряжения в данном контуре, созданное контурным током данного контура и контурными токами смежных контуров (по другую сторону знака равенства).
Для данной схемы (рис. 4.13) необходимо составить 4 уравнений. Со знаком «плюс» записываются ЭДС и падения напряжено разные стороны знака равенства), действующие в направлении контурного тока, со знаком «минус» — направленные проконтурного тока.
Система уравнений для схемы (рис. 4.13):
Решением системы уравнений вычисляются значения контур-токов, которые и определяют действительные токи в каждой и схемы (рис. 4.13).
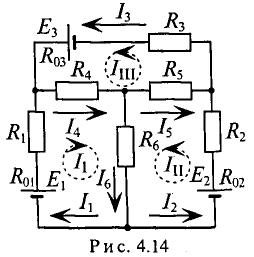
Пример 4.11
Определить токи во всех участках сложной цепи (рис. 4.14), если:
Решение
Необходимо составить 3 уравнения по второму закону для определения контурных токов 1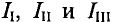
Подставляются числовые значения величин
Из уравнения (2) определяется ток
Значение тока 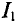
То же значение тока 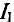
Из полученного уравнения (3) вычитается полученное уравнение (1). В результате получим
Откуда контурный ток
Из уравнения (3) определяется контурный ток
Из уравнения (2′) определяется ток
Вычисляются реальные токи в заданной цепи:
Проверяется правильность решения для 1 -го контура (рис. 4.14).
Решение правильное.
Такую же проверку можно произвести и для других контуров (2-го и 3-го):
Проверка показала правильность решения.
Определение метода контурных токов
Данный метод является фундаментальным и применим для расчета любых электрических цепей. Он базируется на уравнениях, составленных по второму закону Кирхгофа. В схеме выделяются независимые контуры, в каждом из них произвольно выбираются направления контурных токов и составляются уравнения по второму закону Кирхгофа. Для цепи по рис. 3.1 имеем:
Введем в полученную систему уравнений обобщенные параметры:
собственное сопротивление контура – сумма сопротивлений, входящих в состав контура, например, для первого контура:
смежные сопротивления – сопротивления на границах контуров, например, 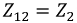
Тогда система уравнений примет вид:
Используя матричный метод расчета, можем записать:
В уравнении (3.8) 
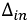
Токи ветвей, находящихся на границах контуров:
Справочный материал по методу контурных токов
Метод контурных токов является одним из основных методов расчета сложных электрических цепей, которым широко пользуются на практике. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так называемые контурное токи, замыкающиеся в контурах.
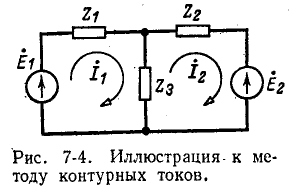
На рис. 7-4 в виде примера показана двухконтурная электрическая цепь, в которой 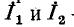
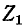
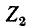
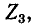
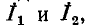
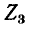
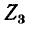
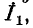
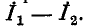
Число уравнений, записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, т. е. для электрической схемы с числом узлов q и числом ветвей р задача нахождения контурных токов сведется к решению системы р — q + I уравнений. Так, в схеме рис. 7-4 q = 2, р = 3; следовательно, число уравнений равно 3 — 2+1=2 (число независимых контуров).
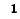
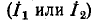
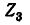
Условимся сумму комплексных сопротивлений, входящих в контур, называть собственным сопротивлением контура, а комплексное сопротивление, принадлежащее одновременно двум или нескольким контурам, — общим сопротивлением этих контуров.
Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от данного контурного тока в собственном сопротивлении контура берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис. 7-4, где направление обоих контурных токов выбрано по ходу часовой стрелки.
Для заданной электрической схемы с двумя независимыми контурами (рис. 7-4) могут быть записаны два уравнения по второму закону Кирхгофа, а именно:,
где 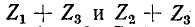
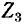
Если заданная электрическая схема содержит п независимых контуров, то на основании второго закона Кирхгофа получается система из п уравнений:
Здесь 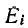
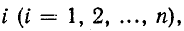
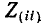
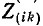
В соответствии со сказанным ранее собственные сопротивления 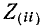
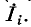
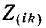
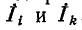
Решение уравнений (7-2) относительно искомых контурных токов может быть найдено с помощью определителей:
ит. д., где определитель системы
Согласно правилу разложения определителя по элементам столбца определитель равен сумме произведений элементов столбца на их алгебраические дополнения. Поэтому решение уравнений запишется в виде
Здесь Дitl — алгебраическое дополнение элемента Z{lk) определителя системы, т. е. умноженный на (—1)‘+* минор элемента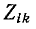
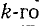
Сокращенно система уравнений (7-3) записывается в виде:
Первый индекс алгебраического дополнения i, обозначающий номер строки, вычеркиваемой в определителе системы, соответствует номеру контура, контурная э. д. с. которого умножается на данное алгебраическое дополнение. Второй индекс 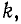
Уравнения (7-2), выражающие второй закон Кирхгофа, записаны в предположении, что источниками электрической энергии служат источники э. д. с. При наличии в электрической схеме источников тока они могут быть заменены эквивалентными источниками э. д. с.
Если проводимости источников тока равны нулю, то целесообразно выбрать заданные токи в качестве контурных; тогда число неизвестных контурных токов и соответственно число уравнений сократятся на число заданных токов.
Если в заданной электрической схеме имеются параллельные ветви, то замена их эквивалентным комплексным сопротивлением сокращает число контуров (за счет тех, которые образованы параллельными ветвями).
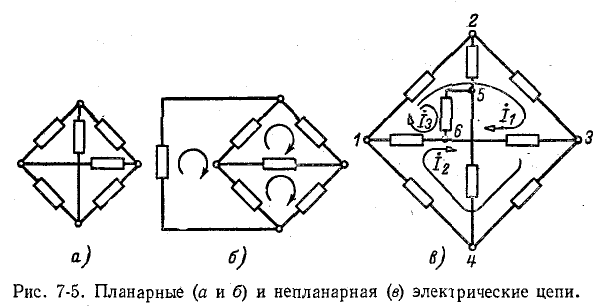
Электрические цепи могут быть планарными или непланарными.
Планарная, или плоская, электрическая цепь может быть вычерчена на плоскости в виде схемы с непере-крещивающимися ветвями. В некоторых случаях пересечение ветвей в электрической схеме, являющееся результатом Принятого способа начертания схемы, устраняется при другом способе изображения данной планарной электрической цепи, как это, например, представлено на рис. 7-5.
Электрическая цепь, приведенная на рис. 7-5, а, планарна, так как имеющееся пересечение ветвей устранимо в соответствии с рис. 7-5, б.
Не планарная электрическая цепь не может быть вычерчена на плоскости в виде схемы с неперекрещиваю-щимися ветвями. Примером такой электрической цепи служит приведенная на рис. 7-5, в непланарная цепь, пересечение ветвей в которой не может быть устранено.
Если направление контурных токов во всех контурах планарной электрической цепи одинаково, например совпадает с ходом часовой стрелки, то общие сопротивления смежных контуров входят в систему уравнений (7-2) со знаком минус, так как контурные токи смежных контуров
направлены в общих ветвях встречно. Направление контурных токов по ходу часовой стрелки принимается во всех контурах, кроме внешнего, охватывающего всю схему. В последнем контурный ток направляется против часовой стрелки'(см. пример 7-2). Это правило, однако, не является обязательным.
В случае непланарной электрической цепи не представляется возможным иметь в общих ветвях только разности контурных токов, как это, например, видно из схемы рис. 7-5, в.
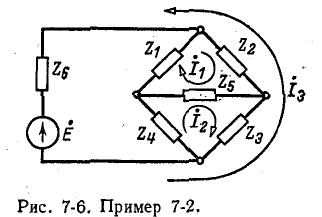
Пример 7-2.
Пользуясь методом контурных токов, определить ток в диагонали бюстовой схемы рис. 7-6.
Выбранные положительные направления контурных токов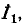
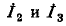
Решение полученной системы уравнений относительно контурных токов 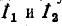
где М имеет то же значение, что и в примере 7-1.
Искомый ток в диагонали мостовой схемы равен разности контурных токов:
что совпадает с полученным в примере 7-1 ответом.
Следует заметить, что если в заданной схеме контуры выбрать так, чтобы через ветвь 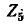
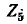
задача сведется к нахождению только одного контурного тока (вместо двух).
- Метод свертывания электрической цепи
- Метод преобразования схем электрических цепей
- Параллельное соединение генераторов
- Метод узловых и контурных уравнений
- Метод узловых потенциалов
- Принцип и метод наложения
- Входные и взаимные проводимости
- Преобразование треугольника сопротивлений в эквивалентную звезду