ГЛАВНОЕ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ
ГРОДНЕНСКОГО ОБЛАСТНОГО ИСПОЛНИТЕЛЬНОГО КОМИТЕТА
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «ИВЬЕВСКИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ»
ЭСО «ТЕЛА ВРАЩЕНИЯ»
ЭСО
→ ТЕЛА ВРАЩЕНИЯ
→ Конус
Пред. ←
Содержание
→ След.
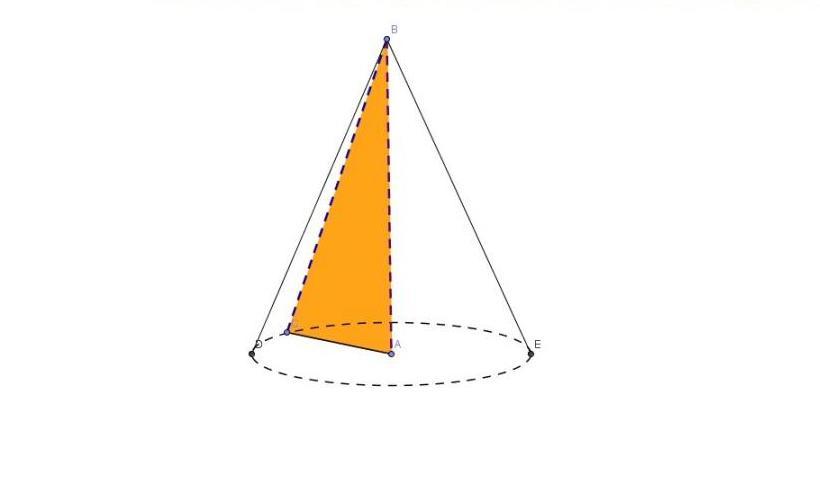
Конус, описанный около сферы
Конус называется описанным около сферы
(сфера – вписанной в конус), если сфера касается основания
конуса и каждой его образующей.
Пред. ←
Содержание
→ След.
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна
Найдите радиус сферы.
Спрятать решение
Решение.
Высота конуса перпендикулярна основанию и равна радиусу сферы. Тогда по теореме Пифагора получаем:
Поскольку по условию образующая равна радиус сферы равен 50.
Ответ: 50.
Радиус и образующая конуса
Свойства
Поскольку радиус конуса характеризует размер его основания, то зная его, можно найти диаметр, длину окружности и площадь круга, лежащего в основании. Диаметр представляет собой удвоенный радиус, длина окружности – удвоенный радиус, умноженный на число π, а площадь круга – квадрат радиуса, умноженный на число π. d=2r P=2πr S_(осн.)=πr^2
Зная радиус и образующую конуса, можно уже найти его высоту, угол между образующей и основанием, угол раствора конуса. Высота конуса через радиус и образующую ищется по теореме Пифагора в прямоугольном треугольнике, оттуда же можно вычислить и угол β через тригонометрические отношения сторон. Угол α можно найти из равнобедренного треугольника, образованного двумя образующими и диаметром, отняв из 180 градусов два угла β. (рис.40.1, 40.2) h=√(l^2-r^2 ) cosβ=r/l α=180°-2β
Площадь боковой поверхности конуса равна произведению полупериметра основания на образующую или произведению числа π на радиус и образующую. Чтобы найти площадь полной поверхности, зная радиус и образующую конуса, необходимо прибавить к площади боковой поверхности произведение числа π на квадрат радиуса, что является площадью основания конуса. S_(б.п.)=πrl S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)
Объем конуса, также как и объем пирамиды рассчитывается как одна треть основания, умноженная на высоту. V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, вычисляется как произведение высоты на радиус конуса, деленное на сумму радиуса и образующей. Радиус сферы, описанной вокруг конуса, представляет собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4) r_1=hr/(l+r)=(r√(l^2-r^2 ))/(l+r) R=l^2/2h
Как найти образующую конуса обычного и усеченного. Формулы
Пространственные фигуры подробно рассматриваются в старших классах общеобразовательных школ в курсе стереометрии. Данная статья содержит ответ на вопрос о том, как найти образующую конуса круглого прямого и образующую соответствующей усеченной фигуры.
Фигура конус
Чтобы понять, как найти образующую конуса, следует дать представление об этой фигуре. Круглым прямым конусом называют фигуру вращения прямоугольного треугольника вокруг одного из его катетов. Рисунок ниже демонстрирует процесс вращения.

Полученная пространственная фигура имеет следующие характеристики:
Заметим, что высота фигуры пересекает круглое основание в его центре. Это является достаточным условием, чтобы считать конус прямым.
Образующая конуса
Теперь можно переходить к ответу на вопрос о том, как найти образующую конуса круглого прямого. Выше было сказано, что она представляет собой отрезок, который лежит на конической поверхности и соединяет вершину с точкой окружности основания. В прямоугольном треугольнике, из которого был конус получен, образующая является гипотенузой. Это наблюдение позволяет записать известную теорему Пифагора, связав образующую g с радиусом r и высотой h фигуры. Формула, как найти образующую конуса, имеет вид:
Помимо этой формулы, на практике вместо высоты или радиуса фигуры может быть известен угол φ между образующей и основанием. В этом случае генератрису g можно рассчитать с помощью следующих выражений:
Эти формулы следуют из свойств тригонометрических функций синуса и косинуса.
Таким образом, вычисление образующей конуса возможно, если знать любые два параметра фигуры.
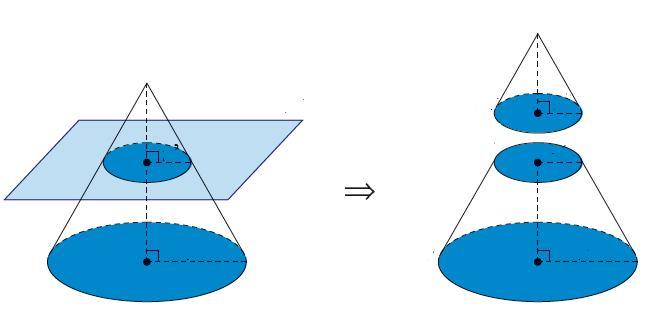
Фигура конус усеченный
Он также является фигурой вращения, только вместо прямоугольного треугольника следует вращать прямоугольную трапецию. На рисунке ниже показан усеченный конус.
Здесь синие стрелки показывают прямоугольную трапецию. Длина вертикальной стрелки является высотой h фигуры, длины двух других синих стрелок – это радиусы оснований конуса. В отличие от цилиндра, основания усеченного конуса имеют разную площадь. Обозначим их радиусы r1 и r2. Четвертая наклонная к основанию сторона трапеции является образующей или генератрисой. Как и для обычного конуса, для усеченного все генератрисы равны друг другу и образуют боковую поверхность фигуры.
Заметим, что усеченный конус получил такое название потому, что его можно получить не только вращением трапеции, но и с помощью отсечения плоскостью верхней части круглого прямого конуса.
Генератриса усеченной фигуры
Итак, мы познакомились с усеченным конусом, а также с понятием о его образующей. Как находить образующую конуса усеченного? Для того чтобы получить нужную формулу, заметим, если высоту h перенести параллельно самой себе к боковой поверхности конуса так, чтобы она касалась одним концом образующей фигуры, то получится прямоугольный треугольник. Его сторонами будут высота h (катет), генератриса g (гипотенуза) и r1-r2 (катет). Тогда можно записать формулу для определения g:
Соответственно, если дан острый угол φ1 между большим основанием и генератрисой, тогда последнюю можно определить так:
Если же известен тупой угол φ2 между малым основанием и генератрисой, тогда для ее вычисления необходимо применять такие выражения:
Здесь первая формула является точно такой же, как для угла φ1, а во второй формуле радиусы в числителе поменялись местами.
Таким образом, найти образующую конуса усеченного можно, если знать любые три его параметра.
Узнать ещё
Знание — сила. Познавательная информация
Конус, вписанный в шар
Решение задач на конус, вписанный в шар (конус, вписанный в сферу) сводится к рассмотрению одного или нескольких треугольников.
Конус вписан в шар, если его вершина и окружность основания лежат на поверхности шара, то есть на сфере. Центр шара лежит на оси конуса.
При решении задач на конус, вписанный в шар, удобно рассматривать сечение комбинации тел плоскостью, проходящей через ось конуса и центр шара. Сечение представляет собой большой круг шара (то есть круг, радиус которого равен радиусу шара) с вписанным в него равнобедренным треугольником — осевым сечением конуса. Боковые стороны этого треугольника — образующие конуса, основание — диаметр конуса.
Если угол между образующими острый, центр описанного круга лежит внутри треугольника (соответственно, центр описанного около конуса шара — внутри конуса).
Если угол между образующими прямой, центр круга лежит на середине основания треугольника (центр шара совпадает с центром основания конуса).
Если угол между образующими тупой, центр круга лежит вне треугольника (центр описанного шара — вне конуса).
Если в условии задачи не сказано, где именно лежит центр описанного шара, желательно рассмотреть, как могут повлиять на решение различные варианты его расположения.
Рассмотрим конуса и описанного около него шара плоскостью, проходящей через ось конуса и центр шара. Здесь SO=H — высота конуса, SB=l — образующая конуса,SO1=O1B=R — радиус шара, OB=r — радиус основания конуса, ∠OSB=α — угол между высотой и образующей конуса.
Треугольник SO1B — равнобедренный с основанием SB (так как SO1=O1B=R). Значит, у него углы при основании равны: ∠OSB=∠O1BS=α, и O1F — медиана, высота и биссектриса. Отсюда SF=l/2.
При решении задач на конус, вписанный в шар, можно рассмотреть прямоугольные треугольники SFO1 и SOB. Они подобны (по острому углу S). Из подобия треугольников
В прямоугольном треугольнике SOB ∠OBS=90º — ∠OSB=90º-α. По теореме Пифагора
В прямоугольном треугольнике O1OB ∠OBO1=90º — ∠O1BS=90º — α — α=90º — 2α.
Если продлить SO до пересечения с окружностью, получим прямоугольный треугольник SBM (∠SBM=90º как вписанный угол, опирающийся на диаметр SM). В нем BO- высота, проведенная к гипотенузе. По свойствам прямоугольного треугольника
[spoiler title=”источники:”]
http://1ku.ru/obrazovanie/45666-kak-najti-obrazujushhuju-konusa-obychnogo-i-usechennogo-formuly/
[/spoiler]
Думаю, что речь идёт о совсем другой задаче.
Задача. Площадь боковой поверхности усечённого конуса, описанного около сферы, равна 12π см^2. Найдите длину образующей этого усечённого конуса.
Указание к решению задачи:
Проведите через ось усечённого конуса (P) произвольную плоскость β. Тогда эта плоскость пересечёт (P) по равнобокой трапеции ABCD (AD||BC, AD>BC), а сферу – по большой окружности ω, причём окружность ω будет вписана в трапецию ABCD.
Пусть M, H, K – точки касания окружности ω со сторонами BC, AD, CD соответственно.
Обозначьте радиусы оснований (P) через r, R (R>r) и выразите с помощью r и R длину образующей CD усечённого конуса (P) (воспользуйтесь свойством отрезков касательных, проведенных из одной точки к окружности). Далее примените формулу для нахождения площади боковой поверхности усечённого конуса.
Ролик к задаче:
Пирамида, вписанная в конус
Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина совпадает с вершиной конуса. При этом конус называется описанным около пирамиды.
Около пирамиды можно описать конус тогда и только тогда, когда около ее основания можно описать окружность.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Упражнение 1
Найдите сторону основания правильной треугольной пирамиды, вписанной в конус, радиус основания которого равен 1.
Ответ:
Упражнение 2
Найдите сторону основания правильной четырехугольной пирамиды, вписанной в конус, радиус основания которого равен 1.
Ответ:
Упражнение 3
Найдите сторону основания правильной шестиугольной пирамиды, вписанной в конус, радиус основания которого равен 1.
Ответ: 1.
Пирамида, описанная около конуса
Пирамида называется описанной около конуса, если ее основание описано около основания конуса, а вершина совпадает с вершиной конуса. При этом конус называется вписанным в пирамиду.
В пирамиду можно вписать конус тогда и только тогда, когда в ее основание можно вписать окружность.
Упражнение 1
Найдите сторону основания правильной треугольной пирамиды, описанной около конуса, радиус основания которого равен 1.
Ответ:
Упражнение 2
Найдите сторону основания правильной четырехугольной пирамиды, описанной около конуса, радиус основания которого равен 1.
Ответ: 2.
Упражнение 3
Найдите сторону основания правильной шестиугольной пирамиды, описанной около конуса, радиус основания которого равен 1.
Ответ:
Сфера, вписанная в конус
Сфера называется вписанной в конус, если она касается его основания и боковой поверхности (касается каждой образующей). При этом конус называется описанным около сферы.
В любой конус (прямой, круговой) можно вписать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, вписанной в треугольник, являющийся осевым сечением конуса.
Напомним, что радиус r окружности, вписанный в треугольник, находится по формуле
где S – площадь, p – полупериметр треугольника.
Упражнение 1
В конус, радиус основания которого равен 1, а образующая равна 2, вписана сфера. Найдите ее радиус.
Решение. Треугольник SAB равносторонний. Высота SH равна Площадь S равна Полупериметр p равен 3. По формуле r = S/p получаем
Упражнение 2
В конус, радиус основания которого равен 2, вписана сфера радиуса 1. Найдите высоту конуса.
Решение. Обозначим h высоту SH конуса . Из формулы r = S/p имеем:
где r = 1, a = FG = 4, p =
Решая уравнение
находим
Упражнение 3
Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус вписанной сферы.
Решение. Высота SH конуса равна 1. Образующая .
Полупериметр p равен
По формуле r = S/p , имеем
Ответ:
Упражнение 4
Высота конуса равна 8, образующая 10. Найдите радиус вписанной сферы.
Решение. Радиус основания конуса равен 6. Площадь треугольника SFG равна 48, полупериметр 16. По формуле r = S/p имеем r = 3.
Ответ: r = 3.
Упражнение 5
Можно ли вписать сферу в наклонный конус?
Ответ: Нет.
Сфера, вписанная в усеченный конус
Сфера называется вписанной в усеченный конус, если она касается его основани й и боковой поверхности (касается каждой образующей). При этом усеченный конус называется описанным около сферы.
В усеченный конус можно вписать сферу, если в его осевое сечение можно вписать окружность. Радиус этой окружности будет равен радиусу вписанной сферы.
Упражнение 1
В усеченный конус, радиусы оснований которого равны 2 и 1, вписана сфера. Найдите радиус сферы и высоту усеченного конуса.
Решение. Имеем: A 1 B = A 1 O 1 = 2, A 2 B = A 2 O 2 = 1. Следовательно, A 1 A 2 = 3 , A 1 C = 1.
Таким образом,
Упражнение 2
В усеченный конус, радиус одного основания которого равен 2, вписана сфера радиуса 1. Найдите радиус второго основания.
Решение. Пусть A 1 O 1 = 2. Обозначим r = A 2 O 2 . Имеем: A 1 A 2 = 2+ r , A 1 C = 2 – r . По теореме Пифагора, имеет место равенство из которого следует, что выполняется равенство Решая полученное уравнение относительно r , находим
Упражнение 3
В усеченном конусе радиус большего основания равен 2, образующая наклонена к плоскости основания под углом 60 о . Найдите радиус вписанной сферы.
Решение. Заметим, что осевым сечением конуса, из которого получен усеченный конус, является равносторонний треугольник со стороной 2. Радиус r сферы, вписанной в усеченный конус, равен радиусу окружности, вписанной в этот равносторонний треугольник, т.е.
Упражнение 4
Образующая усеченного конуса равна 2, площадь осевого сечения 3. Найдите радиус вписанной сферы.
Решение. Воспользуемся формулой r = S/p , где S – площадь осевого сечения, p – полупериметр. В нашем случае S = 3 . Для нахождения полупериметра напомним, что для четырехугольника, описанного около окружности, суммы противоположных сторон равны. Значит, полупериметр равен удвоенной образующей цилиндра, т.е. p = 4. Следовательно, r = ¾.
Ответ:
Упражнение 5
Можно ли вписать сферу в усеченный наклонный конус.
Ответ: Нет.
Сфера, описанная около конуса
Сфера называется описанной около конуса, если вершина и окружность основания конуса лежат на сфере. При этом конус называется вписанным в сферу .
Около любого конуса (прямого, кругового) можно описать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, описанной около треугольника, являющимся осевым сечением конуса.
Напомним, что радиус R окружности, описанной около треугольника, находится по формуле
где S – площадь, a , b , c – стороны треугольника.
Упражнение 1
Около конуса, радиус основания которого равен 1, а образующая равна 2, описана сфера. Найдите ее радиус.
Решение. Треугольник SAB равносторонний со стороной 2. Высота SH равна Площадь S равна По формуле R = abc /4 S получаем
Упражнение 2
Около конуса, радиус основания которого равен 4, описана сфера радиуса 5. Найдите высоту h конуса.
Решение. Имеем, OB = 5 , HB = 4. Следовательно, OH = 3. Учитывая, что SO = OB = 5, получаем h = 8.
Ответ: h = 8.
Упражнение 3
Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус описанной сферы.
Решение. Треугольник SAB – прямоугольный, равнобедренный. Следовательно, радиус R описанной сферы равен радиусу основания цилиндра, т.е. R = 1.
Ответ: R = 1.
Упражнение 4
Высота конуса равна 8, образующая 10. Найдите радиус описанной сферы.
Решение. В треугольнике SAB имеем: SA = SB = 10, SH = 8. По теореме Пифагора, AH = 6 и, следовательно, S = 48. Используя формулу R = abc /4 S , получаем
Упражнение 5
Можно ли описать сферу около наклонного конуса?
Ответ: Да.
Сфера, описанная около усеченного конуса
С фера называется описанной около усеченного конуса, если окружност и основани й усеченного конуса лежат на сфере. При этом усеченный к онус называется в писанным в сферу.
Около усеченного конуса можно описать сферу, если около его осевого сечения можно описать окружность. Радиус этой окружности будет равен радиусу описанной сферы.
Упражнение 1
Около усеченного конуса, радиусы оснований которого равны 2 и 1, а образующая равна 2, описана сфера. Найдите ее радиус.
Решение. Заметим, что A 1 O 1 B 2 O 2 и O 1 B 1 B 2 A 2 – ромбы. Треугольники A 1 O 1 A 2 , O 1 A 2 B 2 , O 1 B 1 B 2 – равносторонние и, значит, A 1 B 1 –диаметр. Следовательно, R = 2.
Ответ: R = 2,
Упражнение 2
Радиус меньшего основания усеченного конуса равен 1, образующая равна 2 и составляет угол 45 о с плоскостью другого основания. Найдите радиус описанной сферы.
Решение. Имеем A 2 O 2 = 1, A 1 A 2 = 2, O 1 O 2 = , OO 1 = O 1 C = 1. Следовательно, OO 2 = 1 + и, значит,
Упражнение 3
Радиус одного основания усеченного конуса равен 4, высота 7, радиус описанной сферы 5. Найдите радиус второго основания усеченного конуса.
Решение. Имеем OO 1 = 3 , OO 2 = 4 и, следовательно, O 2 A 2 = 3.
Ответ: 3.
Упражнение 4
Найдите радиус сферы, описанной около усеченного конуса, радиусы оснований которого равны 2 и 4, а высота равна 5.
Решение. Обозначим R радиус описанной сферы. Тогда
Учитывая, что O 1 O 2 = 6, имеем равенство
Решая его относительно R , находим
Упражнение 5
Можно ли описать сферу около усеченного наклонного конуса.
Ответ: Нет.