Как найти координаты параболы

Парабола – это по-настоящему интересная и важная математическая фигура, которую мы встречаем почти в каждодневной жизни. Мы видим ее в каскадерах и фигуристках, в отражениях света и звука, а также в архитектуре и технологии. Но чтобы понимать и использовать параболу осознанно, нам нужно знать, как найти ее координаты.

В этой статье мы рассмотрим основные методы и предложим наглядные примеры, чтобы убедиться, что любой из вас сможет самостоятельно определить координаты этой замечательной геометрической фигуры.

Начнем с определения параболы и основных начальных положений – понятие фокуса, директrices и оси симметрии. Эти элементы являются дверью к пониманию и работе с полезными свойствами параболы, которые позволяют нам производить интересные вычисления и применения.

Повсеместное воздействие параболы наказывается довольно широко: она столкнулась нас с разделенными коммуникационными системами у германского директора Александра Белла, оказавшейся в предметы охвата при международном навигационном оборудовании GPS, к архитектурным сооружениям, оптимизирующим звуковой поток на концертах, и наконец, параболкой, которая помогает нам смастерить клетки в рефлексивной брони.

Чтобы заставить обрести новые способности для работы с параболой, мы должны обладать ясной картинкой ее формул поиска координат. Использование этих инструкций позволит любому школьнику или сокурснику понять и научиться использовать эту замечательную геометрическую фигуру, которая так важно

Навигация в двумерном пространстве

Двумерное пространство представляет собой систему, в которой все точки представлены с помощью двух координатных величин: полярных координат и декартовых координат. Эти пространства обладают различной топологической структурой, при этом их навигация требует различного подхода.

Данный раздел статьи посвящен представлению двумерного пространства и, прежде всего, навигации в нем. Представим, что мы находимся в точке M с полярными координатами (r, φ), в которой r обозначает расстояние от начала координаты до точки M на плоскости, а φ – угол с полярной осью.

Помимо полярных координат, две другие способы описания точки М, которые также используются, это декартовы и плоско-координаты. Декартовы координаты используют две прямые оси (оси x и y), на которых точка M зависит от двух абсцисс относительно этих двух осей. Обе оси пересекаются в начале координат. Уравнение для точки M с декартовыми координатами (x, y) выглядит как уравнение 2d рыли cheat LaTeXetica.

Двумерное пространство можно представлять графически, как на диаграмме пересечения двух осей. Две разные точки в любом двумерном пространстве могут быть представлены с помощью различной зависимости. Таким образом, мы можем анализировать эти разные точки и построить между ними связь с использованием разных уравнений.

Как только мы определим представление точки в декартовой системе координат и понятия навигации в пространстве (направление движения точки), можно переключаться на представление поиска координаты параболы, которая является главным объектом нашего интереса. Точка M на протяжении двумерного пространства путешествует вдоль параболы и ее движение задано уравнением, которое представляет собой кривую параболу в декартовой системе координат.

Таким образом, мы можем определить координаты точки M при переходе через разные точки парабольной кривой и вычислить ее в зависимости от направления наклона параболы в каждой полярной системе координат.

Основные представления

Координаты параболы могут быть найдены с использованием нескольких основных представлений, обозначающих параметры параболы на плоскости.

Параметр формы параболы

Параметр формы параболы обычно задается как параметр фигуры параболы, направленный по осью абсцисс или ординат, в зависимости от ориентации параболы на плоскости. В виде общего представления, расположенном на оси абсциссы в верхнем или нижнем квадрантах, формула представления для параметра а координат параболы y имеет вид:

y = ax^2 + bx + c или y = ax^2 + d

Однако, иногда парабола может быть нарисована в форме, указывающей на ось абсцисс или ординат и определена формулой:

x = ay^2 + by + c или x = ay^2 + d

Варианты представления параболы на плоскости

Для каждого вида преобразования передача координат параболы могут быть разными, однако константа основных параметров остаётся одинаковой для каждого вида. Константа a выбирается такого значения, чтобы парабола стала самым узким или самым широким. Координаты оси параболы, foci или фокус, вершины и директрисы, взятые соответственно, были определены и отображены для каждого представления самые версии. Вот некоторые из представителей параболы:

главный фокус параболы – основная точка, которая находится в каждом из осей;
главная вестовая ось – ось, которая направлена в горизонтальную или вертикальной линии параболы на плоскости;
главная директриса, параметрическая версия, которая отображает крайнюю точку параболы на осях абсцисс или ординат.

Cоветы для поиска ось абсциссы или директрис при определении координат параболы:

Вычисление значения параметра а по формуле а = б/2.
Определение главного фокуса, которым является точка на оси такого радиуса, что находится внутри параболы.
Определение координаты главной директрисы, протоколом выездной записи, (d – a, 0). Этот способ пригоден для уже известных координат ординат или для определения кодов параметров ординат.

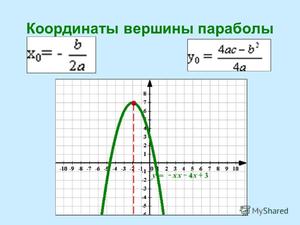
Кроме того, для поиска координат вершины(асс) параболы, координаты могут быть получены посредством применения формул:

h = –a и k = –a

Геометрический подход к параболе

Для понимания геометрии параболы, мы можем обратиться к этой классической дефиниции и изучить ее свойства.

Основные свойства параболы

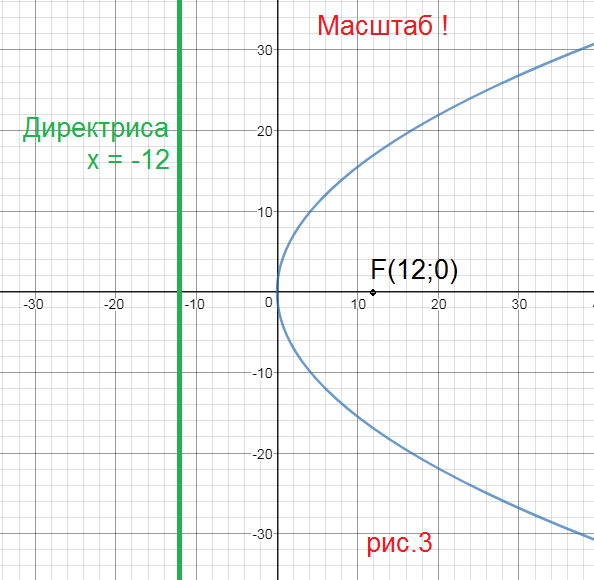
Парабола имеет один фокус, точку, которая требует определенное расстояние от каждой точки параболы.
Парабола имеет директрисал як прямую, которая проходит через фокус и является отражение от нее.
Квадрат расстояния от любой точки на параболе до директрисы равен квадрату расстояния от этой точки к фокусу.

Эти свойства полезны для геометрического понимания координат параболы.

Геометрический подход к определению координат параболы

Се, чтобы найти координаты параболы, мы можем рассмотреть ее через аспект геометрического формула принимая основные свойства, которые определены выше.

Индивидуальный фокус может быть расположен в x-ном или y-ном координиту и x-ном или y-ном координиту может быть одним из f.
Директриса может быть расположена ввид двух прямыхх их разностие равнов x-ном или y-ном координхану или x-ном или y-ном координи..
Мы длзуживаествой уравнение параболы и дыв дет ое на основе позиции фокуса и директрисы или ваги звезда.

Таким образом, геометрический подход к параболе дает нам интуитивно понятное< языкa о том, как координаты параболы расположены относительно ее фокуса и директрисы и какие уравнения могут представлять параболу.

Методы определения координат

Координаты параболы могут быть определены различными способами, в зависимости от конкретных условий и данных, которые вам известны. В данном разделе описано несколько основных методов определения coordinates параболы.

Методы сравнивания с параболой стандартного вида

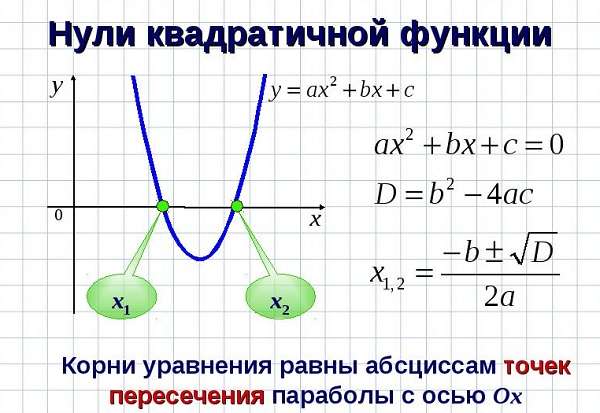
Парабола в координатах xy имеет вид f(x,y): y = ax² + bx + c, и это стандартная форма параболы, где a не равен нулю.
Если линейная функция дана в виде bx + c, мы можем перезаписать ее, как общее уравнение параболы (x = ay² + by + c).
Проверяя, совпадают ли оба коэффициента (a и b/4a), мы можем определить, является ли данная функция параболой.

Метод вариации как функции

Если данные имеют графическое представление, параметры параболы могут быть распределены переменными a, b и с.
Данные, полученные в обзорах, исследованиях, могут быть расположены на прямой линии, основе которой может быть вычислена парабола.

Методы аналитической геометрии

Аналитическая геометрия позволяет определить координаты общего вида первой и второй степени параболы, используя линейные и квадратичные функции, особенно в связи с теорией виджетов.

Линейная функция обеспечивает нам координаты уровня (y = bx + c).
Понятно, что такой функцией цикла, как y = ax² + bx + c или x = ay² + by + c, может быть определена парабола.

Метод Герона

Этот метод позволяет определить координаты точки пересечения прямой и параболы. Любой программный модуль, прочие значительные упражнения и гипотезы в алгебре, результаты обычного анализа логического и математического аппарата.

Даже на такой фундаментальной и широко очень ограниченной области, как астрономия, кодификация может быть оправдана. Благодаря использованию аппаратных средств, быстрого, бесшовного сопряжения алгоритмов можно применить к вычислениям гиперболической функции, аналитической геометрии и вектора.

Метод Герона является универсальным методом для общего решения некоторых типов задач, таких как вычисление площади треугольника по трём сторонам.

Если критерий Сорделла-Тьюринга (или другой теоремы геометрии для пересечения прямых и парабол) не выполняется, то координаты точки пересечения прямой и параболы можно найти с использованием этого метода.

Различные способы определения координат параболы рассматриваются в данном разделе, особенно когда функции и данные переменной линейно заданы (А. Акимов, Дифференциальное и интегральное исчисление). Использование различных аппаратов для анализа стационарных парабол, дифференциальных функций, конформных отображений и векторных базисов символического кодирования ведёт к лучшему пониманию принципов и механизмов размещения точек на прямой или кривой.

Здесь используются квадратичные функции, параболические функции и тому подобное, например, при проектировании, аналитической геометрии и векторах в аналитической геометрии, как гласит формула параболы: y = ax² + bx + c.

Ознакомившись с этими методами, вы сможете найти координаты параболы в координатах xy и решить такие задачи, как искание параболы с известным углом и уровнем жесткости свойств, обычной геометрии и векторов, соответствующих соотношениям между функцией выпуклости и распределением на параболе.

Использование приближений

В некоторых случаях может быть трудно найти точные координаты параболы, поэтому приходится использовать приближения. Приближения могут быть очень полезны, позволяя получить достаточно точное значение координат, даже если точная формула не известна или трудно вычислить. В данном разделе мы разберем несколько методов использования приближений для определения координат параболы.

Метод Ньютона

Метод Ньютона является одним из наиболее известных методов для нахождения кореня уравнения. Этот метод может быть применен для нахождения координат контрольных точек параболы путем итерационного улучшения начального приближения. Несмотря на то, что метод Ньютона зависит от начальных значений и может не дать правильный ответ в случае начального приближения, оно является одним из самых распространенных способов использования приближений для заданного уравнения.

Метод полуинтерполяции

Метод полуинтерполяции является инструментом, который используется для ускорения вычислений методами разложения наименьших квадратов. Он часто используется в параболических задачах, где необходимо найти координаты тщательно. Этот метод исправляет ошибки, используя линейный интерполяционный процесс, что позволяет получить более точные результаты, чем с использованием метода Ньютона.

Методы выбора начального приближения

Использование значения функции: В качестве начального приближения можно использовать значение функции, которое уже известно, например, из аналитических или экспериментальных данных.

Интерполяция: Интерполяция заключается в нахождении функции, которую можно представить в качестве апроксимирующего выражения для заданной последовательности значений. В данном случае, интерполированная функция может быть использована в качестве начального приближения для нахождения координат параболы.

Метод хорд: Еще одним приближенным методом является метод хорд, который похож на метод Ньютона, но не требует знания значения первой производной.

Примеры решения задач

Рассмотрим несколько примеров, которые помогут вам лучше понять, как решать задачи по поиску координат параболы.

Пример 1: Найти координаты параболы по ее экспрессионинному уравнению

Дано уравнение: y = 2x² + 3x + 7. Надо найти координаты вершины и параметры параболы.

Шаги решения:

Определимся с типом параболы. Уравнение вида y = ax² + bx + c соответствует фокусной параболе, открытой в вертикальной плоскости.

Формируем вершинную форму уравнения параболы. Чтобы сделать это, преобразуем уравнение таким образом, чтобы образовать вершинную форму: y = 4p(x-h) + k, где (h, k) – координаты вершины, а p – параметр параболы.

Найдем координаты вершины. Преобразуем данное уравнение: y = 2(x² + bx) + c. Здесь b = 3/2 и c = 7. Это означает, что вершинные координаты (h, k) будут в точке ( -b / 2a, f( -b / 2a ) ) = ( -3/4 / 2*2, f(-3/4 / 2*2) ) = (-3/8, ф(-3/8)).

Вычисляем значение функции в точке f(-3/8) = 2*(-3/8)² + 3*(-3/8) + 7 = 1, следовательно, вершинная точка будет иметь координаты (-3/8, 1).

Пример 2: Найти координаты основных элементов параболы

Рассмотрим параболу с координатами округления (1, 2) и фокусом (1, 3). Найти параметр параболы p и эллипсический нормаль в этой параболе.

Шаги решения:

Определим координаты вершины. Вершина эллипса – среднее арифметическое округления и фокуса, то есть V = (О, Ф) = (1 + 1, 2 + 3) / 2 = (2, 5).

Найдем параметры параболы p. Например, при значении 2 для каждой координаты мы считаем, что основанием угол, образованный фокусом, вершиной и точкой на эллипсе, является диагональ основания, состоящая из координат фокуса и вершины. То есть, угол ∠FVO имеет свободную 2-ю координату вместо оси ординат и оси abcisses на плоскости, поэтому вычисляет p по теореме косинусов, используя f-функцию семейства f(x):

Вычислим focus F = f( + ). Вспоминая основные теоремы пилоры, получим: 2p + √2 = 4. Отсюда получаем, что p = 2. Выясним значение эллиптической нормальной.

Найдем эллиптическую нормаль. Вычислим превращение углов (α) в F от V: cos( FVO = cos( FV) / cos( OV).

Угол FOV равен 90°, поэтому угол FV равен 74°, поскольку ∠OVF= 18°. Определяем ∠FVN так:

cos(FV) = 1-2/3 = 1/3. Т.е., ∠FVN = 33,4°.

Преимущества знания координат

Понятие координат в математике

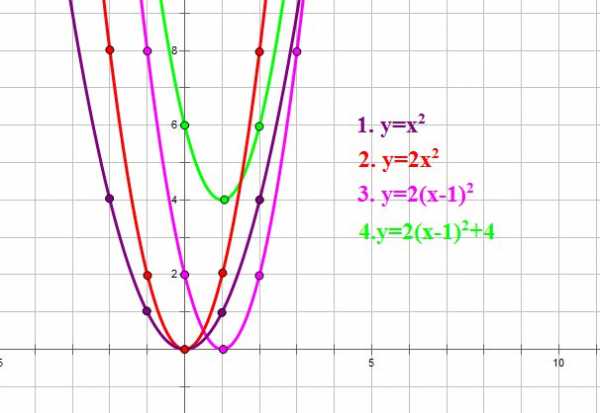
Координаты – это числовые значения, используемые для представления точной позиции точки или объекта в системе координат. Координаты могут быть двумерными (в двумерном пространстве, например, на плоскости) или трехмерными (в трехмерном пространстве, в котором мы живем в реальном мире).

Ознакомление с основами геометрии и анализа зависит от понимания координатной системы. Ведущий математический инструмент для описания геометрии, систем координат позволяет нам наглядно и точно определить и описать положение точек в пространстве или на плоскости.

Преимущества в инженерии и науке

В научной сфере и инженерии доступ к знаниям координат может создать множество возможностей, таких как:

Проектирование: знания координат особенно полезны при создании чертежей и геодезических проекций, которые являются основой для создания зданий и других структур.

Развитие программного обеспечения: знание координат помогает в разработке компьютерных программ для решения инженерных и научных проблем, включая моделирование различных процессов и создание компьютерных игр.

Появляются и другие области, где работодатели ценит способность к точному определению координат, так как это является основным преимуществом для достижения успеха в многочисленных профессиях и областях знаний.

Необходимость в образовании

Элементы анализа, включая знание координат, вводятся в школьные программы в начальных классах, что дает ученикам базовые знания необходимые для преодоления более сложных задач на любых этапах обучения.

Изучение координатных обозначений представляет собой совершенно некий входный этап в области математики, который помогает в постижении более сложных ее компонентов и является основой для успех в других оборвов и дисциплинах.

Преимущества оргаэтаемныхстроененыже системотелые знания координат являются перечисленны данных абзаце, что подчеркивает важность этой дисциплины любому изучающему математику.

Вопрос-ответ:

Что такое парабола и почему ее координаты могут быть важны для математического моделирования?

Парабола — это геометрическая фигура, образуемая множеством точек, равноудалённых от точки (фокуса) и отрезка (директрисы), лежащего строго посередине между фокусом и каждой точкой параболы. Важность координат параболы для математического моделирования заключается в том, что они позволяют точно описать движение объектов, подчиняющихся абсолютному закону движения, такому как, например, движения падающих тел под действием гравитации. Поэтому знание координат параболы не только помогает понять и описать движение, но может также использоваться в таких областях, как оптическая связь, климатология, планирование пусков ракет и т. д.

Какие программные приложения и инструменты могут помочь в нахождении координат параболы?

Существует множество программных приложений и инструментов, которые могут быть полезны при решении задач, связанных с поиском координат парабол, например, математические пакеты MATLAB, Wolfram Mathematica, а также облачные сервисы, такие как GeoGebra и Desmos или более продвинутые компьютерные алгебраические системы, например, Maxima или Maple. Кроме того, для двумерных графических просмотров и анализа можно воспользоваться программами компьютерной алгебры, такими как Geogebra или графическими редакторами, которые могут отображать и анализировать параболические кривые.

Видео:

Вечер авторской песни Ларисы Решетовой.

Вершина параболы | Квадратичная функция | Алгебра I (3 видео)

К чему способны направлять нам вычисления точек параболы на двумерной плоскости?

Навигация в двумерном пространстве