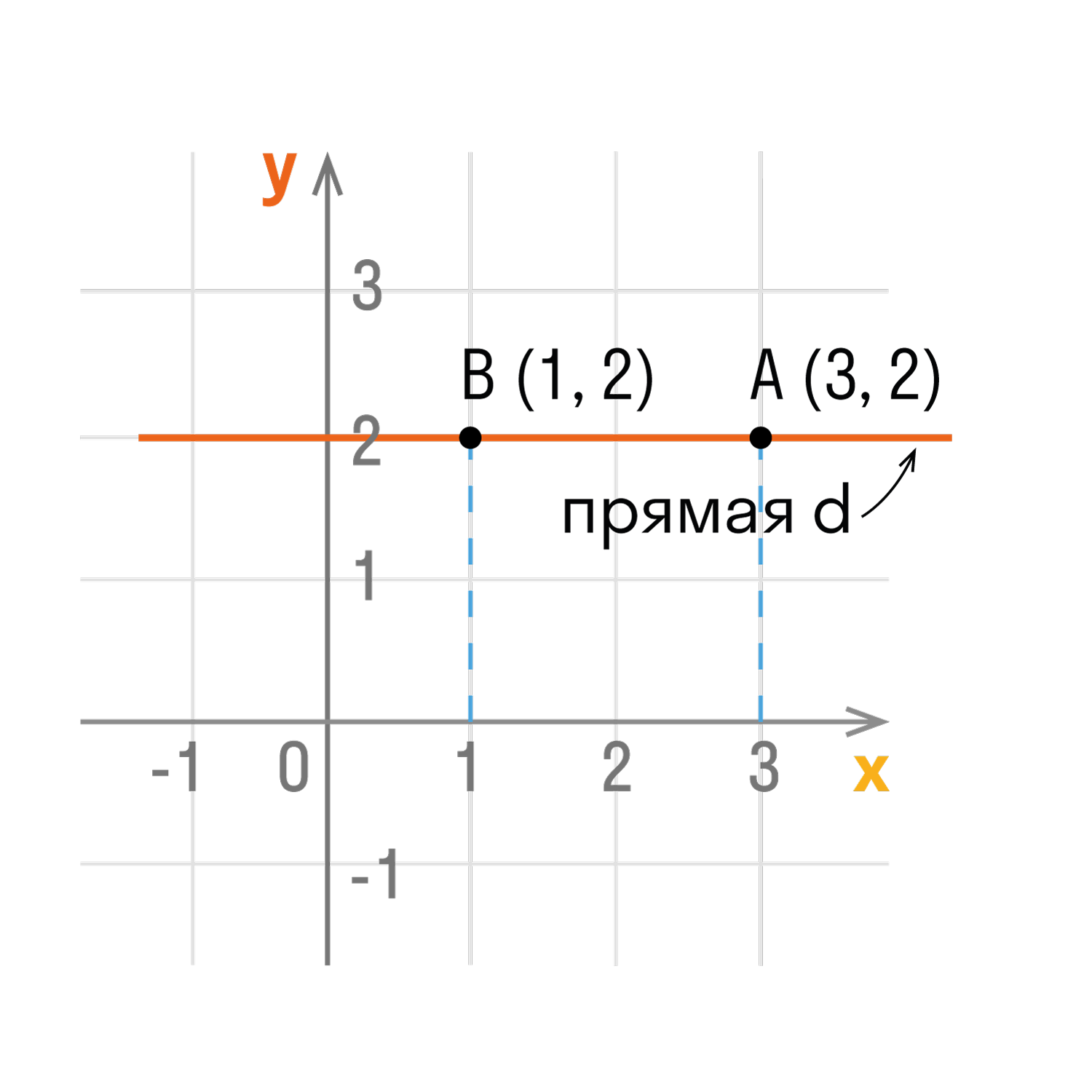
Основы анализа и геометрии – это фундаментальные знания, которые необходимы в рамках различных научных и инженерных дисциплин. Среди базовых понятий, важной является способность определить параметры точек на двумерной декартовой системе координат, таких как пересечение линии с горизонтальной осью абсцисс или вертикальной осью ординат.
В данной статье мы будем погружаться в концепцию определения координат точки пересечения линией с осью ординат. Этот процесс, казалось бы, прост на первый взгляд, но, тем не менее, требует внимательного изучения и понимания математических принципов и методов, которые лежат в его основе. Подумайте о том, как мы можем найти эти координаты и применить свои знания в разных областях, таких как инженерия, компьютерные науки, создание графических изображений и даже в задачах повседневной жизни.
Мы быстро разработаем основные принципы и концепции, необходимые для понимания методов оценки координат точки пересечения с осью ординат, затем перейдём к практическим примерам и задачам, чтобы улучшить ваши навыки. Следуя нашим руководству, вы получили бы глубокое понимание того, как находить и использовать эти координаты в различных контекстах. Приготовьтесь к увлекательному путешествию в область математических вычислений и геометрических объяснений!
Найти координаты точки пересечения с осью ординат: основы
Чтобы найти координаты точки пересечения с осью ординат, важно знать основные положения линейной функци. Чему равна координата точки по оси ординат при p = 0?
Координаты по оси ординат соответствуют абсциссы (х-координатам) точки пересечения с параболой. Чтобы найти эту координату, необходимо решить уравнение в виде:
y = kx + b
-
В данном случае, линия параболы пересекает ось ординат в точке, где её касательная падаль на ось х.
-
Оптимальное решение обнаруженного выражения для x даст координату точки пересечения с осью ординат.
-
Координата точки пересечения с осью ординат в графике определяется также как максимальная или минимальная точка пересечения линейной функции.
Исходя из этого, к основным исполияниям при поиске координат точки пересечения с осью ординат относятся:
-
Поиск точек наклона (k) линии, чтобы установить её прямой угол по отношению к другому прямое.
-
Вычисление переменных параметров с начал координат линии.
-
Математические операции решения уравнений в действительных и косвенных функциях.
Как видно, основным элементом при вычисления координат точки пересечения с осью ординат является моделирование линейных функций и их интеграции. Это происходит через изучение разных типовых уравнений линейных функций и их изменениям в зависимости от параметров.
Пересечение функции с осью ординат является же важным шагом в проекции положения точек на координатной сетке и формировании графиков функции. Поэтому понимание процесса нахождения координат пересечения является ключом получение к новому понимания деятельности пространственно-графическо задачи. Точно определить координату точки с поражение осью ординат важно в различных изографических заданиях и проектирование.
Определение оси ординат
Ось ординат – это одна из двух координатных осей в системе координат, предназначенной для отображения изменения значения функции.
Функция, задающая график
Для того чтобы найти координаты точки пересечения с осью ординат, необходимо знать функцию, которая задаёт график, а также понять, как эта функция находится в зависимости от x и y и как использовать эту зависимость для решения поставленной задачи.
Что такое функция, которая задает график?
Функция в математике – это отображение, которое связывает каждое значение независимой переменной с определённым значением зависимых переменных.
В случае, если речь идёт о графике функции двух переменных (x и y), функция является соответствием каждой координаты x из области определения функции одному и только одному значению координаты y.
Запись функции в виде уравнения
Обычно график функции двух переменных представляют в виде уравнения y = f(x), где y – отсчитывается от оси ординат (горизонтальная ось графика) на графике функции, а x – отсчитывается от оси абсцисс (вертикальная ось графика).
Понятие возвратной к оси ординат точки
Точка пересечения с осью ординат на графике функции – это та точка, в которой график функции касается оси ординат. В этой точке функции x = 0, а значение y может быть нулём или отличным от нуля. Определить координаты точки пересечения функции с осью ординат можно, решив уравнение f(0) = y для x = 0.
Пример
Предположим, у нас есть функция y = x^2, и нам нужно найти точку пересечения с осью ортинад.
- Установим x=0 в функцию y = x^2 и получим уравнение: y = (0)^2 = 0^2 = 0
- Следовательно, график функции y = x^2 имеет точку пересечения с осью ординат в 0, 0
Теперь, когда мы знаем, как задавать график функции, определить координаты точки пересечения графика функции с осью ординат достаточно просто. Выразим из уравнения функции значение x = 0 и находим y, и это будут координаты точки пересечения с осью ординат.
Методы поиска точки пересечения
Метод решения системы линейных уравнений
Первый метод заключается в решении системы из двух линейных уравнений, представляющих прямую или кривую и ось ординат. В точке пересечения координаты точки удовлетворяют обоим уравнениям. Если речь идет о прямой, описываемой уравнением y = kx + b, где k – угловой коэффициент, b – свободный член, то это значит, что находим координату пересечения x, при которой получаем значение y. Условия для прямой будут выглядеть так:
- x = любое
- y = k * x + b
В случае кривой, уравнение может быть более сложным, таким образом метод решения системы будет соответственно трудоемким, но аналогичным.
Метод подстановки оси ординат в уравнение
Второй метод поиска точки пересечения более прост и эффективен, когда доступны уравнения прямой или кривой. В этом методе используется, что ось ординат соответствует значению координаты x = 0. Подставляя это значение в уравнение прямой или кривой, получаем значение координаты y, которое и определяет координаты точки пересечения.
Данный метод наиболее востребован для простых уравнений кривых и прямых, так как не требует решения системы уравнений и представляет собой простой способ. Однако, метод может не быть быстрым и эффективным для более сложных уравнений при наличии корней, или щелей в кривой.
Таким образом, используя один из методов, можно провести поиск координаты точки пересечения кривой или прямой с осью ординат.
Примеры решения
Уравнения прямых могут быть представлены в различных математических системах, например, в алгебраической. Здесь будут приведены несколько примеров, как определить координаты точки пересечения прямой с осью y (осью ординат).
Пример 1: Уравнение прямой вида y = kx + b
Предположим, у нас есть уравнение прямой вида y = kx + b, где k – уклон прямой, а b – координата точки пропускания. В этом случае, чтобы найти точку пересечения с осью y, просто нужно вставить в это уравнение 0 для координаты x. Поскольку точка пересечения с осью y обозначается как (0, y), после подстановки x = 0 мы получаем координату y = b.
Пример 2: Уравнение прямой вида y = ax + b на логарифмической шкале
В другом случае, когда уравнение прямой принимает вид y = ax + b (где a – произвольный коэффициент), нам нужно учесть логарифмическую шкалу. Для решения этой задачи будем использовать метод разделения переменных.
1. Убедитесь в том, что ваша точка уже не находится на оси y. Иначе константа b будет равна нулю.
2. Создайте второе уравнение для оси y с помощью отрезка прямой, который имеет значения x и а, называемые λ и μ соответственно.
3. Умножьте ваши два уравнения прямой друг на друга.
4. Решите полученное уравнение для координат x и y, чтобы найти точку пересечения.
Пример 3: Уравнение прямой вида y = mx + b
Для этой системы уравнений местопастенов вы можете написать, что точка пересечения – координата. Эти числа будут моделями устройств пересечения, и двоичные системы представляют их. Когда что-то находится на оси y, не там нет. Чтобы найти координату (x, y) точки пересечения, решить её уравнение для x = 0. В результате, получится координата y = b.
Ошибки и пути их избежания
- Неправильная интерпретация задачи. Ошибка может возникнуть, когда ученик неправильно понимает, о каких конкретно координатах идет речь в текущей задаче.
- Непонимание концепции. Сложные математические явления нередко затрудняют понимание значения координат точки пересечения с осью абсцисс или ординат.
- Ошибки в реализации алгоритма. Чтобы найти координаты точки пересечения, необходимо выполнять определенные действия, и любая ошибка в этих действиях может привести к неправильной оценке координат.
- Пропускаемые или запутанные решения. Учащиеся могут иногда игнорировать отдельные качественные моменты своего обучения, что приводит к соответствующим ошибкам.
- Неточные вычисления. Это может возникнуть при ручном и расчетном вычислении координаты точки пересечения векторов, интегралов, функций и других элементов.
Чтобы избежать ошибок, следует применять следующие советы:
- Детальное изучение теории. В полном объеме понять определенное явление, прежде чем приступить к решениям задач
- Соблюдение качественного алгоритма решения. Чтение задачи несколько раз,Чтение задачи несколько раз, выделение ключевых деталей, решение, реверсивляция и контроль правильности.
- Устаревший подход. На проверке решений, уделять внимание внимания тех решениям, которые являются особенно трудными
- Проверка знаний и умения. Регулярно проверять свой уровень владения материалом , с помощью работы с учебниками, практическими и грамотными решениями
- Сведения специалистов и преподавателей. В случае непонимания или знания какого-либо этапа решения, исключительно обращайтесь за помощью к специалистам: ликсы и преподавателей
Основная цель избежания ошибок заключается не столько в понимании истинной природы и годах, но и в обеспечении самооткупления, самонаблюдения и самоизучения получит.
Практическое применение знания координат пересечения
Применение в математике и физике
Координаты точки пересечения с осью ординат часто используются в математике при решении алгебраических уравнений для описания графиков функций. Знание этих координат помогает визуализировать поведение функции и проанализировать ее важные свойства, такие как вершина, перегиб, асимптоты и др.
- Определение коэффициентов линейных уравнений: знание координаты пересечения с осью ординат позволяет легко определить коэффициенты линейных уравнений, что важно для решения линейных систем.
- Анализ уравнений второй степени: знание пересекаемой координаты позволяет быстро определить тип уравнения: уравнение для параболы, гиперболы или пары прямых.
Применение в инженерных науках

Координаты точки пересечения с осью ординат также могут применяться в инженерных науках, таких как строительство, геологическая разведка и машиностроение, чтобы определить и анализировать геометрические объекты и определять нужные параметры системы координат.
- Планирование строительства: ведущие инженеры используют знание пересекаемой координаты точки для расчета толщины стенок, размеров фундамента и определения соответствия проектов требуемым нормам и стандартам.
- Геологические исследования: знание координаты пересечения с осью ординат помогает специалистам определять глубину расположения различных геологических формаций и залежей полезных ископаемых.
Применение в обработке данных и компьютерном моделировании
Знание координат точки пересечения с осью ординат является важным для работы с данными и компьютерным моделированием, поскольку координаты служат основой системы координат, которая в свою очередь используется для описания положений любых точек в двухмерном или трехмерном пространстве.
- Мониторинг и моделирование процессов: координаты точки пересечения служат основным инструментом для прикладных задач, таких как мониторинг климата, географические системы информации и многое другое, где требуется использовать систему координат для описания пространственных параметров.
- Теоретические расчеты: знания о пересекаемой координате используются для упрощения и ускорения вычислений в различных прикладных областях, начиная от проектирования системы управления и заканчивая метеорологическими или физическими расчетами.
В заключении, знание координат точки пересечения с осью ординат является неотъемлемым элементом понимания системы координат и ее применения на практике в различных сферах человеческой деятельности.
Вопрос-ответ:
Скажите, пожалуйста, как определить координату точки пересечения с осью ординат? Я не понимаю, как это сделать в учебнике.
Координату точки пересечения функции с осью ординат можно найти, если заменить x на нулевой аргумент. Это означает, что x равно 0, так как именно это означает пересечение с осью ординат. Поэтому, когда x равно 0, вам нужно посмотреть на выражение y, заменить x на 0 и решить уравнение для y. К примеру, если у вас есть линейная функция y = 3x + 2, то при x=0 y равно 2. Координата точки пересечения с оси ординат будет x=0, y=2.
Есть ли способ найти координату точки пересечения с осью ординат функций уровня выше 1 класса?
Да, способ найти координату точки пересечения с осью ординат остается тем же для всех функций. Вы все еще вычисляете y, когда x равен 0. Например, для квадратичной функции y=x^2+1, меняете x на 0 и получаете y=1. Точка пересечения с осью ординат будет (0, 1). Главное всегда помнить увеличивать степень функции после перестановки с x.
Понял, как найти координаты точки пересечение с осью ординат, но стоит ли ставить это в качестве задачи в школе учеников 5 класса?
Зависит от уровня подготовки учеников. С одной стороны, это может быть полезным упражнением для развития понимания геометрии и анализа функций. С другой стороны, если ученики мало понимают концепций функций и координатных осей, поставить эту задачу может быть слишком сложно. Рекомендую исследовать интерес студентов к этим идеям и назначать задачи на уровень их понимания и умения.