Во всех наших обсуждениях и задумках о реальном мире, который нас окружает, мы сталкиваемся с различными геометрическими явлениями. Одна из основных задач при исследовании пространства – определение ячейки координат для любой точки в пространстве. Важность понятия геометрических координат в различных областях науки и техники уже давно не вызывает сомнений, так как это дает нам возможность точно определить расположение объектов друг от друга.
Координаты точки в пространстве – это конкретные данные, которые позволяют определить ее положение относительно выбранной системы отсчета, используя различные математические инструменты. Чтобы найти координаты точки, необходимо иметь ясное представление о том, как она располагается в трехмерном пространстве и как ее позицию можно описать с помощью математических величин.
В этой статье мы научим вас различным методам нахождения координат точек, рассмотрим основные системы координат, такие как прямоугольная, цилиндрическая и сферическая системы, а также объясним, в каких случаях эффективнее применять именно их. К концу статьи вы будете знать, как точно указать местоположение произвольной точки на плоскости или в пространстве, а также как частые геометрические задачи упростить с помощью перевода их в координатную форму.
Будьте готовы к тому, что со мной, и начиная с самых основ, до самых сложных аспектов и деталей, мы погрузимся в подробное изучение пространства, координат и их применения в нескольких реальных задачах. Доверие к нашим знаниям и навыкам с использованием ячейки координат – основа успешной работы и решения многочисленных задач, связанных с пониманием нашего окружения.
Основные понятия пространства
Первое понятие, которое необходимо ввода, это «координатная система». Это схема, которая позволяет определять объекты и фиксировать их координаты, используя систему осей и меток. Координатная система является основой пространства и ее главным элементом.
Следующим важным понятием является линейное пространство. Это множество, состоящее из векторов, с определенным арифметическим и алгебраическим поведением. Основной функцией векторного пространства является связывание точек и объектов в пространстве, осуществляя движение и преобразования.
Важно также обратить внимание на понятие размерности пространства. Размерность пространства – это количество координат, необходимых для описания точек в пространстве. Так, в двумерном пространстве требуется известныть две координаты (например, X, Y), а в трехмерном – три (X, Y, Z).
Типы координатных систем
В топологии и геометрии существует несколько основных типов координатных систем, используемых для определения
положения точек в пространстве. Два наиболее известных типа – это декартова (векторная) система координат и цилиндрическая система координат, каждая из которых имеет свои особенности и области применения.
Декартова система координат
Декартова система координат, также называемая векторной системой координат, была введена
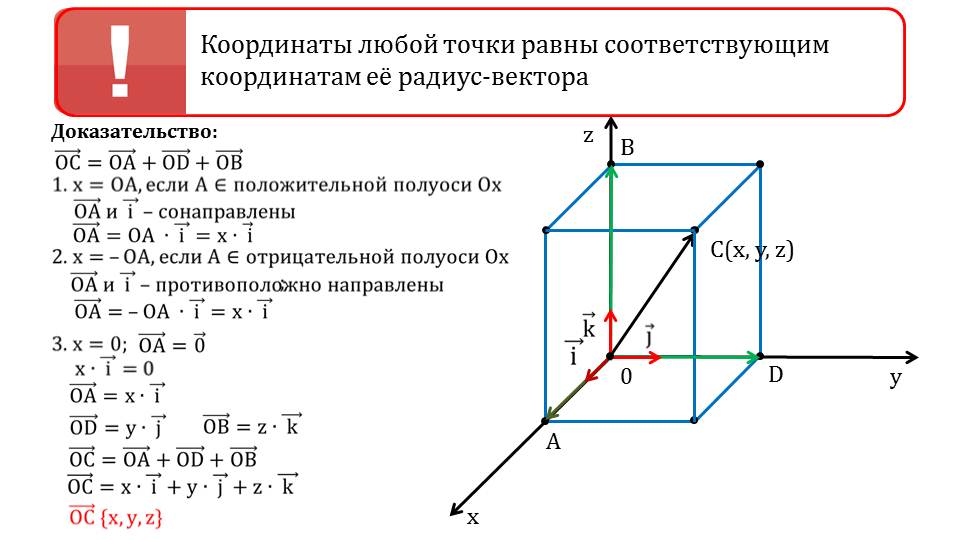
французским философом и математиком Рене Декартом в XVII веке. В этой системе каждая точка в пространстве описывается тремя координатами (X, Y, Z), где X – это горизонтальная координата (абсцисса), Y – вертикальная координата (ордината), а Z – координата в направлении третьей оси, перпендикулярная к XY-плоскости.
Основное преимущество декартовой системы координат заключается в том, что она позволяет легко вычислять расстояние между точками и применять теоремы векторного и скалярного анализа. Однако, в приложениях, где требуется описание точек на поверхностях конических сечений (сферы, цилиндра, конуса), декартова система координат может оказаться сложной для вычислений и меньше покажет себя тогда, когда можно было бы применить другие системы координат.
Цилиндрическая система координат
Цилиндрическая система координат представляет собой трёхмерную систему с двумя осями, для описания положения точки требуется указание радиуса, угла и координаты Z. Радиус обозначается символом r, угол – φ (фи), а координата Z – Z, как и в декартовой системе.
Особенно полезна цилиндрическая система координат для описания форм конических сечений или других поверхностей, которые имеют симметрию по отношению к прямой оси. Например, при решении проблем в солнечной энергетике при проектировании требуется использовать те из энергетических когерентных решений, которые позволяют устранить данные проблемы. В этих случаях более практичным будет использование цилиндрической системы координат вместо декартовой.
В зависимости от исходных задач и проблем различные системы координат имеют свои сильные и слабые стороны. Выбор наиболее подходящей координатной системы имеет непосредственное отношение к качеству достижимого результата в решении математических и инженерных проблем.
Методы определений координат точки
Координаты в декартовой системе
Декартовой системой координат (иначе известной как прямоугольной системой координат) является способ представления точек в двумерном или трёхмерном пространстве. Это одна из наиболее используемых систем, и её основы были заложены французским математиком Рене Декартом (отсюда и название).
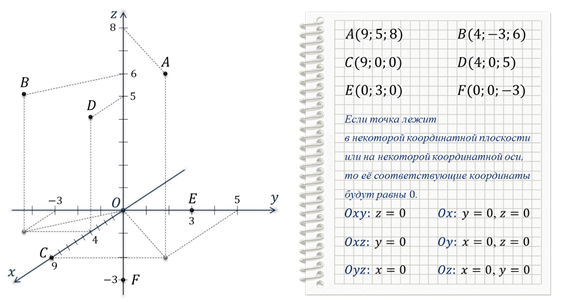
В двумерной системе координаты точки определяются двумя числами (x, y), а в трёхмерной – тремя (x, y, z). На этом основании определяются методы определения координат.
- Определение координатных осей: данные точки определяются по отношению к трём перпендикулярным осям x, y, z.
- Определение координатных плоскостей: в трёхмерном пространстве координаты плоскостей ОХ, ОY, ОZ определены таким образом, чтобы всякое векторное отношение на ОХ представлялось в виде parallelogram, а на ОY и ОZ – в виде прямоугольника.
Координаты в полярной системе
Полярная система координат представляет собой альтернативный способ задания точек на плоскости с использованием двух чисел: радиуса (r) и направления или углу φ (угол между радиусом и положительной частью оси х).
Особенно данная система полезна для описания периодических функций и вообще функций, имеющих конкретную симметрию. Например, для определения координат точки по прямоугольной системе, применяется формула x = rcosφ, y = rsineφ
Использование механизмов полярной системы в трёхмерном пространстве может быть достигнуто с использованием сферических или цилиндрических координат.
Координаты в сферической системе
Сферическая система координат используется для описания местности в трёхмерном пространстве. В этой системе каждая точка описывается тремя координатами: радиусом (r), углом между положительной проекцией вектора на плоскость XY (θ) и углом вершины между вектором и перпендикуляром перпендикулярной поверхности (φ).
Вне зависимости от выбранной системы координат, очень важно обеспечиться точностью вычислений и правильным использованием алгоритмов. Это укрепляет математическую основу решения связанных задач.
Вычисление координат в декартовой системе
Вычисление координат в декартовой системе происходит путем установления точки начала отсчета (начала координат, также известного как начало оси координат), так же как и установив координатные оси, которые пересекаются в точке начала.
Основные понятия
-
Ось абсцисс (Ось X) – ось перпендикулярная оси ординат, представляет направление смещения вправо или влево на плоскости.
-
Ось ординат (Ось Y) – ось перпендикулярная оси абсцисс, представляет направление смещения вверх или вниз на плоскости.
-
Ось аппликат (Ось Z) – ось перпендикулярная плоскости являющейся плоскостью абсцисс и ординат в трехмерном пространстве, представляет направление смещения ближе или далее от своей плоскости.
-
Ориентация координатной оси – ось X располагается слева направо, ось Y снизу-вверх и ось Z ближе-дальше от плоскости X-Y.
Вычисление координат двухмерного пространства (2D)
-
Определите координату точки по оси абсцисс (ось X).
-
Определите координату точки по оси ординат (ось Y).
-
Учитывая определение членов оси X и оси Y, найдите отрезки, которые соединяют точку начала координат с заданной точкой.
-
Сумма произведений отрезков, пропорциональных координатам точки, равна нулю, так как они перпендикулярны друг другу.
Вычисление координат трехмерного пространства (3D)

-
Определите координату точки по оси абсцисс (ось X).
-
Определите координату точки по оси ординат (ось Y).
-
Определите координату точки по оси аппликат (ось Z).
-
Учитывая определение проживания точки в трехмерном пространстве, найдите отрезки, которые соединяют точку начала координат с заданной точкой.
-
Сумма произведений отрезков, пропорциональных координатам точки, равна нулю для каждого направления оси по оставшимся двум осям, так как они перпендикулярны друг другу.
Пример вычисления координат в декартовой системе: пусть дана точка A с координатами (x1,y1) и позиция в точке B с координатами (x2, y2) на плоскости. Рассчитать положение точки в плоскости как разность координат между A и B, а именно (x2 – x1) и (y2 – y1).
Координаты в полярной и сферической системах
Полярная система координат представляет собой двумерный способ определения положения точки в пространстве. В данной системе координаты точки задаются одним расстоянием от начала координатской системы и одним углом между прямой, соединяющей начало системы с точкой, и некой фиксированной осью.
Расстояние от точки до начала координат, называемое радиусом или радиальной координатой, обозначается ρ (ро).
Угол между направляющей осью и радиусом, измеряемый в направлении направляющей оси положительно и против ней – отрицательно, именуется θ (фи). Угол фи обычно измеряется в радианах или градусах. В полярной системе координаты точки запишутся как (ρ,θ).
Сферическая система координат
В сферической системе координат, используемой для задания положения точки в трехмерном пространстве, требуется указать радиальную координату ρ (равное периметру кола обхода сферы) и два угла φ (фита, измеряемый от небесного экватора) и θ (фи, измеряемый от небесной вертикали).
Угол фита – это широта точки на поверхности сферы, который измеряется от 0 до π. В тех случаях, когда φ больше 0, точка находится на севере небесного экватора, и направлен вниз по направлению к полюсу северный. Если угол фита меньше 0, точка находится на Земле южнее оси, и направлена вниз по направлению к полюсу южный.
Угол фи – это долгота точки и обычно измеряется от 0 до 2π. Координаты точки в сферической системе записываются как (ρ,φ,θ).
Инструменты для определения координат
Для определения координат точек в пространстве можно воспользоваться различными инструментами и системами. Ниже предоставлен общий обзор доступных средств, а также их особенности и области применения.