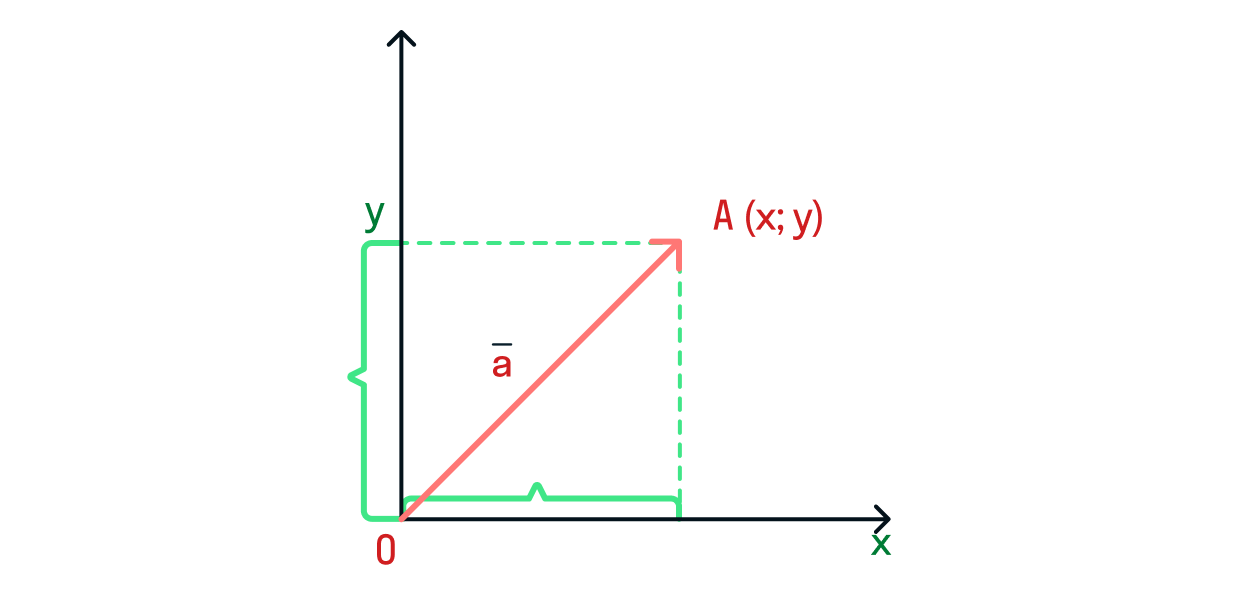
Вычисление координат вектора в некотором базисе является ключевым навыком в области линейной алгебры, который используется во многих областях прикладных наук. В основе этой техники лежит понимание сути аффинных пространств и способности выразить любой вектор через их базисы – истинные обозначения полярностей, уравнение которых показывает фундаментальные способы манипулирования и трансформирования данных.
Базис – важнейшее понятие линейной алгебры, из которого берет начало вполне себе новая проблемность идентификации векторных величин в контексте иной системы базисных векторов. Умение переходить от координат в одном базисе к координатам в другом – это сложность, которую имеется в виду в данной заметке.
Вектор может быть представлен как линейная комбинация базисных векторов. Анализируя это свойство, мы найдем координаты вектора в других базисах, трансформируя пространство и задачи, для которых простое определение координат теряет свою актуальность. Такой подход позволяет нам применять данное понятие во многих практических приложениях, таких как система координат в механике или компьютерной графике и т.д.
В данной статье мы постараемся раскрыть основы вычисления координат векторов в базисе других векторов, используя простые математические алгоритмы и общие принципы, что поможет раскрыть суть данного метода и применять его в решении различных задач.
Анализ векторного пространства

Основные понятия аксиоматики векторного пространства:
- Непустое множество V, называемое векторным пространством.
- Подмножество, называемое полем скаляров, содержащее ноль и содержащее элементы, называемые скалярами.
- Два действия, сложения векторов и умножения векторов на скаляры, которые задают векторное пространство.
Для аксиом векторного пространства, имеющихся в процессе анализа, данные действие должны удовлетворять следующим условиям:
- Замкнутость сложения векторов – если векторы a и b принадлежат векторному пространству, то их сложение (a + b) также принадлежит векторному пространству.
- Замкнутость умножения вектора на скаляр – если четырехмерный вектор a принадлежит векторному пространству и скаляр k принадлежит полю скаляров, то их произведение (k.a) также принадлежит векторному пространству.
Векторное пространство, особенно многомерное векторное пространство, может иметь различную структуру в зависимости от рассмотрения и задачи, которую мы ставим перед собой. Так, в пространстве размерности (n) может рассматриваться линейное подпространство размерности (m, m < n), фракталы, некоторые функции и многое другое.
Анализ векторного пространства – это поиск тех вышеупомянутых характеристик, которые могут быть использованы для гораздо более точной и детальной моделировки этого пространства, и изучение типов векторов, которые лежат там.
Применение векторного пространства:
Такие вычисления обычно используются для моделирования различных физических концепций, таких как:
- Механика: для описания движения точки в пространстве и взаимодействия сил на тело.
- Оптика: для моделирования световых лучей и их интерференции.
- Электродинамика: для моделирования электромагнитных полей и их свойств.
- Химия: для моделирования молекулярных структур и преобразования энергии.
Аналитические свойства векторных пространств играют ключевую роль в комбинаторных алгоритмах и геометрии пространственных узлов.
Анализ векторного пространства чрезвычайно важен в теории информатики и вычислительной линейной алгебре, поскольку он заложен в основу ее задач и методов, а вот с точки зрения прикладных задач в разных областях знаний этот анализ позволяет нам находить новые подходы к решению задач, улучшать их; создавать новые модели и концепции в различных науках и областях.
При продолжении описываемых выше свойств, один из важных аспектов базиса векторов является его независимость и полнота. Независимость векторов означает, что они не лежат на одной линии или плоскости, а полнота показывает, что любые векторы пространства можно описать через их комбинации.
Понимание базисных векторов
Удобство базисных векторов нацелено на то, чтобы упростить нам задачи анализа и работы с векторами. Если бы нам всегда приходилось оперировать векторами в их исходных координатах, вычисления были бы не только чрезвычайно накладными, но и было бы практически невозможно представить то, что происходит на некоторых этапах работы.
Поскольку базисные векторы являются “наилучшими” для любого векторного пространства в конкретном контексте, мы можем сформулировать определение базиса следующим образом:
- Бaзис векторов – это система векторов, которые попарно линейно независимы то есть никакие векторы из системы не могут быть представлены в виде линейных комбинаций других векторов из этой системы и исчерпывающая любую систему векторов в данном пространстве, что означает любые векторы пространства могут быть представлены как линейная комбинация базисных векторов.
Учитывая это определение, мы можем сделать следующие заключения:
- Базисные векторы поглощают информацию о пространственных характеристиках побуждаемых ими систем.
- Как конечно выбирается базис векторов существенно определяет точность и эффективность вычислений в данном пространстве.
Знание и понимание базисных векторов является обязательным для решения практически любых проблем, связанных с векторами в математике, механике, физике, компьютерной графике и многих других областях.
Свойства линейной оболочки
Свойство 1. Линейная оболочка является подпространством: линейная оболочка любых набора векторов всегда образует подпространство в заданном векторном пространстве. Это значит, что она обладает свойствами аддитивности и затвердженности относительно умножения на скаляр.
Аддитивность означает, что для любых двух векторов из линейной оболочки и любых коэффициентов, сумма векторов, произведения которых на эти коэффициенты, также лежит в линейной оболочке.
Затвердженность скалярного умножения предполагает, что для любых векторов из линейной оболочки и любого скаляра, произведение этого скаляра на вектор все равно лежит в линейной оболочке.
Свойство 2. Линейная оболочка порождается линейно независимой системой: даже если начальная система векторов не является линейно независимой, можно найти подмножество этой системы, которое будет линейно независимо и порождать ту же линейную оболочку.
Пример: пусть есть система векторов {v1, v2, …, vn}. Если среди них имеется линейно зависимое подмножество {v1, v2, …, vk}, его можно упростить, удалив ненужные векторы, и получить новую систему, такую как {v1′, v2′, …, vk’}, которая будет линейно независимой и порождать ту же линейную оболочку.
Используя это свойство, можно сэкономить память и вычислительные ресурсы, избавившись от ненужных векторов.
Свойство 3. Аффинные преобразования сохраняют линейную оболочку: если произвести аффинные преобразования каждого вектора из набора, то новая система векторов продолжит порождать ту же линейную оболочку, как и исходный набор.
Это свойство полезно для компактности и красоты вычислений, поскольку позволяет анализировать и работать с преобразованными системами векторов без потери сведения об их линейной оболочке.
Методика нахождения координат
Для того чтобы найти координаты вектора в базисе из других векторов, мы будем использовать две основные методики: линейное разложение вектора на проекции на базисные векторы и метод Гамильтона-Черньи (метод Крамера с использованием матрицы Грама).
Линейное разложение
- Шаг 1: Запишите вектор в виде суммы скалярно-векторных произведений на базисные векторы.
- Шаг 2: Найдите скаляры, используя уравнения с нулевыми свободными членами.
- Шаг 3: Вычислите координаты вектора в заданном базисе.
Метод Гамильтона-Черньи
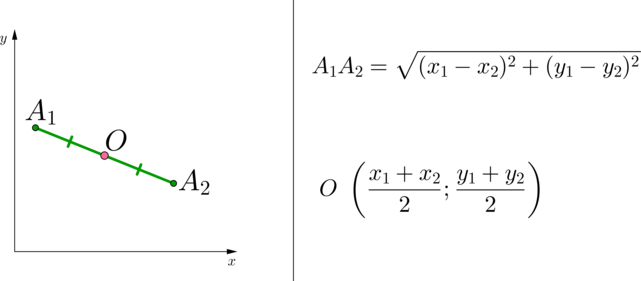
- Шаг 1: Получите матрицу Грама.
- Шаг 2: Решите систему уравнений относительно координат, используя метод Гамильтона-Черньи.
- Шаг 3: Вычислите координаты вектора в заданном базисе.
Далее мы будем приводить примеры для обоих методов и сравнивать их с точки зрения скорость работы и точности вычислений.
Сравнение методов

- Линейное разложение: Метод эффективен для нахождения координат вектора, если базисы имеют низкую размерность, но для высоких размерностей может быть сложным и ресурсоемким.
- Метод Гамильтона-Черньи: Метод является более предпочтительным для высоких размерностей, так как позволяет найти координаты вектора эффективнынее, чем линейное разложение.
Выбор метода для конкретной задачи зависит от размеров базиса и доступного времени для вычислений.
Вычислительные алгоритмы
Основная идея алгоритмов заключается в представлении вектора в виде линейной комбинации базисных векторов, подбирая таким образом коэффициенты, чтобы обеспечить максимальное сходство между исходным вектором и вычисленным.
Один из наиболее эффективных методов, который используется для решения таких задач, является метод Грама-Шмидта. Этот метод предполагает переход от исходной системы базисных векторов к ортонормированной системе, которая характеризуется удобными свойствами для вычисления линейных комбинаций.
В практических задачах также используют достаточно простые алгоритмы: вектор приводится к базису, уже сопоставленному с ним. Таким образом, при определенных условиях можно получить значительный выигрыш в скорости вычислений.
Целью вычислительных алгоритмов является максимизация точности, стабильности и быстроты выполнения всех вычислений. С учетом различных ограничений, будь то ограничения на время или на внешнее окружение (например, ограниченное количество памяти), необходимо подбирать оптимальный набор стратегий вычислений для своего конкретного случая.
Вычислительные алгоритмики широко используются во многих отраслях, включая компьютерную графику, веб-программирование, искусственный интеллект и другие, а также служат инструментом в научных исследованиях, предсказаниях и прогнозировании.
Примером использования данной теории является задание рекомендательных систем, в которых ищется вектор пользователя на основе его размеченных действий в размерности, несколько превосходящей размерность пространства пользователя. Здесь используются высококачественные алгоритмы вычисления координат вектора в базисе других векторов для выбора наиболее подходящих показаний, с максимальным сходством к действий пользователя.
По сути каждый алгоритм должен представлять собой систему правил, которые позволяют находить нужные решения в разных ситуациях. Благодаря разработанным и отрегулированным стратегиям вычислительных алгоритмов мы можем пользоваться различными современными технологиями, которые ранее казались совсем невозможными для создания и реального существования.
Анализ результатов
После нахождения координат вектора в заданном базисе, актуальной становится задача анализа полученных результатов. Здесь важно проверить корректность полученных значений, а также понять их значение и смысл.
Проверка корректности результатов

В первую очередь нужно убедиться, что вычисленные координаты действительно находятся в пределах допустимых значений. Для этого полезно провести сравнение со значениями, полученными опытными образом или с данными из других источников. Также полезно провести проверку на избыточность значений и отклонения от ожидаемых результатов.
Интерпретация результатов
После того, как вы убедились в корректности результатов, теперь вам нужно понять и интерпретировать полученные значения координат. Рассмотрите, как вектора направлены в пространстве, определите характер их взаимодействия друг с другом, и оцените, насколько они описывают общую картину решения вашей задачи.
Также в аналитический ракурс входят рассмотрение того, как изменения величин векторов влияют на изменения координат в заданном базисе. Это может позволить вам понять, какие именно изменения в координатах приводят к изменениям в виду наблюдаемого явления, и чего можно ожидать, изменяя компоненты вектора.