Вектор – фундаментальная концепция, которая широко используется в математике и естественных науках. Он является инструментом, который позволяет описывать физические величины, такие как сила, импульс и угловой момент. Векторы представлены как направленные отрезки, которые обладают длиной и направлением. Векторная алгебра лежит в основе анализа многих сложных физических и математических процессов.
Базис – это набор векторов, которые с помощью линейной комбинации образуют пространство векторов.
Как же определить координаты вектора в базисе из других векторов? Этот вопрос является ключевым для разных разделов математики и науки. В этой статье мы исследуем алгоритмы и подходы к поиску координат вектора в заданном базисе, а также разберем сам процесс и основные концепции.
Прежде чем перейти к практическим примерам, давайте осветим центральные концепции вектора и базиса. Вектор – это не просто направленный отрезок, но также матрица, состоящая из координат в конкретной системе. Базис – это множество векторов, которые могут быть использованы для представления любых других векторов в данном пространстве, используя их линейные комбинации.
Основные понятия
В евклидовом пространстве линейная алгебра изучает свойства и операции с наборами ненулевых объектов (векторов). Базис служит основным инструментом определения координат вектора и выделения из него ключевых элементов. В данном разделе будут рассмотрены основные понятия и принципы, необходимые для понимания привидения вектору координат в заданном базисе.
Базис
Базис определяется как набор векторов, которые линейно независимы (любой вектор, который появляется в результате комбинации других векторов базиса, будет либо суммой других векторов, либо нулевым вектором) и покрывают все пространство (каждый вектор данного пространства может быть выражен как линейная комбинация векторов базиса).
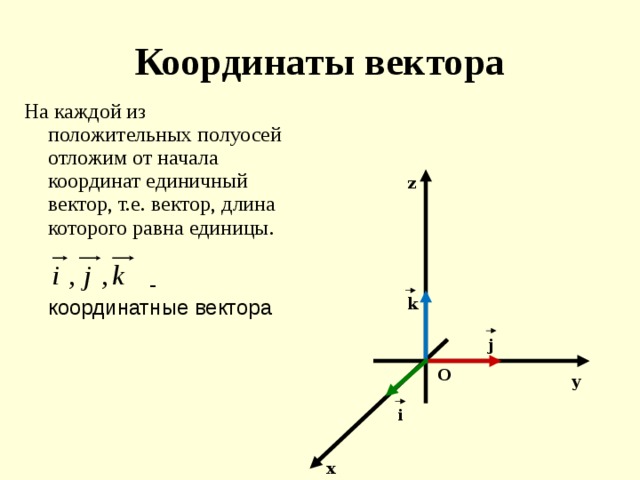
Пример составления базиса в двухмерном пространстве: рассмотрим координатную сетку координатных векторов, лежащих в начале координатных осей и направлениями на оси (1,0) и (0,1). Эти векторы являются перестановками друг друга; вместе они сформируют базис и будут обозначать каждый вектор, обладающий двумя параметрами, или координатами, во втором измерении.
Координаты вектора в заданном базисе
Для решения задачи нахождения координат вектора в заданном базисе необходимо выполнить следующие этапы:
1. Определить линейную зависимость. Следовательно, проанализировать, линейно зависимы заданные векторы или являются ортогональными (линейно независимыми).
2. Сформировать матрицу. В виде изобразительной карточки построить матрицу, векторов которой являются заданными векторами.
3. Решить систему уравнений. Найти коэффициенты с помощью решений системы уравнений, соответствующих векторам базиса, и преобразуя заданный вектор, который находится в записи в виде линейной комбинации векторов базиса.
Соопльноту этих шагов, вы получите координаты заданного вектора в контексте определяемого базиса.
Обратите внимание, что в зависимости от прикладной области интереса вспомогательные инструменты или правила декламирования вариаций приведенных процедур могут изменяться.
Типы векторов и их свойства
Различают следующие основные типы векторов:
1. Скалярные векторы – векторы, которые характеризуются размером и направлением, но не имеют определенного начала отсчета (то есть все векторы, проведенные из собственного начала координат и направленные в различные стороны).
2. Векторы скорости – векторы, которые характеризуют движение тела в пространстве (их берут во внимание скорость, направление и направление перемещения).
3. Матричные векторы – векторы расположенные в матричной форме (матрицы направленности – системе координат). Матрицы векторов описывают ориентацию объекта в пространстве и движения тела в условиях невесомости.
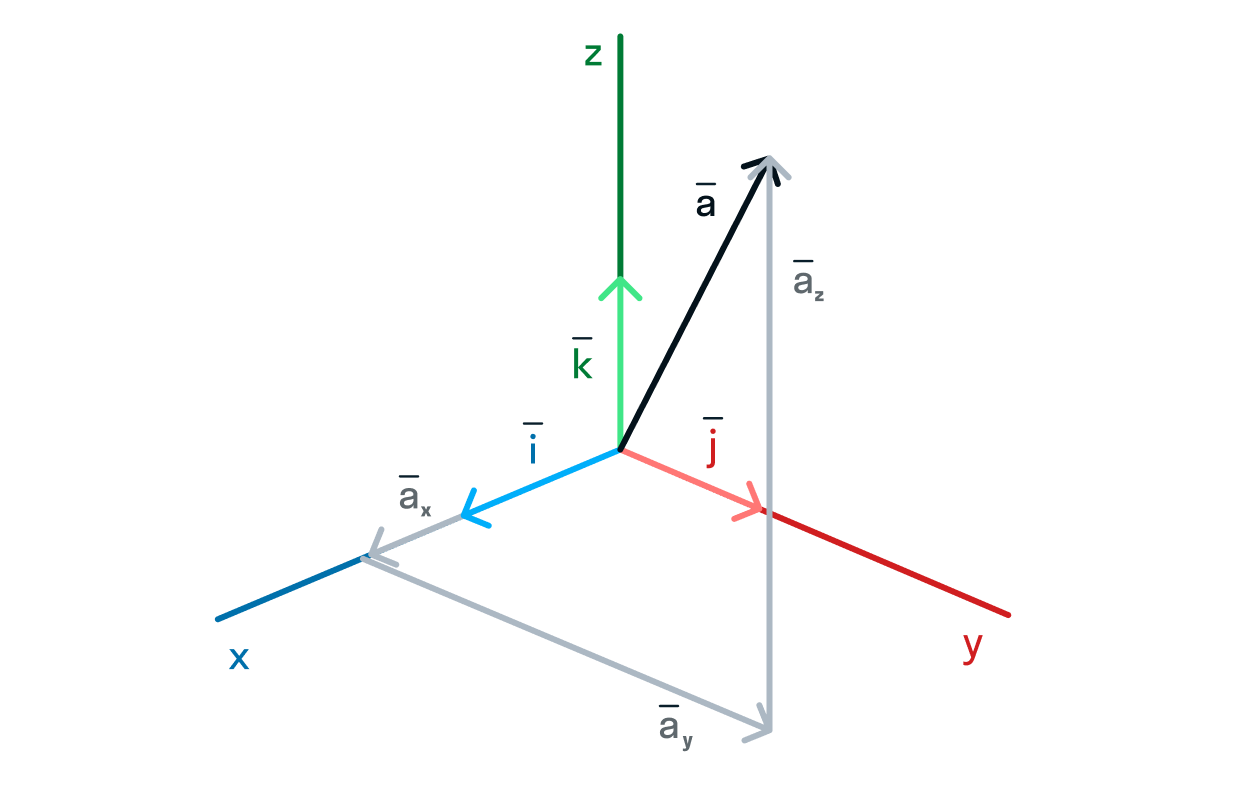
4. Координатные векторы – вектора, в которых значения переменных объекта представлены как их координаты (то есть комбинация их положения и ориентации).
5. Смешанные векторы – вектора, составленные из двух или более векторов разного типа (например, вектора направления и вектора размера).
Также у некоторых систем векторов появляются дополнительные свойства и особенности, их используют в различных вычислительных методах для решения физических, геометрических и комбинаторных задач:
– Линейная независимость векторов, когда знаменатель к коэффициенту приближения в формуле в векторных координатах не равен нулю.
– Системы из n векторов, образующих трехмерное пространство, используются для анализа объектов и явлений в трех измерениях (также это относится к векторному представлению сложных физических процессов).
– Векторы распределения, которые описывают распределение объектов в области их наблюдения (вычисляются на основе координатных векторов).
– Векторы фактора, характеризующие распределение значений переменных по группам (их берут во внимание при анализе сложных аспектов отдельных явлений и процессов).
Вышеуказанные типы векторов и их свойства могут быть использованы при решении различных задач, связанных со сбором и обработкой данных, а также при моделировании сложных объектов и явлений в реальном мире.
Базисы векторов и пространств
Определение базиса
Базис – это набор векторов, которые обладают двумя основными свойствами:
- Векторы образуют линейно независимую систему: никакой из векторов не может быть представлен (равен) как линейная комбинация остальных векторов из набора.
- Векторы генерируют всё пространство: любые векторы из данного пространства могут быть представлены посредством линейной комбинации базисных векторов.
Если базис состоит из n векторов, то размерность соответствующего векторного пространства также равна n.
Найти координаты вектора в базисе из векторов
Чтобы найти координаты вектора относительно заданного базиса из векторов, необходимо решить систему линейных уравнений. Предположим, что в пространстве задано n линейно независимых векторов, и мы хотим найти координаты вектора v относительно этого базиса. При этом базис противопоставляется как B1, B2,…, Bn . Выпишем уравнение:
| A | B1 = x1*v |
|---|---|
| B | B2 = x2*v |
| … | … |
| z | Bn = xn*v |
Индексы x1, x2, …, xn – это искомые координаты вектора v в базисе из векторов B1, B2,…, Bn. Решив эту систему линейных уравнений, мы можем найти координаты вектора v в заданном базисе.
Успех в линейной алгебре
Определившись с концепцией линейной независимости векторов и рассмотрев подход к нахождению координат, связанный с использованием координатных уравнений, мы сможем конструировать и решать задачи и уравнения, связанные с линейным пространством, применяя принципы линейной алгебры. В дальнейшем знания о линейной независимости векторов, базисных векторов и их задачи с местоположением, а также способы их трансформации влияют на понимание множества других теорем и методов линейной алгебры.
Методы определения координат вектора
Метод ортогональных проекций
Этот метод основан на вычислении проекций исходного вектора на каждый базисный вектор. Проекции вектора на базисные векторы рассчитываются как скалярное произведение вектора на вектор базиса и деленное на длину базисного вектора в квадрате. В этой проекции заданный вектор разлагается на составляющие, и полученные количества являются координатами вектора в заданном базисе.
Метод определителя
Второй метод, который часто используется для вычисления координат вектора в заданном базисе, основан на определении определителя системы линейных уравнений, задающих соответствующий базис. Данные уравнения могут быть получены путём выражения составляющих исходного вектора через базисные векторы.
Метод алгебраических методов
Алгебраический метод также может быть использован для вычисления координат вектора в базисе из векторов. Данный метод заключается в решении системы линейных уравнений, которая может быть получена путём разложения вектора в комбинацию базисных векторов. Решение этой системы даст координаты вектора в заданном базисе.
Метод цепного правила
Метод цепного правила позволяет определить координаты вектора в базисе из векторов, используя прямое подстановление. Пусть даны столбец координат вектора в другом базисе и векторы базиса, которые необходимо перевести в исходный базис. Затем, используя запись векторов из основного базиса в терминах векторов исходного базиса. Например, векторы базиса в терминах векторов аффинного базиса могут быть выражены через исходный базис.
Метод сравнения <без комментариев>
Существует вспомогательный метод для вычисления координат вектора в заданном базисе, который основан на схеме сравнения вектора и базисных векторов. В первую очередь домножают отдельные компоненты вектора на базисные векторы, затем суммируют результат для нахождения конечных координат вектора.
- Выберите подходящий базис
- Вычислите выражение, содержащее базисные векторы и компоненты исходного вектора
- Сравните полученные выражения со значениями координат в заданном базисе вектора
- Если выражение, содержащее компоненты вектора и базисные векторы совпадает с координатами вектора в заданном базисе, то полученные координаты являются искомыми
Каждый из этих методов обладает своими достоинствами и недостатками, а также применимостью для решения различных задач. Важной является возможность выбора наиболее подходящего метода для решения конкретного вопроса в зависимости от его условий и требований.
\
Использование определителя
\[\textbf{x} = \alpha \textbf{u} + \beta \textbf{v}\]
В линейной алгебре, определитель может быть использован для нахождения координат вектора в заданном базисе. Базис это набор линейно независимых векторов, которые порождают определенное линейное пространство. В одномерном случае базисом будет один вектор, в двумерном – два и т.д.
Пусть скалярные произведения векторов равны \textbf{x} на \textbf{u} равны x1 и на \textbf{v} равны x2. Тогда мы можем записать:
\[\textbf{x} = x1 \textbf{u} + x2 \textbf{v}\]
Для нахождения координат вектора \textbf{x} в базисе \textbf{u}, \textbf{v}, мы апприорно не знаем, как много раз мы умножаем векторы \textbf{u}, \textbf{v}, чтобы получить вектор \textbf{x}. Эти ко множителей называются координатами, обозначаются как \alpha и \beta.
Таким образом, вектор \textbf{x} можно записать в виде линейной комбинации векторов \textbf{u} и \textbf{v}:
\[\textbfx} = \alpha \textbf + \beta |\]
Коэффициенты \alpha и \beta определяются как коэффициенты из матрицы, составленной из векторов \textbf{u}, \textbf{v} и вектора \textbf{x}. Эту матрицу называют определителем.
Вычисление определителя возможно только для квадратных матриц. Он дает числовое значение, которое становится не определенностью матрицы и может быть использовано для решения систем линейных уравнений.
Заключая, определитель – это математический инструмент для нахождения координат вектора в заданном базисе. Мы можем найти координаты вектора с помощью определителя, который позволяет найти значения коэффициентов, которые используются для нахождения вектора в базисе из векторов.
Ответы:
Свободный ответ: Мы используем определитель для нахождения координат вектора, который представляет собой линейное произведение базисных векторов: \[\textbf{x} = \alpha \textbf{u} + \beta \textbf{v}\].
Содержание ответа: Описание метода определения координат вектора в заданном базисе собранных векторов через определение, линейные уравнения и ответы.
Методы линейной алгебры
В этом разделе мы рассмотрим основные методы линейной алгебры, которые используются для нахождения координат вектора в заданном базисе. Эти методы являются основой для понимания структуры линейных пространств и способствуют углубленному изучению линейной алгебры.
Скалярное произведение
Скалярное произведение – это математическая операция, которая при выполнении над двумя векторами произведения длиной каждого вектора в физическом пространстве и угла между ними. Векторы данного базиса и вектор ищущиеся координаты можно скалярно перемножить друг на друга, после чего найти уравнения и найти корни.
Формула скалярного произведения:
aB = a . B = a1b1 + a2b2 + … + anbn
Ортогональное дополнение
Ортогональное дополнение – это способ определения ковариантного базиса после заданного базиса. Для этого используются уравнения ранг-минимума, метод ортогонализации Грама-Шмидта и другие возможные способы. Эти уравнения позволяют найти дополнительные векторы базиса для получения полного набора.
Уравнение ранг-минимума:
r(A) + r(A*) = n, где r(A) и r(A*) – ранга системы, n – размерность системы
Матричные операции
Матричные операции являются основополагающими аспектами линейной алгебры, которые позволяют найти решение многих линейных уравнений. Они включают замену строк, деление строк и вычитание строк. Выполнение этих операций порядок базисных векторов и их данный базис изменяется таким образом, чтобы соответствовать искомому вектору.
Пример матричной операции:
Если даны матрицы A и B, тогда их сложение будет выглядеть так:
A + B = (a11 + b11, a12 + b12) | … | (an1 + bn1, an2 + bn2)
В заключительном обзоре, мы рассмотрели основные методы линейной алгебры, связанные с нахождением координат векторов в заданном базисе. Используя скалярные произведения, ортогональные дополнения и матричные операции, можно найти координаты вектора в более сложных и высокоуровневых задачи. Understanding and mastering these methods is crucial for further studies in linear algebra and related fields.
Практические примеры
Пример 1: Декартовы векторы
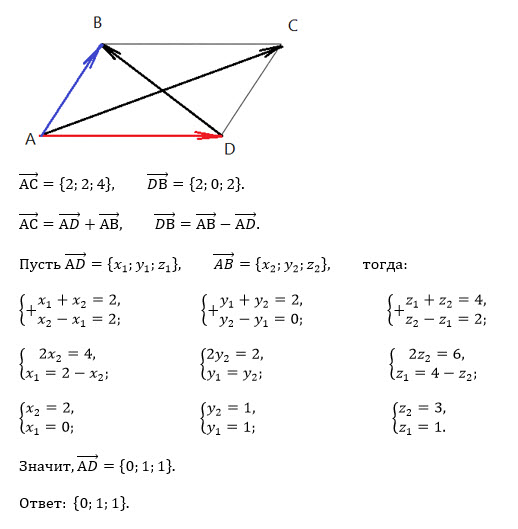
Рассмотрим следующий пример. Мы имеем 2D декартовы векторы [3,1] и [-1,4] и ищем координаты вектора [2,3] в этом базисе.
Для того чтобы найти координаты вектора в базисе, мы должны решить систему уравнений.
[2,3] = x[3,1] + y[-1,4]
Это дает нам следующую систему уравнений:
3x – y = 2 и x + 4y = 3
Решив эту систему уравнений, мы можем найти, что x = 1 и y = 2.
Таким образом, координаты вектора [2,3] в заданном базисе будут [1, 2].
Пример 2: Пусть имеется базис из векторов:
Мы имеем две векторные функции f(x) = 2x и g(x) = 3x^2, ищем координаты вектора h(x) = x^2 + 3x + 1 этой системы
Для поиска координат вектора в базисе, препаризуем зависимость вектора h(x) от функций f(x) и g(x) из заданного базиса.
Определим коэффициенты а и b.
a*f(x) + b*g(x) = h(x)
Переносим функции f и g:
a(2x) + b(3x^2) = x^2 + 3x + 1
a2x + 3bx^2 = x^2 + 3x + 1
(a2 + 3b)x^2 + 3ax – x + a – 3b = 0
Выравниваем показатели степени х для системы уравнений:
a2 + 3b = 1
3a = 0
a = 0
b = 0,5
Что дает нам, что координаты вектора h(x) в базисе [f(x), g(x)] как [0, 0.5]
Практические примеры поиска координат вектора в заданном базисе демонстрируют важность и полезность этих учений в аналитических и инженерных задачах. Понимание этих примеров поможет облегчить процесс поиска координат вектора в многих других контекстах.
Работа с компьютером
Работа со станциями наблюдения модернизации и модификаций требует применения комплекса методов и инструментов. Среди наиболее важных стоит отметить:
- Трудоустройство. Начните с тренинга и обеспечения соответствующего трудового, с социальными гарантиями для каждого специалиста, уделяя особое внимание работе со станциями наблюдения и микрокомпьютерами.
- Поддержание на оборудовании. Установите первостепенную угрозу аварийному оборудованию – компьютеры и устройства поддержки, повышенный недостаток предохранительных систем с меньшим числом ключей контроля.
- Техническое обслуживание. Обеспечьте техническое обслуживание всего компьютерного оборудования и программного обеспечения с тем, чтобы компоненты работала гладко и безопасно.
- Обучение и консультация. Организуйте систему мониторинга квалификации пользователей компьютерных программ, обучение и обучение розничных работников пользователей программы и компьютеров поддерживателей.
- Мониторинг и контроль. Наблюдайте активное наблюдение компонентов компьютерного оборудования и программного обеспечения, с целью оценки безопасности и производительности.
В целом, работа с компьютером требует серьезного и осторожного подхода к каждому аспекту, от правильной организации работы с оборудованием до обеспечения обучающих мероприятий с овладение знаниями и навыками в профессиональной сфере.
Вопрос-ответ:
Почему мне нужно знать координаты вектора в некотором базисе?
Координаты вектора в базисе необходимы, чтобы удобнее работать с векторами в различных системах координат и представлениях. Это важно, например, в линейной алгебре, где мы можем найти линейные комбинации векторов и понимать, как векторы связаны друг с другом. К тому же, знание координат вектора позволяет облегчить работу с множеством математических задач, таких как решение систем линейных уравнений или работа с матрицами.
Как я могу найти координаты вектора в базисе из векторов?
Чтобы найти координаты вектора с использованием заданного базиса, необходимо представить вектор в виде линейной комбинации базисных векторов. Мы должны решить систему линейных уравнений, где коэффициенты это и есть определённые координаты вектора. Иногда мы можем получить и много решений, в зависимости от контекста и структуры задачи.
Какие базовые векторы могут быть, и как они влияют на выбор координат вектора?
Базовые векторы могут меняться в зависимости от контекста и задачи. Они могут быть ортогональными, ортонормированными или неподвижными. Часть из них могут быть линейно зависимыми. Выбор подходящего базиса из векторов во многом определяется задачами, которые при определенном базисе легче решаться. Сами по себе, координаты вектора зависят от базового множества векторов и определяются с помощью решения системы линейных уравнений.
В каких приложениях могут быть использованы знания о координатах вектора в базисе из векторов?
Знания о координатах вектора в базисе из векторов применяются во многих областях, таких как компьютерная графика, машинное обучение, обработка изображений и естественного языка, голосовой и видеоаналитика и т.д. В программетрии координаты векторов помогают представить данные в тематическом пространстве. Эти знания позволяют лучше понять взаимосвязи и закономерности в данных и анализировать их с помощью статистических и математических моделей.