Содержание:
- § 1 Координатная прямая
- § 2 Определение координат симметричных точек
§ 1 Координатная прямая
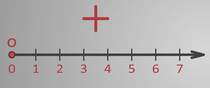
В этом уроке Вы узнаете, что такое координатная прямая, научитесь на ней обозначать положительные и отрицательные числа, определять координаты симметричных точек.
Давайте возьмем координатный луч.
На нем отмечено начало – точка О, единичный отрезок и справа от начала координат у нас находятся положительные числа в порядке возрастания.
А где расположить отрицательные?
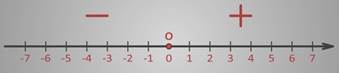
Чтобы отметить отрицательные числа нужно луч дополнить противоположным ему лучом и нанести на него такие же деления.
Таким образом, получилась координатная прямая.
Справа от точки О – начала координат – находятся положительные числа, а слева – отрицательные.
Следовательно, координатная прямая – это прямая с указанным на ней началом отсчета, направлением отсчета и единичным отрезком.
Координата – число, показывающее положение точки на координатной прямой.
Числа, расположенные справа от точки О на координатной прямой – положительные, соответственно направление, в котором они расположены называют положительным.
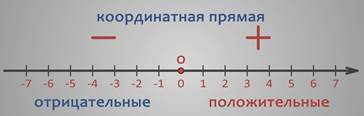
Числа, которые расположены слева – отрицательные, поэтому направление, в котором они расположены называется отрицательным.
На координатной прямой стрелкой указывается только положительное направление. Число 0 разделяет положительные и отрицательные числа.
Каждому числу соответствует единственная точка прямой.
Например, числу 3,5 соответствует точка М, которая удалена от начала отсчета, т. е. от точки О, на расстояние, равное 3,5 (в заданном масштабе), и отложена от точки О в заданном (положительном) направлении.
Числу -4 соответствует точка Р , которая удалена от точки О на расстояние, равное 4, и отложена от точки О в отрицательном направлении, т. е. в направлении, противоположном заданному.
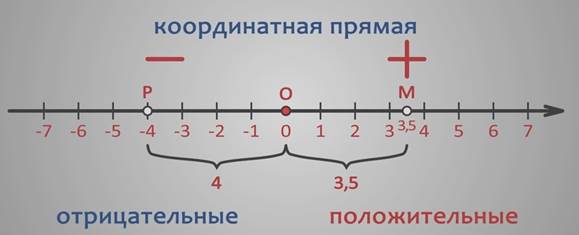
Верно и обратное: каждая точка координатной прямой соответствует единственному числу.

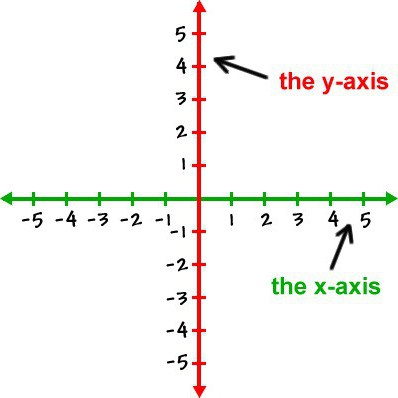
Около стрелки, указывающей направление отсчета на координатной прямой, часто ставят буквы x, y или t .
В таких случаях соответственно говорят «ось x», «ось y» или «ось t».
§ 2 Определение координат симметричных точек

Координатные прямые могут располагаться на плоскости по-разному, не только горизонтально.
Например, шкалу на термометре можно назвать координатной прямой.
Она будет вертикальной.
В этом случае положительные числа будут находиться выше 0, а отрицательные ниже 0.
Выполним практическое задание:

Изобразим координатную прямую.
Для этого начертим прямую, отметим на ней начало координат – точку О, выберем единичный отрезок, нанесем деления справа и слева от 0, покажем стрелкой направление отсчета, назовем координатную прямую «осью х».
Отметим на координатной прямой точки А (3), В (-3).
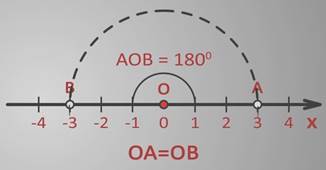
Обратите внимание: расстояние от точки А до начала координат точки О будет равно расстоянию OB.
![]()
Следовательно,
точки А и В будут центрально-симметричны относительно начала отсчета координатной прямой точки О (0).
Следует отметить, что центром симметрии точек на координатной прямой может быть любая точка данной прямой.
Поучимся находить симметричные точки на координатной прямой.
Пусть точка О (0) – центр симметрии.
Найдем точку, симметричную точке С (-6).
Такой точкой будет точка расположенная по другую сторону от центра симметрии.
![]()
Усложним задание.
Центром симметрии теперь будет точка А (-2).
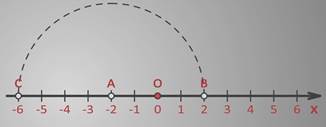
Между точками С (-6) и А (-2) – четыре единичных отрезка.
Отсчитаем от точки А (-2) четыре единичных отрезка вправо отметим точку В.
Определим ее координату – (2).
Таким образом, точки С (-6) и В (2) будут центрально-симметричны относительно точки А (-2).
А как определить координату центра симметрии двух точек на координатной прямой?
Пусть даны симметричные точки М(-1,4) и М1(2,6).
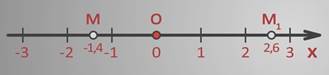
Расстояние от точки М до О(0) 1,4, от М1 до начала координат – 2,6.
Центр симметрии должен быть посередине.
![]()
![]()
![]()
Таким образом, в этом уроке Вы узнали, что такое координатная прямая, научились определять координаты точек и находить симметричные точки.
Список использованной литературы:
- Математика.6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича//Автор-составитель Л.А. Топилина. Мнемозина 2009 г.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И. Зубарева, А.Г. Мордкович.- М.: Мнемозина, 2013 г.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений/Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013 г.
- Справочник по математике – http://lyudmilanik.com.ua
- Справочник для учащихся в средней школе http://shkolo.ru
Использованные изображения:

5 класс “Координатная прямая”

КООРДИНАТНАЯ ПРЯМАЯ

Координатная прямая. Противоположные числа. 6 класс.
Представим
себе такую историю…
–
Привет, Паша! Над чем это ты так задумался? – поинтересовался у друга Саша.
–
Я не могу решить одну задачу. Давай подумаем вместе, – обратился Паша к Саше.
–
Давай. Читай условие, – сказал Саша.
–
Гусеница сползает с листочка на веточку и ползает по ней влево и вправо. Где
окажется гусеница, если она удалится на 5 сантиметров
от листочка? – зачитал условие задачи Паша.
–
И что же здесь сложного? – удивился Саша. – Всё просто. Гусеница окажется в 5 сантиметрах
от листочка.
–
Да, верно. Она окажется в 5 сантиметрах от листочка.
Но она же ползает по веточке как влево, так и вправо. А значит, важно знать и
направление, – сказал Паша.
–
Точно, – согласился Саша. – И как же нам ответить на вопрос задачи?
–
Давай спросим у Мудряша, – сказал Паша.
–
Ребята, прежде чем я отвечу на ваш вопрос, давайте мы немного разомнёмся и
выполним устные задания, – предложил Мудряш.
–
Теперь сверимся! – сказал Мудряш. –
Посмотрите, что у вас должно было получиться!
–
А сейчас вернёмся к вашей задаче, – начал
Мудряш. – Ребята, вы правильно заметили, что для того, чтобы ответить на вопрос
задачи, нам надо знать направление, в котором ползёт гусеница.
–
Давайте представим, что веточка, по которой ползает гусеница, – это
горизонтальная прямая АВ. Листочек на веточке, с которого сползает
гусеница, обозначим на этой прямой точкой О и назовём началом
отсчёта. Точка О будет изображать число 0
на нашей прямой. Можно сказать, что она разделяет прямую АВ на два луча –
ОА и ОB.
Предположим, что наша гусеница решила ползти вправо. Тогда отметим на луче ОА
точку С, которая будет изображать число 1.
Отрезок ОС – это единичный отрезок. На веточке это будет соответствовать
1
сантиметру. На луче ОА можно продолжить изображать положительные числа: 2,
3,
4,
5
и
так далее…
–
В 5
классе мы научились изображать на координатном луче положительные числа и 0,
– дружно сказали Паша и Саша.
–
Совершенно верно, – сказал Мудряш. – Это вам знакомо. А теперь представим, что гусеница
решила ползти влево. Давайте на луче ОВ отметим точку D
таким образом, чтобы отрезок OD
был равен отрезку ОC. На веточке это также будет соответствовать 1
сантиметру. Будем считать, что точка D
изображает число .
Чтобы изобразить число ,
мы на луче ОB
отметим
точку Е таким образом, чтобы отрезок ОЕ был равен двум отрезкам ОD.
Таким же образом мы можем продолжить изображать отрицательные числа: ,
,
и
так далее…
Говорят,
что луч ОА задаёт положительное направление на прямой АВ.
–
А тогда луч ОВ задаёт отрицательное направление на прямой АВ,
– дружно сказали мальчишки.
–
Всё верно, ребята! Отметим, что положительное направление указывают стрелкой,
– добавил Мудряш.
–
Получается, что на прямой АВ мы выбрали начало отсчёта – точку О,
единичный отрезок ОС и направление, – отметили ребята.
–
Да, и такую прямую мы будем называть координатной прямой, –
сказал Мудряш.
–
А тогда число, которое показывает положение точки на прямой, называют координатой
этой точки? – задали вопрос Мудряшу Паша и Саша.
–
Всё верно! – ответил Мудряш.
– Тогда координата точки С –
это 1, а координата точки ДЭ – это , – добавили мальчишки.
–
Молодцы! – похвалил ребят Мудряш и отметил, – записывают это вот так: точка С
(1),
точка D ().
– Запомните! – продолжил Мудряш. – Прямую, на которой выбрали начало
отсчёта, единичный отрезок и направление, называют координатной прямой.
Число, показывающее положение точки на прямой, называют координатой
этой точки.
–
Тогда если наша гусеница проползёт 5
сантиметров вправо, то она окажется в точке с координатой 5?
– вернулись к задаче ребята.
–
Да! И мы можем назвать эту точку, например, точкой F
и записать F (5),
– сказал Мудряш.
–
А если гусеница проползёт 5 сантиметров влево, то окажется
в точке с координатой ,
– продолжили Паша и Саша. – Давайте назовём её точкой K
и
запишем K ().
–
Давайте, – согласился Мудряш.
–
Тогда получается, что на вопрос задачи мы можем дать два ответа? – задали
вопрос Мудряшу мальчики.
–
Конечно! Всё зависит от того, в каком направлении решит ползти гусеница, –
ответил на вопрос Мудряш.
–
Теперь разобрались! – радостно сказали друзья.
–
Отметим на координатной прямой ещё несколько точек, – предложил Мудряш. – Например,
точку М (),
точку N (4), точку P
()…
Но вместо слов «отметим точку с координатой…» может говорить просто «отметим
число…».
– Запомните! – сказал Мудряш. –
Все положительные числа и нуль называют неотрицательными числами.
Все отрицательные числа и нуль называют неположительными числами.
– Ребята, хотелось бы обратить внимание на то, –
продолжил Мудряш, – что координатная прямая может быть расположена
не только горизонтально, как мы с вами только что рассмотрели, но и, например,
вертикально. В таком случае положительными считаются координаты точек,
находящихся выше точки О, а отрицательными – координаты точек,
находящихся ниже точки О.
–
Мне кажется, что шкала термометра, о которой мы говорили на прошлом уроке,
является примером координатной прямой, – неуверенно сказал Паша.
–
Правильно, – сказал Мудряш. – –
начало отсчёта. Положительные значения температуры расположены выше ,
а отрицательные – ниже .
А теперь давайте выполним несколько заданий.
Задание
первое: запишите координаты точек А, B,
C, D,
Е, изображённых на рисунке.
Решение: Единичный
отрезок равен одной клеточке. Точка А находится на расстоянии 4
единичных отрезков справа от начала отсчёта, а значит, имеет координату 4.
Точка
B находится на расстоянии половины
единичного отрезка слева от начала отсчёта, а значит, её координата равна .
Точка
C расположена на расстоянии 4
единичных отрезков слева от начала отсчёта, следовательно, имеет координату .
Точка
D расположена на расстоянии единичных
отрезков справа от начала отсчёта, следовательно, она имеет координату 2,5.
Точка
Е находится на расстоянии 5,5
единичных отрезков слева от начала отсчёта, а значит, имеет координату .
Второе
задание: на координатной прямой отметьте числа: .
Решение: отметим
число 0.
Оно будет являться началом отсчёта. Отметим 1.
Отрезок от 0 до 1
называем единичным отрезком.
Число
находится
на расстоянии 1 единичного отрезка слева от начала
отсчёта. Число 3 находится на расстоянии 3
единичных отрезков справа от начала отсчёта. Число находится
слева от начала отсчёта на расстоянии 2,5 единичных
отрезков.
Число
находится
слева от начала отсчёта на расстоянии 4
единичных отрезков.
Число
5,5
расположено справа от начала отсчёта на расстоянии 5,5
единичных отрезков.
Число
7 также
расположено справа от начала отсчёта, но на расстоянии 7 единичных
отрезков.
И
последнее число расположено
на расстоянии 6,5 единичных отрезков слева от начала
отсчёта.
Следующее
задание: длина единичного отрезка координатной прямой равна 1
см. Чему равно расстояние между точкой А (3)
и точкой В (7), между точкой С
()
и точкой D (),
между точкой Е ()
и точкой F (2)?
Решение: начертим координатную прямую, длина единичного отрезка
которой равна одному сантиметру. Отметим точку А (3)
и точку В (7). Расстояние между этими
точками равно 4 единичным отрезкам, то есть 4
сантиметрам.
Теперь
отметим точку С ()
и точку D ().
Расстояние между ними равно 3 единичным отрезкам, то
есть 3
сантиметрам.
Отметим
точку Е ()
и точку F (2).
Расстояние между этими точками равно 4
единичным отрезкам, а значит, 4 сантиметрам.
Ещё
одно задание: в какую точку перейдёт точка С (3):
а)
при перемещении на 4 единицы в положительном
направлении;
б)
при перемещении на 7 единиц в отрицательном
направлении?
Решение:
начертим координатную прямую АВ и
отметим на ней точку С (3).
Положительное
направление на прямой задаёт нам луч ОА. Значит при перемещении в
положительном направлении, то есть вправо, на 4
единицы точка С перейдёт в точку К (7).
Отрицательное
направление на прямой задаёт луч ОВ. Тогда при перемещении в
отрицательном направлении, то есть влево, на 7
единиц точка С перейдёт в точку М ().
Урок является логическим продолжением урока о координатном луче. Все мы знаем какие числа следуют после нуля. А есть ли что-то, что находится до числа ноль? Смотрите урок…
Больше уроков на сайте https://mriya-urok.com/
Похожие уроки: Координатный луч, Противоположные числа и модуль,
Все положительные числа и ноль можно изобразить на координатном луче в виде точек. Координатным лучом называют луч, начало которого совпадает с началом отсчета на котором отложены равные отрезки (единичные отрезки).
Расширив множество чисел, мы сталкиваемся с тем, что отрицательные числа отметить на координатном луче невозможно.
Для всех рациональных чисел есть координатная прямая.
координатная прямой — это прямая, на которой выбраны начало отсчета, единичный отрезок и направление.
Для изображения координатной прямой проделаем следующие шаги.
- Изобразим прямую линию.
- Выберем начало отсчета, точку О. этой точке соответствует число 0.
- В обе стороны от начала отсчета откладываем единичные отрезки.
- Выбираем направление и обозначаем его стрелкой. Стрелка указывает положительное направление координатной прямой.
- Положительные числа располагаются в положительном направлении от 0. Отрицательные числа – в противоположном направлении на соответствующем расстоянии от нуля.
Теперь можно изобразить любое рациональное число на этой координатной прямой в виде точки. И, наоборот, любой точке на координатной прямой соответствует число, показывающее положение этой точки. Это число называется координатой точки. На координатная прямая, как и на луче, можно сравнивать числа или показывать их изменение:
Увеличение с помощью перемещения в положительном направлении.
Уменьшение с помощью перемещения в отрицательном направлении.
Утверждать, что вы знаете математику, невозможно, если вы не умеете строить графики, изображать неравенства на координатной прямой, работать с осями координат. Визуальная составляющая в науке жизненно необходима, ведь без наглядных примеров в формулах и вычислениях порой можно сильно запутаться. В данной статье мы посмотрим, как работать с осями координат, и научимся строить простейшие графики функций.
Применение
Координатная прямая – это основа простейших видов графиков, с которыми сталкивается школьник на своем учебном пути. Она используется практически в каждой математической теме: при расчёте скорости и времени, проецировании размеров объектов и вычислении их площади, в тригонометрии при работе с синусами и косинусами.
Главная ценность такой прямой – это наглядность. Поскольку математика – это наука, в которой требуется высокий уровень абстрактности мышления, графики помогают в представлении объекта в реальном мире. Как он себя ведет? В какой точке пространства будет находиться через несколько секунд, минут, часов? Что можно сказать о нём в сопоставлении с другими объектами? Какой скоростью он обладает в случайно выбранный момент времени? Как охарактеризовать его движение?
А про скорость речь идёт неспроста – именно её зачастую отображают графики функции. А ещё они могут отображать изменение температуры или давления внутри объекта, его размеров, ориентации относительно горизонта. Таким образом, построить координатную прямую зачастую требуется и в физике.
Одномерный график
Существует понятие многомерности. В одномерном пространстве достаточно всего одного числа, чтобы определить местоположение точки. Это как раз и есть случай с применением координатной прямой. Если пространство двухмерное, то потребуется два числа. Графики такого типа используются гораздо чаще, и чуть дальше в статье мы их обязательно рассмотрим.
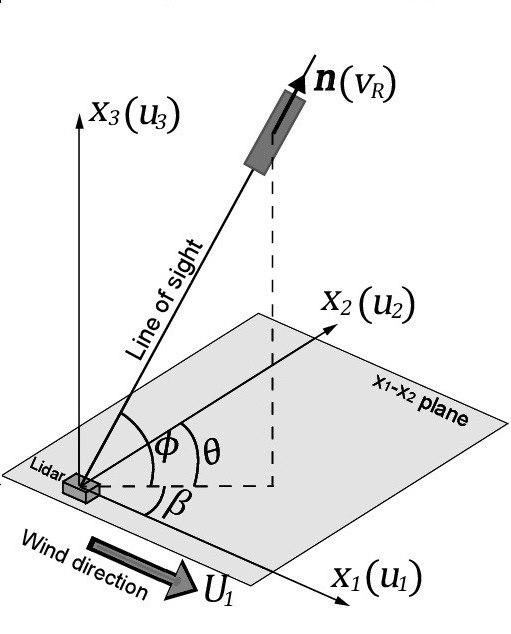
Что можно увидеть с помощью точек на оси, если она всего одна? Можно увидеть размер объекта, его положение в пространстве относительно некоторого «нуля», т. е. точки, выбранной в качестве начала отсчёта.
Изменение параметров с течением времени увидеть не удастся, так как все показания будут отображаться для одного конкретного момента. Однако с чего-то надо начинать! Итак, приступим.
Как построить координатную ось
Для начала требуется провести горизонтальную линию – это и будет наша ось. С правой стороны «заострим» её, чтобы она была похожа на стрелку. Таким образом мы обозначим направление, в котором числа будут увеличиваться. В сторону уменьшения стрелка обычно не ставится. Традиционно ось направлена вправо, поэтому мы просто последуем данному правилу.
Поставим нулевую отметку, которая будет отображать начало координат. Это то самое место, от которого ведется отсчёт, будь то размер, вес, скорость или что угодно другое. Кроме нуля, мы обязательно должны обозначить так называемую цену деления, т. е. ввести стандарт единицы, в соответствии с которой будем откладывать на оси те или иные величины. Это обязательно нужно делать, чтобы уметь находить длину отрезка на координатной прямой.
Через равное расстояние друг от друга поставим точки или «зарубки» на линии, а под ними напишем соответственно 1,2,3 и так далее. И вот, всё готово. Но с получившимся графиком надо ещё научиться работать.
Виды точек на координатной прямой
С первого взгляда на предложенные в учебниках рисунки становится понятно: точки на оси могут быть закрашенные или не закрашенные. Вы думаете, это случайность? Вовсе нет! «Сплошная» точка используется при нестрогом неравенстве – том, которое читается как «больше или равно». Если же нужно строго ограничить интервал (например, «икс» может принимать значения от нуля до единицы, но не включает её), мы воспользуемся «полой» точкой, то есть, по сути, маленьким кружком на оси. Надо заметить, что ученики не очень любят строгие неравенства, потому что с ними сложнее работать.
В зависимости от того, какие точки вы используете на графике, будут называться и построенные интервалы. Если неравенство с двух сторон нестрогое, то мы получим отрезок. Если с одной стороны он окажется «открыт», то называться будет полуинтервалом. Наконец, если часть прямой ограничена с двух сторон полыми точками, она будет называться интервалом.
Плоскость
При построении двух прямых на координатной плоскости мы уже можем рассматривать графики функций. Скажем, горизонтальная линия будет осью времени, а вертикальная – расстоянием. И вот уже мы в состоянии определить, какое расстояние преодолеет объект через минуту или час пути. Таким образом, работа с плоскостью даёт возможность следить за изменением состояния объекта. Это гораздо интереснее, чем исследование статичного состояния.
Простейший график на такой плоскости – прямая, она отражает функцию Y(X) = aX + b. Линия изгибается? Это означает, что объект меняет свои характеристики в процессе исследования.
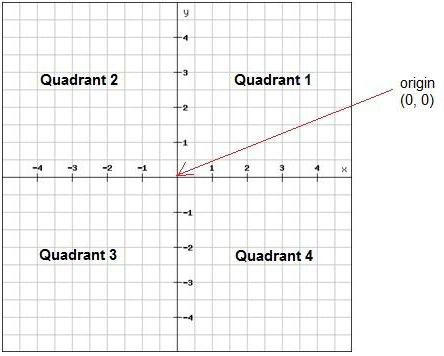
Представьте, вы стоите на крыше здания и держите в вытянутой руке камень. Когда вы отпустите его, он полетит вниз, начав своё движение с нулевой скорости. Но уже через секунду он будет преодолевать 36 километров в час. Камень продолжит ускоряться и дальше, и чтобы нарисовать его движение на графике, вам потребуется замерить его скорость в несколько моментов времени, выставив точки на оси в соответствующих местах.
Отметки на горизонтальной координатной прямой по умолчанию получают название X1, X2,X3, а на вертикальной – Y1, Y2,Y3 соответственно. Проецируя их на плоскость и находя пересечения, мы находим фрагменты результирующего рисунка. Соединив их одной линией, мы получим график функции. В случае с падающим камнем квадратичная функция будет иметь вид: Y(X) = aX * X + bX + c.
Масштаб
Конечно, не обязательно выставлять рядом с делениями на прямой целочисленные значения. Если вы рассматриваете движение улитки, которая ползет со скоростью 0,03 метра в минуту, выставьте в качестве значений на координатной прямой дроби. В данном случае задайте цену деления как 0,01 метра.
Особенно удобно выполнять такие чертежи в тетради в клетку – здесь сразу видно, хватит ли места на листе для вашего графика, не выйдете ли вы за поля. Свои силы рассчитать несложно, ведь ширина клетки в такой тетради – 0,5 сантиметра. Понадобилось – уменьшили рисунок. От изменения масштаба графика он не потеряет и не изменит своих свойств.
Координаты точки и отрезка
Когда на уроке дается математическая задача, в ней могут содержаться параметры различных геометрических фигур как в виде длин сторон, периметра, площади, так и в виде координат. В этом случае может потребоваться как построить фигуру, так и получить какие-то данные, связанные с ней. Возникает вопрос: как найти на координатной прямой требуемую информацию? И как построить фигуру?

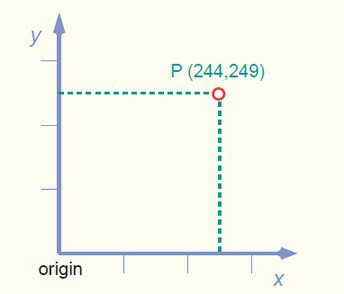
Например, речь идёт о точке. Тогда в условии задачи будет фигурировать заглавная буква, а в скобках будут стоять несколько цифр, чаще всего две (это значит, считать мы будем в двухмерном пространстве). Если в скобках три числа, записанные через точку с запятой или через запятую, то это трехмерное пространство. Каждое из значений – это координата на соответствующей оси: сначала по горизонтальной (X), затем – по вертикальной (Y).
Помните, как построить отрезок? Вы проходили это на геометрии. Если есть две точки, то между ними можно провести прямую. Их-то координаты и указываются в скобках, если в задаче фигурирует отрезок. Например: A(15, 13) – B(1, 4). Чтобы построить такую прямую, нужно на координатной плоскости найти и отметить точки, а затем их соединить. Вот и всё!
А любые многоугольники, как вы знаете, можно нарисовать с помощью отрезков. Задача решена.
Расчёты
Допустим, есть некоторый объект, положение которого по оси X характеризуется двумя числами: начинается он в точке с координатой (-3) и заканчивается в (+2). Если мы хотим узнать длину этого предмета, то должны вычесть из большего числа меньшее. Обратите внимание, что отрицательное число поглощает знак вычитания, потому что «минус на минус даёт плюс». Итак, мы складываем (2+3) и получаем 5. Это и есть требуемый результат.
Другой пример: нам дана конечная точка и длина объекта, но не дана начальная (и требуется её найти). Пусть положение известной точки будет (6), а размер изучаемого предмета – (4). Вычитая длину из конечной координаты, мы получим ответ. Итого: (6 – 4) = 2.
Отрицательные числа
Нередко требуется на практике работать с отрицательными значениями. В этом случае мы будем уходить по оси координат влево. Например, объект высотой 3 сантиметра плавает в воде. На треть он погружен в жидкость, на две трети находится на воздухе. Тогда, выбрав в качестве оси поверхность воды, мы с помощью простейших арифметических вычислений получаем два числа: верхняя точка объекта имеет координату (+2), а нижняя – (-1) сантиметр.
Нетрудно заметить, что в случае с плоскостью у нас образуется четыре четверти координатной прямой. Каждая из них имеет свой номер. В первой (верхней правой) части будут располагаться точки, имеющие две положительные координаты, во второй – слева сверху – значения по оси «икс» будут отрицательные, а по «игрек» – положительные. Третья и четвертая отсчитываются дальше против часовой стрелки.
Важное свойство
Вы знаете, что прямую можно представить как бесконечное множество точек. Мы можем просмотреть сколь угодно внимательно любое количество значений в каждую сторону оси, но не встретим повторяющихся. Это кажется наивным и понятным, но проистекает то утверждение из важного факта: каждому числу соответствует одна и только одна точка на координатной прямой.
Заключение
Помните, что любые оси, фигуры и по возможности графики необходимо строить по линейке. Единицы измерений были придуманы человеком не случайно – допустив погрешность при черчении, вы рискуете увидеть уже не то изображение, которое должно было получиться.
Будьте внимательны и аккуратны в построении графиков и вычислениях. Как и любая наука, изучаемая в школе, математика любит точность. Приложите немного старания, и хорошие оценки не заставят себя долго ждать.
