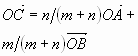Цели:
- выработать умение рассматривать различные подходы к решению задач и
проанализировать “эффект” от применения этих способов решения; - выработать умение учащегося выбирать метод решения задачи в соответствии
со своими
математическими предпочтениями, базирующимися на более прочных знаниях и
уверенных навыка; - выработать умение составить план последовательных этапов для достижения
результата; - выработать умение обосновать все предпринимаемые шаги и вычисления;
- повторить и закрепить различные темы и вопросы стереометрии и
планиметрии, типовые стереометрические конструкции, связанные с решением
текущих задач; - развить пространственное мышление.
Задачи:
- анализ различных методов решения задачи: координатно-векторный метод,
применение теоремы косинусов, применение теоремы о трех перпендикулярах; - сравнение преимуществ и недостатков каждого метода;
- повторение свойств куба, треугольной призмы, правильного шестигранника;
- подготовка к сдаче ЕГЭ;
- развитие самостоятельности при принятии решения.
Схема урока
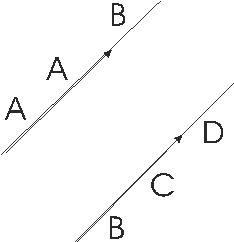
Задача 1.
В кубе ABCDA1B1C1D1
с ребром 1 точка О – центр грани ABCD.
Найти:
а) угол между прямыми A1D и BO;
б) расстояние от точки B до середины отрезка A1D.
Решение пункта а).
1 способ. Координатно-векторный метод
Поместим наш куб в прямоугольную систему координат как показано на рисунке,
вершины A1 (1; 0; 1), D (1; 1; 0), B1
(0; 0; 1), O (½; ½; 0).
Направляющие векторы прямых A1D и B1O:
![]() {0; 1; -1} и
{0; 1; -1} и
![]() {½;
{½;
½; -1};
искомый угол φ между ними находим по формуле:
cos∠φ =
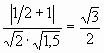 ,
,
откуда∠φ = 30°.
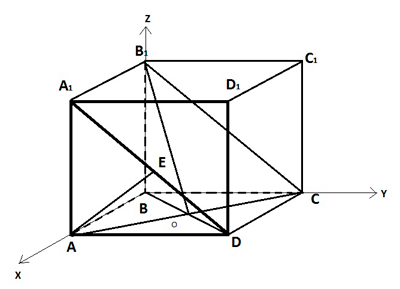
2 способ. Используем теорему косинусов.
1) Проведем прямую В1С параллельно прямой
A1D. Угол CB1O будет искомым.
2) Из прямоугольного треугольника BB1O по теореме Пифагора:
B1O =
![]() .
.
3) По теореме косинусов из треугольника CB1O
вычисляем угол CB1O:
cos
![]() CB1O
CB1O
=
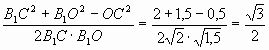 ,
,
искомый угол составляет 30°.
Замечание. При решении задачи 2-м способом можно заметить, что по теореме
о трех перпендикулярах
![]() COB1 = 90°,
COB1 = 90°,
поэтому из прямоугольного ∆ CB1O также легко вычислить косинус
искомого угла.
Решение пункта б).
1 способ. Воспользуемся формулой расстояния между двумя
точками
Пусть точка E – середина A1D, тогда координаты E (1; 1/2; ½), B (0; 0; 0).
BE =
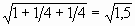 .
.
2 способ. По теореме Пифагора
Из прямоугольного ∆ BAE с прямым
![]() BAE
BAE
находим BE =
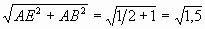 .
.
Задача 2.
В правильной треугольной призме ABCA1B1C1
все ребра равны a. Найти угол между прямыми AB и A1C.
Решение.
1 способ. Координатно-векторный метод
Координаты вершин призмы в прямоугольной системе при расположении призмы, как
на рисунке: A (0; 0; 0), B (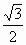 a;
a;
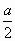 ;
;
0),
A1(0; 0; a), C (0; a; 0).
Направляющие векторы прямых A1C и AB:
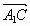
{0; a; -a} и
![]()
{ a;
a;
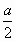 ;
;
0} ;
cos φ =
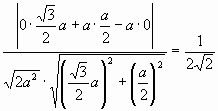 ;
;
![]() φ
φ
= arccos
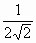 .
.
2 способ. Используем теорему косинусов
Рассматриваем ∆ A1B1C, в котором
A1B1 || AB. Имеем
cos φ =
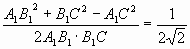 .
.
Задача 3.
(Из сборника ЕГЭ-2012. Математика: типовые экзаменационные варианты под ред.
А.Л.Семенова, И.В.Ященко)
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1,
все рёбра которой равны 1, найдите расстояние от точки E до прямой B1C1.
Решение
1 способ. Координатно-векторный метод
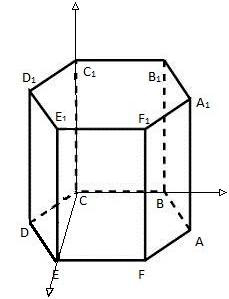
1) Поместим призму в прямоугольную систему координат, расположив координатные
оси, как показано на рисунке. СС1,
СВ и СЕ попарно перпендикулярны, поэтому можно направить вдоль них
координатные оси. Получаем координаты:
С1 (0; 0; 1), Е (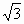 ;
;
0; 0), В1 (0;1;1).
2) Найдем координаты направляющих векторов для прямых С1В1
и С1Е:
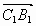 (0;1;0),
(0;1;0),
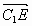
(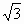 ;0;-1).
;0;-1).
3) Найдем косинус угла между С1В1
и С1Е, используя скалярное произведение векторов
![]() и
и
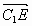 :
:
cos β =
![]() =
=
0 => β = 90° => C1E – искомое расстояние.
4) С1Е =
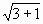 = 2.
= 2.
Вывод: знание различных подходов к решению стереометрических задач
позволяет выбрать предпочтительный для любого учащегося способ, т.е. тот,
которым ученик владеет уверенно, помогает избежать ошибок, приводит к успешному
решению задачи и получению хорошего балла на экзамене. Координатный метод имеет
преимущество перед другими способами тем, что требует меньше стереометрических
соображений и видения, а основывается на применении формул, у которых много
планиметрических и алгебраических аналогий, более привычных для учащихся.
Форма проведения урока – сочетание объяснения учителя с фронтальной
коллективной работой учащихся.
На экране с помощью видеопроектора демонстрируются рассматриваемые
многогранники, что позволяет сравнивать различные способы решения.
Домашнее задание: решить задачу 3 другим способом, например, с помощью
теоремы о трех перпендикулярах.
Литература
1. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по
геометрии для 11 класса.– М.: ИЛЕКСА, – 2010. – 208 с.
2. Геометрия, 10-11: учебник для общеобразовательных учреждений: базовый и
профильный уровни / Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.:
Просвещение, 2007. – 256 с.
3. ЕГЭ-2012. Математика: типовые экзаменационные варианты: 10 вариантов/ под
ред. А.Л.Семенова, И.В.Ященко. – М.: Национальное образование, 2011. – 112 с. –
(ЕГЭ-2012. ФИПИ – школе).
Система координат
С чего было бы логично начать обсуждение метода координат? Наверное, с понятия системы координат. Вспомни, когда ты с нею впервые столкнулся.
Мне кажется, что в 7 классе, когда ты узнал про существование линейной функции ( y=ax+b), например, ( y=2{x}-3).
Напомню, ты строил ее по точкам. Помнишь?
Ты выбирал произвольное число ( x), подставлял ее в формулу ( y=2{x}-3) и вычислял таким образом ( y).
Например, если ( x=0), то ( y=2cdot 0-3=-3), если же ( x=1), то ( y=2cdot 1-3=-1)и т. д.
Что же ты получал в итоге?
А получал ты точки с координатами: ( Aleft( 0,-3 right)) и ( Bleft( 1,-1 right)).
Далее ты рисовал «крестик» (систему координат ( X0Y)), выбирал на ней масштаб (сколько клеточек у тебя будет единичным отрезком) и отмечал на ней полученные тобою точки, которые затем соединял прямой линией, полученная линия и есть график функции ( y=2{x}-3).
Тут есть несколько моментов, которые стоит объяснить тебе чуть подробнее:
- Единичный отрезок ты выбираешь из соображений удобства, так, чтобы все красиво и компактно умещалось на рисунке;
- Принято, что ось ( displaystyle X) идет слева направо, а ось ( displaystyle Y) – cнизу вверх;
- Они пересекаются под прямым углом, а точка их пересечения называется началом координат. Она обозначается буквой ( displaystyle O);
- В записи координаты точки, например ( displaystyle Aleft( 0,-3 right)), слева в скобках стоит координата точки по оси ( displaystyle X), а справа, по оси ( displaystyle Y). В частности, ( displaystyle Aleft( 0,-3 right)) просто означает, что у точки ( displaystyle A) ( displaystyle x=0,~y=-3.);
- Для того, чтобы задать любую точку на координатной оси, требуется указать ее координаты (2 числа);
- Для любой точки, лежащей на оси ( displaystyle Ox,), ( displaystyle y=0.);
- Для любой точки, лежащей на оси ( displaystyle Oy), ( displaystyle x=0.);
- Ось ( displaystyle Ox) называется осью абсцисс;
- Ось ( displaystyle Oy) называется осью ординат.
Векторы
Теперь давай с тобой сделаем следующий шаг: отметим две точки ( displaystyle Aleft( {{x}_{1}},{{y}_{1}} right)) ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)).
Соединим эти две точки отрезком. И поставим стрелочку так, как будто мы проводим отрезок из точки ( displaystyle A) к точке ( displaystyle B):
То есть мы сделаем наш отрезок направленным!
Вспомни, как еще называется направленный отрезок? Верно, он называется вектором!
Вектором называется направленный отрезок, имеющий начало и конец.
Таким образом, если мы соединим точку ( displaystyle A) c точкой ( displaystyle B), причем началом у нас будет точка A, а концом – точка B, то мы получим вектор ( displaystyle overrightarrow{AB}).
Это построение ты тоже делал в 8 классе, помнишь?
Координаты вектора
Оказывается, векторы, как и точки, можно обозначать двумя цифрами: эти цифры называются координатами вектора.
Вопрос: как ты думаешь, достаточно ли нам знать координаты начала и конца вектора, чтобы найти его координаты?
Оказывается, что да! И делается это очень просто:
Координаты вектора = координаты точки конца – координаты точки начала.
Таким образом, так как в векторе ( displaystyle overrightarrow{AB}) точка ( displaystyle Aleft( {{x}_{1}},{{y}_{1}} right)) – начало, а ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)) – конец, то вектор ( displaystyle overrightarrow{AB}) имеет следующие координаты:
( displaystyle overrightarrow{AB}left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}} right))
Например, если ( displaystyle Aleft( 2,0 right))( displaystyle Bleft( 1,2 right)), то координаты вектора ( displaystyle overrightarrow{AB})
( displaystyle overrightarrow{AB}left( 1-2,2-0 right)=overrightarrow{AB}left( -1,2 right))
Теперь давай сделаем наоборот, найдем координаты вектора ( displaystyle overrightarrow{BA}).
Что нам для этого нужно поменять? Да, нужно поменять местами начало и конец: теперь начало вектора будет в точке ( displaystyle B), а конец – в точке ( displaystyle A).
Тогда:
( displaystyle overrightarrow{BA}left( 2-1,text{ }!!~!!text{ }0-2 right)=overrightarrow{BA(}1,-2).)
Посмотри внимательно, чем отличаются векторы ( displaystyle overrightarrow{AB}) и ( displaystyle overrightarrow{BA})?
Единственное их отличие – это знаки в координатах. Они противоположны. Этот факт принято записывать вот так:
( displaystyle overrightarrow{AB}=-overrightarrow{BA})
Иногда, если не оговаривается специально, какая точка является началом вектора, а какая – концом, то векторы обозначают не двумя заглавными буквами, а одной строчной, например: ( displaystyle {vec{a}}), ( displaystyle {vec{p}}) и т. д.
Еще больше о векторах и проекциях (эту тему мы непременно затронем) ты можешь прочитать в статье по физике «Большая теория по векторам» 🙂
Действия с векторами
Что еще можно делать с векторами?
Да почти все то же самое, что и с обычными числами:
- Векторы можно складывать друг с другом;
- Векторы можно вычитать друг из друга;
- Векторы можно умножать (или делить) на произвольное ненулевое число;
- Векторы можно умножать друг на друга.
Что же происходит при выполнении этих действий с координатами векторов?
1. При сложении (вычитании) двух векторов, мы складываем (вычитаем) поэлементно их координаты.
То есть:
( vec{a}left( {{x}_{1}},{{y}_{1}} right)+vec{b}left( {{x}_{2}},{{y}_{2}} right)=vec{c}left( {{x}_{1}}+{{x}_{2}},{{y}_{1}}+{{y}_{2}} right))
( vec{a}left( {{x}_{1}},{{y}_{1}} right)-vec{b}left( {{x}_{2}},{{y}_{2}} right)=vec{c}left( {{x}_{1}}-{{x}_{2}},{{y}_{1}}-{{y}_{2}} right))
2. При умножении (делении) вектора на число, все его координаты умножаются (делятся) на это число:
( kcdot vec{a}left( {{x}_{1}},{{y}_{1}} right)=vec{b}left( k{{x}_{1}},k{{y}_{1}} right))
Например:
Найдите сумму координат вектора ( vec{a}+vec{b}).
Вектор растягивается или сжимается или меняет направление при умножении или делении на число:
Давай вначале найдем координаты каждого из векторов.
Оба они имеют одинаковое начало – точку начала координат. Концы у них разные.
Тогда ( vec{a}left( 2-0,6-0 right)=vec{a}left( 2,6 right)), ( vec{b}left( 8-0,4-0 right)=vec{b}left( 8,4 right)).
Теперь вычислим координаты вектора ( vec{c}=vec{a}+vec{b}=vec{c}left( 2+8,4+6 right)=vec{c}left( 10,10 right))
Тогда сумма координат полученного вектора равна ( 20).
Ответ: ( 20)
Теперь реши сам следующую задачу:
Найти сумму координат вектора ( 3vec{a}-2vec{b})
Проверяем:
- ( vec{a}=vec{a}left( 4-2,10-4 right)=vec{a}left( 2,6 right));
- ( vec{b}=vec{b}left( 10-2,6-2 right)=vec{b}left( 8,4 right));
- ( vec{c}=3vec{a}-2vec{b}=3vec{a}left( 2,6 right)-2vec{b}left( 8,4 right)=left( 6,18 right)-left( 16,8 right)=vec{c}left( -10,10 right));
- ( -10+10=0).
Ответ: ( 0)
Расстояние между двумя точками на координатной плоскости
Давай рассмотрим теперь следующую задачу: у нас есть две точки на координатной плоскости. Как найти расстояние между ними?
Пусть первая точка будет ( {{P}_{1}}({{x}_{1}},{{y}_{1}})), а вторая ( {{P}_{2}}left( {{x}_{2}},{{y}_{2}} right)).
Обозначим расстояние между ними через ( d). Давай сделаем для наглядности следующий чертеж:
Что я сделал?
Я, во-первых, соединил точки ( {{P}_{1}}left( {{x}_{1}},{{y}_{1}} right)) и ( {{P}_{2}}left( {{x}_{2}},{{y}_{2}} right)).
А также из точки ( {{P}_{1}}) провел линию, параллельную оси ( Ox), а из точки ( {{P}_{2}}) провел линию, параллельную оси ( Oy).
Они пересеклись в точке ( R), образовав при этом замечательную фигуру. Чем она замечательна?
Да мы с тобой почти что все знаем про прямоугольный треугольник. Ну уж теорему Пифагора – точно!
Искомый отрезок – это гипотенуза этого треугольника, а отрезки ( {{P}_{1}}R,~{{P}_{2}}R) – катеты.
Чему равны координаты точки ( R)?
Да, их несложно найти по картинке: ( Rleft( {{x}_{2}},{{y}_{1}} right).~)
Так как отрезки ( {{P}_{1}}R,~{{P}_{2}}R) параллельны осям ( Ox) и ( Oy) соответственно, то их длины легко найти: если обозначить длины отрезков ( {{P}_{1}}R,~{{P}_{2}}R) соответственно через ( left| {{P}_{1}}Rleft| ,~ right|{{P}_{2}}R right|), то
( left| {{P}_{1}}R right|={{x}_{2}}-{{x}_{1}})
( left| {{P}_{2}}R right|={{y}_{2}}-{{y}_{1}})
Теперь воспользуемся теоремой Пифагора. Длины катетов нам известны, гипотенузу мы найдем:
( {{d}^{2}}=text{ }!!~!!text{ }left| {{P}_{1}}{{P}_{2}} right|=text{ }!!~!!text{ }{{left| {{P}_{1}}R right|}^{2}}+{{left| {{P}_{2}}R right|}^{2}}=({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}~)
( d=~sqrt{({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}})
Таким образом, расстояние между двумя точками – это корень из суммы квадратов разностей из координат.
Или же – расстояние между двумя точками – это длина отрезка, их соединяющего.
Легко заметить, что расстояние между точками не зависит от направления.
Тогда:
( d=left| overrightarrow{{{P}_{1}}{{P}_{2}}} right|=left| overrightarrow{{{P}_{2}}{{P}_{1}}} right|=sqrt{({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}})
Отсюда делаем три вывода:
- Длина вектора = корень из суммы квадратов его координат;
- Найти расстояние между двумя точками = найти длину вектора, их соединяющего (в любом направлении);
- Длины векторов, соединяющих две точки в разном направлении, равны.
Давай немного поупражняемся в вычислении расстояния между двумя точками:
Например, если ( Aleft( 1,2 right),~Bleft( 3,4 right)), то расстояние между ( A) и ( B) равно
( d=sqrt{{{left( 3-1 right)}^{2}}+{{left( 4-2 right)}^{2}}}=sqrt{4+4}=sqrt{8}=2sqrt{2})
Или пойдем по-другому: найдем координаты вектора ( overrightarrow{AB})
( overrightarrow{AB}left( 3-1,4-2 right)=overrightarrow{AB}left( 2,2 right))
И найдем длину вектора:
( left| overrightarrow{AB} right|=sqrt{{{2}^{2}}+{{2}^{2}}}=sqrt{8}=2sqrt{2})
Как видишь, одно и то же!
Теперь немного потренируйся сам:
Задание. Найти расстояние между указанными точками:
- ( Aleft( 2,sqrt{3} right),~Bleft( 5,2sqrt{3} right));
- ( Cleft( 2,4 right),~Dleft( 1,-5 right));
- ( Fleft( sqrt{12},1 right),~Gleft( sqrt{3},-1 right)).
Проверяем:
- ( d=sqrt{{{left( 5-2 right)}^{2}}+{{left( 2sqrt{3}-sqrt{3} right)}^{2}}}=sqrt{9+3}=sqrt{12}=2sqrt{3});
- ( displaystyle d=sqrt{{{left( 1-2 right)}^{2}}+{{left( -5-4 right)}^{2}}}=sqrt{1+81}=sqrt{82});
- ( displaystyle d=sqrt{{{left( sqrt{3}-sqrt{12} right)}^{2}}+{{left( -1-1 right)}^{2}}}=sqrt{left( 3-2sqrt{3}sqrt{12}+12 right)+4}=); ( displaystyle=sqrt{3-2sqrt{36}+12+4}=sqrt{3-12+12+4}=sqrt{7}).
Вот еще пара задачек на ту же формулу, правда звучат они немного по-другому:
1. Найдите квадрат длины вектора ( vec{a}-vec{b}).
2. Найдите квадрат длины вектора ( overrightarrow{AB})
Я так думаю, ты с ними без труда справился? Проверяем:
1. А это на внимательность) Мы уже нашли координаты векторов ( displaystyle {vec{a}}) и ( displaystyle {vec{b}}) ранее: ( displaystyle vec{a}left( 2,6 right),~vec{b}left( 8,4 right)). Тогда вектор ( displaystyle vec{a}-vec{b}) имеет координаты ( displaystyle left( 2-8,6-4 right)=left( -6,2 right)). Квадрат его длины будет равен:
( displaystyle {{d}^{2}}={{left( -6 right)}^{2}}+{{2}^{2}}=36+4=40.)
2. Найдем координаты вектора ( displaystyle overrightarrow{AB}=overrightarrow{AB}left( 8-2,6-4 right)=overrightarrow{AB}left( 6,2 right))
Тогда квадрат его длины равен
( displaystyle {{d}^{2}}={{6}^{2}}+{{2}^{2}}=36+4=40.)
Ничего сложного, правда? Обычная арифметика, не более того.
Следующие задачки нельзя однозначно классифицировать, они скорее на общую эрудицию и на умение рисовать простенькие картинки.
Задача 1. Найдите синус угла наклона отрезка, соединяющего точки ( displaystyle Oleft( 0;~0 right)),( displaystyle Aleft( 6;~8 right)) с осью абсцисс.
Как мы будем поступать здесь?
Нужно найти синус угла между ( displaystyle OA) и осью ( displaystyle Ox).
А где мы умеем искать синус? Верно, в прямоугольном треугольнике.
Так что нам нужно сделать? Построить этот треугольник!
Поскольку координаты точки ( displaystyle A-6) и ( displaystyle 8), то отрезок ( displaystyle OB) равен ( displaystyle 6), а отрезок ( displaystyle AB-8).
Нам нужно найти синус угла ( displaystyle angle AOB).
Напомню тебе, что синус – это отношение противолежащего катета к гипотенузе, тогда
( displaystyle sinangle AOB=frac{AB}{OA})
Что нам осталось сделать?
Найти гипотенузу.
Ты можешь сделать это двумя способами: по теореме Пифагора (катеты-то известны!) или по формуле расстояния между двумя точками (на самом деле одно и то же, что и первый способ!).
Я пойду вторым путем:
( displaystyle OA=sqrt{{{left( 6-0 right)}^{2}}+{{left( 8-0 right)}^{2}}}=10)
Тогда
( displaystyle sinangle AOB=frac{AB}{OA}=frac{8}{10}=0.8)
Ответ: ( displaystyle 0.8)
Следующая задача покажется тебе еще проще. Она – на координаты точки.
Задача 3. В условиях предыдущей задачи найти сумму расстояний от точки ( displaystyle A) до осей координат.
Задача – вообще элементарная, если знать, что такое расстояние от точки до осей.
Ты знаешь?
Я надеюсь, но все же напомню тебе:
Расстояние от точки до осей координат – это длины перпендикуляров, опущенных из точки к осям.
Итак, на моем рисунке, расположенном чуть выше, я уже изобразил один такой перпендикуляр. К какой он оси?
К оси ( displaystyle Ox).
И чему же равна тогда его длина?
Она равна ( displaystyle 8).
Теперь сам проведи перпендикуляр к оси ( displaystyle Oy) и найди его длину. Она будет равна ( displaystyle 6), ведь так?
Тогда их сумма равна ( displaystyle 14).
Ответ: ( displaystyle 14).
Задача 4. В условиях задачи 2, найдите ординату точки, симметричной точке ( displaystyle A) относительно оси абсцисс.
Решение:
Я думаю, тебе интуитивно ясно, что такое симметрия?
Очень многие объекты ею обладают: многие здания, столы, самолеты, многие геометрические фигуры: шар, цилиндр, квадрат, ромб и т. д.
Грубо говоря, симметрию можно понимать вот как: фигура состоит из двух (или более) одинаковых половинок. Такая симметрия называется осевой.
А что тогда такое ось?
Это как раз та линия, по которой фигуру можно, условно говоря, «разрезать» на одинаковые половинки (на данной картинке ось симметрии – прямая ( displaystyle l)):
Теперь давай вернемся к нашей задаче.
Нам известно, что мы ищем точку, симметричную относительно оси ( displaystyle Ox).
Тогда эта ось – ось симметрии.
Значит, нам нужно отметить такую точку ( displaystyle {{A}_{1}}), чтобы ось ( displaystyle Ox) разрезала отрезок ( displaystyle A{{A}_{1}}) на две равные части.
Попробуй сам отметить такую точку. А теперь сравни с моим решением:
У тебя получилось так же?
Хорошо! У найденной точки нас интересует ордината.
Она равна ( displaystyle -8)
Ответ: ( displaystyle -8)
Теперь задачка на параллелограмм:
Задача 5. Точки ( displaystyle Oleft( 0;~0 right),~Aleft( 6;~8 right),~Cleft( 0;~6 right)~) являются вершинами параллелограмма. Найдите ординату точки ( displaystyle B).
Можно решать эту задачу двумя способами: логикой и методом координат.
Я вначале применю метод координат, а потом расскажу тебе, как можно решить иначе.
Совершенно ясно, что абсцисса точки ( displaystyle B) равна ( displaystyle 6). (она лежит на перпендикуляре, проведенной из точки ( displaystyle A) к оси абсцисс).
Нам нужно найти ординату.
Воспользуемся тем, что наша фигура – параллелограмм, это значит, что ( displaystyle CA=OB).
Найдем длину отрезка ( displaystyle CA), используя формулу расстояния между двумя точками:
( d=sqrt{{{left( 6-0 right)}^{2}}+{{left( 8-6 right)}^{2}}}=sqrt{40})
Тогда ( OB=sqrt{40}.~~)
Опускаем перпендикуляр, соединяющий точку ( B) с осью ( Ox).
Точку пересечения обозначу буквой ( D).
Длина отрезка ( OD) равна ( 6). (найди сам задачу, где мы обсуждали этот момент), тогда найдем длину отрезка ( BD) по теореме Пифагора:
( BD=sqrt{40-36}=2)
Длина отрезка – в точности совпадает с его ординатой.
Ответ: ( 2).
Другое решение (я просто приведу рисунок, который его иллюстрирует)
Ход решения:
- Провести ( CE);
- Найти координаты точки ( E) и длину ( AE);
- Доказать, что ( BD=AE).
Еще одна задачка на длину отрезка:
Точки ( Oleft( 0;~0 right),~Aleft( 6;~8 right),~Bleft( 8;~2 right)) являются вершинами треугольника. Найдите длину его средней линии ( CD), параллельной ( OA).
Ты помнишь, что такое средняя линия треугольника?
Тогда для тебя эта задача элементарна. Если не помнишь, то я напомню: средняя линия треугольника – это линия, которая соединяет середины противоположных сторон.
Она параллельна основанию и равна его половине.
Основание – это отрезок ( OA).
Его длину нам приходилось искать ранее, оно равно ( 10).
Тогда длина средней линии вдвое меньше и равна ( 5).
Ответ: ( 5).
Комментарий: эту задачу можно решить и другим способом, к которому мы обратимся чуть позже.
А пока – вот тебе несколько задачек, потренируйся на них, они совсем простые, но помогают «набивать руку», на использовании метода координат!
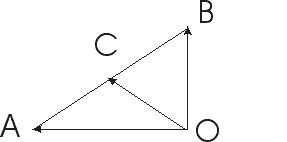
1. Точки ( Oleft( 0;~0 right),~Aleft( 10;~0 right),~Bleft( 8;~6 right),~Cleft( 2;~6 right)) являются вершинами трапеции. Найдите длину ее средней линии ( DE).
2. Точки ( Oleft( 0;~0 right),~Bleft( 8;~2 right),~Cleft( 2;~6 right)) и ( A) являются вершинами параллелограмма. Найдите ординату точки ( A).
3. Найдите длину отрезка, соединяющего точки ( Aleft( 6 ;~8 right)) и ( Bleft( -2;~2 right).)
4. Найдите площадь закрашенной фигуры на координатной плоскости.
5. Окружность с центром в начале координат проходит через точку ( displaystyle Pleft( 8;text{ }6 right)). Найдите ее радиус.
6. Найдите радиус окружности, описанной около прямоугольника ( displaystyle ABCD), вершины которого имеют координаты соответственно ( displaystyle left( -2;~-2 right),~left( 6;~-2 right),~left( 6;~4 right),~left( -2;~4 right).)
Решения:
1. Известно, что средняя линия трапеции равна полусумме ее оснований.
Основание ( displaystyle CB) равно ( displaystyle 6), а основание ( displaystyle OA-10).
Тогда ( displaystyle ED=frac{CB+OA}{2}=frac{16}{2}=8)
Ответ: ( displaystyle 8)
2. Проще всего решить эту задачу так: заметить, что ( displaystyle overrightarrow{OA}=overrightarrow{OC}+overrightarrow{OB}) (правило параллелограмма).
Вычислить координаты векторов ( displaystyle overrightarrow{OC}) и ( displaystyle overrightarrow{OB}) не представляет труда: ( displaystyle overrightarrow{OC}left( 2,6 right),~overrightarrow{OB}left( 8,2 right)).
При сложении векторов координаты складываются.
Тогда ( displaystyle overrightarrow{OA}) имеет координаты ( displaystyle left( 10,8 right)).
Эти же координаты имеет и точка ( displaystyle A), поскольку начало вектора ( displaystyle overrightarrow{OA}) – это точка с координатами ( displaystyle left( 0,0 right)).
Нас интересует ордината. Она равна ( displaystyle 8).
Ответ: ( displaystyle 8)
3. Действуем сразу по формуле расстояния между двумя точками:
( displaystyle d=sqrt{{{left( 6-left( -2 right) right)}^{2}}+{{left( 8-2 right)}^{2}}}=sqrt{64+36}=10)
Ответ: ( displaystyle 10)
4. Посмотри на картинку и скажи, между какими двумя фигурами «зажата» заштрихованная область?
Она зажата между двумя квадратами. Тогда площадь искомой фигуры равна площади большого квадрата минус площадь маленького.
Сторона маленького квадрата – это отрезок, соединяющий точки ( displaystyle left( 0,2 right)) и ( displaystyle left( 2,0 right).) Его длина равна
( displaystyle {{d}_{1}}=sqrt{{{left( 0-2 right)}^{2}}+{{left( 2-0 right)}^{2}}}=sqrt{8})
Тогда площадь маленького квадрата равна
( displaystyle {{S}_{1}}=d_{1}^{2}={{sqrt{8}}^{2}}=8)
Точно так же поступаем и с большим квадратом: его сторона – это отрезок, соединяющий точки ( displaystyle left( 0,4 right)) и ( displaystyle left( 4,0 right).)
Его длина равна
( displaystyle {{d}_{2}}=sqrt{{{left( 0-4 right)}^{2}}+{{left( 4-0 right)}^{2}}}=sqrt{32}).
Тогда площадь большого квадрата равна
( displaystyle {{S}_{2}}=d_{2}^{2}={{sqrt{32}}^{2}}=32)
Площадь искомой фигуры найдем по формуле:
( displaystyle S={{S}_{2}}-{{S}_{1}}=32-8=24)
Ответ: ( displaystyle 24)
5. Если окружность имеет в качестве центра начало координат и проходит через точку ( displaystyle P), то ее радиус ( displaystyle R) будет в точности равен длине отрезка ( displaystyle OP) (сделай рисунок и ты поймешь, почему это очевидно).
Найдем длину этого отрезка:
( displaystyle R=sqrt{{{6}^{2}}+{{8}^{2}}}=10)
Ответ: ( displaystyle 10)
6. Известно, что радиус описанной около прямоугольника окружности равен половине его диагонали.
Найдем длину любой из двух диагоналей (ведь в прямоугольнике они равны!)
( displaystyle left| AC right|=sqrt{{{left( 6-left( -2 right) right)}^{2}}+{{left( 4-left( -2 right) right)}^{2}}}=10)
Тогда
( displaystyle R=frac{1}{2}left| AC right|=5)
Ответ: ( displaystyle 5)
Ну что, ты со всем справился?
Было не очень сложно разобраться, ведь так? Правило здесь одно – уметь сделать наглядную картинку и просто «считать» с нее все данные.
Нам осталось совсем немного. Есть еще буквально два момента, которые бы мне хотелось обсудить:
- как найти координаты середины отрезка и
Координаты середины отрезка
Давай попробуем решить вот такую нехитрую задачку.
Пусть даны две точки ( displaystyle Aleft( {{x}_{1}},{{x}_{2}} right)~) и ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)).
Найти координаты середины отрезка ( displaystyle AB). Решение этой задачки следующее: пусть точка ( displaystyle D) – искомая середина, тогда ( displaystyle D) имеет координаты:
( displaystyle Dleft( frac{{{x}_{1}}+{{x}_{2}}}{2},frac{{{y}_{1}}+{{y}_{2}}}{2} right))
То есть: координаты середины отрезка = среднее арифметическое соответствующих координат концов отрезка.
Это правило очень простое и как правило не вызывает затруднений у учащихся. Давай посмотрим, в каких задачках и как оно употребляется:
1. Найдите ординату середины отрезка, соединяющего точки ( displaystyle Aleft( 6,~8 right)~) и ( displaystyle Bleft( -2,~2 right).)
2. Точки ( displaystyle Oleft( 0;~0 right),~Aleft( 6;~8 right),~Bleft( 6;~2 right),~Cleft( 0;~6 right)) являются вершинами четырехугольника. Найдите ординату точки ( displaystyle P) пересечения его диагоналей.
3. Найдите абсциссу центра окружности, описанной около прямоугольника ( displaystyle ABCD), вершины которого имеют координаты соответственно ( displaystyle left( -2;~-2 right),~left( 6;~-2 right),~left( 6;~4 right),~left( -2;~4 right)).
Решения:
1. Первая задачка – просто классика. Действуем сразу по определению середины отрезка. Она имеет координаты ( displaystyle left( frac{6-2}{2},~frac{8+2}{2} right)=left( 2,5 right)).
Ордината равна ( displaystyle 5).
Ответ: ( displaystyle 5)
2. Легко видеть, что данный четырехугольник является параллелограммом (даже ромбом!). Ты и сам можешь это доказать, вычислив длины сторон и сравнив их между собой.
Что я знаю про параллелограмм?
Его диагонали точкой пересечения делятся пополам! Ага! Значит точка пересечения диагоналей – это что?
Это середина любой из диагоналей!
Выберу, в частности диагональ ( displaystyle OA). Тогда точка ( displaystyle P) имеет координаты ( displaystyle left( frac{6+0}{2},frac{8+0}{2} right)=left( 3,4 right).)
Ордината точки ( displaystyle P) равна ( displaystyle 4).
Ответ: ( displaystyle 4)
3. С чем совпадает центр описанной около прямоугольника окружности?
Он совпадает с точкой пересечения его диагоналей. А что ты знаешь про диагонали прямоугольника?
Они равны и точкой пересечения делятся пополам. Задача свелась к предыдущей.
Возьму, например, диагональ ( displaystyle AC). Тогда если ( displaystyle P) – центр описанной окружности, то ( displaystyle P) – середина ( displaystyle AC).
Ищу координаты: ( displaystyle Pleft( frac{-2+6}{2},frac{-2+4}{2} right)=Pleft( 2,1 right).) Абсцисса равна ( displaystyle 2).
Ответ: ( displaystyle 2)
Теперь потренируйся немного самостоятельно, я лишь приведу ответы к каждой задачи, чтобы ты мог себя проверить.
1. Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты ( displaystyle left( 8;~0 right),~left( 0;~6 right),~left( 8;~6 right).)
2. Найдите ординату центра окружности, описанной около треугольника, вершины которого имеют координаты ( displaystyle left( 8;~0 right),~left( 0;~6 right),~left( 8;~6 right).)
3. Какого радиуса должна быть окружность с центром в точке ( displaystyle Pleft( 8;~6 right),) чтобы она касалась оси абсцисс?
4. Найдите ординату точки пересечения оси ( displaystyle Oy) и отрезка, соединяющего точки ( displaystyle Aleft( 6;text{ }8 right)) и ( displaystyle Bleft( -6;text{ }0 right).)
Ответы:
- ( displaystyle 5);
- ( displaystyle 3);
- ( displaystyle 6);
- ( displaystyle 4).
Умножение векторов
Все удалось? Очень на это надеюсь! Теперь – последний рывок.
Сейчас будь особенно внимателен. Тот материал, который я сейчас буду объяснять, имеет непосредственное отношение не только к простым задачам на метод координат, но также встречается повсеместно и в задачах повышенной сложности.
Какое из своих обещаний я еще не сдержал?
Вспомни, какие операции над векторами я обещал ввести и какие в конечном счете ввел? Я точно ничего не забыл?
Забыл! Забыл объяснить, что значит умножение векторов.
Есть два способа умножить вектор на вектор. В зависимости от выбранного способа у нас будут получаться объекты разной природы:
- Скалярное произведение (результат – число);
- Векторное произведение (результат – вектор).
Векторное произведение выполняется довольно хитро. Как его делать и для чего оно нужно, мы с тобой обсудим чуть позже. А пока мы остановимся на скалярном произведении.
Есть аж два способа, позволяющих нам его вычислить:
- Через координаты векторов;
- Через длины векторов и угол между ними.
Как ты догадался, результат должен быть один и тот же! Итак, давай вначале рассмотрим первый способ:
Найдите скалярное произведение векторов ( displaystyle {vec{a}}) и ( displaystyle {vec{b}})
Справился? Может, и подвох небольшой заметил? Давай проверим:
( displaystyle vec{a}left( 2,6 right)), ( displaystyle vec{b}left( 8,4 right)) – координаты векторов, как в прошлой задаче! Ответ: ( displaystyle 40).
Скалярное произведение через длины векторов и косинус угла между ними
Помимо координатного, есть и другой способ вычислить скалярное произведение, а именно, через длины векторов и косинус угла между ними:
( displaystyle left( vec{a},~vec{b} right)=left| {vec{a}} right|left| {vec{b}} right|coswidehat{vec{a},~vec{b}})
( displaystyle widehat{vec{a},~vec{b}}) – обозначает угол между векторами ( displaystyle {vec{a}}) и ( displaystyle {vec{b}}).
То есть скалярное произведение равно произведению длин векторов на косинус угла между ними.
Зачем же нам эта вторая формула, если у нас есть первая, которая намного проще, в ней по крайней мере нет никаких косинусов?
А нужна она для того, что из первой и второй формулы мы с тобой сможем вывести, как находить угол между векторами!
Пусть ( displaystyle vec{a}left( {{x}_{1}},{{y}_{1}} right),~vec{b}left( {{x}_{2}},{{y}_{2}} right).) Тогда вспоминай формулу для длины вектора!
( displaystyle left| {vec{a}} right|=sqrt{x_{1}^{2}+y_{1}^{2}})
( displaystyle left| {vec{b}} right|=sqrt{x_{2}^{2}+y_{2}^{2}})
Тогда если я подставлю эти данные в формулу скалярного произведения, то я получу:
( displaystyle left( vec{a},~vec{b} right)=sqrt{x_{1}^{2}+y_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}}coswidehat{vec{a},~vec{b}})
Но с другой стороны:
( displaystyle left( vec{a},~vec{b} right)={{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}})
Тогда
( displaystyle {{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}=sqrt{x_{1}^{2}+y_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}}coswidehat{vec{a},~vec{b}})
Или
( displaystyle coswidehat{vec{a},~vec{b}}=frac{{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}}{sqrt{x_{1}^{2}+y_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}}})
Таким образом, что же мы с тобой получили?
У нас теперь есть формула, позволяющая вычислять угол между двумя векторами! Иногда ее для краткости записывают еще и так:
( displaystyle coswidehat{vec{a},~vec{b}}=frac{left( vec{a},~vec{b} right)}{left| {vec{a}} right|left| {vec{b}} right|})
Решение:
1. Эти вектора – наши старые знакомые. Их скалярное произведение мы уже считали и оно было равно ( displaystyle 40).
Координаты у них такие: ( displaystyle vec{a}left( 2,6 right)), ( displaystyle vec{b}left( 8,4 right)). Тогда найдем их длины:
( left| {vec{a}} right|=sqrt{{{2}^{2}}+{{6}^{2}}}=sqrt{40})
( left| {vec{b}} right|=sqrt{{{8}^{2}}+{{4}^{2}}}=sqrt{80})
Тогда ищем косинус между векторами:
( coswidehat{vec{a},~vec{b}}=frac{left( vec{a},~vec{b} right)}{left| {vec{a}} right|left| {vec{b}} right|}=frac{40}{sqrt{40}sqrt{80}}=frac{sqrt{40}sqrt{40}}{sqrt{40}sqrt{80}}=frac{1}{sqrt{2}})
Косинус какого угла равен ( frac{1}{sqrt{2}})? Это угол ( 45{}^circ ).
Ответ: ( 45)
Ну а теперь сам реши вторую задачу, а потом сравним! Я приведу лишь очень краткое решение:
2. ( vec{a}+vec{b}) имеет координаты ( left( 10,10 right)), ( vec{a}-vec{b}) имеет координаты ( left( -6,2 right)).
( left( vec{a}+vec{b},vec{a}-vec{b} right)=-60+20=-40)
( left| vec{a}+vec{b} right|=sqrt{{{10}^{2}}+{{10}^{2}}}=10sqrt{2})
( left| vec{a}-vec{b} right|=sqrt{{{left( -6 right)}^{2}}+{{2}^{2}}}=sqrt{40}).
Пусть ( a) – угол между векторами ( vec{a}+vec{b}) и ( vec{a}-vec{b}), тогда
( cosa=frac{-40}{10sqrt{2}sqrt{40}}=-frac{sqrt{40}}{10sqrt{2}}=-frac{sqrt{20}}{10}=-frac{sqrt{5}}{5})
Ответ: ( -frac{sqrt{5}}{5})
Метод координат (продвинутый уровень)
Мы с тобой продолжаем изучать метод координат. В прошлой части мы вывели ряд важных формул, которые позволяют:
- Находить координаты вектора;
- Находить длину вектора (альтернативно: расстояние между двумя точками);
- Складывать, вычитать векторы. Умножать их на вещественное число;
- Находить середину отрезка;
- Вычислять скалярное произведение векторов;
- Находить угол между векторами.
Конечно, в эти 6 пунктов не укладывается весь координатный метод.
Он лежит в основе такой науки, как аналитическая геометрия, с которой тебе предстоит познакомиться в ВУЗе. Я лишь хочу построить фундамент, который позволит тебе решать задачи ЕГЭ любого уровня сложности!
Этот раздел будет посвящен методу решения тех задач, в которых будет разумно перейти к методу координат. Эта разумность определяется тем, что в задаче требуется найти, и какая фигура дана.
Когда стоит применять метод координат
Итак, я бы стал применять метод координат, если ставятся вопросы:
- Найти угол между двумя плоскостями;
- Найти угол между прямой и плоскостью;
- Найти угол между двумя прямыми;
- Найти расстояние от точки до плоскости;
- Найти расстояние от точки до прямой;
- Найти расстояние от прямой до плоскости;
- Найти расстояние между двумя прямыми.
Подходящими фигурами для метода координат являются:
- Куб;
- Прямоугольный параллелепипед;
- Прямая призма (треугольная, шестиугольная…);
- Пирамида (треугольная, четырехугольная, шестиугольная);
- Тетраэдр (одно и то же, что и треугольная пирамида).
Неподходящими фигурами для метода координат являются тела вращения:
- шар;
- цилиндр;
- конус
По моему опыту, нецелесообразно использовать метод координат для:
- Нахождения площадей сечений;
- Вычисления объемов тел.
Однако следует сразу отметить, что три «невыгодные» для метода координат ситуации на практике достаточно редки.
В большинстве же задач он может стать твоим спасителем, особенно если ты не очень силен в трехмерных построениях (которые порою бывают довольно замысловатыми).
Как применять метод координат
Какими являются все перечисленные мною выше фигуры?
Они уже не плоские, как, например, квадрат, треугольник, окружность, а объемные! Соответственно, нам нужно рассматривать уже не двухмерную, а трехмерную систему координат.
Строится она достаточно легко: просто помимо оси абсцисс и ординат, мы введем еще одну ось, ось аппликат. На рисунке схематично изображено их взаимное расположение:
Все они являются взаимно перпендикулярными, пересекаются в одной точке ( displaystyle O), которую мы будем называть началом координат.
Ось абсцисс, как и прежде, будем обозначать ( Ox), ось ординат – ( Oy), а введенную ось аппликат – ( Oz).
Если раньше каждая точка на плоскости характеризовалась двумя числами – абсциссой и ординатой, то каждая точка в пространстве уже описывается тремя числами – абсциссой, ординатой, аппликатой.
Например:
Соответственно абсцисса точки ( displaystyle P) равна ( displaystyle 1), ордината – ( displaystyle 2), а аппликата – ( displaystyle 3).
Иногда абсциссу точки еще называют проекцией точки на ось абсцисс, ординату – проекцией точки на ось ординат, а аппликату – проекцией точки на ось аппликат. Соответственно, если задана точка ( Aleft( x,y,z right)) то, точку с координатами:
( Aleft( x,y,0 right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oxy)
( Aleft( x,0,z right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oxz)
( Aleft( 0,y,z right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oyz)
Встает естественный вопрос: справедливы ли все формулы, выведенные для двухмерного случая, в пространстве?
Ответ утвердительный, они справедливы и имеют тот же самый вид. За маленькой деталью. Я думаю, ты уже сам догадался, за какой именно.
Во все формулы мы должны будем добавить еще один член, отвечающий за ось аппликат.
Формулы метода координат для трехмерных фигур
1. Если заданы две точки: ( Aleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right)), ( Aleft( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), то:
- Координаты вектора ( overrightarrow{AB}): ( overrightarrow{AB}left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}} right));
- Расстояние между двумя точками (или длина вектора ( overrightarrow{AB})) ( d=left| overrightarrow{AB} right|=sqrt{{{left( {{x}_{2}}-{{x}_{1}} right)}^{2}}+{{left( {{y}_{2}}-{{y}_{1}} right)}^{2}}+{{left( {{z}_{2}}-{{z}_{1}} right)}^{2}}});
- Середина ( D) отрезка ( AB) имеет координаты
- ( Dleft( frac{{{x}_{1}}+{{x}_{2}}}{2},frac{{{y}_{1}}+{{y}_{2}}}{2},frac{{{z}_{1}}+{{z}_{2}}}{2} right)).
2. Если дано два вектора: ( vec{a}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right)) и ( vec{b}left( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), то:
- Их скалярное произведение равно: ( left( vec{a},~vec{b} right)=left| {vec{a}} right|left| {vec{b}} right|cosoverset{}{widehat{vec{a},~vec{b}}},) или ( left( vec{a},~vec{b} right)={{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}+{{z}_{1}}{{z}_{2}});
- Косинус угла между векторами равен:
- ( cosoverset{}{widehat{vec{a},~vec{b}}},=frac{left( vec{a},~vec{b} right)}{left| {vec{a}} right|left| {vec{b}} right|}=frac{{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}+{{z}_{1}}{{z}_{2}}}{sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}+z_{2}^{2}}}).
Плоскость — как «обобщение» прямой
Однако с пространством не все так просто.
Как ты понимаешь, добавление еще одной координаты вносит существенное разнообразие в спектр фигур, «живущих» в этом пространстве. И для дальнейшего повествования мне потребуется ввести некоторое, грубо говоря, «обобщение» прямой.
Этим «обобщением» будет плоскость. Что ты знаешь про плоскость? Попробуй ответить на вопрос, а что такое плоскость? Очень сложно сказать.
Однако мы все интуитивно представляем, как она выглядит:
Грубо говоря, это некий бесконечный «лист», засунутый в пространство. «Бесконечность» следует понимать, что плоскость распространяется во все стороны, то есть ее площадь равна бесконечности.
Однако, это объяснение «на пальцах» не дает ни малейшего представления о структуре плоскости. А нас будет интересовать именно она.
Давай вспомним одну из основных аксиом геометрии: через две различные точки на плоскости проходит прямая, притом только одна.
Или ее аналог в пространстве: через три точки, не лежащие на одной прямой, проходит плоскость, притом только одна.
Уравнение прямой в плоскости и пространстве
Конечно, ты помнишь, как по двум заданным точкам вывести уравнение прямой, это совсем нетрудно: если первая точка имеет координаты: ( Aleft( {{x}_{0}},{{y}_{0}} right)) а вторая ( Bleft( {{x}_{1}},{{y}_{1}} right)), то уравнение прямой будет следующим:
( frac{x-{{x}_{0}}}{{{x}_{1}}-{{x}_{0}}}=frac{y-{{y}_{0}}}{{{y}_{1}}-{{y}_{0}}})
( left( x-{{x}_{0}} right)left( {{y}_{1}}-{{y}_{0}} right)=left( y-{{y}_{0}} right)left( {{x}_{1}}-{{x}_{0}} right))
Это ты проходил еще в 7 классе.
В пространстве уравнение прямой выглядит вот так: пусть у нас даны две точки с координатами: ( Aleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right)), ( Bleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right)), то уравнение прямой, через них проходящей, имеет вид:
( frac{x-{{x}_{0}}}{{{x}_{1}}-{{x}_{0}}}=frac{y-{{y}_{0}}}{{{y}_{1}}-{{y}_{0}}}=frac{z-{{z}_{0}}}{{{z}_{1}}-{{z}_{0}}})
Например, через точки ( Aleft( 1,2,3 right)), ( Bleft( 4,5,6 right)) проходит прямая:
( frac{x-1}{4-1}=frac{y-2}{5-2}=frac{z-3}{6-3})
( frac{x-1}{3}=frac{y-2}{3}=frac{z-3}{3})
( x-1=y-2=z-3)
Как это следует понимать?
Это следует понимать вот как: точка ( Dleft( x,y,z right)) лежит на прямой, если ее координаты удовлетворяют следующей системе:
( displaystyle left{ begin{array}{l}x-1=y-2\x-1=z-3end{array} right.)
Нас не очень будет интересовать уравнение прямой, но нам нужно обратить внимание на очень важное понятие направляющего вектора прямой.
Направляющий вектор прямой
Направляющий вектор прямой – любой ненулевой вектор, лежащий на данной прямой или параллельный ей.
Например, оба вектора ( overrightarrow{{{M}_{0}}{{M}_{1}}}), ( vec{s}) являются направляющими векторами прямой ( l). Пусть ( Mleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right)) – точка, лежащая на прямой, а ( vec{p}left( m,n,q right)) – ее направляющий вектор.
Тогда уравнение прямой можно записать в следующем виде:
( frac{x-{{x}_{0}}}{m}=frac{y-{{y}_{0}}}{n}=frac{z-{{z}_{0}}}{p})
Еще раз повторюсь, мне не очень будет интересно уравнение прямой, но мне очень нужно, чтобы ты запомнил, что такое направляющий вектор!
Еще раз: это ЛЮБОЙ ненулевой вектор, лежащий на прямой, или параллельный ей.
Уравнение плоскости
Вывести уравнение плоскости по трем заданным точкам уже не так тривиально, и обычно этот вопрос не рассматривается в курсе средней школы.
А зря!
Этот прием жизненно необходим, когда мы прибегаем к методу координат для решения сложных задач. Однако, я предполагаю, что ты полон желания научиться чему-то новому?
Более того, ты сможешь поразить своего преподавателя в ВУЗе, когда выяснится, что ты уже умеешь с методикой, которую обычно изучают в курсе аналитической геометрии. Итак, приступим.
Уравнение плоскости не слишком отличается от уравнения прямой на плоскости, а именно оно имеет вид:
( Ax+By+Cz+D=0)
( A,B,C,D-) некоторые числа (не все равные нулю), а ( x,y,z-~) переменные, например: ( 3x+2y-z+1=0,~0.5x-2z-2=0,~x+y=0) и т.д.
Как видишь, уравнение плоскости не очень отличается от уравнения прямой (линейной функции). Однако, вспомни, что мы с тобой утверждали? Мы говорили, что если у нас есть три точки ( Aleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right),~Bleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right),~Cleft( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), не лежащие на одной прямой, то уравнение плоскости однозначно по ним восстанавливается.
Но как? Попробую тебе объяснить.
Поскольку уравнение плоскости имеет вид:
( Ax+By+Cz+D=0)
А точки ( Aleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right),~Bleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right),~Cleft( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)) принадлежат этой плоскости, то при подстановке координат каждой точки в уравнение плоскости мы должны получать верное тождество:
( A{{x}_{0}}+B{{y}_{0}}+C{{z}_{0}}+D=0)
( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D=0)
( A{{x}_{2}}+B{{y}_{2}}+C{{z}_{2}}+D=0)
Таким образом, встает необходимость решать три уравнения аж с ( displaystyle 4) неизвестными!
Дилемма! Однако всегда можно предполагать, что ( D=1) (для этого нужно разделить ( ~Ax+By+Cz+D=0) на ( D)).
Таким образом, мы получим три уравнения с тремя неизвестными ( displaystyle A,B,C):
( A{{x}_{0}}+B{{y}_{0}}+C{{z}_{0}}+1=0)
( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+1=0)
( A{{x}_{2}}+B{{y}_{2}}+C{{z}_{2}}+1=0)
Однако мы не будем решать такую систему, а выпишем загадочное выражение, которое из него следует:
Уравнение плоскости, проходящей через три заданные точки
(left| {begin{array}{*{20}{c}}{x — {x_0}}&{{x_1} — {x_0}}&{{x_2} — {x_0}}\{y — {y_0}}&{{y_1} — {y_0}}&{{y_2} — {y_0}}\{z — {z_0}}&{{z_1} — {z_0}}&{{z_2} — {z_0}}end{array}} right| = 0)
Стоп! Это еще что такое? Какой-то очень необычный модуль!
Однако объект, который ты видишь перед собой не имеет ничего общего с модулем. Этот объект называется определителем третьего порядка.
Определитель третьего порядка
Отныне и впредь, когда ты будешь иметь дело с методом координат на плоскости, тебе очень часто будут встречаться эти самые определители.
Что же такое определитель третьего порядка? Как ни странно, это всего-навсего число. Осталось понять, какое конкретно число мы будем сопоставлять с определителем.
Давай вначале запишем определитель третьего порядка в более общем виде:
( left| {begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}end{array}} right|),
Где ( {{a}_{ij}}) – некоторые числа.
Причем под первым индеком ( displaystyle i) мы понимаем номер строки, а под индеком ( displaystyle j) – номер столбца.
Например, ( {{a}_{23}}) означает, что данное число стоит на пересечении второй строки и третьего столбца.
Давай поставим следующий вопрос: каким именно образом мы будем вычислять такой определитель?
То есть, какое конкретно число мы будем ему сопоставлять?
Для определителя именно третьего порядка есть эвристическое (наглядное) правило треугольника оно выглядит следующим образом:
Как его читать? А понимать его надо следующим образом: мы составляем два выражения:
- Произведение элементов главной диагонали (с верхнего левого угла до нижнего правого) ( displaystyle +) произведение элементов, образующих первый треугольник «перпендикулярный» главной диагонали ( displaystyle +) произведение элементов, образующих второй треугольник «перпендикулярный» главной диагонали;
- Произведение элементов побочной диагонали (с верхнего правого угла до нижнего левого) ( displaystyle +) произведение элементов, образующих первый треугольник «перпендикулярный» побочной диагонали ( displaystyle +) произведение элементов, образующих второй треугольник «перпендикулярный» побочной диагонали;
- Тогда определитель равен разности значений, полученных на шаге ( displaystyle 1) и ( displaystyle 2).
Если записать все это цифрами, то мы получим следующее выражение:
( left| {begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}end{array}} right| = )
( = {a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{21}}{a_{32}}{a_{13}} — left( {{a_{13}}{a_{22}}{a_{31}} + {a_{23}}{a_{32}}{a_{11}} + {a_{21}}{a_{12}}{a_{33}}} right))
Тем не менее, запоминать способ вычисления в таком виде не нужно, достаточно в голове просто держать треугольники и саму идею, что с чем складывается и что из чего затем вычитается).
Давай проиллюстрируем метод треугольников на примере:
Метод треугольников на примере
1. Вычислить определитель: ( left| {begin{array}{*{20}{c}}2&3&{ — 1}\{11}&{21}&{ — 5}\4&6&9end{array}} right|)
Давай разбираться, что мы складываем, а что – вычитаем.
Слагаемые, которые идут с «плюсом»:
Это главная диагональ: произведение элементов равно
( 2cdot 21cdot 9=378)
Первый треугольник, «перпендикулярный главной диагонали: произведение элементов равно
( 3cdot left( -5 right)cdot 4=-60)
Второй треугольник, «перпендикулярный главной диагонали: произведение элементов равно
( 11cdot 6cdot left( -1 right)=-66)
Складываем три числа: ( 378-60-66=252)
Слагаемые, которые идут с «минусом»:
Это побочная диагональ: произведение элементов равно
( left( -1 right)cdot 21cdot 4=-84)
Первый треугольник, «перпендикулярный побочной диагонали: произведение элементов равно
( 3cdot 11cdot 9=297)
Второй треугольник, «перпендикулярный побочной диагонали: произведение элементов равно
( 6cdot left( -5 right)cdot 2=-60)
Складываем три числа:
( -84+297-60=153)
Все, что осталось сделать – это вычесть из суммы слагаемых «с плюсом» сумму слагаемых «с минусом»:
( 252-153=99)
Таким образом,
( left| {begin{array}{*{20}{c}}2&3&{ — 1}\{11}&{21}&{ — 5}\4&6&9end{array}} right| = 99)
Как видишь, ничего сложного и сверхъестественного в вычислении определителей третьего порядка нет. Просто важно помнить про треугольники и не допускать арифметических ошибок.
Теперь попробуй самостоятельно вычислить:
( left| {begin{array}{*{20}{c}}2&{ — 2}&4\3&2&5\1&2&2end{array}} right|)
Проверяем:
- Главная диагональ: ( 2cdot 2cdot 2=8);
- Первый треугольник, перпендикулярный главной диагонали: ( left( -2 right)cdot 5cdot 1=-10);
- Второй треугольник, перпендикулярный главной диагонали: ( 3cdot 2cdot 4=24);
- Сумма слагаемых с плюсом: ( 8-10+24=22);
- Побочная диагональ: ( 1cdot 2cdot 4=8);
- Первый треугольник, перпендикулярный побочной диагонали: ( 2cdot 5cdot 2=20);
- Второй треугольник, перпендикулярный побочной диагонали: ( left( -2 right)cdot 3cdot 2=-12);
- Сумма слагаемых с минусом: ( 8+20-12=16);
- Сумма слагаемых с плюсом минус сумма слагаемых с минусом: ( 22-16=6).
Вывод:
( left| {begin{array}{*{20}{c}}2&{ — 2}&4\3&2&5\1&2&2end{array}} right| = 6)
Вот тебе еще пара определителей, вычисли их значения самостоятельно и сравни с ответами:
- ( left| {begin{array}{*{20}{c}}1&3&{ — 1}\0&4&2\{ — 3}&2&0end{array}} right|);
- ( left| {begin{array}{*{20}{c}}3&1&7\6&2&{14}\{ — 1}&0&8end{array}} right|).
Ответы:
- ( displaystyle -34);
- ( displaystyle 0).
Ну что, все совпало?
Отлично, тогда можно двигаться дальше! Если же есть затрудения, то совет мой таков: в интернете есть куча программ вычисления определителя онлайн.
Все, что тебе нужно – придумать свой определитель, вычислить его самостоятельно, а потом сравнить с тем, что посчитает программа.
И так до тех пор, пока результаты не начнут совпадать. Уверен, этот момент не заставит себя долго ждать!
Теперь давай вернемся к тому определителю, который я выписал, когда говорил про уравнение плоскости, проходящей через три заданные точки:
( left| {begin{array}{*{20}{c}}{x — {x_0}}&{{x_1} — {x_0}}&{{x_2} — {x_0}}\{y — {y_0}}&{{y_1} — {y_0}}&{{y_2} — {y_0}}\{z — {z_0}}&{{z_1} — {z_0}}&{{z_2} — {z_0}}end{array}} right| = 0)
Все, что тебе нужно – это вычислить его значение непосредственно (методом треугольников) и приравнять результат к нулю.
Естественно, поскольку ( displaystyle x,y,z) – переменные, то ты получишь некоторое выражение, от них зависящее.
Именно это выражение и будет уравнением плоскости, проходящей через три заданные точки, не лежащие на одной прямой!
( Ax+By+Cz+D=0)
Давай проиллюстрируем сказанное на простом примере:
1. Построить уравнение плоскости, проходящей через точки
( displaystyle {{M}_{1}}left( -3,2,-1 right), {{M}_{2}}left( -1,2,4 right), {{M}_{3}}left( 3,3,-1 right))
Cоставляем для этих трех точек определитель:
( left| {begin{array}{*{20}{c}}{x — left( { — 3} right)}&{ — 1 — left( { — 3} right)}&{3 — left( { — 3} right)}\{y — 2}&{2 — 2}&{3 — 2}\{z — left( { — 1} right)}&{4 — left( { — 1} right)}&{ — 1 — left( { — 1} right)}end{array}} right|).
Упрощаем:
( left| {begin{array}{*{20}{c}}{x + 3}&2&6\{y — 2}&0&1\{z + 1}&5&0end{array}} right|)
Теперь вычисляем его непосредственно по правилу треугольников:
[{left| {begin{array}{*{20}{c}}{x + 3}&2&6\{y — 2}&0&1\{z + 1}&5&0end{array}} right| = left( {x + 3} right) cdot 0 cdot 0 + 2 cdot 1 cdot left( {z + 1} right) + left( {y — 2} right) cdot 5 cdot 6 — }]
( displaystyle -left( left( z+1 right)cdot 6cdot 0+left( x+3 right)cdot 5cdot 1+left( y-2 right)cdot 2cdot 0 right)=)
( displaystyle=2left( z-1 right)+30left( y-2 right)-5left( x+3 right)=-5x+30y+2z-73)
Таким образом, уравнение плоскости, проходящей через точки ( displaystyle {{M}_{1}}left( -3,2,-1 right), {{M}_{2}}left( -1,2,4 right), {{M}_{3}}left( 3,3,-1 right)), имеет вид:
( -5x+30y+2z-73=0)
То есть ( A=-5,~B=30,~C=2,~D=-73)
Теперь попробуй решить одну задачку самостоятельно, а потом мы ее обсудим:
2. Найти уравнение плоскости, проходящей через точки
( {{M}_{1}}left( 1,2,-1 right),~{{M}_{2}}left( -1,0,4 right),~{{M}_{3}}left( -2,-1,1 right))
Ну что, давай теперь обсудим решение:
Составляем определитель:
( left| {begin{array}{*{20}{c}}{x — 1}&{ — 2}&{ — 3}\{y — 2}&{ — 2}&{ — 3}\{z + 1}&5&2end{array}} right|)
И вычисляем его значение:
( begin{array}{l}left| {begin{array}{*{20}{c}}{x — 1}&{ — 2}&{ — 3}\{y — 2}&{ — 2}&{ — 3}\{z + 1}&5&2end{array}} right| = \ = — 4left( {x — 1} right) — 15left( {y — 2} right) + 6left( {z + 1} right) + 15left( {x — 1} right) + 4left( {y — 2} right) — 6left( {z + 1} right) = \ = 11x — 11y + 11end{array})
Тогда уравнение плоскости имеет вид:
( 11x-11y+11=0)
Или же, сократив на ( 11), получим:
( x-y+1=0)
То есть, ( A=1,B=-1,C=0,D=1.)
Теперь две задачи для самоконтроля:
- Построить уравнение плоскости, проходящей через три точки: ( Kleft( 2,3,4 right),~Lleft( 6,-3,4 right),~Mleft( -4,6,-4 right).);
- Построить уравнение плоскости, проходящей через три точки:
- ( Aleft( 5,-1,3 right),~Bleft( 2,2,0 right),~Cleft( -1,1,1 right).).
Проверим:
- ( 6x+4y-3z-12=0);
- ( y+z-2=0).
Все совпало?
Опять-таки, если есть определенные затруднения, то мой совет таков: берешь из головы три точки (с большой степенью вероятности они не будут лежать на одной прямой), строишь по ним плоскость.
А потом проверяешь себя онлайн. Например, на сайте:
http://www.webmath.ru/web/prog9_1.php
Однако при помощи определителей мы будем строить не только уравнение плоскости.
Вспомни, я говорил тебе, что для векторов определено не только скалярное произведение. Есть еще векторное, а также смешанное произведение.
Векторное произведение векторов
И если скалярным произведением двух векторов и будет число, то векторным произведением двух векторов ( vec{a}) и ( vec{b}) будет вектор ( ~vec{c}=vec{a}cdot vec{b}), причем данный вектор будет перпендикулярен к заданным:
Причем его модуль будет равен площади параллелограмма, построенного на векторах ( vec{a}) и ( vec{b}).
Данный вектор понадобится нам для вычисления расстояния от точки до прямой. Как же нам считать векторное произведение векторов ( vec{a}) и ( vec{b}), если их координаты заданы?
На помощь к нам опять приходит определитель третьего порядка.
Однако, прежде чем я перейду к алгоритму вычисления векторного произведения, я вынужден сделать небольшое лирическое отступление.
Данное отступление касается базисных векторов.
Базисными векторами в трехмерном пространстве называются три вектора:
( vec{i}left( 1,0,0 right),~vec{j}left( 0,1,0 right),~vec{k}left( 0,0,1 right))
Схематично они изображены на рисунке:
Как ты думаешь, а почему они называется базисными? Дело в том, что любой вектор в трехмерном пространстве можно представить через сумму трех базисных векторов:
( vec aleft( {x,y,z} right) = x cdot vec i + y cdot vec j + z cdot vec k.)
Или на картинке:
Справедливость этой формулы очевидна, ведь:
( begin{array}{l}xcdot vec{i}=left( x,0,0 right)\ycdot vec{j}=left( 0,y,0 right)\zcdot vec{k}=left( 0,0,z right)end{array})
Тогда
( vec{a}left( x,y,z right)=xcdot vec{i}+ycdot vec{j}+zcdot vec{k}=left( x,0,0 right)+left( 0,y,0 right)+left( 0,0,z right)=left( x,y,z right)=vec{a}.)
Смешанное произведение трех векторов
Последняя конструкция, которая мне понадобится – это смешанное произведение трех векторов.
Оно, как и скалярное, является числом. Есть два способа его вычисления. ( displaystyle 1) – через определитель, ( displaystyle 2) – через смешанное произведение.
А именно, пусть у нас даны три вектора:
( vec{a}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right),~vec{b}left( {{x}_{2}},{{y}_{2}},{{z}_{2}} right),~vec{c}left( {{x}_{3}},{{y}_{3}},{{z}_{3}} right)), тогда смешанное произведение трех векторов, обозначаемое через ( (vec{a},vec{b},vec{c})) можно вычислить как:
1. ( left( vec{a},vec{b},vec{c} right)=left( vec{a},vec{b}cdot vec{c} right)) – то есть смешанное произведение – это скалярное произведения вектора на векторное произведение двух других векторов
2. ( left( {vec a,vec b,vec c} right) = left| {begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{z_1}}\{{x_2}}&{{y_2}}&{{z_2}}\{{x_3}}&{{y_3}}&{{z_3}}end{array}} right|)
Например, смешанное произведение трех векторов ( vec{a}left( 2,3,5 right),~vec{b}left( 1,4,4 right),~vec{c}left( 3,5,7 right)) равно:
( left( {vec a,vec b,vec c} right) = left| {begin{array}{*{20}{c}}2&3&5\1&4&4\3&5&7end{array}} right| = — 4)
Самостоятельно попробуй вычислить его через векторное произведение и убедись, что результаты совпадут!
И опять – два примера для самостоятельного решения:
- ( vec{a}left( 1,2,3 right),~vec{b}left( 1,1,1 right),~vec{c}left( 1,2,1 right));
- ( vec{a}left( 1,2,3 right),~vec{b}left( 1,-1,1 right),~vec{c}left( 2,0,-1 right)).
Ответы:
- ( displaystyle 2);
- ( displaystyle 1).
Выбор системы координат
Ну вот, теперь у нас есть весь необходимый фундамент знаний, чтобы решать сложные стереометрические задачи по геометрии.
Однако прежде чем приступать непосредственно к примерам и алгоритмам их решения, я считаю, что будет полезно остановиться еще вот на каком вопросе: как именно выбирать систему координат для той или иной фигуры.
Ведь именно выбор взаимного расположения системы координат и фигуры в пространстве в конечном счете определит, насколько громоздкими будут вычисления.
Я напомню, что в этом разделе мы рассматриваем следующие фигуры:
- куб;
- Прямоугольный параллелепипед;
- Прямая призма (треугольная, шестиугольная…);
- Пирамида (треугольная, четырехугольная);
- Тетраэдр (одно и то же, что и треугольная пирамида).
Для каждой из фигур я дам практические рекомендации, как выбирать систему координат.
Я неслучайно расположил задачи в таком порядке. Пока ты еще не успел начать ориентироваться в методе координат, я сам разберу наиболее «проблемные» фигуры, а тебе предоставлю разобраться с простейшим кубом!
Постепенно тебе предстоит научиться работать со всеми фигурами, сложность задач я буду увеличивать от теме к теме.
Приступаем к решению задач:
1. Рисуем тетраэдр, помещаем его в систему координат так, как я предлагал ранее. Поскольку тетраэд правильный – то все его грани (включая основание) – правильные треугольники.
Поскольку нам не дана длина стороны, то я могу принять ее равной ( 1). Я думаю, ты понимаешь, что угол на самом деле не будет зависеть от того, насколько наш тетраэдр будет «растянут»?
Также проведу в тетраэдре высоту и медиану ( displaystyle BM).
Попутно я нарисую его основание (оно нам тоже пригодится).
![]()
Мне нужно найти угол между ( displaystyle DH) и ( displaystyle BM). Что нам известно?
Нам известна только координата точки ( displaystyle B). Значит, надо найти еще координаты точек ( displaystyle D,H,M).
Теперь думаем: точка ( displaystyle H) – это точка пересечения высот (или биссектрисс или медиан) треугольника ( displaystyle ABC).
А точка ( displaystyle D) – это приподнятая точка ( displaystyle H).
Точка же ( displaystyle M) – это середина отрезка ( displaystyle AD).
Тогда окончательно нам надо найти: координаты точек: ( displaystyle A,D,H,M).
Начнем с самого простого: координаты точки ( displaystyle A).
Смотри на рисунок: Ясно, что аппликата точки ( displaystyle A) равна нулю (точка лежит на плоскости ( displaystyle Oxy)).
Её ордината равна ( displaystyle 0,5) (так как ( displaystyle AK) – медиана).
Сложнее найти ее абсциссу. Однако это легко делается на основании теоремы Пифагора: Рассмотрим треугольник ( displaystyle BAS). Его гипотенуза ( displaystyle BA) равна ( displaystyle 1), а один из катетов ( displaystyle AS) равен ( displaystyle 0,5)
Тогда:
( BS=sqrt{B{{A}^{2}}-A{{S}^{2}}}=sqrt{1-frac{1}{4}}=frac{sqrt{3}}{2})
Окончательно имеем: ( Aleft( frac{sqrt{3}}{2},frac{1}{2},0 right)).
Теперь найдем координаты точки ( displaystyle H).
Ясно, что ее аппликата опять равна нулю, а ее ордината такая же, как у точки ( displaystyle A), то есть ( 0,5).
Найдем ее абсциссу. Это делается достаточно тривиально, если помнить, что высоты равностороннего треугольника точкой пересечения делятся в пропорции ( displaystyle mathbf{2}:mathbf{1}), считая от вершины. Так как: ( AK=BS=frac{sqrt{3}}{2}), то искомая абсцисса точки, равная длине отрезка ( displaystyle KH), равна: ( KH=frac{AK}{3}=frac{sqrt{3}}{6}). Т
аким образом, координаты точки ( displaystyle H) равны:
( Hleft( frac{sqrt{3}}{6},frac{1}{2},0 right).)
Найдем координаты точки ( displaystyle D).
Ясно, что ее абсцисса и ордината совпадают с абсциссой и ординатой точки ( displaystyle H). А аппликата равна длине отрезка ( displaystyle DH). ( displaystyle DH) – это один из катетов треугольника ( displaystyle DAH). Гипотенуза треугольника ( displaystyle DAH) – это отрезок ( AD=AB=1.) ( displaystyle AH) – катет.
Он ищется из соображений, которые я выделил жирным шрифтом:
( AH=frac{2}{3}cdot frac{sqrt{3}}{2}=frac{sqrt{3}}{3})
Тогда:
( DH=sqrt{1-{{left( frac{sqrt{3}}{3} right)}^{2}}}=sqrt{frac{2}{3}})
Отсюда:
( Dleft( frac{sqrt{3}}{6},frac{1}{2},sqrt{frac{2}{3}} right).)
Точка ( M) – это середина отрезка ( AD). Тогда нам нужно вспомнить формулу координат середины отрезка:
( Mleft( frac{frac{sqrt{3}}{2}+frac{sqrt{3}}{6}}{2},~frac{frac{1}{2}+frac{1}{2}}{2},frac{0+sqrt{frac{2}{3}}}{2} right)=Mleft( frac{sqrt{3}}{3},frac{1}{2},frac{1}{sqrt{6}} right).~)
Ну все, теперь мы можем искать координаты направляющих векторов:
( overrightarrow{BM}left( frac{sqrt{3}}{3},frac{1}{2},frac{1}{sqrt{6}} right))
( overrightarrow{DH}left( 0,0,-sqrt{frac{2}{3}} right))
Ну что, все готово: подставляем все данные в формулу:
( displaystyle cosvarphi =frac{left| frac{1}{sqrt{6}}cdot left( -sqrt{frac{2}{3}} right) right|}{sqrt{{{left( frac{sqrt{3}}{3} right)}^{2}}+{{left( frac{1}{2} right)}^{2}}+{{left( frac{1}{sqrt{6}} right)}^{2}}}cdot sqrt{{{left( -sqrt{frac{2}{3}} right)}^{2}}}}=frac{frac{1}{3}}{sqrt{frac{19}{36}}cdot sqrt{frac{2}{3}}}=frac{frac{1}{3}}{sqrt{frac{19}{54}}}=frac{sqrt{54}}{3sqrt{19}}=sqrt{frac{6}{19}})
Таким образом, ( varphi =arccossqrt{frac{6}{19}}.)
Ответ: ( varphi =arccossqrt{frac{6}{19}}.)
Тебя не должны пугать такие «страшные» ответы: для задач С2 это обычная практика. Я бы скорее удивился «красивому» ответу в этой части. Также, как ты заметил, я практически не прибегал ни к чему, кроме как к теореме Пифагора и свойству высот равностороннего треугольника. То есть для решения стереометрической задачи я использовал самый минимум стереометрии. Выигрыш в этом частично «гасится» достаточно громоздкими вычислениями. Зато они достаточно алгоритмичны!
2. Изобразим правильную шестиугольную пирамиду вместе с системой координат, а также ее основание:
Нам нужно найти угол между прямыми ( displaystyle SB) и ( displaystyle CD).
Таким образом, наша задача сводится к поиску координат точек: ( displaystyle S,B,C,D).
Координаты последних трех мы найдем по маленькому рисунку, а коодинату вершины ( displaystyle S) найдем через координату точки ( displaystyle O).
Работы навалом, но надо к ней приступать!
a) Координата ( displaystyle D): ясно, что ее аппликата и ордината равны нулю.
Найдем абсциссу. Для этого рассмотрим прямоугольный треугольник ( displaystyle EDP). Увы, в нем нам известна только гипотенуза, которая равна ( displaystyle 1). Катет ( displaystyle DP) мы будем стараться отыскать (ибо ясно, что удвоенная длина катета ( displaystyle DP) даст нам абсциссу точки ( displaystyle D)).
Как же нам ее искать?
Давай вспомним, что за фигура у нас лежит в основании пирамиды? Это правильный шестиугольник.
А что это значит? Это значит, что у него все стороны и все углы равны. Надо бы найти один такой угол. Есть идеи?
Идей масса, но есть формула:
Сумма углов правильного n-угольника равна ( left( n-2 right)cdot 180{}^circ ).
Таким образом, сумма углов правильного шестиугольника равна ( displaystyle 720) градусов. Тогда каждый из углов равен:
( frac{720{}^circ }{6}=120{}^circ )
Вновь смотрим на картинку.
Ясно, что отрезок ( displaystyle EB) – биссектрисса угла ( displaystyle DEF). Тогда угол ( displaystyle DEP) равен ( displaystyle 60) градусам.
Тогда:
( sin60{}^circ =frac{sqrt{3}}{2}=frac{DP}{ED}=frac{DP}{1}=DP)
Тогда ( DP=frac{sqrt{3}}{2}), откуда ( DF=2DP=sqrt{3}).
Таким образом, ( displaystyle D) имеет координаты ( Dleft( sqrt{3},0,0 right))
b) Теперь легко найдем координату точки ( C): ( Cleft( sqrt{3},1,0 right)).
c) Найдем координаты точки ( displaystyle B).
Так как ее абсцисса совпадает с длиной отрезка ( FP) то она равна ( frac{sqrt{3}}{2}).
Найти ординату тоже не очень сложно: если мы соединим точки ( displaystyle C) и ( displaystyle A) а точку пересечения прямой ( displaystyle AC) обозначим, скажем за ( displaystyle M). (сделай сам несложное построение). Тогда ( BM=EP.)
Таким образом, ордината точки B равна сумме длин отрезков ( PM+MB). Вновь обратимся к треугольнику ( displaystyle DEP).
Тогда
( frac{1}{2}=cos60{}^circ =frac{EP}{ED}=EP)
Тогда так как ( PM=DC=1,~mo~PB=1+frac{1}{2}=frac{3}{2}.) Тогда точка ( B) имеет координаты ( Bleft( frac{sqrt{3}}{2},frac{3}{2},0 right).)
d) Теперь найдем координаты точки ( displaystyle O).
Рассмотри прямоугольник ( displaystyle ACDF) и докажи, что ( PO=frac{1}{2}.)
Таким образом, координаты точки ( displaystyle O): ( Oleft( frac{sqrt{3}}{2},frac{1}{2},0 right).)
e) Осталось найти координаты вершины ( S). Ясно, что ее абсцисса и ордината совпадает с абсциссой и ординатой точки ( O).
Найдем аппликату. Так как ( FC=EB=2), то ( OF=1). Рассмотрим прямоугольный треугольник ( displaystyle OFS). По условию задачи боковое ребро ( FS=2). Это гипотенуза моего треугольника.
Тогда высота пирамиды ( displaystyle OS) – катет.
( OS=sqrt{F{{S}^{2}}-O{{F}^{2}}}=sqrt{4-1}=sqrt{3})
Тогда точка ( S) имеет координаты: ( Sleft( frac{sqrt{3}}{2},frac{1}{2},sqrt{3} right).)
Ну все, у меня есть координаты всех интересующих меня точек. Ищу координаты направляющих векторов прямых:
( overrightarrow{SB}left( frac{sqrt{3}}{2}-frac{sqrt{3}}{2},frac{1}{2}-frac{3}{2},sqrt{3}-0 right)=overrightarrow{SB}left( 0,-1,sqrt{3} right).)
( overrightarrow{CD}left( sqrt{3}-sqrt{3},0-1,0 right)=overrightarrow{CD}left( 0,-1,0 right).)
Ищем угол между этими векторами:
( cosvarphi =frac{left| 0+left( -1 right)cdot left( -1 right)+sqrt{3}cdot 0 right|}{sqrt{{{left( -1 right)}^{2}}+{{left( sqrt{3} right)}^{2}}}cdot sqrt{{{left( -1 right)}^{2}}}}=frac{1}{2})
Тогда ( varphi =arccos left( frac{1}{2} right)=60{}^circ )
Ответ: ( 60{}^circ )
Опять-таки, при решении этой задачи я не использовал никаких изошренных приемов, кроме формулы суммы углов правильного n-угольника, а также определения косинуса и синуса прямоугольного треугольника.
3. Поскольку нам опять не даны длины ребер в пирамиде, то я буду считать их равными единице.
Таким образом, поскольку ВСЕ ребра, а не только боковые, равны между собой, то в основании пирамиды и меня лежит квадрат, а боковые грани – правильные треугольники.
Изобразим такую пирамиду, а также ее основание на плоскости, отметив все данные, приведенные в тексте задачи:
Ищем угол между ( displaystyle BM) и ( displaystyle PH).
Я буду делать очень краткие выкладки, когда буду заниматься поиском координат точек. Тебе необходимо будет «расшифровать» их:
a) ( Bleft( 0,1,0 right))
b) ( displaystyle H) – середина отрезка ( displaystyle AC). Её координаты:
( Hleft( frac{1}{2},frac{1}{2},0 right))
c) Длину отрезка ( displaystyle AH) я найду по теореме Пифагора в треугольнике ( displaystyle AHD). ( AH=frac{sqrt{2}}{2}.) Найду ( displaystyle PH) по теореме Пифагора в треугольнике ( displaystyle AHP).
( PH=sqrt{1-frac{1}{2}}=frac{1}{sqrt{2}})
Координаты ( P): ( Pleft( frac{1}{2},frac{1}{2},frac{1}{sqrt{2}} right).)
d) ( M) – середина отрезка ( AP). Ее координаты равны ( Mleft( frac{1}{4},frac{1}{4},frac{1}{2sqrt{2}} right).)
e) Координаты вектора ( overrightarrow{PH}:~overrightarrow{PH}left( 0,0,-frac{1}{sqrt{2}} right).~)
f) Координаты вектора ( overrightarrow{BM}:~overrightarrow{BM}left( frac{1}{4},-frac{3}{4},frac{1}{2sqrt{2}} right).)
g) Ищем угол: ( cosvarphi =frac{frac{1}{4}}{frac{1}{sqrt{2}}cdot frac{sqrt{3}}{2}}=frac{1}{sqrt{6}})
h) Ответ: ( arccosfrac{1}{sqrt{6}})
Куб – простейшая фигура. Я уверен, что с ней ты разберешься самостоятельно. Ответы к задачам 4 и 5 следующие:
4. ( arccosfrac{4}{sqrt{30}})
5. ( arccosfrac{1}{sqrt{15}})
Нахождение угла между прямой и плоскостью
Ну что, время простых задачек окончено!
Теперь примеры будут еще сложнее. Для отыскания угла между прямой и плоскостью мы будем поступать следующим образом:
- По трем точкам строим уравнение плоскости: ( Ax+By+Cz+D=0), используя определитель третьего порядка;
- По двум точкам ищем координаты направляющего вектора прямой: ( vec{s}left( l,m,n right));
- Применяем формулу для вычисления угла между прямой и плоскостью: ( sinvarphi =frac{left| Al+Bm+Cn right|}{sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}~}cdot sqrt{{{l}^{2}}+{{m}^{2}}+{{n}^{2}}}})
Как видишь, эта формула очень похожа на ту, что мы применяли для поиска углов между двумя прямыми.
Структура правой части просто одинакова, а слева мы теперь ищем синус, а не косинус, как раньше. Ну и добавилось одно противное действие – поиск уравнения плоскости.
Опять я решу первые две задачи подробно, третью – кратко, а последние две оставляю тебе для самостоятельного решения.
К тому же тебе уже приходилось иметь дело с треугольной и четырехугольной пирамидами, а вот с призмами – пока что нет.
Решения:
1. Изобразим призму, а также ее основание. Совместим ее с системой координат и отметим все данные, которые даны в условии задачи:
Извиняюсь за некоторое несоблюдение пропорций, но для решения задачи это, по сути, не так важно. Плоскость ( BC{{C}_{1}}) – это просто «задняя стенка» моей призмы. Достаточно просто догадаться, что уравнение такой плоскости имеет вид:
( x=0)
Однако, это можно показать и непосредственно:
Выберем произвольные три точки на этой плоскости: например, ( Bleft( 0,0,0 right),~Cleft( 0,8,0 right),~{{B}_{1}}left( 0,0,3 right)).
Составим уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&0&0\y&8&0\z&0&3end{array}} right| = 0)
Упражнение тебе: самостоятельно вычислить этот определитель. У тебя получилось ( 24x)? Тогда уравение плоскости имеет вид:
( 24x=0)
Или просто
( x=0)
Таким образом, ( A=1,B=0,C=0,D=0.)
Для решения примера мне нужно найти координаты направляющего вектора прямой ( B{{A}_{1}}).
Так как точка ( B) cовпала с началом координат, то координаты вектора (overrightarrow{B{{A}_{1}}}) просто совпадут с координатами точки ( {{A}_{1}}.)
Для этого найдем вначале координаты точки ( displaystyle A).
Для этого рассмотрим треугольник ( displaystyle ABC).
Проведем высоту (она же – медиана и биссектрисса) из вершины ( displaystyle A).
Так как ( BC=8), то ордината точки ( displaystyle A) равна ( displaystyle 4).
Для того, чтобы найти абсциссу этой точки, нам нужно вычислить длину отрезка ( displaystyle AT).
По теореме Пифагора имеем:
( AT=sqrt{A{{B}^{2}}-B{{T}^{2}}}=sqrt{25-16}=3.)
Тогда точка ( displaystyle A) имеет координаты:
( Aleft( 3,4,0 right))
Точка ( {{A}_{1}})– это «приподнятая» на ( displaystyle 3) точка ( displaystyle A):
( {{A}_{1}}left( 3,4,3 right))
Тогда координаты вектора ( overrightarrow{B{{A}_{1}}}):
( overrightarrow{B{{A}_{1}}}left( 3,4,3 right).)
( sinvarphi =frac{left| 3cdot 1+4cdot 0+3cdot 0 right|}{sqrt{{{1}^{2}}+{{0}^{2}}+{{0}^{2}}}cdot sqrt{{{3}^{2}}+{{4}^{2}}+{{3}^{2}}}}=frac{3}{sqrt{34}}.)
( varphi =arcsinfrac{3}{sqrt{34}}.)
Ответ: ( arcsinfrac{3}{sqrt{34}}.)
Как видишь, ничего принципиально сложного при решении таких задач нет. На самом деле процесс еще немного упрощает «прямота» такой фигуры, как призма.
Теперь давай перейдем к следующему примеру:
2. Рисуем параллелепипед, проводим в нем плоскость и прямую, а также отдельно вычерчиваем его нижнее основание:
Вначале найдем уравнение плоскости: Координаты трех точек, лежащих в ней:
( Aleft( 0,0,0 right),~Bleft( 0,2,0 right),{{C}_{1}}left( 1,2,1 right)) (первые две координаты получены очевидным способом, а последнюю координату ты легко найдешь по картинке из точки ( C)). Тогда составляем уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&0&1\y&2&2\z&0&1end{array}} right| = 0)
Вычисляем:
( 2x-2z=0,~x-z=0)
Тогда ( A=1,B=0,C=-1,D=0.)
Ищем координаты направляющего вектора ( overrightarrow{A{{B}_{1}}}): Ясно, что его координаты совпадают с координатами точки ( {{B}_{1}}), не правда ли?
Как найти координаты ( {{B}_{1}})?
Это же координаты точки ( B), приподнятые по оси аппликат на единицу! ( {{B}_{1}}left( 0,2,1 right)). Тогда ( overrightarrow{A{{B}_{1}}}left( 0,2,1 right).)
Ищем искомый угол:
( sinvarphi =frac{left| 1cdot 0+0cdot 2+left( -1 right)cdot 1 right|}{sqrt{{{1}^{2}}+{{left( -1 right)}^{2}}+{{0}^{2}}~}cdot sqrt{0+{{2}^{2}}+{{1}^{2}}}}=frac{1}{sqrt{10}}.)
( ~varphi =arcsinfrac{1}{sqrt{10}}.)
Ответ: ( arcsinfrac{1}{sqrt{10}}.)
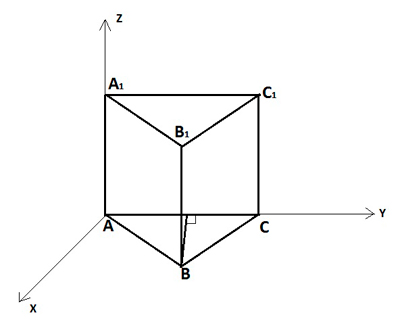
3. Рисуем правильную шестиугольную призму, а затем проводим в ней плоскость и прямую.
![]()
Тут даже плоскость нарисовать проблемно, не говоря уже о решении этой задачи, однако методу координат все равно! Именно в его универсальности и заключается его основное преимущество!
Плоскость проходит через три точки: ( A,C,{{D}_{1}}). Ищем их координаты:
1) ( Aleft( 0,0,0 right),~left( frac{sqrt{3}}{2},frac{3}{2},0 right), {{D}_{1}}left( sqrt{3},1,1 right)). Сам выведи координаты для последних двух точек. Тебе пригодится для этого решение задачи с шестиугольной пирамидой!
2) Строим уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&{frac{{sqrt 3 }}{2}}&{sqrt 3 }\y&{frac{3}{2}}&1\z&0&1end{array}} right| = 0)
( -sqrt{3}x+y+2z=0)
( A=-sqrt{3},B=1,C=2,D=0.)
Ищем координаты вектора ( overrightarrow{A{{C}_{1}}}): ( text{ }!!~!!text{ }overrightarrow{A{{C}_{1}}}left( frac{sqrt{3}}{2},frac{3}{2},1 right)). (снова смотри задачу с треугольной пирамидой!)
3) Ищем угол:
( sinvarphi =frac{left| -sqrt{3}cdot frac{sqrt{3}}{2}+frac{3}{2}+2 right|}{sqrt{{{left( frac{sqrt{3}}{2} right)}^{2}}+{{left( frac{3}{2} right)}^{2}}+{{1}^{2}}~}cdot sqrt{{{left( -sqrt{3} right)}^{2}}+{{1}^{2}}+{{2}^{2}}}}=frac{2}{2sqrt{8}}=frac{1}{2sqrt{2}}.)
Ответ: ( arcsinfrac{1}{2sqrt{2}}.)
Как видишь, ничего сверхъестественно сложного в этих задачах нет. Нужно лишь быть очень внимательным с корнями. К последним двум задачам я дам лишь ответы:
4. ( text{arcsin}frac{12}{sqrt{193}}~)
5. ( text{arcsin}frac{1}{sqrt{6}}~)
Как ты мог убедиться, техника решения задач везде одинаковая: основная задача найти координаты вершин и подставить их в некие формулы. Нам осталось рассмотреть еще один класс задач на вычисление углов, а именно: вычисление углов между двумя плоскостями.
Решения задач:
1. Сторона основания правильной треугольной призмы ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}) равна ( 2), а диагональ боковой грани равна ( sqrt{5}). Найдите угол между плоскостью ( {{A}_{1}}BC) и плоскостью основания призмы.
Рисую правильную (в основании – равносторонний треугольник) треугольную призму и отмечаю на ней плоскости, которые фигурируют в условии задачи:
Нам нужно найти уравнения двух плоскостей: ( ABC~и~BC{{A}_{1}}.) Уравнение основания получается тривиально: ты можешь составить соответствующий определитель по трем точкам, я же составлю уравнение сразу:
( z=0.)
То есть:
( {{A}_{1}}=0, {{B}_{1}}=0, {{C}_{1}}=1, {{D}_{1}}=0.)
Теперь найдем уравнение ( BC{{A}_{1}}.) Точка ( B) имеет координаты ( Bleft( 0,0,0 right).) Точка ( C) – ( Cleft( 0,1,0 right).)
Так как ( AO) – медиана и высота треугольника ( ABC), то ( BO=OC=1.) ( AO) легко находится по теореме Пифагора в треугольнике ( BAO:) ( AO=sqrt{4-1}=sqrt{3}).
Тогда точка ( A) имеет координаты: ( Aleft( sqrt{3},1,0 right).)
Найдем аппликату точки ( {{A}_{1}}.) Для этого рассмотрим прямоугольный треугольник ( {{A}_{1}}AC.~)
( A{{A}_{1}}=sqrt{{{A}_{1}}{{C}^{2}}-A{{C}^{2}}}=1.)
Тогда получаем вот такие координаты: ( {{A}_{1}}left( sqrt{3},1,1 right).) Cоставляем уравнение плоскости ( BC{{A}_{1}}).
( left| {begin{array}{*{20}{c}}x&0&{sqrt 3 }\y&1&1\z&0&1end{array}} right| = 0.)
( x+sqrt{3}z-sqrt{3}z-sqrt{3}y=0)
( x-sqrt{3}z=0)
Тогда
( {{A}_{2}}=1, {{B}_{2}}=0, {{C}_{2}}=-sqrt{3}, {{D}_{2}}=0.)
Вычисляем угол между плоскостями:
( cosvarphi =frac{left| -sqrt{3} right|}{sqrt{1+{{left( -sqrt{3} right)}^{2}}}}=frac{sqrt{3}}{2}.)
Отсюда
( varphi =30{}^circ .)
Ответ: ( 30{}^circ .)
2. В правильной четырехугольной пирамиде ( displaystyle SABCD), все ребра которой равны ( displaystyle 1), найдите синус угла между плоскостью ( displaystyle SAD) и плоскостью, проходящей через точку ( displaystyle A) перпендикулярно прямой ( displaystyle BD).
Делаем рисунок:
![]()
Самое сложное – это понять, что это такая за таинственная плоскость, проходящая через точку ( A) перпендикулярно ( DB).
Ну что же, главное, это что? Главное – это внимательность! В самом деле, прямая ( AC) перпендикулярна ( BD). Прямая ( OS) также перпендикулярна ( BD).
Тогда плоскость, проходящая через эти две прямые, будет перпендикулярна прямой ( BD), и, кстати, проходить через точку ( A). Эта плоскость также проходит через вершину пирамиды.
Тогда искомая плоскость – ( SAC.) А плоскость ( SAD) нам уже дана. Ищем координаты точек ( displaystyle S,A,C,D).
- ( displaystyle Aleft( 0,1,0 right))
- ( displaystyle Cleft( 1,0,0 right))
- ( displaystyle Dleft( 0,0,0 right))
Координату точки ( S) найдем через точку ( O). Из маленького рисунка легко вывести, что координаты у точки ( O) будут такие: ( Oleft( frac{1}{2},frac{1}{2},0 right).~)
Что теперь осталось найти, чтобы найти координаты вершины пирамиды?
Еще нужно вычислить ее высоту.
Это делается при помощи все той же теоремы Пифагора: вначале докажи, что ( OB=frac{sqrt{2}}{2}) (тривиально из маленьких треугольничков, образующих квадрат в основании).
Так как по условию ( SB=1), то имеем:
( OS=sqrt{1-{{left( frac{sqrt{2}}{2} right)}^{2}}}=frac{1}{sqrt{2}}.)
Теперь все готово: координаты вершины:
( Sleft( frac{1}{2},frac{1}{2},frac{1}{sqrt{2}} right).~)
Составляем уравнение плоскости ( displaystyle DAS):
( left| {begin{array}{*{20}{c}}x&0&{frac{1}{2}}\y&1&{frac{1}{2}}\z&0&{frac{1}{{sqrt 2 }}}end{array}} right| = 0)
Ты уже спец в вычислении определителей. Без труда ты получишь:
( frac{1}{sqrt{2}}x-frac{1}{2}z=0)
Или иначе (если домножим обе части на корень из двух)
( x-frac{1}{sqrt{2}}z=0.)
Теперь найдем уравнение плоскости ( displaystyle SAC):
( left| {begin{array}{*{20}{c}}{x — 1}&{ — 1}&{ — frac{1}{2}}\y&1&{frac{1}{2}}\z&0&{frac{1}{{sqrt 2 }}}end{array}} right| = 0)
(ты ведь не забыл, как мы получаем уравнение плоскости, правда?
Если ты не понял, откуда взялась эта минус единица, то вернись к определению уравнения плоскости! Просто всегда до этого оказывалось так, что моей плоскости принадлежало начало координат!)
Вычисляем определитель:
( begin{array}{l}frac{x-1}{sqrt{2}}-frac{1}{2}z+frac{1}{2}z+frac{y}{sqrt{2}}=0\frac{x-1}{sqrt{2}}+frac{y}{sqrt{2}}=0\x+y-1=0end{array}).
(Ты можешь заметить, что уравнение плоскости совпало с уравнением прямой, проходящей через точки ( displaystyle A) и ( displaystyle C)! Подумай, почему!)
Теперь вычисляем угол:
( cosvarphi =frac{left| 1+1cdot 0-frac{1}{sqrt{2}}cdot 0 right|}{sqrt{1+{{left( -frac{1}{sqrt{2}} right)}^{2}}}cdot sqrt{{{1}^{2}}+{{1}^{2}}}~~}=frac{1}{sqrt{3}}.)
Нам же нужно найти синус:
( sinvarphi =sqrt{1-{{cos }^{2}}varphi }=sqrt{1-frac{1}{3}}=sqrt{frac{2}{3}}).
Ответ: ( sqrt{frac{2}{3}}.)
3. В правильной четырехугольной призме ( ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) стороны основания равны ( displaystyle 1), а боковые ребра равны ( displaystyle 5). На ребре ( A{{A}_{1}}) отмечена точка ( displaystyle E) так, что ( AE:E{{A}_{1}}=2:3). Найдите угол между плоскостями ( ABC) и ( BE{{D}_{1}}.)
Каверзный вопрос: а что такое прямоугольная призма, как ты думаешь? Это же всего-то навсего хорошо известный тебе параллелепипед! Сразу же делаем чертеж! Можно даже отдельно не изображать основание, пользы от него здесь немного:
Плоскость ( ABC), как мы уже раньше заметили, записывается в виде уравнения:
( z=0.)
Теперь составляем плоскость ( BE{{D}_{1}}.)
( Bleft( 0,0,0 right),~Eleft( 1,0,2 right),~{{D}_{1}}left( 1,1,5 right).)
Cразу же составляем уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&1&1\y&0&1\z&2&5end{array}} right| = 0)
( begin{array}{l}2y+z-2x-5y=0\-2x-3y+z=0\2x+3y-z=0end{array})
Ищем угол:
( cosvarphi =frac{1}{sqrt{4+9+1}}=frac{1}{sqrt{14}})
Ответ: ( arccos frac{1}{sqrt{14}}~~)
Теперь ответы к последним двум задачам:
4. ( arccosfrac{2}{3})
5. ( sqrt{frac{2}{3}})
Ну что же, теперь самое время немного передохнуть, ведь мы с тобой молодцы и проделали огромную работу!
Вычисление расстояния от точки до плоскости
Что нам потребуется для решения этой задачи?
- Координаты точки ( Mleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
- Уравнение плоскости ( Ax+By+Cz+D=0.)
Итак, как только мы получим все необходимые данные, то применяем формулу:
( d=frac{left| A{{x}_{0}}+B{{y}_{0}}+C{{z}_{0}}+D right|}{sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}})
Как мы строим уравнение плоскости тебе уже должно быть известно из предыдущих задач, которые я разбирал в прошлой части. Давай сразу приступим к задачам.
Схема следующая: 1, 2 –я помогаю тебе решать, причем довольно подробно, 3, 4 – только ответ, решение ты проводишь сам и сравниваешь. Начали!
Решения:
1. Рисуем кубик с единичными ребрами, строим отрезок и плоскость, середину отрезка ( B{{C}_{1}}) обозначим буквой ( M)
Вначале давай начнем с легкого: найдем координаты точки ( displaystyle M). Так как ( displaystyle Bleft( 0,1,0 right),~{{C}_{1}}left( 1,1,1 right),~) то ( displaystyle Mleft( frac{1}{2},1,frac{1}{2} right).) (вспомни координаты середины отрезка!)
Теперь составляем уравнение плоскости по трем точкам ( displaystyle Aleft( 0,0,0 right),~{{B}_{1}}left( 0,1,1 right),~{{D}_{1}}left( 1,0,1 right).)
(left| {begin{array}{*{20}{c}}x&0&1\y&1&0\z&1&1end{array}} right| = 0)
( displaystyle x+y-z=0.)
( displaystyle A=1,B=1,C=-1,~D=0.)
Теперь я могу приступать к поиску расстояния:
( displaystyle d=frac{left| frac{1}{2}+1-frac{1}{2} right|}{sqrt{1+1+1}}=frac{1}{sqrt{3}})
Ответ: ( displaystyle frac{1}{sqrt{3}})
2. Вновь начинаем с чертежа, на котором отмечаем все данные!
Для пирамиды было бы полезно отдельно рисовать ее основание.
![]()
Даже тот факт, что я рисую как курица лапой, не помешает нам с легкостью решить эту задачу!
1. ( AO=OC=frac{1}{2}AC=frac{sqrt{{{2}^{2}}+{{2}^{2}}}}{2}=sqrt{2}).
Тогда ( OS=sqrt{S{{C}^{2}}-O{{C}^{2}}}=sqrt{3}.)
Теперь легко найти координаты точки ( S.)
Так как координаты точки ( O:Oleft( 1,1,0 right),~), то ( Sleft( 1,1,sqrt{3} right).)
2. Так как координаты точки ( C:) ( Cleft( 2,2,0 right),) а ( M) – середина отрезка ( SC), то
( Mleft( frac{3}{2},frac{3}{2},frac{sqrt{3}}{2} right).)
Без проблем найдем и координаты еще двух точек на плоскости ( ADM.) ( Dleft( 1,0,0 right),~Aleft( 0,0,0 right).) Составляем уравнение плоскости и упростим его:
(left| {left| {begin{array}{*{20}{c}}x&1&{frac{3}{2}}\y&0&{frac{3}{2}}\z&0&{frac{{sqrt 3 }}{2}}end{array}} right|} right| = 0)
( frac{3}{2}z-frac{sqrt{3}}{2}y=0)
( sqrt{3}y-3z=0)
( y-sqrt{3}z=0.)
Так как точка ( B) имеет координаты: ( Bleft( 0,2,0 right)), то вычисляем расстояние:
( d=frac{2}{sqrt{1+3}}=1.)
Ответ (очень редкий!): ( 1)
Ну что, разобрался?
Мне кажется, что здесь все так же технично, как и в тех примерах, что мы рассматривали с тобой в предыдущей части. Так что я уверен, что если ты овладел тем материалом, то тебе не составит труда решить оставшиеся две задачи.
Я лишь приведу ответы:
- ( frac{3sqrt{39}}{4})
- ( frac{sqrt{3}}{2})
Вычисление расстояния от прямой до плоскости
На самом деле, здесь нет ничего нового. Как могут располагаться прямая и плоскость друг относительно друга?
У них есть всего ( 2) возможности: пересечься, или прямая параллельна плоскости. Как ты думаешь, чем равно расстояние от прямой до плоскости, с которой данная прямая пересекается?
Мне кажется, что тут ясно, что такое расстояние равно нулю. Неинтересный случай.
Второй случай хитрее: тут уже расстояние ненулевое. Однако, так как прямая параллельна плоскости, то каждая точка прямой равноудалена от этой плоскости:
Таким образом:
Расстояние от плоскости до параллельной ей прямой равно расстоянию от любой точки прямой до плоскости.
А это значит, что моя задача свелась к предыдущей: ищем координаты любой точки на прямой, ищем уравнение плоскости, вычисляем расстояние от точки до плоскости.
На самом деле, такие задачи в ЕГЭ встречаются крайне редко. Мне удалось найти лишь одну задачу, и то данные в ней были такими, что метод координат к ней был не очень-то и применим!
Теперь перейдем к другому, гораздо более важному классу задач:
Вычисление расстояния точки до прямой
Что нам потребуется?
- Координаты точки, от которой мы ищем расстояние: ( {{M}_{0}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
- Координаты любой точки, лежащей на прямой ( {{M}_{1}}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right))
- Координаты направляющего вектора прямой ( vec{s}left( m,n,p right))
Какую применяем формулу?
Ответ: ( d=frac{left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|}{sqrt{{{m}^{2}}+{{n}^{2}}+{{p}^{2}}}})
Что означает знаменатель данной дроби тебе и так должно быть ясно: это длина направляющего вектора прямой. Здесь очень хитрый числитель!
Выражение ( left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|) означает модуль (длина) векторного произведения векторов ( overrightarrow{{{M}_{0}}{{M}_{1}}}) и ( vec{s}.)
Как вычислять векторное произведение, мы с тобой изучали в предыдущей части работы. Освежи свои знания, нам они сейчас очень пригодятся!
Таким образом, алгоритм решения задач будет следующий:
- Ищем координаты точки, от которой мы ищем расстояние: ( {{M}_{0}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
- Ищем координаты любой точки на прямой, до которой мы ищем расстояние: ( {{M}_{1}}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right))
- Строим вектор ( overrightarrow{{{M}_{0}}{{M}_{1}}}:) ( overrightarrow{{{M}_{0}}{{M}_{1}}}left( {{x}_{1}}-{{x}_{0}},{{y}_{1}}-{{y}_{0}},{{z}_{1}}-{{z}_{0}} right).)
- Строим направляющий вектор прямой ( vec{s}left( m,n,p right))
- Вычисляем векторное произведение ( overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s})
- Ищем длину полученного вектора: ( left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|)
- Вычисляем расстояние: ( d=frac{left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|}{sqrt{{{m}^{2}}+{{n}^{2}}+{{p}^{2}}}})
Работы у нас много, а примеры будут достаточно сложными! Так что теперь сосредоточь все внимание!
1. Дана правильная треугольная пирамида ( DABC) с вершиной ( D). Сторона основания пирамиды равна ( sqrt{6}), высота равна ( sqrt{30}).
Найдите расстояние от середины бокового ребра ( BD) до прямой ( MT), где точки ( M) и ( T) — середины ребер ( AC) и ( AB) соответственно.
2. Длины ребер ( AB,A{{A}_{1}}) и ( AD) прямоугольного параллелепипеда ( ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) равны соответственно ( 12,text{ }16~) и ( 15.)
Найдите расстояние от вершины ( {{A}_{1}}) до прямой ( B{{D}_{1}}.)
3. В правильной шестиугольной призме ( ABCDEF{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}{{E}_{1}}{{F}_{1}}) все ребра которой равны ( 1) найдите расстояние от точки ( B) до прямой ( {{E}_{1}}{{F}_{1}}.)
Решения:
1. Делаем аккуратный чертеж, на котором отмечаем все данные:
![]()
Ну что же, работы нам предстоит немало! Принимаемся за нее, засучив рукава!
1. Чтобы найти координаты высоты пирамиды, нам нужно знать координаты точки ( displaystyle O.) Её аппликата равна нулю, а ордината равна ( displaystyle frac{sqrt{6}}{2}.)
Абсцисса ее равна длине отрезка ( displaystyle OS.) ( displaystyle AS=sqrt{A{{B}^{2}}-S{{B}^{2}}}=sqrt{6-frac{6}{4}}=frac{3}{sqrt{2}}.~)
Так как ( displaystyle AS) – высота равностороннего треугольника ( displaystyle ABC), то она делится в отношении ( displaystyle 2:1), считая от вершины, отсюда ( displaystyle OS=frac{3}{3sqrt{2}}=frac{1}{sqrt{2}}).
Окончательно, получили координаты:
( displaystyle Oleft( frac{1}{sqrt{2}},frac{sqrt{6}}{2},0 right).)
Тогда ( displaystyle D(left( frac{1}{sqrt{2}},frac{sqrt{6}}{2},sqrt{30} right)).
Координаты точки ( displaystyle A:Aleft( frac{3}{sqrt{2}},frac{sqrt{6}}{2},0 right).)
2. ( displaystyle K) – середина отрезка ( displaystyle BD:)
( displaystyle Kleft( frac{1}{2sqrt{2}},frac{sqrt{6}}{4},frac{sqrt{30}}{2} right).~)
3. ( displaystyle M) – середина отрезка ( displaystyle AC:)
( displaystyle Mleft( frac{3}{2sqrt{2}},~frac{frac{sqrt{6}}{2}+sqrt{6}}{2},0 right)=Mleft( frac{3}{2sqrt{2}},~frac{3sqrt{6}}{4},0 right).)
( displaystyle T) – середина отрезка ( displaystyle AB)
( displaystyle Tleft( frac{3}{2sqrt{2}},~frac{sqrt{6}}{4},0 right).~)
4. Координаты( displaystyle overrightarrow{KT}:overrightarrow{KT}left( frac{3}{2sqrt{2}}-frac{1}{2sqrt{2}},frac{sqrt{6}}{4}-frac{sqrt{6}}{4},~0-frac{sqrt{30}}{2} right)=overrightarrow{KT}left( frac{1}{sqrt{2}},~0,~-frac{sqrt{30}}{2} right).)
Координаты вектора ( displaystyle overrightarrow{TM}:)
( displaystyle overrightarrow{TM}left( 0,frac{3sqrt{6}}{4}-frac{sqrt{6}}{4},0 right)=overrightarrow{TM}left( 0,~frac{sqrt{6}}{2},0 right).)
5. Вычисляем векторное произведение:
( displaystyle overrightarrow{KT}times overrightarrow{TM}=frac{1}{sqrt{2}}cdot frac{sqrt{6}}{2}cdot overrightarrow{k}-frac{sqrt{30}}{2}cdot frac{sqrt{6}}{2}cdot vec{i}=frac{3sqrt{5}}{2}vec{i}+frac{sqrt{3}}{2}overrightarrow{k}=left( frac{3sqrt{5}}{2},0,~frac{sqrt{3}}{2} right).)
6. Длина вектора ( displaystyle TM): проще всего заменить, что отрезок ( displaystyle TM) – средняя линия треугольника ( displaystyle ABC), а значит, он равен половине основания ( displaystyle BC). Так что ( displaystyle left| text{ }!!~!!text{ }overrightarrow{TM} right|=frac{sqrt{6}}{2}).
7. Считаем длину векторного произведения:
( displaystyle left| overrightarrow{KT}times overrightarrow{TM} right|=sqrt{{{left( frac{3sqrt{5}}{2} right)}^{2}}+{{left( frac{sqrt{3}}{2} right)}^{2}}}=2sqrt{3}.)
8. Наконец, находим расстояние:
( displaystyle d=frac{left| overrightarrow{KT}times overrightarrow{TM} right|}{text{ }!!~!!text{ }left| text{ }!!~!!text{ }overrightarrow{TM} right|}=frac{2sqrt{3}}{frac{sqrt{6}}{2}}=2sqrt{2})
Уф, ну все!
Честно тебе скажу: решение этой задачи традиционными методами (через построения), было бы намного быстрее.
Зато здесь я все свел к готовому алгоритму!
Я так думаю, что алгоритм решения тебе ясен? Поэтому попрошу тебя решить оставшиеся две задачи самостоятельно. Сравним ответы?
2. ( displaystyle 12)
3. ( displaystyle 2)
Опять-таки повторюсь: эти задачи проще (быстрее) решать через построения, а не прибегая к координатному методу.
Я продемонстрировал такой способ решения лишь затем, чтобы показать тебе универсальный метод, который позволяет «ничего не достраивать».
Наконец, рассмотрим последний класс задач: Вычисление расстояния между скрещивающимися прямыми.
Вычисление расстояния между скрещивающимися прямыми
Здесь алгоритм решения задач будет схож с предыдущим. Что у нас есть:
- Направляющий вектор первой прямой: ( overrightarrow{{{a}_{1}}(}{{x}_{1}},{{y}_{1}},{{z}_{1}}).)
- Направляющий вектор второй прямой: ( overrightarrow{{{a}_{2}}(}{{x}_{2}},{{y}_{2}},{{z}_{2}}).)
- Любой вектор, соединяющий точки первой и второй прямой: ( overrightarrow{{{a}_{3}}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right))
Как мы ищем расстояние между прямыми?
Формула следующая:
( d=frac{left| left( overrightarrow{{{a}_{3}}},~overrightarrow{{{a}_{1}}},overrightarrow{{{a}_{2}}} right) right|}{left| overrightarrow{{{a}_{1}}}times overrightarrow{{{a}_{2}}} right|})
Числитель – это модуль смешанного произведения (мы его вводили в предыдущей части), а знаменатель – как и в предыдущей формуле (модуль векторного произведения направляющих векторов прямых, расстояние между которыми мы с тобой ищем).
Я напомню тебе, что
![]()
тогда формулу для расстояния можно переписать в виде:
[d = frac{{left| begin{array}{l}begin{array}{*{20}{c}}{{x_0}}&{{y_0}}&{{z_0}}end{array}\begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{z_1}}end{array}\begin{array}{*{20}{c}}{{x_2}}&{{y_2}}&{{z_2}}end{array}end{array} right|}}{{left| begin{array}{l}begin{array}{*{20}{c}}{overrightarrow i }&{overrightarrow j }&{overrightarrow k }end{array}\begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{z_1}}end{array}\begin{array}{*{20}{c}}{{x_2}}&{{y_2}}&{{z_2}}end{array}end{array} right|}}]
Этакий определитель делить на определитель! Хотя, если честно, мне здесь совсем не до шуток!
Данная формула, на самом деле, очень громоздка и приводит к достаточно сложным вычислениям. На твоем месте я бы прибегал к ней только в самом крайнем случае!
Давай попробуем решить несколько задач, используя изложенный выше метод:
- В правильной треугольной призме ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}), все рёбра которой равны ( 1), найдите расстояние между прямыми ( A{{A}_{1}}) и ( B{{C}_{1}}).
- Дана правильная треугольная призма ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}) все рёбра основания которой равны ( 2sqrt{7}) Сечение, проходящее через боковое ребро ( A{{A}_{1}}) и середину ( M) ребра ( {{B}_{1}}{{C}_{1}}) является квадратом. Найдите расстояние между прямыми ( {{A}_{1}}B) и ( AM.)
Первую решаю я, а опираясь на нее, вторую решаешь ты!
1. Рисую призму и отмечаю прямые ( A{{A}_{1}}) и ( B{{C}_{1}}.)
![]()
Координаты точки С: ( C:Cleft( frac{sqrt{3}}{2},frac{1}{2},0 right),) тогда ( {{C}_{1}}left( frac{sqrt{3}}{2},frac{1}{2},1 right).~)
Координаты точки ( B:Bleft( 0,1,0 right).~)
Координаты вектора ( overrightarrow{B{{C}_{1}}}:~overrightarrow{B{{C}_{1}}}left( frac{sqrt{3}}{2},-frac{1}{2},1 right).)
Координаты точки ( {{A}_{1}}:{{A}_{1}}left( 0,0,1 right).)
Координаты вектора ( overrightarrow{A{{A}_{1}}}:~overrightarrow{A{{A}_{1}}}left( 0,0,1 right).)
Координаты вектора ( overrightarrow{AB}left( 0,1,0 right).)
[left( {B,overrightarrow {A{A_1}} overrightarrow {B{C_1}} } right) = left| {begin{array}{*{20}{l}}{begin{array}{*{20}{c}}0&1&0end{array}}\{begin{array}{*{20}{c}}0&0&1end{array}}\{begin{array}{*{20}{c}}{frac{{sqrt 3 }}{2}}&{ — frac{1}{2}}&1end{array}}end{array}} right| = frac{{sqrt 3 }}{2}]
Считаем векторное произведение между векторами ( AA) и ( overrightarrow{B{{C}_{1}}}:)
[overrightarrow {A{A_1}} cdot overrightarrow {B{C_1}} = left| begin{array}{l}begin{array}{*{20}{c}}{overrightarrow i }&{overrightarrow j }&{overrightarrow k }end{array}\begin{array}{*{20}{c}}0&0&1end{array}\begin{array}{*{20}{c}}{frac{{sqrt 3 }}{2}}&{ — frac{1}{2}}&1end{array}end{array} right| — frac{{sqrt 3 }}{2}overrightarrow k + frac{1}{2}overrightarrow i ]
Теперь считаем его длину:
( left| overrightarrow{A{{A}_{1}}}times overrightarrow{B{{C}_{1}}} right|=sqrt{{{left( -frac{sqrt{3}}{2} right)}^{2}}+{{left( frac{1}{2} right)}^{2}}}=1)
Тогда
( d=frac{frac{sqrt{3}}{2}}{1}=frac{sqrt{3}}{2}.)
Ответ: ( frac{sqrt{3}}{2}.)
Теперь постарайся аккуратно выполнить вторую задачу. Ответом на нее будет: ( frac{sqrt{6}}{2}).
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
В развитии геометрии важное значение имело применение алгебры к решению геометрических задач, которое со временем переросло в отдельную науку – аналитическую геометрию. Координатно-векторный метод помогает упростить решение задачи, избежав представления сложных геометрических конфигураций.
Прямоугольными координатами пользовались еще до начала нашей эры. Древнегреческий математик Аполлоний Пергский мог определить с помощью них кривые: параболу, гиперболу и эллипс. Координатами пользовались и в средние века, определяя положение светил на небе, нужное место на поверхности Земли. Прямоугольную сетку использовали художники эпохи Возрождения.
Применять координаты в математике впервые стали Пьер Ферма и Рене Декарт. В 1637 г. Декарт издал трактат «Рассуждение о методе» и изложил в нем метод прямолинейных координат, ввел удобную алгебраическую символику, предложил способы построения касательных и нормалей к плоским алгебраическим кривым. Пьер Ферма раньше и более последовательно, чем Декарт, разработал метод координат, а также вывел уравнение прямой и линий второго порядка.
Термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона в работах по построению числовых систем. Вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному анализу современный вид.
Координатно-векторный метод актуален на сегодняшний день, т.к. находит свое применение в разных областях науки и общественной жизни. Метод координат лежит в основе механики, геодезии, астрономии, используется в медицине, экономике, географии, информатике. Вектор используется в физике для характеристики физических величин. Его изучению уделяют внимание как в школьной программе, так и в таких разделах высшей математики, как «Линейная алгебра», «Функциональный анализ» и др. Рассматриваются прямоугольная, полярная, аффинная, сферическая, цилиндрическая, и другие системы координат. В работе мы рассмотрели прямоугольную систему координат.
Координатно-векторный метод соединяет в себе метод координат и векторный метод. В координатном методе целесообразно знакомиться с прямоугольной системой координат, способами нахождения и задания координат точки на плоскости и в пространстве. В векторном методе должны рассматриваться понятия вектора и связанные с ним определения, теоремы и свойства. Объединив координатный и векторный метод, можно вывести необходимые формулы и найти удобный способ решения любой геометрической задачи.
Объект исследования – координатно-векторный метод в элементарной математике.
Предмет исследования – методы и приемы решения задач по теме «Координатно-векторный метод».
Цель исследования – систематизация теоретического материала, связанного с координатно-векторным методом и его применение к решению геометрических задач.
Результаты исследования докладывались на внутривузовских студенческих конференциях «Молодежь в мире науки» и «Студенчество в научном поиске», где работа заняла 1 место. По результатам конференций, статья опубликована в сборниках. Кроме того, результаты исследования представлены на X международной студенческой конференции в январе 2018 г.
Работа состоит из введения, двух частей и заключения.
Список использованных источников состоит из 21 наименования.
Глава 1. Теоретические основы координатно-векторного метода.
1.1. Основные понятия метода координат
Прямоугольная декартова система координат на плоскости.
Сущность координатного метода на плоскости заключается в задании системы координат, после чего каждую точку плоскости можно охарактеризовать парой действительных чисел, ее координатами, а геометрические фигуры задавать аналитическими условиями (уравнением, неравенством, системой уравнений или неравенств). Чтобы ввести прямоугольную систему координат, необходимо провести на плоскости две взаимно перпендикулярные прямые, выбрать на каждой из них положительное направление и масштаб. Прямоугольную систему координат на плоскости обычно обозначают , где и – ее координатные оси. Ось называют осью абсцисс, а ось – осью ординат.
Рис. 1
Каждой точке плоскости в заданной прямоугольной декартовой системе координат соответствует единственная упорядоченная пара действительных чисел называемых координатами точки на плоскости. Координату называют абсциссой точки , а – ординатой точки М.
Трехмерная прямоугольная система координат в пространстве.
Для задания декартовой прямоугольной системы координат в пространстве выбирают перпендикулярные прямые, называемые осями. Точка пересечения осей называется началом координат. Декартовыми прямоугольными координатами точки в прямоугольной трехмерной системе координат называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до осей координат или проекции радиус-вектора точки на три взаимно перпендикулярные координатные оси.
В пространстве координаты называются соответственно абсциссой, ординатой и аппликатой. В зависимости от взаимного расположения положительных направлений координатных осей возможны правая (рис. 2) и левая (рис. 3) координатные системы.
Рис. 2
Рис. 3
Определение 1. Расстоянием между двумя точками называется длина отрезка, что соединяет эти точки.
Расстояние между двумя точками на плоскости вычисляется по формуле:
Расстояние между двумя точками и в пространстве вычисляется по формуле:
Следующие определения, теоремы, следствия и формулы применимы как на плоскости, так и в пространстве.
Определение 2. Середина отрезка – это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
В прямоугольной системе координат отметим точку с координатами и точку с координатами Координаты середины отрезка вычисляются по формуле:
Следствие 1. Точка тогда и только тогда является серединой отрезка , когда
где – произвольная точка плоскости.
Определение 3. Разделить отрезок , значит найти на заданном отрезке такую точку , для которой имеет место равенство:
Пусть даны точки . Координаты точки вычисляются по формуле:
1.2. Основные понятия векторного метода
В настоящее время понятие «вектор» имеет различные определения.
По Л. С. Атанасяну: «Отрезок, для которого указано, какой из его концов называется началом, а какой – концом, называется направленным отрезком или вектором» (рис 3).
Рис. 4
М. Воловичем было предложено более точное определение: «Вектор – это пара точек, одна из которых является первой. Каждая задающая направленный отрезок пара различных точек задает луч, который начинается в первой из точек пары и проходит через вторую точку, и расстояние между точками. Луч называется направлением направленного отрезка, расстояние между точками – его модулем или длиной».
По В.А. Гусеву: «Под вектором понимается либо множество упорядоченных точек, задающих некий параллельный перенос, либо сам этот перенос».
В.М. Болтянский считает, что «Вектором правильнее называть не один направленный отрезок, а семейство всех равных, параллельных и одинаково направленных отрезков».
Определение 4. Вектор, у которого начало совпадает с концом, называется нулевым вектором.
Определение 5. Длина отрезка длиной или модулем вектора .
Определение 6. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или одной прямой.
Определение 7. Векторы, лежащие в одной плоскости или в параллельных плоскостях называются компланарными.
Определение 8. Пусть – два произвольных вектора на плоскости (рис. 5) . Возьмем на плоскости произвольную точку и отложим вектор , равный вектору . Затем от точки отложим вектор , равный вектору . Вектор называется суммой векторов и обозначается через .
Рис. 5
Свойства сложения векторов:
(коммутативность).
2. (ассоциативность).
Определение 9. Разностью векторов называется такой вектор , который в сумме с вектором дает вектор :
Для получения разности достаточно отложить векторы от одной точки и взять вектор, идущий из конца вектора к концу вектора .
Рис. 6
Определение 10. Углом между векторами, отложенными от одной точки, называется наименьший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором. Угол выражается из формулы скалярного произведения.
Определение 11. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
Свойства скалярного произведения:
. (коммутативность).
2. (дистрибутивность).
3. , т.е. числовой множитель можно выносить за знак скалярного произведения.
4. Если , то = 0 и .
5. = .
6. = .
Определение 12. Проекции вектора на оси координат называются координатами вектора .
Скалярное произведение двух векторов на плоскости и в пространстве можно вычислить, зная координаты этих векторов. Скалярное произведение векторов и в пространстве выражается формулой:
Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на число.
1. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Другими словами, если и – данные векторы, то вектор имеет координаты .
2. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
Другими словами, если и – данные векторы, то вектор имеет координаты .
3. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Другими словами, если – данный вектор, – данное число, то вектор имеет координаты .
Теорема 1. Пусть – прямоугольная система координат на плоскости, а – единичные векторы оси . Для любого вектора справедливо равенство:
где – координаты вектора в системе .
Рис. 7
Теорема 2. Пусть – трехмерная прямоугольная система координат, а – единичные векторы оси . Для любого вектора справедливо равенство:
где где – координаты вектора в системе .
Рис. 8
Для решения задач необходимо ввести систему координат.
Пример 1. Правильная четырехугольная пирамида , все ребра которой равны 1.
Рис. 9
Координаты вершин:
Определение 13. Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус-вектором данной точки.
1.3. Сущность координатно-векторного метода
Чтобы использовать в решении задач координатно-векторный метод, необходимо знать формулы косинуса и синуса угла между векторами; уметь составлять уравнение прямой и уравнение плоскости; знать формулы нахождения расстояний.
Определение 14. Уравнением линии на плоскости называется уравнение , которому удовлетворяют координаты любой точки, принадлежащей этой линии, и не удовлетворяют координаты никакой другой точки.
Теорема 3. В декартовой системе координат любая плоскость задается уравнением: , где координаты вектора нормали к плоскости.
Доказательство:
Пусть на плоскости даны точки и опущен нормальный вектор к плоскости (рис. 10). Найдем координаты вектора
Рис. 10
Определение 15.Нормальный вектор к плоскости – любой вектор, перпендикулярный данной плоскости.
Теорема 4. Любое уравнение первой степени в декартовой системе координат задает плоскость
Теорема 5. Два уравнения первой степени задают одну и ту же плоскость в том и только в том случае, когда одно получается из другого умножением на число.
Выведем общее уравнение прямой:
Пусть дана прямоугольная система координат (рис. 11). Отметим точки . Выберем направляющий вектор . Векторы коллинеарны, следовательно:
Так
Таким образом, – постоянные коэффициенты.
(0;b)
(0;0)
Рис. 11
Определение 16. Любой вектор, коллинеарный данной прямой, называется направляющим вектором этой прямой.
Определение 17. Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку.
Косинус угла между ненулевыми векторами и вычисляется по формуле:
Определение 18. Угол между плоскостями измеряется углом между нормалями к этим плоскостям.
Определение 19. Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и её проекцией на данную плоскость.
Синус угла между прямой, направляющий вектор которой имеет координаты и плоскостью, заданной уравнением
вычисляется по формуле:
где вектор нормали к плоскости, направляющий вектор прямой.
Определение 20. Расстояние от точки до прямой – это длина перпендикуляра, опущенного източки на эту прямую.
Определение 21. Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Для того чтобы найти расстояние от точки до плоскости, необходимо найти координаты точки, и координаты нормали данной плоскости. После чего воспользоваться следующей формулой:
где , плоскость задана уравнением
Определение 22. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Исходя из вышесказанного, для решения геометрических задач координатно-векторным методом наиболее общим является следующий способ, представленный в виде алгоритма:
1. Ввести прямоугольную систему координат.
2. Найти координаты необходимых точек.
3. Найти координаты необходимых векторов.
4. Задать уравнения прямой и плоскости, если они необходимы.
5. Использовать формулу для решения конкретной задачи, выполнить вычисления.
6. Записать ответ.
Таким образом, в 1 главе мы рассмотрели метод координат и векторный метод на плоскости и в пространстве. В координатном методе мы представили информацию о прямоугольной системе координат, способах нахождения и задания координат точки. В векторном методе мы рассмотрели понятия вектора и связанные с ним определения, теоремы и свойства. Соединив два метода, мы получили координатно-векторный метод. В нем рассмотрели уравнения прямых и плоскостей, формулы для нахождения углов и расстояний. На основании всего вышесказанного мы вывели способ решения задач координатно-векторным методом, который представили в виде алгоритма. Рассмотренные формулы и понятия применяются для решения геометрических задач, некоторые из которых представлены в главе 2.
Глава 2. Применение координатно-векторного метода для решения геометрических задач.
Представленный в теоретической части материал помог нам составить классификацию задач, решаемых координатно-векторным методом. К каждой задаче мы представили решение и ответ.
Рассмотрим задачи, при решении которых будет использован координатно-векторный метод.
1. Задачи на нахождение угла между скрещивающимися прямыми.
2. Задачи на нахождение угла между прямой и плоскостью.
3. Задачи на нахождение угла между плоскостями.
4. Задачи на нахождение расстояния от точки до плоскости.
5. Задачи на нахождения расстояния между плоскостями.
6. Задачи на нахождение расстояния между скрещивающимися прямыми.
7. Задачи на нахождение угла между плоскостями.
Задача 1. В кубе (рис. 12) точки середины ребер соответственно. Найдите угол между прямыми
Рис. 12
Решение:
1. Введём прямоугольную систему координат с началом в точке , оси которой совпадают с ребрами
2. Найдём координаты точек : .
3. Прямые скрещивающиеся. Чтобы найти угол между скрещивающимися прямыми, необходимо найти косинус угла между соответствующими векторами. Найдем координаты векторов :
4. Воспользуемся формулой нахождения косинуса угла между ненулевыми векторами:
Ответ:
Задача 2. В правильной четырехугольной пирамиде (рис. 13), все ребра которой равны 1, точки середины ребер Найдите угол между прямыми .
Рис. 13
Решение:
1. Введём прямоугольную систему координат. Для данной задачи лучше всего выбрать начало координат в центре основания пирамиды, а оси построить параллельно относительно сторон ее основания.
2. Найдем координаты необходимых точек , и ,
3. Найдём координаты векторов
4. Воспользуемся формулой нахождения косинуса угла между ненулевыми векторами:
Ответ:
Задача 3. В правильной четырехугольной пирамиде (рис. 14), все ребра которой равны 1, найдите угол между прямой и плоскостью .
Рис. 14
Решение:
1. Введём прямоугольную систему координат. Начало координат поместим в точку , поэтому все координаты этой точки равны нулю.
2. Найдём координаты точек
Чтобы найти координаты точки , сначала найдем координаты ее проекции на плоскость основания, а затем ее координаты по оси OZ:
3. Запишем уравнение плоскости
Так как плоскость проходит через начало координат, получим систему уравнений:
Уравнение плоскости имеет вид:
Разделим обе части равенства на с, получим:
Таким образом, вектор нормали к плоскости SBC имеет координаты:
Найдем координаты направляющего вектора прямой
4. Воспользуемся формулой для нахождения угла между прямой и плоскостью:
Ответ:
Задача 4. В правильной четырехугольной призме (рис. 15) со стороной основания 12 и высотой 21 на ребре взята точка так, что 8. На ребре взята точка так, что = 8. Найдите угол между плоскостью и плоскостью .
Рис. 15
Решение:
1. Введём прямоугольную систему координат с началом в точке .
2. Найдём координаты точек : .
3. Составим уравнение плоскости
Таким образом, получим уравнение: Составим уравнение плоскости :
Таким образом, получим уравнение:
4. Воспользуемся формулой нахождения угла между плоскостями:
Ответ:
Задача 5. В единичном кубе (рис. 16) найдите расстояние от точки до плоскости .
Рис. 16
Решение:
1. Введём прямоугольную систему координат с началом в точке , оси которой совпадают с ребрами
2. Найдём координаты точек : и
3. Составим уравнение плоскости :
Отсюда
Уравнение имеет вид:
4. Воспользуемся формулой нахождения расстояния от точки до плоскости:
Ответ:
Задача 6. В правильной треугольной призме все ребра которой равны 1, найдите расстояние между прямыми
Рис. 17
Решение:
Расстояние между прямыми есть расстояние от точки , которая является серединой отрезка до плоскости .
1. Введём прямоугольную систему координат с началом в точке M.
2. Найдём координаты точек
3. Составим уравнение плоскости :
4. Воспользуемся формулой нахождения расстояния от точки до плоскости:
Ответ:
Задача 7. На плоскости заданы точки Доказать, что ромб и вычислить его площадь.
Решение:
Найдем координаты векторов
Найдем координаты середины отрезков
Середины диагоналей совпадают.
Поскольку то в четырехугольнике диагонали пересекаются под прямым углом. Значит, четырехугольник – ромб.
Ответ: 5 кв.ед.
Задача 8. Даны вершины треугольника и . Доказать, что , где середина стороны . Определить вид треугольника .
Решение:
Найдём координаты точки :
Точка имеет координаты ,
Значит, .
Поскольку медиана перпендикулярна стороне , то ∆ равнобедренный.
Задача 9. Найти медиану AM треугольника ABC (рис. 18), вершины которого имеют координаты: А(0; 1), В(1; -4), С (5; 2).
Рис. 18
Решение:
Найдем координаты точки
Точка имеет координаты (3; 1).
Найдём медиану
Ответ:
Заключение
Координатно-векторный метод решения задач на сегодняшний день очень востребован, и позволяет решать фактически все виды математических, физических, астрономических и технических задач. Он имеет преимущество перед другими, так как не требует сложных построений в проекциях. Однако важно уметь правильно вводить систему координат индивидуально для каждой задачи. Недостатком данного метода является то, что нередко он требует большого объема вычислений.
В первой главе мы рассмотрели отдельно векторный метод, в котором представили все определения, операции над векторами, их скалярное умножение, базис на плоскости и в пространстве. В методе координат рассмотрели прямоугольную систему координат, нахождение расстояния между точками, вычисление середины отрезка, деление отрезка в заданном отношении. Объединив два метода, мы получили координатно-векторный метод и представили все необходимые определения, формулы, свойства и теоремы, применяемые для решения геометрических задач. Для решения задач в пространстве мы составили обобщенный способ, представленный в виде алгоритма.
Представленный в теоретической части материал помог нам составить перечень геометрических задач, решаемых координатно-векторным методом. Мы рассмотрели задачи на нахождение угла между скрещивающимися прямыми, между плоскостями, между прямой и плоскостью. Рассмотрели задачи на нахождение расстояния от точки до плоскости и между скрещивающимися прямыми, задачи на нахождение неизвестных величин и доказательство утверждений на плоскости. К каждой задаче мы представили решение и ответ.
Список использованных источников
Атанасян, Л.С. Геометрия 10-11. М: Просвещение, 2009. – 258 с.
Вдовин, А.Ю. Высшая математика. Стандартные задачи с основами теории [Электронный ресурс] : учеб. пособие / А.Ю. Вдовин, Л.В. Михалева, В.М. Мухина. – Электрон. дан. – Спб : Лань, 2009. – 192 с. – Режим доступа: https: / / e.lanbook.com/book/45. – Загл. с экрана.
Вилейтнер, Г. История математики от Декарта до середины XIX столетия / Г. Вилейтнер. – М.: Физматгиз, 1960. – 469 с.
Волович, М.Б. Векторы // Первое сентября. – 2001. – №15. – С.11-16.
Габович, И., Горнштейн П. Вооружившись методом координат // Квант. – 2009. – №11. – с. 42 – 47.
Гельфанд, И.М. Метод координат [Электронный ресурс] : учеб. пособие / И.М. Гельфанд, Е.Г. Глаголева, А.А. Кириллов. – Электрон. дан. – Москва : МЦНМО, 2009. – 21-22 с. – Режим доступа: https://e.lanbook.com/book/9321. – Загл. с экрана.
Глаголев, Н. А. Элементарная геометрия: стереометрия для 10-11 кл. ср. шк. в 2 ч. – М.: Просвещение, 2008. – ч. 2.
Гордин, Р.К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень) [Электронный ресурс] : учеб. пособие – Электрон. дан. – Москва : МЦНМО, 2017. – 120 с. – Режим доступа: https://e.lanbook.com/book/92688. – Загл. с экрана.
Готман, Э.Г. Скопец, З.А., Решение геометрических задач аналитическим методом. – М.: Просвещение, 2009.
Гусев, В.А. Преподавание геометрии в 6-8 классах: Сб. статей / сост. В.А. Гусев – М.: Просвещение, 1979. – 287 с.
Калинин, А.Ю. Сборник задач по геометрии. 10-11 классы [Электронный ресурс] : учеб. пособие / А.Ю. Калинин, Д.А. Терешин. –Электрон. дан. – Москва : МЦНМО, 2011. – 160 с. – Режим доступа: https://e.lanbook.com/book/9349. – Загл. с экрана.
Кушнир, И.А. Векторные методы решения задач [Текст] : учеб.пособие / И.А. Кушнир – Киев: Обериг, 1994. – 210 с.
Лихолетов, И.И., Мацкевич, И.П. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике [Текст] : Лихолетов И.И., Мацкевич И.П. 2-е изд., исправл. и доп. – Минск: Вышэйшая школа, 1969. – 454 с.
Математика. Подготовка к ЕГЭ-2012: учебно-методическое пособие / под ред. Ф.Ф. Лысенко, С.Ю. Калабухова. – Ростов-на-Дону: Легион – М., 2011.
Мугаллимова, C.Р. Векторы для школьника [Текст] : учеб.пособие / С.Р. Мугаллимова – Омск: «Сфера», 2008. – 51 с.
Новые компьютерные технологии. Координатная плоскость // Математика – Приложение к газ. «Первое сентября» – 2004г. – №29. – С. 10-14.
Погорелов, А.В. Аналитическая геометрия [Электронный ресурс] : учеб. пособие / А.В. Погорелов, – Электрон. текстовые данные. – Москва, Ижевск: Регулярная и хаотическая динамика, 2005. – 208 c. – Режим доступа: http://www.iprbookshop.ru/16488.html. – ЭБС «IPRbooks».
Постников, М.М. Аналитическая геометрия [Электронный ресурс] : учеб. пособие – Электрон. дан. – Санкт-Петербург : Лань, 2009. – 416 с. – Режим доступа: https://e.lanbook.com/book/318. – Загл. с экрана.
Сумина, Г.Н. Методические рекомендации к изучению метода координат на плоскости: учебно-методическое пособие / сост. Г.Н. Сумина –М: Просвещение, 2013 г. – 76 с.
Цубербиллер, О.Н. Задачи и упражнения по аналитической геометрии [Электронный ресурс] : учеб. пособие – Электрон. дан. – Санкт-Петербург : Лань, 2009. – 336 с. – Режим доступа: https://e.lanbook.com/book/430. – Загл. с экрана.
Ларин, А.А. Подготовка к ЕГЭ [Электронный ресурс] / А.А. Ларин – Режим доступа: http://www.alexlarin.net/ – свободный.
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Башкирский государственный педагогический университет
им. М.Акмуллы»
(ФГБОУ ВПО «БГПУ им. М.Акмуллы»)
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА
Тазетдиновой Анастасии Николаевны
МЕТОДИКА ИСПОЛЬЗОВАНИЯ ВЕКТОРНОГО И
КООРДИНАТНОГО МЕТОДА ПРИ РЕШЕНИИ
ЗАДАЧ ПОВЫШЕННОЙ СЛОЖНОСТИ
Научный руководитель:
Дата представления_________________
Дата защиты_______________________
Оценка____________________________
Уфа 2014
СОДЕРЖАНИЕ
Введение
История возникновения и становления аналитических методов
Различные подходы к определению понятия вектора в математике и в школьном курсе математики
Обучение решению задач как психологическая и методическая проблема
Методика обучения векторному методу решения задач в геометрии
Методика формирования умений, составляющих суть векторного метода решения задач в неполной средней школе
Методика обучения векторному методу решения содержательных геометрических задач
Описание элективного курса «Решение задач повышенной сложности векторным и координатным способом»
Заключение
Список литературы
Приложение
ТЕМА: Методика использования векторного и координатного метода при решении задач повышенной сложности
Автор работы: Тазетдинова Анастасия Николаевна
Научный руководитель:
(фамилия, имя. отчество, должность, ученая степень. звание, место работы)
АННОТАЦИЯ
Актуальность работы
В соответствии с концепцией Российского образования и, в частности, математического, одной из задач обучения, развития и воспитания учащихся в средней школе является достижение следующих двух главных целей образования: воспитать личность, способную адаптироваться в быстро меняющихся условиях жизни и способную одновременно изменять эти условия. Соответственно, усилия школы должны быть сосредоточены в двух направлениях: создание условий для развития интеллекта и формирование творческих качеств личности обучающихся. Одной из приоритетных целей математического образования в рамках выделенных направлений является «формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики». Векторный и координатный метод, который в литературе называется ещё векторно-координатным и координатно-векторным, является одним из основных методов геометрии. Тем не менее, большинство школьников затрудняются в применении этого метода к решению задач, в том числе повышенной сложности. Это обусловлено тем, что в школе уделяется недостаточно внимания для применения указанных методов на практике. Разрешение этого противоречия между необходимостью обучения учащихся векторному методу решения геометрических задач и недостаточному уделению внимания этому на практике особенно актуально при изучении темы «Векторы в пространстве» в 10 классе, поскольку в теории и методике обучения математике даются, в основном, рекомендации для изучения векторного метода на плоскости.
Таким образом, сформулированное выше противоречие определило актуальность проблемы моей работы, которая состоит в его разрешении посредством обоснованной разработки методических рекомендаций по обучению учащихся векторному и координатному методу решения геометрических задач в теме «Векторы в пространстве».
Цели и задачи
Целью работы является разработка методики, которая позволила бы избежать устойчивых затруднений, возникающих у учеников при введении понятия вектора и изучении его свойств. Это позволит сделать изучение темы «Векторы» понятной и доступной для большинства учащихся.
Для достижения поставленной цели необходимо решить задачи:
-
провести анализ психолого-педагогической и научно-методической литературы по проблеме исследования с целью выявления условий успешного овладения школьниками векторного и координатного метода решения геометрических задач, в том числе повышенной сложности;
-
провести анализ программных документов, школьных учебников по теме «Векторы в пространстве»;
-
выявить теоретико-методическую концепцию, на основе которой можно разрабатывать методические рекомендации изучения векторного и координатного метода решения задач в школьном курсе геометрии;
-
разработать методические рекомендации для успешного овладения учащимися векторного и координатного метода;
-
провести опытную проверку разработанных методических рекомендаций.
Характеристика методики исследования и использованных источников
Для решения вышеперечисленных задач использовались следующие методы:
-
изучения и анализ литературы по исследуемой проблеме;
-
беседа с учителями математики в старших классах общеобразовательной школы;
-
тестирование учащихся;
-
опытная работа.
Объект исследования: процесс обучения геометрии в основной школе;
Предмет исследования: методическая система обучения учащихся векторному методу решения задач.
Гипотеза исследования: Если целенаправленно обучать школьников умениям и действиям, входящих в состав векторного и координатного метода, формулировать частные эвристики по решению отдельных типов задач, в том числе повышенной сложности, то это будет способствовать эффективному усвоению учащимися этого метода.
Методологической основой исследования послужили: концепция развивающего обучения (В.В. Давыдова, Д.Б. Эльконина); основные положения деятельностного подхода; методические рекомендации по изучению темы «Векторы в пространстве» (Т.А. Ивановой, З.А. Скопеца, В.А. Гусева, Г.И. Саранцева).
Структура работы
Структура дипломной работы определена ее логикой и решением задач исследования. Работа состоит из введения, двух глав, заключения, списка литературы, приложения.
Основные выводы
В результате проделанной работы можно сделать следующие выводы:
-
вектор является одним из фундаментальных понятий современной математики. В настоящее время существует несколько подходов к определению этого понятия.
-
векторный и координатный метод является эффективным методом решения геометрических задач, в том числе повышенной сложности, и доказательства теорем;
-
для успешного овладения школьниками векторным и координатным методом решения содержательных геометрических задач необходимо обучать их умениям и действиям, входящих в его состав;
-
сущность векторного и координатного метода состоит в том, что условие и требование задачи записывается в векторной форме, а ее решение состоит в переходе от условия к требованию на основе законов векторной алгебры.
Практическая значимость
Геометрия – раздел математики, являющийся носителем собственного метода познания мира, с помощью которого рассматриваются формы и взаимное расположение предметов, развивающих пространственные представления, образное мышление учащихся, изобразительно-графические умения, приемы конструктивной деятельности, формируют геометрическое мышление. Несмотря на цели и задачи, сформулированные в учебных программах по математике и геометрии 5-9 классов, согласно которым у учеников на протяжении пяти лет должны быть сформированы пространственное мышление и воображение, умение выделять плоскостные объекты в составе пространственных объектов, на практике дело обстоит иначе.
В данной работе представлены методические рекомендации, которые позволят расширить и систематизировать знания учащихся в использовании векторного и координатного метода решения стереометрических задач, в том числе повышенной сложности.
Введение
В геометрии применяются различные методы решения задач – это синтетический (чисто геометрический) метод, метод преобразований, векторный и координатный метод, метод ключевых задач. Методы делятся на методы алгебры и геометрии . Геометрические методы: метод треугольников, метод площадей, метод вспомогательных фигур, координатный метод, векторный метод и др. Они занимают различное положение в школе. Основным методом считается синтетический, а из других наиболее высокое положение занимает векторный и координатный метод потому, что он тесно связан с геометрией. Изящество синтетического метода достигается с помощью интуиции, догадок, дополнительных построений. Векторный и координатный метод этого не требует: решение задач во многом алгоритмизировано, что в большинстве случаев упрощает поиск и само решение задачи. Можно с уверенностью говорить о том, что изучение данного метода является неотъемлемой частью школьного курса геометрии. Но нельзя забывать, что при решении задач этим методом необходим навык алгебраических вычислений и не нужна высокая степень сообразительности, а это в свою очередь негативно сказывается на творческих способностях учащихся. Поэтому необходима методика изучения метода координат, позволяющая учащимся научиться решать разнообразные задачи векторным и координатным методом, однако не показывающая этот метод как основной для решения геометрических задач. В силу этого, обучение учащихся решению задач, в том числе повышенного уровня, координатно-векторным методом должно найти свое место в обучении геометрии. При этом важно раскрыть суть метода на примере рассмотрения выразительной, показывающей достоинство данного метода задачи, дать ориентировочную основу действия для применения этого метода, организовать самостоятельную работу учащихся по решению задач этим методом, выделив их виды. Векторный и координатный метод является одним из основных методов геометрии. С его помощью можно эффективно решить ряд аффинных и метрических задач планиметрии и стереометрии, ряд прикладных задач физики и астрономии. Так же изучение векторного метода представляет собой самостоятельный познавательный интерес, т.к. на его основе имеется возможность корректно ввести метод координат на плоскости и в пространстве. Необходимо отметить, что в школьном курсе математики тема «Векторы», а вместе с ней векторный метод, появилась относительно недавно, в начале шестидесятых годов прошлого века. Тем не менее, практически сразу же понятие вектора стало одним из ведущих понятий школьного курса математики, а векторный метод – одним из основных способов решения задач и доказательства теорем.
В любом школьном учебнике изложение темы «Векторы» состоит из двух этапов: изучение векторов и векторного метода в планиметрии и в стереометрии. Изучение темы «Векторы в пространстве» дает возможность учащимся получить представление о широте применения векторов в различных областях человеческой деятельности, познакомиться с некоторыми фактами развития векторного исчисления, усвоить систематизированные сведения о векторах в пространстве, научиться проводить аналогии между плоскими и пространственными конфигурациями векторов, применять векторный метод для изучения плоских и пространственных форм, при решении задач, в том числе, повышенной сложности. Изучением темы «Векторы. Векторный метод решения задач» в разные периоды времени занимались многие ученые-физики, математики и методисты: К. Вессель, Р. Декарт, Ж. Арган, А. Д. Александров, В. А. Гусев, Ю.М. Калягин, Т.А. Иванова, Л.С. Атанасян, Г.П. Бевз, В.Г. Болтянский, В.Ф.Бутузов, М.Б. Волович, Г.Д. Глейзер, С.Б. Кадомцев, В.М. Клопский, А.Н. Колмогоров, Ю.М. Колягин, Г.Л. Луканкин, И.А.Лурье, А.Ф.Пичурин, В.А. Погорелов, В. И. Рыжик, Г. И. Саранцев, А.Ф. Семенович, А.Д. Семушин, З.А. Скопец, И.М. Смирнова, В.А. Смирнов, Ф.И. Фетисов, Р.С. Черкасов, И.Ф. Шарыгин, И.М. Яглом, М.И. Ягодовский. В настоящее время существует несколько подходов к определению понятию вектора, определены операции с векторами, очерчен круг задач, решаемых векторным и координатным методом, выделены умения, входящие в состав векторного и координатного метода. Разработаны частные методики по обучению учащихся векторам и, в частности, векторному методу. Все они основаны на идее основного назначения векторов – использование алгебраического аппарата для решения геометрических задач.
История возникновения и становления аналитических методов
Прежде чем начать изучение какой-либо темы, необходимо обратиться к истории ее возникновения. Многие историки считают «родителями векторного пространства» ирландского учёного XIX в. У. Гамильтона, а также его немецких коллег и современников Г. Грассмана. Даже сам термин «вектор» ввел также Гамильтон около 1845 г.
Между тем историю векторного исчисления, как историю и корни всякой крупной математической теории, можно проследить задолго до его выделения в самостоятельный раздел математики. В Древней Греции, пифагорейцы, открыв иррациональные числа, пришли к выводу, что не всякую величину можно выразить дробями. Вследствие этого математики того времени попытались свести вопросы арифметики и алгебры к решению задач геометрическим путем. Таким образом, было положено начало геометрической теории отношений Евдокса (408-355 гг. до н.э.), а позднее «геометрической алгебре». В работе Евклида «Начала» сложение и вычитание сводились к сложению и вычитанию отрезков, умножение – к построению прямоугольников на отрезках, соответствующих по длине множителям, а деление – к операции «приложения» геометрических фигур. Еще в работе «Механические проблемы», созданной в школе Аристотеля, введен термин «сложение движений», т.е. скоростей, и сформулировано правило параллелограмма. Его использовал Архимед в работе «О спиралях», а позже – Птолемей. Астрономы средневекового Востока, развивая теорию Птолемея, постоянно использовали «сложение движений».
В 1587 г. был опубликован на голландском языке трактат фламандского ученого С. Стевина (1548-1620) «Начала статики». В нем автор, рассматривая сложение сил, приходит к выводу, что для нахождения результата сложения двух сил, действующих под углом 90°, необходимо воспользоваться «параллелограммом сил», при этом для обозначения сил С. Стевин ввел стрелки. Иначе говоря, С. Стевин впервые ввел сложение двух векторов, перпендикулярных друг другу. Далее, Стевин в «Основах статики» и Валлис (1616-1703) в «Механике» сформулировали правила параллелограмма и параллелепипеда для сложения направленных отрезков, которыми они изображали силы, скорости, ускорения.
В конце 16- начале 17 в. многие ученые – физики, в том числе Леонардо да Винчи, Галилео Галилей, пользовались направленными отрезками для наглядного представления сил. Формулируя свои законы движения планет, Кеплер по существу рассматривает направленный отрезок, началом которого является Солнце, а конец совпадает с движущейся точкой. Однако в рассматриваемую эпоху в естествознании еще не оформилось четко понятия векторной величины, а идеи алгебраических действий с направленными отрезками лишь зарождались. Исторически развитие векторного исчисления шло тремя путями: геометрическим (исчисление отрезков), физическим (исследование векторных величин, встречаемых в естествознании), и алгебраическим (расширение понятия операции при создании современной алгебры). Начала исчисления направленных отрезков были впервые изложены норвежцем Каспаром Весселем в мемуаре «Опыт об аналитическом представлении направления и его применениях, преимущественно к решению плоских и сферических многоугольников», опубликованном в «Трудах Датской Академии наук» в 1799 г. Вессель создал свой труд, исходя из чисто практических задач – облегчить труд геодезиста-землемера. Векторную алгебру на плоскости (или двумерное векторное пространство) Вессель строит почти так же, как она изложена в наших учебниках. Для иллюстрации приведем его определение суммы нескольких векторов, следующее за определением суммы двух направленных отрезков: «Чтобы сложить более двух отрезков, нужно следовать тому же правилу: располагаем их так, чтобы конец первого совпадал с началом второго, а конец второго совпадал с первой точкой третьего и т. д., затем соединяем отрезком ту точку, где первый отрезок начинается с той точкой, где последний отрезок заканчивается, и называем этот последний отрезок суммой всех данных отрезков». Причем он подчеркивает, что в расширенное понятие сложения включен как частный случай и старый смысл этого действия, т.е. «Если складываемые отрезки одинаково направлены, то это определение суммы вполне согласуется с обычным сложением». Вессель также строит исчисление направленных отрезков в пространстве (трехмерное векторное пространство) и, развивая оригинальную «алгебру вращения сферы», применяет ее к решению сферических треугольников и многоугольников. «Опыт» Весселя свидетельствует о том, что именно удовлетворение потребностей прикладной геометрии привело к развитию векторного исчисления. Об этом говорят и философские воззрения великих ученых о роли математики в исследовании явлений природы. Система координат Р. Декарта основана на его концепции единой математики, объединяющей геометрию и алгебру. Развивая мысли Декарта о матемизации естествознания, Лейбниц писал: «Алгебра выражает величину необходим ещё иной, чисто геометрический анализ, непосредственно выражающий положение». Лейбниц говорил о построении геометрического исчисления, изучающего направленные отрезки, их длины, углы между ними. Эти мысли стали исходной точкой для многих геометрических работ. Видное место в истории векторного исчисления занимает книга Карно «Геометрия положения» (1803). В ней автор вводит понятие геометрического количества, под которым он подразумевает в основном направленный отрезок, и занимается действиями над ориентированными фигурами, в частности отрезками. До него положительные и отрицательные отрезки рассматривались лишь в пределах одной прямой, он же ввел отрезки, имеющие любое направление, и фактически проложил путь к векторному исчислению. Некоторые введенные Карно термины и символы, в частности обозначение вектора с помощью черты наверху, сохранились и поныне. В 1835 г. Дж. Белаватис в «Теории эквиполентности» ввел свободные векторы, назвав эквиполентными направленные отрезки с равной длиной и совпадающими направлениями. В сочинении по аналитической и проективной геометрии «Барицентрическое исчисление» (1827) немецкий математик А. Мебиус в известной мере продолжил труд Карно и систематизировал его идеи. Автор впервые представлял геометрическое количество АВ в виде разности точек: В – А. Швейцарский математик Жан Арган (1768-1822) написал в 1806 г. «Опыт о способе изображения мнимых количеств в геометрических построениях». Арган ставит и корректно решает задачу построения исчисления направленных отрезков, которые он называет «направленными линиями». Примерно в то же время появился и ряд других работ (М. Бюэ, Дж. Уоррена и др.), в которых делаются попытки обобщения алгебраических понятий таким образом, чтобы «числами» и «величинами» охватить отрицательные и комплексные числа, и направленные отрезки. В математике эта теория окончательно утвердилась после «курса алгебраического анализа» (1821) О. Коши и «Теории биквадратичных вычетов» (1832) Гаусса. Дальнейшее развитие векторного исчисления связано с исследованиями гиперкомплексных чисел, с помощью которых можно было бы изучать повороты направленных отрезков в пространстве. В своем труде «Лекции о кватернионах» Гамильтон дал строгое изложение алгебры комплексных чисел и создал учение, которое явилось одним из алгебраических источников развития современного векторного исчисления. В работе автор впервые вводит термины «вектор» (от лат. vector – «несущий или ведущий, влекущий, переносящий»), «скаляр», скалярное и векторное произведения, а так же определяет операции с векторами в трехмерном пространстве. Он писал: «Шаг от точки А к точке В можно рассматривать как работу по транспортировке или переносе подвижной точки из начального положения в конечное». Теорию кватернионов развил и усовершенствовал математик и физик П. Тэт (1831-1901), посвятивший теории кватернионов и ее приложениям к физике 70 своих работ. В 1867 г. в «Элементарном трактате по теории кватернионов» Тэт впервые дал векторное изложение аналитической геометрии. В главе «Геометрия прямой и плоскости» Тэт предложил те задачи, которые и сейчас входят в учебники: найти уравнение прямой, проходящей через две данные точки; найти длину перпендикуляра, опущенного из данной точки на плоскость; найти условие того, что четыре данные точки лежат в одной плоскости, и т.д. Грассман в труде «Учение о протяженности» (1844 г.) впервые излагает учение об n- мерном евклидовом пространстве, которое как частный случай включает теорию векторов на плоскости и в трехмерном пространстве. Векторы, названные автором палочками, он обозначал жирными буквами латинского алфавита. Скалярное произведение векторов, названное им внутренним произведением, он обозначал a | b; векторное произведение, внешним произведением, он обозначал [a, b]. Во второй половине 19 в. идеи векторного исчисления получили свое развитие, в основном, в области физики. Так, Сен-Венан (1797-1886), опираясь на труды Валлиса и Стевина, в работе «О геометрических суммах и разностях и их применении для упрощения изложения механики» (1845 г.) разработал теорию сложения и вычитания направленных отрезков. Джемс Кларк Максвелл (1831-1879), один из создателей теории электромагнитного поля, применил в своем «Учении об электричестве и магнетизме» векторное исчисление. «Ценность идеи вектора несказанна», – писал Максвелл Тэту. Из разбухшего аппарата теории кватернионов он выбрал то, что необходимо для векторного исчисления, и тем самым создал удобный инструмент, который широко использует современная физика. Однако современный вид придали векторному исчислению в конце 19 в. американский физик, один из основателей химической термодинамики и статической механики – Дж. Гиббс (1839-1903), Грассман, и английский физик О. Хевисайд (1850-1925), применивший векторы в своей «Электромагнитной теории». В последней четверти 19 в. происходит слияние, синтез трех путей (геометрического, алгебраического и физического) исторического развития и трех источников формирования векторного исчисления. Векторное исчисление становится независимой ветвью математики.
В современной математике раздел, в котором излагается учение о действиях с векторами, называют векторной алгеброй, так как эти действия имеют много свойств с алгебраическими действиями. Наряду с ней Гамильтон создал и векторный анализ, изучающий переменные векторы – векторные функции.
Различные подходы к определению понятия вектора в математике и в школьном курсе математики
Вектор является одним из фундаментальных понятий современной математики. Эволюция этого понятия осуществлялась благодаря широкому использованию его в различных областях математики, механики, а так же в технике. Уже на уроках физики в 7 классе изложение материала ведется с широким привлечением векторного аппарата. Известно, что существует несколько подходов к ведению понятия «вектор».
В учебнике Л.Я. Куликова по алгебре [17] «n-мерным вектором над полем F (где F-поле скаляров) называется любой кортеж из n элементов поля F». При таком подходе вектор обычно записывается в виде строки или столбца. Например, (α1, α2,…, αn), где αi-скаляры. В теории линейной алгебры можно встретить другой подход, при котором вектор определяется как элемент векторного пространства V, обладающий рядом свойств. В данном случае определение вектора вводится аксиоматически, через систему свойств. Анализируя оба подхода к определению понятия вектора, лежащих в основе линейной алгебры, можно сделать вывод, что в данном случае геометрия полностью заменяется алгеброй, а все арифметические операции над векторами сводятся к аналогичным операциям над числами.
В геометрии к определению понятия вектора другой подход: «Вектор – геометрический объект, характеризующийся направлением и длиной». Кроме того, существуют различные конкретизации. Предметом векторного исчисления служит вектор как множество сонаправленных отрезков, имеющих одинаковую длину. Соответственно этому подходу векторы рассматривают с точностью до их положения (т.е. не различая равных векторов, получающихся друг из друга параллельным переносом). В этом смысле векторы называют свободными. Таким образом, свободные векторы вполне определяются заданием его длины и (если он не нулевой) направления. Равные векторы, не совпадающие по положению, рассматриваются как различные конкретные изображения одного и того же свободного вектора. Данный подход к определению понятия вектора нагляден, но неоднозначно определяет результат операций над векторами. Необходимо отметить, что векторы, представляемые параллельными переносами, перемещением точек, направленными отрезками являются лишь изображения векторов, но не сами векторы в их общем понятии.
Существует еще один подход к определению понятия вектора, автором которого является Вейль. Этот подход составляет основу векторного изложения геометрии [5]. Вектор относится к числу первоначальных неопределяемых понятий. К ним же относится и понятие суммы векторов, умножение вектора на число, скалярное произведение векторов. Свойства арифметических операций над векторами автор описывает через систему аксиом. Такой подход к определению понятия вектора достаточно громоздкий. Кроме того, при таком подходе затруднено понятие результата выполнения арифметических действий над векторами. Тем не менее, этот подход обладает рядом преимуществ: при векторном изложении некоторые теоремы геометрии доказываются значительно проще, чем при традиционном изложении.
Итак, в математике существуют различные подходы к определению понятия вектора. Каждый из них имеет преимущества и недостатки. Однако никакой из них не может быть «перенесен» в школьный курс геометрии без должных оговорок.
Рассмотрим специфику изложения темы «Векторы» в различных школьных учебниках по геометрии. Прежде всего, обратимся к истории. Как предполагалось изучать векторы?
В России векторы в школьном курсе математики появились в начале 60-х годов XX века. Инициаторами их введения были В.Г. Болтянский и И.М. Яглом. В 1962 г., еще до выхода учебника [А] для школы, была выпущена книга для учителя [Б], которая была рассчитана на то, чтобы учителям было легче разобраться в понятии вектора, которое впервые появлялось в курсе геометрии средней школы. В данном пособии [Б] авторы сразу отмечают, что существуют различные подходы к определению понятия вектор. Один из подходов характеризуется тем, что «…вектор с элементарно-геометрической точки зрения есть объект, характеризуемый направлением (т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной. Однако такое определение слишком общее…»[Б, с.7]. Определение вектора как параллельного переноса, несмотря на его математическую точность, авторами считается неудовлетворительным, так как «представление о векторе как о геометрическом преобразовании кажется нам недостаточно наглядным и далеким от физических представлений о векторных величинах»[17, с.7]. В результате авторы предлагают принять как основное следующее определение «вектором называется семейство всех параллельных между собой, одинаково направленных и имеющих одинаковую длину отрезков» [17, с.7]. Но использование данного определения в курсе средней школы считается ими «нецелесообразным», и предлагается определять вектор как направленный отрезок. Авторы уточняют, что учитель должен понимать разницу между вектором как семейством направленных отрезков и одним направленным отрезком. В 1963 году вышел учебник для школы В.Г. Болтянского и И.М. Яглома [А], где векторы определялись как направленные отрезки. К учебнику прилагалась книга для учителя [В], в ней авторы предупреждают, что трактовка вектора как направленного отрезка является чересчур упрощенной и требует при изложении материала постоянных оговорок, связанных с понятием «равенство» векторов, т.е. следует различать «равные» в смысле совпадающие векторы и «равные» в смысле конгруэнтные векторы. Данный учебник просуществовал в школе только два года, и авторы не успели внести какие-либо уточнения в определение понятия вектора. Итак, рассмотрев возможные варианты определения понятия вектора, авторы посчитали нецелесообразным определять данное понятие ни как параллельный перенос, ни как семейство (класс) направленных отрезков, а остановились на упрощенном определении, хотя и понимали, что оно ведет к постоянным оговоркам. К сожалению, В.Г. Болтянский и И.М. Яглом, уточняя, о каких именно «постоянных оговорках» идет речь, не говорят, как реализовать их предупреждение в практике обучения. В эти же годы начинается реформирование математического образования школы с доминирующим влиянием теоретико-множественного подхода к введению понятий и их изучению, инициатором и руководителем которого был A.H. Колмогоров. В частности, слово «равно» было синонимом слова «совпадают». Например, два различных треугольника с тремя соответственно равными сторонами предлагалось считать не равными, а конгруэнтными. А вот два равных вектора, отложенные от различных точек, равны, а не конгруэнтны. В учебном пособии [10] под редакцией А.Н. Колмогорова вектор определялся как параллельный перенос плоскости: «Параллельным переносом (вектором) называется отображение плоскости на себя, при котором все точки плоскости изображаются в одном и том же направлении на одно и то же расстояние». Это определение обладает тем важным преимуществом, что параллельный перенос представляет свободный вектор, и потому все векторные операции с ним определяются как однозначные. При таком определении вектора векторное исчисление может быть изложено без противоречий и смешения понятий. Однако в задачах, предлагаемых в учебнике, фигурируют направленные отрезки, а не переносы плоскости или пространства. В следующем пособии для 9-10 классов [11] (под редакцией З.А. Скопеца), вектор определяется уже как параллельный перенос пространства. «Параллельным переносом, определяемым парой (А, В) несовпадающих точек, называется преобразование пространства, при котором каждая точка М отображается на такую точку М1, что луч ММ1 сонаправлен с лучом АВ, расстояние ММ1 равно расстоянию АВ». Таким образом, вектор вводился как множество пар точек, задающих один и тот же перенос. В последнем издании учебника под редакцией А.Н. Колмогорова явно вводится понятие свободного вектора, и перенос привлекается только как его изображение. В результате изложение оказалось существенно лучше, чем в других учебниках для 6-8 классов того времени, без путаницы и ошибок. В перестройке школьного курса геометрии, происходящей в середине 80-х годов ХХ века, одним из центральных моментов оказалось коренное изменение понятия о векторе. Вектор, определяемый как параллельный перенос плоскости или пространства, был заменен направленным отрезком: на место отображения плоскости или пространства на себя поставлена фигура с «отмеченной» точкой (один конец отрезка «отмечен» как начало). Так, в учебнике А.В. Погорелова [21] изложение темы начинается следующим образом: «Вектором мы будем называть направленный отрезок. Направление вектора определяется указанием его начала и конца… Для обозначения векторов будем пользоваться строчными латинскими буквами а, b, c,… Можно так же обозначить вектор указанием его начала и конца. При этом начало вектора ставится на первое место» [21, c. 117]. В задачном материале рассматриваются следующие виды заданий:
-доказательство равенства векторов;
-доказательство перпендикулярности векторов;
-вычисление угла между векторами.
Основным теоретическим базисом при решении этих задач являются определения равенства векторов и скалярного произведения векторов; аппаратом решения заданий становятся формальные действия с координатами, т.е. геометрическое приложение векторов опускается.
В учебнике Л.С. Атанасяна и др. [8] вектор так же определяется как направленный отрезок, но изложение строится иначе, чем в учебнике А.В. Погорелова. В параграфе «Понятие вектора» п.1 начинается так: «Многие физические величины, например сила, перемещение материальной точки, скорость, характеризуются не только своим числовым значением, но и направлением в пространстве. Такие физические величины называются векторными величинами или векторами». Далее, после приведения примера изображения силы в физике, говорится: «Отвлекаясь от конкретных свойств физических векторных величин, мы приходим к геометрическому понятию вектора… Определение. Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется направленным отрезком или вектором. Недостаток этого изложения состоит в том, что дается два понятия вектора без должных оговорок. Однако авторы не могут оставить определение вектора как направленного отрезка. В конце §1 они делают важное замечание.«Замечание. Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой. Иногда про такие векторы говорят, что это один и тот же вектор, но отложенный от разных точек». По сути, здесь говорится о свободном векторе. Но само определение этого понятия не вводится. Задачный материал в учебнике Л.С. Атанасяна направлен на осознание, осмысление вводимых дидактических единиц. Он служит своеобразным пропедевтическим курсом для решения задач векторным методом. Содержательных задач в главе немного, но они разнотипны. Ключевые из них решены в учебнике.
В учебнике И.Ф. Шарыгина [31] вектор так же определяется через направленный отрезок: «Рассмотрим на плоскости две точки А и В. Обозначим через вектор АВ, понимая под этим направленный отрезок АВ, т.е. отрезок, у которого точка А является началом, а точка В концом».
Так же, как и А.В. Погорелов, И.Ф. Шарыгин вводит координаты вектора, и на их основе определяет операции с векторами.В связи с этим, и основным способом решения задач по учебному пособию И.Ф. Шарыгина становится выражение векторов через координаты, произведение с ними арифметических действий. Предлагаются задания на отработку понятия скалярного произведения векторов, следующие виды метрических задач:
-найти угол между прямой и плоскостью;
-найти угол между плоскостями;
доказательство того, что сумма косинусов двугранных углов любого тетраэдра не больше двух;
доказательство того, что все три угла между биссектрисами плоских углов трехгранного угла одновременно либо острые, либо прямые, либо тупые.
В учебнике А.Д. Александорова [2] понятие вектора вводится аналогично подходу, изложенному у Л.С. Атанасяна: «Величины, которые характеризуются не только численным значением, но и направлением, называются векторными величинами или векторами. Численное значение вектора называется его модулем». Далее автор выделяет пункт «Направленные отрезки». «…Если тело переместилось из точки А в точку В, то это перемещение естественно изобразить отрезком, направленным из точки А в точку В…У направленного отрезка указан порядок концов.» После этого автор обращает внимание учащихся на то, что направленный отрезок – лишь изображение вектора, а не сам вектор в общем понимании. Однако, в отличие от остальных авторов, А.Д. Александров не вводит понятие компланарных векторов. Он определяет следующие способы разложения вектора: по прямой и плоскости, по трем прямым. Предлагает для решения задачи на отработку этих умений и приводит задачи на геометрическую интерпретацию векторов:
-отложить вектор, равный сумме двух или более данных;
-отложить вектор, равный разности двух векторов;
-доказать векторные равенства, пользуясь изображением параллелепипеда.
Анализируя представленные подходы, можно сделать вывод, что все авторы в той или иной степени стремятся дать определение свободного вектора. Это делается у различных авторов по-разному.
Обучение решению задач как психологическая и методическая проблема
Перед выявлением специфики векторного метода, разработки конкретной методики обучения школьников решению математических задач, необходимо проанализировать само понятие задач, их роль и место в обучении математике. Задачи играют огромную роль в жизни человека. Задачи, которые ставит перед собой человек, и задачи, которые ставят перед ним другие люди и обстоятельства жизни, направляют всю его деятельность, всю его жизнь. Поэтому проблемы, связанные с этим понятием, занимают значительное место во многих науках. Например, в психологии исследуются процессы решения задач и особенности этих процессов при решении отдельных их видов. Предметом исследования дидактики и частных методик являются вопросы использования решений задач в обучении. В обучении математике задачи играют большую роль. Эта роль определяется, с одной стороны, тем, что конечные цели этого обучения сводятся к овладению учащимися методами решения определенной системы математических задач. С другой стороны, она определяется и тем, что полноценное достижение целей обучения возможно лишь с помощью решения учащимися системы учебных и математических задач, которые являются важнейшим средством формирования у школьников системы основных математических знаний и способов деятельности. Кроме того, «от эффективности использования задач в обучении математике во многом зависит не только качество обучения, воспитания и развития учащихся средней школы, но и степень их практической подготовленности к последующей за обучением деятельности в любой сфере производства, народного хозяйства, культуры, личных и общественных взаимоотношений» [24, с.5]. В различных областях знания (психология, педагогика, математика, методика математики) проблему содержания понятия «задача» исследовали Г.А. Балл, Ю.М. Калягин, Л.М. Фридман, В.И. Крупич, А.Ф. Эсаулов, Н.А. Менчинская и многие другие. Каждый из них дает свою точку зрения на рассматриваемую проблему.В методике преподавания математики под задачей принято понимать «задание, которое должен выполнить субъект, или вопрос, на который он должен найти ответ, опираясь на указанные условия и все вытекающие из них следствия» [28, с. 158]. В свою очередь, по мнению психологов, процесс решения задач тесно взаимосвязан с процессом мышления. Многие исследования показывают, что именно в ходе решения задач самым естественным образом можно формировать у школьников элементы творческого, логического и алгоритмического мышления.
Необходимо отметить, что умственное развитие учащихся является одной из основных задач обучения математике. Многие авторы связывают его именно с развитием математического мышления. В соответствии с этим возникает вопрос, что представляет собой математическое мышление, каковы его специфические черты. «Чаще всего математическое мышление рассматривается в соответствии со спецификой математики, которая состоит в особенностях ее абстракций (Ж. Адамар, Б.В. Гнеденко, А.Н. Колмогоров, А.И. Маркушевичи др.)» [28, c.82]. В их работах сущность понятия математического мышления ассоциируется с понятием математических способностей. Выделяется огромное число черт математических способностей: сила абстрагирования, оперирование абстракциями, геометрическая интуиция, четкое логическое рассуждение, гибкость мышления, математическая интуиция, анализирование, синтез, стремление к рациональности решения, лаконизм, оригинальность мышления и др. Все эти способности можно развивать в процессе решения задач. Развитие творческих мыслительных способностей и познавательной самостоятельности учащихся невозможно вне проблемных ситуаций. Необходимо внедрение проблемно-развивающего обучения. Задачи при таком обучении служат основным средством активизации знаний и способов действий. Они используются для раскрытия содержания понятий, теорем, способов умственной деятельности ученика, а также для формирования умений и навыков. В решение таких задач важно включать этапы анализа задачи и обсуждения решения. В процессе анализа задачи должны устанавливаться предметная область задачи, все ее элементы, характер каждого элемента (постоянный или переменный, известный или неизвестный и т.д.). Также необходимо вычленение из задачи всех отношений, которыми связаны элементы предметной области. Это позволит выбрать правильный подход к решению задачи. В процессе анализа проделанного решения выявляются преимущества и недостатки решения, проводятся поиски лучшего решения, устанавливаются и закрепляются в памяти учащихся те приемы, которые были использованы в данном решении, выделяются условия возможности применения этих приемов. Все это будет в наилучшей степени способствовать превращению решения задач в могучее обучающее средство.
В настоящее время решение математических задач используется для разных функций. Л.М. Фридман под функцией решения задачи понимает «проектируемые учителем изменения в деятельности и психике учащихся, которые должны произойти в результате решения ими этих задач» [30, с.151]. Одной из основных функций в обучении математике он считает функцию формирования и развития у учащихся общих умений решений любых математических (в том числе и прикладных) задач. Общее умение по решению задач следует отличать от частных умений решения задач определенного вида. Частные умения формируются на основе усвоения учащимися теоретических знаний, пользуясь которыми учащиеся производят операции и действия, входящие целостным элементом в формируемое умение. Формирование общих умений решения математических задач осуществляется таким образом, что учащиеся не получают никаких особых знаний, лежащих в основе этих умений. Поэтому представления учащихся о задачах, их элементах и структуре, о сущности и механизмах их решения является весьма смутными, а зачастую просто неверными. Притом эти представления по мере перехода в старшие классы отнюдь не улучшаются, т.к. они формируются часто стихийно, в результате случайной информации и редкой рефлексии на свои действия в процессе решения многочисленных задач. Это происходит потому, что действующие программы по математике не предусматривают изучения каких-либо теоретических основ о задачах и их решении. В то же время, теоретические знания о задачах и их решении нужны учащимся для того, чтобы они могли производить решение разнообразных задач сознательно и целенаправленно, а не только лишь на основе подражания по аналогии с ранее решенными задачами. В отличие от Л.М. Фридмана Ю.М. Колягин к главным функциям задач относит воспитывающую и развивающую функции. К числу важнейших воспитывающих функций задач он относит «формирование у школьников диалектико-материалистического мировоззрения, познавательного интереса и творческих задатков, воспитание чувства патриотизма, эстетическое воспитание и т.д.» [24, с.11]. В частности, автор поясняет, что в процессе применения математики к решению любой практической задачи, можно показать школьникам, что математика, отражая явления реальной действительности, является мощным средством ее познания. Предложение учащимся задачи с избыточной или неполной информацией воспитывает у них готовность к практической деятельности. Рассмотрение изящного решения той или иной математической задачи способствует эстетическому воспитанию школьников. Применение в обучении математике задач с воспитывающими функциями способствует, по мнению Ю.М. Колягина, формированию у школьников интереса к решению задач, что в свою очередь является эффективным средством приобщения школьников к учебной математической деятельности творческого характера. В методической литературе встречаются разделения задач по различным основаниям.
Л.М. Фридман предлагает разделить все задачи на два вида:
1) задачи на усвоение учебного материала (учебные задания), которые следует решать непосредственно в процессе изучения учебного материала, и при этом все ученики решают одни и те же задачи. Число таких задач невелико.
2) задачи на применение изученного учебного материала, которые даются учащимся спустя некоторое время. При этом выдается список всех рекомендуемых задач, которые они могут решать.
К.И. Нешков и А.Д. Семушин выделяют следующие типы задач:
1) задачи с дидактическими функциями (предназначены для облегчения усвоения уже изученных теоретических сведений);
2) задачи с познавательными функциями (в процессе решения которых углубляются знания учащихся по отдельным разделам математики, школьники знакомятся с важнейшими теоретическими сведениями, методами решения задач);
3) задачи с развивающими функциями (задачи, содержание которых расширяет основной курс математики, способствует повышению уровня сложности нескольких изученных ранее вопросов).
Опыт показывает, что наиболее приемлемым является выделение следующих видов задач:
1) по характеру требования – на вычисление или нахождение; на доказательство или объяснение; на построение или преобразование;
2) по отношению к способам решения – стандартные и нестандартные;
3) по характеру объектов – математические и реальные (или с практически содержанием).
Отнесение задачи к группе задач с той или иной функцией не является классификацией, поскольку одна и та же задача для различных субъектов и в разных ситуациях может нести разные функции. Однако выделение функций задач имеет смысл, т.к. учитывая цели обучения, важно, чтобы в системе задач по конкретной теме присутствовали задачи с каждой из названных функций. Характерная для настоящего времени тенденция к повышению роли проблемного обучения свидетельствует о том, что решение задач правомерно занимает все более ведущее место в обучении математике, нередко определяя его формы и методы, в которых основной акцент ставится на самостоятельное и творческое усвоение школьниками учебного материала, на формирование их математического развития, целостного развития личности и развития всех психических процессов (воли, эмоций, памяти, воображения, представлений и т.д.). При обучении учащихся решению задач необходимо изучать с ними сами задачи, их структуру и особенности, характер используемых общих методов решения, их структуру деятельности по решению задач. При этом главными объектами усвоения следует считать общие схемы деятельности по решению задач, общие методы и способы моделирования задач. Решение же отдельных задач должно быть лишь средством для такого обучения.
Методика обучения векторному методу решения задач в геометрии
Теоретической основой преподавания школьного курса математики и, в частности, темы «Векторы» является ассоциативная теория усвоения. Первые постулаты ассоциативной психологии были сформулированы Аристотелем, выдвинувшим идею о том, что образы, возникающие без видимой внешней причины, являются продуктом ассоциаций. Закрепление ассоциаций обусловлено частотой их повторения в опыте. При этом ассоциация рассматривается как связь между психическими явлениями, при которой восприятие, представление одного из них влечет за собой появление другого. В XVIII веке английским врачом Давидом Гартли была сформулирована идея о том, что формирование соответствующих ассоциаций может существенно улучшить качество запоминания, а значит и обучения. Данная идея легла в основу психологического направления, которое получило название ассоцианизм или ассоциативная психология. Уже в XIX веке ассоцианизм подвергся резкой критике и почти полностью прекратил свое существование как научное направление. Но в XX веке он получил развитие, в трудах И.М. Сеченова и И.П. Павлова и был принят в качестве официальной психологической теории усвоения в СССР. Позиции ассоциативной теории усвоения как теоретической основы обучения сохраняются в настоящее время, в том числе и при изучении темы «Векторы». Механизм усвоения в рамках данной психологической теории понимается так: задача учителя заключается в том, чтобы обеспечить восприятие, которое понимается как целостное отражение предметов, ситуаций и событий, возникающее при непосредственном воздействии физических раздражителей на рецепторные поверхности органов чувств. Таким образом, считается, что если ученики получили достаточно много примеров и контрпримеров, то у них должны сформироваться правильные представления об объектах. На основе сформировавшихся представлений, организовав вычленение общих свойств рассматриваемых объектов и обозначив вычлененные свойства словами, мы, в соответствии с рассматриваемой теорией, формируем понятия. То есть механизм усвоения понимается следующим образом. Вначале формируются восприятия, на их основе – представления, а уже затем понятия. По данному сценарию: сначала зрительное восприятие, потом представления, описанные словами – понятия, происходит формирование понятия вектор. Действительно, учитель показывает ученикам «отрезки со стрелками», обеспечивая тем самым восприятие того, что впоследствии будет названо вектором. Рассмотрение нескольких «зрительных образов» должно обеспечить формирование представления о векторе. Наконец, «отрезки со стрелками» обозначают словами: направленный отрезок или вектор, обеспечивая тем самым, в соответствии с ассоциативной теорией усвоения, формирование понятия вектор. Но при введении понятия вектор нецелесообразно опираться на ассоциативную теорию, потому что, это неизбежно приводит к устойчивой ошибке, которая заключается в том, что изображение направленного отрезка воспринимается как сам направленный отрезок, т.е. в понятие вектора включается множество точек, составляющих на рисунке этот направленный отрезок. Отметим, что когда ассоциативная теория усвоения только появилась в школе, она была очень прогрессивной и позволила существенно увеличить эффективность обучения. Однако в настоящее время сделать обучение более эффективным может применение деятельностного подхода, разработанного психологами школы Л.С. Выготского А.Н.Леонтьевым и П.Я. Гальпериным. Проблемой методики обучения учащихся векторному методу занимались многие ученые-методисты: В.А. Гусев, Г.Л. Луканин, Г.И Саранцев, З.А. Скопец, Т.А. Иванова и другие. При обучении учащихся векторному и координатному методу В.А. Гусев, Ю.М. Колягин и Г.Л. Луканин дают следующие методические рекомендации [13, c.43]:
1) необходимо заинтересовать учащихся, показав им эффективность использования векторного метода на специально подобранных задачах;
2) следует обучить учащихся некоторым эвристикам (системе определенных правил, помогающих найти ключ к решению задачи), которые помогут создать у них навык в его применении;
3) обучать векторному методу стоит на достаточно простых по геометрическому содержанию задачах, чтобы не отвлекать внимание учащихся на трудности чисто геометрического содержания;
4) следует указать учащимся, что векторный и координатный метод не является универсальным, к решению некоторых задач он может быть неприменим или малоэффективен.
После изучения векторного и координатного метода учащиеся должны усвоить типы задач, решаемых с помощью него; полезно также в конце изучения темы выделить преимущества и недостатки векторного и координатного метода. Подобная организация работы будет способствовать более эффективному усвоению учащимися векторного и координатного метода.
Методика формирования умений, составляющих суть векторного метода решения задач в неполной средней школе
Задачи, решаемые векторным методом, можно разделить на следующие виды: афинные задачи без векторных данных (содержательные геометрические задачи), задачи на доказательство и вычисления, для которых требуется рассматривать векторно-параметрическое задание прямой и плоскости и задачи, в содержание которых уже включены векторы.
Учащиеся испытывают большие затруднения при выборе метода, с помощью которого они будут решать ту или иную задачу. Эти затруднения вызваны прежде всего тем, что в методической литературе и в учебных пособиях недостаточно раскрыта математическая сторона применения векторов к решению геометрических задач, не устанавливаются, хотя бы ориентировочно, основные задачи (теоремы), которые широко используются при решении более сложных задач. Рассмотрим задачи трех типов, которые целесообразно решать с помощью векторов учащимся 9 классов.
1) задачи, связанные с доказательством параллельности прямых и отрезков.
2) задачи, в которых доказывается, что некоторая точка делит отрезок в заданном отношении.
3) задачи на доказательство принадлежности трех и более точек одной прямой.
Эти виды задач наиболее многочисленны и, в силу простого перевода на векторный язык, могут служить образцами для учащихся. Кроме того, навык, приобретенный при решении этих задач, можно переносить на более сложные (где данные задачи могут встречаться в виде части задач). В задачах такого рода традиционные методы решения связаны обычно со значительными трудностями: или с необходимостью дополнительных геометрических построений, или с довольно громоздкими тригонометрическими преобразованиями. Решение геометрических задач векторным и координатным методом позволяет отработать у учащихся навыки перевода условия с геометрического языка на векторный и формировать навыки, необходимые для перевода с векторного языка на геометрический. Для решения задач учащиеся должны владеть следующими умениями, которые и являются компонентами векторного и координатного метода:
-
Переводить геометрический язык на векторный и наоборот;
-
Выполнять операции над векторами, уметь преобразовывать векторные выражения;
-
Знать наиболее важные векторные соотношения и их особенности;
-
Уметь выразить один вектор через некоторые другие;
-
Переходить от соотношения между векторами к соотношению между их длинами и наоборот.
Для овладения умением переходить от геометрического языка к векторному и обратно необходимо знать, как то или иное векторное соотношение выражается на геометрическом языке. Векторные соотношения удобно представить в таблице:
|
№ |
Рисунок |
Что необходимо доказать или определить на геом. языке. |
Что достаточно определить или доказать на векторном языке. |
|
1 |
Рис.1 |
|
|
|
2 |
Рис.2 |
|
|
|
3 |
Рис.3 |
|
|
|
4 |
Рис.4 |
|
|
|
5 |
Рис.5 |
|
|
|
6 |
Рис.6 |
|
|
|
7 |
Рис.7 |
|
|
|
8 |
Рис.8 |
|
|
|
9 |
Рис.9 |
|
|
1) Задачи, связанные с доказательством параллельности прямых и отрезков.
При решении этих задач наиболее часто используется признак коллинеарности двух векторов (соотн. 1) и единственность разложения вектора по двум неколлинеарным векторам (соотн. 7).
Задача. Если в выпуклом четырехугольнике, две противоположные стороны не параллельны, длина отрезка, соединяющего середины этих сторон, равна полусумме длин двух других сторон четырехугольника, то этот четырехугольник – трапеция.
Дано:
– четырехугольник
– середина
Рис.10
– середина
Доказать: – трапеция.
Анализ. Для решения задачи достаточно доказать, что На векторном языке это означает, что
Решение:
Выразим вектор двумя различными способами:
(1)
(2)
Сложим почленно (1) и (2).
(3)
(4)
Из условия следует
(5)
Сопоставляя (4) и (5), получаем:
Это возможно тогда и только тогда, когда
Задачи для самостоятельного решения:
Задача 1. Доказать, что если в четырехугольнике диагонали, пересекаясь, делятся пополам, то этот четырехугольник параллелограмм.
Задача 2. Доказать теорему о средней линии треугольника.
Задача 3.Доказать, что средняя линия трапеции параллельна основаниям и длина ее равна полусумме длин оснований.
2) Задачи на доказательство деления некоторого отрезка в заданном отношении или на нахождение отношения, в котором точка делит отрезок.
Решение задач этого типа базируется на следующей теореме.
Для того чтобы точка делила отрезок
так, что
необходимо и достаточно, чтобы для произвольной точки
выполнялось равенство:
Задача. На стороне АС треугольника АВС взята точка М так, что АМ=1/4 АС, а на продолжении стороны ВС такая точка N, что BN=BC. В каком отношении точка Р пересечения АВ и MN делит каждый из этих отрезков?
Дано:
– треугольник
Рис.11
Найти: МР:PN, АР:РВ
Решение задач повышенной сложности такого типа показала, что работу нужно вести в следующем направлении: постараться разложить один из векторов (чаще всего конец такого вектора – точка, которая делит данный отрезок в заданном отношении) по двум основным векторам (они неколлинеарны) двумя различными способами. Используя единственность разложения вектора по двум неколлинеарным векторам, установить зависимость между коэффициентами в разложении вектора, что потом дает возможность найти искомое соотношение.
Решение:
1. Пусть и
2. Основные векторы
3. Разложим вектор по основным двумя различными способами
а)
Итак,
(1)
б) (соотношение (2)).
Но
(2)
4. Учитывая единственность разложения вектора по двум неколлинеарным векторам, из равенств (1) и (2) получаем
Следовательно,
Задачи для самостоятельного решения.
Задача 1.
Дано:
Доказать: – средняя линия
Задача 2. Докажите, что медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины.
Задача 3. В треугольнике биссектриса
делит сторону в отношении
В каком отношении медиана
делит эту биссектрису?
3) Задачи на доказательство или использование принадлежности трех точек одной прямой.
При решении задач на доказательство того, что три точки А, В, С принадлежат одной прямой, обычно доказывается коллинеарность векторов, например и
или используется следующая теорема: Для того, чтобы точка
принадлежала прямой, необходимо и достаточно, чтобы для любой точки
выполнялось равенство:
где
Задача.
Дано:
– трапеция
– середина
– середина
Рис.12
Доказать:
Анализ: Для того, чтобы доказать, что достаточно доказать, что
и
коллинеарны. Для этого необходимо разложить векторы
и
по основным.
Решение:
1. Основные векторы:
2. По векторной формуле середины отрезка
(1)
3. Из треугольников и
Значит,
то есть
Сопоставляя (1) и (2), получаем
Задачи для самостоятельного решения.
Задача 1. В пространстве расположены отрезки и
Точка
есть середина отрезка
точка
– середина
Докажите, что середины отрезков
расположены на одной прямой.
Задача 2.На стороне треугольника
взята точка
Доказать, что центры тяжестей
и
лежат на одной прямой.
Методика обучения векторному и координатному методу решения содержательных геометрических задач
Векторный метод является одним из аналитических методов решения геометрических задач и доказательства теорем. Сущность его состоит в том, что условие и требование задачи записываются в векторной форме, а ее решение состоит в переходе от условия к требованию на основе законов векторной алгебры. Векторный метод относится к методам алгоритмического типа, т.к. можно выделить общую схему решения геометрических задач векторным методом. Этот план включает следующие пункты:
1.Прочитав и проанализировав условия, выполнить рисунок
2.Согласно условию и требованию задачи, ввести в рассмотрение векторы
3.Выразить через них векторы, необходимые для решения задачи
4.«Перевести» условие и требование задачи на язык векторов
5.С помощью преобразований над полученными векторными соотношениями перейти от условия задачи к требованию.
6.Полученному векторному соотношению дать геометрическое истолкование
Поэтому, при организации урока по обучению учащихся векторному методу необходимо учитывать технологию работы с алгоритмом, разработанную в теории и методике обучения математики. Имеется 3 различных возможностей построения данного урока:
-
Повторить с учащимися умения, входящие в состав векторного метода; затем сообщить им тему урока, сформулировать в готовом виде схему решения задач векторным методом, и далее отрабатывать этот алгоритм на примере решения ряда задач.
-
Вспомнить с учащимися алгоритм решения задач векторным методом из планиметрии, по аналогии найти план решения стереометрических задач векторным методом.
-
В результате совместного поиска учителем и учащимися решения стереометрической содержательной задачи выделить план решения этой задачи векторным методом; обобщить алгоритм для всех задач.
Организация урока по третьему подходу соответствует основному принципу деятельностного подхода: включение ученика в целесообразно организованную деятельность. Урок должен включать в себя три основных блока: мотивационно-ориентировочный, оперативно-познавательный и рефлексивно-оценочный. На этапе актуализации необходимо повторить с учащимися умения, необходимые для решения задач векторным методом (перевод геометрических свойств фигур на векторный язык и обратно; преобразование векторных выражений; представление векторов через другие).
К примеру, урок по теме «Применение векторов к решению задач» можно провести в такой форме:
Тип урока: урок изучения нового
Учебные задачи урока:
1.«Открыть» совместно с учащимися план решения задач векторным методом.
2.Выявить совместно с учащимися типы аффинных задач, решаемых векторным методом.
Подготовка к уроку: Учитель на урок приносит карточки с заданиями для каждого ученика, плакат с записанной схемой решения геометрических задач векторным методом. Таблица векторных равенств и словарь перевода уже вывешены в классе.
Ход урока
1) Мотивационно – ориентировочный этап. Форма проведения: самостоятельная работа на индивидуальных карточках, которыми ученики после выполнения задания обмениваются. Осуществляется взаимопроверка. Далее предлагается решить задачу: Дан тетраэдр DABC. Точки К, М – середины АВ и CD. Докажите, что середины отрезков КС, KD, MA, MB являются вершинами некоторого параллелограмма. На обдумывание дается 2 минуты.
Вопрос: Какими способами вы пробовали решить задачу? Что у вас получилось? (Ученики отвечают на вопрос, аргументируя возникшие затруднения)
Вопрос: Какую общую тему мы изучаем на протяжении последних уроков? (Векторы в пространстве). Какой метод, связанный с применением векторов, мы рассматривали в планиметрии? (Векторный). Как вы думаете, можно ли применить векторный метод, чтобы решить стереометрическую задачу? В пространстве, как и на плоскости, при решении задач может быть реализован векторный метод. Итак, сформулируйте тему нашего урока. (Векторный метод решения стереометрических задач). Какова в связи с темой цель нашего урока? (Открыть способ решения задач векторным методом).
Тема урока записывается на доске и в тетрадях.
2) Операционно-познавательный этап.
Вернемся к решению сформулированной задачи. Что значит на векторном языке: доказать, что A1A2A3A4 – параллелограмм? Чем вы воспользовались при ответе на данный вопрос? Что означает второе условие на геометрическом языке? Выполняется ли это условие? Почему? Таким образом, что нам достаточно проверить? Итак, мы должны выразить векторы. Как это можно сделать?
Необходимо ввести в рассмотрение векторы, но не произвольно, а учитывая условие задачи. Известно, что точка М – середина DC. Как этот факт записать с помощью векторов? Начинается оформление задачи.
Учитель, привлекая учеников, проводит решение у доски, показывает образец оформления, учащиеся в тетрадях по плану:
1. Ввели векторы.
2. «Перевели» условие и требование задачи на векторный язык.
3. Выразили векторы, необходимые для решения.
4.Перешли от условия к требованию задачи.
5. «Перевели» векторное выражение на геометрический язык
Далее анализируется решение задачи и составляется план решения задач векторным методом: С чего мы начали решение данной задачи? Как мы это сделали? (Ввели в рассмотрение векторы). После проведенного анализа учитель вывешивает заранее подготовленную схему: Прочитав и проанализировав условия, выполнить рисунок. Согласно условию и требованию задачи, ввести в рассмотрение векторы. Выразить через них векторы, необходимые для решения задачи. «Перевести» условие и требование задачи на язык векторов. С помощью преобразований над полученными векторными соотношениями прийти от условия задачи к требованию. Полученному векторному соотношению дать геометрическое истолкование.
Задание: Учитывая, что A1A2A3A4 – параллелограмм, составьте на основе этой задачи новые, изменив требование задачи. Сделайте вывод, какие задачи мы можем попытаться решить, используя векторный метод? Рассмотрим еще один вид задач, которые можно решить с помощью векторного метода. Докажите, что если точки пересечения медиан треугольников АВС и А1В1С1 совпадают, то прямые АА1, ВВ1, СС1 параллельны некоторой плоскости. С чего начнем решение этой задачи? (с построения чертежа). Доказательство факта, что данная фигура – параллелограмм, доказательство параллельности прямых, доказательство равенства двух отрезков.
Вопрос: Какой вид задач мы еще смогли решить, используя векторный метод? Что нам для этого потребовалось установить? Какой теоретический факт лежал в основе доказательства? Какие виды задач можно ещё решить, используя критерий компланарности векторов? Таким образом, мы выделили ещё два типа задач, решаемых векторным методом: установление принадлежности точек прямой и нахождение отношений длин отрезков.
3) Рефлексивно-оценочный этап. Итак, какова была цель нашего урока? Каковы этапы решения задач мы с вами выделили? (Найти, в каком отношении делит отрезок точка, принадлежащая этому отрезку -Найти способ решения задач векторным методом 1. Прочитав и проанализировав условия, выполнить рисунок 2. Согласно условию и требованию задачи, ввести в рассмотрение векторы 3. Выразить через них векторы, необходимые для решения задачи 4. «Перевести» условие и требование задачи на язык векторов 5. С помощью преобразований над полученными векторными соотношениями прийти от условия задачи к требованию. 6. Полученному векторному соотношению дать геометрическое истолкование) Чем вы можете воспользоваться при решении задачи на этапах 2, 3, 5? А чем на этапах 4 и 6? Заметим, что выделенная нами схема является примерной. В зависимости от содержания задания часть из этих этапов может быть проведена «мысленно», «перевод» может осуществляться не сразу, а постепенно по ходу решения и т.д. Какие типы задач можно попытаться решить, используя векторы? Какие теоремы используются в решении данных задач? Как вы думаете, чем мы с вами будем заниматься на следующих уроках? Дается ДЗ.
Описание элективного курса «Решение задач повышенной сложности векторным и координатным способом»
Данный элективный курс представлен в виде практикума, который позволит, расширить и систематизировать знания учащихся в использовании решения стереометрических задач. Не секрет, что многие старшеклассники при решении таких задач сталкиваются с трудностями, связанными с построением чертежа. При выполнении ЕГЭ по математике многие выпускники либо не справляются с решением задания С2, либо вообще не приступают к его решению, так как не умеют выделять в составе пространственных фигур объекты на плоскости. Программа курса предусматривает изучение координатного метода для решения задач различного уровня сложности. Он позволяет с помощью формул и введения координатного пространства решать различные стереометрические задачи. Этот метод упрощает работу, связанную с чертежом, тем самым облегчает решение задачи.
Цели курса:
-
Расширение и углубление знаний учащихся о методах и приемах решения стереометрических задач.
-
Развитие интереса к предмету и возможности овладения им с точки зрения дальнейшей перспективы применения полученных знаний в своей будущей профессии.
-
Развитие умений самостоятельно приобретать знания, дать возможность ученикам проявить себя и добиться успеха.
-
Подготовка к ЕГЭ – выполнение заданий уровня С2.
Задачи курса:
-
Развивать пространственные представления и воображения учащихся;
-
Систематизировать теоретические знания учащихся по стереометрии;
-
Познакомить учащихся с координатным методом решения стереометрических задач и развивать навыки использования его.
-
Познакомить учеников с разными типами геометрических задач, в том числе повышенной сложности, с особенностями методики и способами их решения.
-
Готовить выпускников к успешной сдаче ЕГЭ и конкурсных экзаменов в вузы.
Программа данного элективного курса содержит лекционные занятия, уроки – практикумы, дидактические материалы, темы творческих работ. На уроках-практикумах старшеклассники решают большое количество различных задач, в том числе и из ЕГЭ, развивая навыки работы по нахождению углов и расстояний в пространстве. Работа над проектами дает возможность ученикам совершать пусть небольшие, но свои открытия и окрыляет их для следующих побед. Содержание материала, уровневая индивидуализация учебной и дифференциация обучающей деятельности на фоне благоприятного психологического климата помогут ученику сформировать учебные умения и навыки, повысить его образовательный уровень, что связано с дальнейшим успешным самообразованием и профессиональным самоопределением
Тематическое планирование курса
|
№ урока |
Тема. Содержание. |
Кол-во часов |
Виды деятельности учащихся |
|
|
1. |
Декартовы координаты в пространстве. Нахождение координат точек и длин векторов в пространстве. |
1 |
Составление алгоритма действия. Практическая работа. |
|
|
2 |
Составление матрицы и нахождение определителей. |
1 |
Составление алгоритма действия. Работа в группах. |
|
|
3 |
Составление матрицы и нахождение определителей. |
1 |
Практическая работа. Работа в группах. |
|
|
4 |
Составление уравнения плоскости по координатам точек в пространстве. |
1 |
Составление алгоритма действия. Практическая работа |
|
|
5 |
Векторы нормали. Нахождение их координат. |
1 |
Практикум по решению задач Работа в парах, четверках. |
|
|
6 |
Вычисление угла между векторами в пространстве. |
1 |
Практикум по решению задач |
|
|
7 |
Решение задач на нахождение угла между прямыми в многогранниках. |
1 |
Составление алгоритма действия. |
|
|
8 |
Решение задач на нахождение угла между прямыми |
1 |
Презентация по теме. Практикум по решению задач. |
|
|
9 |
Формула нахождения угла между прямой и плоскостью в пространстве. |
1 |
Составление алгоритма действия. Практическая работа |
|
|
10 |
Нахождение угла между прямой и плоскостью в пространстве. |
1 |
Презентация по теме. Практикум по решению задач. |
|
|
11 |
Нахождение угла между плоскостями в пространстве. |
1 |
Работа с демонстрационным материалом. Решение задач. |
|
|
12 |
Нахождение расстояния от точки до плоскости, находящейся в многогранниках. |
1 |
Составление алгоритма действия. Практикум по решению задач. |
|
|
13 |
Нахождение расстояния между скрещивающимися прямыми в многогранниках. |
1 |
Презентация по теме. Практикум по решению задач. |
|
|
14 |
Нахождение расстояния между плоскостями в пространстве. |
1 |
Практикум по решению задач. Работа в группах. |
|
|
15, 16 |
Защита проектов. |
2 |
Работа в группах. |
|
|
17 |
Контрольная работа |
1 |
Выполнение заданий контрольной работы. |
|
|
18 |
Итоговое занятие |
1 |
Работа в группах Защита решения задач, исследовательских работ. |
Содержание программы
Знакомство учащихся с целями и задачами курса. На первом занятии учащимся предлагается ряд задач повышенной сложности, решение которых потребует от них знания многих тем элективного курса. Класс делится на группы, каждая группа получает задачу. Защита задач проходит на последнем занятии. По желанию учащиеся могут приготовить реферат, проект, провести исследовательскую работу. Дидактический материал дается ученикам после изучения каждой темы.
Представленный курс содержит 10 основных тем
1. Декартовы координаты в пространстве. Нахождение координат точек и длин векторов в пространстве – 1ч.
Проводится этот урок сначала в форме лекции – повторение основных ключевых моментов: декартовы координаты в пространстве и понятия, связанные с ними (координаты вектора, длина вектора, расстояние между точками, середина отрезка, параллельный перенос). На этом уроке учитель знакомит учеников с планом, задачами и целями работы. Даются задачи, решение которых будет рассмотрено на последнем занятии, а также список литературы и электронных адресов информации по теме.
2 .Составление матрицы и нахождение определителей – 2ч.
Данный теоретический материал является частью высшей алгебры. На занятиях рассматриваются основные формулы и решаются задания по нахождению определителей.
3. Уравнение плоскости и векторы нормали – 2ч.
Эта тема является основой для решения задач по стереометрии координатным методом. Задачи, решаемые здесь, ставят вопросы, которые будут рассмотрены в следующих темах.
4. Нахождение угла между прямыми, прямой и плоскостью, плоскостями – 6ч.
На этих занятиях ребята не только используют изученные формулы для нахождения углов в многогранниках, но и готовятся к ЕГЭ, выполняя задания С2. Необходимо использовать презентации, т. к. они помогут в выборе координатного пространства и правильного нахождения координат точек.
5. Нахождение расстояния между точкой и плоскостью, между прямыми, плоскостями в пространстве – 3ч.
Немаловажное значение на этих уроках отводится нахождению расстояний от середины ребер, от вершин, от центра окружности, что значительно облегчит в дальнейшем решение более сложных задач. Благодаря работе с интерактивной доской и компьютером, ученики наглядно увидят расположение элементов фигур в пространстве.
6. Подведение итогов – 4ч.
Заключительные уроки содержат достаточное количество геометрических задач, часть из которых имеет сложность уровня С2.
После рассмотрения полного курса учащиеся должны иметь следующие результаты обучения:
а) уметь составлять уравнение плоскости;
б) уметь применять формулы для нахождения углов между прямыми, прямой и плоскостью, плоскостями;
в) уметь находить расстояния между прямыми, между прямой и плоскостью в многогранниках;
г) уметь решать задачи с использованием изученных формул;
д) уметь находить дополнительный материал по изучаемой теме во всех допустимых средствах информации; уметь предоставлять результаты своих находок по окончании курса.
Данный элективный курс рассчитан на выпускников, которые желают углубить свои знания по математике, качественно подготовиться к сдаче ЕГЭ. Но он также и полезен ребятам, которые будут в дальнейшем работать по специальности, связанной с математикой.
Практическая часть учебного курса
Угол между прямыми а и b
Углом между прямыми в пространстве называется угол между любыми параллельными им пересекающимися прямыми. Этот угол равен углу между направляющими векторами данных прямых (или дополняет его до 1800).
1
) Выбираем любые вектора AB и CD, имеющие направления прямых а и b (параллельные им).
2) Определяем координаты векторов AB(x1;y1;z1) и CD(x2;y2;z2) по соответствующим координатам их начал и концов (от координат конца вектора нужно отнять координаты начала).
3) Подставляем найденные координаты в формулу:
C
OS(AB,CD) =
Для нахождения самого угла, нужно найти арккосинус полученного результата.
У
гол между прямыми в многограннике – это угол между векторами п1 и п2 , которые параллельны данным прямым. Пусть на одной прямой заданы точки А ( а1 , b1, c1 ) , В ( а2 , b2, c2 ), а на другой – С ( а3 , b3, c3 ), D( а4 , b4, c4 ). Тогда векторы имеют координаты:
п1 ( х1 = а2 – а1, у1 = b2 – b1 ,z1 = c2– c1), п2( х2 = а4 – а3, у2 = b4 –b3, z2 = c4 – c3). Значение угла вычисляется по формуле, известной как скалярное произведение векторов.
Задача: В кубе АВСDА1В1С1D1 М и N – середины ребер А1D1 и ВВ1. Найдите угол между прямой МN и диагональю ВD1.
Решение:
Введем пространственную систему координат.
Находим координаты точек В, D1, М , N : B(1;1;0) , D1(0;0;1) , M(0,5;0;1) , N(1;1;0,5).
Координаты векторов BD1(-1;-1;1) , MN (0,5;1;-0,5).
Искомый угол находится по формуле cos a :
Ответ: .
Уравнение плоскости в пространстве
Точки, удовлетворяющие равенству образуют плоскость с нормалью
. Коэффициент
отвечает за величину отклонения (параллельного сдвига) между двумя плоскостями с одной и той же заданной нормалью
. Для того, чтобы написать уравнение плоскости нужно сначала найти ее нормаль, используя матрицу и определители, а затем подставить координаты найденной нормали в уравнение
Угол между прямой и плоскостью
Допустим, что нам заданы прямая и плоскость координатами направляющего вектора AB(x1;y1;z1) и нормали n(x2;y2;z2).
Угол Ψ между прямой и плоскостью вычисляется по следующей формуле:
c
os(n,AB) =
Чтобы составить уравнение плоскости, которой принадлежат данные точки, необходимо воспользоваться определителями матрицы и следующей формулой:
=
–
+
Задача: В правильной треугольной пирамиде SABC сторона основания равна 8 и SC =17 . Найдите tg
угла , образованного плоскостью основания и прямой АО , где О – точка пересечения медиан грани ABC.
Введем пространственную систему координат. Находим координаты точек В,А,C,O : B(8 ;0;0) А(0;0;0) ,C(4
;12;0), О(4
;4;15).
Координаты вектора n = АО (
;4;15)
Составляем уравнение плоскости основания :
=
–
+
Искомый угол находится по формуле sin a :
; tg
; Ответ:
.
Угол между плоскостями
Пусть n1(x1;y1;z1) и n2(x2;y2;z2) — две любые нормали к данным плоскостям.
Если в задаче необходимо найти угол между плоскостями , то координаты векторов нормали составляются по матрицам , в которых берутся координаты соответствующих точек. После того как составлены уравнения плоскостей , значение угла можно найти по формуле .
Т
огда косинус угла между плоскостями равен модулю косинуса угла между нормалями:
cos(n1 , n2) =
Задача: В кубе АВСDА1В1С1D1 найдите угол между плоскостью А1ВD и плоскостью, проходящей через середины его ребер АВ, ВВ1 , В1С1, С1D1, D1D, DА.
Решение:
Введем пространственную систему координат. Находим координаты точек необходимых для составления матриц и нахождения уравнения плоскостей: B(1;1;0) , А1(1;0;1) , D(0;0;0) ,К(0;0;0,5) , М(0,5;0;0),N(1;0,5;0)
Составляем уравнение плоскости А1ВD
= x(-1) – y(-1) + z(1) = – x + y + z.
Составляем уравнение плоскости KMN
= x(-0,25) – y(-0,25) + z(-0,25) = -0,25x + 0,25y – 0,25z.
Т
огда n1 (-1; 1; 1) , n2(-0,25; 0,25;-0,25).
Следовательно ,
cosa = = =
=
=
=
, tg
;
Ответ: .
Расстояние от точки до плоскости
Для вычисления расстояния от точки
до плоскости
, заданной уравнением
можно использовать следующую формулу:
В знаменателе стоит длина нормали, а числителе — значение выражения из левой части уравнения плоскости в точке
Задача: В правильной шестиугольной пирамиде SABCEF , все ребра которой равны 1, найдите расстояние от точки Е до плоскости SDА.
Решение:
Введем пространственную систему координат. Находим координаты точек S,D,E,A: А(0;0;0) , S ( ;
;
) , Е(0;
;0) D(1
;0). Составим уравнение плоскости SDA
= –
–
) +
x +
После упрощения уравнение принимает вид: x +
= 0
Ответ: =
Расстояние от точки до прямой
Для вычисления расстояния от точки К (x1;y1;z1) до прямой а необходимо на ней найти координаты вектора n (А; В; С), которые составлены из координат двух точек прямой . Одна из этих точек, например N (x2;y2;z2) , используется в формуле, по которой находится искомое расстояние.
d =
Задача: В правильной шестиугольной призме ABCDEF A 1B 1C 1D1 E 1F 1 , все ребра которой равны 1, найдите расстояние от точки В до прямой А1F 1.
Решение:
Введем пространственную систему координат. Находим координаты точек А1 ,F1,В : А 1(0;0;1) ,F1 ( ;
;
) , В(1;
;0).
Подставляя координаты в формулу можно вычислить расстояние от точки В до прямой А1F 1.
d = Ответ:
.
Расстояние между прямыми
Для вычисления расстояния между двумя прямыми а и в необходимо иметь координаты векторов а и в , которые лежат на этих прямых. Пусть точка А (x1;y1;z1) принадлежит прямой а , точка В (x2;y2;z2) принадлежит прямой в. Вектор а(
) , вектор в(
) .И тогда расстояние между прямыми находятся по формуле :
d =
Задача: В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите расстояние между прямыми ВD и АS.
Решение:
В
ведем пространственную систему координат. Находим координаты точек А ,D,В, Н, S: А (0;0;0), В(1;
; 0) , Н (
;
;
S (
;
;
, D (0;1;0). ВD( -1; 1; 0), АS(
;
;
Подставляя координаты в формулу можно вычислить искомое расстояние.
d = =
=
Ответ:
.
Заключение
Достаточно простой в применении, метод координат является необходимой составляющей решения задач различного уровня. Использование данного метода, позволяет учащимся значительно упростить и сократить процесс решения задач, в том числе повышенного уровня, что помогает им при дальнейшем изучении как школьного курса математики, так и при изучении математики в высших учебных заведениях. Координатно-векторный метод имеет преимущества перед другими в том, что не требует сложных построений в проекциях, т.к. заключается во введении (привязке к исследуемым фигурам) декартовой системы координат, а затем – исчислении образующихся векторов (их длин и углов между ними); то есть одно без другого не работает. Этот метод – довольно мощный (ему поддаются даже самые «непробиваемые», казалось бы, задачи). Все те соотношения, которые при решении традиционным методом даются с большим трудом (через привлечение большого количества вспомогательных теорем), здесь получаются как бы сами собой, в ходе вычислений. Весь этот подход, развитый до своего логического завершения, в высшей математике получает название аналитической геометрии. Единственный его, пожалуй, недостаток – это требуемый нередко большой объем вычислений. Координатно-векторный метод представлен практически во всех учебниках, но большее внимание ему уделено в задачнике Потоскуева Е.В. и Звавича Л.И. С помощью векторно-координатного метода можно быстро и успешно решать стереометрические задачи из ЕГЭ в блоке С (задание С2).
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Башкирский государственный педагогический университет
им. М.Акмуллы»
(ФГБОУ ВПО «БГПУ им. М.Акмуллы»)
О Т З Ы В Р У К О В О Д И Т Е Л Я
На работу студента__________________________________________________
выполненную на тему_______________________________________________
__________________________________________________________________
1. Актуальность работы_____________________________________________
__________________________________________________________________
_________________________________________________________________
2. Научная новизна работы___________________________________________
__________________________________________________________________
3. Оценка содержания работы_________________________________________
__________________________________________________________________
4. Положительные стороны работы____________________________________
__________________________________________________________________
5. Замечания_______________________________________________________
__________________________________________________________________
__________________________________________________________________
6. Рекомендации по внедрению результатов работы______________________
__________________________________________________________________
__________________________________________________________________
7. Рекомендуемая оценка_____________________________________________
8. Дополнительная информация для ГАК______________________________ __________________________________________________________________ Научный руководитель________________________________________________ __________________________________________________________________
(подпись ) (фамилия, имя, отчество)
__________________________________________________________________
(ученая степень, звание, должность, место работы)
______________________________________ г
дата
РЕЦЕНЗИЯ
на выпускную квалификационную работу студента(ки)
_________________________________________________факультета
__________________________________________________________
__________________________________________________________
(фамилия, имя, отчество студента)
Башкирского государственного педагогического университета им.М.Акмуллы,
выполненную на тему:_______________________________________________
_____________________________________________________________________________
1. Актуальность, новизна исследования_______________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
2 Оценка содержания работы_________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
3 Отличительные, положительные стороны работы_______________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
4. Практическое значение и рекомендации по внедрению____________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
5 Недостатки и замечания по работе___________________________________
__________________________________________________________________
__________________________________________________________________
6. Рекомендуемая оценка_____________________________________________
Рецензент_______________ _____________________________
(подпись) (фамилия, имя, отчество)
(ученая степень, звание, должность, место работы)
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Башкирский государственный педагогический университет
им. М.Акмуллы»
(ФГБОУ ВПО «БГПУ им. М.Акмуллы»)
З А К Л Ю Ч Е Н И Е Заведующего кафедрой___________________________________________
(фамилия, имя, отчество зав.кафедрой)
Квалификационная выпускная работа студента группы_________________
_________________________________________________________________
_____________________________________________________________________________________________________________________________________________________
(фамилия, имя, отчество студента)
выполненная на тему______________________________________________
________________________________________________________________
________________________________________________________________
в объеме_______________ с., с приложением __________с.
соответствует установленным требованиям и допускается кафедрой к защите.
Заведующий кафедрой
«_____ »________________20___ г.