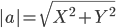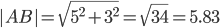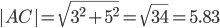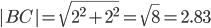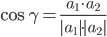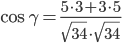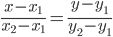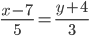Как найти координаты третьей вершины?
Прошу помочь в нахождении формул.
- Вопрос задан более трёх лет назад
- 21855 просмотров
Оценить 5 комментариев
Хорошо учился бы в школе, вопросов бы не задавал.
Рад, что предоставил вам возможность почувствовать себя образованнее.
«Если задать вопрос на американском форуме, вам 40 человек дадут подробный ответ на вопрос.
Если спросить на израильском форуме, вам в ответ зададут 40 вопросов.
А если спросить на русском форуме, вам 40 человек расскажут почему ты мудак и вопрос твой мудацкий» ©
Человек же просто спросил.
В таком случае уж начните с определений:
— какая перед Вами стоит задача;
— какой инструментарий Вам доступен;
— способны ли Вы найти сумму квадратов катетов.
В противном случае не совсем понятно на каком уровне Вам отвечать: дать ссылку на готовую библиотеку или научить пользоваться калькулятором.
Раз так, то пляшем от картинки:
Один из вариантов решения Вашей задачи: предположим, что центр системы координат совпадает с точкой A, таким образом Cx=b*cos(g+t), Cy=b*sin(g+t)
Угол g вычисляем по теореме косинусов или синусов, смотря что Вам идеологически ближе (теорему см. по фиолетовой ссылке).
Синус угла t будет равен By/c.
Следует обратить внимание на периодичность функций, не забывать про различия промеж градусами и радианами, поглядывать сюда и сюда а так же иметь в виду особенные случаи про которые в условии ничего не сказано.
Не так давно уважаемый тов. timyrik20 написал хабрапост на интересующую Вас тему.
Человек же просто спросил.
Человеку прям сразу и ответили. Вполне исчерпывающе, как на уровень хабра.
Как найти третью координату треугольника, когда указаны две координаты и соответствующие им углы
Я пытаюсь вычислить третью координату треугольника ABC, где A (x1, y1) B (x2, y2) угол CAB = a1 и угол CBA = a2. мне нужно найти третью координату C (x3, y3)
я думал об использовании закона косинусов, но они могут привести к решению некоторых сложных уравнений.
Мне нужна простая методика для их решения или использование некоторых прямых формул или любого другого метода, который может быть реализован в компьютерной программе.
может кто-нибудь помочь мне в этой проблеме?
Примеры решений по аналитической геометрии на плоскости
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.
Решения задач о треугольнике онлайн
Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.
Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.
Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.
Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.
Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.
Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$.
Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.
[spoiler title=”источники:”]
http://techarks.ru/qa/kak-najti-tretyu-koordinatu-HC/
http://www.matburo.ru/ex_ag.php?p1=agtr
[/spoiler]
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
1 |
|
Как найти координаты третьей вершины треугольника, зная все стороны и две вершины?07.07.2013, 16:27. Показов 97727. Ответов 19
Добрый день, подскажите как найти координаты третьей вершины треугольника?
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
07.07.2013, 17:10 |
2 |
|
Зная то, что расстояние между двумя точками равно: Откуда и найдем координаты 3-ей точки
2 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 17:18 [ТС] |
3 |
|
А как вывести из формулы нужную?
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
07.07.2013, 17:44 |
4 |
|
Например, можно произвести смещение точки А в начало координат.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 17:46 [ТС] |
5 |
|
Извени, но я не понимаю…
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,783 Записей в блоге: 12 |
|
|
07.07.2013, 19:38 |
6 |
|
А так понимаете?
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 20:07 [ТС] |
7 |
|
Рисунок не доступен пишет.
0 |
|
4216 / 3411 / 396 Регистрация: 15.06.2009 Сообщений: 5,818 |
|
|
07.07.2013, 21:35 |
8 |
|
Известны координаты точек А(x1,y1), С(x2,y2). Условие некорректно – переопределено. Две заданных вершины тем самым уже определяют и длину одной стороны.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 23:27 [ТС] |
9 |
|
Условие некорректно – переопределено. Две заданных вершины тем самым уже определяют и длину одной стороны. Длина и координаты две разные вещи.
0 |
|
2525 / 1751 / 152 Регистрация: 11.08.2012 Сообщений: 3,349 |
|
|
07.07.2013, 23:52 |
10 |
|
Длина и координаты две разные вещи. А Том Ардер другого и не утверждал. Читайте внимательнее.
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,783 Записей в блоге: 12 |
|
|
08.07.2013, 11:23 |
11 |
|
Решение
Добрый день, подскажите как найти координаты третьей вершины треугольника? Вот картинка. Миниатюры
3 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
08.07.2013, 14:48 [ТС] |
12 |
|
А как вы выделили x и y из формулы?
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,783 Записей в блоге: 12 |
|
|
09.07.2013, 09:13 |
13 |
|
Справа на картинке записана система двух уравнениий – уравнений окружностей.Решив систему, получаем координаты двух точек. т.е. точек В может быть две.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
09.07.2013, 14:03 [ТС] |
14 |
|
проблема в том, что я не знаю как решить уравнение окружностей(
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
09.07.2013, 14:11 |
15 |
|
Раскройте скобки, вычтите из 1 уравнения другое. Уйдут квадраты, выразите одну переменную через другую. Подставите в 1 исходное.
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,783 Записей в блоге: 12 |
|
|
09.07.2013, 15:16 |
16 |
|
Только проще сначала вычесть из первого уравнение второе, затем воспользоваться формулой разности квадратов.
1 |
|
0 / 0 / 0 Регистрация: 10.04.2016 Сообщений: 7 |
|
|
28.04.2016, 22:07 |
17 |
|
А можно решить как-нибудь без системы уравнений?
0 |
|
0 / 0 / 0 Регистрация: 08.04.2019 Сообщений: 6 |
|
|
10.04.2019, 13:19 |
18 |
|
Я тоже был бы не против без системы уравнений
0 |
|
1471 / 826 / 140 Регистрация: 12.10.2013 Сообщений: 5,456 |
|||||
|
10.04.2019, 21:50 |
19 |
||||
|
del Для чего тут система уравнений?
Нормализуем вектор AC и множим на длину AB стороны и крутим матрицей поворота в 2д на нужный угол. Угол треугольника найти по трем сторонам. Эх раньше бы и рис и формулы кинул…но теперь лень =). Может кто из гуру не полениться…
0 |
|
pro4vayder 1 / 1 / 0 Регистрация: 25.05.2016 Сообщений: 2 |
||||
|
04.11.2020, 09:49 |
20 |
|||
|
Прошу глянуть решение здесь. Ответ выше был близок к ответу, но человеку далекому от математики (мне) – это не особо было понятно. P.S решение выводит 2 ответа точек пересечения Кликните здесь для просмотра всего текста http://algolist.ru/maths/geom/… rcle2d.php
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
04.11.2020, 09:49 |
|
20 |
| Автор | Сообщение | ||||
|---|---|---|---|---|---|
|
|||||
|
Здравствуйте, уважаемые форумчане. Помогите пожалуйста с формулой Как найти координаты третьей вершины треугольника по длинам трёх сторон и двум координатам вершин? Известны координаты точек А(x1,y1), С(x2,y2). Использовать для вычислений Косинус и Синус угла АСВ и смещение прямой АС относительно системы координат нельзя из-за получающейся огромной погрешности при вычислениях. Я про формулу такого вида: x3 = x2 + a*cosС, y3 = y2 + a*sinС
|
||||
| Вернуться к началу |
|
||||
|
Avgust |
|
||
|
Точка А – центр окружности радиусом с Точка С – центр окружности радиусом a Пересечение двух окружностей дадут точку B, то есть ее координаты. Всего-то нужно решить систему относительно [math]x,[/math] и [math]y[/math] [math](y-y_1)^2+(x-x_1)^2=c^2[/math] [math](y-y_2)^2+(x-x_2)^2=a^2[/math] Получим два решения при допустимых соотношениях параметров (при которых треугольник может существовать) Последний раз редактировалось Avgust 26 мар 2013, 09:10, всего редактировалось 1 раз. |
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю Avgust “Спасибо” сказали: panda |
|||
|
panda |
|
||
|
Спасибо за ответ. А не могли бы вы оформить его в виде формулы?
|
|||
| Вернуться к началу |
|
||
|
Avgust |
|
||
|
Формулы я получил. Но они такие громоздкие, что писать полчаса надо. Вот численно элементарно делается. Например, зададим параметры пифагорова треугольника: Тогда по команде Maple solve({(y-y1)^2+(x-x1)^2 = c^2, (y-y2)^2+(x-x2)^2 = a^2}, [x, y]); получим два решения: 1) [math]x=4 , ; , y=0[/math] 2) [math]x=frac{28}{25}, ; , y=frac{96}{25}[/math] Графическое представление этой задачи:
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю Avgust “Спасибо” сказали: panda |
|||
|
Avgust |
|
||
|
Я добавил рисунок… x:=(1/2)*((y1-y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+(x1^3-x1^2*x2+(y2^2-2*y1*y2-c^2+y1^2+a^2-x2^2)*x1-x2*(a^2-c^2-x2^2-y2^2+2*y1*y2-y1^2))*(x1-x2))/((x1-x2)*(x1^2-2*x2*x1+x2^2+(y1-y2)^2)); y := (-sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2); Второе решение: x := (1/2)*((-y1+y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2)))+(x1-x2)*(x1^3-x1^2*x2+(y1^2-2*y1*y2+y2^2+a^2-c^2-x2^2)*x1-x2*(-c^2-x2^2+a^2-y1^2+2*y1*y2-y2^2)))/((x1^2-2*x2*x1+x2^2+(y1-y2)^2)*(x1-x2)); y := (sqrt(-(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a+y1-y2)*(c+a-y1+y2))*(-x1^2+2*x2*x1-x2^2+(-c+a+y1-y2)*(-c+a-y1+y2)))+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2); Формулы проверил – работают отлично. Вот если бы их суметь упростить!
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю Avgust “Спасибо” сказали: amjava, panda, Realdreamer |
|||
|
Realdreamer |
|
||
|
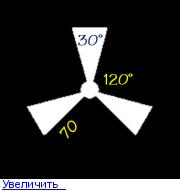
Уважаемые математики Пишу программу, но к сожалению не очень силен в математических науках. Нужно как раз вершины треугольника Вообще в итоге мне нужно написать симуляцию работы вентилятора. Крутится то я его заставлю. Пытался сам найти, но видимо не так запрос формирую.
|
|||
| Вернуться к началу |
|
||
|
Realdreamer |
|
||
|
vvvv Координат всего должно быть 9 для каждой оси, но в таблице их 10 В итоге я пошёл по другому пути a = 70 и разделил её пополам. Получил координату по Y в обе стороны y1 = sqrt(a ** 2 – b ** 2) А потом по формуле окружности просто сдвинул на 120 градусов влево и вправо xn1 = sin(120 – 15) * a xn1 = sin(-120 – 15) * a От меня вам всё равно спасибо что откликнулись!
|
|||
| Вернуться к началу |
|
||
I want to locate precisely the 3rd coordinate of a right angled triangle.
I have:
- the length of three sides
- The three angles
- The other two coordinates of the triangle
The triangle can lie in any orientation in 2D coordinate system.
The three sides, angles and coordinates could be different in the piece of experiment and I am not working with any fix pair of values… I am actually dealing with multiple pairs of all above mentioned values.
I need a reliable and accurate way of finding the 3rd coordinate. Currently I have this formula but it calculated two pairs of coordinates (forming a butterfly) instead of the triangle.
Edit 2:
In the diagram that I mentioned and to which a (potential) solution has been presented, I have a confusion/connected question (because I believe this could be the cause of the problem).
Question:
Can $(x_1, y_1)$ and $(x_2, y_2)$ be any pair of the right angles triangle? or does $(x_1, y_1)$ must the coordinates of the right angle and $(x_2, y_2)$ for the base vertex?
Currently I get this:
As you can see, the coordinate I am trying to get is draw way-off the border of the circle. The coordinate should be found on the border of the circles and not that far away in space.
As you might have guessed that I am trying to draw tangents between each circle. I have worked out rest of the code but the coordinate is being calculated incorrectly and thus the right angled triangle is formed incorrectly..
Edit (ignore this heading please):
I want to find only ONE triangle instead of the four possibilities.
http://awaismunir.net/universal/tangents/3rd-third-vertext-calculate-right-angled-triangle.gif
Note:
I have already reviewed these urls:
Calculate coordinates of 3rd point (vertex) of a scalene triangle if angles and sides are known.
and
How to find the third coordinate of a right triangle given 2 coordinates and lengths of each side
Kindly help.
Thanks!
Steve
Как найти вершину треугольника?
Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.
1 способ (графический)
- В системе координат отмечаем две заданные вершины.
- Ставим ножку циркуля в одну из построенных точек.
- Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
- Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
- Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
- Определяем координаты полученных точек, исходя из полученного чертежа.
Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.
2 способ (аналитический)
Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)
- Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
- Составляем соотношения
AC=√((x-x1)^2+(y-y1)^2)
BC=√((x-x2)^2+(y-y2)^2)
AB=√((x2-x1)^2+(y2-y1)^2) - Учитывая, что треугольник равносторонний, составляем систему уравнений:
AC=BC
AC=AB
Или система уравнений:
√((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
√((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2) - Методом подстановки решаем полученную систему.
Теперь вы знаете, как найти вершину треугольника.
Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Прямая на плоскости
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=xj-xi; Y=yj-yi
здесь X , Y координаты вектора; xi , yi — координаты точки Аi ; xj , yj — координаты точки Аj
Например, для вектора AB: X=x2-x1=12-7=5 ; Y=y2-y1=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой:
3) Угол между прямыми. Угол между векторами a1(X1;Y1) , a2(X2;Y2) можно найти по формуле:
где a1a2=X1X2+Y1Y2
Найдем угол между сторонами AB и AC
γ = arccos(0.88) = 28.07 0
8) Уравнение прямой. Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2) , представляется уравнениями:
Уравнение прямой AB . Каноническое уравнение прямой: 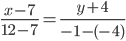
y= 3 /5x- 41 /5 или 5y-3x+41=0



 Сообщение было отмечено как решение
Сообщение было отмечено как решение











![[ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)