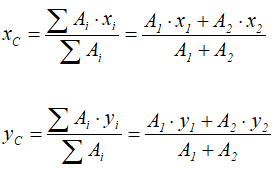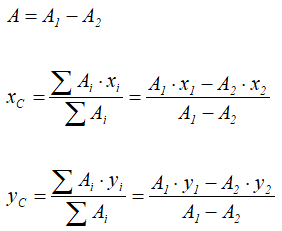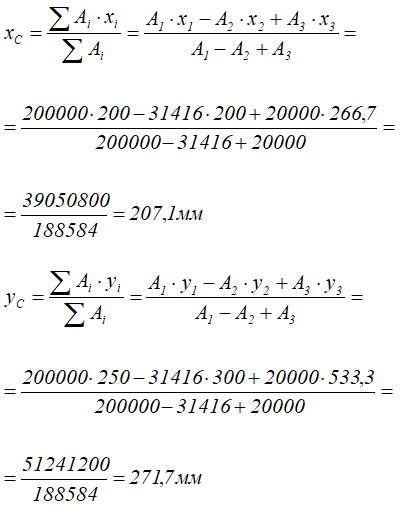
Определение координат центра тяжести xC и yC плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.
Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.
Способы определения координат центра тяжести
Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.
Существует 5 способов расчета координат положения центра тяжести:
- Аналитический (путем интегрирования).
- Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
- Экспериментальный. (метод подвешивания тела).
Этот способ подходит в основном для плоских и линейных тел. - Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.
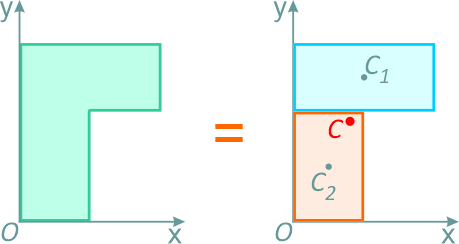
Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A1 и A2 (A = A1+ A2).
Рисунок 1.8
Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны:
- Дополнение (Метод отрицательных площадей или объемов).
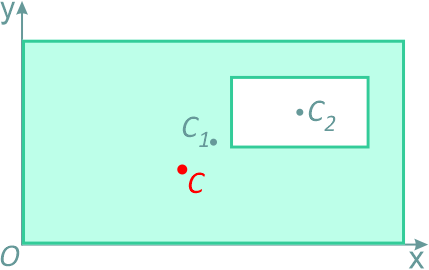
Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Рисунок 1.9
Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).
Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:
Другие видео
Пример определения координат центра тяжести плоской фигуры
Задача
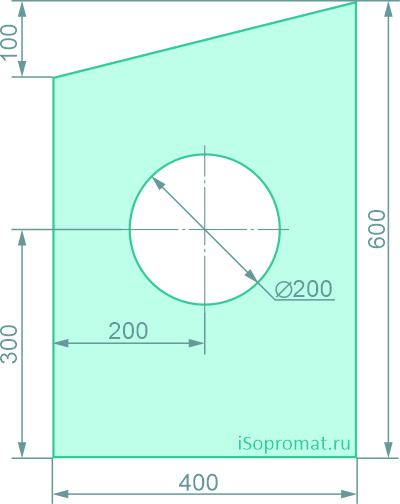
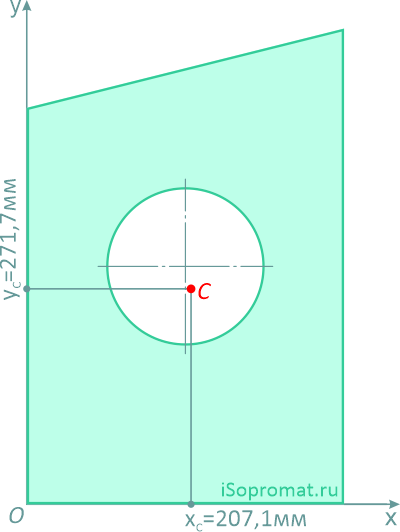
Определить координаты центра тяжести плоской фигуры с круглым отверстием
Решение
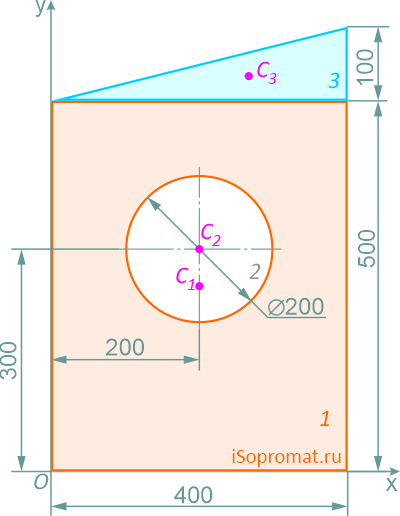
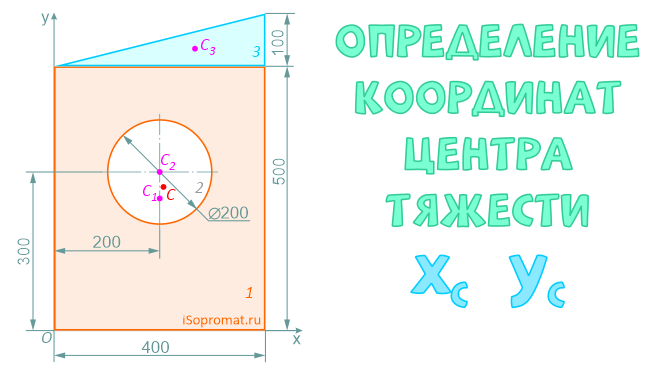
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.
Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести Ci отдельных фигур:
Прямоугольник (фигура 1)
Площадь
A1=400×500=200000 мм2
Положение центра тяжести
x1=200мм
y1=250мм
Круг (2) (вычитаемая фигура)
Площадь
A2=π×2002/4=31416 мм2
Центр тяжести
x2=200мм
y2=300мм
Прямоугольный треугольник (3)
Площадь
A3=400*100/2=20000 мм2
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x3=400×2/3=266,7мм
y3=500+100×1/3=533,3мм
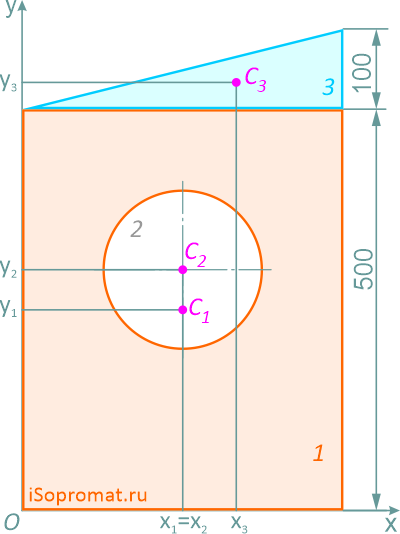
Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:
Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами xC=207,1мм, yC=271,7мм.
Другие примеры решения задач >
Центры тяжести простейших фигур >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
В этой статье посмотрим, как определяются координаты центра тяжести сложной фигуры — состоящей из простых. В задачах по сопромату часто приходится находить положение центра тяжести составных сечений, для дальнейшего вычисления моментов инерции и т. д.
Также часто, при изучении теоретической механики, студентам предлагается решить подобную задачу, и найти центр тяжести какой-нибудь фигуры.
Условие задачи
Предлагаю рассмотреть следующую фигуру:

В сопромате принято заштриховывать сечения тонкими линиями, вот так:

В своих же уроках я буду использовать заливку. Так, штриховка не будет мешать наносить обозначения.
Разбивка сложной фигуры на простые
Как видишь, сечение состоит из прямоугольника, прямоугольного треугольника, четверти круга, а также имеет круглый вырез:

Отметим центры тяжести (С1, С2, С3, С4) каждой отдельной фигуры, с учётом справочной информации.
Открой эту страничку, и пока не закрывай, она нам ещё понадобится!

Покажем вспомогательные оси (x0, y0) для всего сечения, которые будем использовать для нахождения положения центра тяжести (C):

Как определить положение центра тяжести?
Чтобы определить координату центра тяжести сечения, например, вертикальное расстояние от оси x0 до центра тяжести сечения (yc):

Нужно статический момент сечения относительно этой вспомогательной оси (x0) разделить на площадь всего сечения (A):

Площадь всего сечения (A) найти просто – это алгебраическая сумма площадей всех фигур:

Статический момент сечения, относительно вспомогательной оси будет равен алгебраической сумме статических моментов каждой фигуры (с учётом знака):

где Ai – площадь отдельной фигуры;
yi – расстояние от центра тяжести отдельной фигуры до вспомогательной оси (x0).
Координата центра тяжести (xc), находится аналогично:

Определение площади сечения
Для начала предлагаю сделать самое простое, используя формулы, указанные на этой странице, найти площадь всего сечения (A):


Как видишь, круглый вырез, нужно учесть с «минусом», что очевидно.
Определение расстояний от вспомогательных осей до центров тяжести отдельных фигур
Найдём расстояния от вспомогательных осей (x0, y0) до центров тяжести отдельных фигур, опять же, используя нашу шпаргалку:
Определение статических моментов
Определяем статические моменты сечения относительно вспомогательных осей (x0, y0):


Важно! Статические моменты могут быть и отрицательными.
Определение координат центра тяжести
И, наконец, определяем положение центра тяжести всего сечения (C):

Покажем центр тяжести всего сечения (C):

Если остались какие-то вопросы по данному уроку, можешь смело задавать их в комментариях. Также, другие уроки, на сайте – ssopromat.ru, по определению геометрических характеристик, можешь найти здесь.
1.
Разбивают
сечение на простые фигуры. В
задачах для самостоятельной работы
такими фигурами являются стандартные
профили проката, размеры которых
приведены в прил. I.
Обычно профили прокатной стали,
образующие сечение, обозначают цифрами
1, 2, 3, … .
2.
Указывают
центры тяжести каждого профиля (фигуры)
и обозначают их C1,
…, СN
,
используя
таблицы ГОСТов (см. прил. I).
3.
Выбирают
систему координатных осей. В
задачах для самостоятельной работы
все сечения имеют одну ось симметрии,
поэтому рекомендуется одну из
координатных осей совмещать с ней.
Вторую ось координат направляют
перпендикулярно первой так, чтобы она
пересекла центры тяжести одной или
нескольких фигур. При этом начало
координат может совпадать (или не
совпадать) с центром тяжести одной
из фигур. Вторую ось можно направить
так, чтобы она прошла через нижнюю
(крайнюю) точку сечения. В первом
случае вычисления будут более простыми.
4.
Составляют
формулы для определения координат
центра тяжести сечения:
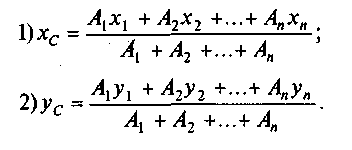
22
Пользуясь
таблицами ГОСТов (см. прил. I),
определяют площади профилей проката
Аъ
А2,
…, А„, координаты
их центров тяжести х{,
х2,
…,х„ и
уъ
у2,
…,у„ относительно
выбранных осей координат. Число слагаемых
в числителе и знаменателе формул зависит
от числа профилей, из которых состоит
сечение. Полученные величины
подставляют в формулу и находят хс
и
ус.
Следует
помнить, что если ось х
совмещена
с осью симметрии, то координата ус
=
0, а если ось у
совмещена
с осью симметрии, то хс
= 0.
5.
Указывают
положение центра тяжести на рисунке,
придерживаясь
определенного масштаба, и показывают
расстояние от центра тяжести до
координатных осей.
6.
Выполняют
проверку правильности решения, для
чего можно изменить положение координатных
осей (или одной оси) и найти координаты
центра тяжести относительно .новых
осей. Положение центра тяжести не
зависит от того, как выбрана система
координатных осей.
Пример
5.
Определить координаты центра тяжести
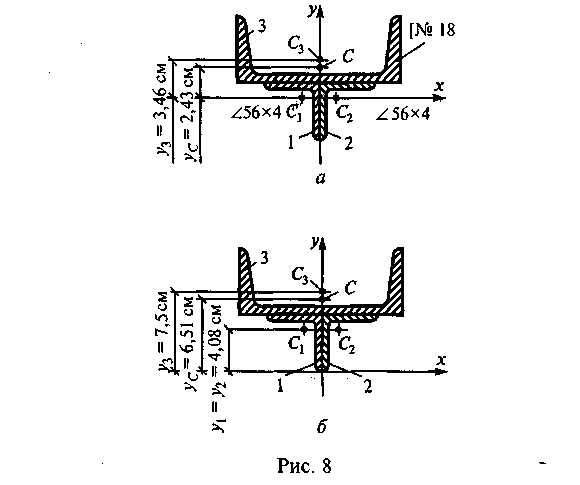
сечения, показанного на рис. 8, а.
Сечение состоит из двух уголков (/.}
56×4
и швеллера ([) № 18. Выполнить проверку
правильности определения положения
центра тяжести. Указать его положение
на сечении.
Решение.
1.
Разобьем
сечение на профили проката: два
уголка 56×4 и швеллер № 18. Обозначим их
1, 2, 3 (см. рис. 8, а).
2.
Укажем
центры тяжести каждого
профиля, используя
табл. 1 и 4 прил. I,
и обозначим их Q,
С2,
С3.
3.
Выберем
систему координатных осей. Ось
у
совместим
с осью симметрии, а ось х
проведем
через центры тяжести уголков.
4.
Определим
координаты центра тяжести всего сечения.
Так
как ось у
совпадает
с осью симметрии, то она проходит через
центр тяжести сечения, поэтому хс
=
0. Координату ус
определим
по формуле
Пользуясь
табл. 1 и 4 прил. I,
определим площади каждого профиля и
координаты центров тяжести:
Координаты
yi
и
у2
равны
нулю, так как ось х
проходит
через центры тяжести уголков. Подставим
полученные значения в формулу для
определения ус:
23
5.
Укажем
центр тяжести сечения на рис. 8, а и
обозначим его буквой С. Покажем расстояние
у
с = 2,43
см от оси х
до
точки С.
Поскольку
уголки симметрично расположены, имеют
одинаковую площадь и координаты, то
А]
= А2,
yl
= у2.
Поэтому
формула для определения ус
может
быть упрощена:
6.
Выполним
проверку. Для
этого ось х
проведем
по нижнему краю полки уголка (рис. 8, б).
Ось
у
оставим,
как в первом решении. Формулы для
определения хс
и
ус
не
изменяются:
Площади профилей
останутся такими же, а координаты центров
тяжестей уголков и швеллера изменятся.
Выпишем их:
Находим координату
центра тяжести:
24

По
найденным координатам хс
и
ус
наносим
на рисунок точку С.
Найденное
двумя способами положение центра тяжести
находится в одной и той же точке. Проверим
это. Разница между координатами ус,
найденными
при первом и втором решении, составляет:
6,51 – 2,43 = 4,08 см.
Это
равно расстоянию между осями х
при
первом и втором решении: 5,6 – 1,52 = 4,08 см.
Ответ:
ус
= 2,43
см, если ось jc
проходит через центры тяжести уголков,
или ус
= 6,51
см, если ось х
проходит
по нижнему краю полки уголка.
Пример
6. Определить
координаты центра тяжести сечения,
изображенного на рис. 9, а.
Сечение
состоит из двутавра (I)
№ 24 и швеллера № 24а. Показать положение
центра тяжести на сечении.
Решение.
1.
Разобьем
сечение на профили проката: двутавр
и швеллер. Обозначим их цифрами 1 и 2.
2.
Укажем
центры тяжести каждого профиля С и
С2,
используя табл. 3 и 4 прил. I.
3.
Выберем
систему осей координат. Ось
х
совместим
с осью симметрии, а ось у
проведем
через центр тяжести двутавра.
4.
Определим
координаты центра тяжести сечения.
Координата
ус
=
0, так как ось х
совпадает
с осью симметрии. Координату хс
определим
по формуле
25
По
табл. 3 и 4 прил. I
и схеме сечения определим
Подставим числовые
значения в формулу и получим
5.
Нанесем
точку С (центр тяжести сечения) по
найденным значениям хс
и
ус
(см.
рис. 9, а).
6.
Проверку
решения необходимо выполнить самостоятельно
при
положении осей, как показано на рис. 9,
б.
В
результате решения получим хс
– 11,86
см. Разница между значениями хс
при
первом и втором решении равна 11,86 – 6,11 =
5,75 см, что равно расстоянию между осями
у
при
тех же решениях bдв/2
=
5,75 см.
Ответ:
хс
=
6,11 см, если ось у
проходит
через центр тяжести двутавра; хс
=
11,86 см, если ось у
проходит
через левые крайние точки двутавра.
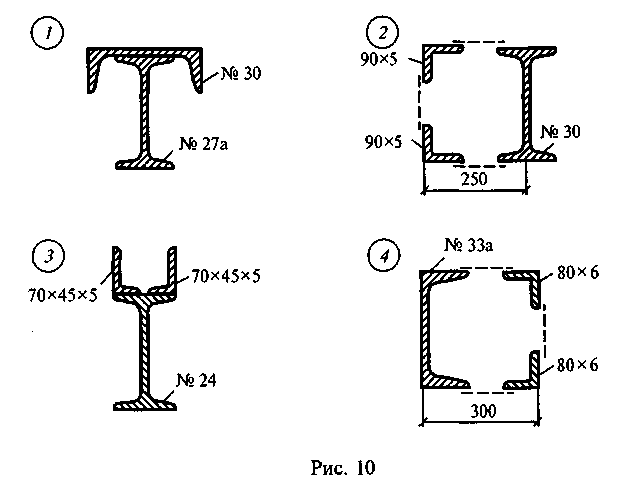
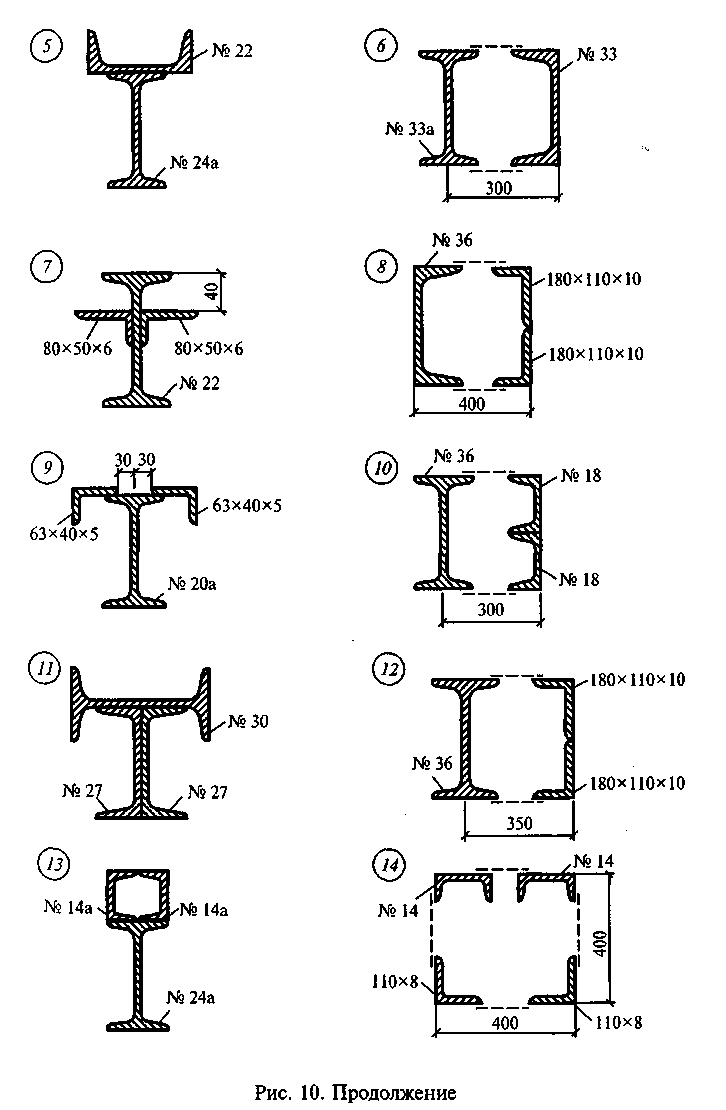
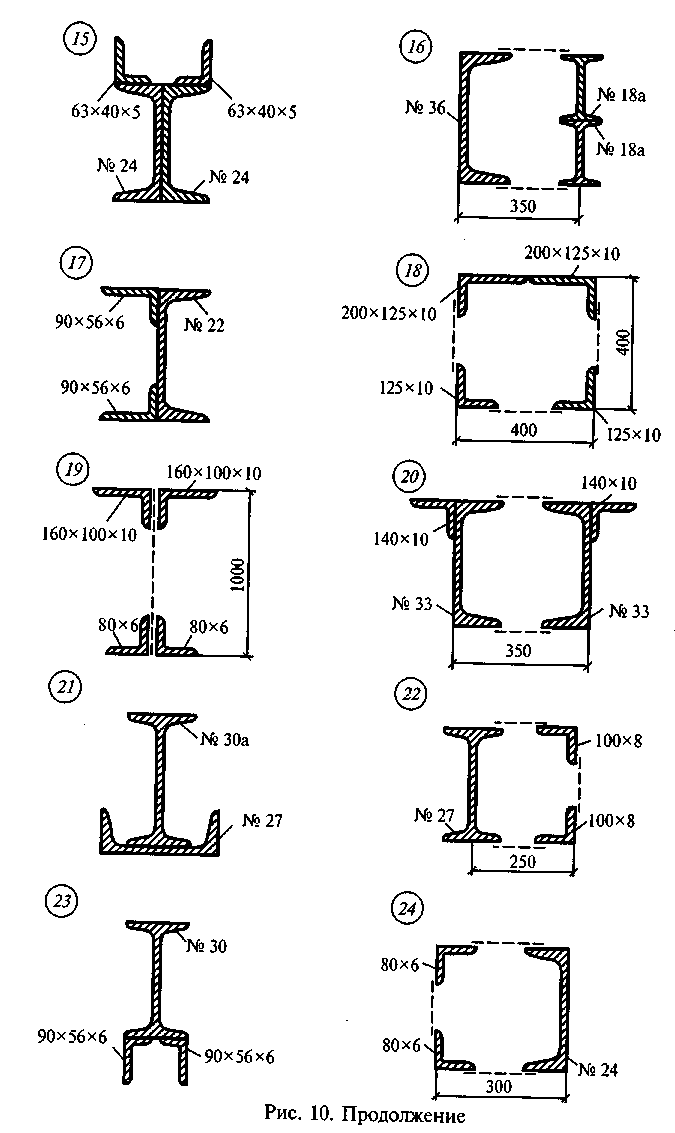
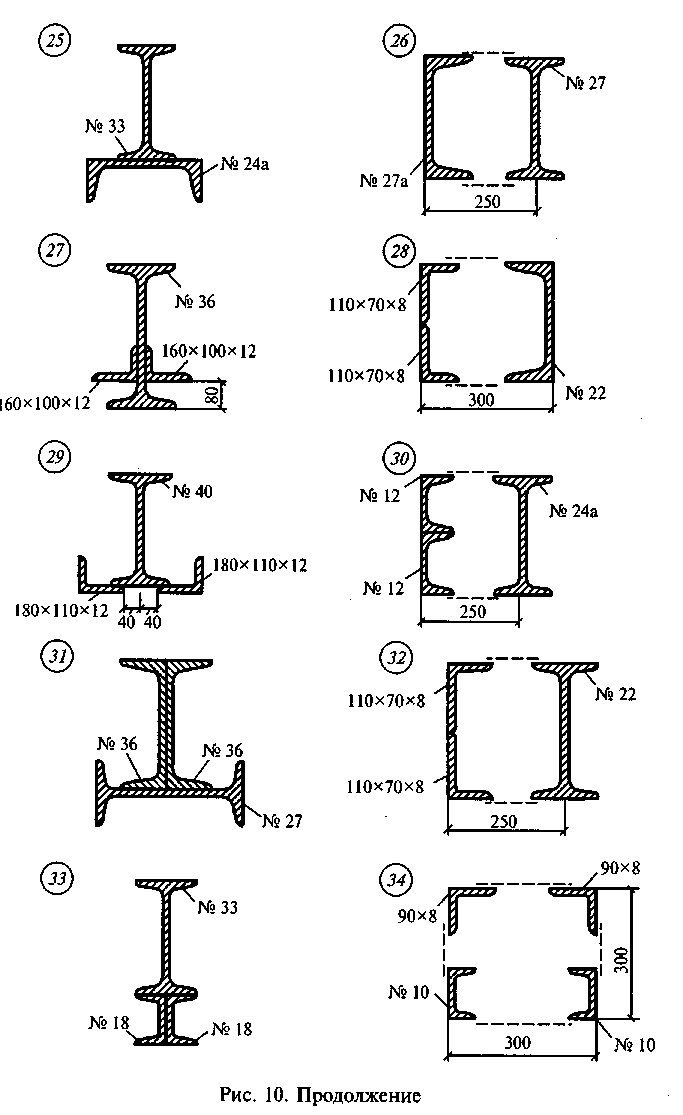
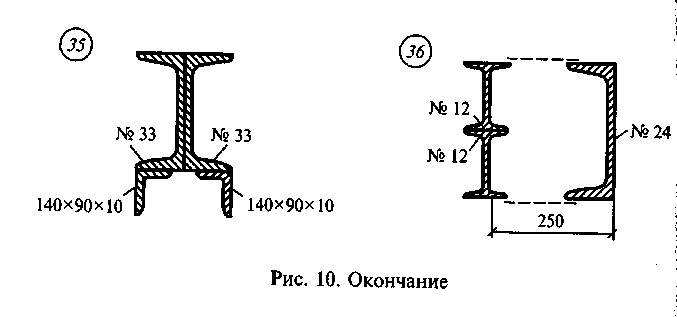
Задание
для самостоятельной работы 3.
Определить координаты центра тяжести
сечения по данным одного из вариантов,
показанных на рис. 10. Показать положение
центра тяжести на сечении.
26
27
28
29
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определить главные центральные моменты инерции, осевые моменты сопротивления сечения, составленного из стандартных профилей проката.
Сечение состоит из двух неравнополочных уголков 75×50х5 (маркировка в мм) и швеллера № 16 (№ швеллера говорит о его высоте в см).
- Определим положение центра тяжести сечения.
Сечение симметрично относительно оси у, проводим её как ось – главную и центральную. Координата хС=0. Для нахождения уС проводим случайную ось х′ (выбранную случайным образом). Обозначим центры тяжести всех профилей и выпишем необходимые характеристики профилей из сортамента прокатной стали.
Фигуры 1,2 – уголки 75×50х5
А1=А2=6,11 см2
Iх1= Iх2=34,8 см4
Iу1= Iу2=12,5 см4
Фигура 3 – швеллер №16
А3=18,1 см2,
Iх3=747 см4,
Iу3=63,3 см4.
Покажем на схеме и определим координаты у для профилей
у1 = у2 = у0 =2,39 см,
у1= –z0 =-1,8 см.
Определим координату уС по формуле

где Аi – площадь каждого профиля,
уi – координата.
Проводим главную центральную ось х вниз от оси х′ на 0,11 см, наносим т.С – центр тяжести всего сечения.
2. Определяем главные центральные моменты инерции по формулам перехода:

где Ixi , Iyi — моменты инерции каждой фигуры;
Аi – площадь сечения каждой фигуры;
аi – расстояние от центра тяжести каждой фигуры до главной центральной оси х;
bi – расстояние от центра тяжести каждой фигуры до главной центральной оси у.
Определяем аi (смотрим схему)
а1 = а2 = у1+|уС|= 2,39 + 0,11 = 2,5см,
а3= — (|у3|-|уС|) = -1,69см.
Определяем Iх. Следует обратить внимание на то, что фигура 3 – швеллер – повернут, поэтому, для определения Iх следует из сортамента взять Iу швеллера.
Iх3=63,3см4
Определяем Iу. Для швеллера (повернут) Iу3 = Iх = 747см4.
Определим размеры bi, показываем на схеме.
b1= –х0 = -1,17см,
b2= х0 = 1,17см,
b3=0, т.к. центр тяжести швеллера лежит на оси у.

Из схемы видно ,что
Тогда
Определить главные центральные моменты инерции сечения геометрической формы.
- Определим положение центра тяжести сечения.
Сечение симметрично относительно оси у, поэтому нанесем ось у – ось, на которой находится центр тяжести всего сечения. Координата хС=0, значит, следует определить координату уС.
Выберем случайную ось х′ — внизу сечения.
Разобьем сечение на простые фигуры:
фигура 1 – прямоугольник с основанием 8 см и высотой 6 см, отмечаем центр тяжести прямоугольника – т. С1
фигура 2 – равнобедренный треугольник с основанием 8 см и высотой 3 см, отмечаем его центр тяжести – т. С2.
Теперь вычислим площади каждой фигуры и определим координаты у каждой фигуры, затем координаты нанесем на схему
Прямоугольник
Треугольник
Теперь определим координату центра тяжести всего сечения по формуле:
Тогда
Отмечаем уС на схеме, центр тяжести всего сечения – т.С — и проводим через эту точку главную центральную ось х.
По формулам перехода определяем главные центральные моменты инерции сечения:

где Ixi , Iyi — моменты инерции каждой фигуры;
Аi – площадь сечения каждой фигуры;
аi – расстояние от центра тяжести каждой фигуры до главной центральной оси х;
bi – расстояние от центра тяжести каждой фигуры до главной центральной оси у.
Фигура 1 – прямоугольник
Расстояние а1 от С1 до оси х покажем на схеме. Из схемы видно, что а1=- ( уС – у1 )= -0,8 см. Так как С1 находится на оси у, то b1=0.
Фигура 2 – треугольник
Находим а2 = у2 – уС = 7 — 3,8= 3,2 см, отмечаем на схеме.
b2=0, т.к. С2 находится на оси у.
Подставляем значения в формулы перехода и определяем:
— главный центральный момент инерции сечения относительно оси х
— главный центральный момент инерции сечения относительно оси у
Таким образом,
Для заданного поперечного сечения, состоящего из швеллера и равнобокого (равнополочного) уголка требуется определить главные центральные моменты инерции
1) Вычерчиваем сечение в масштабе.
2) Разбиваем на простейшие фигуры:
1. Швеллер №30 (пользуемся сортаментом прокатных профилей):
2. Уголок :
3) В каждой фигуре найти собственный центр тяжести С1 и С2 ,провести собственные оси.
4) Выбрать вспомогательные оси .
5) Относительно вспомогательных осей определить центр тяжести всей фигуры:
Через найденный центр тяжести проводим центральные оси.
6) Находим моменты инерции всей фигуры относительно центральных осей, используя формулы перехода между параллельными осями
При определении центробежного момента инерции следует помнить ,что если фигура имеет хотя бы одну ось симметрии, то эта ось является главной, вторая ось, перпендикулярная ей, тоже главная. Центробежный момент относительно главных осей равен 0. Таким образом, для швеллера
Для уголка см4, знак зависит от расположения уголка (см. Таблицы «Знак центробежного момента для уголков»). В нашем случае он положительный.
Здесь: аi – расстояния между центральной осью Х и собственным центром тяжести каждой фигуры,
bi – расстояние между центральной осью Y и собственным центром тяжести каждой фигуры
Как видим из вычислений, центробежный момент инерции сечения значит, центральные оси Х;Y не являются главными!
7) Определим положение главных осeй через угол α0:
Знак «-» означает, что надо повернуть оси Х, У по часовой стрелке.
8) Определим главные моменты инерции сечения

Проверка выполняется.
Найти главные центральные моменты инерции.
- Подготовка исходных данных.
Из сортамента выписываем:
— для двутавра №10:
— для швеллера №20:
Нумеруем составные части, показываем их центры тяжести (С1, С2, С3) и собственные центральные оси каждой из них (х1,у1; х2,у2; х3,у3).
2. Поскольку сечение имеет одну ось симметрии, то она – одна из главных центральных (у0). Найдем положение центра тяжести на этой оси. Для этого выберем вспомогательную ось х‘, перпендикулярную оси симметрии, и реализуем формулу:
которая и определит расстояние от оси х‘ до искомого центра тяжести.
Тогда А=А1+А2+А3=2×20+14,3+28,83=83,15 см2,
тогда
Показываем на схеме центр тяжести «С» и проводим вторую главную центральную ось х0.
Ординаты собственных центров тяжести простых фигур в системе главных центральных осей:
3. Вычисляем главные центральные моменты инерции
Итак,
Определить главные центральные моменты инерции сечения.
Составные простые части сечения: прямоугольник 100×60см (I), полукруг r=30см (IIи III), треугольник 100×30см (IV).
Вертикальная ось симметрии у0 является одной из главных центральных осей.
- Найдем положение центра тяжести сечения на оси симметрии. Для этого выберем вспомогательную ось х‘, перпендикулярную оси симметрии. Пусть она совпадает с осями: х1, х2, х3
.
Общая площадь А = А1 — А2 — А3 + А4 = 6000 – 1415 – 1415 + 1500 = 4670см2.
Статический момент относительно вспомогательной оси х‘:
Тогда
значит, центр тяжести сечения располагается на 12,8см выше вспомогательной оси х‘.
2. Вычисляем осевые моменты инерции
Они и будут главными центральными моментами инерции сечения.
Здесь применялись формулы:
Найти главные центральные моменты инерции сечения, состоящего из листа 40×2см и двух уголков №14/9.
Исходные данные из сортамента для неравнобокого уголка №14/9.
Сечение имеет одну ось симметрии. Она – одна из главных центральных. Обозначаем её х0. Чтобы показать вторую главную центральную ось, надо найти положение центра тяжести на оси симметрии:
Выбираем вспомогательную ось у‘, перпендикулярную к оси симметрии и вычисляем статический момент сложного сечения относительно этой оси:
Проводим главную центральную ось у0 через найденный центр тяжести.
Вычисляем непосредственно главные центральные моменты инерции:
Таким образом,
Требуется найти главные центральные моменты инерции.
Сечение имеет две оси симметрии. Следовательно, центр тяжести совпадает с точкой пересечения этих осей, а сами они оказываются главными центральными осями.
Остается лишь вычислить осевые моменты инерции относительно осей х0 и у0.
«Разбиваем» сечение на простые фигуры: прямоугольник 6×8см и два круга r=1см. Тогда:
Итак
,
Требуется определить величины главных центральных моментов инерции.
Сечение имеет одну ось симметрии.
На основании первого признака главных осей для симметричных сечений можно утверждать, что ось симметрии является одной из главных центральных осей. Обозначаем ее «у0». Значит, вторая главная центральная ось, перпендикулярная оси симметрии, должна проходить через центр тяжести сечения.
Следовательно, нам достаточно только найти положение центра тяжести на оси симметрии, а для этого необходимо вычислить одну лишь координату его по формуле:
С этой целью выбираем вспомогательную ось х‘, «разбиваем» сложное сечение на прямоугольник со сторонами 10 и 4см и треугольник с основанием 4см и высотой 3см.
Тогда:
Проводим через найденный центр тяжести вторую главную центральную ось х0.
Расстояние между осями х1 и х0: а1=5 — 4,3 =0,7см, а расстояние между осями х2 и х0: а2=10 – 1 — 4,3 = 4,7см.
Таким образом, положение главных центральных осей найдено, осталось вычислить величины главных центральных моментов инерции:
х‘, у‘ – вспомогательные оси при определении положения центра тяжести сечения,
Sх’, Sу’ – статические моменты относительно вспомогательных осей,
хс, ус – координаты центра тяжести сечения, а также и обозначение случайных (т.е. не главных) центральных осей,
х0, у0 – главные центральные оси,
α0 – угол поворота главных центральных осей от случайных центральных осей хс и ус,
, — главные центральные моменты инерции,
сi – центры тяжести отдельных фигур, из которых состоит сечение сложной формы,
хi, уi – собственные центральные оси отдельных фигур, а также и координаты центров тяжести отдельных фигур в системе вспомогательных осей х‘, у‘,
аi, вi – расстояния между собственными центральными осями отдельных фигур хi, уi и случайными центральными осями всего сечения хс, ус.
Требуется определить положение главных центральных осей и величины главных центральных моментов инерции.
Сечение имеет сложную форму, состоит их 4х простых фигур:
I – швеллера №30а,
II – прямоугольника 2×40см,
III – двутавра №20а,
IV – равнобокого уголка №12 (d=10мм).
Всё начинается с подготовки исходных данных. С этой целью необходимо сделать выписки из таблиц Сортамента прокатных сечений (см. рубрику «Таблицы»).
Этап 0. Подготовительный
Фигура I. Швеллер №30а
Фигура II – прямоугольник 2×40см, В сортаменте прокатной стали этой фигуры нет, поскольку все геометрические характеристики ее свободно вычисляются
Фигура III. Двутавр №20а.
Фигура IV. Равнобокий уголок №12 (d=10мм).
Пользуясь данными сортамента, на схеме сечения, вычерченной в достаточно крупном масштабе, показываем положение центров тяжести каждой из фигур и собственные центральные оси хi, уi.
Этап 1. Определение положения центра тяжести сечения. Сечение не имеет осей симметрии. Поэтому придётся определять две координаты центра тяжести, используя формулы:
Для реализации этих формул выбираем вспомогательные оси х‘ и у‘ (см.схему сечения).
Площади отдельных фигур: А1=43,89см2, А2=2×40=80см2,
А3=35,5см2, А4=23,3см2.
Координаты центров тяжести отдельных фигур:
Площадь всего сечения А=182,7см2.
Тогда координаты собственных центров тяжести отдельных фигур в системе случайных центральных осей хс, усбудут:
а1=2,66см, b1=-7,5см
а2=-2,34см, b2=-1,93см
а3=-7,34см, b3=9,07см
а4=14,33см, b4=2,4см.
Этап 2. Определение моментов инерции относительно случайных центральных осей хс, ус.
Справочные сведения о знаке собственного центробежного момента инерции уголка (равнобокого и неравнобокого):
Справочные сведения для определения собственного центробежного момента инерции неравнобокого уголка:
Этап 3. Определение положения главных центральных осей
Положительный угол α0 соответствует повороту против часовой стрелки главных осей относительно случайных (см.схему).
Этап 4. Определение величин главных центральных моментов инерции
Правило: Ось с максимальным главным моментом инерции «тяготеет» к более тяжелой случайной оси. Поэтому в нашем случае:
тогда
Проверки.
- Выполнение закона суммы осевых моментов инерции.
Для этого сравним
.
получаем:
Разница в последней цифре дает незначительную погрешность <<5%, что вполне допустимо в инженерных расчетах.
2. Проверка правильности вычислений.
Суть ее в том, что если все сделано правильно, то центробежный момент инерции сечения относительно найденных нами главных осей должен равняться нулю.
Подставляя сюда и sin13˚20’=0,2306, cos13˚20’=0,9730,имеем
погрешность составляет:
И эта проверка выполняется.
Определение центра тяжести плоской фигуры
Центр тяжести применяется при исследовании устойчивости положений равновесия тел и сплошных сред, находящихся под действием сил тяжести и в некоторых других случаях, а именно: в сопротивлении материалов и в строительной механике – при использовании правила Верещагина.
При определении координат центра тяжести используются следующие методы:
1) метод симметрии: если сечение имеет центр симметрии или ось симметрии, то центр тяжести находится в центре симметрии или на оси симметрии;
2) метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых, легко определить;
3) метод отрицательных площадей: этот способ является частным случаем способа разделения. Он используется, когда сечение имеет вырезы, срезы, полости (отверстия), которые рассматриваются как часть сечения с отрицательной площадью.
При решении задач на определение центра тяжести сложных сечений следует придерживаться следующего порядка:
1. Выбрать метод, который наиболее применим к данной задаче.
2. Разбить сложное сечение на простые части, для которых центры тяжести известны.
3. Выбрать оси координат. При этом необходимо помнить, что: если тело имеет плоскость симметрии, то его центр тяжести лежит в этой плоскости; если тело имеет ось симметрии, то его центр тяжести лежит на этой оси; если тело имеет центр симметрии, то его центр тяжести совпадает с центром симметрии.
4. Определить координаты центров тяжести отдельных частей относительно выбранных осей.
5. Используя формулы определить искомые координаты центра тяжести заданного сечения.

где А1, А2 … Аn – площади простых сечений;
x1, x2 … xn, y1, y2 … yn– координаты центра тяжести простых сечений.
Координаты центра тяжести сложной плоской фигуры определяются после разделения ее на простые фигуры и определения их центров тяжести.
Координаты центра тяжести некоторых простых плоских фигур:
Порядок выполнения задания:
1) начертить заданное сложное сечение (фигуру), выбрать оси координат.
2) разбить сложное сечение на простые, для которых центры тяжести и силы тяжести известны;
3) определить необходимые данные для простых сечений:
4)определить координаты центров тяжести простых сечений относительно выбранных осей координат;
5) определить положение центра тяжести сложного сечения.
Найти координаты центра тяжести плоской фигуры, изображенной на рисунке.
Выбираем оси координат так, чтобы нижний и левый край фигуры совпали с ними:
Делим заданную плоскую фигуру на прямоугольник (1), треугольник (2) и круг (3).
Вычисляем площади этих фигур:
S1 = 10·20 = 200; S2 = 0,5·5·10 = 25; S3 = π·9 =28,3.
Определяем координаты центров тяжести фигур:
x1 = 10; y1 = 5.
x2 = 5; y2 = 11,7.
x3= 5; y3= 5.
Координаты центра тяжести всей плоской фигуры: