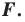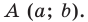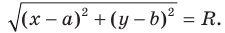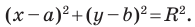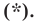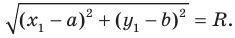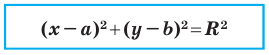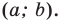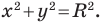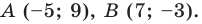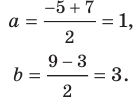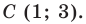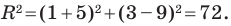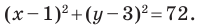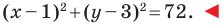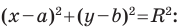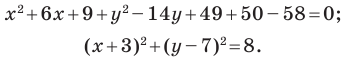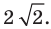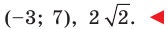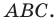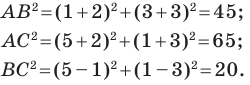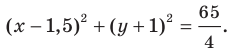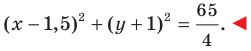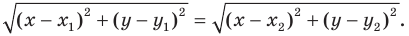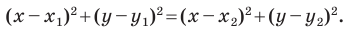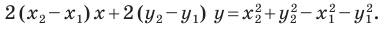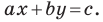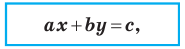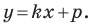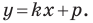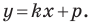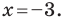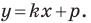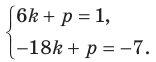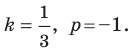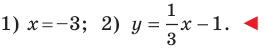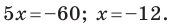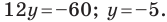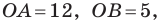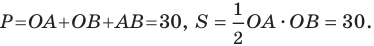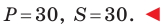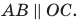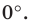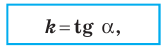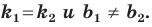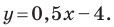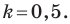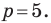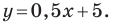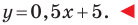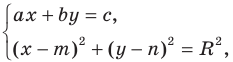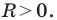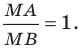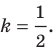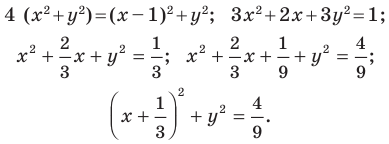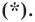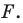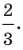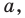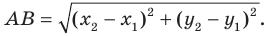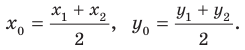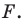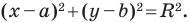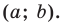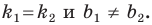Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как найти координаты точки
Поддержать сайт
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».
Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).
Запомните!
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Координатная плоскость
Координатная плоскость – это прямоугольная система координат, состоящая из двух взаимно перпендикулярных осей, имеющих направление, начало отсчета и единичные отрезки.
ОПРЕДЕЛЕНИЕ КООРДИНАТЫ ТОЧКИ:
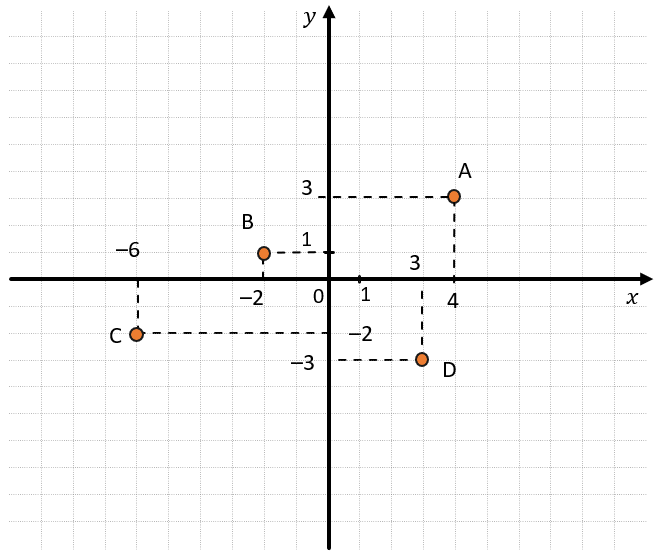
Любая точка на этой плоскости имеет свои координаты в соответствии с координатами осей. Рассмотрим координатную плоскость, на которой отмечены несколько точек:
Найдем координаты каждой из этих точек.
Чтобы найти координаты точки, нужно:
1. Провести перпендикуляры от точки к каждой координатной оси.
2. Перпендикуляр, упавший на ось Ох, попадет на координату x данной точки, а перпендикуляр, упавший на ось Оу, попадет на координату y данной точки.
Например:
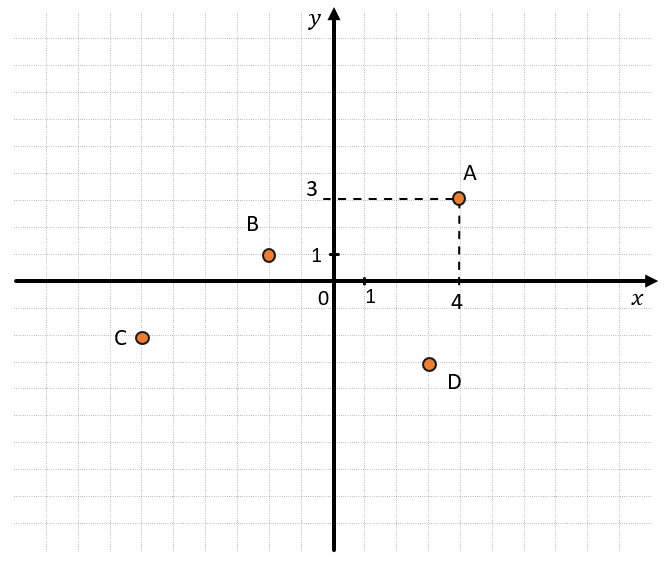
Координата точки А на оси Ох равна 4, а на оси ОУ равна 3. Координаты записывают так:
(А(4;3))
Координата на оси Ох называется абсциссой.
Координата на оси Оу называется ординатой.
Сначала записывают координату оси абсцисс, потом координату оси ординат.
Найдем координаты других точек:
Таким образом:
({Aleft( 4;3 right) }{Bleft( –2;1 right) }{Cleft( –6;–2 right) }{Dleft( 3;–4 right)})
КООРДИНАТНЫЕ ЧЕТВЕРТИ:
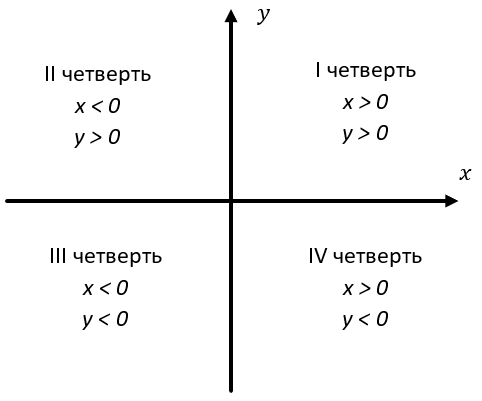
Координаты могут быть как положительными, так и отрицательными, в зависимости от того, с какой стороны от начала координат находится точка. Мы видим, что каждая из представленных точек имеет разные знаки для абсцисс и ординат. Все потому, что они находятся в разных четвертях координатной плоскости, которые образуют координатные оси. На каждой из этих четвертей координаты x и y имеют определенные знаки:
Первой четвертью является четверть, где и абсцисса, и ордината принимают положительные значения. В этой четверти находилась точка А.
Дальше четверти нумеруются против часовой стрелки. Таким образом точка В находилась во второй четверти и имела отрицательную абсциссу и положительную ординату, точка С имела только отрицательные координаты, а точка D имела положительную абсциссу и отрицательную ординату.
СИММЕТРИЯ:
Виды симметрии:
-
Относительно оси Ох (ордината меняет знак на противоположный).
-
Относительно оси Оу (абсцисса меняет знак на противоположный).
-
Относительно начала координат (абсцисса и ордината меняют знаки на противоположные).
Суть симметрии:
Рассмотрим каждый вид симметрии подробнее.
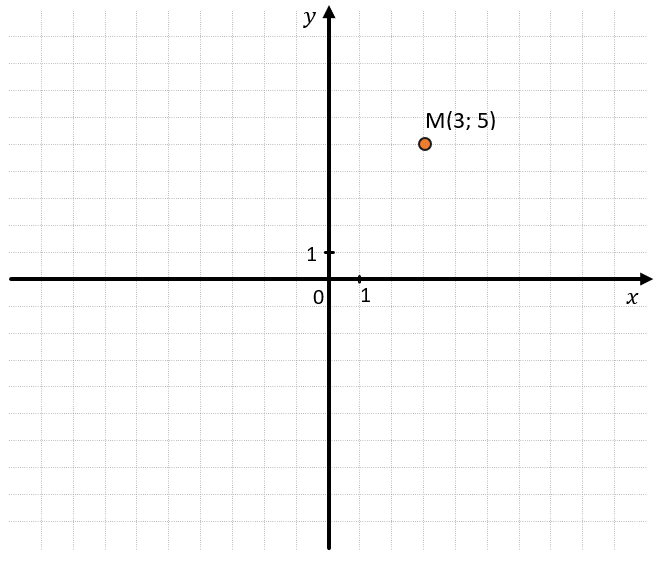
На плоскости можно симметрично отражать любые построение. Представим всю координатную плоскость, как сгибаемый лист бумаги, и отметим на нем точку M(3; 5):
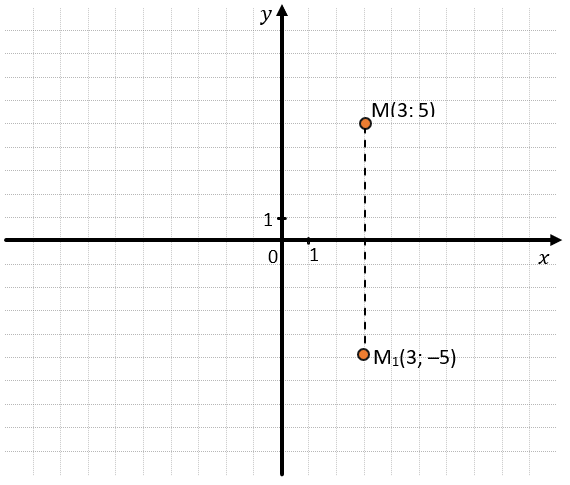
1. Согнем наш лист по линии оси Ох. Получим, что наша точка отпечатается на другой стороне от этой оси. Получим новую точку М1 с координатами (3; –5). Эта точка будет симметрична данной относительно оси Ox:
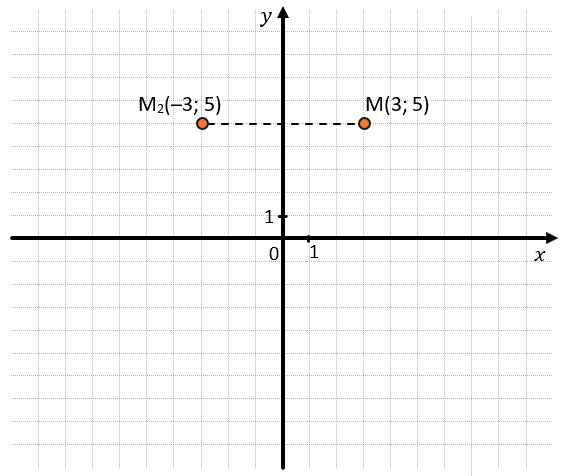
2. Согнем наш лист по линии оси Оу. Тогда наша точка «отпечатается» на другой стороне от этой оси и попадет в точку М2(–3; 5). Эта точка будет симметрична данной относительно оси Оу:
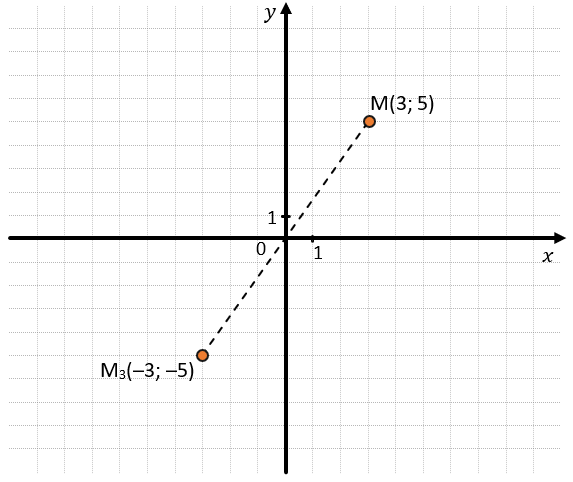
3. Если мы согнем лист сначала относительно оси Ох, а потом еще и по оси Оу (неважно в каком порядке), то наша точка попадет в точку, M3(–3; –5). Эта точка будет симметрична данной относительно начала координат:
ПОСТРОЕНИЕ ТОЧКИ НА КООРДИНАТНОЙ ПЛОСКОСТИ ПО КООРДИНАТАМ:
Мы можем как узнать координаты точек на плоскости, так и сами их задавать.
Чтобы отметить на координатной плоскости точку с конкретными координатами, нужно:
1. Провести через абсциссу точки прямую, перпендикулярную оси Ох.
2. Провести через ординату точки прямую, перпендикулярную оси Оу.
3. Точка пересечения этих прямых и будет являться точкой с заданными координатами. Отметить эту точку.
Например:
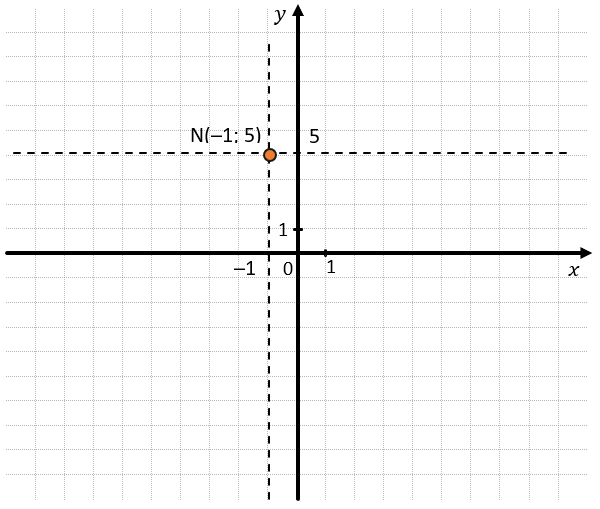
Построим точку на координатной плоскости по координатам: (Nleft( –1;5 right))
Точка N имеет координаты ((–1; 5)).
1. На оси Ох отметим координату –1 и проведем через нее перпендикуляр к этой оси.
2. На оси Оу отметим координату 5 и проведем через нее перпендикуляр к этой оси.
3. На пересечении этих прямых отметим точку (N(–1; 5)):
Прямые, которые мы провели в первом и втором пункте можно записать в виде формул:
({x = –1 }{y = 5})
Такие формулы описывают, в каких точках прямые пересекают оси под прямым углом.
ОПИСАНИЕ УЧАСТКОВ ПЛОСКОСТИ:
Задавать на плоскости можно не только координаты точек и прямых, но и выделять некоторые площади. Например, разбиение координатной плоскости на четверти задается неравенствами.
Рассмотрим несколько случаев выделения частей плоскости.
Пример №1:
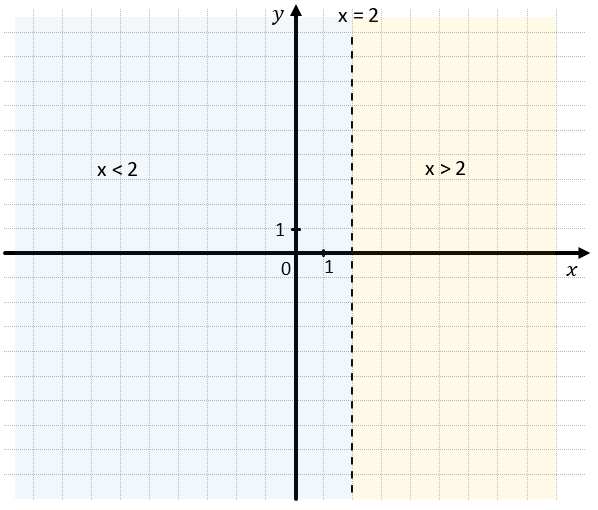
Выделите область, которая включает в себя множество точек так, что: (x > 2)
Это выражение описывает множество точек на плоскости, абсциссы которых больше 2.
-
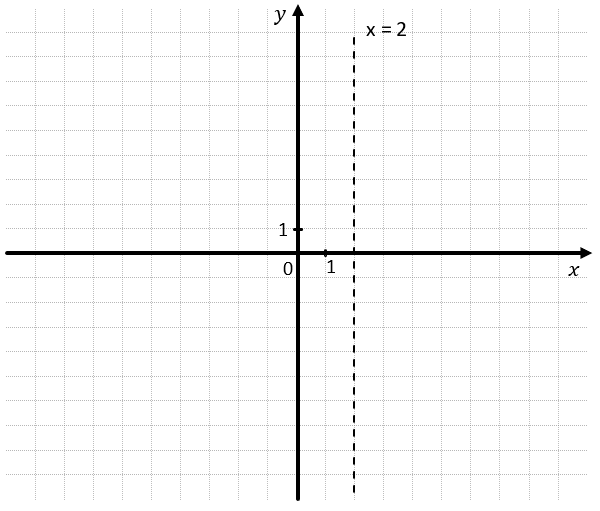
Чтобы выделить это множество на плоскости, проведем прямую (x = 2):
2. Таким образом эта прямая поделила всю координатную плоскости на две полуплоскости: одна находится справа от прямой, вторая слева.
– Если мы отметим любую точку слева от прямой (x = 2), то увидим, что абсцисса этой точки будет меньше, чем 2.
– Если мы отметим любую точку справа от прямой (x = 2), то увидим, что абсцисса этой точки будет больше, чем 2.
3. Нам подходит второй вариант, значит множество точек, для которых неравенство (x > 2) верное – красная полуплоскость:
Пример №2:
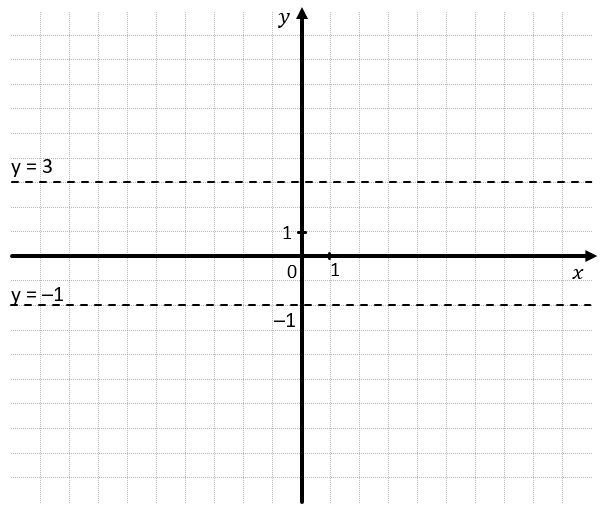
Выделите область, которая включает в себя множество точек так, что: (–1 < y < 3)
Здесь нам так же заданы определённые точки, но уже с ограничением ординаты. Нужно выделить область, все точки на которой будут иметь ординату больше, чем –1 и меньше, чем 3. Алгоритм построение такой же, как в примере №1, только у нас появилась вторая прямая.
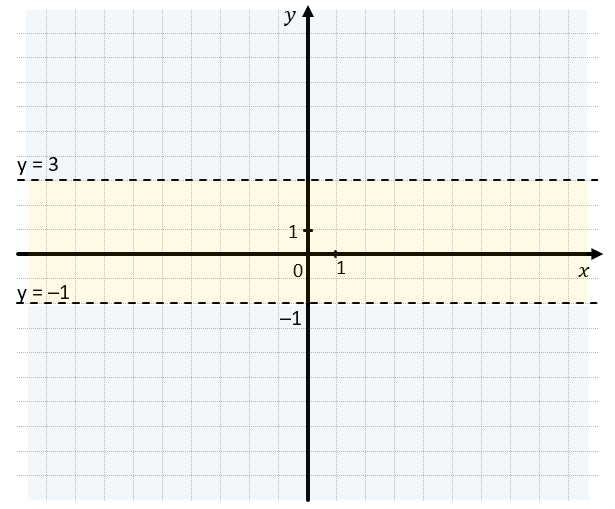
1. Проведем прямые (y = –1) и (y = 3):
2. У нас появилось три полуплоскости. Проанализируем каждые из них:
– Если поставить точку выше прямой (y = 3,) её ордината будет больше 3.
– Если поставить точку ниже прямой (y = –1), её ордината будет меньше –1.
– Если поставить точку между прямыми (y = –1 )и (y = 3), её ордината будет больше –1 и меньше 3.
3. Нам подходит область между прямыми, где (–1 < y < 3):
Елена Борисовна Калюжная
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Основные сведения о координатной плоскости
Каждый объект (например, дом, место в зрительном зале, точка на карте) имеет свой упорядоченный адрес (координаты), который имеет числовое или буквенное обозначение.
Математики разработали модель, которая позволяет определять положение объекта и называется координатной плоскостью.
Чтобы построить координатную плоскость нужно провести $2$ перпендикулярные прямые, на конце которых указываются с помощью стрелок направления «вправо» и «вверх». На прямые наносятся деления, а точка пересечения прямых является нулевой отметкой для обеих шкал.
Определение 1
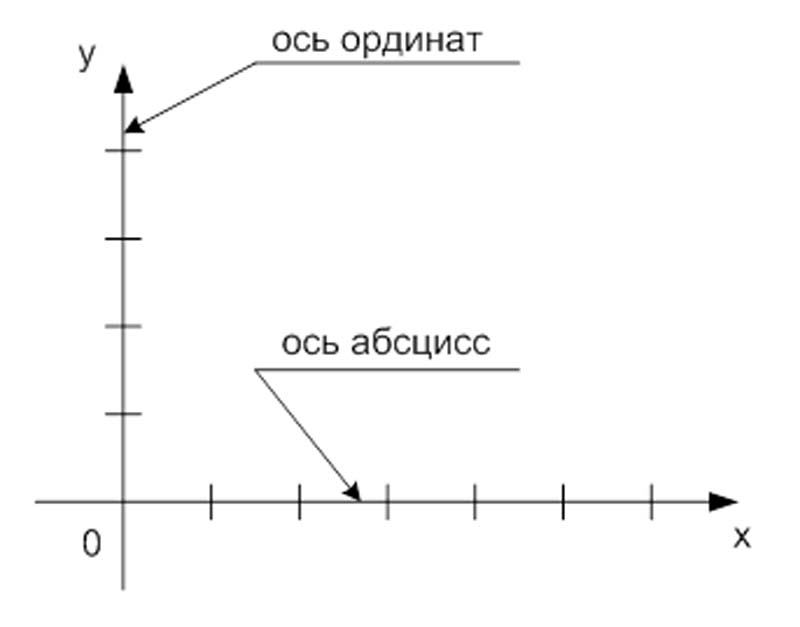
Горизонтальная прямая называется осью абсцисс и обозначается х, а вертикальная прямая называется осью ординат и обозначается у.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Две перпендикулярные оси х и у с делениями составляют прямоугольную, или декартовую, систему координат, которую предложил французский философ и математик Рене Декарт.
Координатная плоскость
Координаты точки
Точка на координатной плоскости определяется двумя координатами.
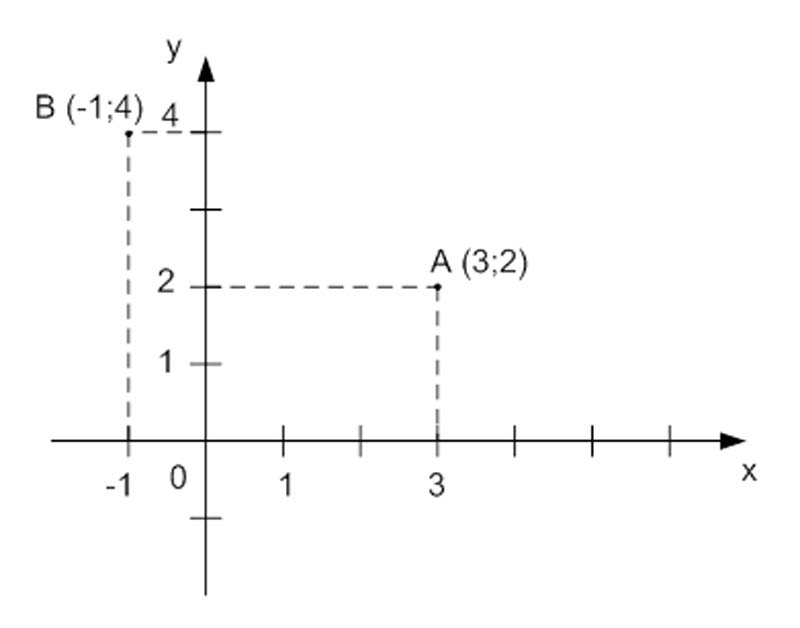
Чтобы определить координаты точки $A$ на координатной плоскости нужно через нее провести прямые, которые будут параллельны координатным осям (на рисунке выделены пунктирной линией). Пересечение прямой с осью абсцисс дает координату $x$ точки $A$, а пересечение с осью ординат дает координату у точки $A$. При записи координат точки сначала записывается координата $x$, а затем координата $y$.
«Координаты на плоскости» 👇
Точка $A$ на рисунке имеет координаты $(3; 2)$, а точка $B (–1; 4)$.
Для нанесения точки на координатную плоскость действуют в обратном порядке.
Построение точки по заданным координатам
Пример 1
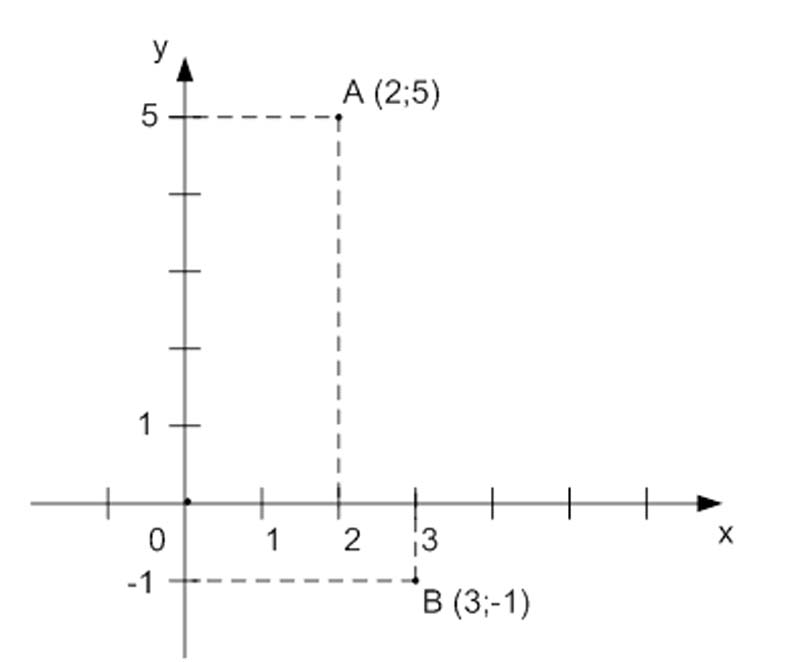
На координатной плоскости построить точки $A(2;5)$ и $B(3; –1).$
Решение.
Построение точки $A$:
- отложим число $2$ на оси $x$ и проведем перпендикулярную прямую;
- на оси у отложим число $5$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $A$ с координатами $(2; 5)$.
Построение точки $B$:
- отложим на оси $x$ число $3$ и проведем перпендикулярную оси х прямую;
- на оси $y$ отложим число $(–1)$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $B$ с координатами $(3; –1)$.
Пример 2
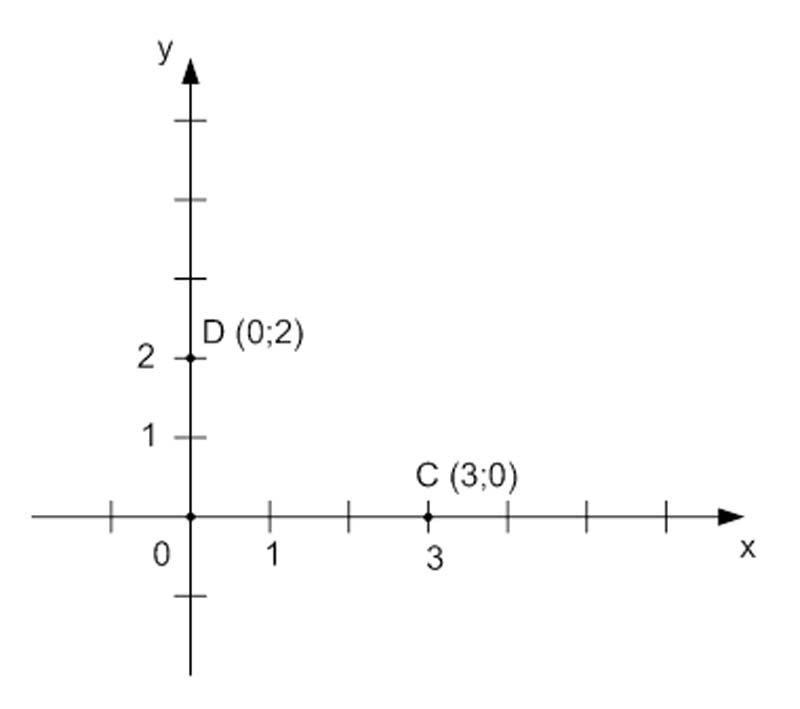
Построить на координатной плоскости точки с заданными координатами $C (3; 0)$ и $D(0; 2)$.
Решение.
Построение точки $C$:
- отложим число $3$ на оси $x$;
- координата $y$ равна нулю, значит точка $C$ будет лежать на оси $x$.
Построение точки $D$:
- отложим число $2$ на оси $y$;
- координата $x$ равна нулю, значит, точка $D$ будет лежать на оси $y$.
Замечание 1
Следовательно, при координате $x=0$ точка будет лежать на оси $y$, а при координате $y=0$ точка будет лежать на оси $x$.
Пример 3
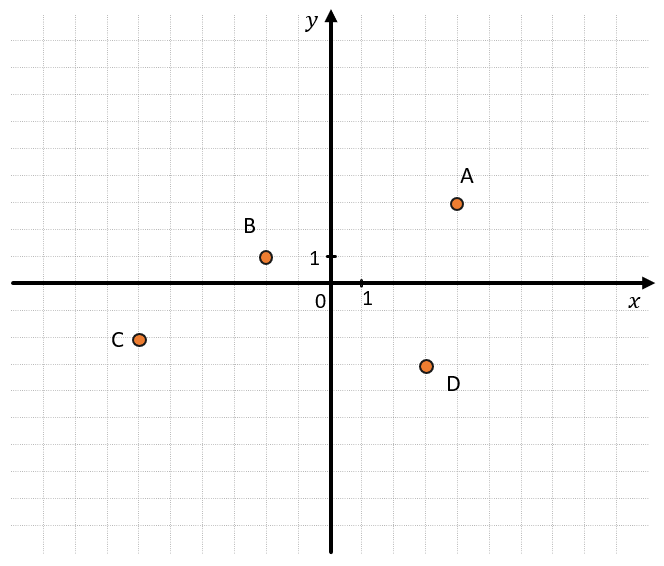
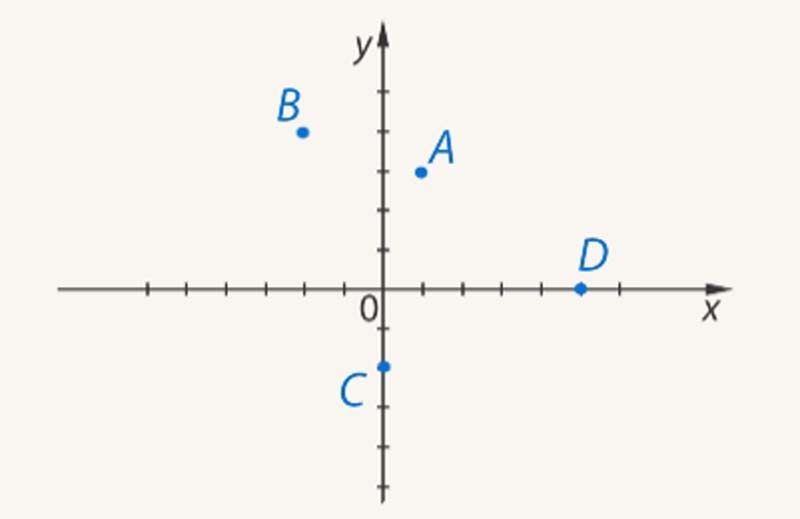
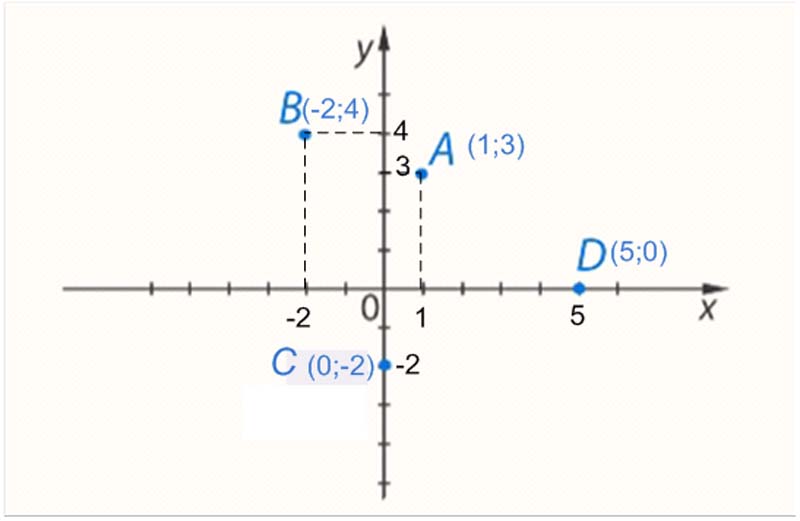
Определить координаты точек A, B, C, D.$
Решение.
Определим координаты точки $A$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Таким образом, получаем, что точка $A (1; 3).$
Определим координаты точки $B$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Получаем, что точка $B (–2; 4).$
Определим координаты точки $C$. Т.к. она расположена на оси $y$, то координата $x$ этой точки равна нулю. Координата у равна $–2$. Таким образом, точка $C (0; –2)$.
Определим координаты точки $D$. Т.к. она находится на оси $x$, то координата $y$ равна нулю. Координата $x$ этой точки равна $–5$. Таким образом, точка $D (5; 0).$
Пример 4
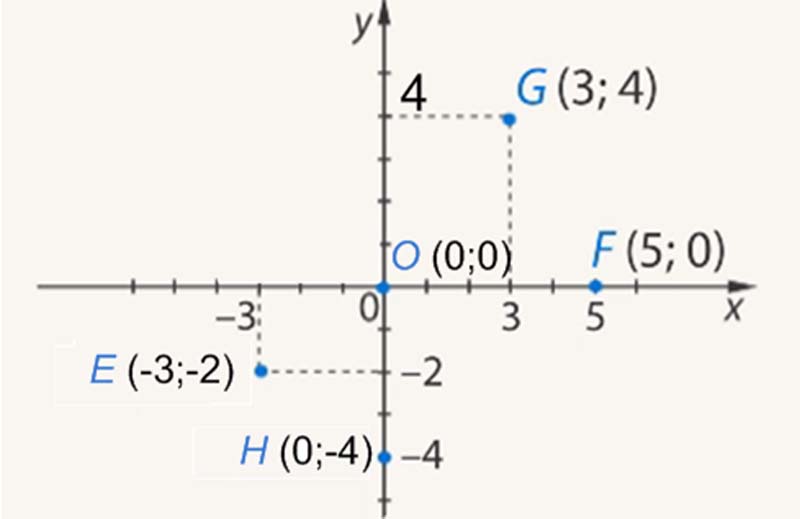
Построить точки $E(–3; –2), F(5; 0), G(3; 4), H(0; –4), O(0; 0).$
Решение.
Построение точки $E$:
- отложим число $(–3)$ на оси $x$ и проведем перпендикулярную прямую;
- на оси $y$ отложим число $(–2)$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $E (–3; –2).$
Построение точки $F$:
- координата $y=0$, значит, точка лежит на оси $x$;
- отложим на оси $x$ число $5$ и получим точку $F(5; 0).$
Построение точки $G$:
- отложим число $3$ на оси $x$ и проведем перпендикулярную прямую к оси $x$;
- на оси $y$ отложим число $4$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $G(3; 4).$
Построение точки $H$:
- координата $x=0$, значит, точка лежит на оси $y$;
- отложим на оси $y$ число $(–4)$ и получим точку $H(0; –4).$
Построение точки $O$:
- обе координаты точки равны нулю, значит, точка лежит одновременно и на оси $y$, и на оси $x$, следовательно является точкой пересечения обеих осей (началом координат).
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Координатная плоскость
Указать положение точки на плоскости можно с помощью координат. Для этого проведем на плоскости две перпендикулярные координатные прямые так, чтобы их начала отсчета совпадали.
Эти прямые называют осями координат, точку их пересечения О – начало отсчета.
Горизонтальная ось – ось абсцисс, обозначают буквой 

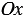
Вертикальная ось – ось ординат, обозначают буквой 

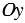
Оси 

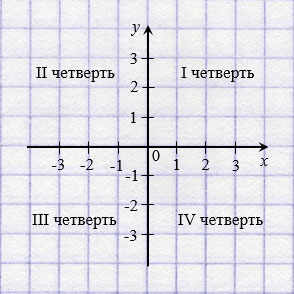
Координатные оси разбивают плоскость на четыре части, которые называют координатными четвертями и нумеруют так, как показано на рисунке ниже.
Отметим на координатной плоскости точку А. Проведем через нее прямую АВ, перпендикулярную оси абсцисс (АВ 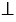
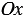
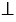
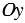
Точка В на оси 





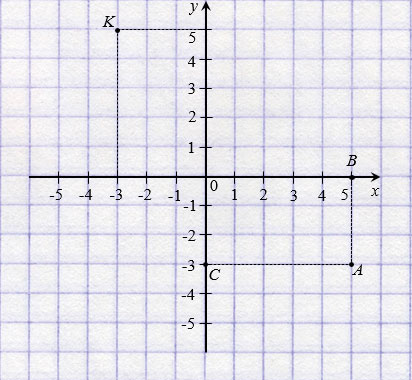
Обратите внимание, записывая координаты точки, абсциссу всегда ставят на первое место, а ординату – на второе. Если числа 5 и 

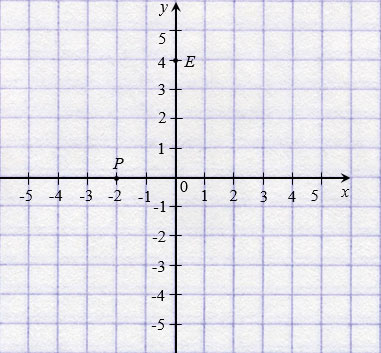
У начала координат абсцисса и ордината равны нулю, записывают так: О(0; 0). Если точка лежит на оси абсцисс, то ее ордината равна нулю, а если на оси ординат, то нулю равна ее абсцисса. На рисунке ниже: Р(
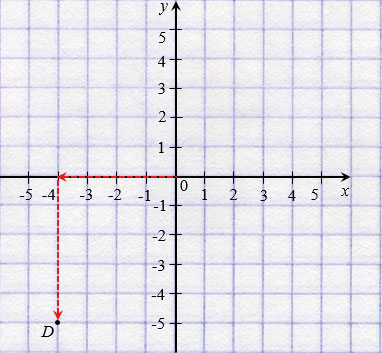
Чтобы попасть в точку D с координатами (


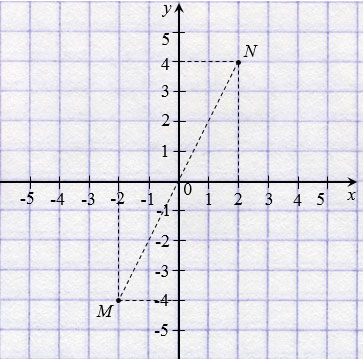
Две точки с противоположными абсциссами и ординатами симметричны относительно начала координат.
На рисунке ниже точки N(2; 4) и М(

Две точки, имеющие равные ординаты и противоположные абсциссы, симметричны относительно оси ординат.
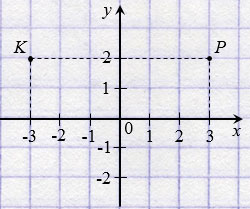
На рисунке ниже точки Р(3; 2) и К(
Две точки, имеющие равные абсциссы и противоположные ординаты, симметричны относительно оси абсцисс.
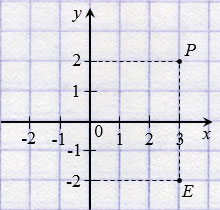
На рисунке ниже точки Р(3; 2) и Е(3; 
Советуем посмотреть:
Перпендикулярные прямые
Осевая и центральная симметрии
Параллельные прямые
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1308,
Мерзляк, Полонский, Якир, Учебник
Номер 1317,
Мерзляк, Полонский, Якир, Учебник
Номер 1336,
Мерзляк, Полонский, Якир, Учебник
Номер 10,
Мерзляк, Полонский, Якир, Учебник
Задание 1395,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1402,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1443,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1456,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1533,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1573,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 822,
Мерзляк, Полонский, Якир, Учебник
Номер 837,
Мерзляк, Полонский, Якир, Учебник
Номер 876,
Мерзляк, Полонский, Якир, Учебник
Номер 879,
Мерзляк, Полонский, Якир, Учебник
Номер 887,
Мерзляк, Полонский, Якир, Учебник
Номер 899,
Мерзляк, Полонский, Якир, Учебник
Номер 925,
Мерзляк, Полонский, Якир, Учебник
Номер 996,
Мерзляк, Полонский, Якир, Учебник
Номер 1215,
Мерзляк, Полонский, Якир, Учебник
Номер 10,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 63,
Мерзляк, Полонский, Якир, Учебник
Номер 326,
Мерзляк, Полонский, Якир, Учебник
Номер 327,
Мерзляк, Полонский, Якир, Учебник
Номер 333,
Мерзляк, Полонский, Якир, Учебник
Номер 339,
Мерзляк, Полонский, Якир, Учебник
Номер 342,
Мерзляк, Полонский, Якир, Учебник
Номер 343,
Мерзляк, Полонский, Якир, Учебник
Номер 10,
Мерзляк, Полонский, Якир, Учебник
Номер 352,
Мерзляк, Полонский, Якир, Учебник
Номер 363,
Мерзляк, Полонский, Якир, Учебник
Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
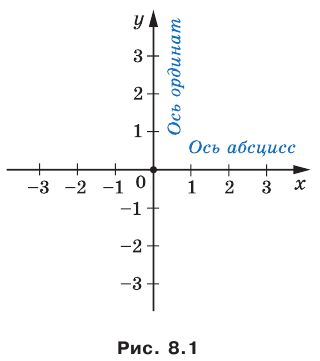
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
Договорились координатную плоскость с осью
Координаты точки на плоскости 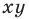
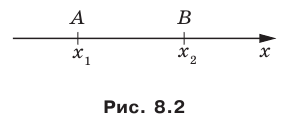
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 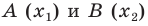
Научимся находить расстояние между точками 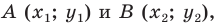
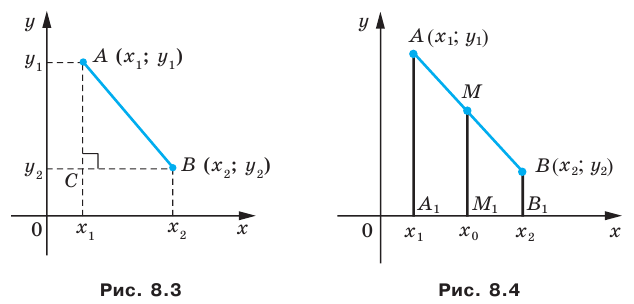
Рассмотрим случай, когда отрезок 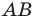
Через точки 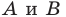
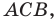
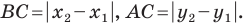
Тогда формулу расстояния между точками 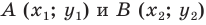
Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок 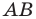
Пусть 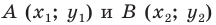
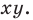
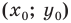
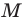
Рассмотрим случай, когда отрезок 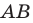
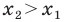
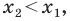
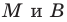
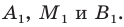
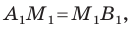
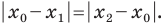
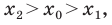
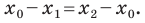

Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок 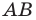
Пример №1
Докажите, что треугольник с вершинами в точках 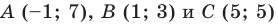
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
Следовательно, 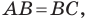
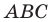
Поскольку 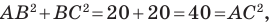
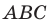
Пример №2
Точка 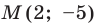
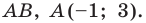
Решение:
Обозначим 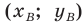
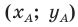
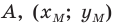
Поскольку 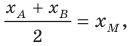
Аналогично
Ответ:
Пример №3
Докажите, что четырехугольник 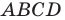
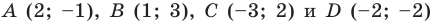
Решение:
Пусть точка 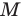
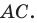
Следовательно,
Пусть точка 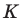
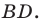
Следовательно,
Таким образом, точки 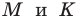
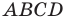
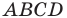
Найдем диагонали параллелограмма:
Следовательно, диагонали параллелограмма 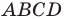
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
Координаты 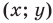
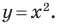
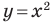
Определение. Уравнением фигуры 
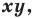
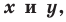
- если точка принадлежит фигуре
то ее координаты являются решением данного уравнения;
- любое решение
данного уравнения является координатами точки, принадлежащей фигуре
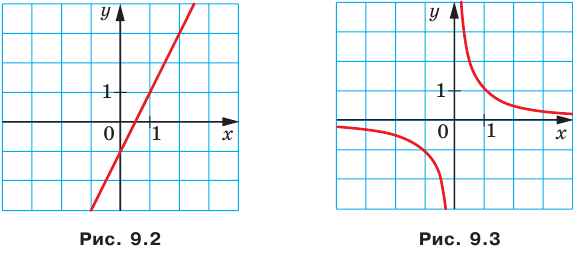
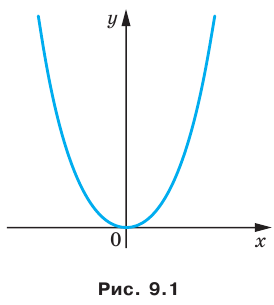
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 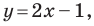
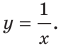
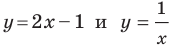
Если данное уравнение является уравнением фигуры 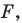
Пользуясь этими соображениями, выведем уравнение окружности радиуса 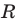
Пусть 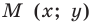
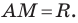
Отсюда
Мы показали, что координаты 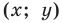
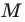
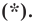
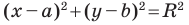
Пусть пара чисел 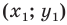
Тогда 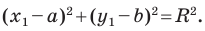
Это равенство показывает, что точка 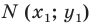
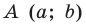
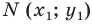
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса 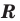
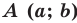
Верно и такое утверждение: любое уравнение вида 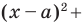
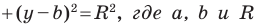
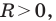
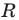
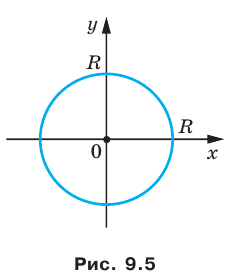
Если центром окружности является начало координат (рис. 9.5), то 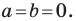
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок 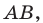
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 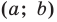
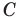
Следовательно,
Радиус окружности 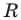
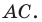
Следовательно, искомое уравнение имеет вид
Ответ:
Пример №5
Докажите, что уравнение 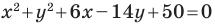
Решение:
Представим данное уравнение в виде
Следовательно, данное уравнение является уравнением окружности с центром в точке 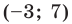
Ответ:
Пример №6
Докажите, что треугольник с вершинами в точках 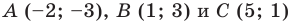
Решение:
Найдем квадраты сторон данного треугольника:
Поскольку 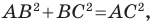
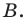
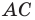
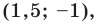
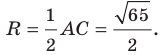
Ответ:
Уравнение прямой
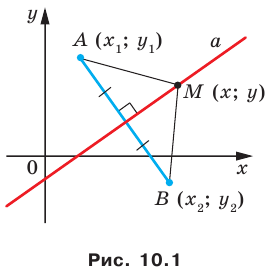
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
Пусть 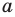
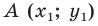
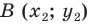
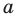
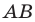
Пусть 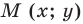
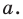
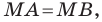
Мы показали, что координаты 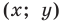
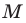
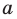
Теперь покажем, что любое решение уравнения 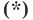
Пусть 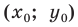
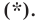
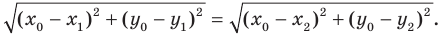
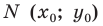
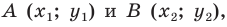
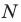
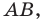
Итак, мы доказали, что уравнение 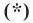
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 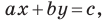
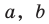
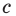
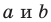
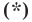
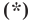
Раскроем скобки и приведем подобные слагаемые. Получим:
Обозначив 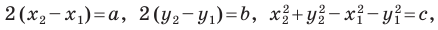
Поскольку точки 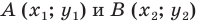
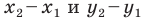
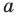
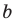
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
где 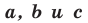
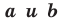
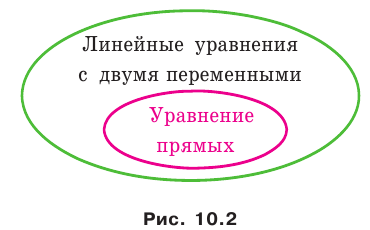
Верно и такое утверждение: любое уравнение вида 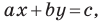
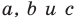
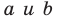
Если 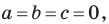
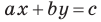
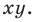
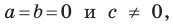
Из курса алгебры 7 класса вы знаете, что уравнение вида 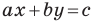
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 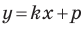
Перепишем уравнение 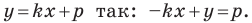
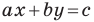
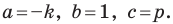
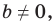
А любую ли прямую на плоскости можно задать уравнением вида 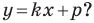
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида
Вместе с тем, если в уравнении прямой 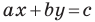
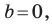
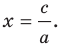
Если 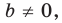
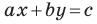
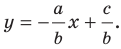
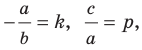
Следовательно, если 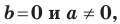
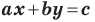
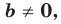
Уравнение невертикальной прямой удобно записывать в виде
Данная таблица подытоживает материал, рассмотренный в этом пункте.
Пример №7
Составьте уравнение прямой, проходящей через точки:
Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 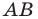
2) Поскольку данные точки имеют разные абсциссы, то прямая 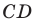
Подставив координаты точек 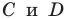
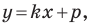
Решив эту систему уравнений, находим, что
Ответ:
Пример №8
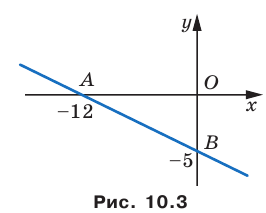
Найдите периметр и площадь треугольника, ограниченного прямой 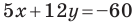
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при 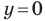
С осью ординат: при 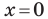
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 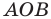
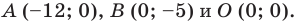
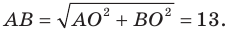
Ответ:
Угловой коэффициент прямой
Рассмотрим уравнение 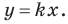
Покажем, что прямые 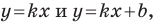
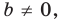
Точки 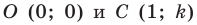
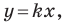
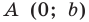
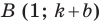
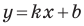
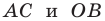
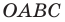
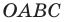
Теперь мы можем сделать такой вывод: если 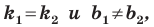
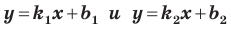
Пусть прямая 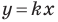
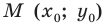
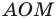
Если прямая 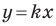
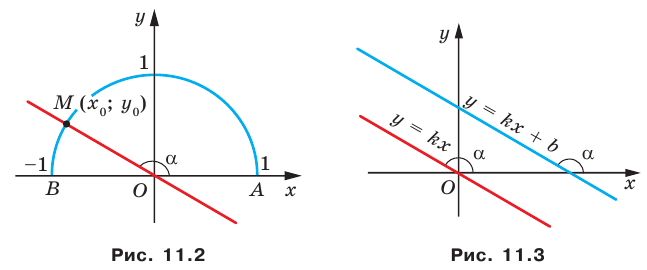
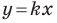
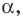
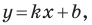
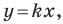
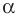
Рассмотрим прямую 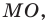
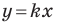
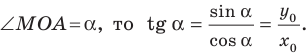
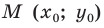
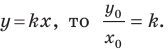
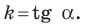
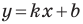
где 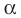
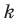
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 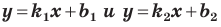
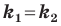
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 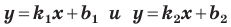
Пример №9
Составьте уравнение прямой, которая проходит через точку 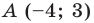
Решение:
Пусть уравнение искомой прямой 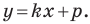
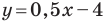
Следовательно, искомое уравнение имеет вид 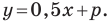
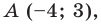
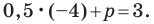
Искомое уравнение имеет вид
Ответ:
Метод координат
Мы часто говорим: прямая 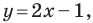
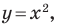
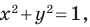
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
где числа 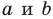
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
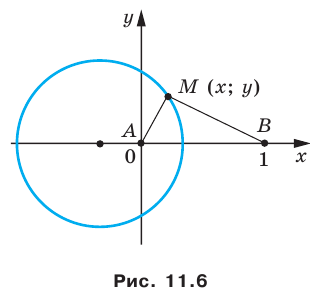
Отметим на плоскости две точки 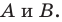
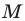
Это серединный перпендикуляр отрезка 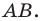
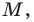
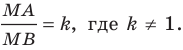
Плоскость, на которой отмечены точки 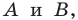
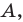
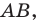
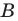
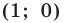
Пусть 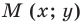
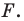
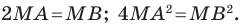
Следовательно, если точка 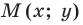
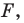
Пусть 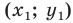
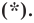
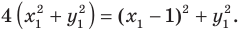
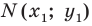
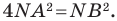
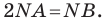
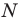
Таким образом, уравнением фигуры 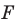
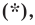
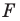
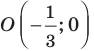
Мы решили задачу для частного случая, когда 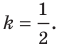
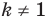
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 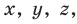
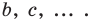
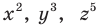
Справочный материал
Расстояние между двумя точками
Расстояние между точками 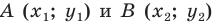
Координаты середины отрезка
Координаты 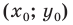
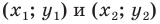
Уравнение фигуры
Уравнением фигуры 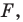
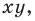
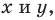
1) если точка принадлежит фигуре 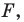
2) любое решение 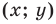
Уравнение окружности
Уравнение окружности радиуса 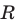
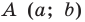
Любое уравнение вида 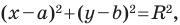
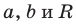
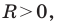
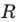
Уравнение прямой
Уравнение прямой имеет вид 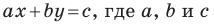
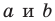
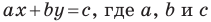
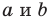
Если 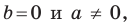
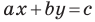
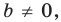
Угловой коэффициент прямой
Коэффициент 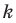
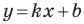
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 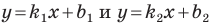
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование














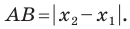
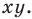
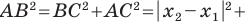
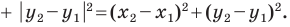

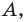
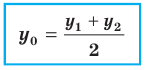
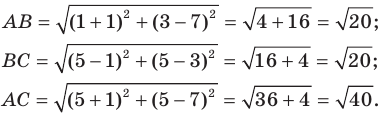

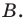
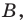
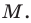
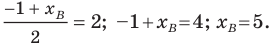
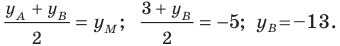
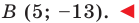
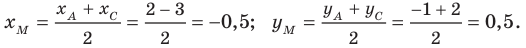
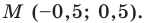
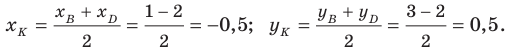
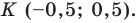
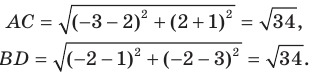

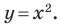
 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;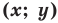 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре