В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат Oxyz в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x, y, и z, которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Любую плоскость, заданную в прямоугольной системе координат Oxyz трехмерного пространства, можно определить уравнением Ax + By + Cz + D = 0. В свою очередь, любое уравнение Ax + By + Cz + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A, B, C, D – некоторые действительные числа, и числа A, B, C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
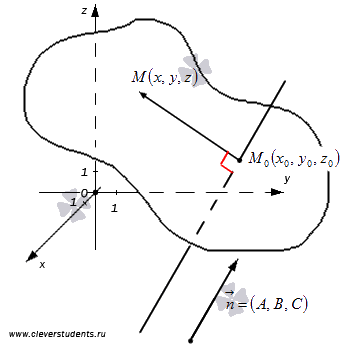
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида Ax + By + Cz + D = 0. Допустим, задана некоторая плоскость и точка M0(x0, y0, z0), через которую эта плоскость проходит. Нормальным вектором этой плоскости является n→= (A, B, C). Приведем доказательство, что указанную плоскость в прямоугольной системе координат Oxyz задает уравнение Ax + By + Cz + D = 0.
Возьмем произвольную точку заданной плоскости M(x, y, z).В таком случае векторы n→= (A, B, C) и M0M→=(x-x0, y-y0, z-z0) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n→, M0M→=Ax-x0+B(y-y0)+C(z-z0)=Ax+By+Cz-(Ax0+By0+Cz0)
Примем D=-(Ax0+By0+Cz0) , тогда уравнение преобразуется в следующий вид: Ax + By + Cz + D = 0. Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида Ax + By + Cz + D = 0 задает некоторую плоскость в прямоугольной системе координат Oxyz трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А, B, C одновременно не являются равными нулю. Тогда существует некоторая точка M0(x0, y0, z0), координаты которой отвечают уравнению Ax + By + Cz + D = 0, т.е. верным будет равенство Ax0 + By0 + Cz0 + D = 0. Отнимем левую и правую части этого равенства от левой и правой частей уравнения Ax + By + Cz + D = 0. Получим уравнение вида
A(x-x0) + B(y-y0) + C(z-z0) + D = 0, и оно эквивалентно уравнению Ax + By + Cz + D = 0. Докажем, что уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает некоторую плоскость.
Уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n→=(A, B, C) и M0M→=x-x0, y-y0, z-z0. Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A(x-x0) + B(y-y0) + C(z-z0) + D = 0 множество точек M(x, y, z) задает плоскость, у которой нормальный вектор n→=(A, B, C). При этом плоскость проходит через точку M(x0, y0, z0). Иначе говоря, уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает в прямоугольной системе координат Oxyz трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение Ax + By + Cz + D = 0 также определяет эту плоскость. Теорема доказана полностью.
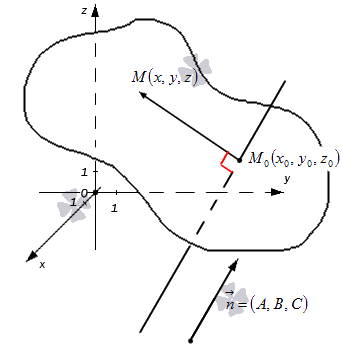
Уравнение вида Ax + By + Cz + D = 0 называют общим уравнением плоскости в прямоугольной системе координат Oxyz трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ·Ax+λ·By+λ·Cz+λ·D=0, где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением Ax+By+Cz+D=0, поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x-2·y+3·z-7=0 и -2·x+4·y-23·z+14=0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида Ax+By+Cz+D=0( при конкретных значениях чисел A, B, C, D). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
Укажем пример как иллюстрацию этих утверждений.
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4x + 5y – 5z + 20 = 0, и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4x + 5y – 5z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.
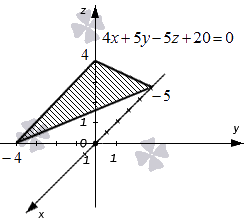
Общее уравнение плоскости, проходящей через точку
Повторимся: точка M0(x0, y0, z0) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением Ax+By+Cz+D=0 в том случае, когда подставив координаты точки M0(x0, y0, z0) в уравнение Ax+By+Cz+D=0, мы получим тождество.
Заданы точки M0(1, -1, -3) и N0(0, 2, -8) и плоскость, определяемая уравнением 2x+3y-z-2=0. Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
Решение
Подставим координаты точки М0 в исходной уравнение плоскости:
2·1+3·(-1)-(-3)-2=0⇔0=0
Мы видим, что получено верное равенство, значит точка M0(1, -1, -3) принадлежит заданной плоскости.
Аналогично проверим точку N0. Подставим ее координаты в исходное уравнение:
2·0+3·2-(-8)-2=0⇔12=0
Равенство неверно. Таким, образом, точка N0(0, 2, -8) не принадлежит заданной плоскости.
Ответ: точка М0 принадлежит заданной плоскости; точка N0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n→=(A, B, C) – нормальный вектор для плоскости, определяемой уравнением Ax+By+Cz+D=0. Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
В прямоугольной системе координат задана плоскость 2x+3y-z+5=0. Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x, y, z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n→ исходной плоскости имеет координаты 2, 3, -1 . В свою очередь, множество нормальных векторов запишем так:
λ·n→=λ·2, λ·3, -λ, λ∈R, λ≠0
Ответ: λ·2, λ·3, -λ, λ∈R, λ≠0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n→=(A, B, C)является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M0(x0, y0, z0), принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n→=(A, B, C) будет выглядеть так: Ax+By+Cz+D=0. По условию задачи точка M0(x0, y0, z0) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство:Ax0+By0+Cz0+D=0
Вычитая соответственно правые и левые части исходного уравнения и уравнения Ax0+By0+Cz0+D=0, получим уравнение вида A(x-x0)+B(y-y0)+C(z-z0)=0. Оно и будет уравнением плоскости, проходящей через точку M0(x0, y0, z0) и имеющей нормальный вектор n→=(A, B, C).
Возможно получить это уравнение другим способом.
Очевидным фактом является то, что все точки М (x, y, z) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n→=(A, B, C) и M0M→=(x-x0, y-y0, z-z0) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
n→, M0M→=A(x-x0)+B(y-y0)+C(z-z0)=0
Задана точка М0(-1, 2, -3), через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n→=(3, 7, -5). Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x0=-1, y0=2, z0=-3, A=3, B=7, C=-5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A(x-x0)+B(y-y0)+C(z-z0)=0
И получим:
3(x-(-1))+7(y-2)-5(z-(-3))=0⇔3x+7y-5z-26=0
- Допустим, М (x, y, z) – некоторая точки заданной плоскости. Определим координаты вектора M0M→ по координатам точек начала и конца:
M0M→=(x-x0, y-y0, z-z0)=(x+1, y-2, z+3)
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
n→, M0M→=0⇔3(x+1)+7(y-2)-5(z+3)=0⇔⇔3x+7y-5z-26=0
Ответ: 3x+7y-5z-26=0
Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А, B, C, D отличны от нуля, общее уравнение плоскости Ax+By+Cz+D=0 называют полным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
- В случае, когда D = 0, мы получаем общее неполное уравнение плоскости: Ax+By+Cz+D=0⇔Ax+By+Cz=0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О (0, 0, 0), то придем к тождеству:
A·0+B·0+C·0=0⇔0≡0
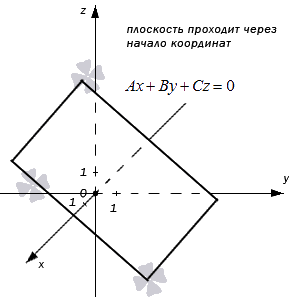
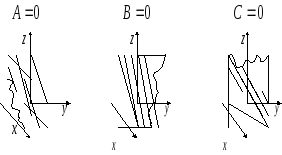
- Если А = 0, В ≠ 0, С ≠ 0, или А ≠ 0, В = 0, С ≠0, или А ≠ 0, В ≠ 0, С = 0, то общие уравнения плоскостей имеют вид соответственно: By+Cz+D=0, или Ax+Cz+D=0, или Ax+By+D=0. Такие плоскости параллельны координатным осям Оx, Oy, Oz соответственно. Когда D=0, плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей By+Cz+D=0, Ax+Cz+D=0 и Ax+By+D=0 задают плоскости, которые перпендикулярны плоскостям Oyz, Oxz, Ozy соответственно.

- При А=0, В=0, С≠0, или А=0, В≠0, С=0, или А≠0, В=0, С=0 получим общие неполные уравнения плоскостей: Cz+D=0 ⇔z+DC=0⇔z=-DC⇔z=λ, λ∈R или By+D=0⇔y+DB=0⇔y=-DB⇔y=λ, λ∈R или Ax+D=0⇔x+DA=0⇔x=-DA⇔x=λ, λ∈R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям Oxy, Oxz, Oyz соответственно и проходят через точки 0, 0, -DC, 0, -DB, 0 и -DA, 0, 0 соответственно. При D=0 уравнения самих координатных плоскостей Oxy, Oxz, Oyz выглядят так: z=0, y=0, x=0
соответственно.

Задана плоскость, параллельная координатной плоскости Oyz и проходящая через точку М0(7, -2, 3). Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости Oyz, а, следовательно, может быть задана общим неполным уравнением плоскости Ax+D=0, A≠0⇔x+DA=0. Поскольку точка M0(7, -2, 3) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x+DA=0, иначе говоря, должно быть верным равенство 7+DA=0 . Преобразуем: DA=-7, тогда требуемое уравнение имеет вид: x-7=0.
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости Oyz. Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости Oyz: i→=(1, 0, 0). Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A(x-x0)+B(y-y0)+C(z-z0)=0⇔⇔1·(x-7)+0·(y+2)+0·(z-3)=0⇔⇔x-7=0
Ответ: x-7=0
Задана плоскость, перпендикулярная плоскости Oxy и проходящая через начало координат и точку М0(-3, 1, 2).
Решение
Плоскость, которая перпендикулярна координатной плоскости Oxy определяется общим неполным уравнением плоскости Ax+By+D=0 (А≠0, В≠0). Условием задачи дано, что плоскость проходит через начало координат, тогда D=0 и уравнение плоскости принимает вид Ax+By=0⇔x+BAy=0.
Найдем значение BA. В исходных данных фигурирует точка М0(-3, 1, 2), координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: -3+BA·1=0, откуда определяем BA=3.
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x+3y=0.
Ответ: x+3y=0.
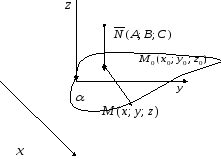
Пусть
точка
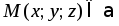 ,
,
тогда вектор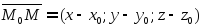 .
.
Так
как
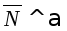 ,
,
то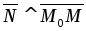 ,
,
тогда
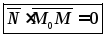 – векторное
– векторное
уравнение плоскости
или
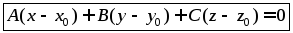
–
уравнение
плоскости в координатах
§19Общее уравнение плоскости
В
уравнении
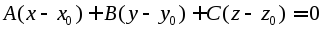
раскроем
скобки и приведем подобные:
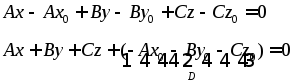
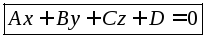
– общее
уравнение плоскости,
где
А,
В, С
– координаты нормального вектора;
х,
у, z
– координаты точки М.
Частные
случаи:
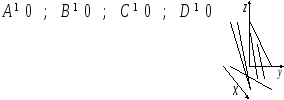
-
D
= 0 – плоскость, проходит через начало
координат:
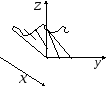
-
Если отсутствует
одна из координат, то плоскость
параллельна соответствующей оси:
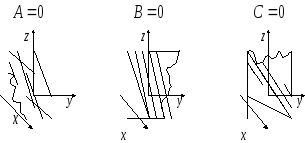
-
Если
отсутствует одна из координат, то
плоскость параллельна соответствующей
оси:
-
Если отсутствуют
две координаты, то плоскость параллельна
соответствующей координатной плоскости:
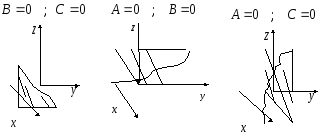
Для
построения плоскости необходимо общее
уравнение, путем деления на свободный
член D,
привести к уравнению плоскости в отрезках
на осях:
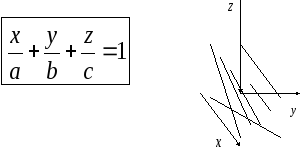
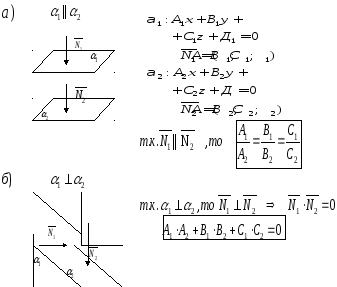
§20 Взаимное расположение двух плоскостей
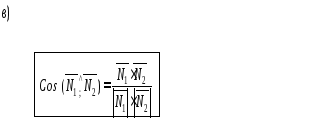
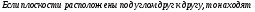
§21 Нахождение координат любой точки, принадлежащей данной плоскости.
Чтобы
найти координаты точки, принадлежащей
плоскости, две координаты выбирают
произвольно, подставляют в уравнение
плоскости, а третью координату находят
из полученного равенства.
Пример:
Найти координаты какой-нибудь точки,
принадлежащей плоскости 2x+y-z-3=0
Возьмем
х=0, у=0 и подставим в уравнение плоскости,
получим –z-3=0,
откуда z=-3.
Следовательно, искомая точка А (0;0;-3)
22Прямая в пространстве
Определение
1.
Прямая в
системе ОХУZ
рассматривается как линия пересечения
двух плоскостей.
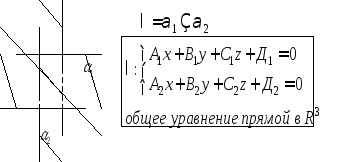
Прямая
в
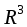 может быть задана с помощью направляющего
может быть задана с помощью направляющего
вектора.
Определение
2.
Вектор
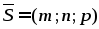 ,
,
параллельный прямой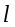 называетсянаправляющим
называетсянаправляющим
вектором прямой.

Пусть
точка
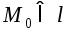 .
.
Возьмем на этой прямой произвольную
точку
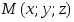 .
.
Тогда
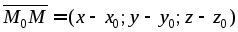 .
.
Так
как
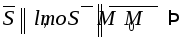 их координаты пропорциональны:
их координаты пропорциональны:
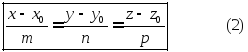
–
канонические
уравнения прямой,
где m,
n, p –
любые действительные числа, в том числе
и ноль, т.к.
запись символическая.
Но одновременно все три координаты m,
n, p нулю
быть равными не могут.
§23Угол между прямыми в пространстве
Угол
между прямыми
и угол между направляющими векторами
этих прямых связаны соотношением:
= 1
или
= 1800
– 1.
Угол между направляющими векторами
находится из скалярного произведения.
Таким образом:

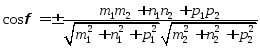 .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Продолжим изучение темы уравнение плоскости. В этой статье мы всесторонне рассмотрим общее уравнение плоскости в трехмерном пространстве в фиксированной прямоугольной системе координат. Сначала получим вид общего уравнения плоскости, приведем примеры и необходимые пояснения. Далее остановимся на общем уравнении плоскости, проходящей через заданную точку пространстве. В заключении разберем частные случаи общего уравнения плоскости, рассмотрим общее неполное уравнение плоскости и приведем подробные решения задач.
Навигация по странице.
Прежде чем записать общее уравнение плоскости, напомним определение прямой перпендикулярной к плоскости: прямая перпендикулярна к плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. Из этого определения следует, что любой нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в этой плоскости. Этот факт мы используем при доказательстве следующей теоремы, которая задает вид общего уравнения плоскости.
Начнем с доказательства первой части теоремы.
Равенство 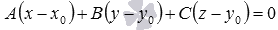 представляет собой необходимое и достаточное условие перпендикулярности векторов
представляет собой необходимое и достаточное условие перпендикулярности векторов  и
и 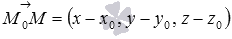 . Иными словами, координаты плавающей точки
. Иными словами, координаты плавающей точки 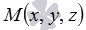 удовлетворяют уравнению
удовлетворяют уравнению 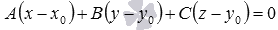 тогда и только тогда, когда перпендикулярны векторы
тогда и только тогда, когда перпендикулярны векторы  и
и 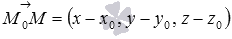 . Тогда, учитывая факт, приведенный перед теоремой, мы можем утверждать, что если справедливо равенство
. Тогда, учитывая факт, приведенный перед теоремой, мы можем утверждать, что если справедливо равенство 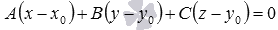 , то множество точек
, то множество точек 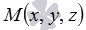 определяет плоскость, нормальным вектором которой является
определяет плоскость, нормальным вектором которой является  , причем эта плоскость проходит через точку
, причем эта плоскость проходит через точку 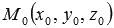 . Другими словами, уравнение
. Другими словами, уравнение 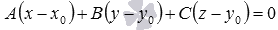 определяет в прямоугольной системе координат Oxyz в трехмерном пространстве указанную выше плоскость. Следовательно, эквивалентное уравнение
определяет в прямоугольной системе координат Oxyz в трехмерном пространстве указанную выше плоскость. Следовательно, эквивалентное уравнение  определяет эту же плоскость. Первая часть теоремы доказана.
определяет эту же плоскость. Первая часть теоремы доказана.
Приступим к доказательству второй части.
Пусть нам дана плоскость, проходящая через точку 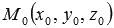 , нормальным вектором которой является
, нормальным вектором которой является  . Докажем, что в прямоугольной системе координат Oxyz ее задает уравнение вида
. Докажем, что в прямоугольной системе координат Oxyz ее задает уравнение вида  .
.
Для этого, возьмем произвольную точку этой плоскости. Пусть этой точкой будет 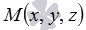 . Тогда векторы
. Тогда векторы  и
и 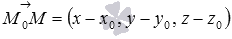 будут перпендикулярны, следовательно, их скалярное произведение будет равно нулю:
будут перпендикулярны, следовательно, их скалярное произведение будет равно нулю: 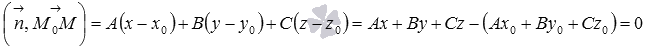 . Приняв
. Приняв 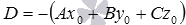 , уравнение примет вид
, уравнение примет вид  . Это уравнение и задает нашу плоскость. Итак, теорема полностью доказана.
. Это уравнение и задает нашу плоскость. Итак, теорема полностью доказана.
Уравнение  называется общим уравнением плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве.
называется общим уравнением плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве.
Общее уравнение плоскости вида  , где
, где  — некоторое действительное число, отличное от нуля, определяет в прямоугольной системе координат Oxyz плоскость, совпадающую с плоскостью
— некоторое действительное число, отличное от нуля, определяет в прямоугольной системе координат Oxyz плоскость, совпадающую с плоскостью  , так как задает то же самое множество точек трехмерного пространства. К примеру, уравнения
, так как задает то же самое множество точек трехмерного пространства. К примеру, уравнения  и
и  задают одну и ту же плоскость, так как им удовлетворяют координаты одних и тех же точек трехмерного пространства.
задают одну и ту же плоскость, так как им удовлетворяют координаты одних и тех же точек трехмерного пространства.
Немного поясним смысл теоремы.
Приведем пример, иллюстрирующий последнюю фразу.

Содержание
- Общее уравнение плоскости, проходящей через точку.
- Неполное общее уравнение плоскости.
- Метод координат
- Координаты вектора
- Скрещивающиеся прямые
- Уравнение плоскости
- Расстояние от точки до плоскости
- Расстояние между скрещивающимися прямыми
- Геометрия. 11 класс
Общее уравнение плоскости, проходящей через точку.
Еще раз повторим, что точка 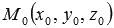 принадлежит плоскости, которая задана в прямоугольной системе координат в трехмерном пространстве общим уравнением плоскости
принадлежит плоскости, которая задана в прямоугольной системе координат в трехмерном пространстве общим уравнением плоскости  , если при подстановке координат точки
, если при подстановке координат точки 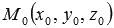 в уравнение
в уравнение  оно обращается в тождество.
оно обращается в тождество.
Принадлежат ли точки  и
и  плоскости, общее уравнение которой имеет вид
плоскости, общее уравнение которой имеет вид  .
.
Подставим координаты точки М в общее уравнение плоскости:  . В результате приходим к верному равенству, следовательно, точка
. В результате приходим к верному равенству, следовательно, точка  лежит в плоскости.
лежит в плоскости.
Проделаем такую же процедуру с координатами точки N :  . Получаем неверное равенство, поэтому, точка
. Получаем неверное равенство, поэтому, точка  не лежит в плоскости, определенной общим уравнением плоскости
не лежит в плоскости, определенной общим уравнением плоскости  .
.
М лежит в плоскости, а N – не лежит.
Из доказательства теоремы об общем уравнении плоскости виден один полезный факт: вектор  является нормальным вектором плоскости
является нормальным вектором плоскости  . Таким образом, если мы знаем вид общего уравнения плоскости, то мы сразу можем записать координаты нормального вектора этой плоскости.
. Таким образом, если мы знаем вид общего уравнения плоскости, то мы сразу можем записать координаты нормального вектора этой плоскости.
Плоскость в прямоугольной системе координат Oxyz задана общим уравнением плоскости  . Запишите координаты всех нормальных векторов этой плоскости.
. Запишите координаты всех нормальных векторов этой плоскости.

Теперь рассмотрим обратную задачу – задачу составления уравнения плоскости, когда известны координаты ее нормального вектора. Очевидно, что существует бесконечно много параллельных плоскостей, нормальным вектором которых является вектор  . Поэтому, зададим дополнительное условие, чтобы обозначить одну конкретную плоскость. Будем считать, что точка
. Поэтому, зададим дополнительное условие, чтобы обозначить одну конкретную плоскость. Будем считать, что точка 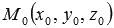 принадлежит плоскости. Таким образом, задав нормальный вектор
принадлежит плоскости. Таким образом, задав нормальный вектор  и точку плоскости
и точку плоскости 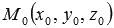 , мы зафиксировали плоскость (смотрите раздел способы задания плоскости в пространстве). Получим общее уравнение этой плоскости.
, мы зафиксировали плоскость (смотрите раздел способы задания плоскости в пространстве). Получим общее уравнение этой плоскости.
Общее уравнение плоскости с нормальным вектором  имеет вид
имеет вид  . Так как точка
. Так как точка 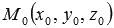 лежит на плоскости, то ее координаты удовлетворяют уравнению плоскости, следовательно, справедливо равенство
лежит на плоскости, то ее координаты удовлетворяют уравнению плоскости, следовательно, справедливо равенство 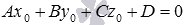 . Вычтем из левой и правой части равенства
. Вычтем из левой и правой части равенства  левую и правую части равенства
левую и правую части равенства 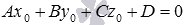 соответственно. При этом получаем уравнение вида
соответственно. При этом получаем уравнение вида 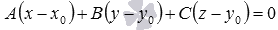 , которое является общим уравнением плоскости, проходящей через точку
, которое является общим уравнением плоскости, проходящей через точку 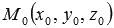 и имеющей направляющий вектор плоскости
и имеющей направляющий вектор плоскости  .
.
Это уравнение можно было получить и иначе.
Очевидно, что множество точек трехмерного пространства 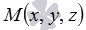 определяют требуемую плоскость тогда и только тогда, когда векторы
определяют требуемую плоскость тогда и только тогда, когда векторы  и
и 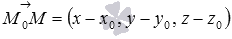 перпендикулярны. То есть, тогда и только тогда, когда их скалярное произведение равно нулю:
перпендикулярны. То есть, тогда и только тогда, когда их скалярное произведение равно нулю:  .
.
Напишите уравнение плоскости, если в прямоугольной системе координат Oxyz в пространстве она проходит через точку  , а
, а  — нормальный вектор этой плоскости.
— нормальный вектор этой плоскости.
Приведем два решения этой задачи.
Из условия имеем  . Подставляем эти данные в общее уравнение плоскости, проходящей через точку
. Подставляем эти данные в общее уравнение плоскости, проходящей через точку 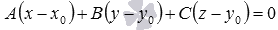 :
:

Теперь второй вариант решения.
Пусть 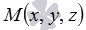 — текущая точка плоскости. Находим координаты вектора
— текущая точка плоскости. Находим координаты вектора  по координатам точек начала и конца:
по координатам точек начала и конца:  . Для получения требуемого общего уравнения плоскости осталось только воспользоваться необходимым и достаточным условием перпендикулярности векторов
. Для получения требуемого общего уравнения плоскости осталось только воспользоваться необходимым и достаточным условием перпендикулярности векторов  и
и  :
:


Существует множество аналогичных задач на составление общего уравнения плоскости, в которых сначала требуется найти координаты нормального вектора плоскости. Самые распространенные из них это задачи на нахождение уравнения плоскости, проходящей через точку параллельно заданной плоскости и задачи на составление уравнения плоскости, проходящей через точку перпендикулярно к заданной прямой.
Неполное общее уравнение плоскости.
Рассмотрим все возможные общие неполные уравнения плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве.



Разберем решения нескольких примеров на составление неполного уравнения плоскости.
Напишите общее уравнение плоскости параллельной координатной плоскости Oyz и проходящей через точку  .
.
Приведем второй способ решения этой задачи.

Источник
Метод координат
Для решения задачи по стереометрии координатным методом нужно выбрать декартову систему координат. Ее можно выбрать как угодно, главное, чтобы она была удобной. Приведем примеры выбора системы координат в кубе, пирамиде и конусе:

Далее необходимо найти координаты основных точек в выбранной системе координат. Это могут быть вершины объемной фигуры, середины ребер или любые другие точки, указанные в условии задачи. Найдем координаты куба и правильной пирамиды (предположим, что все ребра равны (4)):
С кубом все просто, но в других фигурах могут возникнуть трудности с нахождением координат.

Координату (x) точки (С) можно получить, опустив перпендикуляр (CE) из (т.С) на ось (OX). (см. Рис. 2). Получится (т.E), указывающая на искомую координату по (x) – 2.


Координаты вектора
Вектор – отрезок, имеющий длину и указывающий направление.
На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.

Скрещивающиеся прямые
Уравнение плоскости
Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.
Например, пусть даны три точки:
Подставим координаты точек в общее уравнение плоскости:
$$begin A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end$$
Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.
Теперь у нас есть три уравнения и три неизвестные – можем решить систему:
Расстояние от точки до плоскости
Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.
Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).
Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.
Решим задачу полностью методом координат.
Нарисуем рисунок и выберем декартову систему координат. (Рис 5).
Источник
Геометрия. 11 класс
Конспект урока
Геометрия, 11 класс
Урок № 3. Координатный метод решения задач
Перечень вопросов, рассматриваемых в теме:
Уравнение вида  задает в пространстве плоскость α.
задает в пространстве плоскость α.
При этом вектор  – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль. Очевидно, что нормалью является любой вектор, коллинеарный вектору
– это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль. Очевидно, что нормалью является любой вектор, коллинеарный вектору  .
.
Вектор  и любой коллинеарный ему вектор называются направляющим векторами прямой
и любой коллинеарный ему вектор называются направляющим векторами прямой  и прямой
и прямой  соответственно.
соответственно.
Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. Учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 163-170.
Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 353-260.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Работа по теме урока. Объяснение новой темы
Мы рассмотрели несложную задачу на применение метода координат в пространстве.
Векторы  , угол между которыми мы искали, называются направляющими векторами прямой
, угол между которыми мы искали, называются направляющими векторами прямой  и прямой
и прямой  соответственно.
соответственно.
Рассмотрим этот метод более подробно.
Суть метода координат на плоскости и в пространстве заключается в следующем.
В рассмотренном нами примере, поскольку был дан куб, мы могли ввести систему координат с центром в любой его вершине.
В координатах удобно решать задачи, связанные с поиском расстояний и углов. Но для того чтобы его использовать, нужно знать некоторые формулы:
Расстояние между параллельными плоскостями определяется как расстояние от точки, лежащей в одной плоскости, до другой плоскости.
Мы рассмотрим только первые четыре формулы.
Угол между прямыми
Если прямая задана двумя точками A и B, то известен направляющий вектор этой прямой  с координатами <
с координатами < >. Пусть вторая прямая имеет направляющий вектор
>. Пусть вторая прямая имеет направляющий вектор  . Тогда угол между векторами вычисляется по формуле:
. Тогда угол между векторами вычисляется по формуле:
 .
.
Дальше ищется арккосинус от найденного числа. Заметим, что если косинус получился отрицательным, то это значит, что угол между векторами тупой. Поэтому мы берем модуль получившегося числа.
Фактически мы уже рассмотрели пример вычисления угла между прямыми в пространстве.
Угол между прямой и плоскостью
Сначала рассмотрим уравнение плоскости, проходящей через три точки.
 .
.
Вам известно, что в пространстве плоскость задается уравнением, аналогичным тому, которое на плоскости задает прямую.
Если линейное уравнение вида  на плоскости задает прямую l, то уравнение вида
на плоскости задает прямую l, то уравнение вида  задает в пространстве плоскость α. При этом вектор
задает в пространстве плоскость α. При этом вектор  – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль.
– это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль.
Вам известно, что три точки в пространстве определяют единственную плоскость. Поэтому, если заданы три точки, то мы можем найти уравнение плоскости
Мы можем подставить координаты заданных точек в уравнение плоскости и решить систему из трех уравнений с тремя переменными:

В этой системе четыре неизвестных, однако, мы можем избавиться от одной, если разделим все уравнения на D:
 .
.
Для изучения данного способа в 11 классе на базовом уровне введение понятий матрица, определитель матрицы не желателен, данные понятия не входят в базовый курс изучения геометрии.
Иногда эта система оказывается несложной. Но иногда бывает трудно ее решить, и тогда можно использовать следующую формулу:
Обозначение |M| означает определитель матрицы М.
В нашем случае матрица представляет собой таблицу 3х3 элемента. И определитель |M| вычисляется следующим образом:
 .
.
Таким образом, уравнение плоскости будет записано так:



 .
.
Решая ее, получим значения А, В и С:  . То есть уравнение плоскости имеет вид:
. То есть уравнение плоскости имеет вид:
 .
.
Ответ:  .
.
Теперь запишем формулу угла между прямой и плоскостью.
Пусть дано уравнение плоскости:  и известен
и известен  — направляющий вектор прямой.
— направляющий вектор прямой.
Тогда  – синус угла между прямой и плоскостью.
– синус угла между прямой и плоскостью.
Найдем угол между прямой и плоскостью. В качестве плоскости возьмем ту, уравнение которой мы только что написали:

Направляющий вектор прямой:  .
.
Найдем синус угла между прямой и плоскостью:
 .
.
Угол между прямой и плоскостью  .
.
Ответ:  .
.
Угол между плоскостями
уравнение первой плоскости: 
уравнение второй плоскости: 
Тогда  — косинус угла между этими плоскостями.
— косинус угла между этими плоскостями.
Найдем угол между плоскостями:
 и
и  .
.
Найдем косинус угла между плоскостями:
 .
.
Угол между плоскостями: 
Ответ: 
Расстояние от точки до плоскости
Пусть координаты точки:  , уравнение плоскости:
, уравнение плоскости:  .
.
Тогда Расстояние от точки до плоскости вычисляется по формуле:  .
.
Найдем расстояние от точки М(4; 3; 4) до плоскости  .
.
 .
.
Теперь рассмотрим решение задачи координатным методом с использованием рассмотренных формул.
АВС…D1 – куб с ребром 4. Найти расстояние от точки А до плоскости ЕКС (Е – середина D1C1, K – середина C1B1)
Введем систему координат с началом в вершине А так, как показано на рисунке:

Интересующие нас точки будут иметь координаты:
A(0; 0; 0), C(4; 4; 0), E(4; 2; 4), K(2; 4; 4).
Напишем уравнение плоскости ЕКС:
 .
.
Решая ее, получим значения А, В, С и D:  .
.
Уравнение плоскости имеет вид: 
Теперь найдем расстояние от точки А до плоскости ЕКС:  .
.
Ответ:  .
.
Рассмотрим задачу (№14 из варианта ЕГЭ).
В кубе ABC…D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB = 3. Через точки K и C1 построена плоскость α, параллельная прямой BD1.
а) Докажите, что A1P : PB1 = 2 : 1, где P — точка пересечения плоскости α с ребром A1B1.
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.
Переформулируем первый пункт этой задачи таким образом:
Проведем плоскость через точки Р, K и C1 и докажем, что она параллельна прямой BD1.
Введем систему координат так, как показано на рисунке:

Найдем координаты точек  :
:
Р( ; 0; 4), К(4; 0; 3),
; 0; 4), К(4; 0; 3), (4; 4; 4).
(4; 4; 4).
Напишем уравнение плоскости  :
:
 ;
;

Решая ее, получим значения А, В, С и D:  .
.
 — уравнение плоскости
— уравнение плоскости
Теперь докажем, что плоскость  параллельна прямой BD1.
параллельна прямой BD1.
Найдем угол между прямой BD1 и плоскостью  .
.
Точки В и D1 имеют координаты: В (4; 0; 0), D1 (0; 4; 4).
Направляющий вектор прямой BD1 – это вектор  .
.
Он имеет координаты  .
.
Теперь найдем синус угла между вектором  и плоскостью
и плоскостью  .
.

 .
.
В этом случае нам не нужно считать знаменатель дроби. Так как числитель получился равен 0, то дробь равна 0, то есть синус угла между плоскостью и прямой равен 0, значит, плоскости параллельны или совпадают. Но, так как точка В, например, в плоскости, очевидно, не лежит, то плоскости параллельны.
Это значит, что плоскость, параллельная прямой BD1 и проходящая через точки  действительно пересекает ребро A1B1в точке Р так, что A1P : PB1 = 2 : 1. Что и требовалось доказать.
действительно пересекает ребро A1B1в точке Р так, что A1P : PB1 = 2 : 1. Что и требовалось доказать.
Теперь рассмотри второй пункт задачи. Уравнение плоскости  у нас есть. Плоскость BB1C1 параллельна координатной плоскости YOZ и проходит через точку
у нас есть. Плоскость BB1C1 параллельна координатной плоскости YOZ и проходит через точку
В(4; 0; 0). Поэтому она имеет уравнение  .
.
То есть ее коэффициенты  .
.
Найдем угол между плоскостями, используя формулу


Ответ:  .
.
Источник
