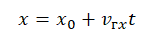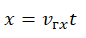Как найти координату точки в начальный момент

Формула координаты тела при равномерном прямолинейном движении

Прямолинейное равномерное движение является наиболее простым и понятным типом механического движения. Подробнее узнать про этот вид движения можно здесь.

Для нахождения координаты тела при равномерном прямолинейном движении используется довольно простая формула:

Формула координаты тела при прямолинейном равномерном движении

x₀ — координата тела в начальный момент времени,

x — координата тела в текущий момент времени,

t — время движения,

V — скорость тела

Таким образом, необходимо знать только начальную координату тела, его скорость и время в пути. Вы можете подставить эти значения в наш онлайн калькулятор и получить результат:

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

1. Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
2. Построить уравнение вида x₁ = x₂.
3. Найти время встречи двух тел t_встр.
4. Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

1. Построить графики x1(t) и x2(t).
2. Найти точку пересечения графиков.
3. Пустить перпендикуляр из этой точки к оси ОХ.
4. Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два

Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

1. Определить характер движения материальной точки.
2. Записать уравнение координаты материальной точки.
3. С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: 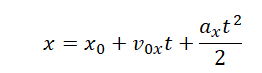Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно, a_x>0. Поэтому варианты «б» и «г» исключаются. Остается выяснить, чему равна скорость: она равна нулю (как в ответе «а») или меньше нуля (как в ответе «в»)? Моменту времени t=0 соответствует точка, являющая вершиной параболы. Когда ветви параболы смотрят вверх, в ее вершине скорость тела всегда равна нулю, так как эта точка лежит на границе между отрицательной и положительной скоростью. Отсюда делаем вывод, что верный ответ «а».Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Записать исходные данные.
2. Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
3. Выразить скорость грузовика из уравнения его движения.
4. Записать уравнение движения мотоциклиста.
5. Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
6. Подставить время в формулу скорости грузовика и вычислить ее.

Решение

• Координата встречи грузовика и мотоциклиста: x = 150 м.
• Время запаздывания мотоциклиста: t_запазд = 5 с.
• Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Механическое движение

О чем эта статья:

Механическое движение

Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.

«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:

• тело отсчета
• система координат
• часы

В совокупности эти три параметра образуют систему отсчета.

В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

• Время — в международной системе единиц СИ измеряется в секундах [с].
• Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

• Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
• Перемещение — вектор, проведенный из начальной точки пути в конечную [м].

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

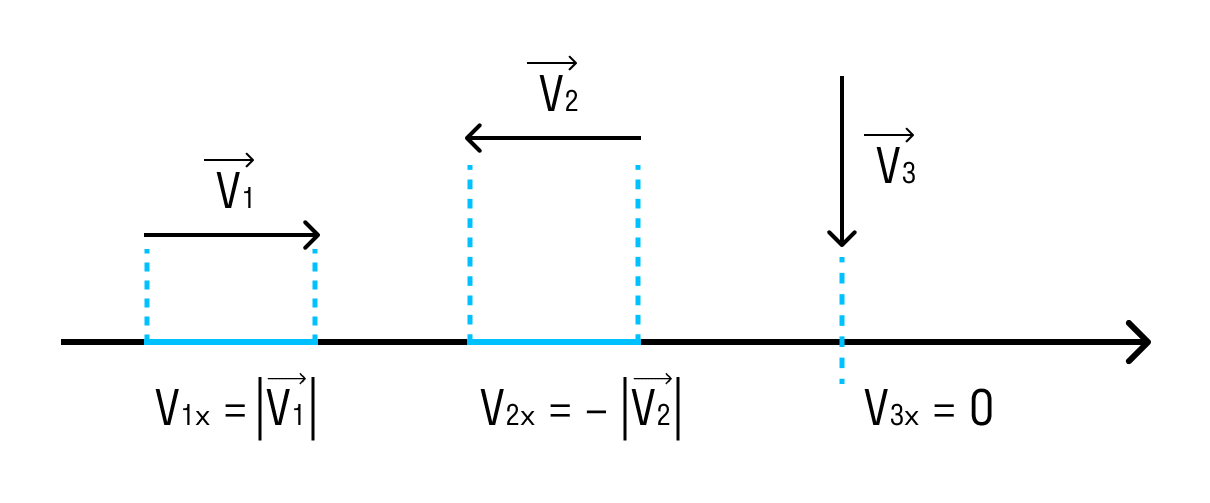
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

— скорость [м/с]
— перемещение [м]
— время [с]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости
V ср.путевая = S/t

Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!

Уравнение движения

Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

Уравнение движения при движении против оси

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_0x — начальная скорость тела в [м/с]
t — время [с]
a_x — ускорение [м/с 2 ]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости

— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]

Задача

Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, . Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x₀ + v_0xt + a_xt 2 /2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
км

Ответ: через полчаса координата автобуса будет равна 150 км.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

[spoiler title=”источники:”]

http://skysmart.ru/articles/physics/mehanicheskoe-dvizhenie

[/spoiler]

ЗАДАЧИ на Прямолинейное равномерное
движение с решениями

Формулы, используемые в 9 классе на уроках
«Задачи на прямолинейное равномерное движение».

Название величины	Обозначение	Единица измерения (в СИ)	Связь с другими величинами
Начальная координата	х0	м	х0 = х – Sх х0 = х – νxt
Координата в любой момент времени	х	м	х = х0 + Sх х = х0 + νxt
Проекция скорости	νx	м/с
Проекция перемещения	Sх	м	Sх = νxt   Sх = х – х0
Время	t	с

1 мин = 60 с;   1 ч = 3600 с;   1 км = 1000 м;   1 м/с = 3,6 км/ч.

---

---

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

---

Типовая задача «Уравнение координаты (нахождение неизвестной величины)»

Задача № 1.
 В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.

---

Типовая задача «Уравнение координаты. Движение двух тел»

Задача № 2.
 Движение двух тел задано уравнениями  x₁ = 20 – 8t и х₂ = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.

---

Типовая задача «График координаты»

Задача № 3.
  Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите:  а) начальную координату тела;  б) проекцию скорости тела;  в) направление движения тела (по оси х или против оси х);  г) запишите уравнение координаты.

---

Типовая задача «График координаты. Движение нескольких тел»

Задача № 4.
 На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите:  а) начальную координату;  б) скорость;  в) направление движения;  г) запишите уравнение координаты.

---

ЗАДАЧИ ПОСЛОЖНЕЕ

Задача № 5.
 На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.

РЕШЕНИЕ:

---

Задача № 6.
 По графикам на рисунке напишите уравнения движения x = x(t). Из уравнений и графиков найдите координаты тел через 5 с, скорости движения тел, время и место встречи второго и третьего тел.

РЕШЕНИЕ:

---

Задача № 7.
  ОГЭ
  Расстояние (S) между городами М и К = 250 км. Одновременно из обоих городов навстречу друг другу выезжают автомашины. Машина из города М движется со скоростью = 60 км/ч, из города К — со скоростью ν₂ = 40 км/ч. Построить график зависимости пути от времени для каждой из машин и по ним определить место встречи и время их движения до встречи.

---

Задача № 8.
   ЕГЭ
 Скорость течения реки v_p = 1 м/с, скорость лодки относительно воды v₀ = 2 м/с. Под каким углом к берегу следует держать курс, чтобы лодка двигалась перпендикулярно берегу? За какое время t она переправится через реку, ширина которой d = 200 м?

---

Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.

Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.

Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.

При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.

В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.

---

Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями
• Посмотреть конспект по теме КИНЕМАТИКА: вся теория для ОГЭ (шпаргалка)
• Вернуться к Списку конспектов по Физике.
• Проверить свои знания по Физике (ОНЛАЙН-ТЕСТЫ)

Прямолинейное равномерное движение является наиболее простым и понятным типом механического движения. Подробнее узнать про этот вид движения можно здесь.

Для нахождения координаты тела при равномерном прямолинейном движении используется довольно простая формула:

Формула координаты тела при равномерном прямолинейном движении

Таким образом, для того, чтобы найти координату тела при равномерном прямолинейном движении необходимо знать только начальную координату тела, его скорость и время в пути. Вы можете подставить эти значения в наш онлайн калькулятор и получить результат.

Часть
1. «Координатный
способ задания движения точки»

Движение точки
задано уравнениями

(м),

(м).

Определить
и построить траекторию. Определить и
показать на чертеже положение точки в
начальный момент и в момент времени
.
Для указанных моментов времени найти
скорость и ускорение точки. Изобразить
на чертеже соответствующие векторы:
,

и
,
.

Решение. Для исключения времени выразим его первого из первого уравнения через координату x и подставим во второе уравнение: или .

Полученное
уравнение представляет собой уравнение
параболы (Рис.1) с вершиной в точке (4; 0).
Выясним, вся ли парабола является
траекторией точки, или только ее часть.
Для этого найдем начальное положение
точки
,
подставив в уравнения движения
:

,

(м).

Таким
образом, точка начинает свое движение
из вершины параболы
.

Установим
направление движения. Для этого, пользуясь
заданными уравнениями движения,
проанализируем, как изменяются координаты
точки при возрастании времени
.
В нашем случае очевидно, что с течением
времени координата

возрастает, а координата

убывает. Следовательно, точка движется
вправо.

Таким
образом, траекторией точки является
правая ветвь параболы (Рис.1).

Найдем
положение точки в момент времени
,
подставив в уравнения движения
:

(м),

(м).

Положение

точки показано на Рис.2.

Найдем как функции
времени проекции скорости на координатные
оси, а также ее модуль и направляющие
косинусы:

,

,

;

,

.

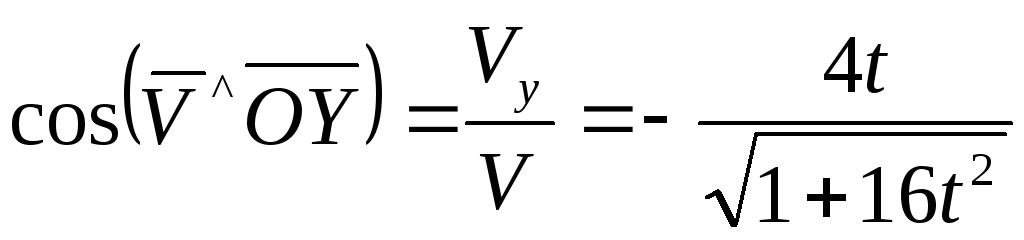
В заданные моменты
времени получаем:

при

,

,

,

,

;

при

,

,

,

,

.

Найдем как функции
времени проекции ускорения на координатные
оси, а также его модуль и направляющие
косинусы:

,

,

;

,

.

Очевидно, что в рассматриваемом движении ни модуль, ни направление вектора ускорения не зависят от времени, поэтому найденные значения справедливы для любого момента времени: . Векторы скорости и ускорения в начальный момент времени и в момент времени показаны на Рис.2 (они могут быть построены либо через модуль и направляющие косинусы, либо через проекции).

Часть
2. «Естественный
способ задания движения точки»

Точка
М
движется по траектории, представляющей
собой половину окружности радиуса r,
согласно закону

(м). Начало отсчета криволинейной координаты (точка О) и направление ее положительного отсчета указаны на Рис.3.

Определить
как функции времени проекцию вектора
скорости на орт касательной
,
а также проекции вектора ускорения на
орт касательной

и на орт главной нормали
.
Построить графики зависимостей
,

,

и
.
Показать положение точки на траектории
в начальный момент и в момент времени

.
Найти и изобразить на чертеже векторы
скорости, касательного и нормального
ускорений, а также вектор полного
ускорения для указанных моментов
времени.

Решение.

Определим

,

и
:

;
(а)

;
(b)

.
(c)

Полученные
функции (a)
и (b),
а также заданный закон движения позволяют
построить графики
,

и

(Рис.4). Найдем положение точки М
в начальный момент и в момент времени

,
подставив в заданный закон движения

и
:

(м);


(м).

Покажем
соответствующие положения точки на
траектории. Поскольку длина полной
окружности равна
,
то

составляет 1/4 окружности. Откладывая
полученную величину в сторону
положительного отсчета криволинейной
координаты (т.к.
),
находим точку

(Рис.4). Криволинейная координата

отрицательна и по модулю в два раза
меньше
,
поэтому точка

отстоит от точки О
влево на 1/8 окружности.

Подставив
указанные моменты времени в уравнение
(а),
найдем

;

(м/с).

Таким
образом, начальная скорость точки равна
нулю. Покажем на чертеже вектор
.
Поскольку его проекция на касательную
ось
,
он направлен в сторону убывания дуговой
координаты (Рис.5). (Напомним, что
касательная ось всегда направлена в
сторону возрастания дуговой координаты).

Аналогичным
образом из (b)
и (c)
найдем:

(м/с²);


(м/с²).

;

(м/с²).

Векторы
нормального, касательного и полного
ускорений точки М
показаны на Рис.5. Отметим, что направление
касательного ускорения, так же как и
скорости, определяется знаком его
проекции на касательную ось. Нормальное
ускорение (если оно отлично от нуля)
всегда направлено в сторону вогнутости
траектории (его проекция на главную
нормаль не может быть отрицательной).

Поскольку

,
вектор полного ускорения в начальный
момент времени совпадает с касательным
ускорением. В момент времени

вектор

определяется
как векторная
сумма

и
.
Его модуль равен

(м/с²),

а
угол, составляемый с направлением
главной нормали, определим через тангенс:

.

Часть
3. «Переход
от координатного способа задания
движения точки к естественному»

Движение
точки задано уравнениями:

(м);

(м).

Найти
уравнение траектории и построить ее на
чертеже. показать
на ней начальное положение точки и найти
закон движения точки по траектории
,
приняв за начало отсчета дуговой
координаты начальное положение точки
и считая, что точка начинает свое движение
в сторону возрастания дуговой координаты.

Решение.

Чтобы
найти уравнение траектории точки
исключим время из уравнений движения.
Для этого из первого уравнения выразим

,
а из второго
,
затем возведём их в квадрат и сложим:

;

;

;

;

.

Очевидно,
что окружность радиуса

м
с
координатами центра

включает траекторию движения точки
(Рис.6). Необходимо только уточнить,
является ли вся окружность траекторией
или только её часть представляет эту
траекторию.

Для
определения начального положения точки
на траектории подставим в уравнения
движения значение времени
.
Находим, что точка в начальный момент
движения занимает положение
,
определяемое координатами
,

,
т.е.
.

Установим
направление движения точки по траектории
при возрастании времени от

до

с.
Подставив в уравнения движения

найдем, что при этом координаты движущейся
точки будут равны:
;

,
т.е.
.
Следовательно, точка

начинает своё движение по окружности
от точки

в направлении часовой стрелки.

Легко
убедится в том, что при

точка занимает положение
,
а при

точка приходит в
.
Из этого следует, что вся окружность
является траекторией движения точки.

Проекции
вектора скорости

на оси координат равны

Y S M0 V0 A M r Wn W V M3 M1 C W O X M2 V1 Рис. 6

, . Модуль этого вектора равен ; при с . Направляющие косинусы вектора являются функцией времени, т.е. направление этого вектора непрерывно изменяется:

при

:

Установим
закон движения точки вдоль траектории.
Начало отсчёта криволинейной координаты
(точку
)
совместим с начальным положением точки

.
В качестве положительного направления
отсчёта криволинейной координаты
выберем направление движения точки.
Поскольку точка движется в сторону
возрастания криволинейной координаты

,
то

,
()

После
интегрирования этого выражения найдем

.

При

,
поэтому

и закон движения точки вдоль траектории
будет следующим:

Соседние файлы в папке Примеры выполнения

• #
• #
• #

  03.03.20153.66 Кб2Содержание OneNote.onetoc2

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.