Координаты вершин правильного тетраэдра
20 июня 2013
Пирамиды традиционно считаются сложными фигурами в задаче C2. А уж если в основании пирамиды лежит треугольник (т.е. пирамида становится тетраэдром), то все становится совсем грустно. В общем, если в ЕГЭ по математике вам попадется правильный тетраэдр, примите мои поздравления: это самая мерзкая и сложная фигура, которая встречается на настоящем экзамене.
Тем не менее, после небольшой тренировки все становится вполне решаемо. И в этом уроке мы пошагово разберем каждую вершину тетраэдра и найдем каждую координату. Вы убедитесь: все, что нам действительно надо знать — это две теоремы:
- Теорема Пифагора — без нее не решается вообще ни одна задача C2, потому что на этой теореме построена сама идея декартовой системы координат;
- Теорема о медианах. А именно: медианы треугольника пересекаются в одно точке и делятся ею в отношении 2 : 1, считая от вершины.
Вот и весь список! Вы знаете эти теоремы? Тогда поехали!
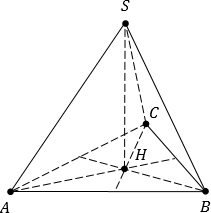
Задача. В правильном тетраэдре SABC, все ребра которого равны 1, введите систему координат и найдите координаты вершин.
[Подпись к рисунку]
Смотрите также:
- Четырехугольная пирамида: как найти координаты вершин

- Уравнение плоскости в задаче C2. Часть 1: матрицы и определители

- Решение ЕГЭ-2011: вариант 1, часть B

- Не пишите единицы измерения в задаче B12

- Быстрое возведение чисел в квадрат без калькулятора

- Задача B4: тарифы на сотовую связь

Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
:
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму.
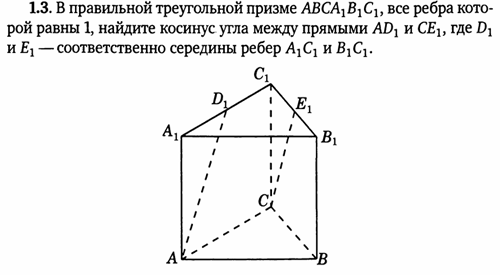
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
.
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
;
.
Выразим C и B через A и подставим в третье уравнение:
.
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.

Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
I. Основные формулы:
1. Расстояние между точками А (![]() ,
, ![]() ), В
), В ![]() ,
, ![]() ) равно
) равно ![]() =
=![]() .
.
2. Угол между плоскостями. Если β – угол между плоскостями, заданными уравнениями ![]() х+
х+![]() z+
z+![]() =0 и
=0 и ![]() х+
х+![]() z+
z+![]() =0, то
=0, то
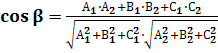 .
.
3. Расстояние от точки до плоскости. Если ρ – расстояние от точки ![]() (
(![]() ,
, ![]() ), до плоскости
), до плоскости ![]() х+
х+![]() z+D =0, то
z+D =0, то
ρ=![]() .
.
4. Уравнение плоскости, проходящей через три заданные точки ![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ,
, ![]() ), в координатной форме:
), в координатной форме:
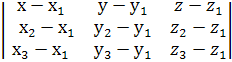 =0;
=0;
5. Если отрезок, концами которого служат точки А (![]() ,
, ![]() ), В
), В ![]() ,
, ![]() ) разделен точкой С (х, у,
) разделен точкой С (х, у,![]() ) в отношении λ, то координаты точки С определяются по формулам
) в отношении λ, то координаты точки С определяются по формулам
Х = ![]() ; у=
; у=![]() ; z=
; z=![]() .
.
II. Координаты вершин многогранников.
Определите координаты вершин многогранников:
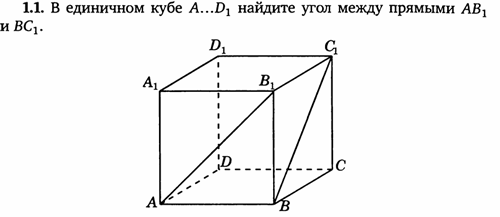
1. Единичный куб A…D1
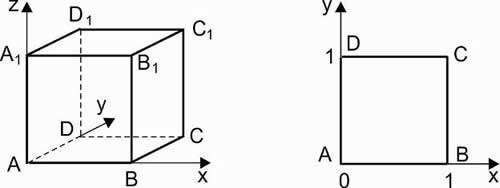
Решение: координаты вершин А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), D (0, 1, 0), D1 (0, 1, 1), С (1, 1, 0), С1 (1, 1, 1).
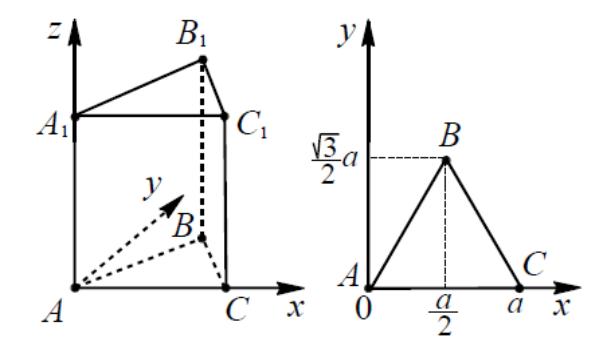
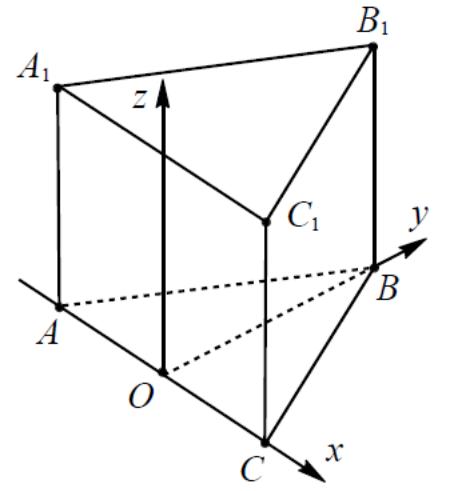
2. Правильная треугольная призма A…C1 , все ребра, которой равны 1.
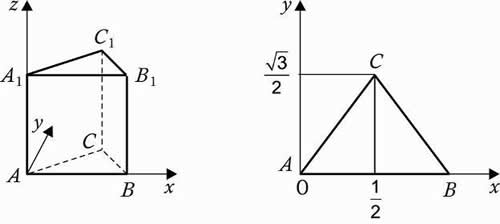
Решение: координаты вершин: А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), С (0,5; ![]() , 0), С1 (0,5;
, 0), С1 (0,5; ![]() , 1).
, 1).
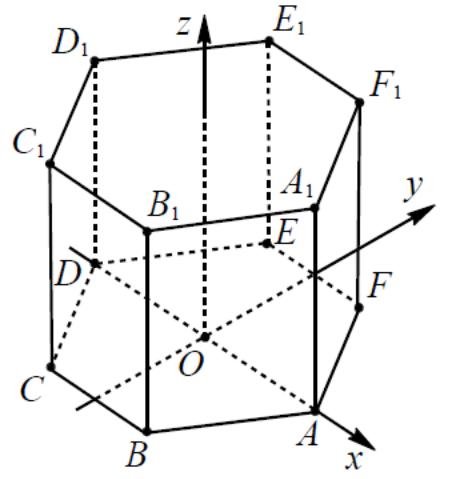
3. Правильная шестиугольная призма A…F1, все ребра которой равны 1.
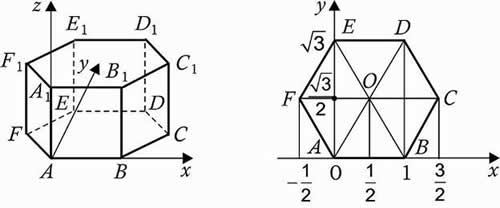
Решение: координаты вершин: А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), С (1,5; ![]() , 0), С1 (1,5;
, 0), С1 (1,5; ![]() , 1), D (1,
, 1), D (1, ![]() (1,
(1, ![]() Е (0,
Е (0, ![]() ,
, ![]() (0,
(0, ![]() ,
,
F(-0,5 , ![]() 0),
0), ![]() (-0,5,
(-0,5, ![]() 1).
1).
4. Правильная треугольная пирамида (тетраэдр) ABCD все ребра которой равны 1.
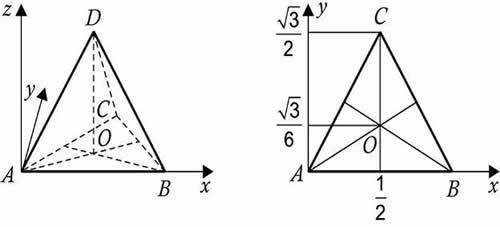
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (0,5; ![]() , 0), D (0,5,
, 0), D (0,5, ![]()
5. Правильная четырехугольная пирамида SABCD, все ребра которой равны 1.
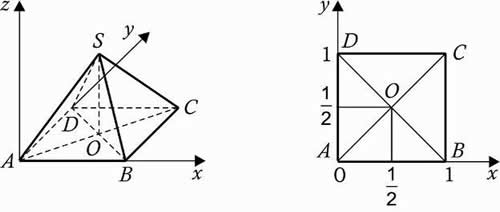
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (1, 1, 0), D (0, 1, 0![]() S (0,5; 0,5;
S (0,5; 0,5; ![]() ).
).
6. Правильная шестиугольная пирамида SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2.
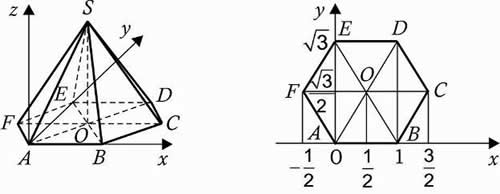
III. Решение задач.
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (1,5; ![]() , 0), D (1,
, 0), D (1, ![]() Е (0,
Е (0, ![]() , F (-05,
, F (-05, ![]() 0), S (0,5;
0), S (0,5; ![]() ).
).
Решение:
- А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), D (0, 1, 0), D1 (0, 1, 1), С (1, 1, 0), С1 (1, 1, 1).
- Найдем координаты векторов
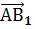 (1, 0, 1) и
(1, 0, 1) и 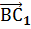 = (0, 1, 1)
= (0, 1, 1) - Найдем косинус угла между векторами
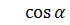 =
=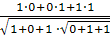 =
= ; α=60.
; α=60.
Ответ: 60.
Решение:
- координаты вершин А (0, 0, 0), D1 (
 ,
, 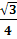 , 1), С (0,5;
, 1), С (0,5; 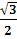 , 0), Е1 (
, 0), Е1 ( ;
; 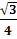 , 1).
, 1). - Найдем координаты векторов:
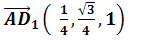 и
и 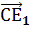 (
( ,
, 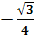 , 1)
, 1) - Найдем косинус угла между векторами
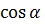 =
=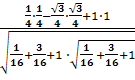 =0,7;
=0,7;
Ответ: 0,7.
Полностью текст работы приведен в Приложении.
Правильная
треугольная пирамида
MABC
,
сторона основания которой
равна
a
,
а высота h
.Обычно
используют один из двух вариантов
расположения системы координат.
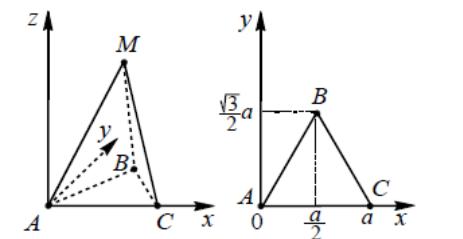
4.1
Пусть начало координат находится в
точке A
,
ось x
направлена
вдоль ребра AC
,
ось y
проходит
через точку A
перпендикулярно
AC
,
ось z
проходит
через точку A
перпендикулярно
плоскости ABC
(см.
рис. 6). Тогда вершины пирамиды имеют
координаты: А(0; 0; 0); В(
;
;
0);С(а;0;0), М(
;
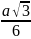
;h).
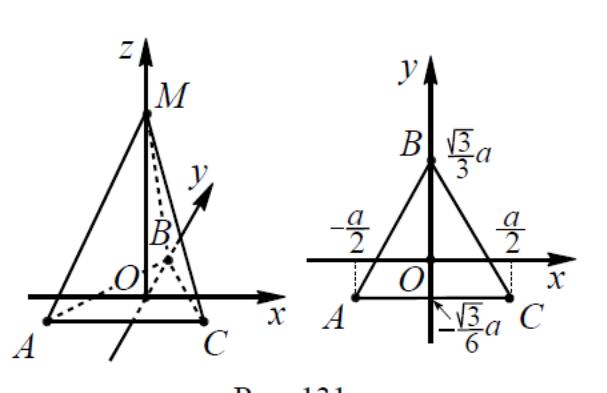
4.2
Пусть начало координат находится в
центре треугольника ABC
в
точке O
,ось
x
проходит
через точку O
параллельно
ребру AC
,
ось y
проходит
через точку O
перпендикулярно
AC
,
ось z
проходит через точку O
перпендикулярно
плоскости ABC
(см.
рис. 7). Тогда вершины пирамиды имеют
координаты: A(-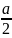
;
–
;0),
В(0;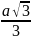
;
0),
С(
;
–
;0),
М(0;0;h).
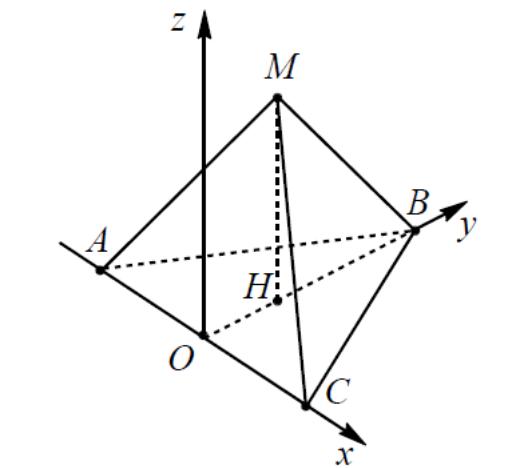
4.3
Еще один вариант расположения правильной
треугольной пирамиды относительно
прямоугольной декартовой системы
координат представлен на рисунке №8.
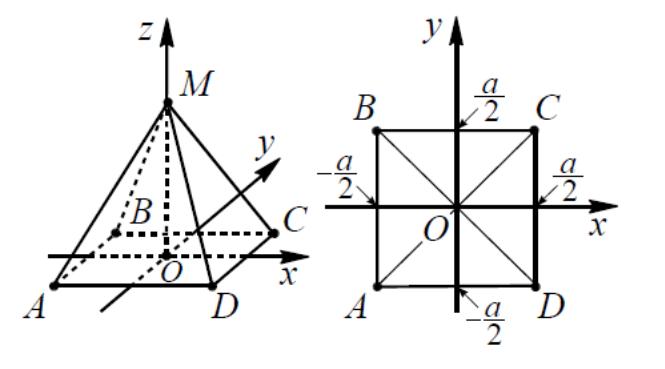
5. Правильная четырехугольная пирамида
Правильная
четырехугольная пирамида
MABC
,
сторона основания которой равна a
,
а высота h
.Обычно
используют один из двух вариантов
расположения системы координат.
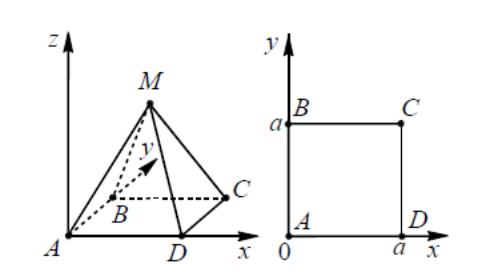
5.1
Пусть начало координат находится в
точке A
,
ось x
направлена
вдоль ребра AD
,
ось y
–
вдоль ребра AB
,
ось z
проходит
через точку A
перпендикулярно
плоскости ABC
(см.
рис. 9). Тогда вершины пирамиды имеют
координаты:
A(0;
0; 0) , B(0;
a;
0) , C(a;
a;
0) ,Д(а;0;0), М(
;
;
h).
5.2.
Пусть начало координат находится в
центре основания в точке O
,
ось x
проходит через точку O
параллельно
ребру AD
,
ось y
проходит
через точку O
параллельно
ребру AB,
ось z
проходит
через точку O
перпендикулярно
плоскости основания (см. рис. 10). Тогда
вершины пирамиды имеют координаты:
А(-
;
–
;0),
В (-
;
;0),
С(
;
;0),Д(
;
–
;0),М(0;0;h)
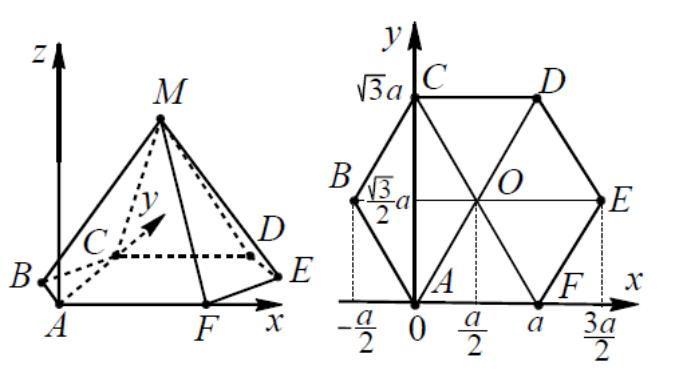
6. Правильная шестиугольная пирамида
6.1MABCDEF
,
сторона основания
которой
равна a
,
а высота h
.
Пусть начало координат находится в
точке A
,
ось x
направлена
вдоль ребра AC
,
ось y
проходит
через точку A
перпендикулярно
AC
,
ось z
проходит
через точку A,
пер-
пендикулярно
плоскости ABC
(см.
рис.11). Тогда вершины пирамиды имеют
координаты: А(0; 0; 0); В(-
;
;
0); С(0;
;0),
Д (а;
;0),
Е(
;
;
0), F(а;0;0),М(
;
;
h).
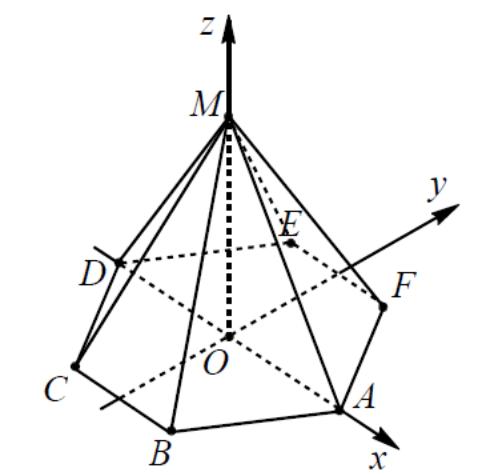
6.2
Еще один вариант расположения правильной
шестиугольной пирамиды относительно
прямоугольной декартовой системы
координат показан на рисунке 12.
|
Рисунок |
|
|
Р |
Рисунок |
|
|
|
|
Рисунок
|
|
|
Рисунок
|
|
|
Рисунок
|
|
18
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Скачать материал

Скачать материал


- Сейчас обучается 141 человек из 50 регионов


- Сейчас обучается 249 человек из 63 регионов




Описание презентации по отдельным слайдам:
-

1 слайд
Векторно-координатный метод решения стереометрических задач
Введение системы координат
в правильных пирамидахУчитель математики
МАОУ «Обдорская гимназия»
г. Салехард ЯНАО
Е.И. Гусак -

2 слайд
Введение системы координат
Координаты четырехугольной пирамиды
Изобразим пирамиду и введем систему координат
𝐴
𝐵
𝐶
𝐷
𝐻
𝑆
𝒙
𝒚
𝒛
Начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. SH ∥ оси z.
Можно начало поместить в центр квадрата – точку Н.
Пусть все ребра пирамиды равны 1. -

3 слайд
Введение системы координат
AC = 𝟐 HC = 𝟐 𝟐
Чтобы найти координаты точки S, сначала найдем координаты ее проекции на Оху – точки Н. А затем из △SHC определим координату z, равную длине SH.
SH = 𝟏− 𝟐 𝟒 = 𝟐 𝟐
A(0;0;0) B(1;0;0) C(1;1;0) D(0;1;0) H 𝟏 𝟐 ; 𝟏 𝟐 ;𝟎 S 𝟏 𝟐 ; 𝟏 𝟐 ; 𝟐 𝟐
𝐴
𝐵
𝐶
𝐷
𝐻
𝒙
𝒚
0
1
1 2
1 2
1 -

4 слайд
Введение системы координат
Координаты треугольной пирамиды
Изобразим пирамиду и введем систему координат𝐴
𝐵
𝐶
𝑆
𝑂
Начало координат — в точке A. Сторону AB принимаем за единичный отрезок, если иное не указано в условии задачи. Ось x направляем по ребру AB, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC, а ось z ⊥ (OXY). SO ∥ оси z.
𝒙
𝒚
𝒛 -

5 слайд
Введение системы координат
CH = 𝟏− 𝟏 𝟒 = 𝟑 𝟐 OC = 𝟐 𝟑 CH = 𝟐 𝟑 ⋅ 𝟑 𝟐 = 𝟑 𝟑
Из △SOC: SO = 𝟏− 𝟑 𝟗 = 𝟔 𝟑
A(0;0;0) B(1;0;0) C 𝟏 𝟐 ; 𝟑 𝟐 ;𝟎 S 𝟏 𝟐 ; 𝟑 𝟔 ; 𝟔 𝟑 O 𝟏 𝟐 ; 𝟑 𝟔 ;𝟎𝐴
𝐵
𝐶
0
1
1 2
3 2
𝒙
𝒚
𝐴
𝐵
𝐶
𝑂
𝑆
𝒙
𝒚
𝒛
𝐻
𝑂
3 6 -

6 слайд
Введение системы координат
Координаты шестиугольной пирамиды
Пусть стороны основания пирамиды равны 1, а боковые ребра – 2. Изобразим пирамиду и введем систему координат.Начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AЕ, а ось z — вверх, перпендикулярно плоскости OXY. SО ∥ оси z.
Можно начало поместить в центр шестиугольника – точку О.𝐴
𝐵
𝐶
𝐷
𝐸
𝐹
𝑂
𝑆
𝒙
𝒚
𝒛 -

7 слайд
Введение системы координат
Шестиугольник разбивается большими
диагоналями на 6 правильных треугольников. ВЕ = 2.
Из △АВЕ: АЕ = 4−1 = 3 . FL = CN = 3 2 .
Из △SOC: SO = 4−1 = 3 .
Таким образом,
A(0;0;0) B(1;0;0) C 𝟑 𝟐 ; 𝟑 𝟐 ;𝟎 D( 1; 𝟑 ;𝟎)
Е(0; 𝟑 ; 0) F − 𝟏 𝟐 ; 𝟑 𝟐 ;𝟎 S 𝟏 𝟐 ; 𝟑 𝟐 ; 3𝑂
𝒙
𝒚
𝒛
𝐴
𝐵
𝐶
𝐷
𝐸
𝐹
0
1
𝑂
𝒙
𝒚
𝟑
3 2
𝐿
𝑁
3 2
− 1 2
1 2
Краткое описание документа:
Достаточно простой в применении, метод координат является необходимой составляющей решения задач различного уровня. Использование данного метода, позволяет учащимся значительно упростить и сократить процесс решения задач, что помогает им при дальнейшем изучении, как школьного курса математики, так и при изучении математики в высших учебных заведениях. Координатно-векторный метод имеет преимущества перед другими, что не требует сложных построений в проекциях. По той простой причине, что этот метод заключается во введении (привязке к исследуемым фигурам) декартовой системы координат, а затем – исчислении образующихся векторов (их длин и углов между ними).
В презентации рассматривается введение системы координат в правильной четырехугольной пирамиде, правильной треугольной пирамиде и правильной шестиугольной пирамиде. Показывается нахождение координат точек фигуры.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 256 705 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-

«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
Тема
Глава 5. Метод координат в пространстве. Движения
Больше материалов по этой теме
Другие материалы
Презентация “Введение системы координат в призмах”
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: Глава 5. Метод координат в пространстве. Движения
- 10.06.2019
- 486
- 3


Координатный метод в решение задач егэ по математкие
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: Глава 5. Метод координат в пространстве. Движения
Рейтинг:
3 из 5
- 25.05.2019
- 941
- 9

Контрольная работа № 1 по теме: “Метод координат” (11 класс)
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: Глава 5. Метод координат в пространстве. Движения
Рейтинг:
3 из 5
- 04.02.2019
- 40586
- 1997

Урок геометрии в 11 классе
- Учебник: «Алгебра», Никольский С.М., Потапов М.К., Решетников Н.Н. и др.
- Тема: § 13. Комбинаторика
- 28.01.2019
- 528
- 1

Буклет на тему: Стереометрические задачи
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: Глава 5. Метод координат в пространстве. Движения
- 13.01.2019
- 430
- 2


Урок по теме “Решение задач методом координат”
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
- Тема: Глава 5. Метод координат в пространстве. Движения
- 29.12.2018
- 612
- 12

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
-
Курс повышения квалификации «Основы построения коммуникаций в организации»
-
Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация маркетинга в туризме»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
-
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
-
Курс профессиональной переподготовки «Осуществление и координация продаж»