Как найти координаты четвертой вершины тетраэдра

Условие

Решение

Написать комментарий

Координаты вершин правильного тетраэдра

20 июня 2013

Пирамиды традиционно считаются сложными фигурами в задаче C2. А уж если в основании пирамиды лежит треугольник (т.е. пирамида становится тетраэдром), то все становится совсем грустно. В общем, если в ЕГЭ по математике вам попадется правильный тетраэдр, примите мои поздравления: это самая мерзкая и сложная фигура, которая встречается на настоящем экзамене.

Тем не менее, после небольшой тренировки все становится вполне решаемо. И в этом уроке мы пошагово разберем каждую вершину тетраэдра и найдем каждую координату. Вы убедитесь: все, что нам действительно надо знать — это две теоремы:

1. Теорема Пифагора — без нее не решается вообще ни одна задача C2, потому что на этой теореме построена сама идея декартовой системы координат;
2. Теорема о медианах. А именно: медианы треугольника пересекаются в одно точке и делятся ею в отношении 2 : 1, считая от вершины.

Вот и весь список! Вы знаете эти теоремы? Тогда поехали!

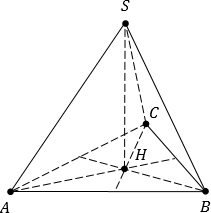
Задача. В правильном тетраэдре SABC, все ребра которого равны 1, введите систему координат и найдите координаты вершин.

Смотрите также:

1. Четырехугольная пирамида: как найти координаты вершин
2. Уравнение плоскости в задаче C2. Часть 1: матрицы и определители
3. Решение ЕГЭ-2011: вариант 1, часть B
4. Не пишите единицы измерения в задаче B12
5. Быстрое возведение чисел в квадрат без калькулятора
6. Задача B4: тарифы на сотовую связь

Примеры решения задач

Задача 1.
Найти координаты векторного произведения

,
если

,

.

Решение.
Найдем

и

.
Векторное произведение, по определению,
равно

.

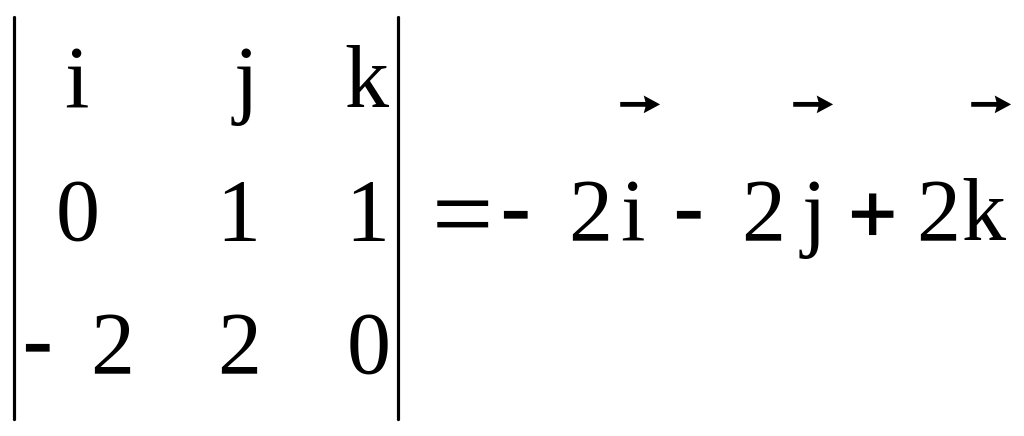
Задача 2.
Силы

и

приложены к точке

.
Вычислить величину момента равнодействующей
этих сил

относительно точки

.

Решение.
Найдем силу

и плечо

:

.
Момент

сил

вычисляется по формуле

,
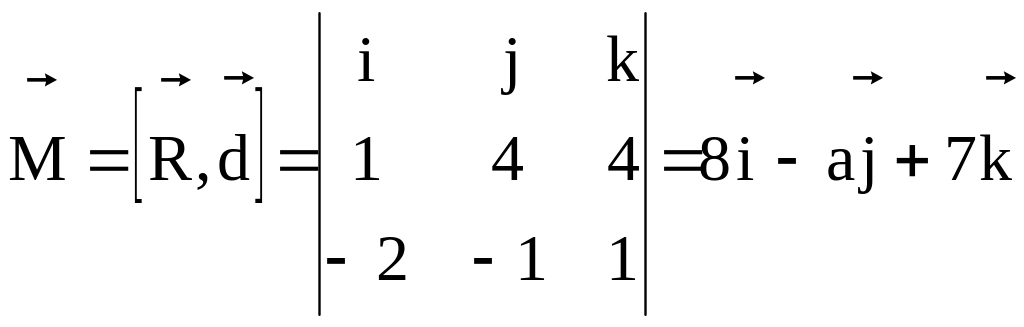
а его модуль

.

Задача 3. Даны
координаты вершин параллелепипеда:

.
Найти объем параллелепипеда, его высоту,
опущенную из вершины С, угол между
вектором AD
и гранью, в которой лежат векторы АВ и
АС.

Решение.
По определению, объем параллелепипеда
равен смешанному произведению векторов,
на которых он построен. Найдем эти
векторы:

.

Объем этого
параллелепипеда

.

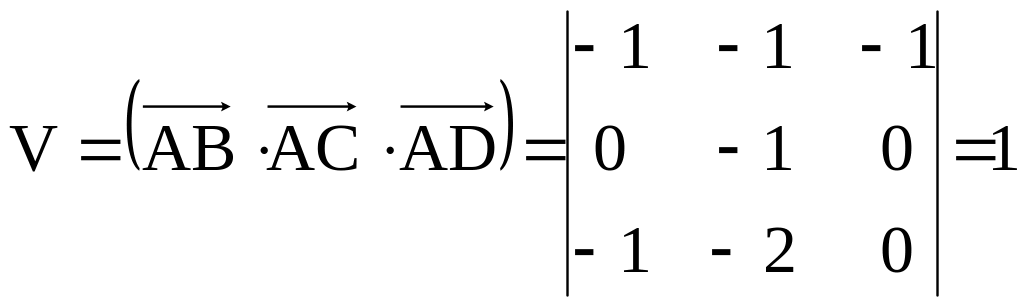
С другой стороны,
объем параллелепипеда

,

– это площадь параллелограмма:

.

,
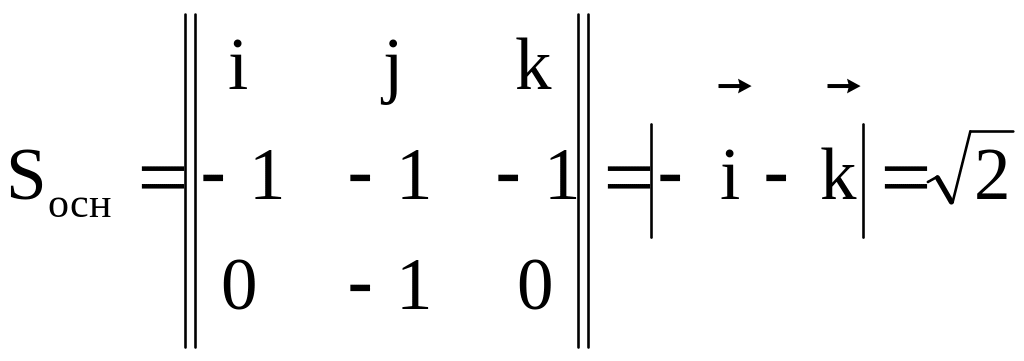
тогда высота

.

Угол между
вектором и гранью

найдем по формуле

.

так как вектор

перпендикулярен грани, в которой лежат
векторы


.
Угол между этим вектором и вектором

находим по известной формуле

.
Очевидно, что искомый угол

.

Итак:

.

Задача 4.
Проверить,
лежат ли в одной плоскости точки

,

.
Найти линейную зависимость вектора

,
если это возможно.

Решение.
Найдем три вектора:

.

.

Три вектора лежат
в одной плоскости, если они компланарны,
т. е. их смешанное произведение равно
нулю:

.
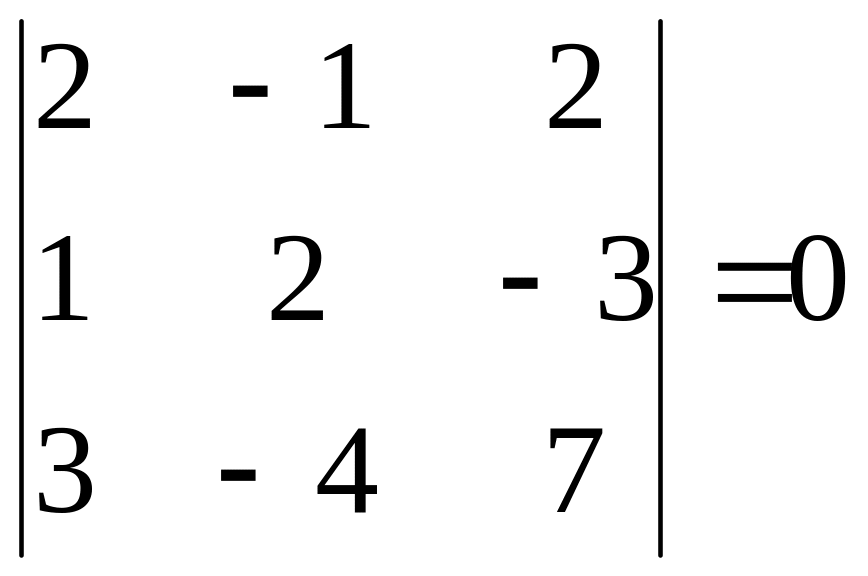
Следовательно, эти три вектора линей-

н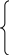
о
зависимы. Найдем линейную зависимость

от

.

.

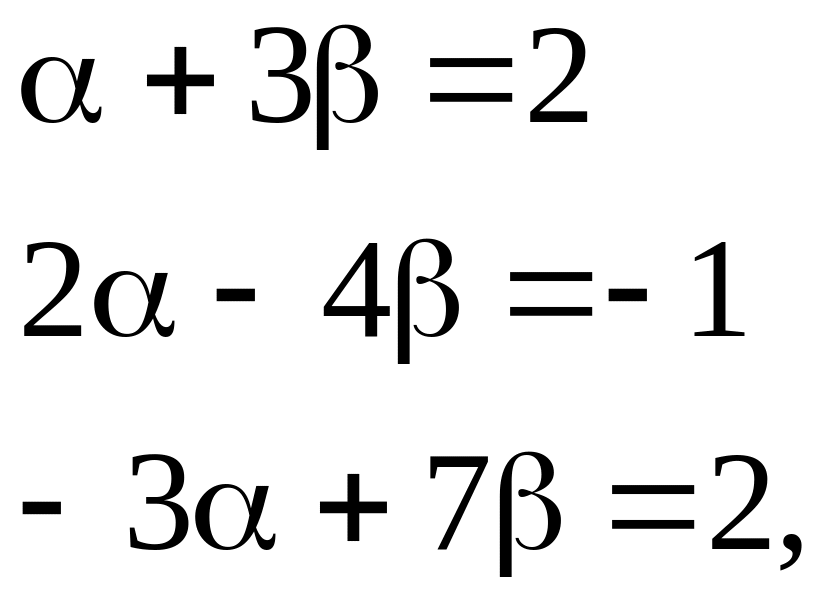
Решая эту систему,
получим

,
т.е.

.

Задачи

1.

.
Вычислить: а)

;
б)

;

в)

.

2.

.
Вычислить площадь треугольника,
построенного на векторах

и

.

3. Заданы векторы

.
Найти координаты векторов:

а)

б)

;
в)

.

4. Вычислить
площадь треугольника с вершинами

.

5. В треугольнике
с вершинами

,

и

найти высоту

.

6. Найти вектор

,
если векторы

имеют следующие координаты:

.

7. Сила

приложена к точке

.
Определить момент этой силы относительно
точки

.

8. Установить,
образуют ли векторы

базис в множестве всех вектров, если
а)

;
б)
.

9. Вычислить
объем тетраэдра ОАВС, если

.

10. В тетраэдре
с вершинами в точках

и

вычислить высоту

.

11. Проверить,
компланарны ли данные векторы:

а)


;

б)



.

12. Доказать, что
четыре точки

лежат в одной плоскости.

13. Найти координаты
четвертой вершины тетраэдра ABCD
, если известно, что она лежит на оси Oy,
а объем тетраэдра равен V:

а)

;

б)

.

Домашнее задание

1. Упростить
выражение

.

2. Найти площадь
параллелограмма, построенного на
векторах

и

,
где

–
единичные векторы, угол между которыми
равен

.

3. Даны векторы

.
Найти вектор

.

4. Дан треугольник
с вершинами

.
Найти его площадь.

5. Даны силы

,
приложенные к точке

.
Определить величину и направляющие
косинусы момента равнодействующей этих
сил относительно точки

.

6. Вычислить
объем параллелепипеда, построенного
на векторах:

1)

,
где

– взаимно перпендикулярные орты;

2)

.

7. Доказать, что
точки

лежат в одной

плоскости.

8. Даны вершины
тетраэдра

.
Найти длину высоты, опущенной из вершины
О на грань АВС.

9. Векторы

,
образующие правую тройку, взаимно
перпендикулярны. Зная,

что

,
вычислить

.

10. Вектор

перпендикулярен к векторам

,
угол между

равен

.
Зная, что

,
вычислить

.

11. Даны векторы

.
Вычислить

.

12. Установить,
компланарны ли векторы

,
если

1)

;

2)

;

3)

.

13. Доказать, что
точки

лежат в одной плоскости.

14. Вычислить
объем тетраэдра, вершины которого
находятся в точках

.

15. Даны вершины
тетраэдра

.
Найти его высоту, опущенную из вершины
D.

16. Объем тетраэдра

,
три его вершины находятся в точках

.
Найти координаты четвертой вершины D,
если известно, что она лежит на оси

.

Ответы к задачам

1)

.
2)

.
3) (-3, 5, 7), (-6, 10, 14), (-12, 20, 28).

4)

.
5) 5. 6) (-20, 7, -11). 8) Нет, да. 9) 17/2. 10)

.
11) Да, нет.

13) (0, 0, 0), (0, 1, 0).

Ответы к домашнему
заданию

1)

.
2)

.
3)

.
4)

.
5)

.
6) 0. 8) 11.

9) 24. 10)

.
11) -7. 12) Да, нет, да. 14) 3. 15) 11. 16) (0,
8, 0), (0, -7, 0).

Типовой расчет

Задача 1

1. По сторонам ОА
и ОВ прямоугольника ОАСВ отложены
единичные векторы

.
Выразить через

векторы

,
если

.

2. Найти вектор

,
направленный по биссектрисе угла между
векторами

,
если

.

3. Найти вектор

,
образующий со всеми тремя базисными
ортами равные острые углы, если

.

4. Даны векторы

,
угол между которыми составляет

.
Построить вектор

и определить его модуль, если

.

5. В трапеции

.
Разложить геометрически и аналитически
вектор

по векторам

.

6. Найти вектор

,
коллинеарный вектору

,
образующий с ортом

острый угол и имеющий длину

.

7. Найти вектор

,
образующий c
ортом

угол

,
с ортом

– угол

,
если

.

8. Даны три
вершины параллелограмма

:

.
Найти его четвертую вершину D,
противоположную В.

9. На оси ординат
найти точку М, равноудаленную от
точек

.

10. На оси абсцисс
найти точку М, расстояние которой от
точки

равно пяти.

11. Определить
координаты концов отрезка, который
точками

и

делится на три равные части.

12. Вектор составляет
с осями

углы

.
Какой угол он составляет с осью

?

13. Даны три вершины
параллелограмма:

.
Найти его четвертую вершину D.

14. Вектор

составляет с осью ОХ угол

,
а с осью OY
угол

.
Определить координаты точки М, если её
ордината Z
отрицательна, и выразить вектор

через орты

.

15. Найти вектор

,
образующий со всеми тремя базисными
ортами равные острые углы, если

.

16. Найти вектор

,
направленный по биссектрисе угла между
векторами

и

,
если

.

17. На оси ординат
найти точку М, равноудаленную от точек

и

.

18. Даны три
вектора:

.
Найти разложение век-

тора

по базису

.

19. Составляют ли
векторы

базис в пространстве и каковы координаты
вектора

в этом базисе.

.

20. Составляют ли
векторы

базис в пространстве и каковы координаты
вектора

в этом базисе.

.

21. Даны четыре
вектора:

.
Можно ли любые три из них принять за
базис?

22. Найти вектор

,
образующий с ортом

угол

,
с ортом

угол

,
если

.

23. Найти линейную
зависимость между векторами

.

24. Являются ли
векторы

компланарными?

25. Даны вершины
треугольника:

.
Вычислить длину биссектрисы его
внутреннего угла при вершине А.

26.

– медианы треугольника АВС. Выразить
через

векторы

.

27. В параллелограмме
АВСD
обозначены

.
Выразить через

векторы

,
где М – точка пересечения диагоналей
параллелограмма.

28. В треугольнике
АВС

.
Полагая

,

выразить

через векторы

.

29. В ромбе

даны диагонали

.
Разложить по этим двум векторам все
векторы, совпадающие со сторонами ромба:

.

30. На трех
некомпланарных векторах:

– построен параллелепипед

.
Выразить через

векторы, совпадающие со всеми остальными
ребрами, диагоналями и диагоналями
граней этого параллелепипеда.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Finding $(x, y, z)$ as the intersection of three spheres of radius $L_P$, $L_Q$, and $L_R$, centered at $P = (P_x, P_y, P_z)$, $Q = (Q_x, Q_y, Q_z)$, and $R = (R_x, R_y, R_z)$, respectively, is the solution.

However, if you rotate and translate the coordinate system, you can simplify the math a lot. (This is nothing special; it’s just that when most of the coordinates are zeroes, the expressions simplify a lot.)

Rotate and translate the coordinate system (we’ll use $(u, v, w)$ for the rotated and translated coordinates for clarity; note that distances are unchanged), $P$ is at origin $(0, 0, 0)$, $Q$ is at $(U_Q, 0, 0)$, and $R$ at $(U_R, V_R, 0)$. Then, the fourth vertex is at
$$begin{aligned}
u &= frac{L_P^2 – L_Q^2 + U_Q^2}{2 U_Q} \
v &= frac{L_P^2 – L_R^2 + U_R^2 + V_R^2 – 2 U_R u}{2 V_R} \
w &= pmsqrt{L_P^2 – u^2 – v^2} \
end{aligned}$$

Rotating and translating the coordinate system is not difficult, either:
$$begin{aligned}
U_Q &= leftlVert Q – P rightrVert \
hat{u} &= frac{Q – P}{U_Q} \
vec{t} &= (R – P) – hat{u}bigr(hat{u} cdot (R – P)bigr) \
hat{v} &= frac{vec{t}}{leftlVert vec{t} rightrVert} \
hat{w} &= hat{u} times hat{v} \
U_R &= (R – P) cdot hat{u} \
V_R &= (R – P) cdot hat{v} \
end{aligned}$$
Conversion back to original coordinates is similarly trivial:
$$vec{p} = P + u hat{u} + v hat{v} + w hat{w}$$

---

Here is a Python 3 implementation:

# SPDX-License-Identifier: CC0-1.0
# This file is in Public Domain.

from vector import Vector, sqrt

def find_fourth_vertex(vertex1, vertex2, vertex3, distance1, distance2, distance3):
    # Use Vector type for the vertices
    p1 = Vector(vertex1[0], vertex1[1], vertex1[2])
    p2 = Vector(vertex2[0], vertex2[1], vertex2[2])
    p3 = Vector(vertex3[0], vertex3[1], vertex3[2])

    # Use float type for the distances
    r1 = float(distance1)
    r2 = float(distance2)
    r3 = float(distance3)

    u_axis = (p2 - p1).unit
    v_axis = (p3 - p1).perp(u_axis).unit
    w_axis = u_axis ^ v_axis

    u2 = (p2 - p1) | u_axis
    u3 = (p3 - p1) | u_axis
    v3 = (p3 - p1) | v_axis

    u = (r1*r1 - r2*r2 + u2*u2) / (2*u2)
    v = (r1*r1 - r3*r3 + u3*u3 + v3*v3 - 2*u*u3) / (2*v3)
    w = sqrt(r1*r1 - u*u - v*v)

    return (p1 + u*u_axis + v*v_axis + w*w_axis,
            p1 + u*u_axis + v*v_axis - w*w_axis)

if __name__ == '__main__':
    from math import sin, cos, pi
    from random import Random

    prng = Random()

    while True:
        # Generate four random vectors in (-9.9,-9.9,-9.9) - (+9.9,+9.9,+9.9)
        v = [ Vector(prng.uniform(-9.9, 9.9), prng.uniform(-9.9, 9.9), prng.uniform(-9.9, 9.9)),
              Vector(prng.uniform(-9.9, 9.9), prng.uniform(-9.9, 9.9), prng.uniform(-9.9, 9.9)),
              Vector(prng.uniform(-9.9, 9.9), prng.uniform(-9.9, 9.9), prng.uniform(-9.9, 9.9)),
              Vector(prng.uniform(-9.9, 9.9), prng.uniform(-9.9, 9.9), prng.uniform(-9.9, 9.9)) ]
        # Find their minimum pairwise distance
        rmin = (v[1] - v[0]).norm
        for i in range(0, len(v) - 1):
            for j in range(i+1, len(v)):
                rmin = min(rmin, (v[j] - v[i]).norm)
        # If they're all least 1 unit from each other, accept.
        if rmin >= 1:
            break

    v1 = v[0]
    v2 = v[1]
    v3 = v[2]

    r1 = (v[3] - v[0]).norm
    r2 = (v[3] - v[1]).norm
    r3 = (v[3] - v[2]).norm

    print("v1 = %s, distance %f" % (v1, r1))
    print("v2 = %s, distance %f" % (v2, r2))
    print("v3 = %s, distance %f" % (v3, r3))

    v4a, v4b = find_fourth_vertex(v1, v2, v3, r1, r2, r3)

    print("v4 == %s" % (v[3],))
    print("v4a = %s" % (v4a,))
    print("v4b = %s" % (v4b,))

    print("v4a distances: %f, %f, %f" % ((v4a-v1).norm, (v4a-v2).norm, (v4a-v3).norm))
    print("v4b distances: %f, %f, %f" % ((v4b-v1).norm, (v4b-v2).norm, (v4b-v3).norm))

where a.perp(b) is $vec{a} – vec{b}(vec{a}cdotvec{b})$, a | b is $vec{a} cdot vec{b}$ and a ^ b is $vec{a} times vec{b}$.

When run, it generates a test tetrahedron, and displays the results when find_fourth_vertex is given three of the vertices and their distances to the fourth.

The helper Vector class is implemented by vector.py:

# SPDX-License-Identifier: CC0-1.0
# This file is in Public Domain.

from math import sqrt

class Vector(tuple):
    """Tuple subclass implementing basic 3D vectors"""

    def __new__(cls, x, y, z):
        return tuple.__new__(cls, (float(x), float(y), float(z)))

    def perp(self, other):
        """Part perpendicular to other vector"""
        dp = self[0]*other[0] + self[1]*other[1] + self[2]*other[2]
        return Vector(self[0] - dp*other[0],
                      self[1] - dp*other[1],
                      self[2] - dp*other[2])

    @property
    def unit(self):
        """Scaled to unit length"""
        n = sqrt(self[0]*self[0] + self[1]*self[1] + self[2]*self[2])
        return Vector(self[0]/n, self[1]/n, self[2]/n)

    @property
    def norm(self):
        """Euclidean length"""
        return sqrt(self[0]*self[0] + self[1]*self[1] + self[2]*self[2])

    @property
    def normsqr(self):
        """Euclidean length squared"""
        return self[0]*self[0] + self[1]*self[1] + self[2]*self[2]

    @property
    def x(self):
        """Vector x coordinate"""
        return self[0]

    @property
    def y(self):
        """Vector y coordinate"""
        return self[1]

    @property
    def z(self):
        """Vector z coordinate"""
        return self[2]

    def __bool__(self):
        """Nonzero vector"""
        return (self[0]*self[0] + self[1]*self[1] + self[2]*self[2] > 0)

    def __abs__(self):
        """abs(a): Euclidean length of vector a"""
        return sqrt(self[0]*self[0] + self[1]*self[1] + self[2]*self[2])

    def __add__(self, other):
        """a + b: Vector addition"""
        if isinstance(other, (tuple, list)) and len(other) >= 3:
            return Vector(self[0]+other[0], self[1]+other[1], self[2]+other[2])
        else:
            return NotImplemented

    def __radd__(self, other):
        """b + a: Vector addition"""
        if isinstance(other, (tuple, list)) and len(other) >= 3:
            return Vector(other[0]+self[0], other[1]+self[1], other[2]+self[2])
        else:
            return NotImplemented

    def __mul__(self, other):
        """a * b: Scalar multiplication"""
        if isinstance(other, (int, float)):
            return Vector(self[0]*other, self[1]*other, self[2]*other)
        else:
            return NotImplemented

    def __rmul__(self, other):
        """b * a: Scalar multiplication"""
        if isinstance(other, (int, float)):
            return Vector(other*self[0], other*self[1], other*self[2])
        else:
            return NotImplemented

    def __neg__(self):
        """-a: Negation"""
        return Vector(-self[0], -self[1], -self[2])

    def __or__(self, other):
        """a | b: Dot product"""
        if isinstance(other, (tuple, list)) and len(other) >= 3:
            return self[0]*other[0] + self[1]*other[1] + self[2]*other[2]
        else:
            return NotImplemented

    def __ror__(self, other):
        """b | a: Dot product"""
        if isinstance(other, (tuple, list)) and len(other) >= 3:
            return other[0]*self[0] + other[1]*self[1] + other[2]*self[2]
        else:
            return NotImplemented

    def __sub__(self, other):
        """a - b: Vector subtraction"""
        if isinstance(other, (tuple, list)) and len(other) >= 3:
            return Vector(self[0]-other[0], self[1]-other[1], self[2]-other[2])
        else:
            return NotImplemented

    def __rsub__(self, other):
        """b - a: Vector subtraction"""
        if isinstance(other, (tuple, list)) and len(other) >= 3:
            return Vector(other[0]-self[0], other[1]-self[1], other[2]-self[2])
        else:
            return NotImplemented

    def __truediv__(self, other):
        """a / b: Scalar division"""
        if isinstance(other, (int, float)):
            return Vector(self[0]/other, self[1]/other, self[2]/other)
        else:
            return NotImplemented

    def __xor__(self, other):
        """a ^ b: Vector cross product"""
        if isinstance(other, (tuple, list)) and len(other) >= 3:
            return Vector(self[1]*other[2] - self[2]*other[1],
                          self[2]*other[0] - self[0]*other[2],
                          self[0]*other[1] - self[1]*other[0])
        else:
            return NotImplemented

    def __rxor__(self, other):
        """b ^ a: Vector cross product"""
        if isinstance(other, (tuple, list)) and len(other) >= 3:
            return Vector(other[1]*self[2] - other[2]*self[1],
                          other[2]*self[0] - other[0]*self[2],
                          other[0]*self[1] - other[1]*self[0])
        else:
            return NotImplemented

that you can just put in the same directory as the example Python file.
Run pydoc3 vector in that directory to see the API description for it.

Note that vector.py defines a generic 3D Euclidean vector class with basic vector algebra operations, and is in no way specific to this particular problem.