Как найти координаты центра окружности онлайн - Сайт, где вы сможете решить свои вопросы

Нахождение центра и радиуса окружности по общему уравнению окружности

Коэффициенты a, b, c, d, e уравнения

Введите коэффициенты a, b, c, d, e в указанном порядке ax² + by² + cx + dy + e = 0

Точность вычисления

Знаков после запятой: 2

Уравнение после выделения полного квадрата

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности – это будет точка с координатами (a,b), и радиус окружности – это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это – уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения
Для каждой скобки применим метод выделения полного квадрата (подробнее смотри тут – Метод выделения полного квадрата), то есть заменим выражение вида на выражение вида . С учетом того, что коэффициенты при квадратах равны единице, а свободный член можно принять за ноль, формула для вычисления h и k упрощаются.

Для x^2+cx :
$h_x=-frac{c}{2}\k_x=-frac{c^2}{4}$

Для y^2+dy :
$h_y=-frac{d}{2}\k_y=-frac{d^2}{4}$

Тогда
$(x^2+cx) + (y^2+dy)+e=0 \ to (x-h_x)^2+k_x + (y-h_y)^2+k_y + e=0 \ to (x-h_x)^2 + (y-h_y)^2=-e - k_x - k_y$

Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число – значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.

Для решения обратной задачи – нахождения общего уравнения окружности по координатам центра и радиусу – можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	– twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{”}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	–
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

центр:x^2+y^2=1
центр:x^2-6x+8y+y^2=0
центр:(x-2)^2+(y-3)^2=16
центр:x^2+(y+3)^2=16
центр:(x-4)^2+(y+2)^2=25
Показать больше

Описание

Пошаговое вычисление центра окружности по заданному уравнению

circle-function-center-calculator

Блог-сообщения, имеющие отношение к Symbolab

Practice, practice, practice

Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Нахождение центра и радиуса окружности по общему уравнению окружности

Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности – это будет точка с координатами (a,b), и радиус окружности – это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это – уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

Для каждой скобки применим метод выделения полного квадрата (подробнее смотри тут – Метод выделения полного квадрата), то есть заменим выражение вида на выражение вида . С учетом того, что коэффициенты при квадратах равны единице, а свободный член можно принять за ноль, формула для вычисления h и k упрощаются.

Уравнение окружности по трем точкам

Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.

Уравнение окружности

r 2 = (x — h) 2 + (y — k) 2

h,k — координаты центра Окружности
x,y — координаты точки окружности
r — радиус

Пример

Найдите координаты точки центра окружности, радиус и уравнение окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)

Решение :

Подставляем координаты точек в формулу

(2 — h) 2 + (2 — k) 2 = r 2
(2 — h) 2 + (4 — k) 2 = r 2
(5 — h) 2 + (5 — k) 2 = r 2

Шаг :2

Найдем значение k упрощая 1 и 2 уравнения

(2 — h) 2 + (2 — k) 2 = (2 — h) 2 + (4 — k) 2
4 — 4h + h 2 + 4 — 4k + k 2 = 4 — 4h + h 2 +16 — 8k + k 2
8 — 4k = 20 — 8k
k= 3

Шаг :3

Найдем значение h упрощая уравнения 2 и 3

(2 — h) 2 + (2 — k) 2 = (5 — h) 2 + (5 — k) 2
4 — 4h + h 2 + 4 — 4k + k 2 = 25 — 10h + h 2 + 25 — 10k + k 2
8 — 4k — 4h = 50 — 10h — 10k
6k + 6h = 42

Подставив значение k=3 в уравнение

Получаем координаты точки центра (h,k) = ( 4,3 )

Шаг :4

Подставим значения h,k в формулу

r 2 = (x — h) 2 + (y — k) 2
r 2 = (2 — 4) 2 + (2 — 3) 2
r 2 = (-2) 2 + (-1) 2
r 2 = 5
r = 2.24

Шаг :5

Подставим значения h, k в уравнение окружности

(x — h) 2 + (y — k) 2

Уравнение окружности = (x — 4) 2 + (y — 3) 2

Уравнение окружности

Для расчета уравнения, надо знать определение окружности. Итак, окружность – это множество точек в пространстве, равноудаленных от одной точки, называемой центром. Отрезок, соединяющий две точки окружности и проходящий через точку центра, называется диаметром. Отрезок, соединяющий две точки окружности – хорда. Отрезок, соединяющий центр и любую точку окружности – радиус. Радиус равен половине диаметра.

Рассчитывая уравнение окружности, получаем следующие данные:
• координаты точки центра;
• длину радиуса.

И наоборот, зная длину радиуса и координаты точки центра, можно определить координаты любой точки и начертить окружность.

Для чего необходимо рассчитывать уравнение окружности? Зная длину радиуса, который рассчитывается, исходя из данных уравнения, можно определить длину любой окружности и площадь круга по следующим формулам:
• l=2πr, где l – длина окружности, π=3,14
• S=πr2

Следует помнить, круг – это множество точек на плоскости координат, расположенных внутри окружности. Оптимальный способ рассчитать уравнение окружности – воспользоваться онлайн калькулятором. Это ускорит процесс и позволит быстро решить задачи по соответствующим формулам.

[spoiler title=”источники:”]

http://wpcalc.com/uravnenie-okruzhnosti-po-trem-tochkam/

http://allcalc.ru/node/847

[/spoiler]

Источник

Уравнение окружности

r² = (x — h)² + (y — k)²

где,

h,k — координаты центра Окружности
x,y — координаты точки окружности
r — радиус

Пример

Решение :

Шаг:1

Подставляем координаты точек в формулу

(2 — h)² + (2 — k)² = r²
(2 — h)² + (4 — k)² = r²
(5 — h)² + (5 — k)² = r²

Шаг :2

Найдем значение k упрощая 1 и 2 уравнения

(2 — h)² + (2 — k)² = (2 — h)² + (4 — k)²
4 — 4h + h²+ 4 — 4k + k² = 4 — 4h + h²+16 — 8k + k²
8 — 4k = 20 — 8k
k=3

Шаг :3

Найдем значение h упрощая уравнения 2 и 3

(2 — h)² + (2 — k)² = (5 — h)² + (5 — k)²
4 — 4h + h²+ 4 — 4k + k² = 25 — 10h + h²+ 25 — 10k + k²
8 — 4k — 4h = 50 — 10h — 10k
6k + 6h = 42

Подставив значение k=3 в уравнение

6h = 24
h=4

Получаем координаты точки центра (h,k) = (4,3)

Шаг :4

Подставим значения h,k в формулу

r² = (x — h)² + (y — k)²
r² = (2 — 4)² + (2 — 3)²
r² = (-2)² + (-1)²
r² = 5
r = 2.24

Шаг :5

Подставим значения h, k в уравнение окружности

(x — h)² + (y — k)²

Уравнение окружности = (x — 4)² + (y — 3)²

Ответ :

Координаты точки центра окружности c(h,k) = c(4,3)
Радиус окружности r = 2.24
Уравнение окружности = (x — 4)² + (y — 3)² = (2.24)²

людей нашли эту статью полезной. А Вы?

Источник

Как найти радиус и центр окружности

Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.

Окружность радиуса R с центром в начале координат представляется уравнением:

Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

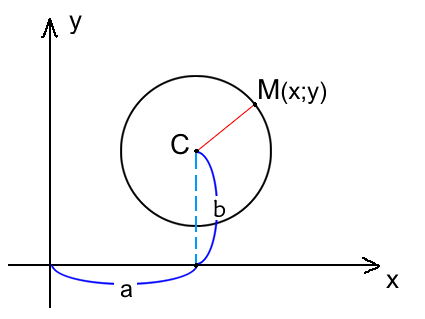
Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия).
Это уравнение можно записать в виде:

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x² и y² были равны в уравнение вида:

3. Если выполняется неравенство

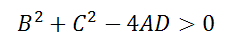
Как найти радиус и центр окружности

Уравнение Ax²+Bx+Ay²+Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

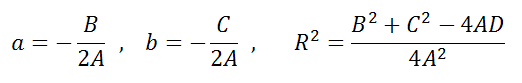
Пример 1
Уравнение 5x²-10x+5y²+20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

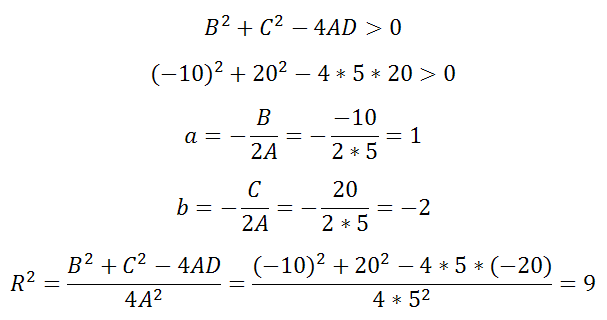
Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x²+4xy+y²=1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x²+9y²=36 не представляет окружность, так как в нём коэффициенты при x² и y² не равны.

7925

Источник

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Номер Строки

Нахождение центра и радиуса окружности по общему уравнению окружности

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Уравнение окружности по трем точкам

Уравнение окружности

Пример

Решение :

Шаг :2

Шаг :3

Шаг :4

Шаг :5

Уравнение окружности

Уравнение окружности

Пример

Решение :

Шаг:1

Шаг :2

Шаг :3

Шаг :4

Шаг :5

Ответ :

Как найти радиус и центр окружности

Окружность радиуса R с центром в начале координат представляется уравнением:

Как найти радиус и центр окружности

Вам также может понравиться

Как найти площадь неправильной четырехугольной пирамиды

Как найти мою историю в инстаграме

Как найти анионы при диссоциации

Добавить комментарий Отменить ответ