Как найти центр симметрии
Одним из видов симметрии является центральная. Центр симметрии – некоторая точка O, относительно которой вращают плоскость, поворачивая ее на 180°. Каждая точка A переходит в такую точку A’, что O – середина отрезка AA’.

Инструкция
Если даны две точки, центром симметрии между ними, по определению, будет середина отрезка, соединяющего их. Сложнее обстоит дело с геометрической фигурой: здесь уже надо рассмотреть все точки, составляющие ее. Любая произвольная точка должна переходить в центрально симметричную ей, иначе принцип симметрии будет нарушен.
Если даны две фигуры, про которые сказано, что они являются симметричными относительно неизвестного центра, попробуйте мысленно вращать каждую из фигур. В итоге вы должны представить переход на 180° (пол-окружности). Найдите любые две симметричные точки, проведите между ними отрезок. В его центре будет располагаться центр симметрии и этих двух точек, и всей фигуры.
Пусть надо построить окружность, симметричную данной относительно точки O. Центр окружности пусть обозначен точкой C. Проведите прямую от точки C через точку O. Ножками циркуля отмерьте расстояние OC, отложите такое же расстояние на прямой от точки O в другую сторону. Зафиксируйте результат, это будет центр новой окружности. Измерьте циркулем радиус исходной окружности и достройте симметричную.
Чтобы построить многоугольник, симметричный данному относительно центра O, найдите образ каждой из его вершин. Исходная точка называется «прообразом», конечная – «образом». Последовательно соедините точки между собой. Мысленно повращайте фигуры, оцените, правильным ли получился результат.
Если дана пространственная фигура, и необходимо найти центр симметрии между какими-либо двумя точками, вспомните свойства этого объемного тела. Возможно, центр симметрии лежит на пересечении диагоналей, биссектрис, медиан, перпендикуляров. Докажите, что указанная вами точка является именной центром симметрии, используя свойства фигуры, другие данные в задаче условия и определение симметричности.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Координаты симметричных точек
Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
Осевая и центральная симметрия

О чем эта статья:
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.

- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Дробно-линейные отображения
Дробно-линейной функцией называется функция вида: , где — произвольные комплексные числа, такие, что .
Перечислим без доказательства свойства дробно-линейной функции.
- Дробно-линейная функция осуществляет взаимно однозначное отображение расширенной комплексной плоскости на себя. При этом точка отображается в точку , а точка отображается в .
- Дробно-линейное отображение можно представить в виде суперпозиции трех простейших отображений: целого линейного , отображения и сдвига .
- Дробно-линейное отображение отображает окружности и прямые в окружности и прямые. При этом прямая может перейти как в прямую, так и в окружность. Окружность тоже может перейти как в прямую, так и в окружность. Это свойство называется круговым свойством дробно-линейных отображений.
- Точки симметричные относительно прямой или окружности переходят в точки симметричные относительно образа этой прямой или окружности.
- Дробно-линейное отображение, переводящее три заданные точки в три заданные точки: дается формулой:
Пример 1 Найти образ мнимой оси при отображении .
Мнимая ось представляет собой прямую. По третьему свойству она должна перейти в окружность или в прямую. Найдем образы трех точек мнимой оси: . Так как образ одной из точек , то мнимая ось переходит в прямую проходящую через и , то есть в действительную ось.
Пример 2 Найти дробно линейное отображение, переводящее точки .
Пример 3 Найти образ области при отображении
Найдем образ мнимой оси при данном отображении. Возьмем три точки : .
Отметим также, что . Куда же перешел луч ? Подставим в формулу отображения: . При , точки переходят в точки луча действительной оси. Точки переходят в луч . Образы двух точек действительной оси у нас есть: Действительная ось переходит в окружность, проходящую через точки .
Найдем образ точки из границы нашей области:
Итак, образ луча будет полуокружность .
Теперь мы можем изобразить схему самого отображения:
Пример 4 Найти образы всех квадрантов при отображении .
Чтобы не решать опять задачи подобные примеру 3, воспользуемся следствием принципа симметрии Римана-Шварца в такой формулировке:
Пусть функция отображает область в и — дуга окружности или отрезок, принадлежащий границе области , и — область, симметричная относительно .
Пусть непрерывна на и области и не пересекаются. Тогда функция конформно отображает на , где и — образы и соответственно при отображении .
На следующем рисунке видно, что области и симметричны относительно луча , который переходит в полуокружность . Так находится образ области . Он для удобства обозначен штриховкой. Точно так же находятся образы остальных двух квадрантов.
Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.
Нужна помощь с курсовой или дипломной работой?
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/osevaya-i-centralnaya-simmetriya
http://khab.work5.ru/spravochnik/matematika/drobno-linejnye-otobrazheniya
[/spoiler]
Объясните в кратце пожалуйста как найти центр симметрии?
Ученик
(51),
закрыт
5 лет назад
Naumenko
Высший разум
(856099)
5 лет назад
если дана пара фигур и сказано. что они центрально-симметричны. то
нужно найти пару соответственных точек-например вершины равных углов
соединить их отрезком
найти середину этого отрезка-
это и будет центром симметрии
запросм в КАРТИНКИ
центральная симметрия.
насмотришься и разберешься.
Евген Про
Знаток
(250)
5 лет назад
0_______А______С______В______ ; Рассмотрим числовой луч с началом отсчета в т. О (0). На нем даны точки с заданными координатами А и В. Надо найти центр симметрии этих точек, точку С. Для этого из длины отрезкаОВ нужно вычесть длину отрезка ОА – мы получим длину отрезка АВ. АВ нужно разделть пополам- это длина АС=СВ. Теперь, чтобы узнать координаты точки С нужно к длине ОА добавить АС. Все.. Вот
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Осевая и центральная симметрии
Осевая симметрия
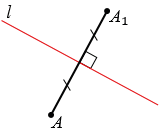
Рассмотрим построение точки, симметричной данной точке А относительно данной прямой  .
.
Пусть дана точка А и прямая  .
.
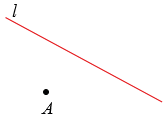
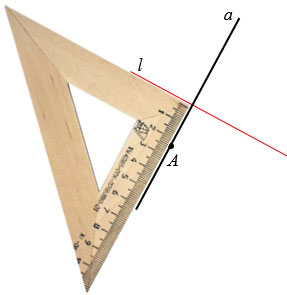
Точку симметричную точке А относительно прямой  , можно построить так. Проведем через точку А прямую
, можно построить так. Проведем через точку А прямую  , перпендикулярную прямой
, перпендикулярную прямой  . Для этого используем чертежный угольник. Прикладываем чертежный угольник так, как показано на рисунке ниже и проводим прямую
. Для этого используем чертежный угольник. Прикладываем чертежный угольник так, как показано на рисунке ниже и проводим прямую  через точку А.
через точку А.
Пусть прямые  и
и  пересекаются в точке О. Отложим при помощи линейки на прямой
пересекаются в точке О. Отложим при помощи линейки на прямой  отрезок ОА1, равный отрезку ОА.
отрезок ОА1, равный отрезку ОА.
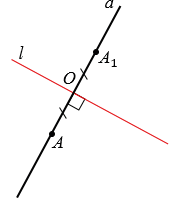
Получаем точки А и А1, которые симметричны относительно прямой  .
.
Также можно построить фигуры, симметричные относительно прямой.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой  .
.
Пусть дан треугольник АВС и прямая  .
.
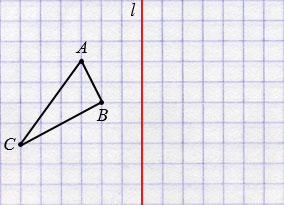
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно прямой  (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой
(алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой  .
.
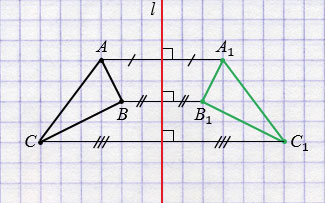
Обратите внимание, любые две фигуры, симметричные относительно прямой, равны.
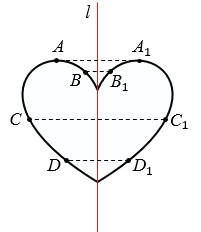
Если фигура имеет ось симметрии (прямая  ) то, все точки этой фигуры, не принадлежащие этой оси, можно разделить на пары симметричных точек.
) то, все точки этой фигуры, не принадлежащие этой оси, можно разделить на пары симметричных точек.
Центральная симметрия
Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1 (смотри рисунок ниже).
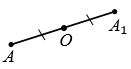
Рассмотрим построение точки, симметричной данной точке М относительно данной точки О.
Пусть даны точки М и О. Точку, симметричную точке М относительно точки О, можно построит так. Проведем луч МО.
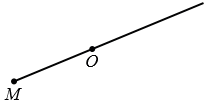
На луче МО отложим отрезок ОN , равный отрезку ОМ.
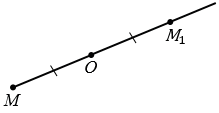
Точки М и М1, которые симметричны относительно точки О.
Также можно построить фигуры, симметричные относительно точки.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
Пусть дан треугольник АВС и точки О.
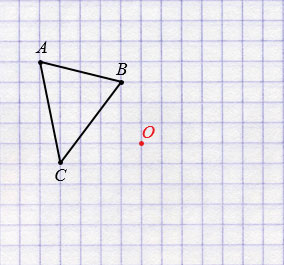
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно точки О (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
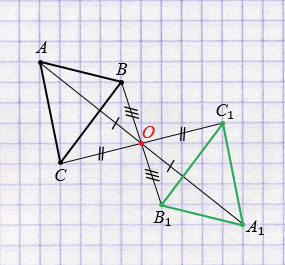
Обратите внимание, любые две фигуры, симметричные относительно точки, равны.
Рассмотрим окружность с центром в точке О. Все точки окружности можно разбить на пары точек, симметричных относительно точки О.
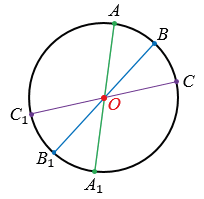
В таком случае говорят, что окружность имеет центр симметрии – точку О.
Также центр симметрии имеют такие фигуры, как отрезок, прямоугольник, эллипс.
Советуем посмотреть:
Перпендикулярные прямые
Параллельные прямые
Координатная плоскость
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1249,
Мерзляк, Полонский, Якир, Учебник
Номер 1253,
Мерзляк, Полонский, Якир, Учебник
Номер 1256,
Мерзляк, Полонский, Якир, Учебник
Номер 1258,
Мерзляк, Полонский, Якир, Учебник
Номер 1262,
Мерзляк, Полонский, Якир, Учебник
Номер 1266,
Мерзляк, Полонский, Якир, Учебник
Номер 1270,
Мерзляк, Полонский, Якир, Учебник
Номер 1318,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 8,
Мерзляк, Полонский, Якир, Учебник
Сегодня на уроке мы вспомним понятия отображения
плоскости на себя, движение плоскости, вспомним основные понятия центральной
симметрии. Введём понятия отображения пространства и движение пространства,
центральной симметрии в пространстве. Определим, будет ли центральная симметрия
в пространстве – движением пространства.
Мы уже с вами знакомы с таким понятием, как
движение. Давайте вспомним, что мы называли движением.
Движением
мы называли любое отображение плоскости, которое сохраняет расстояние между
точками.
Отображение
плоскости на себя определяли так: если каждой точке плоскости
ставится в соответствие какая-то точка этой же плоскости, причём любая точка
плоскости оказывается сопоставленной некоторой точке, то говорят, что дано отображение
плоскости на себя.
Эти определения мы давали для движения на плоскости.
Но в стереометрии мы говорим о пространстве, значит, надо определить, что
называется движением пространства.
Но сначала давайте определим, что такое отображение
пространства на себя.
Определение:
Пусть каждой точке пространства
поставлена в соответствие некоторая точка ,
причем любая точка пространства
оказалась поставленной в соответствие какой-то точке .
Тогда говорят, что задано отображение пространства на себя. При
данном отображении точка переходит
(отображается) в точку .
Определение:
Под движением пространства понимается
отображение пространства на себя, при котором любые две точки пространства и
отображаются
в какие-то точки и
так,
что .
По-другому можно сказать, что движение
пространства – это отображение пространства на себя, сохраняющее
расстояние между точками.
Теперь давайте вспомним, какие фигуры обладают центральной
симметрией.
Определение:
Фигура называется симметричной относительно
точки ,
если для каждой точки фигуры симметричная ей точка относительно точки также
принадлежит этой фигуре. Точка называется
центром симметрии фигуры.
Примерами
центрально симметричных фигур можно назвать некоторые цветы:
В геометрии яркими примерами центрально симметричных
фигур являются окружность (центр симметрии – центр окружности) и параллелограмм
(центром симметрии является точка пересечения диагоналей).
Ещё мы давали такое определение:
Точки и
называются
симметричными относительно точки ,
если –
середина отрезка .
Точка называется
центром симметрии.
Точка считается
симметричной сама себе.
В курсе планиметрии мы доказывали, что центральная
симметрия является движением.
Напомним это доказательство.
Рассмотрим точки М и N
и точки М1 и N
1
симметричные точкам М и N
относительно точки О.
Рассмотрим треугольники М NО
и М1ОN1.
То есть при центральной симметрии сохраняется
расстояние между точками. Тогда по определению движения, получим, что и центральная
симметрия является движением.
Определение:
В пространстве центральной симметрией
мы назовём отображение пространства на себя, при котором любая точка переходит
в симметричную ей точку относительно
данного центра .
Теперь давайте докажем, что и в пространстве
центральная симметрия является движением.
Пусть О – центр симметрии. Введём прямоугольную
систему координат Оxyz с началом в
точке О. Теперь давайте попробуем установить связь между координатами двух
точек М (x, y,
z) и М1(x1,
y1,
z1),
симметричных относительно точки О.
Если точка М не совпадает с точкой О, то по
определению центральной симметрии О – середина отрезка ММ1. Тогда
координаты точки О можно вычислить по формулам координат середины отрезка. С
другой стороны, поскольку О – начало координат, значит, точка О имеет
координаты 0, 0, 0. То есть получим, что ,
,
.
Если точки М и О совпадают, тогда точка М1
также совпадает с точкой О, потому что точка О – центр симметрии, а, значит,
она отображается сама на себя. И в этом случае будут выполнятся равенства,
,
.
Теперь давайте рассмотрим две точки и
.
По только что доказанным формулам для координат
симметричных точек получим, что точка .
Точка .
Теперь давайте найдём расстояние .
Получим, что расстояние между точками ,
равно:
Теперь давайте найдём расстояние между точками и
.
Очевидно, что оба эти выражения равны, то есть
получим, что .
Вывод: расстояние между
точками при центральной симметрии в пространстве сохраняется, значит,
центральная симметрия в пространстве также является движением, но
уже не плоскости, а пространства.
Рассмотрим несколько задач.
Задача:
найти координаты точек, в которые переходят точки ,
,
при
центральной симметрии относительно начала координат.
Решение: воспользуемся
формулами для вычисления координат симметричных точек.
Если точка симметрична
точке то
справедливы формулы:
.
Тогда получим, что точка отобразится
в точку .
Точка отобразится
в точку .
Точка отобразится
в точку .
Решим ещё одну задачу.
Задача:
доказать, что при центральной симметрии прямая, не проходящая через центр
симметрии, отображается на параллельную ей прямую.
Доказательство. Пусть
прямая не
проходит через центр симметрии О. Построим точки симметричные точкам и
относительно
точки О.
Рассмотрим и
.
По определению центральной симметрии точка О – середина отрезков АА1
и ВВ1, то есть и
.
Углы как вертикальные, то
есть треугольники равны по двум сторонам и углу между ними.
Тогда получим, что .
Эти углы являются накрестлежащими для прямых и
при
секущей .
Тогда по признаку параллельности прямых получим, что прямые .
Что и требовалось доказать.
Итоги:
Сегодня на уроке мы вспомнили понятия отображения
плоскости на себя, движение плоскости, вспомнили основные понятия центральной
симметрии. Ввели понятия отображения пространства и движение пространства,
центральной симметрии в пространстве. Показали, что и в пространстве
центральная симметрия будет примером движения.
