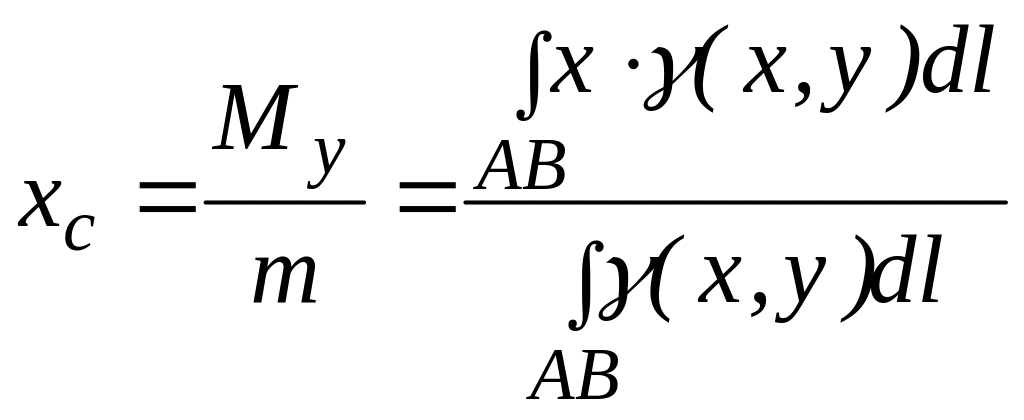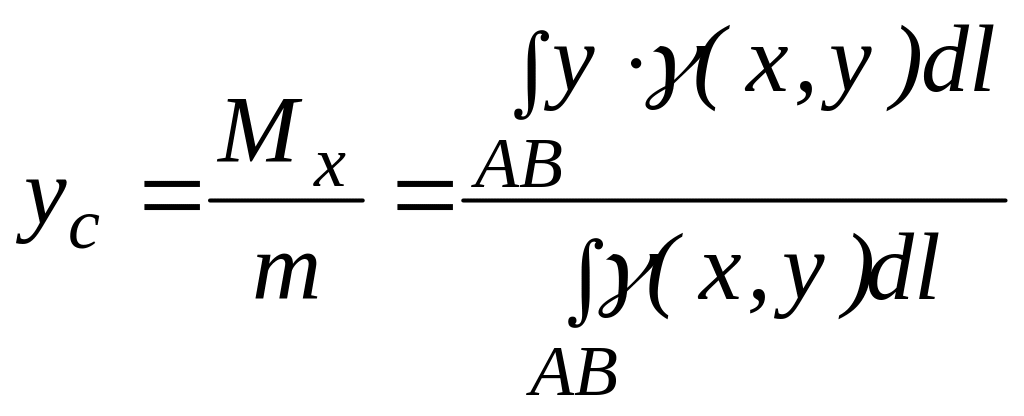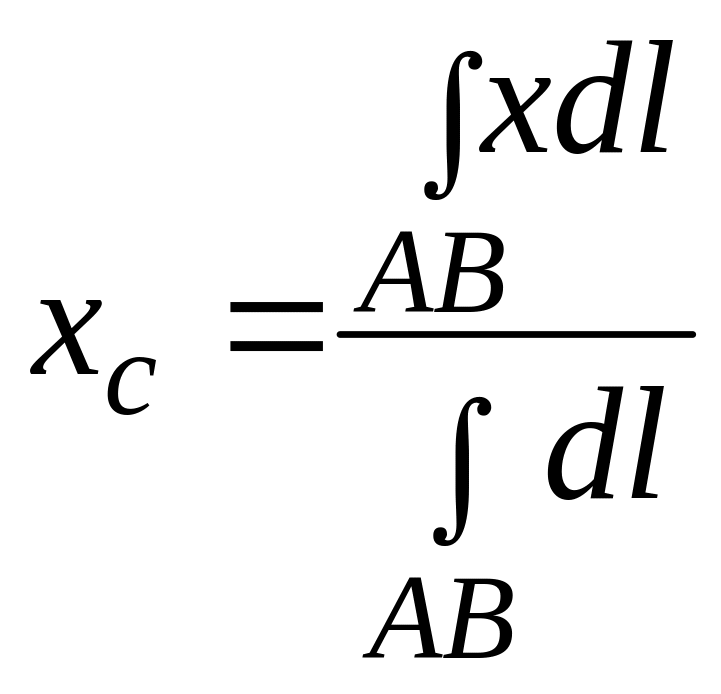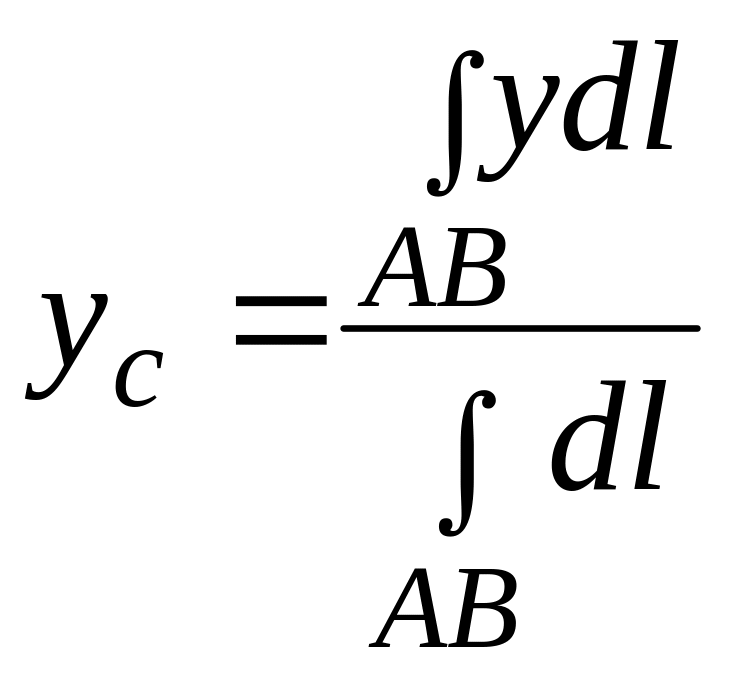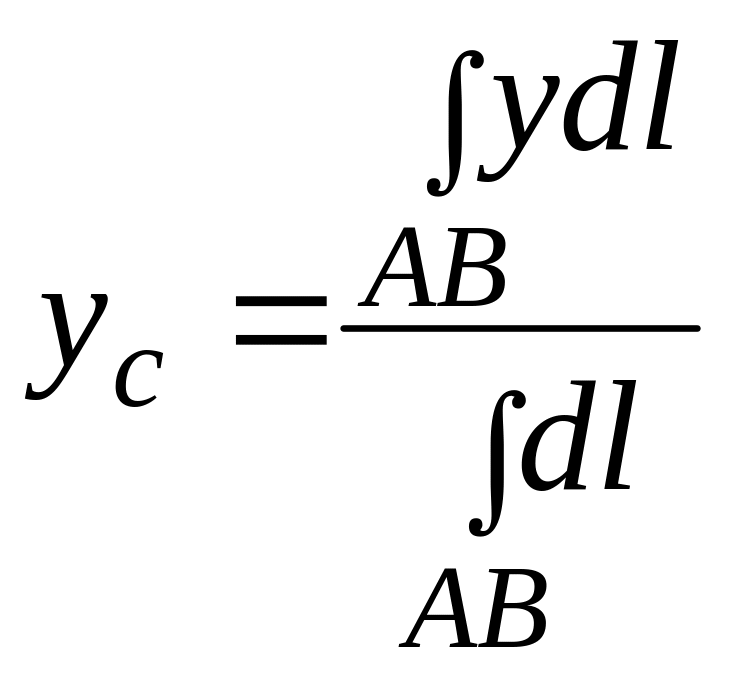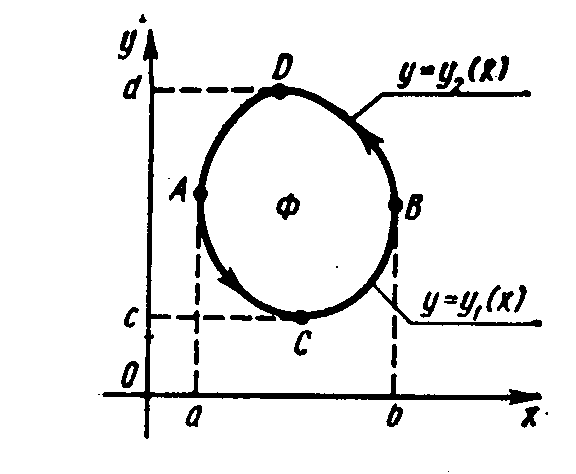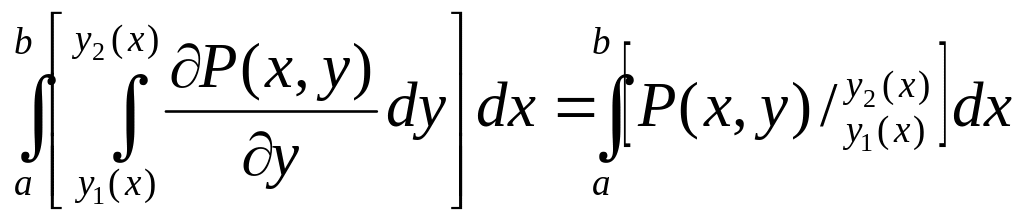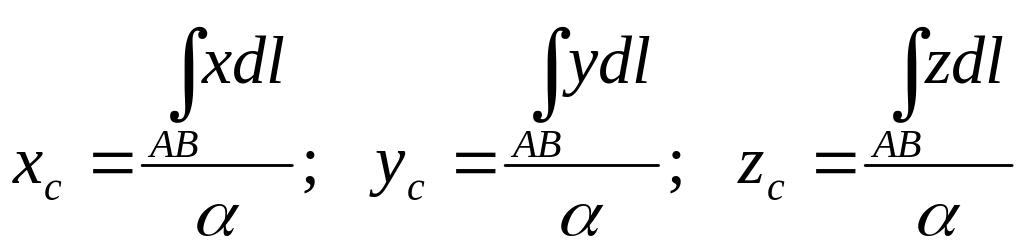Формулы для расчета координат положения центра тяжести треугольника, дуги окружности и кругового сегмента.
Рисунок 1.10
Центр тяжести треугольника
Центр тяжести площади треугольника совпадает с точкой пересечения его медиан (рисунок 1.10, а).
DM = MB, CM = (1/3)AM.
Центр тяжести дуги окружности
Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. yC = 0.
dl – элемент дуги, dl = Rdφ, R – радиус окружности, x = Rcosφ, L = 2αR,
Следовательно:
xC= R(sinα/α).
Центр тяжести кругового сектора
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок 1.10, в).
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R.
Центр тяжести сектора совпадает с центром тяжести дуги AB:
Примеры решения задач >
Центры тяжести других фигур >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
iSopromat.ru
Формулы для расчета координат положения центра тяжести треугольника, дуги окружности и кругового сегмента.
Центр тяжести треугольника
Центр тяжести площади треугольника совпадает с точкой пересечения его медиан (рисунок 1.10, а).
Центр тяжести дуги окружности
Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. yC = 0.
dl – элемент дуги, dl = Rdφ, R – радиус окружности, x = Rcosφ, L = 2αR,
Центр тяжести кругового сектора
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок 1.10, в).
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R.
Центр тяжести сектора совпадает с центром тяжести дуги AB:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Определение положения центра тяжести дуги окружности
iSopromat.ru
Формулы для расчета координат положения центра тяжести треугольника, дуги окружности и кругового сегмента.
Центр тяжести треугольника
Центр тяжести площади треугольника совпадает с точкой пересечения его медиан (рисунок 1.10, а).
Центр тяжести дуги окружности
Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. yC = 0.
dl – элемент дуги, dl = Rdφ, R – радиус окружности, x = Rcosφ, L = 2αR,
Центр тяжести кругового сектора
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок 1.10, в).
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R.
Центр тяжести сектора совпадает с центром тяжести дуги AB:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Теоретическая механика:
Центр тяжести
Смотрите также решения задач по нахождению центра тяжести в онлайн решебниках Яблонского (С.8) и Мещерского (§ 9).
Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил (Е. М. Никитин, § 42). Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
xc = (∑ Gixi) / ∑ Gi;
(1) yc = (∑ Giyi) / ∑ Gi;
zc = (∑ Gizi) / ∑ Gi.
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес Gi каждого отрезка li можно представить в виде произведения
Gi = lid,
где d – постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо Gi их значений lid постоянный множитель d в каждом слагаемом числителя и знаменателя можно вынести за скобки (за знак суммы) и сократить. Таким образом, формулы для определения координат центра тяжести фигуры, составленной из отрезков линий , примут вид:
xc = (∑ lixi) / ∑ li;
(2) yc = (∑ liyi) / ∑ li;
zc = (∑ lizi) / ∑ li.
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174), то вес каждой плоскости (поверхности) можно представить так:
Gi = Fip,
где Fi – площади каждой поверхности, а p – вес единицы площади фигуры.
После подстановки этого значения Gi в формулы (1) получаем формулы координат центра тяжести фигуры, составленной из площадей :
xc = (∑ Fixi) / ∑ Fi;
(3) yc = (∑ Fiyi) / ∑ Fi;
zc = (∑ Fizi) / ∑ Fi.
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
Gi = Viγ,
где Vi – объем каждой части, а γ – вес единицы объема тела.
После подстановки значений Gi в формулы (1) получаем формулы для определения координат центра тяжести тела, составленного из однородных объемов :
xc = (∑ Vixi) / ∑ Vi;
(4) yc = (∑ Viyi) / ∑ Vi;
zc = (∑ Vizi) / ∑ Vi.
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
Если известен радиус дуги r и центральный угол 2α, стягиваемый дугой и выраженный в радианах, то положение центра тяжести C (рис. 176, а) относительно центра дуги O определится формулой:
(5) xc = (r sin α)/α.
Если же задана хорда AB=b дуги, то в формуле (5) можно произвести замену
sin α = b/(2r)
и тогда
(5а) xc = b/(2α).
В частном случае для полуокружности обе формулы примут вид (рис. 176, б):
(5б) xc = OC = 2r/π = d/π.
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы:
(6) xc = (2r sin α)/(3α).
Если же задана хорда сектора, то:
(6а) xc = b/(3α).
В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
(6б) xc = OC = 4r/(3π) = 2d/(3π).
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
При решении задач на определение положения центра тяжести любого однородного тела, составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
1) выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
2) разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
3) определить или длины, или площади, или объемы составных частей;
4) выбрать расположение осей координат;
5) определить координаты центров тяжести составных частей;
6) найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
7) по найденным координатам указать на рисунке положение центра тяжести тела.
§ 23. Определение положения центра тяжести тела, составленного из тонких однородных стержней
§ 24. Определение положения центра тяжести фигур, составленных из пластинок
В последней задаче, а также в задачах, приведенных в предыдущем параграфе, расчленение фигур на составные части не вызывает особых затруднений. Но иногда фигура имеет такой вид, который позволяет разделить ее на составные части несколькими способами, например тонкую пластинку прямоугольной формы с треугольным вырезом (рис. 183). При определении положения центра тяжести такой пластинки ее площадь можно разделить на четыре прямоугольника (1, 2, 3 и 4) и один прямоугольный треугольник 5 – несколькими способами. Два варианта показаны на рис. 183, а и б.
Наиболее рациональным является тот способ деления фигуры на составные части, при котором образуется наименьшее их число. Если в фигуре есть вырезы, то их можно также включать в число составных частей фигуры, но площадь вырезанной части считать отрицательной. Поэтому такое деление получило название способа отрицательных площадей.
Пластинка на рис. 183, в делится при помощи этого способа всего на две части: прямоугольник 1 с площадью всей пластинки, как будто она целая, и треугольник 2 с площадью, которую считаем отрицательной.
§ 25. Определение положения центра тяжести сечений, составленных из профилей стандартного проката
При решении задач, приведенных в этом параграфе, нужно пользоваться таблицами из ГОСТа на прокатную сталь: ГОСТ 8509–57, ГОСТ 8510–57, ГОСТ 8239–56, ГОСТ 8240–56.
Эти таблицы для каждого профиля содержат их размеры и площадь, а для уголков и швеллера, кроме того, – координаты центров тяжести.
§ 26. Определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму
Чтобы решать задачи на определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму, необходимо иметь навыки определения координат центра тяжести фигур, составленных из линий или площадей.
Центры тяжести некоторых однородных тел
Центр тяжести площади треугольника. Разобьем площадь треугольника ABD на ряд узких полосок, параллельных стороне AD (рис. 5.3). Центр тяжести каждой такой элементарной полоски находится в ее середине, а центры тяжести всех этих полосок будут лежать на медиане BE. Разбив площадь треугольника прямой, параллельной его другой стороне, например стороне АВ, убедимся, что центр тяжести треугольника должен лежать на медиане DK. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке С пересечения его медиан. Точка пересечения медиан делит каждую медиану в отношении 2 : 1, т. е. СЕ= (1/3)ВЕ, СВ = (2/3)BE.
Если известны координаты вершин данного треугольника А(хЛ, у A, ZA), В(хв, ув, ZB), D(xd, yD, ZD), TO по формулам аналитической геометрии получим координаты центра тяжести С:
Центр тяжести дуги окружности. Рас-
смотрим дугу АВ радиусом R с центральным углом АОВ= 2а. Ввиду симметрии центр тяжести этой дуги лежит на оси
Ох (рис. 5.4). Выделим на дуге АВ элемент ab длиной dl = Rdiр, положение которого определяется углом ф. Координата х элемента ab будет х = R cos ф. Подставляя значения хи dl в первую из формул (5.8), заменив в ней знак суммирования на интеграл по всей
длине дуги АВ, получим
где L — длина дуги АВ, равная R • 2а. Отсюда окончательно находим, что центр тяжести дуги окружности лежит на оси ее симметрии на расстоянии от центра О, равном
где угол а измеряется в радианах.
Центр тяжести кругового сектора. Рассмотрим круговой сектор ОАВ радиусом R с центральным углом 2а (рис. 5.5). Разобьем площадь сектора ОАВ радиусами, проведенными из центра О, на элементарные секторы, каждый из которых можно рассматривать как
треугольники, центры тяжести которых лежат на дуге DE окружности радиусом 2R/2. Следовательно, центр тяжести сектора ОАВ совпадает с центром тяжести дуги DE, положение которого определится по формуле (5.10), подставив в нее значение радиуса 2/?/3:
В частности, для полукруга будем иметь a = я/2 и из (5.11) получим:
Приведем без доказательства еще некоторые результаты.
Центр тяжести призмы. Чтобы найти центр тяжести призмы, мысленно разобьем ее плоскостями, параллельными основанию, на тонкие пластины, которые можно принять за плоские многоугольники. Учитывая, что все они будут одинаковыми, то их центры тяжести лежат на отрезке прямой, соединяющей центры тяжести С| нижнего и С2 верхнего оснований этой призмы, а центр тяжести С всей призмы находится в середине указанного отрезка (рис. 5.6).
Центр тяжести пирамиды (конуса). Этот центр С лежит на отрезке прямой, соединяющей вершину пирамиды с центром тяжести ее основания, на расстоянии 1/4 этого отрезка от центра тяжести основания. Так, для пирамиды и конуса, изображенных на рис. 5.7,
Этот результат справедлив для любой многоугольной пирамиды и для конуса.
Центр тяжести полушара. Этот центр С лежит на оси Ох (ось симметрии, рис. 5.8), а его координата
где R — радиус полушара.
Задача 5.1. Из тонкой однородной проволоки сделан контур (рис. 5.9, а), представляющий собой две дуги полуокружностей радиусов R и г = R/2 и прямую AD. Определить центр тяжести контура.
Решение. Проводим оси Dxy и разбиваем контур на три элемента, для каждого из которых находим его длину и координаты центра тяжести.
Центры тяжести некоторых однородных тел
Центр тяжести площади треугольника. Разобьем площадь треугольника ABD на ряд узких полосок, параллельных стороне AD (рис. 5.3). Центр тяжести каждой такой элементарной полоски находится в ее середине, а центры тяжести всех этих полосок будут лежать на медиане BE. Разбив площадь треугольника прямой, параллельной его другой стороне, например стороне АВ, убедимся, что центр тяжести треугольника должен лежать на медиане DK. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке С пересечения его медиан. Точка пересечения медиан делит каждую медиану в отношении 2 : 1, т. е. СЕ= (1/3)ВЕ, СВ = (2/3)BE.
Если известны координаты вершин данного треугольника А(хЛ, у A, ZA), В(хв, ув, ZB), D(xd, yD, ZD), TO по формулам аналитической геометрии получим координаты центра тяжести С:
Центр тяжести дуги окружности. Рас-
смотрим дугу АВ радиусом R с центральным углом АОВ= 2а. Ввиду симметрии центр тяжести этой дуги лежит на оси
Ох (рис. 5.4). Выделим на дуге АВ элемент ab длиной dl = Rdiр, положение которого определяется углом ф. Координата х элемента ab будет х = R cos ф. Подставляя значения хи dl в первую из формул (5.8), заменив в ней знак суммирования на интеграл по всей
длине дуги АВ, получим
где L — длина дуги АВ, равная R • 2а. Отсюда окончательно находим, что центр тяжести дуги окружности лежит на оси ее симметрии на расстоянии от центра О, равном
где угол а измеряется в радианах.
Центр тяжести кругового сектора. Рассмотрим круговой сектор ОАВ радиусом R с центральным углом 2а (рис. 5.5). Разобьем площадь сектора ОАВ радиусами, проведенными из центра О, на элементарные секторы, каждый из которых можно рассматривать как
треугольники, центры тяжести которых лежат на дуге DE окружности радиусом 2R/2. Следовательно, центр тяжести сектора ОАВ совпадает с центром тяжести дуги DE, положение которого определится по формуле (5.10), подставив в нее значение радиуса 2/?/3:
В частности, для полукруга будем иметь a = я/2 и из (5.11) получим:
Приведем без доказательства еще некоторые результаты.
Центр тяжести призмы. Чтобы найти центр тяжести призмы, мысленно разобьем ее плоскостями, параллельными основанию, на тонкие пластины, которые можно принять за плоские многоугольники. Учитывая, что все они будут одинаковыми, то их центры тяжести лежат на отрезке прямой, соединяющей центры тяжести С| нижнего и С2 верхнего оснований этой призмы, а центр тяжести С всей призмы находится в середине указанного отрезка (рис. 5.6).
Центр тяжести пирамиды (конуса). Этот центр С лежит на отрезке прямой, соединяющей вершину пирамиды с центром тяжести ее основания, на расстоянии 1/4 этого отрезка от центра тяжести основания. Так, для пирамиды и конуса, изображенных на рис. 5.7,
Этот результат справедлив для любой многоугольной пирамиды и для конуса.
Центр тяжести полушара. Этот центр С лежит на оси Ох (ось симметрии, рис. 5.8), а его координата
где R — радиус полушара.
Задача 5.1. Из тонкой однородной проволоки сделан контур (рис. 5.9, а), представляющий собой две дуги полуокружностей радиусов R и г = R/2 и прямую AD. Определить центр тяжести контура.
Решение. Проводим оси Dxy и разбиваем контур на три элемента, для каждого из которых находим его длину и координаты центра тяжести.
Дуга АВ радиусом /?(/, = nR, х< = 0, у <— 2R/n, последнее получим из
формулы (5.10), положив а — п/2), дуга DB радиусом r—R/2(l2 — nR/2,
Подставив соответствующие значения в формулы (5.8), получим
Найденное положение центра тяжести С контура показано на рис. 5.9, а.
Задача 5.2. Определить центр тяжести пластины, ограниченной контуром, рассмотренным в предыдущей задаче.
Проводим оси Dxy (рис. 5.9, б) и разбиваем пластину на два элемента: полукруг радиусом R (ч. 1), из которого вырезан полукруг радиусом г = R/2 (ч. 2).
При выполнении расчетов площадь части 2, как вычитаемая, должна браться со знаком «минус». Тогда для каждой части имеем:
Подставив числовые значения величин в формулы (5.7), получим
Центр тяжести С, координаты которого определены, показываем на чертеже (рис. 5.9, б); он располагается на прямой СХС2 левее точки Сх.
Сопоставив результаты задач 5.1 и 5.2, видим, что центр тяжести пластины (рис. 5.9, б) не совпадает с центром тяжести контура (рис. 5.9, а), окаймляющего ее.
Задача 5.3. Определить положение центра тяжести однородной пластины, изображенной на рис. 5.10 (размеры даны в сантиметрах).
Решение. Проводим оси Вху. Площадь пластины рассматриваем как фигуру, составленную из трех частей: треугольника ЛВК (ч. 1) и прямоугольника BKED (ч. 2), из которого вырезан полукруг (ч. 3) радиусом R = 3 см.
Вычисляем площадь и координаты центров тяжести каждой части пластины:
S3 = —uF?/2 — —14,13 см 2 (площадь полукруга берем со знаком минус, так как она вычитается из площади прямоугольника), х3 = 8 — 4/?/Зтг = 6,73 см, у3 = 3 см.
Площадь всей пластины S = о) + S2 + о3 = 42,87 см .
Подставив соответствующие значения в формулы (5.7), получим:
Найденное положение центра тяжести С показываем на чертеже.
Задача 5.4. Определить положение центра тяжести однородного твердого тела (рис. 5.11), состоящего из трех частей: полушара I радиусом /?, прямого круглого цилиндра II радиусом г — /?/2 и высотой Н — 4/?, круглого конуса III с основанием радиусом /? и высотой h = 2/?.
Решение. Проводим оси координат Oxyz так, что ось у совмещена с осью симметрии тела. Тогда хс— 0, Zq
Обозначим центры тяжести полушара через Сх, цилиндра — через С2, конуса — через С3. Для вычисления ус воспользуемся формулой (5.6), которая в данном случае имеет вид:
где ух, у2, у3 — координаты центров тяжести полушара, цилиндра и конуса; V], v2, v3 — соответственно объемы этих тел; общий объем V— v, + v2 + v3.
Находим: для полушара I vx — 2kR 3 /3, yx= — 3R/8 для цилиндра II v2 = nr 2 H= kR 3 , у2 = Н/2 = 2R; для конуса III v3 = nF^h/3 = 2nR 3 /3, у3 =
= // + -h -4,5R, V-7nR /3. Подставив эти значения в формулу, получим У с — (57/28) /?.
Ответ: положение центра тяжести С данного твердого тела (см. рис. 5.11) определяется координатами хс— 0, ус — (57/28)/?, ?с= 0.
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/opredelenie-polozheniya-tsentra-tyazhesti-dugi-okruzhnosti
http://studref.com/496042/matematika_himiya_fizik/tsentry_tyazhesti_nekotoryh_odnorodnyh
[/spoiler]
Содержание:
- Центр масс
- Центр параллельных сил
- Центр тяжести
- Центры тяжести некоторых плоских однородных фигур
- Центр тяжести дуги окружности
- Центр тяжести кругового сектора
- Центр тяжести кругового сегмента
- Центр тяжести треугольника
- Центр тяжести трапеции
- Примеры решения задач на тему: Центр масс
- Способы определения координат центра тяжести тела
- Метод симметрии
- Метод разбиения
- Метод дополнения
- Экспериментальные способы
- Центры тяжести некоторых однородных тел
- Центр тяжести дуги окружности
- Центр тяжести треугольника
- Центр тяжести сектора
Центр масс – это геометрическая точка, положение которой определяется распределением массы в теле, а перемещение характеризует движение тела или механической системы как целого.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Центр масс
Центр масс – это некоторое положение, определяемое относительно объекта или системы объектов и это среднее положение всех частей системы, взвешенное в соответствии с их массами.
Центр параллельных сил
Если на тело действует система параллельных сил 




Координаты центра параллельных сил определяются по зависимостям:
где 

Центр параллельных сил имеет ту особенность, что через него обязательно будет проходить линия действия равнодействующей при вращении линий действия всех сил системы вокруг точек их приложения на один и тот же угол в одну и ту же сторону. Модули сил при вращении не должны меняться.
Центр тяжести
Если твердое тело находится возле поверхности Земли, то на каждую материальную часть этого тела действует сила тяжести 


Координаты центра тяжести твердого тела можно определить как координаты центра параллельных сил:
где 



Если тело однородное, то есть удельный вес не меняется по объему 
где 

Тогда формулы для определения координат центра тяжести твердого тела приобретут вид:
Положение центра тяжести однородного тела зависит только от формы объема, что занимает тело, и называется центром тяжести этого объема.
Если однородное тело имеет форму тонкой пластины, то его можно рассматривать как материальную плоскую фигуру. В этом случае положение центра тяжести плоской фигуры определяется двумя координатами 

где 

Центр тяжести однородной пластины называется центром тяжести плоской фигуры.
Если выбранный элементарный объем 
а) для однородного твердого тела:
где 
б) для однородной поверхности:
где 
в) для однородной плоской фигуры, лежащей в плоскости xy:
г) для однородной линии:
где 
Центры тяжести некоторых плоских однородных фигур
Для упрощения определения центра тяжести используются следующие вспомогательные правилами:
1. Если тело имеет плоскость симметрии, то центр тяжести лежит на этой плоскости.
2. Если тело симметрично относительно оси, то центр тяжести лежит на этой оси.
3. Если тело симметрично относительно точки, то центр тяжести лежит в центре симметрии.
4. Если тело состоит из нескольких частей, центры тяжести которых можно определить, то центр тяжести такого тела находят как центр тяжести нескольких материальных точек, а именно тех, в которых расположены весы каждой отдельной части тела.
Центр тяжести дуги окружности
Центр тяжести дуги окружности 

где 


Центр тяжести кругового сектора
Центр тяжести кругового сектора лежит на оси симметрии и имеет координаты:
где 

Центр тяжести кругового сегмента
Центр тяжести кругового сегмента лежит на оси симметрии сегмента и имеет координаты:
где 

Центр тяжести треугольника
Центр тяжести треугольника (рис. 9.6) лежит в точке пересечения его медиан – на расстоянии 1/3 каждой медианы от соответствующего основания треугольника.
Центр тяжести трапеции
Центр тяжести трапеции (рис.9.7) с основаниями 



Расстояния 


Наиболее распространенный способ определения положения центра тяжести однородного тела сложной формы заключается в том, что его разбивают на такие части, положение центров тяжести которых известно, или может быть легко определено.
Например, однородную плоскую фигуру (рис.9.8) разбивают на три части 1,2 и 3, положения центров тяжести которых, 
Координаты центра тяжести фигуры 
где 


Этим способом удобно пользоваться и при определении положения центра тяжести плоской фигуры, из которой вырезана некоторая часть (рис.9.9).
В этом случае площадь плоской фигуры можно записать в виде разницы площадей сплошной фигуры 1 (площадь положительная) и вырезанной части 2 (площадь отрицательная), то есть 
Координаты центра тяжести фигуры равны:
где 



Первый из этих методов имеет название “метод разбиения”, второй – “метод дополнения”, или “метод отрицательных масс”. В общем случае формулы для определения центра тяжести плоской фигуры имеют вид:
где 
Примеры решения задач на тему: Центр масс
Задача № 1
Найти центр тяжести двутаврового профиля, размеры которого в сантиметрах указаны на рис.9.10.
Решение. Поскольку форма сечения имеет ось симметрии, ось 

В силу симметричности профиля относительно оси 
Линиями 

Запишем уравнение для определения абсциссы центра тяжести площади:
где 

Поскольку центры тяжести прямоугольников 

Площади этих прямоугольников соответственно равны:
Тогда:
Таким образом, центр тяжести фигуры лежит в точке 
Ответ:
Задача № 2
Найти координаты центра тяжести поперечного пересечения разностороннего угольника (рис.9.11), полки которого имеют ширину 
Решение. Разделим пересечение линией 


Запишем формулы для координат 

где 



С рис.9.11 видим, что
Тогда:
Ответ:
Задача № 3
Определить положение центра тяжести плоской фигуры (рис.9.12), ограниченной полуокружностью 



Решение. Данная площадь имеет ось симметрии, вдоль которой направим ось 

Разделим площадь 



Абсцисса центра тяжести площади 
где 





Для определения 
В случае половины круга
Площадь половины круга равна:
Центр тяжести треугольника лежит на пересечении его медиан (раздел 9.3.4). Поскольку треугольник 



Площадь треугольника 
Подставив найденные значения 




Ответ:
Задача № 4
Найти координаты центра тяжести квадратной пластины с вырезом в виде сегмента радиуса 
Решение. Осью симметрии рассматриваемой фигуры будет диагональ 
Поэтому направим ось 

Центр тяжести пластины будет лежать на оси 
Площадь фигуры 


Абсцисса центра тяжести фигуры будет равняться:
где 





Для квадрата 
Как следует из рис. 9.13, 
где 


Для кругового сектора (раздел 9.3.2) получим:
Поскольку 

Таким образом, абсцисса 
Площадь кругового сектора 
Подставив значение 




Ответ:
Задача № 5
Найти координаты центра тяжести площади, ограниченной (рис.9.14) правой веткой параболы 

Решение. На расстоянии 



Площадь выделенной элементарной площадки будет равняться:
Площадь фигуры, что ограничена заданными линиями:
Поскольку точка 


Отсюда:
Тогда:
Абсцисса центра тяжести
Для определения координаты 




Площадь выделенной площадки:
Ордината центра тяжести:
Тогда:
Ответ:
Способы определения координат центра тяжести тела
Существует несколько способов определения координат центра тяжести тел. среди них различают: метод симметрии, метод разбиения и дополнения, экспериментальные способы.
Рассмотрим последовательно эти способы.
Метод симметрии
Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, или на оси симметрии, или в центре симметрии.
Таким образом, центр тяжести однородных симметричных тел, таких как кольца,
прямоугольные пластины, прямоугольные параллелепипеды, шары и другие тела, которые
имеют центр симметрии, расположенный в геометрических центрах (центры симметрии) этих тел.
Метод разбиения
Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести нетрудно определяется, то координаты центра тяжести всего тела можно определить непосредственно по формулам выше. Причем количество слагаемых в числителе каждого из указанных выражений будет равно количеству частей, на которое разбивается тело.
Приведем пример определения центра тяжести тела методом разбиения его на отдельные тела, центры тяжести которых известны.
Пример:
Определить координаты центра тяжести однородной пластины. Размеры в
мм заданные на рис. 1.64
Решение.
Выберем оси координат x и y. Разбиваем пластину на отдельные прямоугольные части. Для каждого прямоугольника проводим диагонали, точки пересечения которых c1, c2 и c3 соответствуют центрам веса каждого прямоугольника. В принятой системе координат нетрудно получить значение координат этих точек. А именно: c1 (–1,1), c2 (1,5), c3 (5,9). Площади каждого тела соответственно равны: I — s1 = 4 см2; II — s2 = 20 см2; III — s3 = 12 см2. Площадь всей пластины равна: S = s1 + s2 + s3 = 36 см2.
Для определения координат центра тяжести заданной пластины используем выражение выше. Подставив значения всех известных величин в уравнения, получим
По вычисленным значениям координат центра тяжести пластины можно обозначить точку C на рисунке. Как видим, центр тяжести (геометрическая точка) пластины расположен за ее пределами.
Метод дополнения
Способ, о котором говорится далее, является некоторым случаем способа разбиения. Он может применяться к телам, которые имеют вырезы, полости, причем без учета выреза, или вырезанной части тела положение центра тяжести тела известно. Рассмотрим пример применения такого метода.
Пример. Определить положение центра тяжести круглой пластины радиусом R, имеет круговое отверстие радиуса r (рис. 1.65). Расстояние C1C2 = a.
Решение.
Как видно из рисунка, центр тяжести пластины находится на оси симметрии пластины x, то есть на прямой, проходящей через точки C1 и C2. Таким образом, для определения положения центра тяжести этой пластины необходимо вычислить только одну координату xC, поскольку вторая координата yC равна нулю. Покажем оси координат x, y. Примем, что пластина состоит из двух тел — с полного круга (без учета выреза) и тела,
образовано вырезом. В принятой системе координаты x для указанных тел будут равны: x1 = 0; x2 = C1C2 = a. Площади тел равны: 

заданной пластины используем первое уравнение выражения.
Подставив значения всех известных величин в это уравнение, получим
Таким образом, значение координаты xC отрицательное, а потому, поскольку вторая координата 0 yC = 0, то центр тяжести пластины C размещен на оси x слева от точки C1.
Экспериментальные способы
Эти способы нашли широкое применение при отыскании положения центра тяжести тел сложных форм и конфигураций, для которых другие способы почти непригодны вследствие громоздкости и сложности. К таким телам, в первую очередь, следует отнести комбайны, тракторы, сложные сельскохозяйственные машины и орудия. При применении экспериментальных способов отыскания положения
центра тяжести наиболее широко используют метод подвешивания и метод взвешивания тел.
При применении метода подвешивания тело на тросе подвешивают за различные его точки. Направление троса, будет давать каждый раз направление силы веса тела. Тогда точка пересечения этих направлений и дает положение центра тяжести тела.
Использование второго метода — взвешивание требует измерения веса всего тела, а также отдельных его частей. Рассмотрим пример применения этого метода.
Пример.
Определим продольную координату центра тяжести трактора, у которого продольная база составляет l (рис. 1.66).
Решение.
Сначала поставим на платформу весов задние колеса трактора, как это показано на рисунке. Итак, определяем силу давления задних колес на платформу, или реакцию 

Q = RA + RB.
Теперь составим алгебраическую сумму моментов всех сил относительно точки A. Она равна
Откуда определяем продольную координату центра тяжести:
xC = 
Для определения поперечной координаты центра тяжести трактора необходимо знать реакции левых колес (переднего и заднего) и правых, а также поперечную базу трактора. Дальше аналогичным выражением определяется эти координаты центра тяжести.
Центры тяжести некоторых однородных тел
Определим далее координаты центров тяжести некоторых простых однородных тел.
Центр тяжести дуги окружности
Рассмотрим дугу AB окружности радиусом R, в которой центральный угол OAB равен 2α (радиан) (рис. 1.67). Покажем оси координат x, y начало которых разместим в точке O. Вследствие того, что дуга имеет ось симметрии Ox, то центр ее тяжести будет расположен именно на этой оси (yC = 0). Остается только вычислить координату xC.
Используем для вычисления этой координаты первое уравнение выражения, а именно
Определим составляющие, которые необходимо подставить в это уравнение. Для этого выделим на дуге AB элемент M M1 длиной dl, равной:
dl = R · dφ.
Если φ — угол, определяющий положение элемента M M1 на дуге AB, то координата x элемента M M1 будет равна:
x = Rcosφ.
Общая длина дуги AB равна:
L = 2α · R.
Подставим эти значения в первое уравнение выражения. При этом считается, что интеграл в числителе данного выражения должен быть определенным по всей длине дуги. Будем иметь:
Таким образом, координата xC будет равняться
xC = 
Центр тяжести треугольника
Есть произвольный треугольник, вершины которого в принятой системе координат Oxy соответствуют точкам с координатами A1 (x1, y1), A2 (x2, y2), A3 (x3, y3) (рис. 1.68). Если провести прямые, которые будут параллельны основе A1A3 и провести их достаточное количество, то вся площадь треугольника будет состоять из полос бесконечно малой ширины, центры тяжести которых будут размещены посередине каждой полосы, а потому и центр тяжести треугольника будет расположенный на его медиане. А если провести линии, параллельные другой стороне треугольника, то и в этом случае центр тяжести будет размещен на соответствующей медиане. Таким образом, совершенно очевидно, что центр тяжести треугольника C будет расположен в точке пересечения его медиан.
Определим координаты этой точки. По курсу аналитической геометрии известно, что точка пересечения медиан треугольника в принятой системе координат определяется такими зависимостями
где x1, x2, …, y3 — координаты вершин треугольника.
Полезно также знать, что
Центр тяжести сектора
Рассмотрим круговой сектор OAB радиуса R, центральный угол которого равен 2α (радиан) (рис. 1.69). Центр тяжести сектора, вполне очевидно, лежит на оси его симметрии, то есть на биссектрисе угла AOB. Эту биссектрису примем за ось x и найдем на этой оси положение центра C. Разобьем площадь сектора на бесконечно большое число элементарных секторов с центральными углами ∆φ.
Будем рассматривать каждый сектор как треугольник с основанием R · ∆φ и высотой R. Центр тяжести каждого треугольника расположен на расстоянии 
Тогда учитывая, что
Будем иметь
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Рабчук Александр Викторович1, Самигуллина Ракия Гареевна2
1Уфимский государственный авиационный технический университет, к.т.н.. доцент кафедры математики
2Уфимский государственный авиационный технический университет, старший преподаватель каф. математики
Аннотация
Традиционно, такие разделы высшей математики как криволинейные и поверхностные интегралы, особенно их применение, вызывают затруднения у студентов при изучении. Поэтому в данной статье кратко дана теория и приведено много разобранных примеров взятых из различных источников, в частности из [1,2,3].
Rabchuk Aleksandr Viktorovich1, Samigullina Rakiya Gareevna2
1Ufa State Aviation Technical University, PhD in Technical Science, Assistant Professor of the Mathematic Department
2Ufa State Aviation Technical University, Senior teacher of the Mathematic Department
Abstract
By tradition, devides higher mathematics by contour and surface integrals ,particularly application, is difficult by students.Therefor in this article give theori and many look into examples from [1,2,3].
Библиографическая ссылка на статью:
Рабчук А.В., Самигуллина Р.Г. Приложения криволинейных интегралов. Часть 1 // Современная педагогика. 2014. № 10 [Электронный ресурс]. URL: https://pedagogika.snauka.ru/2014/10/2675 (дата обращения: 24.02.2023).
Приложения криволинейного интеграла первого рода
1. Если подынтегральная функция равна единиц, то криволинейный интеграл
равен длине S кривой L, т.е.
2. Пусть в плоскости Оху задана гладкая кривая L, на которой определена и непрерывна функция двух переменных z=f(x,y)≥0. Тогда можно построить цилиндрическую поверхность с направляющей L и образующей, параллельной оси Оz и заключенной между L и поверхностью z=f(x,y). Площадь этой цилиндрической поверхности можно вычислить по формуле
3. Если L=AB – материальная кривая с плотностью, равной ρ=ρ(х,у), то масса этой кривой вычисляется по формуле
(физический смысл криволинейного интеграла первого рода).
4. Статистические моменты материальной кривой L относительно координатных осей Ох и Оу соответственно равны
где ρ(х,у) – плотность распределения кривой L а
– координаты центра тяжести (центра масс) кривой L.
5. Интегралы
выражают моменты инерции кривой L с линейной плотностью ρ(х,у) относительно осей Ох, Оу и начала координат соответственно.
ПРИМЕРЫ:1. Вычислить криволинейный интеграл
где L – дуга параболы у2 = 2х, заключенная между точками (2, 2) и (8, 4).
Найдем дифференциал дуги dl для кривой
. Имеем
Следовательно, данный интеграл равен
Ответ:
2. Вычислить криволинейный интеграл
где L – контур треугольника АВО с вершинами А(1,0), В(0,1), О(0,0)
Поскольку
то остается вычислить криволинейный интеграл по каждому из отрезков АВ, ВО и ОА :
1) (АВ): так как уравнение прямой АВ имеет вид у=1 – х, то . Отсюда, учитывая, что х меняется от 0 до 1, получим
2) (ВО): рассуждая аналогично, находим х=0, 0 ≤ у ≤ 1, откуда
3) (ОА):
.
4) Окончательно
Ответ:
3. Вычислить криволинейный интеграл
где L – окружность
Введем полярные координаты
Тогда, поскольку
уравнение окружности примет вид
т.е.
а дифференциал дуги
При этом Следовательно,
Ответ:
4. Вычислить криволинейный интеграл первого рода от функции с тремя переменными
где L – дуга кривой, заданной параметрически
Перейдем в подынтегральном выражении к переменной t. Имеем для подынтегральной функции:
Теперь выразим через t дифференциал dl:
Таким образом,
Ответ:
5. Вычислить площадь части боковой поверхности кругового цилиндра , ограниченной снизу плоскостью Оху, а сверху поверхностью
Искомая площадь вычисляется по формуле
где L – окружность x2+y2=R2. Поверхность цилиндра и поверхность симметричны относительно координатных плоскостей Оxz и Oyz, поэтому можно ограничиться вычислением интеграла при условиях у≥0, х≥0, т.е. вычислить четверть искомой площади и результат умножить на 4. Имеем
Следовательно,
Получили определенный интеграл, который берем подстановкой
откуда
Ответ:
6. Найти массу четверти эллипса
расположенной в первой четверти, если линейная плотность в каждой точке пропорциональна ординате этой точки с коэффициентом k.
Поскольку р(х, у)=ky, имеем
L – четверть эллипса
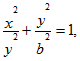
Переходим к параметрическим координатам эллипса Напомним, что
– фокусное расстояние эллипса, а
– эксцентриситет эллипса. Находим
Переходим к вычислению массы
Воспользуемся формулой
где Получаем
Учитывая, что 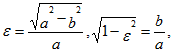
Ответ: .gif)
7. Найти координаты центра тяжести дуги окружности x2+y2=R2(0≤ x ≤R, 0≤ y ≤R).
Так как по условию задана четверть дуги окружности, то ее длина
В силу того, что биссектриса I координатного угла является осью симметрии, имеем
. Теперь находим
Ответ:
Приложения криволинейного интеграла второго рода
Интеграл
можно представить в виде скалярного произведения векторов F=Pi+Qi и ds=idx+jdy:
В таком случае
Выражает работу переменной силы F=Pi+Qj при перемещении материальной точки М=М(х,у) вдоль кривой L=AB от точки А до точки В.
При А=В кривая L замкнута, а соответствующий криволинейный интеграл по замкнутой кривой обозначается так:
В этом случае направление обхода контура иногда поясняется стрелкой на кружке, расположенном на знаке интеграла.
Предположим, что в плоскости Оху имеется односвязная область D (это значит, что в ней нет «дыр»), ограниченная кривой , (
– обозначение границы области D), а в области D и на ее границе
функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными.
Теорема: Пусть А и В – произвольные точки области D, AmB и AnB – два произвольных пути (гладкие кривые), соединяющие эти точки (рис. 2).
Тогда следующие условия равносильны:
1. (условие Грина).
2. (криволинейный интеграл не зависит от пути интегрирования).
3. (интеграл по любому замкнутому пути равен нулю).
4. (выражение
представляет собой полный дифференциал некоторой функции
).
В случае выполнения любого из равносильных условий предыдущей теоремы криволинейный интеграл по любой кривой, соединяющей точки (хо, уо) и (х1, у1) из области D, можно вычислить при помощи формулы Ньютона-Лейбница
где U(x, y) – некоторая первообразная для P dx + Q dy.
С другой стороны, первообразная U(x, y) выражения P dx + Q dy может быть найдена при помощи криволинейного интеграла
В этих же условиях на функции Р(х,у) и Q(х,у), а также на область D, имеет место формула Грина, позволяющая свести криволинейный интеграл по замкнутому контуру к двойному интегралу
Здесь предполагается, что обход границы области D в криволинейном интеграле
совершается в положительном направлении, т.е. при таком обходе границы область D остается слева; для односвязной области это направление совпадает с направлением против часовой стрелки.
Заметим, что площадь S=S(D) области D может быть вычислена при помощи криволинейного интеграла второговрода:
(эта формула получается из формулы Грина с ).
ПРИМЕРЫ:1. Даны функции Р(х ,у) = 8х+4у+2, Q(х ,у) = 8у+2 и точки А(3, 6), В(3,0), С(0,6). Вычислить криволинейный интеграл
где:
1) L – отрезок ОА;
2) L – ломаная ОВА;
3) L – ломаная ОСА;
4) L – парабола, симметричная относительно оси Оу и проходящая через точки О и А;
5) проверить выполнимость условия Грина.
1) Отрезок ОА может быть записан в виде: у=2х, . Тогда dy=2dx и
2) Используем свойство аддитивности, вычисляя отдельно интеграл по отрезкам ОВ и ВА. Тогда:
а) ОВ: здесь у=0, 0≤х≤3, т.е. dy=0, откуда
б) ВА: х=3, 0≤у≤6, т.е. dx=0, и
Таким образом,
3) Этот интеграл вычислим аналогично предыдущему.
а) ОС: х=0, (т.е. dx=0), 0≤y≤6, откуда
б) СА: 0≤х≤3 , у=6, dy=0, следовательно,
Окончательно
4) Подставив координаты точки А(3;6) в равенство у=ах2 найдем уравнение данной параболы . При этом 0≤х≤3 и
откуда (путь ОА по параболе обозначим
)
5) Имеем
т.е. условие Грина не выполняется. Этот факт, а также вычисления в пунктах 1) – 4) этой задачи показывают, что данный криволинейный интеграл второго рода зависит от пути интегрирования.
2. Вычислить интеграл
где L – верхняя половина эллипса .gif)
Воспользуемся параметрическими уравнениями эллипса: х=a cost, y=b sin t,
т.е. dx = – a sin t dt, dy = b cos t dt. Подставляя в интеграл и учитывая направление обхода (откуда следует, что t меняется от π до 0), получаем
.gif)
3. Вычислить криволинейный интеграл
где L – отрезок, соединяющий точку С(2, 3, -1) с точкой D(3, -2, 0).
Составим параметрические уравнения отрезка СD, используя уравнения прямой, проходящей через две точки:
Отсюда . Далее, находим
подставляем все нужные выражения в данный интеграл, обозначенный через J, и вычисляем определенный интеграл:
Ответ:
4. Вычислить где К – отрезок прямой от А(0 ;0) до В (4; 3).
Уравнение прямой АВ имеет вид у=(3; 4)х. Находим у/= ¾ и, следовательно,
Ответ:
5. Вычислить если
Найдем
Тогда
Ответ:
6. Найти массу М дуги кривой x=t, y=t2/2, z=t3/3 (0≤ t ≤1), линейная плотность которой меняется по закону
Ответ:
7. Вычислить криволинейный интеграл от точки А(1, 0) до точки В(0, 2) (рис. 3):
1) по прямой 2х+у=2;
2) по дуге параболы 4х+у2=4;
3) по дуге эллипса x=cost, y=2sint.
1) Пользуясь данным уравнением линии интегрирования, преобразуем криволинейный интеграл в обыкновенный определенный интеграл с переменной х, затем вычисляем его:
у=2-2х, dy=-2dx,
2) Здесь удобно преобразовать криволинейный интеграл в обыкновенный интеграл с переменной у:
3) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем его: x=cost, dx=-sintdt; y=2sint; dy=2costdt:
Ответ: I1=1, I2=-1/5, I3=4/3.
8. Вычислить криволинейный интеграл между точками Е
(-1, 0) и Н (0, 1):
1) по прямой ЕН;
2) по дуге астроиды х=cos3t, y=sin3t.
1) Вначале составляем уравнение линии интегрирования – прямой ЕН, как уравнение прямой, проходящей через две известные точки: у-х=1.
Пользуясь этим уравнением и известной формулой для дифференциала дуги плоской кривой преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной х и вычисляем его:
2) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем:
ибо π/2≤ t ≤π;
Ответ:
9. Даны точки А(3, -6, 0) и В(-2, 4, 5). Вычислить криволинейный интеграл
1) по прямолинейному отрезку ОВ;
2) по дуге АВ окружности, заданной уравнениями x2+y2+z2=45, 2x+y=0.
1) Вначале составляем уравнения линии интегрирования – прямой ОВ.
Пользуясь общими уравнениями прямой, проходящей через две точки .gif)
Приравнивая эти равные отношения параметру t, преобразуем полученные канонические уравнения прямой ОВ к параметрическому виду: x=-2t, y=4t, z=5t.
Далее, пользуясь этими уравнениями, преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной t, затем вычисляем его
2) Преобразуем данные уравнения окружности к параметрическому виду. Полагая х=t, получим у=-2t (из второго данного уравнения), (из первого уравнения). Отсюда
.gif)
Ответ:
10. Вычислить криволинейные интегралы:
1)
2) вдоль периметра треугольника с
вершинами А(-1,0), В (0,2) и С (2,0)
Составив уравнение прямой АВ, у-2х=2, и исходя из этого уравнения, преобразуем криволинейный интеграл на отрезке АВ в обыкновенный интеграл с переменной х:
у=2х+2, dy=2dx,
Аналогичным путем вычисляя криволинейный интеграл на отрезках ВС и СА, получим
х=2-у, dx=-dy,
Следовательно,
2) Здесь подынтегральное выражение есть полный дифференциал функции двух переменных, ибо (уcosx)’y =(sinx)’x =cosx. Вследствии этого данный криволинейный интеграл, взятый по периметру данного треугольника равен нулю. Он будет равен нулю и по любому другому замкнутому контуру.
Ответ:
11. Найти длину кардиоиды x=2acost-acos2t, y=2asint-asin2t.
Применяем формулу
, исходя из данных параметрических уравнений кардиоиды и формулы для дифференциала дуги плоской кривой, преобразуем криволинейный интеграл формулы в обыкновенный интеграл с переменной t.
Ответ: L=16a.
12. Найти площадь, ограниченную замкнутой кривой:
1) эллипсом x=a cost, y=b sint;
2) петлей декартова листа х3+у3-3аху=0.
1) Применяем формулу
, исходя из данных параметрических уравнений эллипса, преобразуем криволинейный интеграл в обыкновенный интеграл с переменной t и вычисляем его:
2) Вначале преобразуем данное уравнение к параметрическому виду. Полагая у=хt, получим
Геометрический параметр t=y/x есть угловой коэффициент полярного радиуса ОМ (рис. 6), точка М(х, у) опишет всю петлю кривой при изменении t от 0 до +∞.
Преобразуя криволинейный интеграл формулы в обыкновенный интеграл с переменной t , получим
Ответ: S=3a2/2.
13. Найти массу дуги АВ кривой у=lnx, если в каждой ее точке линейная плотность пропорциональна квадрату абсциссы точки: хА=1, хВ=3.
Применяем формулу
, исходя из данного уравнения кривой, преобразуем криволинейный интеграл в обыкновенный с переменной х
Ответ:
14. Найти координаты центра тяжести дуги АВ винтовой линии х=аcost, y=asint, z=bt, если в каждой ее точке линейная плотность пропорциональна аппликате этой точки: tA=0, tB=π.
Применяя формулы
.gif)
Следовательно,
Ответ:
15. Вычислить работу, совершаемую силой тяжести при перемещении точки массы m по дуге АВ некоторой кривой.
Если выбрать прямоугольную систему координат так, чтобы направление оси Оz совпало с направлением силы тяжести, то действующая на точку сила
а ее проекции на оси координат Fx=P=O, Fy=Q=0, Fz=R=mg.
Искомая работа согласно формуле
Она зависит только от разности аппликат начала и конца пути, но не зависит от формы пути.
16. Найти работу силового поля, в каждой точке (х,у) которого напряжение (сила, действующая на единицу массы) , когда точка массы m описывает окружность x=accost, y=asint, двигаясь по ходу часовой стрелки.
Подставляя в формулу
проекции силы
действующей на точку: Fx=m(x+y), Fy= – mx, и преобразуя криволинейный интеграл в обыкновенный с переменной t, получим
Ответ: Е=2πma2.
Библиографический список
- Лунгу К.Н. Сборник задач по высшей математике. 1 курс – 7-е изд., – М.: Айрис-пресс, 2008.
- Лунгу К.Н. Сборник задач по высшей математике. 2 курс – 5-е изд., – М.: Айрис-пресс, 2007.
- Письменный Д.Т. Конспект лекций по высшей математике: полный курс – 7-е изд. – М.: Айрис-пресс, 2008.
Все статьи автора «Рабчук Александр Викторович»
Пусть
на плоскости хоу
задана кривая АВ,
в каждой
точке которой определена непрерывная
функция f(х,
у) двух
независимых переменных х
и у.
Рассмотрим
криволинейный интеграл I
рода (по длине дуги) от этой функции по
кривой АВ.
Он обозначается
,
кривая АВ
называется кривой интегрирования, А
– начальной,
а В – конечной
точками интегрирования. Из определения
криволинейного интеграла первого рода
следует, что он не зависит от направления
кривой АВ,
т.е.:
.
Если АВ – пространственная кривая, то
криволинейным интегралом первого рода,
распространенным на эту кривую называется
интеграл вида:
,
где
функция f(х,
у, z)
– функция
трех независимых переменных, которая
определена и непрерывна в каждой точке
кривой АВ.
Масса
m
материальной кривой, имеющей плотность
(х,
у, z)
равна криволинейному интегралу первого
рода от функции (х,
у, z)
по пространственной кривой АВ,
т.е.:
.
(3.16)
В
этом состоит физический (механический)
смысл криволинейного интеграла первого
рода.
Если
масса распределена непрерывно вдоль
дуги плоской кривой АВ
с плотностью функции
= (х,
у) в каждой
точке кривой, то статические моменты
Мх
и Му
дуги
относительно координатных осей ОХ
и ОУ
соответственно
определяются по формулам:
;
.
(3.17)
Моменты
инерции этой дуги относительно
координатных осей ОХ
и ОУ
соответственно равны:
;
.
(3.18).
Координаты
центра тяжести дуги АВ
вычисляются по формулам:
;
(3.19)
.
(3.20)
Если
кривая однородна, то плотность функции
(х,
у) = const,
поэтому формулы (3.19) и (3.20) примут вид:
,
(3.21)
где
– длина дуги АВ.
Если
плоская гладкая кривая АВ
задана параметрическими уравнениями
вида х = х(t);
у = у(t),
причем, существуют непрерывные производные
хt
и уt,
где параметр
t
применяется
на дуги АВ
в пределах
t
.
Тогда
и криволинейный интеграл выражается
через определенный по формуле:
.
(3.22)
Если
кривая АВ
задана уравнением у
= у(х); где а
х
b,
то
.
(3.23);
Рассмотрим
теперь случай пространственной гладкой
кривой АВ.
Пусть ее параметрические уравнения
имеют вид:
х
= х(t);
у = у(t);
z = z(t);
причем существуют непрерывные производные
хt,
уt
и zt.
Предположим, что параметр t
изменяется
в пределах
t
.
Тогда
справедлива формула:
.
(3.24)
Криволинейный
интеграл от функции f(х,
у)
по дуге, заданной уравнением в полярных
координатах r
= r(),
где
,
вычисляется
с помощью формулы:
.
(3.25)
Задача
3.3.
Вычислить
,
где АВ
часть окружности х2
+ у2
= R2,
лежащая в
I
четверти.
Решение.
Выразим из
уравнения окружности явно ординату у
через абсциссу х,
получим
(в первой четверти у
0).
Найдем
и подставим в выражения
;
.
По
формуле (3.23)
получим:
.
Ответ:
.
Задача
3.4.
Найти
центр тяжести полуокружности х2
+ у2
= R2,
лежащей в
верхней полуплоскости, а также ее момент
инерции относительно оси ОХ
(плотность
считать равной единице).
Решение.
Центр тяжести
дуги кривой определяется по формуле
(3.20). Из соображений симметрии следует,
что он находится на оси ОУ.
Поэтому хс
= 0.
,
где
,
так как это длина полуокружности.
Для
вычисления числителя дроби воспользуемся
параметрическими уравнениями окружности:
x
= R
cos
t;
y
= R
sin
t.
Тогда
.
;
.
Ответ:
хс
= 0,
.
Задачи
для самостоятельного решения
Задача
3.5.
Найти
координаты центра тяжести одной арки
циклоиды: x
= a(t
– sin
t),
y
= a(1
– cos
t),
0
t
2.
(Считать
плотность равной единице).
Указание.
Воспользоваться
формулами (3.22).
Учитывая
симметрию, заключаем, что абсцисса
центра тяжести хс
= а.
;
.
Ответ:
хс
= а;
.
Задача
3.6.
Найти массу
участка кривой у
= ln
x
от точки с абсциссой
до точки с абсциссой
,
если плотность в каждой точке равна
квадрату ее абсциссы.
Указание.
;
.
Ответ:
.
Задача
3.7.
Определить
центр тяжести дуги астроиды x
= a
cos3t,
y
= a
sin3t,
лежащий в
первой четверти
.
Плотность считать равной единице.
Ответ:
.
Определение
криволинейного интеграла
второго рода
и его механический смысл
Рассмотрим
задачу, приводящую к понятию криволинейного
интеграла второго рода. Эта задача о
вычислении работы переменной силы при
перемещении материальной точки вдоль
некоторой кривой.
Предположим,
что при движении по кривой АВ
материальная точка М переходит из
положения А в положение В. Во
время движения на точку М действует
сила
=
(x,
y, z),
заданная своими проекциями P,
Q, R
на координатные оси OX,
OY и OZ,
т.е.
= P(x, y, z)
+ Q(x, y, z)
+ R(x, y, z)
.
(3.26)
Найдем работу Е
силы
при данном перемещении точки.
Если бы перемещение
точки М было прямолинейным, а
действующая сила
– постоянной (по величине и направлению),
то работа Е этой силы, по известной
формуле из физике, была бы равна скалярному
произведению вектора на вектор перемещения
,
т.е. Е =(
,
).
Однако особенность задачи состоит в
том, что перемещение точки является
криволинейным, а действующая сила
переменной . Разобьем кривую АВ на
части (элементарных дуг) точками М0,
М1, М2,…, Мn-1,
Mn
где M0
совпадает с А, а Mn
– с точкой В. Обозначим диаметр
разбиения через d.
На каждой дуге выберем производную
точку
(
,
,
)
и найдем в ней значение силы
=
(Pк, Qк,
Rк),
где Pк = P
(
,
,
),
Qк = Q(
,
,
),
Rк =
R(
,
,
).
Предположим, что сила сохраняется
постоянной в точках дуги и под ее действие
точка перемещается на каждом элементарном
участке не по дуге, а по хорде, соединяющей
точки Мк-1, Mк(к
= 1, 2, …, n).
Используя формулу для вычисления
скалярного произведения через проекции
силы и векторы перемещения, получим
приближенное значение работы на каждом
элементарном участке дуги
Ек
P (
,
,
)xк
+ Q(
,
,
)yк
+ R(
,
,
)zк,
xк
= xк –
xк-1, yк
= yк –
yк-1, zк
= zк –
zк-1, а xк
, yк ,
zк,
координаты точки Mк
(к = 1, 2, …, n).
Суммируя полученные
частичные работы, найдем приближенно
полную работу силы
при перемещении точки М вдоль кривой
АВ
E
P
(
,
,
)xк
+ Q(
,
,
)yк
+
+ R(
,
,
)zк].
(3.27)
За работу E
силы
при перемещении материальной точки
вдоль кривой АВ примем предел суммы
(3.27) при стремлении диаметра разбиения
к нулю, т.е.
E
=
P
(
,
,
)xк
+ Q(
,
,
)yк
+ R(
,
,
)zк].
Перейдем к
определению криволинейного интеграла
второго рода.
Пусть в пространстве
OXYZ задана
непрерывная, гладкая кривая АВ и
функция P(x,
y, z)
на этой кривой. С помощью точек М0,
М1, М2,…, Mn
в направлении от А и В разобьем
на n дуг производные
длины. На каждой дуге М0,
Мк-1, Mк
выберем производную точку
(
,
,
)
и найдем в ней значение функции P(
,
,
)
. Для каждой элементарной дуги
вычислим произведение P(
,
,
)xк,
где xк
– проекция дуги Мк-1, Mк
на ось ОХ, т.е. xк
= xк –
xк-1,
где xк и xк-1
соответственно абсциссы конца и
начала хорды Мк-1, Mк.
Просуммируя полученные произведения,
получим
P
(
,
,
)xк.
(3.28)
Суммы вида (3.28)
называются интегральными суммами
второго рода для функции P(x,
y, z),
соответствующими разбиению {Mк}
кривой АВ (относительно координаты
х) с отмеченными точками
(
,
,
).
определение.
Предел интегральных сумм вида (3.28) при
d
0 (n
),
если он существует и не зависит от
способа разбиения кривой АВ
на частные дуги и выбора точек
,
называется криволинейным интегралом
второго рода по координате х
и обозначается
(x,
y, z)dx , т.е.
(x,
y, z)dx =
P
(
,
,
)xк
. (3.29)
Аналогично
определяются криволинейные интегралы
по координатам y
и z,
их обозначают
(x,
y, z)dy и
(x,
y, z)dz , беря
для функции
Q(x,
y,
z)
проекции yк
на ось ОY,
а для R(x,
y,
z)
проекции
zк
на ось
ОZ.
Определение.
Сумма трех интегралов
(x,
y, z)dx,
(x,
y, z)dy,
(x,
y, z)dz называется
общим криволинейным интегралом второго
рода (по координатам) и обозначается
(x,
y, z)dx =
(x,
y, z)dy +
(x,
y, z)dz.
(3.30)
Если
P,
Q,
R
– проекции силы
на координатной оси, то из формулы (3.27)
следует, что общий криволинейный интеграл
второго рода выражает работу этой силы
на пути АВ,
т.е.
E
=
(x,
y, z)dx +
(x,
y, z)dy +
(x,
y, z)dz (3.31)
В
этом состоит физический смысл
криволинейного интеграла второго рода.
Замечание
1. Если кривая
АВ
лежит в плоскости ХОY
и функции P(x,y)
и Q(x,y)
не зависят от z,
то криволинейные интегралы второго
рода имеют вид
(x,
y)dx + Q(x, y)dy.
(3.32)
Замечание
2. В отличие
от криволинейного интеграла первого
рода криволинейный интеграл второго
рода меняет свое значение на противоположное
при изменении направления кривой АВ,
т.е.
(x,
y, z)dx = –
(x,
y, z)dx
В
самом деле, если изменить направление
обхода кривой, то изменятся знаки
проекций xк
в сумме (3.28), значит и сама сумма, и ее
предел.
Замечание
3. Криволинейный
интеграл второго рода обладает всеми
свойствами криволинейного интеграла
первого рода, за исключением одного: он
меняет знак на противоположный при
изменении направления обхода кривой.
Замечание
4. В случае,
когда кривая АВ
– замкнутая (т.е. точка В
совпадает с точкой А)
употребляется обозначение
(M)dx
+ Q(M)dy
+ R(M)dz.
В
случае, когда кривая АВ
замкнутая, за положительное направление
обхода принимается такое, при котором
область, лежащая внутри этого контура
остается слева по отношению к точке,
совершающей обход.
Теорема:
Если функции P(x,
y, z), Q(x,
y, z), R(x,
y, z) непрерывны,
или имеют конечное число разрывов
первого рода вдоль непрерывной кривой
АВ,
имеющей конечную длину, то криволинейные
интегралы
(x,
y, z)dx,
(x,
y, z)dy,
(x,
y, z)dz, а
следовательно
и криволинейный интеграл
dx
+ Qdy
+ Rdz
существуют.
Вычисление
криволинейного интеграла второго рода
Пусть
гладкая кривая АВ
задана параметрическими уравнениями
х= х(t),
y=y(t),
z=z(t),
причем изменению t
от
до
соответствует
движение точки по кривой от А
до В
(не обязательно, чтобы
было меньше ).
Тогда
=
. (3.33)
Аналогичные
формулы имеют место и для интегралов
по координатам y
и z.
Выпишем формулу для вычисления общего
интеграла второго рода
+Q(x,y,z)dy+R(x,y,z)dz=
=
+Q(x(t),y(t),z(t))y(t)+
+R(x(t),y(t),
z(t))z(t)
] dt. (3.34)
Если
АВ
– кривая, расположенная, например, в
плоскости ХОУ,
то формула (3.34) в этом случае примет вид
=
+
+Q(x(t),y(t),z(t))y(t)
+ R(x(t),y(t),z(t))z(t)dt.
(3.35)
Для
плоской гладкой кривой у
= у(х), где а
х
b,
заданной явным уравнением, получим
=
=
.
(3.36)
Задача
3.8. Вычислить
криволинейный интеграл
,
где АВ
– одни виток винтовой линии
х=
cos
t,
у = sin
t,
z
= 2t
от точки А
(1,0,0) до точки
В (1,0,4).
Решение.
Вдоль дуги АВ
параметр t
изменяется от 0
до 2.
Тогда, используя формулу (3.24),
получим
=
=
=
=
.
Задача
3.9. Вычислить
криволинейный интеграл
вдоль
кривой у=х3
от точки А
(1,1) до
точки В(2,8).Решение.
По формуле (3.26) получим
=
.
Связь
между криволинейными интегралами
первого
и второго рода.
Пусть
АВ
– направленная пространственная кривая
с началом А
и концом В,
тогда все касательные к АВ
также являются направленными прямыми.
Обозначим углы, которые образует
касательная к АВ
с осями ОХ,
ОУ, ОZ
соответственно ,
и .
Очевидно,
что эти углы являются функциями координат
x,y,z
точки касания М.
Выделим
из АВ
элементарную дугу dl,
и будем считать ее прямолинейной. Значит
dl
–это вектор с проекциями dx,
dy,
dz,
направленный так же, как и кривая АВ.
Следовательно, dx
= cos
dl,
dy
= cos
dl,
dz
= cos
dl.
Тогда
общий интеграл второго рода выразится
через интеграл первого рода по формуле
=
.
(3.37)
По
формуле (3.37) осуществляется переход от
криволинейного интеграла первого рода
к интегралу второго рода.
Формула
Остроградского – Грина.
Рассмотрим
на плоскости ХОУ
компактную фигуру Ф,
ограниченную замкнутой гладкой (или
кусочно – гладкой) кривой A.
Пусть
функции Р(х,у)
и Q(х,у)
непрерывны вместе со своими частными
производными
на компактной фигуре Ф.Тогда
имеет место формула
=
,
(3.38)
которая
называется формулой Остроградского-Грина.
Она устанавливает связь между двойным
интегралом по некоторой плоской области
и криволинейным по контуру, ограничивающему
эту область, играет фундаментальную
роль в векторном анализе.
Докажем
справедливость формулы (3.38). Рассмотрим
в плоскости ХОУ
выпуклую в
направлении обеих осей фигуру Ф,
ограниченную замкнутым контуром А,
состоящим из двух кривых
у
= у1(х)
и у = у2(х),
где у1(х)
у2(х),
Рис.
3.2
а
х
b
(рис. 3.2). Так как по условию Р(х,у)
и Q(х,у)
непрерывно дифференцируемые функции
на Ф,
то существует
,
который можно преобразовать следующим
образом
=
=
=
.
(3.39)
Если
взять в качестве параметра х
и записать параметрическое уравнения
кривой АDВ
в виде х = х,
у = у2(х),
а кривой АСВ
– в виде х =
х, у = у1(х),
то используя ранее выведенные формулы,
получим
;
.
(3.40)
Подставляя
выражение (3.40) в (3.30) и учитывая свойства
криволинейных интегралов, имеем
.
(3.41)
Аналогично
можно доказать, что
.
(3.42)
Вычитая
(3.41) из (3.42), получим формулу
.
(в
предположении, что обход контура А
осуществляется
против часовой стрелки). Формула (3.38)
доказана для выпуклой фигуры Ф.
Однако
она справедлива и для всякой замкнутой
области, которую можно разбить на
конечное число выпуклых фигур.
Замечание.
При доказательстве формулы (3.36)
рассматривалась область Ф,
ограниченная одним замкнутым контуром
(односвязная). Можно доказать, что
формула Остроградского-Гаусса остается
справедливой и для многосвязной области,
ограниченной не одним, а несколькими
не связанными друг с другом контурами
(многосвязной).
Геометрические
и механические приложения
криволинейных
интегралов
Криволинейные
интегралы имеют широкие приложения в
геометрии, механике и физике. Ограничимся
рассмотрением только некоторых из них.
Площадь плоской области
Используя
формулу Грина (3.38), выведем формулы для
вычисления площади фигуры Ф
с помощью криволинейного интеграла.
Если
функции Р(х,у)
= -у, а Q(х,у)=0,
то
и формуле
(3.38) примет вид
.
Откуда S
= –
.
(3.43)
Аналогично,
полагая Р(х,
у) = 0, Q(х,
у) = х, получим
S
= –
(3.44)
При
Р(х, у) = -1/2 у;
Q
(х, у) = 1/2 х,
имеем
S
= 1/2
.
Задача
3.10. Найти
площадь S
плоской фигуры, ограниченной эллипсом
.
Решение.
Параметрические уравнения эллипса
имеют вид x
= а соs
t,
y
= b
sin
t,
где 0
t
2.
По
формуле (3.44) находим
S=
=
.
Координаты центра
масс материальной кривой
Для определения
координат центра масс материальной
кривой АВ, если известна линейная
плоскость распределения массы (М)
в каждой ее точке М, используются
формулы
,
(3.45)
где
M
=
-масса
кривой АВ.
Если
кривая АВ
однородна, то есть
= const,
то формулы (3.45) упрощаются
.
(3.46)
где
=
–кривой
АВ.
Задача
3.11. Вычислить
,
где АВ –
первая четверть окружности х2
+ у2
= R2,
пробегаемая
против часовой стрелки.
Решение.
Из уравнения окружности выразим у
через х.
Получим
,
так как в первой четверти у
0, то
;
.
Учитывая,
что интегрирование ведется против
часовой стрелки х
изменяется от R
до 0.
По
формуле (3.29)
получим:
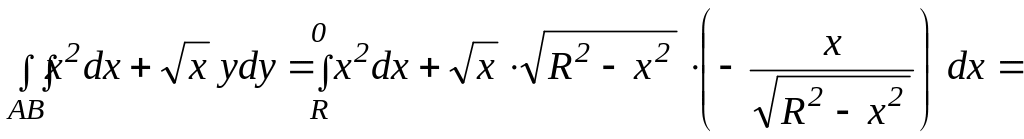
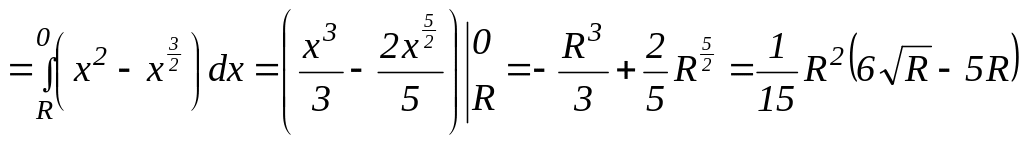
Ответ:
.
Задача
3.12. Вычислить
криволинейный интеграл,
где АВ один
виток линии х
= cos
t,
y
= sin
t,
z
= 2t
от точки
А(1, 0, 0)
до В(1, 0, 4).
Решение.
Очевидно,
что вдоль дуги
АВ параметр
t
изменяется
от 0
до 2.
По формуле
(3.28), получим
.
Ответ:
.
Задачи
для самостоятельного решения
Задача
3.13. а) Вычислить
,
где АВ – дуга
параболы у
= х2
от точки х
= 0 до точки
х = 2;
б)
Вычислить
,
где АВ та
же дуга.
Ответ:
а)
;
б)
.
Задача
3.14.
Вычислить
,
где АВ
1)
отрезок прямой, соединяющий точки А(2,
3) и В(3,
5);
2)
дуга параболы у
= х2 (0
х
2);
3)
дуга параболы у=х2,
соединяющая точки С(0,0)
и D(4,2).
Ответ:
1)
;
2)
;
3)
.
Задача
3.15. Вычислить:
;
где
L
одна из линий, соединяющих точки О(0,
0) и А(2,
2).
-
отрезок
ОА; -
парабола
; -
парабола
; -
кубическая
парабола
-
ломанная
ОСА,
где С(2, 0).
Решение.
-
Уравнение
прямой на которой лежит отрезок ОА
у = х, поэтому
dy
= dx.
Заменим в подынтегральном выражении
у
на х, а
dy
на
dx,
получим:
.
-
Из
уравнения кривойследует, что dy
= xdx.
Заменяя
в подынтегральном выражении у
на
,
а dy
на
хdx,
получим, что
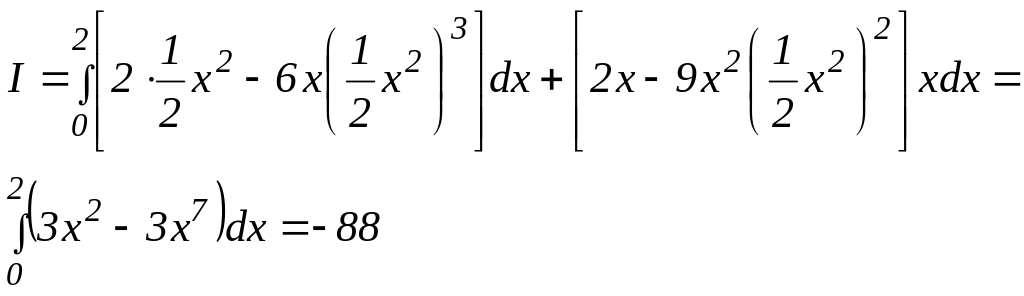
-
Так
как уравнение линии,
то dx
= ydy.
Заменим в подынтегральном выражении
х, на
,
а dx
на ydy,
получим, учитывая, что у
изменяется от 0
до 2.
.
-
Убедиться
самостоятельно, что I
= – 88. -
Вычислим
этот интеграл по ломанной ОСА,
состоящий из отрезка ОС
оси ОХ и
отрезка СА
прямой Х =
2.
В
этом случае на отрезке ОС:
у = 0, dy
= 0. На отрезке
СА: х = 2, dх
= 0, а у
изменяется
от 0
до 2,
так как
.
.
Итак,
по какой бы из указанных кривых,
соединяющих точки (0,
0) и (2,
2), мы не
вычисляли этот интеграл, оказывается,
что он равен одному и тому же числу.
Иначе говоря, величина этого интеграла
не зависит от пути интегрирования.
Ниже
будет указано условие, которому должно
удовлетворять подынтегральное выражение
Р(х,у)dx
+ Q(x,y)dy
в криволинейном интеграле второго
рода, чтобы интеграл не зависел от пути
интегрирования, соединяющего эти точки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
30.04.2022655.36 Кб144.doc
- #
- #
- #
- #
- #
- #
- #
- #
- #


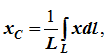
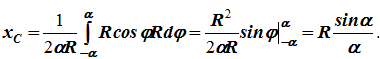
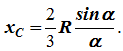




























































































.gif)
.gif)
.gif)
.gif)
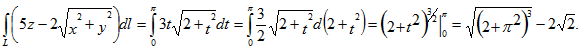
.gif)
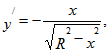
.gif)
.gif)
.gif)
.gif)
.gif)
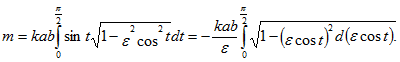
.gif)
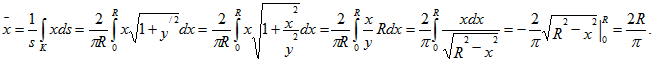
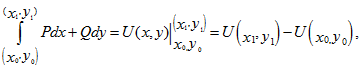
.gif)
.gif)
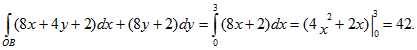
.gif)

.gif)
.gif)
.gif)
.gif)
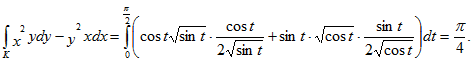
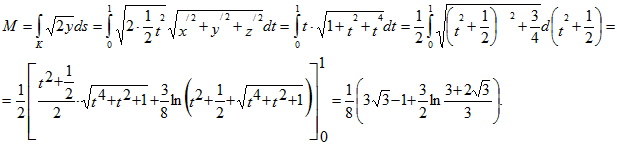
.gif)
.gif)

.gif)
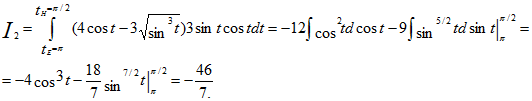
.gif)

.gif)
.gif)
.gif)
.gif)

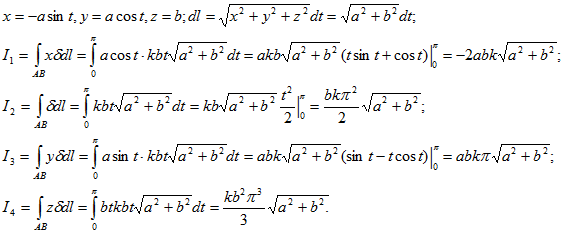
.gif)