Цветовые координаты — количественное описание цветового воздействия в трехмерной системе координат, например (L*, a*, b*) или (X, Y, Z), полностью определяющие цвет любой точки цветовой модели, при соблюдении некоторых стандартизованных условий рассматривания цвета.
Введение
Трехмерное представление цветового пространства человека Рисунок Аддитивного синтеза цвета основных цветов RGB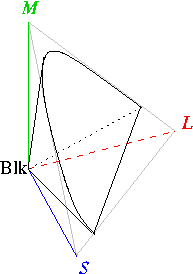

Основой математического описания цвета в колориметрии является экспериментально установленный факт, что любой цвет при соблюдении упомянутых условий можно представить в виде смеси (суммы) определённых количеств 3 линейно независимых цветов, т. е. таких цветов, каждый из которых не может быть представлен в виде суммы каких-либо количеств 2 других цветов. Групп (систем) линейно независимых цветов существует бесконечно много, но в колориметрии используются лишь некоторые из них. Три выбранных линейно независимых цвета RGB называют основными цветами; они определяют цветовую координатную систему — ЦКС. При этом 3 числа, описывающие данный цвет (RGB), являются количествами основных цветов в смеси, цвет которой зрительно неотличим от данного цвета; это и есть цветовые координаты — ЦК данного цвета.
Экспериментальные результаты, которые закладывают в основу разработки колориметрической ЦКС, получают при усреднении данных наблюдений (в строго определённых условиях) большим числом наблюдателей; поэтому они не отражают точно свойств цветного зрения какого-либо конкретного наблюдателя, а относятся к т. н. среднему стандартному колориметрическому наблюдателю.
Смысл цветовых координат
Будучи отнесены к стандартному наблюдателю в определённых неизменных условиях, стандартные данные смешения цветов и построенные на них колориметрической ЦКС описывают фактически лишь физический аспект цвета, не учитывая изменения цветовосприятия глаза при изменении условий наблюдения и по др. причинам.
Когда ЦК какого-либо цвета откладывают по 3 взаимно перпендикулярным координатным осям, этот цвет S,M,L (см. рис.К) геометрически представляется точкой в трёхмерном, т. н. цветовом, пространстве или же вектором, начало которого совпадает с началом координат, а конец — с упомянутой точкой цвета (см. рис.4). Точечная и векторная геометрическая трактовки цвета равноценны и обе используются при описании цветов. Точки, представляющие все реальные цвета, заполняют некоторую область цветового пространства. Но математически все точки пространства равноправны, поэтому можно условно считать, что и точки вне области реальных цветов представляют некоторые цвета. Такое расширение толкования цвета как математического объекта приводит к понятию т. н. нереальных цветов, которые невозможно как-либо реализовать практически. Тем не менее с этими цветами можно производить математические операции так же, как и с реальными цветами, что оказывается чрезвычайно удобным в колориметрии. Соотношение между основными цветами RGB в ЦКС (цветовая координатная система) выбирают так, что их количества, дающие в смеси некоторый исходный цвет (чаще всего белый), принимают равными 1.
Субъективно «качество» цвета, не зависящее от абсолютной величины цветового вектора и называемое его цветностью, геометрически удобно характеризовать в двумерном пространстве — на «единичной» плоскости цветового пространства, проходящей через 3 единичные точки координатных осей (осей основных цветов). Линии пересечения единичной плоскости с координатными плоскостями образуют на ней равносторонний треугольник, в вершинах которого находятся единичные значения основных цветов. Этот треугольник часто называют треугольником Максвелла. Цветность какого-либо цвета определяется не 3 его ЦК, а соотношением между ними, т. е. положением в цветовом пространстве прямой, проведённой из начала координат через точку данного цвета. Другими словами, цветность определяется только направлением, а не абсолютной величиной цветового вектора и, следовательно, её можно характеризовать положением точки пересечения этого вектора (либо указанной прямой) с единичной плоскостью. Вместо треугольника Максвелла часто используют цветовой треугольник более удобной формы — прямоугольный и равнобедренный. Положение точки цветности в нём определяется двумя координатами цветности, каждая из которых равна частному от деления одной из ЦК на сумму всех 3 ЦК. Двух координат цветности достаточно, т.к. по определению сумма её 3 координат равна 1. Точка цветности исходного (опорного) цвета, для которой 3 цветовые координаты равны между собой (каждая равна 1/3), находится в центре тяжести цветового треугольника. (См. также [1])
Принцип построения цветовой модели
Основная статья: LAB
Рис. 4. Единичная плоскость и нейтральный цвет N (Например, белый при равных значениях 0,333 основных цветов RGB, что в сумме = 1) в трёх-координатном цветовом пространстве, что даёт белую точку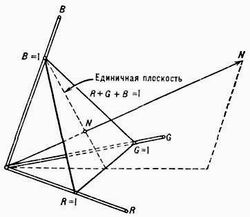
Свойства цветового зрения учитываются в колориметрии по результатам экспериментов со смешением цветов. В таких экспериментах выполняется зрительное уравнивание чистых спектральных цветов (т. е. цветов, соответствующих монохроматическому свету с различными длинами волн) со смесями 3 основных цветов. Оба цвета наблюдают рядом на 2 половинках фотометрического поля сравнения. По достижении уравнивания измеряются количества 3 основных цветов и их отношения к принимаемым за 1 количествам основных цветов в смеси, уравнивающей выбранный опорный белый цвет. Полученные величины будут ЦК уравниваемого цвета в ЦКС, определяемой основными цветами прибора и выбранным опорным белым цветом. Если единичные количества красного, зелёного и синего основных цветов обозначить как для (RGB): (R), (G), (B), а их количества в смеси (RGB): ЦК — R, G, B, (cм. рис.4), то результат уравнивания можно записать в виде цветового уравнения: (RGB) — Ц* = R (R) + G (G) + S (S). Легко заметить, что это линейное уравнеие. Описанная процедура не позволяет уравнять большинство чистых спектральных цветов со смесями 3 основных цветов прибора. В таких случаях некоторое количество одного из основных цветов (или даже двух) добавляют к уравниваемому цвету. Цвет получаемой смеси уравнивают со смесью оставшихся 2 основных цветов прибора (или с одним). В цветовом уравнении это учитывают переносом соответствующего члена из левой части в правую. Так, если в поле измеряемого цвета был добавлен красный цвет, то Ц* = — R(R), G(G), B(B). При допущении отрицательных значений ЦК уже все спектральные цвета можно выразить через выбранную тройку основных цветов. При усреднении результатов подобной процедуры для нескольких наблюдателей были получены значения количеств 3 определённых цветов, требующиеся в смесях, зрительно неотличимых от чистых спектральных цветов, которые соответствуют монохроматическим излучениям одинаковой интенсивности. При графическом построении зависимостей количеств основных цветов от длины волны получаются функции длины волны, называемые кривыми сложения цветов или просто кривыми сложения.
Кривые сложения цветов
Рис. 1. Кривые сложения для ЦКС МКО RGB. Рис. 2. Кривые сложения для ЦКС МКО XYZ. Рис. 3. График цветностей для системы XYZ и цветовой треугольник системы RGB (R — красный, G — зелёный, B — синий).

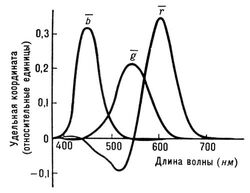
Кривые сложения цветов играют в колориметрии большую роль. По ним можно рассчитать количества основных цветов, требуемые для получения смеси, зрительно неотличимой от цвета излучения сложного спектрального состава, т. е. ЦК такого цвета в ЦКС, определяемой данными кривыми сложения. Для этого цвет сложного излучения представляют в виде суммы чистых спектральных цветов, соответствующих его монохроматическим составляющим (с учётом их интенсивности). Возможность подобного представления основана на одном из опытно установленных законов смешения цветов, согласно которому ЦК цвета смеси равны суммам соответствующих координат смешиваемых цветов. Таким образом, предполагают, что кривые сложения должны характеризовать реакции на излучение 3 разных приёмников излучения. Однако функции спектральной чувствительности 3-х типов пригментов обнаруженных в сетчатке глаза человека, описывают кривые сложения в физиологической ЦКС. С точки зрения теории трёхкомпонентного цветного зрения, каждой из бесконечно большого числа возможных ЦКС должна соответствовать своя группа из 3 кривых сложения, причём все группы кривых сложения должны быть связаны между собой линейными соотношениями. Следовательно, кривые сложения любой из всех возможных ЦКС можно считать линейными комбинациями функций спектральной чувствительности 3-х типов приёмников человеческого глаза — колбочек. (Cм. Математика цветного зрения)
Фактически основой всех ЦКС является система, кривые сложения которой были определены экспериментально. Её основными цветами являются чистые спектральные цвета, соответствующие монохроматическим излучениям с длинами волн 700,0 нм (красный), 546,1 нм (зелёный) и 435,8 нм (синий). Исходная (опорная) цветность — цветность равноэнергетического белого цвета Е (т. е. цвета излучения с равномерным распределением интенсивности по всему видимому спектру). Кривые сложения этой системы, принятой Международной комиссией по освещению (МКО) в 1931 и известной под название международной колориметрической системы МКО RGB (от англ., red — красный, green — зелёный, blue — синий), показаны на рис. 1. (См. Цветовое пространство CIE 1931).
Кривые сложения системы МКО RGB имеют отрицательные участки (отрицательные количества основных цветов) для некоторых спектральных цветов, что неудобно при расчётах. Наряду с системой RGB МКО в 1931 приняла другую ЦКС, систему XYZ (цветовая модель), в которой отсутствовали недостатки системы RGB и которая дала ряд др. возможностей упрощения расчётов. Основными цветами (X), (Y), (Z) системы XYZ являются нереальные цвета (т. е. допускается существование несуществующих цветов!), выбранные так, что кривые сложения этой системы (рис. 2) не имеют отрицательных участков, а координата Y равна яркости (См. Яркость) наблюдаемого окрашенного объекта, т.к. кривая сложения у совпадает с функцией относительной спектральной световой эффективности (См. Спектральная световая эффективность) стандартного наблюдателя МКО для дневного зрения. На рис. 3 показан график цветностей (цветовой треугольник) х, у системы XYZ (цветовая модель). На нём приведены линия спектральных цветностей, линия пурпурных цветностей, цветовой треугольник (R) (G) (В) системы МКО RGB, линия цветностей излучения абсолютно чёрного тела и точки цветностей стандартных источников освещения МКО А, В, С и D. Цветность равноэнергетического белого цвета Е (опорная цветность системы XYZ) находится в центре тяжести цветового треугольника системы XYZ. Эта система получила всеобщее распространение и широко используется в колориметрии. Но (в связи с принятыми допущениями) она естественно не отражает цветоразличительных свойств глаза, т. е. одинаковые расстояния на графике цветностей х, у в различных его частях не соответствуют одинаковому зрительному различию между соответствующими цветами при одинаковой яркости.
Создать полностью зрительно однородное цветовое пространство таким методом до сих пор не удаётся. Это связано с неспособностью взятой за основу трёхкомпонентной теории цветовосприятия описать, на основе экспериментально полученных спектров чувствительности фотопигментов, механизма цветовосприятия. Поэтому предложено много различных эмпирических формул для подсчёта числа цветовых различий (порогов цветоразличения) между разными цветами. Более ограниченная задача — создание зрительно однородного графика цветностей — приблизительно решена. МКО в 1960 рекомендовала такой график u, v, полученный в 1937 Д. Л. Мак-Адамом путём видоизменения графика, предложенного Д. Б. Джаддом (оба — США) на основании многочисленных экспериментальных данных. Для подсчёта числа порогов цветоразличения ΔE между разными цветами с 1970 годов (по временной рекомендации МКО) используется эмпирическая формула Г. Вышецкого:
Невозможно разобрать выражение (синтаксическая ошибка): {displaystyle ΔE=sqrt{(U_{rm 1}-U_{rm 2})^2 + (V_{rm 1}-V_{rm 2})^2 + (W_{rm 1}-W_{rm 2})^2}}
где:
Невозможно разобрать выражение (синтаксическая ошибка): {displaystyle W = 25Y^1/_3 — 17}
,
Невозможно разобрать выражение (синтаксическая ошибка): {displaystyle U = 13W (u — u_0)}
,
Невозможно разобрать выражение (синтаксическая ошибка): {displaystyle V = 13W (v — v_0)}
.
Здесь:


Описание, приведённое выше, показывает, что цель процесса измерения цвета — определение его ЦК в некоторой ЦКС. Чаще всего это — стандартная колориметрическая система МКО XYZ.[2]
Нахождение цветовых координат
Когда цвет (при объективных цветовых измерениях (Ц. и.) всегда имеется в виду цвет окрашенного предмета или источника света (cм. Источники света)) представлен спектральным распределением плотности, мощности — дисперсии излучения (испускаемого источником, либо отражённого или пропущенного предметом), то для нахождения его ЦК нужно использовать кривые сложения в качестве взвешивающих функций, оценивающие это излучение. Такая оценка может выполняться двумя путями.
Спектрофотометрический метод цветного измерения
Первый путь (спектрофотометрический метод цветового источника) состоит в измерении энергии спектрального распределения плотномти, мощности — дисперсии излучения с последующим расчётом ЦК при перемножении найденной функции спектрального распределения на 3 функции сложения и интегрирования произведений. Если Е (λ) — функция спектрального распределения источника, ρ(λ) — функция спектрального отражения или пропускания предмета — X, Y, Z определяются следующим образом:
- (интегрирование проводится в диапазоне длин волн видимого излучения — от 380 до 780 нм).
Практически интегрирование заменяют суммированием через интервал Δλ (от 5 до 10 нм), т.к. подынтегральные спектральные функции обычно неудобны для интегрирования:

Спектральное распределение излучения и спектральную характеристику отражения (пропускания) измеряют, диспегируя свет в спектр, например, в Спектрофотометре или Монохроматоре. Кривые сложения задаются в виде таблиц значений удельных координат через 5 или 10 нм. Имеются также таблицы величин Е (λ) и т.д. для стандартных источников света МКО А, В, С, D, представляющих наиболее типичные условия естественного (В, С и D) и искусственного (А) освещения.
Цветовые измерения на основе кривых сложения
Второй путь цветовых измерений (Ц. и.) на основе кривых сложения — это анализ излучения с помощью 3 приёмников света (См. Приёмники света), характеристики спектральной чувствительности (См. Спектральная чувствительность) которых совпадают с кривыми сложения. Каждый такой светоэлектрический преобразователь выполняет действия перемножения 2 спектральных функций и интегрирования произведений, в результате чего на его выходе электрический сигнал равен (при соответствующей калибровке прибора) одной из ЦК. Подобные цветоизмерительные приборы называются фотоэлектрическими (или объективными) колориметрами. Они оценивают результирующее излучение, учитывая как избирательное отражение (или пропускание) несамосветящихся (c проходящим светом) предметов (например, линз), так и освещение, т. е. прибор «видит» то, что видит глаз. Основной трудностью при изготовлении фотоэлектрических колориметров является достаточно точное «формирование» кривых сложения, для чего обычно подбирают соответствующие Светофильтры. Если прибор предназначен для работы с кривыми сложения x̅, , то наиболее трудно сформировать двугорбую кривую x̅ (рис. 2). Обычно каждая из её ветвей формируется отдельно; тогда прибор содержит 4 канала (светофильтра). Иногда в колориметрах используют др. ЦКС, все кривые сложения в которой одногорбые. Один из каналов колориметра одновременно может служить Яркомером. Часто в таких приборах предусматривается расчёт координат цветности. Максимальная точность цветовых измерений фотоэлектрическими колориметрами по цветности в координатах х, у составляет от 0,002 до 0,005 (относительные единицы измерения).
Прямое определение цветовых координат
SRGB цветовой треугольник, показано как подмножество x, y пространства, пространства цветности, основанный на колориметрии CIE 1931. Цветной треугольник является плоскостью расположения цветов в треугольнике, на основе сочетанием трех основных цветов RGB (красный, зелёный, синий) по углам. Организации цветов, например, вокруг системы из основных цветов: красного, жёлтого и синего были до теории аддитивного синтеза цвета. В современной x, y диаграмме большой треугольник, ограниченный воображаемым предварительным выбором (праймериз) X, Y и Z имеет углы (1,0), (0,1) и (0,0) (см. рис.4, Цветовые координаты), соответственно; при этом SRGB определяет цветность красного, зеленого и синего первого предварительного подбора основных цветов. Треугольник представляет набор первичных цветов; цвета в пределах этого треугольника могут быть воспроизведены путем смешивания основных цветов. Цвета вне цветового треугольника поэтому показаны здесь как серый цвет. Предварительный выбор цветов и D65 и чёрно-белая точка SRGB показаны. (Эталон МКО D65 (иногда пишется D65, что является широко используемым стандартным источника света и определяется Международной комиссии по освещению (CIE) (МКО). Это часть D серии осветительных устройств, которые пытаются изобразить стандартное освещение в условиях на открытом воздухе в различных частях мира).[3]
Другой принципиальной возможностью цветовых измерений является прямое определение цветовых координат — ЦК.
Но это возможно не всегда, т.к. в общем случае цветовые ощущения возбуждает световое излучение произвольного спектрального состава, а ЦК физически не существует. Прямое измерение ЦК возможно в трёхцветных аддитивных устройствах создания цвета (RGB), используемых, например, для воспроизведения цветных изображений. Основные цвета такого устройства определяют ЦКС, и их количества в смеси, дающей некоторый цвет, и есть ЦК этого цвета в ЦКС устройства. Пример такого устройства — трёхцветный Кинескоп, в котором раздельное управление свечениями 3 люминофоров (См. Люминофоры) обеспечивает получение всего множества цветов, цветности которых заключены в пределах цветового треугольника, определяемого основными цветами кинескопа (цветностями свечений люминофоров, см. Цветное телевидение). Для непосредственного измерения количеств 3 основных цветов в цвете смеси, воспроизводимом на экране кинескопа, т. е. ЦК в ЦКС кинескопа, можно использовать фотоэлектрический приёмник излучения с произвольной спектральной чувствительностью, лишь бы она не выходила за пределы видимого спектра. Измерительным прибором, подключенным к такому приёмнику, достаточно поочерёдно замерить интенсивности свечения отдельных люминофоров кинескопа. (При измерении интенсивности свечения красного люминофора «отключаются» лучи, возбуждающие зелёный и синий цвета, и т.д.) Калибровка подобного прибора состоит в снятии его показаний при поочерёдном измерении интенсивностей свечения 3 люминофоров после установки на экране опорного белого цвета, т. е. цвета с опорной цветностью ЦКС кинескопа и максимальной яркостью. В дальнейшем при измерениях разных цветов показания прибора делятся на показания для соответствующих основных цветов при опорном белом цвете. Результаты такого деления и будут ЦК в ЦКС кинескопа. Опорный белый цвет при калибровке устанавливается как можно более точно с помощью других приборов (спектрофотометра, фотоэлектрического колориметра) или визуально по специальному эталону белого цвета. Точность установки опорного белого цвета при калибровке определяет точность последующих Ц. и. (цветовых измерений). Получить значения ЦК в др. ЦКС (например, международных) можно, пересчитав показания прибора по формулам преобразования ЦК. Для вывода пересчётных формул нужно знать координаты цветности опорного белого цвета и основных цветов данного кинескопа, которые измеряют каким-либо др. методом. Большое преимущество такого непосредственного измерения ЦК по сравнению с Ц. и. при помощи фотоэлектрического колориметра заключается в отсутствии необходимости формировать определённые кривые спектральной чувствительности фотоприёмника. Ц. и. по описанному способу можно выполнять и по полному цвету свечения экрана, без отключения лучей, возбуждающих отдельные люминофоры. В этом случае в приборе должно быть 3 светофильтра с произвольными, но различающимися спектральными характеристиками. В таком приборе каждый отсчёт представляет собой сумму 3 отсчётов однофильтрового прибора для всех 3 отдельных цветных свечений. Чтобы получить значения ЦК по 3 отсчётам трёхфильтрового прибора, используют пересчётную матрицу, элементы которой определяются при калибровке прибора. Калибровка состоит в поочерёдных измерениях каждым из каналов прибора каждого из цветных свечений люминофоров в отдельности после установки на экране опорного белого цвета. Указанный пересчёт, а также переход от ЦК в ЦКС кинескопа к международной ЦКС в приборе описываемого типа может производиться автоматически, с помощью специально встроенной электрической схемы. Т. о. можно получать отсчёты прямо в ЦКС (цветовая координатная система) кинескопа или в международной ЦКС.
Метод визуальной колориметрии
ЦК (цветовые координаты) определяют также при измеренном цвете визуальными колориметрами. Наблюдатель, регулируя количества 3 основных цветов такого прибора, добивается зрительного тождества цвета смеси этих цветов и измеряемого цвета. Затем вместо последнего измеряют цвет смеси. А её ЦК есть просто количества основных цветов колориметра, отнесённые к количествам этих же цветов, входящих в смесь, которая даёт опорный белый цвет ЦКС колориметра. Измерить количества основных цветов в визуальном колориметре ещё легче, чем в цветном кинескопе. Достаточно прочесть показания 3 шкал, отградуированных по раскрытию щелей, пропускающих световые потоки соответствующих цветов к полю сравнения. Откуда при использовании визуальных колориметров измеряется косвенно цвет образца, а его «метамер» — восприятие цвета смеси трёх основных цветов колориметра. Процесс зрительного уравнивания двух цветов служит при этом для получения такого метамера цвета образца, ЦК которого можно легко измерить. Достоинством визуального колориметрирования является высокая точность Ц. и. Недостатком же является то, что получаемые результаты действительны для конкретного (выполняющего зрительное уравнивание двух цветов), а не для стандартного наблюдателя. Кроме того, этим методом трудно измерять цвета не отдельных образцов, а предметов.
Принцип зрительного сравнения измеряемого цвета с цветом, ЦК которого известны или могут быть легко измерены, используется также при Ц. измерении с помощью цветовых атласов. Последние представляют собой наборы цветных образцов в виде окрашенных листов бумаг, которые систематизированы в определённом порядке. При сравнении с измеряемым цветом подбирается образец из атласа, наиболее близкий к нему. Измеренный цвет получает наименование этого образца в соответствии с принятой в данном атласе системой обозначений. Для выражения его в международной ЦКС все образцы атласа заранее измеряются в этой системе при определённом освещении. Измеряемые цвета желательно наблюдать при том же освещении. Цветовые атласы позволяют измерять или уточнять цвета предметов (например, автомобилей при их ремонте согласно номеру цвета в атласе), а не только специальных образцов, но дискретность набора цветов в атласе снижает точность измерений, которая дополнительно понижается из-за того, что условия зрительного сравнения здесь хуже, чем при визуальном колориметрировании. В СССР использовали цветовые атласы Рабкина и ВНИИМ (АЦ-1000), в США широкое распространение получили измерения по атласу Манселла (Мензелла). Цвета измеренные с помощью цветовых атласов являются прикидочными и могут с успехом производиться там, где большая точность не нужна или, где неудобно применять другие методы.
Выражение цвета в определённой ЦКС, т. е. при задании его ЦК (или яркости и координат цветности), универсально и наиболее употребительно. Но прибегают и к др. способам количественного выражения цвета. Примером может служить только что описанное выражение цвета в системе какого-либо цветового атласа. Ещё один такой способ — выражение цвета через его яркость, преобладающую длину волны и колориметрическую чистоту цвета. (Последние два параметра характеризуют цветность.) Достоинство этого способа заключается в близком соответствии 3 перечисленных параметров цвета привычным субъективным его характеристикам: светлоте, цветовому тону и насыщенности.
Более удобно характеризовать цветность одним числом. Но её двумерность требует для её выражения в общем случае двух чисел. С точки зрения трёхкомпонентных моделей — для некоторых совокупностей цветностей (линий на графике цветностей) можно использовать одномерное выражение.
- Первая такая совокупность — чистые спектральные цвета и чистые пурпурные цвета, цветности которых определяются значениями преобладающей длины волны.
- Второй совокупностью, для которой возможно одномерное выражение, являются цветности излучения абсолютно чёрного тела (См. Абсолютно чёрное тело), используемые для характеристики источников освещения с цветностями свечения, близкими к цветности белого цвета. Величина, определяющая положение точки на линии цветностей излучения чёрного тела (и цветности упомянутых источников), — Цветовая температура, т. е. температура в градусах Кельвина абсолютно чёрного тела, при которой оно имеет данную цветность.[4] Тем не менее этот метод находит ограниченное применение.
Линейное уравнение цветного зрения и цветового пространства
Рис.3. Нормализованные спектры чувствительности фотопигментов колбочек сетчатки глаза при цветном зрении в условиях дневного освещения.
В итоге, из условия, что пучок света может быть составным, состоящим из излучений многих различных длин волны, определять степень, в которой физический цвет C в Hцвет стимулирует каждую клетку колбочки , мы должны вычислить интеграл (относительно w), по интервалу [Wmin,Wmax], из уравнения:
-
- C (w) *s (w), C (w) *m (w), и C (w) *l (w) (см. рис.3).
Тройные из получающихся чисел связываются каждым «физическим» цветом C (который является областью в Hцвет) к специфическому воспринятому цвету (который является единственным пунктом в R³цвет). Т.е. при оппонентном отборе трёх основных цветов S,M,L наиболее ярких из числа многих цветов сфокусированных на колбочки лучей предметных точек. Эта функция, как легко можно заметить, является линейной (как уравнения первой степени). Может также быть легко замечено, что много различных областей в «физическом» месте Hцвет могут все привести к тому же самому единственному воспринятому цвету в R³цвет.
Таким образом, воспринятый цвет не уникален для одного физического цвета. То есть природа цветного зрения подчиняется принципу трёхкомпонентного цветного зрения (на базе трёх основных цветов спектра света RGB при работе колбочек в условиях дневного освещения и математически выражается линейным уравнением.(В отличие от нелинейной теории цветного зрения, по которой в цветном зрении участвуют блоки колбоча+палочка, что неправильно. (См. Ретиномоторная реакция фоторецепторов).
В итоге человеческое цветное восприятие определено определенной, групповой линейной картографией от бесконечномерного места Hilbert Hцвет к 3-мерному Евклидовому месту en:Euclidean_spaceR³цвет.
И наше ощущение цвета привело к появлению понятия цветового пространства, которое выражается математической цветовой моделью представления цвета, которая основана на использовании цветовых координат.
См. также
- Цветовые пространства LAB
- Стандартные источники света
Литература
- Гуревич М. М., Цвет и его измерение, М. — Л., 1950;
- Кривошеев М. И., Кустарев А. К., Световые измерения в телевидении, М., 1973;
- Нюберг Н. Д., Измерение цвета и цветовые стандарты, М., 1933;
- Wright W. D., The measurement of colour, 3 ed., L., 1964;
- Wyszecky G., Stiles W. S., Color science, N. Y., 1967. А. К. Кустарёв.
Примечания
- ↑ http://thelib.ru/books/bse/bolshaya_sovetskaya_enciklopediya_cv-read-10.html
- ↑ http://dic.academic.ru/dic.nsf/bse/148439/%D0%A6%D0%B2%D0%B5%D1%82%D0%BE%D0%B2%D1%8B%D0%B5
- ↑ http://en.wikipedia.org/wiki/Color_triangle
- ↑ http://dic.academic.ru/dic.nsf/bse/148439/%D0%A6%D0%B2%D0%B5%D1%82%D0%BE%D0%B2%D1%8B%D0%B5
| Цветовые модели |
|---|
| RGB (цветовая модель) • CMYK • XYZ (цветовая модель) • HSV (цветовая модель) • HSL и HSV (цветовые модели) • RYB • LAB • PMS (Пантон) • LMS • Манселла • NCS • RAL • YUV • YCbCr • YPbPr • YDbDr • YIQ |
| Глаз и Зрение | |
|---|---|
| Основные разделы | Зрение,Глаз • Анатомия глаза • Теории цветовосприятия • Современные взгляды на цветное зрение |
| Зрение,Глаз | Глаз •
Глаз человека • Зрение • Цветное зрение • Цветное зрение у птиц • Эволюция цветного зрения • Бинокулярное зрение • Зрение в условиях слабого освещения • Свет • Цвет • Эффект Пуркинье • Стереоскопия • Зрительная система • Зрение человека • Дальтонизм • Фотопигмент • Опсины • Зрительная кора • Саккада • Колориметрия • Эффект Трослера • Дендрит • Денситометрия • Денситометр |
| Анатомия глаза | Фиброзная оболочка – Конъюнктива · Склера · Шлеммов канал Трабекулярная сеть · Роговица · Эндотелий роговицы · Лимб Кератоциты
Сосудистая оболочка – Хориоидеа · Радужная оболочка · Зрачок · Цилиарное тело |
| Теории цветовосприятия | Теории цветового зрения · Теории цветного зрения · Религиозная гипотеза зрения · Гипотеза М. В. Ломоносова о цветном зрении · Теория цветовосприятия Иоганнеса Мюллера · Теория Юнга – Гельмгольца · Теория Геринга · Психофизическая теория цветоощущения Георга Мюллера · Теория Лэдд-Франклин · Зонная теория Крисса · Теория Кёнинга · Гипотеза Г. Хартриджа · Концепция М.Смирнова · Модель П. Уолравена · Теория цветного зрения Лэнда · Трёхкомпонентная теория цветового зрения • Теория многокомпонентного цветного зрения · Оппонентная теория цветового зрения • Нелинейная теория зрения |
Цветовая модель — математическая модель описания представления цветов в виде кортежей чисел (обычно из трёх, реже — четырёх значений), называемых цветовыми компонентами или цветовыми координатами. Все возможные значения цветов, задаваемые моделью, определяют цветовое пространство.
Цветовая модель задаёт соответствие между воспринимаемыми человеком цветами, хранимыми в памяти, и цветами, формируемыми на устройствах вывода (возможно, при заданных условиях).
Цветовое пространство CIE XYZ[править | править код]

Функции цветового соответствия Стандартного колориметрического наблюдателя, определённые комитетом CIE в 1931 году на диапазоне длин волн от 380 до 780 нм (с 5 нм интервалом)[1]
Человек является трихроматом — сетчатка глаза имеет три вида рецепторов (колбочек), ответственных за цветное зрение. Можно считать, что каждый вид колбочек даёт свой отклик на определённую длину волны видимого спектра.
Важным свойством (для всех физически реализуемых цветов) является неотрицательность как функций отклика, так и результирующих цветовых координат для всех цветов. Системой, основанной на откликах колбочек человеческого глаза, является цветовая модель LMS.
Исторически сложилось, что для измерения цвета используется другое цветовое пространство — XYZ — эталонная цветовая модель, заданная в строгом математическом смысле Международной комиссией по освещению (фр. Commission internationale de l’éclairage, CIE) в 1931 году. Модель CIE XYZ является мастер-моделью практически всех остальных цветовых моделей, используемых в технических областях.
Эксперименты, проведённые Дэвидом Райтом (англ. David Wright)[2] и Джоном Гилдом (англ. John Guild)[3] в конце 1920-х и начале 1930-х годов, послужили основой для определения функций цветового соответствия. Изначально функции цветового соответствия были определены для 2-градусного поля зрения (использовался соответствующий колориметр). В 1964 году комитет CIE опубликовал дополнительные данные для 10-градусного поля зрения. Итак, аналогично координатам LMS, цвет XYZ задаётся следующим образом:
- где
— спектральная плотность какой-либо энергетической фотометрической величины, например, потока излучения, энергетической яркости и т. п., в абсолютном или относительном выражении.
Для модели брались условия, чтобы компонента Y соответствовала визуальной яркости сигнала (
Цветовое пространство XYZ не задает сразу отклики колбочек на сетчатке человека, являясь очень сильно преобразованной цветовой моделью с целью получить значения цвета и, соответственно, возможность отличать один спектр от другого, отталкиваясь от фотометрической яркости излучения (Y). Саму яркость Y интерпретировать как отклик «зелёных» колбочек нельзя, эта функция для дневного зрения, являющегося трехстимульным, задается всеми реальными откликами рецепторов. Изначально модель CIE 1931 XYZ получили путём преобразования модели CIE 1931 RGB, которая, в свою очередь, является следствием прямого эксперимента по смешиванию и визуальному сравнению излучений различных спектральных составов. Любая цветовая модель может быть преобразована в модель XYZ, так как данная модель определяет все правила смешивания цветов и задает ограничения, накладываемые на все спектральные составы излучений, которые имеют один цвет.
Хроматические координаты (x;y) и цветовое пространство xyY[править | править код]
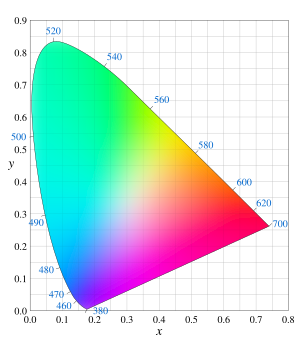
Хроматическая диаграмма с длинами волн цветов
Если формально построить сечение пространства XYZ плоскостью 
.
- аналогично, но необязательно:
Такое сечение называется хроматической диаграммой (диаграммой цветности).
В пространстве XYZ точке (X,0,0), как легко посчитать по формулам, на хроматической диаграмме соответствует точка xy=(1,0). Подобным образом, точке XYZ=(0,Y,0) соответствует точка xy=(0,1) и, наконец, точке XYZ=(0,0,Z) — точка xy=(0,0). Видно, что все реальные цвета, полученные любыми спектральными составами излучений, в том числе и монохроматическими (спектральные цвета) не дотягивают до подобных «чистых» значений. Данная закономерность вытекает из правила смешивания цветов и является проявлением того, что невозможно получить отклик одних колбочек без отклика других (хоть и очень малого), а также из того, что яркость Y не может иметь нулевое или малое значение при определенном отклике любых колбочек.
Цветовое пространство xyY можно задать, если задать значение цветности — (x, y) при данном значении яркости Y.
При этом для координат x и y продолжает выполняться условие неотрицательности.
Не следует путать светлоту Y в моделях XYZ и xyY — с яркостью Y в модели YUV или YCbCr.
Физически реализуемые цвета[править | править код]
Если на хроматической диаграмме xy отметить все возможные монохроматические цвета спектра, то они образуют собой незамкнутый контур, так называемый спектральный локус. Замыкание этого контура в основании «языка» называется линией пурпуров. Все цвета, которые могут быть реализованы в виде суммы спектральных линий данной яркости, будут лежать внутри этого контура. То есть существуют точки XYZ цветов за пределами контура, которые хотя и имеют положительные значения каждой компоненты, но тем не менее соответствующий отклик от колбочек не может быть получен при данной яркости (константе 
Вместе с тем, при расчётах такие цвета (как и вообще цвета с отрицательными координатами) вполне могут использоваться. Например, в качестве базовых цветов для пространства Prophoto RGB были выбраны физически не реализуемые цвета.
Производные от CIE XYZ цветовые пространства[править | править код]
Цветовые модели можно классифицировать по их целевой направленности:
- L*a*b* — равноконтрастное цветовое пространство, в котором расстояние между цветами соответствует мере ощущения их различия.
- Аддитивные модели — где цвет получается путём добавления к черному (Класс RGB).
- Субтрактивные модели — получение цвета «вычитанием» краски из белого листа (CMY, CMYK).
- Модели для кодирования цветовой информации при сжатии изображений и видео.
- Математические модели, полезные для обработки изображения, например HSV.
- Модели, где соответствие цветов задаётся таблично (Цветовая модель Пантон (Pantone))
Все модели сводятся к XYZ путём соответствующих математических преобразований. В качестве примеров можно рассмотреть:
- Цветовая модель sRGB (IEC 61966-2.1)[4], разновидность модели RGB, широко используется в компьютерной индустрии, часто представляет собой цветовую модель «по умолчанию».
- В телевидении для стандарта PAL применяется цветовая модель YUV, для SÉCAM — модель YDbDr, а для NTSC — модель YIQ. (Следует помнить, что Y в этих моделях вычисляется совершенно по-другому, чем Y в модели XYZ).
Цветовой охват моделей устройств вывода[править | править код]

Охват различных устройств цветовоспроизведения
Диаграмма Yxy используется для иллюстрации характеристик цветового охвата (англ. color gamut) различных устройств воспроизведения цвета — дисплеев и принтеров через соответствующие им цветовые модели.
Как уже было сказано, любой тройке чисел XYZ можно сопоставить конкретные координаты пространства RGB или CMYK. Так, цвет будет соответствовать яркости цветовых каналов или плотности красок. Физическая реализуемость цвета на устройстве накладывает условие неотрицательности координат. Таким образом, только некое подмножество Yxy может быть физически реализовано на устройстве. Эта область называется цветовым охватом устройства.
Конкретная область цветового охвата обычно имеет вид многоугольника, углы которого образованы точками основных, или первичных, цветов. Внутренняя область описывает все цвета, которые способно воспроизвести данное устройство.
На рисунке справа показаны области цветового охвата различных средств цветовоспроизведения:
- белый контур отражает диапазон фотографической эмульсии различного назначения;
- красный пунктирный контур — пространство sRGB, приблизительно соответствующее гамме большинства распространённых мониторов, являющиеся, по сути, стандартом представления графики в сети Интернет;
- чёрный сплошной контур — пространство Adobe RGB, включающее цвета, воспроизводимые на печатных машинах, но с использованием первичных цветов;
- синий сплошной контур соответствует высококачественной офсетной печати;
- синий пунктирный контур отражает охват обычного бытового принтера.
См. также[править | править код]
- Цветоделение
- Формула цветового отличия
- Цветовая палитра
- Атлас цветов
Примечания[править | править код]
- ↑ CIE — INTERNATIONAL COMMISSION ON ILLUMINATION. Дата обращения: 3 июня 2008. Архивировано из оригинала 3 июня 2005 года.
- ↑ William David Wright. A re-determination of the trichromatic coefficients of the spectral colours (англ.) // Transactions of the Optical Society. — 1928. — Vol. 30. — P. 141—164. — doi:10.1088/1475-4878/30/4/301.
- ↑ John Guild. The colorimetric properties of the spectrum (англ.) // Philosophical Transactions of the Royal Society of London. — 1931. — Vol. A230. — P. 149—187.
- ↑ A Standard Default Color Space for the Internet – sRGB. Дата обращения: 13 января 2010. Архивировано 23 августа 2011 года.
Ссылки[править | править код]
- Алексей Шадрин, Андрей Френкель. Color Management System (CMS) в логике цветовых координатных систем. Часть I, Часть 2, Часть 3
- Всё о цвете
- Цветопередача
- Основы теории цвета
- Цветовой конвертер LCh, Lab, RGB, hex, XYZ, xyY, CMYK, Pantone с открытым кодом. CIELab.XYZ.
Согласно
первому закону аддитивного смешения
цветов, любой цвет Ц может быть выражен
через три линейно-независимых цвета:
Ц=R[R]
+ G[G]+
B[B],
(9.1)
где R,
G
и В – количества основных цветов [R],
[G]
и [B]
соответственно. Напомним, что количества
цветов являются алгебраическими
величинами, то есть входят в выражение
со знаком «+» или «-». Данная запись
цвета называется «цветовое
уравнение»,
а входящие в неё количества цветов
называется «координаты
цвета в трихроматичной (трёхцветной)
системе».
Резолюцией МКО в качестве основных
цветов системы RGB
выбраны следующие излучения в определенных
количествах:
[R]
→ λR=700.0
нм; ФR=
1.00 лм – «КРАСНЫЙ»
[G]
→ λG=547.1
нм; ФG=4.59
лм – «ЗЕЛЕНЫЙ»
[В] →
λВ=435.8
нм; ФВ=0.06
лм – «СИНИЙ»
Величины
световых потоков Фi
были специально подобраны таким образом,
чтобы три основных цвета, взятые в равных
количествах, давали в сумме единичный
белый цвет «Е»:
[R]+[G]+[B]=E (9.2)
Такой
белый цвет в литературе называют
«равностимульный
(или
равноинтенсивный) белый цвет»,
чтобы подчеркнуть тот факт, что он
сформирован взятыми в равных
количествах
основными цветами.
Ясно,
что при удвоении количества цветов
суммарный цвет белый цвет так же
«удвоится»:
2[R]+2[G]+2[B]=2Е
– белый цвет в «удвоенном количестве»
Введем
несколько определений:
1).
Модуль
цвета (m)
По
определению, модуль цвета m
равен сумме трех координат данного
цвета:
m = R+G+B (9.3)
Пример
с белым цветом показывает, что цветовой
модуль m
характеризует цвет с количественной
стороны
2).
Координаты
цветности
{r, g, b}
По
определению, координаты цветности
{r, g, b}
– это отношение координат цвета к его
модулю:
 (9.3)
(9.3)
Введенные
таким образом координаты цветности
{r, g, b}
определяют цвет с качественной стороны,
то есть описывают оттенок
цвета
(тон + насыщенность).
Можно сказать, что координаты цветности
представляют собой координаты некоторого
цвета, взятого «в единичном количестве»
– так называемого «единичного
цвета».
Из
определения координат цветности ясно,
что r+g+b=1.
Следовательно, для описания цветового
оттенка достаточно задать только две
координаты цветности, например {r, g},
недостающую координату легко выразить:
b=1- (r + g).
Используя данное свойство координат
цветности, все тона можно изобразить в
виде точек на плоскости.
Воспользовавшись
формулами (9.3) перепишем цветовое
уравнение в другом виде:
Ц =
R[R]+G[G]+B[B]
= mr[R]+mg[G]+mb[B]
=
= m(
r[R]+g[G]+b[B]
)=m[Ц],
(9.4)
где [Ц]
=
r[R]+g[B]+b[B]
– (по смыслу) некоторый единичный цвет,
(9.5)
m
=
R+G+B
–
модуль цвета
Видно,
что модуль цвета показывает, в каком
количестве необходимо взять единичный
цвет [Ц] (соответствующий тону и
насыщенности цвета Ц), чтобы получить
интересующий нас цвет. Отметим,
что выражение (9.5), описывающее единичный
цвет, по своей форме совершенно аналогично
цветовому уравнению (9.1). Поэтому (9.5)
принято называть «цветовое
уравнение для единичного цвета [Ц]».

Рисунок
50– схема эксперимента Райта и Гилда.
Для
выполнения практических расчётов, В.
Райт и Ж. Гилд в эксперименте определили
координаты цветности для всех
монохроматических излучений (всех
чистых цветов). На рисунке 9.1 приведена
схема их эксперимента.
В области
экрана I
смешиваются излучения основных цветов.
В области
экрана II
наблюдатель видит излучение с длиной
волны λ,
координаты цветности которого требуется
определить.
Указанная
на рисунке яркость экрана необходима
для обеспечения нормальной работы
колбочек глаза.
Управляя
регуляторами
количества для всех трех основных
цветов, экспериментатор должен выровнять
цвет полей I
и II
– добиться цветового тождества излучений
в обеих областях поля зрения.
Отметим
некоторые особенности измерений:
-
Регуляторы
количества основных цветов были
градуированы в соответствии со значениями
единичных цветовых потоков ФR
,
ФG
и ФВ. -
Как мы
уже знаем, цвет спектрально-чистого
излучения не всегда может быть
воспроизведен путём аддитивного
смешивания трех основных излучений.
Поэтому в некоторых случаях к исследуемому
излучению можно было подмешивать одно
из основных излучений, с целью
«разбавления» (для снижения насыщенности
исследуемого цвета). Пусть, например,
для целей разбавления использовалось
излучение синего цвета ( показано
пунктирной стрелкой на рисунке) в
количестве B1.
В этом случае, после установлении
цветового тождества получаем:
Ц(λ) +
B1[B]
= R[R]
+ G[G]
+ B2[B]
Ц(λ)=R[R]+G[G]+
(B1-B2)[B]
, (9.6)
где
R,
G,
и В =B1-B2
– количества основных цветов, измеренные
в «единичных цветовых потоках» (то есть
положения ручек регуляторов основных
цветов).
Зная
количества основных цветов, необходимые
для установления цветового тождества,
экспериментаторы легко рассчитали
координаты цветности:
 (9.7)
(9.7)
3).
Удельные
координаты
 .
.
При
выполнении расчетов, часто оказываются
полезны так называемые «удельные
координаты»
 .
.
В литературе их могут называть по-разному:«удельные
координаты спектральных излучений
постоянной мощности»,
(применительно к графикам) «кривые сложения».
Удельные
координаты
–
это координаты цвета, световой поток
которого имеет мощность 1 Вт.
Таким
образом, имеется три типа координат
цвета:
Координаты
цвета:{R,G,B}–полная
характеристика цвета Ц
Удельные
координаты цвета:
 –характеризуют
–характеризуют
цвет того же оттенка, что и Ц, но с
мощностью 1Вт
Координаты
цветности:
{r, g, b} – характеристика
единичного цвета [Ц], соответствующего
данному Ц
Чтобы
рассчитать удельные координаты некоторого
спектрально-чистого излучения Ц с длиной
волны ,
поступают следующим образов:
-
находят
координаты {r, g, b}, для соответствующего
этому излучению единичного цвета [Ц] -
вычисляют
мощность
единичного
цвета
P[Ц]
(выраженную
в Ваттах!):
 ,
,
(9.8)
где Ф[ц]
– световой поток, соответствующий
единичному цвету [Ц], Фi
–
единичные световые потоки для трех
основных цветов.
-
каждую
из координат {r, g, b} единичного
цвета [Ц] делят на эту мощность:
 (9.9)
(9.9)
Итак,
выражения (9.9) позволяют нам по известным
координатам цветности {r, g, b}
некоторого спектрально-чистого излучения
вычислить его удельные
координаты
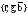 –
–
то есть координаты цвета
с
тем же оттенком,
но обладающего мощностью
1Вт.
Обратите внимание на тот факт, что
множитель «683» является общим для всех
трех удельных координат: он входит в
формулы для каждой из них. Легко понять,
что общий множитель не важен для расчёта
качественных характеристик цвета,
поэтому его часто опускают.
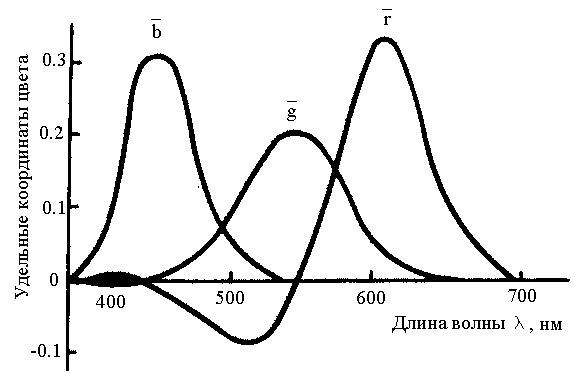
Рисунок
51 –удельные координаты цвета для всех
спектрально-чистых цветов в системе
RGB.
Мощность:
1/683 Вт
Данный
график показывает, в каких количествах
необходимо смешать основные цвета
системы RGB
(с учётом единичных количеств Ф i ),
чтобы воспроизвести цвет монохроматического
излучения с длинной волны
и мощностью 1/ 683 Вт.
Удельные
координаты спектральных цветов с
различной длиной волны (в системе RGB)
Пользуясь
кривыми сложения легко расчитать
координаты
спектрально-чистого цвета
(монохроматического излучения) с длиной
волны
и мощностью Р:
 (9.10)
(9.10)
Если
излучение не монохроматическое, а
обладает сложным спектром, вычисления
усложняются. Такое излучение представляет
собой совокупность большого числа
световых волн с различной длиной
и обладающих мощностью dP
(dP
= Рd
– «мощность излучения, обладающего
длиной волны вблизи λ»1).
Координаты цвета в этом случае – есть
алгебраическая сумма координат цвета
для каждой из волн, вычисленных по
формуле (9.10). Таким образом, дляизлучения
со сложным спектром
получаем следующую формулу:
 (9.11)
(9.11)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Привет, сегодня поговорим про вычисление координат цвета, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
вычисление координат цвета , настоятельно рекомендую прочитать все из категории Цифровая обработка изображений.
Координаты цвета произвольного излучения для заданного набора основных цветов можно вычислить косвенным путем, если для этого набора известны функции сложения, т. е. координаты цвета спектральных (узкополосных) излучений единичной энергии. Типичные функции сложения показаны на рис. 3.4.1. Функции сложения, определяющие колориметрическую систему, обозначаются как 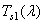 ,
, 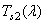 ,
, 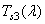 , где
, где 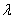 — длина волны спектрального цвета.
— длина волны спектрального цвета.

Рис. 3.4.1. Функция сложения для типичных основных цветов – красного, зеленого и синего.
Монохроматический свет 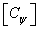 с длиной волны
с длиной волны 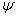 и единичной энергией имеет спектральную плотность
и единичной энергией имеет спектральную плотность 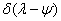 . При этом справедливо следующее соотношение:
. При этом справедливо следующее соотношение:
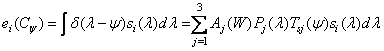 . (3.4.12)
. (3.4.12)
Рассмотрим теперь произвольный цвет 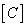 со спектральной плотностью
со спектральной плотностью 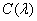 .
. 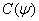 единиц этого света при длине волны
единиц этого света при длине волны 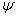 имеют координаты цвета
имеют координаты цвета 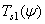 ,
, 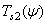 ,
, 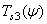 . Об этом говорит сайт https://intellect.icu . Следовательно,
. Об этом говорит сайт https://intellect.icu . Следовательно,
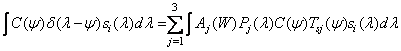 . (3.4.13)
. (3.4.13)
Интегрируя обе части этого равенства по 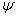 и используя основное свойство дельта-функции, получаем
и используя основное свойство дельта-функции, получаем
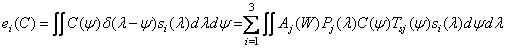 . (3.4.14)
. (3.4.14)
Сравнение этого равенства с соотношением (3.4.7) показывает, что координата цвета 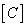 есть
есть
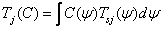 . (3.4.15)
. (3.4.15)
Как видно из рис. 3.4.1, координаты некоторых спектральных цветов могут иметь отрицательные значения. С другой стороны, координата цвета пропорциональна интенсивности основного цвета, которая не может быть отрицательной. Отрицательные значения координат интерпретируются следующим образом: основной цвет, соответствующий отрицательному значению координаты, должен быть прибавлен к исходному цвету, после чего достигается уравнивание смесью двух оставшихся основных цветов. В этом смысле любой цвет может быть уравнен смесью любых основных цветов. Однако цвета с отрицательными координатами не могут быть воспроизведены с помощью реального устройства с заданными основными цветами (например, в приемнике цветного телевидения). К счастью, можно выбрать основные цвета так, чтобы большинство обычных естественных цветов были воспроизводимыми.
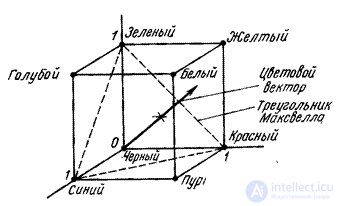
Рис. 3.4.2. Цветовое пространство для типичных основных цветов.
Координаты цвета 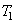 ,
, 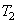 ,
,  можно рассматривать как координаты точек в некотором трехмерном пространстве (рис. 3.4.2). Данный цвет можно представить также как вектор. На рис. 3.4.2 показан треугольник, называемый треугольником Максвелла. Расстояния от вершин этого треугольника до точки пересечения цветового вектора с плоскостью треугольника характеризуют цветовой тон и насыщенность цветов.
можно рассматривать как координаты точек в некотором трехмерном пространстве (рис. 3.4.2). Данный цвет можно представить также как вектор. На рис. 3.4.2 показан треугольник, называемый треугольником Максвелла. Расстояния от вершин этого треугольника до точки пересечения цветового вектора с плоскостью треугольника характеризуют цветовой тон и насыщенность цветов.
Рис. 3.4.3. График цветностей для типичных основных цветов.
Часто при описании цвета его яркость не представляет интереса. В таких случаях цветовой тон и насыщенность цвета 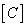 можно выразить через координаты цветности, являющиеся нормированными координатами цвета:
можно выразить через координаты цветности, являющиеся нормированными координатами цвета:
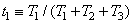 , (3.4.16а)
, (3.4.16а)
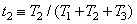 , (3.4.16б)
, (3.4.16б)
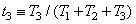 . (3.4.16в)
. (3.4.16в)
Очевидно, что 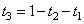 и, следовательно, для описания цветности необходимы только две координаты. На рис. 3.4.3 показан график цветностей для набора типичных основных цветов. С помощью реальных источников света можно физически воспроизводить только те цвета, которые находятся внутри треугольника, определенного тремя основными цветами.
и, следовательно, для описания цветности необходимы только две координаты. На рис. 3.4.3 показан график цветностей для набора типичных основных цветов. С помощью реальных источников света можно физически воспроизводить только те цвета, которые находятся внутри треугольника, определенного тремя основными цветами.
Я хотел бы услышать твое мнение про вычисление координат цвета Надеюсь, что теперь ты понял что такое вычисление координат цвета
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Цифровая обработка изображений
Из статьи мы узнали кратко, но емко про вычисление координат цвета
Определение CIE 1931 г. координаты цветности:
Координата цветности
Цвета на рисунке включают цвета, которые может получить природа. Это двумерная плоская пространственная диаграмма, плоскость, составленная из прямоугольной шкалы xy. Он был разработан, чтобы учесть привычку людей обсуждать отношения переменных в плоской системе координат. В процессе проектирования графа было проведено множество математических преобразований и вычислений. Значение и функцию этой фигуры можно свести к двум предложениям: (1) Она представляет собой основной закон цветового зрения. (2) Указывает на общий закон смешения и распада цветов.
1. Система координат – x, y декартова система координат.
x – представляет относительную величину по отношению к красному.
y – представляет относительную величину, связанную с зеленым цветом.
z – представляет относительную величину, связанную с синим цветом. и z=1-(x+y)
2. Форма и контурные линии
Форма – форма языка, иногда называемая диаграммой «кривая языка». Замкнутая область, окруженная периферийной кривой в форме языка и прямой линией внизу. Язычковая периферическая кривая – это линия цветовой траектории всего видимого монохроматического света, каждая точка представляет цвет определенной длины волны монохроматического света, с длинами волн от 390 до 760 нм. Рядом с кривой. Отмечены соответствующие длины волн некоторых характерных цветовых точек. Например, на рисунке 510нм – 520нм – 530нм. Нижняя линия — прямая линия, соединяющая точку 390 нм с точкой 760 нм, эта линия называется фиолетово-красной линией.
3. Цвет
Это цветовая карта цветов области, включая цвета, которые могут быть получены физически. К сожалению, такая информация, редко доступная в истинных стандартах, часто искажается переводами.
4. Ценность применения – количественное представление цвета
Цвета представлены значениями координат (x, y). Белый следует включить в понятие «цвет».
5. Значение нескольких особенностей
(1) Точка E – координатная точка точки равноэнергетического белого света.
Пятно Е представляет собой смесь трех основных цветов света с одинаковой энергией стимулирующего света. Однако световые потоки трех не равны. CCT = 5400K в точке E.
(2) Точка – CIE определяет точку координаты цветности стандартного источника белого света. Это лампа на чистом вольфраме со значением цветовой температуры CCT=2856.
(3) Точка B – стандартная точка координат источника света, определенная CIE CCT=4874K точки B, представляющая прямой дневной свет.
(4) Точка C – стандартная точка координат источника дневного света (дневной свет), подтвержденная CIE CCT=6774K точки C.
(5) точка D – иногда также обозначаемая буквой D источник света называется типичным дневным светом или рекомбинантным дневным светом; ЦКТ=6500К。
6. Три специальные линии
(1) Линия траектории цветовой температуры черного тела: в середине язычковой кривой через белую область проходит нисходящая кривая, которая является линией траектории цветовой температуры черного тела. Эта кривая представляет собой траекторию светящегося цвета черного тела при различных температурах. Цветовая температура варьируется от 1000К до бесконечности. Но на самом деле обычно используется диапазон 1000К-1400К.
(2) Линия траектории монохроматического света: то есть кривая в форме языка на диаграмме координат цветности, линия траектории цвета, соответствующего длине волны видимого света. Любая точка на кривой указывает длину волны света и цвет, который он представляет.
(3) Пурпурно-красная линия: прямая линия, соединяющая два конца кривой в форме языка. Представляет траекторию цвета после смешивания красного и фиолетового. Это называется пурпурно-красной линией.
7. 20 определенных цветовых зон
Область, окруженная кривой языка, разделена на 20 цветовых областей. В каждом регионе цвет считается в основном одинаковым, и каждая цветовая зона представляет собой среднюю доминирующую длину волны или дополнительную доминирующую длину волны, и есть соответствующее английское название. Их англо-китайские имена отличаются следующим образом:
1. Красный — красный 2. Розовый — розовый 3. Reddis Orange — оранжево-красный 4. Желто-розовый — розовый 5. Оранжевый — оранжевый 6. Оранжево-желтый — оранжево-желтый 7. Желтый — желтый8.Оранжево-желтый—желто-зеленый9. Желто-зеленый — зелено-желтый 10. Желто-зеленый — бледно-желтовато-зеленый 11. Зеленый — зеленый 12. Голубовато-зеленый — светло-сине-зеленый 13, Зеленовато-синий — светло-зеленовато-голубой 14. Синий — синий 15. Пурпурно-синий — сиренево-синий 16 Пурпурно-фиолетовый – фиолетово-фиолетовый 17. Красновато-фиолетовый – красновато-фиолетовый 18. Пурпурно-розовый – сиренево-розовый 19. Пурпурно-красный – пурпурно-красный 20
8. Дополнительность света и цвета
Если два цвета света можно смешать в определенной пропорции, чтобы получить белый свет, два цвета света называются дополнительными. На диаграмме цветности пара дополнительных цветных огней может быть найдена на любой прямой линии, проходящей через белую область. Конечно, проходя через прямые концы точки Е точки изоэнергетического белого света, вы также можете найти дополнительный набор цветного света. На диаграмме координат цветности цвет света любых двух точек соединяет прямую линию двух точек, и результат этого смешения цветов света всегда находится в определенной точке на линии. Если линия не проходит через белую область, светлый цвет двух точек нельзя назвать дополнительным.
9. Смешение белого света с другими цветами света — доминирующая длина волны и дополнительная доминирующая длина волны.
Смешайте белый свет с соответствующим спектральным цветом, чтобы получить любой цвет света, который вам нужен. Если выбран белый свет, эквивалентный энергии белого света точки Е. Выберите любую точку C, соедините CE и удлините, пересеките на монохроматической линии траектории, затем длину волны монохроматического света C’, называемую доминирующей длиной волны точечного света C. Доминирующая длина волны λ представляет доминирующий цвет спектрального цвета в каждой точке на линии. Если в треугольнике FEN выбрана точка А, то ЭП связан, но его нельзя продолжить в направлении А, а линию следует продолжить влево вверх и пересечь в точке А’ на линии монохроматической траектории, то Длина волны точки A’ называется дополнительной доминирующей длиной волны точки A. Доминирующая длина волны дополнительного цвета также является доминирующим цветом, представляющим цвет каждой точки на линии AA’.
10. Количественное представление цветовых оттенков
Оттенок цветового поля, похожий на интертон в музыке. В музыкальном произведении есть тональность C, клавиша F и т. д., а в цветности это обозначается доминирующей длиной волны. Звуки произношения в музыке бывают высокими и низкими. В колориметрии существуют соответствующие оттенки цвета. Оттенок цвета выражается в показателях возбуждающей чистоты Ре. (См. рисунок в разделе 11) Очевидно, что на линии цвет точки С’ темный, затем постепенно тускнеет, а к точке Е становится полностью белым.
11. Смешение цветов и света
Диаграмма координат цветности xy может использоваться для представления соотношения смешивания любых двух цветовых огней.
два спектральных цвета по координатам цветности. Чтобы смешать два вида света, просто соедините две точки, чтобы получить прямую линию, и цветовая точка смешивания цветов также должна быть точкой на линии.
12. Широта цвета
На диаграмме координат цветности XY каждая точка представляет определенный цвет. Цвет любой точки и окружающих соседних точек должен быть разным. Но если точки расположены близко друг к другу, человеческий глаз не может их различить. Только когда расстояние между двумя точками достаточно велико, мы можем почувствовать разницу. Диапазон, в котором человеческий глаз не может воспринять изменение цвета, называется цветовой широкой способностью. Исследования показали, что широкая мощность цветов неодинакова в разных местах на диаграмме цветности. Широкая емкость синей зоны мала, а широкая емкость зеленой зоны велика. Другими словами, одинаковое расстояние между различными областями диаграммы цветности не представляет визуальной разницы в равной цветности. Это дефект диаграмм цветности.
LISUN выпустил портативный колориметр/измеритель цветности — это инновационный инструмент для измерения цвета с мощной конфигурацией, позволяющей сделать измерение цвета более простым и профессиональным; Он поддерживает Bluetooth для подключения к устройствам Android и ISO, портативный колориметр / измеритель цветности перенесет вас в новый мир управления цветом; Его можно широко использовать для измерения значения цвета, значения цветовой разницы и поиска аналогичного цвета по цветовым картам для полиграфической, лакокрасочной, текстильной промышленности и т. д.
CD-320PRO_Портативный колориметр/цветометр
Компания Lisun Instruments Limited была основана LISUN GROUP в 2003 году. Система качества LISUN строго сертифицирована по стандарту ISO9001: 2015. Для членов CIE продукты LISUN разработаны на основе CIE, IEC и других международных или национальных стандартов. Все продукты прошли сертификацию CE и прошли проверку в сторонней лаборатории.
Наша основная продукция гониофотометра, Интегрирующая сфера, Spectroradiometer, Генератор всплесков, Пистолеты-симуляторы ESD, Приемник EMI, Испытательное оборудование EMC, Тестер электробезопасности, Экологическая палата, Температура камеры, Климатическая камера, Тепловая камера, Тест соленых брызг, Камера для испытаний на пыль, Водонепроницаемый тест, Тест RoHS (EDXRF), Испытание светящейся проволоки и Испытание иглы на пламя.
Пожалуйста, не стесняйтесь обращаться к нам, если вам нужна поддержка.
Технический отдел: Service@Lisungroup.com, Cell / WhatsApp: +8615317907381
Отдел продаж: Sales@Lisungroup.com, Cell / WhatsApp: +8618117273997
Метки:CD-320PRO





