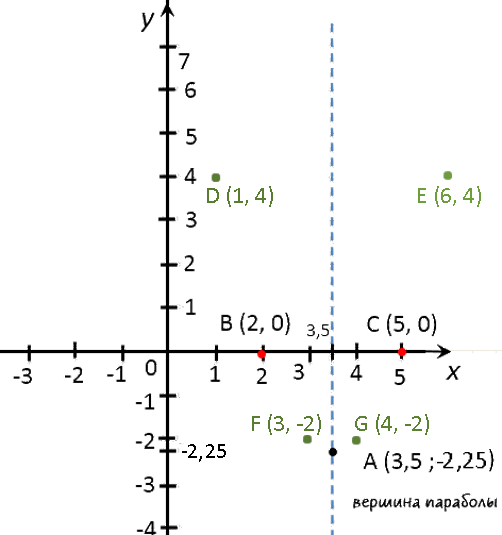Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Запомните!
Квадратичная функция — это функция вида
y = ax2 + bx + c,
где a,
b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x2 − 7x + 9 |
|
| y = 3x2 − 1 |
|
| y = −3x2 + 2x |
|
Как построить график квадратичной функции
Запомните!
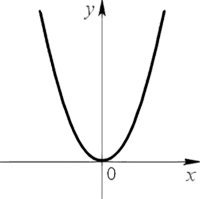
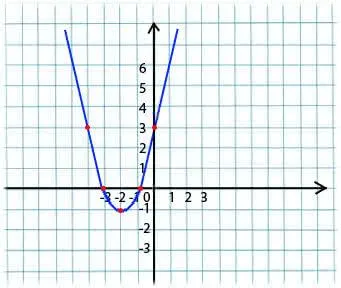
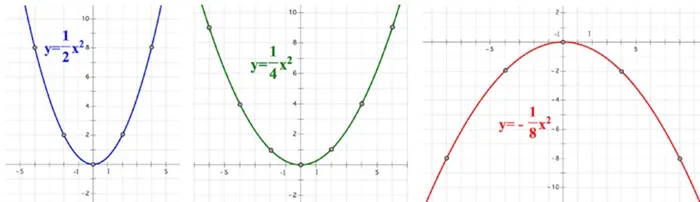
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
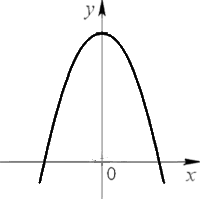
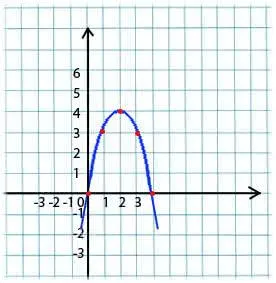
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции «y = x2 −7x + 10».
- Направление ветвей параболы
Запомните!
Если «a > 0», то ветви направлены вверх.
Если «a < 0», то ветви направлены вниз.
В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
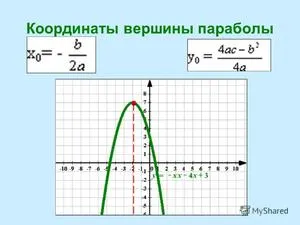
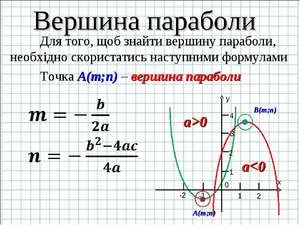
- Координаты вершины параболы
Запомните!
Чтобы найти «x0»
(координата вершины по оси «Ox»)
нужно использовать формулу:Найдем «x0» для нашей функции «y = x2 −7x + 10».
Теперь нам нужно найти «y0»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x0» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».y0(3,5) =
(3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =−12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy». - Нули функции
Для начала давайте разберемся, что называют нулями функции.
Запомните!
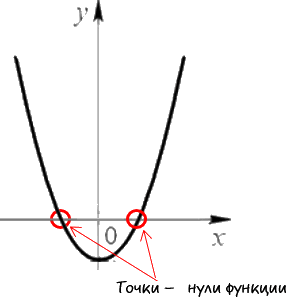
Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».Подставим в заданную функцию «y = x2 −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .0 = x2 −7x + 10
x2 −7x + 10 = 0x1;2 =
7 ±
√49 − 4 · 1 · 102 · 1 x1;2 =
x1;2 =
x1 = x2 =
x1 = x2 =
x1 = 5 x2 = 2
Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.
- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.x 1 3 4 6 y Для каждого выбранного значения «x»
рассчитаем «y».- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
4 -
y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 =
−2 -
y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 =
−2 -
y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 =
4
Запишем полученные результаты в таблицу.
x 1 3 4 6 y 4 −2 −2 4 Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график.
На забудьте после построения подписать график функции. - y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.
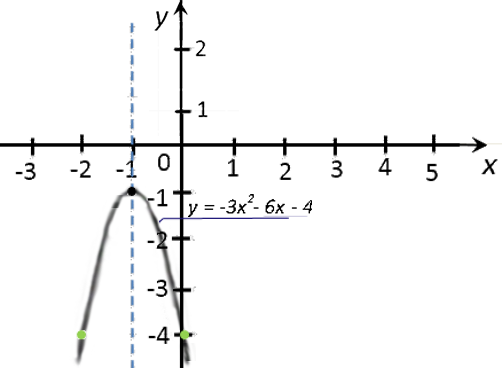
Пусть требуется построить график функции
«y = −3x2 − 6x − 4».
- Направление ветвей параболы
- Координаты вершины параболы
x0 =
x0 = == −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 =
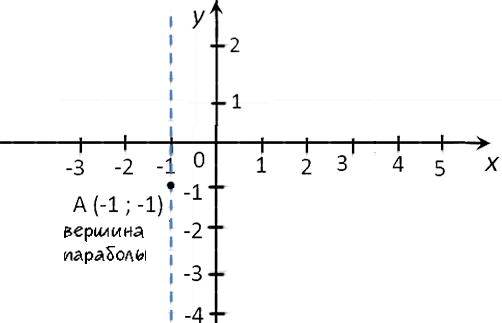
−3 · 1 + 6 − 4 = −1(·) A (−1; −1)
— вершина параболы.
- Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ±
√62 − 4 · 3 · 42 · 1 x1;2 =
x1;2 =
Ответ: нет действительных корней.Так как корней нет, значит, график функции не пересекает ось
«Ox». - Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x2 − 6x − 4».- y(−3) = −3 · (−3)2 − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13 -
y(−2) = −3 · (−2)2 − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4 -
y(0) = −3 · 02 − 6 · 0 − 4
= −4 -
y(1) = −3 · 12 − 6 · 1 − 4
= −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13 - y(−3) = −3 · (−3)2 − 6 · (−3) − 4
«a = −3» — ветви параболы направлены вниз.
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
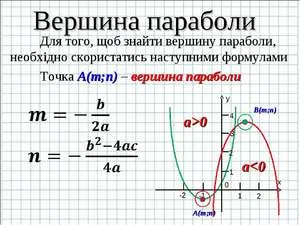
Координаты вершины параболы онлайн
Парабола – это функция, заданная уравнением:
Её график имеет следующий вид:
Причем, в зависимости от знака коэффициента , ветви параболы направлены вверх (если ) или вниз (если ).
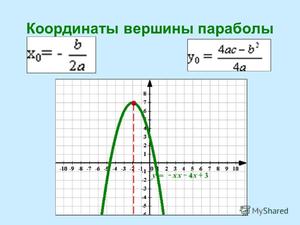
В школьном курсе алгебры возникает задача нахождения координат вершины параболы. Их можно найти по формулам:
Вершина параболы, отмечена оранжевой точкой на приведённом выше графике.
Наш онлайн калькулятор позволяет найти координаты вершины параболы с описанием подробного хода решения на русском языке. Для работы калькулятора, необходимо ввести уравнение параболы и указать её переменную. Уравнение параболы можно вводить в различных форматах, а коэффициентами могут быть не только числа или дроби, но и параметры. Нажмите на кнопку “Примеры”, расположенную на панели калькулятора, чтобы посмотреть различные форматы ввода.
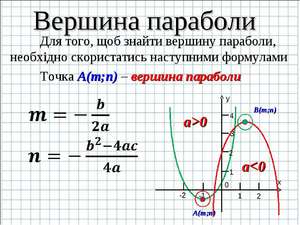
Как найти вершину параболы: три формулы
Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.
Нахождение вершины параболы: способы, примеры, советы
График функции y = ax 2 + bx + c, где a — первый коэффициент, b – второй коэффициент, c – свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.
У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.
Первый способ
Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.
Например, y =x 2 –8 x +15;
находим первый, второй коэффициенты и свободный член;
подставляем значения a и b в формулу;
вычисляем значения y;
Значит, вершина находится в точке (4;-1).
Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n – корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.
Рассмотрим на примере y =x 2 –6x+5
1) Приравниваем к нулю:
2) Находим дискриминант, используя формулу: D = b 2 –4 ac:
3) Находим корни уравнения по формуле (-b±√ D)/2a:
- 1 – первый корень;
- 5 – второй корень.
Второй способ
Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.
1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.
2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.
У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:
3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.
4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).
Третий способ
Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:
1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.
Рассмотрим этот способ подробнее.
Дана функция y = 4x²+16x-17;
- Записываем производную и приравниваем к нулю.
f'(x) = (4x²+16x-17)’ = 8x+16 =0
Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).
1) Строим таблицу
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Советы
Правильно находите коэффициенты.
Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.
Делайте всё поэтапно. Следуйте алгоритму.
Обратите ваше внимание на то, что:
- Нужно проверять правильно ли ваше решение.
- Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.
Видео
Это видео поможет вам научиться находить вершину параболы
Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?
Урок: как построить параболу или квадратичную функцию?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Парабола — это график функции описанный формулой ax 2 +bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:
1 ) Формула параболы y=ax 2 +bx+c,
если а>0 то ветви параболы направленны вверх,
а 2 +bx+c=0;
a) Полное квадратное уравнение имеет вид ax 2 +bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax 2 +bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);
4) Найти несколько дополнительных точек для построения функции.
ПРАКТИЧЕСКАЯ ЧАСТЬ
И так теперь на примере разберем все по действиям:
Пример №1:
y=x 2 +4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x 2 +4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x1=(-4+2)/2=-1
x2=(-4-2)/2=-3 
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2
х -4 -3 -1 0
у 3 0 0 3
Подставляем вместо х в уравнение y=x 2 +4x+3 значения
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2
Пример №2:
y=-x 2 +4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1 2 +4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x 2 +4x=0
Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4. 
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x 2 +4x значения
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2
Пример №3
y=x 2 -4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x 2 -4=0
Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x 2 =4
x1=2
x2=-2
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x 2 -4 значения
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0
Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.
[spoiler title=”источники:”]
http://liveposts.ru/articles/education-articles/matematika/kak-najti-vershinu-paraboly-tri-formuly
http://tutomath.ru/uroki/kak-postroit-parabolu.html
[/spoiler]
Математики рекомендуют использовать значения, полученные при расчете конструкции графа, так как произвольные подстановки x и вычисления значительно снижают скорость вычислений.
Как найти вершину параболы неполного квадратного уравнения
Урок: Как построить притчу или квадратичную функцию?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Притча — это график функции, описываемой видом AX 2 +BX +C = 0. Чтобы построить притчу, необходимо следовать простому алгоритму.
(1) Один из видов притчи — y = ax 2 +bx +c. Если A> 0, то сектор притчи направлен вверх и 2 +Bx +C = 0.
(a) Полное квадратное уравнение имеет вид ax 2 +bx +c = 0 и решается тождественным b) Неполное квадратное уравнение имеет вид ax 2 +bx = 0. Для решения уберите x из скобки, и каждый множитель будет равен 0: ax 2+bx = 0, x(ax+b) = 0, x = 0, ax+b = 0- c) Форма Ax 2 +C = 0. Для решения перенесите незнакомца в одну сторону, а знакомого — в другую. x = ±√(c/a),.
4) Найдите несколько дополнительных точек для планирования функции.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Затем используйте примеры, чтобы проанализировать ситуацию шаг за шагом. Пример №1: y = x 2 +4x +3 c = 3 и притча пересекается при x = 0 y = 3. Ветви притчи смотрят вверх, потому что a = 1 1> 0. a = 1 b = 4 c = 3 x = (-b)2a = (-4)/(2*1) = -2 y = (-2)2 +4*( — 2)+3 = 4- 81 -4ac = 16-12 = 4 x = (-b±√(d))2a x1= (-4+2)2/2 = -1 x2= (-4-2)2 = -3 Возьмем любое место вблизи вершины x = -2
Обменяем y = x 2+4x+3 в уравнении y = (-4)2 +4*(-4)+3 = 16-16+3 = 3 y = (-3)2 +4*(-3)+3 = 9-12+3 = 0 y = (-1)2 +4*(- 1)+3 = 1-4+3 = 0 y = (0)2+4*(0)+3 = 0 -0+3 = 3 Из значений функции метафорой является линия x = -2 мы видим, что она симметрична
Пример 2: y = -x 2 +4x c = 0 Следовательно, притча пересекается в точке x = 0 y = 0. Ветви притчи выглядят как a = -1 -1 2 +4*2 = -4 +8 = 4 Частное уравнение вида Ax 2 +Bx = 0. Чтобы решить ее, выведите x из скобки и приравняйте каждую силу к 0. x (-x+4) = 0, x = 0, x = 4. Возьмите любую точку около верхней x = 2 x 0 1 3 3 3 3 3 0 y = 0 2 +4*0 = 0 y = — (1)2 +4*1 = -1 +4 = 3 y = — (3)2 +4*3 = -9 +13 = 3 y = — (4) 2 +4*4 = -16 +16 = 0 Уравнение y = -x 2 +4* 4 = -16+16 = 0 Притча симметрична относительно прямой x = 2, что видно из значения функции.
Пример 3 y = x 2 -4 c = 4 Следовательно, притча пересекается в точке x = 0 y = 4. Сектора притчи показаны выше как a = 1 1> 0. a = 1 b = 0 c = -4 x = (-b)/2a = 0/(2*(1)) = 0 y = (0)2 -4 = -4 В верхней части находятся корни уравнения (0; -4 ) x 2 -4 = 0 частное уравнение вида ax 2 +c = 0. Чтобы решить ее, переместите незнакомца на одну сторону, а знакомого — на другую. x = ±√(c/a)x 2 = 4 x1= 2 x2= -2
Возьмем любую точку около верхней x = 0 x -2 -1 1 2 y 0 -3 -3 0 Возьмем любую точку около y = (-2) 2 -4 уравнение y = x 2 -4 = 4-4 = 0 y = (-1) 2 -4 = 1-4 = -3 y = 1 2 -4 = 1-4 = -3 y = 2 2 -4 = 4-4 = 0 Убедитесь, что притча симметрична прямой x = 0 от значения функции Обратите внимание, что функция y = ax 2 + bx = -3
Нахождение вершины параболы: способы, примеры, советы
График функции y = ax 2 + bx + c. Где a — первый коэффициент, b — второй коэффициент, а c — свободный термин, называемый притчей. Обратите внимание, однако, на тот факт, что a ≠ 0.
Каждая точка в притче имеет симметричную ей точку, кроме одной, которая называется верхней точкой. Чтобы найти верхнюю точку, необходимо установить точку на графике. Точка графика — это определенная координата оси абсцисс и вертикальной координатной оси. (x; y). Узнайте, как найти свои любимые номера.
Первый способ
Если вы хотите узнать, как правильно вычислить координаты пиков, проверьте вид x0 = -b/2a. Замените это число в функции, чтобы получить y0.
Найдите первый и второй коэффициенты и свободные члены.
Замените значения a и b в формуле и
Это означает, что верхняя часть находится в точке (4; -1).
Ветви притчи симметричны относительно оси симметрии, проходящей через верхнюю часть притчи. Зная корни уравнения, легко вычислить удаленную верхнюю позицию притчи. Предположим, что k и n — корни квадратного уравнения. Тогда точка x0 равна k и n и может быть вычислена по виду x0 = (k + n)/2.
Например, рассмотрим y = x 2 -6x+5
2) Найдите различие, используя вид: d = b 2 -4 ac:.
3) Используйте вид (-b ± √d)/2a для нахождения корней уравнения.
Второй способ
Прибавление к полному квадрату — лучший способ определить, где находится вершина. Используя этот метод, можно одновременно вычислить x и y, не заменяя исходный пример на x. Рассмотрим этот метод на примере функции: y = x 2 +8 x +10.
1. сначала выражение должно быть приравнено к переменной, равной 0. Затем, чтобы переместить c вправо с противоположным знаком, мы имеем выражение x 2 + 8x = -10. 2.
2. нам нужно создать идеальный квадрат с левой стороны. Для этого измерьте (b/2)2 и увеличьте обе части уравнения до полученного результата. В этом случае замените b на 8.
Вы получите 16. Затем добавьте это число к обеим частям уравнения.
3. мы видим, что полученное уравнение является совершенным квадратом. Его можно выразить в виде: (x + 4)2 = 6.
Используйте это уравнение, чтобы найти координаты вершины притчи. Чтобы вычислить x, мы приравниваем 0 к 0. Таким образом, x = 4. Координата y равна координате справа, y = 6. Вершина притчи в этом уравнении — (-4, 6).
Третий способ
Если вы знаете, что такое деривативы, для вас есть другой человек. Независимо от того, где находится «угол» притчи, ее вершина — это крайняя точка. В этом методе необходимо применить следующий алгоритм
1. найдите первую производную, используя вид f ‘(x) = (ax² + bx + c)’ = 2ax + b.
2. выровнять производные по 0. В итоге получается 0 = 2ax + b. Отсюда вы можете найти то, что нас интересует.
Для получения дополнительной информации ознакомьтесь с этим методом.
Построение параболы
Самой сложной частью построения является нахождение правильной точки функции. Для детальной структуры необходимо рассчитать 5-7 пунктов (достаточно для школьного урока). Для этого выберите значение x и замените его функцией. Результатом вычисления является количество точек на оси линии. Затем нанесите точки на координатный уровень. В результате вы получаете притчу.
Давайте рассмотрим подробнее, как найти точки интереса. Например, функция y = -x 2 +11 x -24 имеет вид (5,5; -6,25).
Из-за осевой симметрии притчи можно измерить только значения справа или слева от вершины. Это удобнее, так как желательно измерять цену, наиболее близкую к 0. В нашем случае эти значения равны 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Если функция представлена в виде неполного квадрата, то к обеим частям уравнения нужно прибавить или вычесть одно и то же число. Используя этот метод, можно одновременно рассчитать значения x и y. Алгоритм нахождения вершины функции y=x 2 + 4x+2 следующий.
Нахождение вершины параболы: способы, примеры, советы
График функции y=ax 2 + bx + c. Где a — первый коэффициент, b — второй коэффициент и c — свободный член, называется параболой. Заметим, однако, что a ≠ 0.
Каждая точка в притче имеет симметричную ей точку, кроме одной, которая называется верхней точкой. Чтобы найти верхнюю точку, необходимо установить точку на графике. Точка графика — это определенная координата оси абсцисс и вертикальной координатной оси. (x; y). Узнайте, как найти свои любимые номера.
Первый способ
Если вы хотите узнать, как правильно вычислить координаты пиков, проверьте вид x0 = -b/2a. Замените это число в функции, чтобы получить y0.
Найдите первый и второй коэффициенты и свободные члены.
Замените значения a и b в формуле и
Это означает, что верхняя часть находится в точке (4; -1).
Ветви параболы симметричны относительно оси симметрии, проходящей через вершину параболы. Когда корни уравнения известны, можно легко вычислить дальнее положение вершины параболы. Предположим, что k и n — корни квадратного уравнения. Тогда точка x0 равна k и n и может быть вычислена по уравнению x0 = (k + n)/2.
Например, рассмотрим y = x 2 -6x+5
2) Найдите различие, используя вид: d = b 2 -4 ac:.
3) Используйте вид (-b ± √d)/2a для нахождения корней уравнения.
Второй способ
Прибавление к полному квадрату — лучший способ определить, где находится вершина. Используя этот метод, можно одновременно вычислить x и y, не заменяя исходный пример на x. Рассмотрим этот метод на примере функции: y = x 2 +8 x +10.
1. сначала выражение должно быть приравнено к переменной, равной 0. Затем, чтобы переместить c вправо с противоположным знаком, мы имеем выражение x 2 + 8x = -10. 2.
2. нам нужно создать идеальный квадрат с левой стороны. Для этого измерьте (b/2)2 и увеличьте обе части уравнения до полученного результата. В этом случае замените b на 8.
Вы получите 16. Затем добавьте это число к обеим частям уравнения.
3. мы видим, что полученное уравнение является совершенным квадратом. Его можно выразить в виде: (x + 4)2 = 6.
Используйте это уравнение, чтобы найти координаты вершины притчи. Чтобы вычислить x, мы приравниваем 0 к 0. Таким образом, x = 4. Координата y равна координате справа, y = 6. Вершина притчи в этом уравнении — (-4, 6).
Третий способ
Если вы знаете, что такое деривативы, для вас есть другой человек. Независимо от того, где находится «угол» притчи, ее вершина — это крайняя точка. В этом методе необходимо применить следующий алгоритм
1. найдите первую производную формулы f'(x) = (ax²+ bx + c)’ = 2ax+b
2. выровнять производные по 0. В итоге получается 0 = 2ax + b. Отсюда вы можете найти то, что нас интересует.
Для получения дополнительной информации ознакомьтесь с этим методом.
Построение параболы
Самой сложной частью построения является нахождение правильной точки функции. Для детальной структуры необходимо рассчитать 5-7 пунктов (достаточно для школьного урока). Для этого выберите значение x и замените его функцией. Результатом вычисления является количество точек на оси линии. Затем нанесите точки на координатный уровень. В результате вы получаете притчу.
Давайте рассмотрим подробнее, как найти точки интереса. Например, функция y = -x 2 +11 x -24 имеет вид (5,5; -6,25).
Из-за осевой симметрии притчи можно измерить только значения справа или слева от вершины. Это удобнее, так как желательно измерять цену, наиболее близкую к 0. В нашем случае эти значения равны 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Советы
Найдите правильную цену.
Перечислите промежуточные расчеты на бумаге. Это не только облегчит поиск вершины, но и поможет вам заметить свои ошибки.
Делайте все постепенно. Следуйте алгоритму.
Пожалуйста, обратите внимание:
- Нужно проверять правильно ли ваше решение.
- Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.
Функция — это (уникальное!) множество функций, где каждому элементу множества (аргументу) ставится в соответствие (уникальный!) элемент другого множества (множество значений функции). Правило заключается в том, что элемент присваивается элементу.
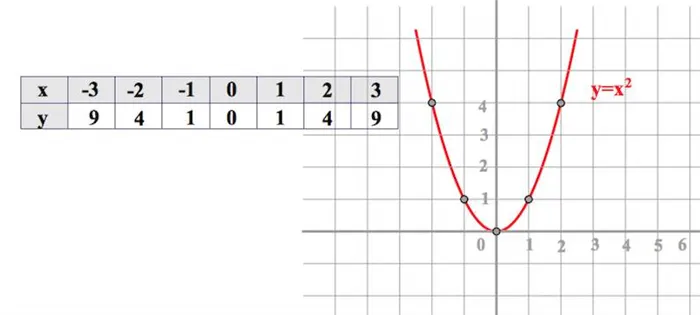
Квадратичная функция
Чтобы построить его, заполните таблицу, заменив значение x в выражении.
Отметьте точки (0; 0), (1; 1), (-1; 1) и т.д. Чем меньше уровень координат (чем меньше значение, в данном случае шаг 1) и чем больше значений x вы получите, тем более гладкой будет кривая), получите притчу.
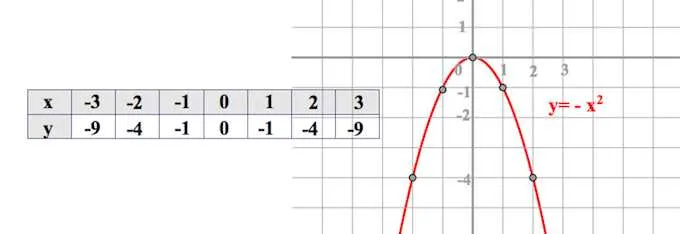
Взяв случай, т.е. даже при наличии симметрии (x), легко убедиться, что симметрия существует. Это легко проверить, заполнив соответствующие таблицы.
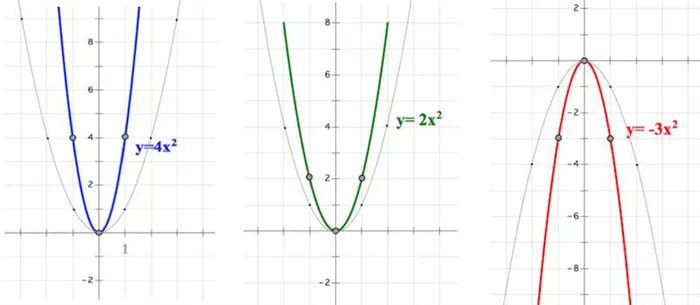
II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ
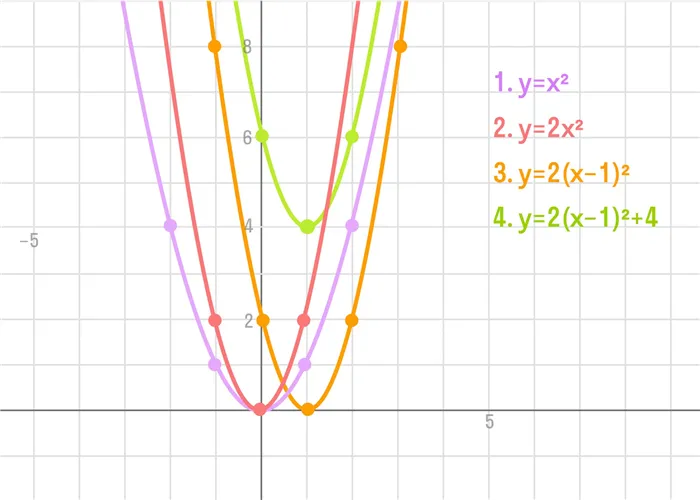
Что происходит, когда мы берем? Как меняется поведение в притче? Притча меняет форму и «теряет вес» по отношению к притче (не верите мне — заполните соответствующую таблицу и убедитесь сами):.
На первом рисунке (см. выше) хорошо видно, что точки (-1; 1) из таблицы притчи (1; 1) преобразуются в точки (1; 4) и (1; -4). Одинаковое значение, придаваемое каждому пункту, умножалось на 4. Это происходит для всех значимых точек в исходной таблице. Аналогично, рассмотрим фотографии 2 и 3.
Притча была бы «шире», чем даже если бы.
1) Сигнальные знаки отвечают за направление ветки. Если ветви направлены вверх, если вниз.
(2) Абсолютное значение коэффициента (модуля) показывает, будет ли притча «расширяться» или «сужаться». Чем он больше, тем длиннее притча, чем меньше | a |, тем шире притча.
III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»
Вот игра, с которой вас можно познакомить (т.е. где посмотреть дело), рассмотрим притчу о форме. Нетрудно сделать вывод, что притча движется вверх и вниз вдоль оси (вы всегда можете обратиться к таблице).
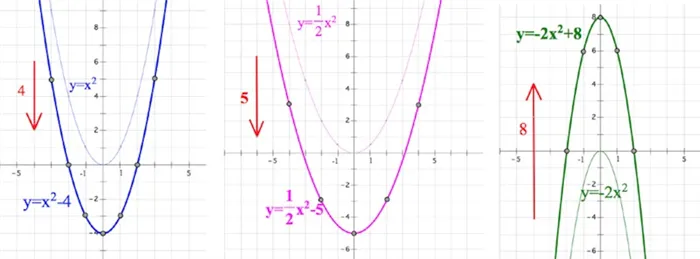
IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»
Когда притча «сбегает» с оси и в итоге «проходит» по всему уровню координат? Когда она перестает быть равной.
Здесь нам необходим тип расчета вершины для построения притчи.
Таким образом, в этой точке (как в новой системе координат (0; 0)) мы строим притчу, которая уже находится в нашей власти. Если мы имеем дело, например, с отрезком сверху вправо и один к одному — полученная точка является нашей точкой (так же как шаг влево и шаг вверх является нашей точкой) — если мы имеем дело, например, с отрезком сверху вправо и два вверх Например.
Нахождение экстремальных точек является важным шагом в решении многих практических задач. Конечно, можно открыть специальный электронный калькулятор, но предпочтительнее уметь делать это самостоятельно.
Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
Уравнение квадратичной функции можно записать в виде y = a(x -x -x -x -x -x -x -x -x -x -x -x -x -x -x -x -x -x -x).0) + y0где x0, y0 — Это координаты вершины притчи.
Координаты вершины — (x₀;y₀). В уравнении квадратичной функции y = 2x 2 + 3x -5 второй коэффициент является иго, если a = 1.
Рассмотрим такой пример: y = 2 * (x -1)2 + 4.
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить график функции y = x 2 ,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
Составьте график притчи для каждого случая.
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x-2) x (x + 1).
Этот тип функции позволяет быстро найти нулевую точку функции.
(x-2) x (x + 1) = 0, т.е. x₁ = 2 и x₂ = -1.
Определите координаты вершин параболы.
Найдите точку пересечения осей OY.
c = ab = (-2) x (1) = -2, что симметрично относительно оси симметрии параболы.
Отметьте эти точки на координатной плоскости и соедините их прямыми линиями.
Загрузить PDF
Загрузить PDF
В дифференциальном исчислении точка перегиба – эта точка кривой, в которой ее кривизна меняет знак (с плюса на минус или с минуса на плюс). Это понятие используется в машиностроении, экономике и статистике для определения существенных изменений в данных.
-
1
Определение вогнутой функции. Середина любой хорды (отрезок, соединяющий две точки) графика вогнутой функции лежит либо под графиком, либо на нем.
-
2
Определение выпуклой функции. Середина любой хорды (отрезок, соединяющий две точки) графика выпуклой функции лежит либо над графиком, либо на нем.
-
3
Определение корней функции. Корень функции – это такое значение переменной «х», при котором у = 0.
- При построении графика функции корни – это точки, в которых график пересекает ось Х.
Реклама
-
1
Найдите первую производную функции. Посмотрите правила дифференцирования в учебнике; вы должны научиться брать первые производные, и только потом переходить к более сложным вычислениям. Первые производные обозначаются как f ‘(х). Для выражений вида ax^p + bx^(p−1) + cx + d первая производная имеет вид: apx^(p−1) + b(p − 1)x^(p−2) + c.
- Например, найдите точки перегиба функции f(х) = х^3 +2х -1. Первая производная этой функции имеет вид:
f ′(x) = (x^3 + 2x − 1)′ = (x^3)′ + (2x)′ − (1)′ = 3x^2 + 2 + 0 = 3×2 + 2
- Например, найдите точки перегиба функции f(х) = х^3 +2х -1. Первая производная этой функции имеет вид:
-
2
Найдите вторую производную функции. Вторая производная – это производная от первой производной исходной функции. Вторая производная обозначается как f ′′(x).
- В приведенном выше примере вторая производная имеет вид:
f ′′(x) = (3×2 + 2)′ = 2 × 3 × x + 0 = 6x
- В приведенном выше примере вторая производная имеет вид:
-
3
Приравняйте вторую производную к нулю и решите полученное уравнение. Полученный результат будет предполагаемой точкой перегиба.
- В приведенном выше примере ваш расчет выглядит следующим образом:
f ′′(x) = 0
6x = 0
x=0
- В приведенном выше примере ваш расчет выглядит следующим образом:
-
4
Найдите третью производную функции. Чтобы убедиться, что полученный результат на самом деле является точкой перегиба, найдите третью производную, которая является производной от второй производной исходной функции. Третья производная обозначается как f ′′′(x).
- В приведенном выше примере третья производная имеет вид:
f ′′′(x) = (6x)′ = 6
Реклама
- В приведенном выше примере третья производная имеет вид:
-
1
Проверьте третью производную. Стандартное правило оценки предполагаемой точки перегиба: если третья производная не равна нулю (то есть f ′′′(x) ≠ 0), то предполагаемая точка перегиба является настоящей точкой перегиба. Проверьте третью производную; если она не равна нулю, то вы нашли настоящую точку перегиба.
- В приведенном выше примере третья производная равна 6, а не 0. Поэтому вы нашли настоящую точку перегиба.
-
2
Найдите координаты точки перегиба. Координаты точки перегиба обозначаются как (x,f(x)), где х – значение независимой переменной «х» в точке перегиба, f(х) – значение зависимой переменной «у» в точке перегиба.
- В приведенном выше примере при приравнивании второй производной к нулю вы нашли, что х = 0. Таким образом, чтобы определить координаты точки перегиба, найдите f(0). Ваш расчет выглядит следующим образом:
f(0) = 0^3 +2×0−1 = −1.
- В приведенном выше примере при приравнивании второй производной к нулю вы нашли, что х = 0. Таким образом, чтобы определить координаты точки перегиба, найдите f(0). Ваш расчет выглядит следующим образом:
-
3
Запишите координаты точки перегиба. Координаты точки перегиба – это найденные значения «х» и f(x).
- В приведенном выше примере точка перегиба – это точка с координатами (0, -1).
Реклама
Советы
- Первая производная от свободного члена (простого числа) всегда равна нулю.
Реклама
Об этой статье
Эту страницу просматривали 21 934 раза.
Была ли эта статья полезной?
Точки пересечения графиков функций
В алгебре и начале анализа можно встретить множество задач на поиск точек пересечения графиков функций с помощью их построения или другими методами. Благодаря определенному алгоритму действий, найти ответ достаточно просто. В большинстве случаев решение заключается в определении корней различного вида уравнений.
График функции (y = f(x)) является множеством точек ((x; y)), координаты которых связаны соотношением (y = f(x).)
Равенство (y = f(x)) называют уравнением данного графика. Таким образом, график функции представляет собой множество точек (x; y), где x — является аргументом, а y — определяется как значение функции, соответствующее данному аргументу.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В том случае, когда графики пересекаются в какой-то точке, можно сделать вывод о существовании общего решения системы уравнений. Определить координаты точки можно с помощью графического или аналитического метода. В первом случае требуется построить график уравнения с переменной. Аналитический метод поиска координат точек, в которых графики функций пересекаются, подразумевает решение уравнения, а найденные корни и являются искомыми точками.
Как найти координаты, примеры решения
Существует несколько способов решения подобных задач:
- Поиск точек пересечения графиков функций заключается в приравнивании обеих функций друг к другу. При этом все члены с х переносят в левую сторону, а оставшиеся – в правую. Затем остается найти корни уравнения, которое получилось после преобразований.
- Второй метод состоит в записи системы уравнения для ее последующего решения с помощью подстановки одной функции в другую.
- Третий способ подразумевает построение графиков функций, чтобы определить точки их пересечения визуально.
В качестве примера можно рассмотреть две линейные функции:
(f(x) = k_1 x+m_1)
(g(x) = k_2 x + m_2)
Данные функции являются прямыми. Их можно графически изобразить, если принять какие-либо два значения (x_1) и (x_2) и найти (f(x_1)) и ((x_2)). Далее действия необходимо повторить с функцией (g(x)). Затем достаточно легко определить визуально координаты точки пересечения рассматриваемых функций.
Важно отметить, что для линейных функций характерна лишь одна точка пересечения только в том случае, когда (k_1 neq k_2). В противном случае (k_1=k_2), а функции будут параллельными друг другу, в связи с тем, что k является коэффициентом угла наклона. При( k_1 neq k_2) и (m_1=m_2) точка пересечения будет соответствовать (M(0;m)). Данная закономерность упрощает решение многих подобных задач.
Задача № 1
Имеются функции: (f(x) = 2x-5)
(g(x)=x+3)
Требуется определить координаты точки, в которой пересекаются графики рассматриваемых функций.
Решение
В первую очередь стоит отметить, что функции являются линейными. Важно обратить внимание на коэффициент угла наклона рассматриваемых функций:
(k_1 = 2)
(k_2 = 1)
Заметим, что:
(k_1 neq k_2)
По этой причине имеется лишь одна точка пересечения графиков функций. Определить ее можно путем решения уравнения:
(f(x)=g(x))
(2x-5 = x+3)
Необходимо перенести члены с x в левую часть, а остальные – в правую:
(2x – x = 3+5)
(x = 8)
В результате удалось найти x=8, что соответствует абсциссе точки пересечения графиков. Требуется определить ординату y с помощью подстановки x = 8 в любое из уравнений – в (f(x)), либо в (g(x)):
(f(8) = 2cdot 8 – 5 = 16 – 5 = 11)
Таким образом, M (8;11) – представляет собой точку, в которой пересекаются графики пары линейных функций.
Ответ: M (8;11)
Задача № 2
Записаны две функции: (f(x)=2x-1)
(g(x) = 2x-4.)
Необходимо определить точки, в которых графики рассматриваемых функций пересекаются.
Решение
Угловые коэффициенты:
(k_1 = k_2 = 2)
Таким образом, линейные функции параллельны между собой, что объясняет отсутствие точек пересечения их графиков.
Ответ: графики функций параллельны, точки пересечения отсутствуют.
Задача № 3
Требуется определить координаты точки, в которой пересекаются графики следующих функций: (f(x)=x^2-2x+1)
(g(x)=x^2+1)
Решение
В данном случае функции являются нелинейными. Поэтому алгоритм решения задачи будет несколько отличаться от предыдущих примеров. В первую очередь следует приравнять уравнения:
(x^2-2x+1=x^2+1)
Далее необходимо разнести в разные стороны уравнения члены с x и без него:
(x^2-2x-x^2=1-1)
(-2x=0)
(x=0)
Таким образом, будет определена абсцисса искомой точки. Затем необходимо найти ординату у. Для этого нужно подставить (x = 0) в какое-либо из двух начальных уравнений. К примеру:
(f(0)=0^2-2cdot 0 + 1 = 1)
M (0;1) является точкой, в которой пересекаются графики функций.
Ответ: M (0;1)
Приравнивание функций друг к другу и нахождение корней
Выяснить, имеют ли точки пересечения графики функций, можно путем сравнения соответствующих тождеств и решения уравнения. Однако при этом допускается получение различных равенств с неизвестными. Тогда целесообразно воспользоваться специальными методиками.
Когда уравнение относится к первой степени или является линейным, решение получить достаточно просто. Метод заключается в переносе переменных величин в одну часть уравнения, а известных – в другую. Алгоритм действий:
- раскрытие скобок, приведение подобных коэффициентов;
- перенос членов с неизвестными в одну сторону, а с известными – в другую;
- математические преобразования;
- определение корня.
Квадратные уравнения решают с помощью одного из способов:
- разложение на множители;
- выделение полного квадрата;
- поиск дискриминанта;
- теорема Виета.
В первом случае представляется возможным понизить степень при неизвестной величине. Второй метод заключается в выделении квадрата по одной из формул сокращенного умножения. Каждая из этих методик реализуема при наличии знаний соответствующих тождеств, в том числе правил разложения на множители.
Третий способ состоит в поиске корней через дискриминант (Д), который является дополнительным параметром, позволяющим сразу решить задачу. Дискриминант определяется с помощью формулы:
((-S)^2-4PU)
В том случае, когда Д>0, переменная может иметь пару значений, которые превращают равенство в справедливое тождество. Если Д=0, то корень является единственным. Когда Д<0, искомое тождество с неизвестными не имеет решений.
Квадратные уравнения решают таким образом:
- выполнение необходимых алгебраических преобразований, в том числе раскрытие скобок и приведение подобных слагаемых;
- выбор наиболее оптимального способа решения и его реализация;
- проверка корней с помощью их подстановки в начальное выражение.
Примечание
Распространенной ошибкой является пренебрежение проверкой результатов решения. Некорректные действия могут привести к образованию ложных корней.
Существует несколько методик решения тождеств кубического и биквадратного типов:
- понижение степени, то есть разложение на множители;
- замена переменной.
Первый вариант решения подразумевает выполнение преобразований для последующего применения одной из формул сокращенного умножения. Такой способ применяют нечасто. Второй способ состоит в том, что при решении необходимо ввести переменную с более низкой степенью, которая упрощает выражение. Порядок действий при этом следующий:
- выполнение математических преобразований;
- выражение переменной через другую;
- решение квадратного или линейного уравнения;
- подстановка промежуточных корней, которые получилось найти на третьем шаге, во второй;
- вычисление искомых корней;
- проверка;
- исключение ложных решений;
- запись ответа.
Путем составления системы уравнений
Данный метод определения точек пересечения графиков функций предполагает запись системы уравнения. К примеру:
Решение системы уравнений представляет собой пару чисел (х, у), являющуюся одновременно решением для первого и второго уравнения системы. Решить систему уравнений – значит, отыскать все ее решения, либо установить их отсутствие.
Порядок действий при решении системы уравнений можно рассмотреть на примере:
Решение будет иметь следующий вид:
Данные уравнения являются линейными, поэтому график каждого из них представляет собой прямую. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и является решением системы уравнений.
Решение системы представляет сбой единственную пару чисел:
Если подставить данные числа в любое из уравнений, то получится справедливое равенство. Таким образом, имеется единственное решение линейной системы. Можно записать отчет: (-1;0).
В процессе решения линейной системы можно столкнуться с разными ситуациями:
- система обладает единственным решением, прямые пересекаются;
- решения системы отсутствуют. прямые параллельны;
- система обладает бесчисленным множеством решений, прямые совпадают.
При рассмотрении частного случая системы p(x; y) и q(x; y) являются линейными выражениями от x и y.
В задачах нередко требуется решить нелинейную систему уравнений. К примеру, необходимо решить следующую систему:
Решение имеет следующий вид:
График первого уравнения будет иметь вид прямой, а второго – являться окружностью. Можно построить первый график по точкам:
Центр окружности в точке О(0; 0), радиус равен 1.
Графики пересекаются в точке А(0; 1) и в точке В(-1; 0).
Ответ: (0; 1); (-1; 0).
Можно решить систему графическим способом:
В первую очередь необходимо построить график первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 2. График второго уравнения является параболой, которая смещена относительно начала координат на 2 вверх, то есть ее вершина – точка (0; 2).
Графики обладают одной общей точкой А(0; 2). Данная точка является решением системы. Если подставить два числа в уравнение, можно проверить корректность ответа и записать его. Ответ: (0; 2).
В качестве еще одного примера можно решить следующую систему:
Первым шагом является построение графика первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 1.
Далее необходимо построить график функции:
График будет являться ломанной:
Далее следует сместить ее на 1 вниз по оси oy. В результате получится график функции:
При помещении обоих графиков в одну систему координат получится следующая ситуация:
Таким образом, получились три точки пересечения: А(1; 0), т. В(-1; 0), т. С(0; -1)
Нахождение через графическое построений функций
Любой определенный график задают с помощью соответствующей функции. Найти точки, в которых пересекаются графики, можно путем решения уравнения, имеющего вид:
(f1(x)=f2(x))
Решение данного уравнения будет являться искомой точкой.
Построить график можно с помощью бумаги и ручки. В процессе необходимо обратить внимание на то, что количество точек пересечения пары графиков определяется видом функции. Линейные функции обладают лишь одной точкой пересечения, линейная и квадратная – двумя, квадратные – двумя, либо четырьмя.
В общем случае двух линейных функций можно предположить, что:
(y1=k1x+b1)
(y2=k2x+b2)
Для поиска точки пересечения графиков необходимо решить уравнение:
(y1=y2 или k1x+b1=k2x+b2)
После преобразований получится, что:
(k1x-k2x=b2-b1.)
Далее нужно выразить x:
(x=(b2-b1)/(k1-k2).)
При известной координате точки по оси абсцисс следует определить координату по оси ординат. Таким образом, можно найти координаты точки пересечения графиков:
(((b2-b1)/(k1-k2); k1(b2-b1)/(k1-k2)+b2))
График функции y = f (х) представляет собой множество точек плоскости, координаты (х, у) которых соответствуют выражению y = f(x). График функции наглядно иллюстрирует поведение и свойства функции. Для построения графика определяют несколько значений довода х и для них рассчитывают соответствующие значения функции y=f(x). Для больше точного и наглядного построения графика следует обнаружить его точки пересечения с осями координат.
С целью определить точку пересечения графика функции с осью y, нужно определить значение функции при х=0, то есть обнаружить f(0). В качестве примера можно рассмотреть график линейной функции, изображенной на рисунке:
В данном случае при х=0 ((y=a*0+b)) функция равна b. Таким образом, график пересекает ось ординат (ось Y) в точке (0,b). Когда пересекается ось абсцисс (ось Х) функция равна 0, то есть (y=f(x)=0). Для того чтобы определить х, следует решить уравнение (f(x)=0). В случае линейной функции получаем уравнение (ax+b=0), откуда и находим (x=-b/a). В результате можно сделать вывод, что ось Х пересекается в точке ((-b/a,0).)
При наличии квадратичной зависимости y от х, уравнение (f(x)=0) обладает двумя корнями. Таким образом, ось абсцисс пересекается два раза. В случае периодической зависимости y от х, например, (y=sin(x)), график функции обладает бесконечным количеством точек пересечения с осью Х. Проверить корректность расчета координат точек, в которых пересекаются графики функций, можно с помощью подстановки найденных значений х в выражение f(x). Значение выражения при любом из вычисленных х должно быть равно 0.