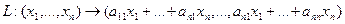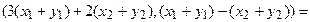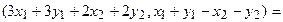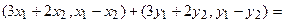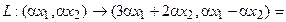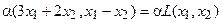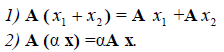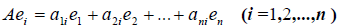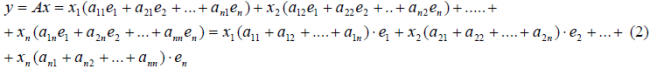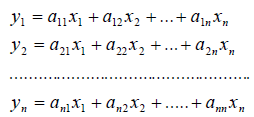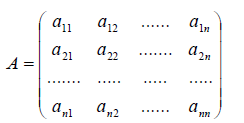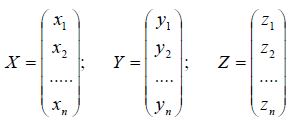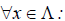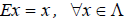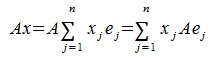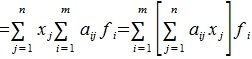def find_mountain(a):
return max(map(max, a))
a = [[1, 3, 1], [3, 2, 5], [2, 2, 2]]
print(find_mountain(a))
понимаю как определить макс. элемент, а как найти его координаты(номер ряда и столбца)
в данном массиве макс. элемент – 5
нужно чтобы вывело кортеж в ответе такой: (1, 2)
задан 23 янв 2021 в 7:11
4
def find_mountain(a):
arr = max(a, key = max)
return a.index(arr), arr.index(max(arr))
ответ дан 23 янв 2021 в 7:25
DanisDanis
19k5 золотых знаков20 серебряных знаков55 бронзовых знаков
можно так:
алгоритм находит ВСЕ максимальные значения (все двумерные координаты максимальных значений)
arr = [[1, 3, 1], [3, 2, 5], [2, 2, 2], [1, 5, 1]]
# найти максимальное значение
max_value = max(max(arr, key=max))
# найти позиции
res = [(obj[0], obj[1].index(max_value)) for obj in enumerate(arr) if max_value in obj[1]]
print(res)
ответ дан 23 янв 2021 в 8:02
ZhiharZhihar
36.8k4 золотых знака25 серебряных знаков65 бронзовых знаков
|
Ychenyi 38 / 39 / 7 Регистрация: 13.11.2020 Сообщений: 678 |
||||
|
1 |
||||
Как найти координаты максимального элемента матрицы?22.01.2021, 23:30. Показов 4035. Ответов 10 Метки нет (Все метки)
понимаю как определить макс. элемент, а как найти его координаты(номер ряда и столбца)
0 |
|
Заклинатель змей 611 / 508 / 213 Регистрация: 30.04.2016 Сообщений: 2,412 |
|
|
22.01.2021, 23:31 |
2 |
|
Ychenyi, цикл по строчкам и внутри этого цикла цикл по элементам
0 |
|
38 / 39 / 7 Регистрация: 13.11.2020 Сообщений: 678 |
|
|
23.01.2021, 10:12 [ТС] |
3 |
|
DobroAlex, пытался но не получается
0 |
|
Gdez 7250 / 4039 / 1779 Регистрация: 27.03.2020 Сообщений: 6,865 |
||||
|
23.01.2021, 10:17 |
4 |
|||
|
РешениеYchenyi,
3 |
|
38 / 39 / 7 Регистрация: 13.11.2020 Сообщений: 678 |
|
|
23.01.2021, 10:30 [ТС] |
5 |
|
Gdez, а почему m равно длине первого списка? По логике же они могут быть разные по длине
1 |
|
Gdez 7250 / 4039 / 1779 Регистрация: 27.03.2020 Сообщений: 6,865 |
||||||||
|
23.01.2021, 11:26 |
6 |
|||||||
|
Ychenyi, вообще, матрица – квадратный массив. Массив – часто прямоугольная структура. А в этом коде можно вместо
Записать
Убрав 3-ю строчку из кода
1 |
|
ioprst 1303 / 843 / 409 Регистрация: 12.03.2018 Сообщений: 2,305 |
||||
|
23.01.2021, 11:46 |
7 |
|||
3 |
|
Ychenyi 38 / 39 / 7 Регистрация: 13.11.2020 Сообщений: 678 |
||||
|
23.01.2021, 11:55 [ТС] |
8 |
|||
|
Gdez, ioprst, оказывается можно было куда проще это сделать
0 |
|
Arsegg 3478 / 2086 / 559 Регистрация: 02.09.2015 Сообщений: 5,332 |
||||
|
23.01.2021, 12:01 |
9 |
|||
/upd Не по теме:
оказывается можно было куда проще это сделать Очень много проходов по матрице. Не очень…
1 |
|
Модератор 35199 / 19415 / 4063 Регистрация: 12.02.2012 Сообщений: 32,435 Записей в блоге: 13 |
|
|
23.01.2021, 12:05 |
10 |
|
Ychenyi, это не сделать проще, а записать. Код Gdez будет работать быстрее (потому, что он проходит матрицу один раз, а твой код пройдет ее дважды
1 |
|
1303 / 843 / 409 Регистрация: 12.03.2018 Сообщений: 2,305 |
|
|
23.01.2021, 12:07 |
11 |
|
Ychenyi, конечно можно
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
23.01.2021, 12:07 |
|
11 |
Содержание
Матрица
Определение, обозначения
Матрица1) – прямоугольная таблица
$$ A=
left(begin{array}{llll}
3 & -7 & dots & sqrt{pi} \
&&& \
C_n^1 & 101.(66) & dots & frac{5}{7} \
dots & & & dots \
aleph_0 & 0 & dots & e
end{array}right) ,
$$
в каждой ячейке которой располагается некоторое число (или, в общем случае, элемент из некоторого множества – лишь бы только были определены те операции, что нам потребуются ниже), называемое элементом матрицы.
Будем обозначать матрицы прописными латинскими буквами $ , A_{},B,dots, {mathfrak A},{mathfrak B},dots $, а – при необходимости – их элементы буквами строчными $ a_{},b,dots,{mathfrak a},{mathfrak b},dots $ Сами таблицы условимся ограничивать скобками – либо круглыми $ ( quad )_{} $, либо квадратными $ [ quad ]_{} $.
В матрице $ A_{} $ естественным образом выделяются строки и столбцы, при этом отсчет строк и столбцов уславливаются вести, начиная от левого верхнего угла матрицы. Упорядоченная пара чисел
(количество строк, количество столбцов)
матрицы называется порядком (или размерностью) матрицы. Так, если матрица имеет $ m_{} $ строк и $ n_{} $ столбцов, то о ней говорят как о матрице порядка $ mathbf m_{} $ на $ mathbf n_{} $, и записывают порядок в виде $ mtimes n_{} $.
Любая $ mtimes n_{} $-матрица содержит всего $ ,mn_{} $ элементов, и каждому из этих элементов можно поставить в соответствие «координаты его местоположения» в матрице, т.е. упорядоченную пару натуральных чисел $ (j,k)_{} $, в которой первое число отвечает за номер строки элемента, а второе — за номер его столбца.
Часто будет возникать необходимость записи матрицы общего вида, т.е. матрицы с элементами, числовые значения которых могут быть переменными. В самом общем случае — когда все элементы матрицы $ A_{} $ могут быть произвольными — будем их записывать в виде $ a_{jk}^{} $ или же, когда необходимо избежать недоразумения, в виде $ a_{j,k}^{} $. Так, $ a_{11}^{} $ означает элемент матрицы $ A_{} $, стоящий в ее левом верхнем углу; $ b_{10,3}^{} $ – элемент матрицы $ B, $, стоящий в $ 10_{} $-й строке и $ 3_{} $-м столбце; $ {mathfrak c}_{m-3,2n-7}^{} $ – элемент матрицы $ {mathfrak C}_{} $, стоящий в $ (m-3)_{} $-й строке и $ (2n-7)_{} $-м столбце. Такая договоренность позволяет записывать компактно матрицы, для элементов которых имеется функциональная зависимость от местоположения в таблице. К примеру, совершенно произвольную $ mtimes n_{} $-матрицу
$$
A=
left( begin{array}{lllll}
a_{11} & a_{12} & a_{13}& dots & a_{1n} \
a_{21} & a_{22} & a_{23}& dots & a_{2n} \
dots & & & & dots \
a_{m1} & a_{m2} & a_{m3}& dots & a_{mn}
end{array}
right)
$$
мы можем записать в виде $ A_{}=left [a_{jk} right ]_{j=1,dots,m atop k=1,dots,n} $.
П
Пример.
$$
A=left [frac{1}{j+k-1}
right ]_{j=1,2,3,4 atop k=1,2,3}
=
left(begin{array}{rrr}
1 & frac{1}{2} & frac{1}{3} \
&& \
frac{1}{2} & frac{1}{3} & frac{1}{4} \
&& \
frac{1}{3} & frac{1}{4} & frac{1}{5} \
&& \
frac{1}{4} & frac{1}{5} & frac{1}{6}
end{array}right)
.
$$
?
Найти развернутое выражение для матриц, представленных в компактной форме
a) $ A_{} =left [ max (j,k) right ]_{j=1,2,3,4 atop k=1,2quad} $ ;
б) $ B_{} =left [ |j-k| right ]_{j=1,2,3 atop k=1,2,3 } $ ;
в) $ C_{}=left [delta_{jk} right ]_{j=1,dots,5 atop k=1,2,3 } $,
где $ delta_{jk}^{} $ означает символ Кронекера.
В принятых обозначениях $ j_{} $-й строкой произвольной матрицы $ A_{} $ будет матрица
$$ A^{[j]}=left(a_{j1},a_{j2},dots,a_{jn} right) , $$
а ее $ k_{} $-м столбцом – матрица
$$
A_{[k]}=left( begin{array}{c} a_{1k} \ a_{2k} \ vdots \ a_{mk} end{array} right) .
$$
Матрицы $ A_{} $ и $ B_{} $ называются равными если равны их порядки и совпадают элементы на соответствующих местах:
$$ A=left[a_{jk} right]_{j=1,dots,m atop k=1,dots,n} ,
B=left[b_{jk} right]_{j=1,dots,m atop k=1,dots,n} ,
$$
$$
quad Rightarrow quad A=B iff a_{jk} =b_{jk} forall jin {1,dots,m },
kin {1,dots,n } .
$$
Матрицы разных порядков не считаются равными.
Еще одно упрощение записи – часто применяемое для матриц заранее не специфицированного порядка – заключается в том, что если некоторый участок матрицы занят равными нулю элементами, то они либо не указываются вовсе, либо вся их совокупность обозначается $ {mathbb O}_{} $.
Матрица, состоящая только из нулей, называется нулевой матрицей соответствующего порядка.
Ее будем записывать в виде $ {mathbb O}_{mtimes n}^{} $.
П
Пример.
$$
left(begin{array}{rrrr}
0 & 0 & 0 & 0 \
0 & 0 & 0 & 0
end{array}right) = {mathbb O}_{2times 4} .
$$
Элементарные операции
умножение на число
Произведением матрицы $ A_{} $ на число (скаляр) $ c_{} $ называется матрица, каждый элемент которой равен произведению соответствующего элемента матрицы $ A_{} $ на число $ c_{} $:
$$
A=left[a_{jk} right ]_{j=1,dots,m atop k=1,dots,n} {color{RubineRed} Rightarrow }
ccdot A = left [ca_{jk} right]_{j=1,dots,m atop k=1,dots,n} .
$$
$$
3cdot
left(begin{array}{rrr}
1& 0 & 1 \
-1 & 1 & 0 \
0 & 1 & 2
end{array}
right) =
left(begin{array}{rrr}
3& 0 & 3 \
-3 & 3 & 0 \
0 & 3 & 6
end{array}
right) , quad
2cdot
left(
begin{array}{r}
1 \ 0 \ -1
end{array}
right) =
.
$$
сложение
Для матриц $ A_{} $ и $ B_{} $ одного порядка их суммой называется матрица, каждый элемент которой равен сумме соответствующих элементов складываемых матриц:
$$A =left[a_{jk} right]_{j=1,dots,m atop k=1,dots,n}, B=left[b_{jk} right]_{j=1,dots,m atop k=1,dots,n} quad{color{RubineRed} Rightarrow } quad A+B = left[a_{jk} + b_{jk} right]_{j=1,dots,m atop k=1,dots,n} , .$$
$$
left(
begin{array}{rrr}
1& -2 & -1 \
2 & -1 & -2 \
1 & 2 & sqrt{3} \
0 & 1 & 7
end{array}
right)
+
left(
begin{array}{rrr}
-1& 3 & 2 \
1 & 0 & 1 \
-1 & -2 & 3 \
-1 & 1 & -5
end{array}
right)=
$$
Т
Теорема. Множество матриц фиксированного порядка $ m times n_{} $ образует линейное пространство относительно двух этих введенных операций.
Будем обозначать это пространство $ mathbb R^{m times n} $ в случае, когда рассматриваются только числа (элементы матрицы и скаляры, на которые допускается их домножение) вещественные, и $ mathbb C^{m times n} $ если рассматриваются и мнимые.
транспонирование
Преобразование матрицы, при котором ее строки становятся столбцами новой матрицы, называется транспонированием матрицы:
$$
left( begin{array}{lllll}
a_{11} & a_{12} & a_{13}& dots & a_{1n} \
a_{21} & a_{22} & a_{23}& dots & a_{2n} \
dots & & & & dots \
a_{m1} & a_{m2} & a_{m3}& dots & a_{mn}
end{array}
right)^{top}=
left(begin{array}{llll}
a_{11} & a_{21} & dots & a_{m1} \
a_{12} & a_{22} & dots & a_{m2} \
a_{13} & a_{23} & dots & a_{m3} \
vdots & & & vdots \
a_{1n} & a_{2n} & dots & a_{mn}
end{array}
right)
$$
В компактном виде:
$$
left( left[a_{jk} right]_{j=1,dots,m atop k=1,dots,n} right)^{top}=left[a_{kj} right]_{k=1,dots,n atop j=1,dots,m}
,
$$
а в схематичном:

§
В литературе для операции транспонирования используются также обозначения $ A^{t}=mbox{ }^{t}A=A^{prime}=A^{ast} $.
?
Показать справедливость следующих свойств операции транспонирования:
а) $ left( A^{top} right)^{top} = A $;
б) $ (A+B)^{top}=A^{top} + B^{top} $;
в) $ (cA)^{top}=c A^{top} $, где $ c_{} $ — число;
г) $ (AB)^{top}= B^{top} A^{top} $
при условии, что все операции в левых частях равенств определены (операция умножения матриц определяется
☟
НИЖЕ ).
конкатенация
Для матриц $ A_{} $ и $ B_{} $ с одинаковым количеством строк можно определить операцию $ Amid B_{} $ (будем также использовать обозначение $ [A mid B] $) конкатенации2) матриц:
$$ A=
left(begin{array}{llll}
a_{11} & a_{12} & dots & a_{1n} \
a_{21} & a_{22} & dots & a_{2n} \
dots & & & dots \
a_{m1} & a_{m2} & dots & a_{mn}
end{array}right) ,
B=
left(begin{array}{llll}
b_{11} & b_{12} & dots & b_{1k} \
b_{21} & b_{22} & dots & b_{2k} \
dots & & & dots \
b_{m1} & b_{m2} & dots & b_{mk}
end{array}right) Rightarrow
$$
$$
Rightarrow Amid B=
left(begin{array}{llllllll}
a_{11} & a_{12} & dots & a_{1n} & b_{11} & b_{12} & dots & b_{1k} \
a_{21} & a_{22} & dots & a_{2n} & b_{21} & b_{22} & dots & b_{2k} \
dots & & & &&& & dots \
a_{m1} & a_{m2} & dots & a_{mn} & b_{m1} & b_{m2} & dots & b_{mk}
end{array}right).
$$
Проще говоря: к матрице $ A_{} $ «приписывается» справа матрица $ B_{} $. В этом смысле саму матрицу $ A_{} $ можно считать результатом конкатенации ее столбцов:
$$ A= A_{[1]}mid A_{[2]} mid dots mid A_{[m]}=left[ A_{[1]}mid A_{[2]} mid dots mid A_{[m]} right] . $$
Можно также производить конкатенацию матриц «по вертикали», т.е. по строкам3). Одновременную конкатенацию — когда к матрице $ A_{mtimes n}^{} $ приписывается столбец $ U_{mtimes 1 } $ справа и строка $ V_{1times (n+1)} $ снизу — называют окаймлением4) матрицы.
векторизация
матрицы5) произвольного порядка образно означает «вытягивание» ее в вектор-столбец. Если
представить матрицу как результат конкатенации ее столбцов:
$$ A=left[A_{[1]} mid A_{[2]} mid dots mid A_{[n]}right] , $$
то
$$ operatorname{Vec}(A)=left(begin{array}{c}
A_{[1]} \ A_{[2]}\ vdots \ A_{[n]}
end{array}
right) , .
$$
Так, например
$$
operatorname{Vec}left(begin{array}{ccc}
a_1 & b_1 & c_1 \
a_2 & b_2 & c_2
end{array}
right)=
left(begin{array}{c}
a_1 \
a_2 \
b_1 \
b_2 \
c_1 \
c_2
end{array}
right), .
$$
перезагрузка
Умножение матриц
Для матрицы-строки $ U=(u_{1},dots,u_n) $ и матрицы-столбца $ V=left(begin{array}{c} v_{1}\ vdots\ v_n end{array}right) $ определим произведение $ Ucdot V_{} $ как число
$$ Ucdot V= u_1v_1+dots+u_nv_n . $$
Для произвольных матриц $ A_{} $ и $ B_{} $ произведение матрицы $ A_{} $ на матрицу $ B_{} $ определяется тогда и только тогда, когда их порядки связаны ограничением:
количество столбцов матрицы $ A_{} $ = количество строк матрицы $ B_{} $
т.е. если матрица $ A_{} $ имеет порядок $ mtimes n_{} $, то матрица $ B_{} $ может иметь порядок $ ntimes k_{} $ при $ forall kin{mathbb N}_{} $. В этом случае произведение матрицы $ A_{} $ на матрицу $ B_{} $ обозначается6) $ Acdot B_{} $ и представляет собой матрицу $ C_{} $ порядка $ mtimes k_{} $:
$$
begin{array}{ccccc}
C&=&A&cdot&B ,\
{mtimes k}&&{mtimes n}&&{ntimes k}
end{array}
$$
элементы которой вычисляются по следующему правилу
$$
C=[c_{jell}]_{_{j=1,dots,matop
ell=1,dots,k
}},quad
c_{jell}= A^{[j]}B_{[ell]}=a_{j1}b_{1ell}+a_{j2}b_{2ell}+dots+a_{jn}b_{nell} .
$$
Таким образом, элемент, стоящий в $ j_{} $-й строке и $ ell_{} $-м столбце матрицы $ C_{} $, равен произведению $ j_{} $-й строки матрицы $ A_{} $ на $ ell_{} $-й столбец матрицы $ B_{} $.
В схематичном виде:

Порядок («размеры») матрицы $ C_{} $ определяется следующим образом: высота берется от первого сомножителя, а ширина — от второго.
При этом произведение $ B cdot A_{} $ может и не быть определено!
П
Пример.
$$
A=left(begin{array}{rr}
1&2\
-1&0\
3&7
end{array}right),B=left(begin{array}{rrrr}
mathbf i&0&0&-1\
4&2&0&-2
end{array}right) color{Red}{Longrightarrow} Acdot B=left(begin{array}{rrrr}
8+ mathbf i&4&0&-5\
-mathbf i&0&0&1\
28+3mathbf i&14&0&-17
end{array}right)
$$
П
Пример.
$$
A=left(
begin{array}{rrr}
3&-1&-1\
2&0&1\
1&1&1
end{array}right),B=left(begin{array}{rr}
2&1\
-1&0\
0&1
end{array}right) color{Red}{Longrightarrow} Acdot B= left(begin{array}{rr}
7&2\
4&3\
1&2
end{array}right)
$$
П
Пример.
$$
A=left(begin{array}{c}
1\ 0\ 1\ 1
end{array}right), B=(1,2,-1,-2) color{Red}{Longrightarrow} Acdot B=
left(begin{array}{rrrr}
1&2&-1&-2\
0&0&0&0\
1&2&-1&-2\
1&2&-1&-2
end{array}right)
$$
$$
B cdot A = ( – 2 ) .
$$
Т
Теорема. Операция умножения матриц подчиняется ассоциативному закону:
$$ (Acdot B) cdot D = Acdot (B cdot D) $$
если хотя бы в одной части равенства произведение определено.
Доказательство
☞
ЗДЕСЬ.
Операция умножения матриц
некоммутативна
: даже если определены оба произведения $ Acdot B_{} $ и $ B cdot A_{} $, то, как правило, $ Acdot B ne B cdot A $.
Что послужило причиной введения такой операции умножения?
Ответ и дальнейшие свойства операции умножения
☞
ЗДЕСЬ.
В приложениях используются и другие определения произведения двух матриц. Например, для матриц $ A_{} $ и $ B_{} $ одинакового порядка их адамаровым произведением называется матрица того же порядка, состоящая из поэлементных произведений: $ C=left[ a_{jk} b_{jk} right] $. См. также и
☞
КРОНЕКЕРОВО ПРОИЗВЕДЕНИЕ.
Квадратные матрицы
Матрица $ A_{} $ называется квадратной, если количество ее строк равно количеству ее столбцов. О квадратной $ ntimes n_{} $-матрице будем говорить как о матрице порядка $ mathbf n $, а записывать ее компактно в виде
$$A=left[ a_{jk} right]_{j,k=1}^n$$
Если матрицы $ A_{} $ и $ B_{} $ – квадратные порядка $ n_{} $, то обе матрицы $ AB_{} $ и $ BA_{} $ являются тоже квадратными порядка $ n_{} $. Тем не менее, и в этом случае, как правило, $ ABne BA_{} $.
П
Пример.
$$
A=
begin{pmatrix}
1 & 2 \
3 & 4
end{pmatrix}
,quad
B=
begin{pmatrix}
1 & 2 \
5 & 3
end{pmatrix} color{Red}{Longrightarrow}
AB=
begin{pmatrix}
11 & 8 \
23 & 18
end{pmatrix},
BA=
begin{pmatrix}
7 & 10 \
14 & 22
end{pmatrix}
.
$$
Говорят, что квадратные матрицы $ A $ и $ B $ коммутируют (или перестановочны), если $ AB=BA $.
симметричная
Главной диагональю квадратной матрицы $ A_{} $ называется ее диагональ, идущая из левого верхнего в правый нижний угол, т.е. эта диагональ совпадает с вектором $ (a_{11},dots,a_{jj},dots,a_{nn}^{}) $.
Матрица $ A_{} $ называется симметричной если она удовлетворяет соотношению
$$A=A^{top} .$$
Из определения следует, что симметричная матрица может быть только квадратной, а ее элементы должны удовлетворять соотношению:
$$ a_{jk}=a_{kj} quad npu {j,k } subset {1,dots, n} . $$
Иными словами, симметричная матрица — это такая матрица, которая симметрична относительно своей главной диагонали.
?
Сколько элементов надо задать, чтобы однозначно определить симметричную матрицу порядка $ n_{} $?
Частным случаем симметричной матрицы является диагональная матрица:
$$
D=left(
begin{array}{cccc}
a_{11} & & & \
& a_{22} & & {mathbb O} \
{mathbb O} & & ddots & \
& & & a_{nn}
end{array}
right) .
$$
§
Подробнее о симметричной матрице
☞
ЗДЕСЬ.
единичная
Матрица $$
E_n =
left(
begin{array}{cccc}
1 & & & \
& 1 & & {mathbb O} \
{mathbb O} & & ddots & \
& & & 1
end{array}
right)_{n}=
left[delta_{jk} right]_{j,k=1}^n
$$ называется единичной матрицей порядка $ n_{} $.
кососимметричная
Матрица $ A_{} $ называется кососимметричной если она удовлетворяет соотношению
$$A=-A^{top} .$$
Из определения следует, что кососимметричная матрица может быть только квадратной, а ее элементы должны удовлетворять соотношению:
$$ a_{jk}=-a_{kj} quad , {j,k } subset {1,dots, n} . $$
Отсюда вытекает, что все элементы главной диагонали кососимметричной матрицы должны быть равны 0.
П
Пример. Векторное произведение вектора $ X=(x_{1},x_2,x_3) $ на вектор $ Y=(y_{1},y_2,y_3) $ может быть задано с помощью кососимметричной матрицы:
$$
Xtimes Y = (x_{1},x_2,x_3) left(begin{array}{rrr}
0 & -y_3 & y_2 \
y_3 & 0 & -y_1 \
-y_2 & y_1 & 0
end{array}
right)
, .
$$
?
Указать все элементы кососимметричной матрицы
$$
left(
begin{array}{rrr}
color{Red}{Box} & 1 & color{Red}{Box} \
color{Red}{Box} & color{Red}{Box} & 3 \
-2 & color{Red}{Box} & color{Red}{Box}
end{array}
right)_{3times 3} .
$$
?
Доказать, что при любой квадратной матрице $ A_{} $
а) матрицы $ A_{}+A^{top} $ и $ A_{}A^{top} $ будут симметричными;
б) матрица $ A_{}-A^{top} $ будет кососимметричной.
Т
Теорема. Для любой квадратной матрицы $ A_{} $ существует и единственно ее представление в виде суммы симметричной и кососимметричной матриц, а именно:
$$ A = frac{1}{2} (A+A^{top}) + frac{1}{2} (A-A^{top}) . $$
§
Свойства кососимметричной матрицы
☞
ЗДЕСЬ
обратно симметричная матрица
Не очень удачный перевод на русский выражения reciprocal symmetric matrix. Формально определяется как квадратная матрица с ненулевыми элементами, удовлетворяющая соотношению
$$ A=[a_{jk}]_{j,k=1}^n , a_{jk}=1/a_{kj} . $$
Из этого определения следует, что все элементы главной диагонали такой матрицы равны $ 1_{} $.
Обычно рассматриваются положительные обратно симметричные матрицы.
П
Пример.
$$
left( begin{array}{rrr}
1 & sqrt{2} & 3 \
1/sqrt{2} & 1 & 1/4 \
1/3 & 4 & 1
end{array}
right) .
$$
Матрицы встречаются в теории принятия решений. Пусть имеется $ n_{} $ различных критериев $ C_1,C_2,dots, C_n $ и человек, принимающий решения (эксперт), может оценить во сколько раз критерий $ C_j $ важнее (предпочтительней) критерия $ C_k $; соответствующую величину $ a_{jk} $ называют интенсивностью (мощностью) предпочтения7). Особенно удачно, если эксперт оказывается достаточно квалифицированным (или самоуверенным) и в состоянии ранжировать набор критериев, придав каждому определенные веса $ w_1,w_2,dots, w_n $. Тогда матрица
$$
left[frac{w_j}{w_k} right]_{j,k=1}^n
$$
представляет собой обратно симметричную матрицу, обладающую свойством
$$ a_{jk}=a_{jell}a_{ell k} . $$
В этом случае про обратно симметричную матрицу говорят, что она мощностно-транзитивная8).
треугольная
Так называется квадратная матрица, у которой все элементы выше главной диагонали или ниже ее равны нулю.
Различают верхнетреугольную9)
$$
U=left(begin{array}{ccccc}
a_{11} & a_{12} &a_{13} & dots & a_{1n} \
& a_{22} & a_{23} & dots & a_{2n} \
& & ddots & & \
& mathbb O & & ddots & vdots \
& & & & a_{nn}
end{array}
right)
$$
и нижнетреугольную
$$
L=left(begin{array}{ccccc}
a_{11} & & & & \
a_{21} & a_{22} & & & \
& & ddots & mathbb O & \
vdots & & & ddots & \
a_{n1} & a_{n2} & dots & & a_{nn}
end{array}
right)
$$
матрицы. Часто эти матрицы называют право– и левотреугольными соответственно и обозначают тогда $ R_{} $ и $ L_{} $. В одной и той же книге можно встретить одновременно
LU-разложение матрицы и QR-разложение матрицы; при этом вторые буквы означают именно верхнетреугольные матрицы. Так исторически сложилось: неудобно, но привычно!
Хессенберга
Матрица вида
$$
left(begin{array}{llllll}
a_{11} & a_{12} & a_{13} & dots & a_{1,n-1} & a_{1n} \
a_{21} & a_{22} & a_{23} & dots & a_{2,n-1} & a_{2n} \
0 & a_{32} & a_{33} & dots & a_{3,n-1} & a_{3n} \
vdots & & ddots & & & \
0 & 0 & 0 & dots & a_{n,n-1} & a_{nn}
end{array}
right) ,
$$
т.е. с элементами $ a_{ij}=0 $ при $ i<j+1 $ называется верхней матрицей Хессенберга.
ортогональная
матрица — это квадратная матрица $ A_{} $ с вещественными элементами, удовлетворяющая соотношению:
$$ A cdot A^{top} = E , $$
здесь $ E_{} $ — единичная матрица того же порядка, а $ {}^{top} $ означает транспонирование. Иными словами, строки матрицы $ A_{} $ удовлетворяют условию
$$ A^{[j]}cdot left( A^{[k]} right)^{top} = a_{j1}a_{k1}+a_{j2}a_{k2} + dots + a_{jn}a_{kn}= delta_{jk} , $$
где $ delta_{jk}^{} $ — символ Кронекера. Если определить скалярное произведение для строк $ X=(x_1,x_2,dots,x_{n}) $ и $ Y=(y_1,y_2,dots,y_{n}) $ по правилу, естественно обобщающему определение скалярного произведения в двух- и трехмерном пространстве:
$$ langle X,Y rangle =x_1y_1+x_2y_2+dots+x_ny_n , $$
то определение ортогональной матрицы оправдано тем, что ее строки оказываются взаимно ортогональными. К тому же, они все имеют «единичную длину»: сумма квадратов элементов любой строки равна 1.
В литературе под ортогональной матрицей иногда понимают и матрицу с комплексными элементами, удовлетворяющую соотношению
$ A cdot A^{top} = E $. Тогда для матрицы из приведенного выше случая используют название вещественная ортогональная матрица.
П
Пример. Матрица
$$
left(
begin{array}{rr}
cos theta & – sin theta \
sin theta & cos theta
end{array}
right)
$$
— ортогональная.
Т
Теорема. Если матрица $ A_{} $ — ортогональная, то и матрица $ A_{}^{top} $ — ортогональная, т.е. у ортогональной матрицы взаимно ортогональны не только строки, но и столбцы.
§
Подробнее об ортогональной матрице
☞
ЗДЕСЬ
Следующий класс матриц не относится ко множеству ортогональных, но близок к нему по смыслу.
Матрица $ A_{} $ называется матрицей Адамара10) если любой ее элемент равен либо $ +1_{} $ либо $ – 1_{} $ и ее строки взаимно ортогональны. Иными словами для матрицы Адамара порядка $ n_{} $ должно быть выполнено:
$$ A^{top} cdot A = n E , $$
где $ E_{} $ — единичная матрица того же порядка.
П
Пример. Матрицы
$$
left(
begin{array}{rr}
1 & 1 \
1 & -1
end{array}
right) quad u quad
left(
begin{array}{rrrr}
1 & 1 & 1 & 1 \
1 & -1 &1 & -1 \
1 & 1 & -1 & -1 \
1 & -1 & -1 & 1
end{array}
right)
$$
— матрицы Адамара. С помощью последней матрицы и следующего результата можно сконструировать матрицу Адамара порядка $ 2^{n} $.
Т
Теорема. Если $ H_{} $ — матрица Адамара порядка $ n_{} $, то блочная матрица $$ left[ begin{array}{rr}
H & H \
H & -H
end{array}
right]
$$
является матрицей Адамара порядка $ 2,n $.
Если при $ n> 2 $ матрица Адамара существует, то $ n_{} $ должно быть кратно $ 4_{} $. Обратное утверждение составляет содержание следующей гипотезы:
Гипотеза Адамара: для любого натурального $ n_{} $ кратного $ 4_{} $ существует матрица Адамара порядка $ n_{} $. Не доказана.11)
§
Применение матрицы Адамара:
☞
КОДИРОВАНИЕ.
☞
Максимальное значение определитедя матрицы порядка $ n $, элементы которой по модулю не превосходят $ 1 $ достигается на матрицах Адамара (в случае их существования для данного $ n $); оно равно $ n^{n/2} $. См.
☞
Неравенство Адамара
ганкелева
матрица — это квадратная матрица вида
$$
left(begin{array}{lllll}
h_0 & h_1 & h_2 & dots & h_{n-1} \
h_1 & h_2 & h_3 & dots & h_n \
h_2 & h_3 & h_4 & dots & h_{n+1} \
vdots & & & ddots & vdots \
h_{n-1} & h_{n} & h_{n+1} & dots & h_{2n-2}
end{array}
right)_{ntimes n}= left[ h_{j+k}right]_{j,k=0}^{n-1}
$$
Симметричная матрица, на каждой диагонали которой, перпендикулярной главной, стоят одинаковые элементы. Таким образом, ганкелева12) матрица полностью определяется заданием своих крайних элементов:
$$ h_0,h_1,dots, h_{2n-2} $$
— они называются образующими ганкелевой матрицы.
§
Подробнее о ганкелевой матрице
☞
ЗДЕСЬ.
тёплицева
Так называется квадратная матрица вида
$$
left(begin{array}{lllll}
t_0 & t_{-1} & t_{-2} & dots & t_{-n+1} \
t_1 & t_0 & t_{-1} & dots & t_{-n+2} \
t_2 & t_1 & t_0 & dots & t_{-n+3} \
vdots & & & & vdots \
t_{n-1} & t_{n-2} & t_{n-3} & dots & t_{0}
end{array}
right)= left[ t_{j-k}right]_{j,k=0}^{n-1} .
$$
Элементы каждой диагонали, параллельной главной, одинаковы. В отличие от ганкелевой матрицы, теплицева13) матрица не обязательно симметрична.
Частным случаем тёплицевой матрицы является циклическая матрица:
$$
left(begin{array}{lllll}
a_1 & a_2 & a_3 & dots & a_n \
a_n & a_1 & a_2 & dots & a_{n-1} \
a_{n-1} & a_n & a_1 & dots & a_{n-2} \
vdots & & & & vdots \
a_2 & a_3 & a_4 & dots & a_1
end{array}
right) ;
$$
(иногда называется циркулянтом, хотя в отечественной литературе циркулянтом чаще называют ее определитель).
Каждая строка, начиная со второй, получается сдвигом предыдущей вправо на один элемент; тот элемент, что при этом сдвиге «вываливается» за пределы матрицы, переставляется в начало строки.
§
Подробнее о циклической матрице
☞
ЗДЕСЬ
положительная
Так называется матрица $ A_{} $ все элементы которой положительны (определяется для матриц произвольного порядка — не обязательно квадратных). Обозначается $ A > 0 $ или $ A > mathbb O $. По аналогии определяются неотрицательная ( $ A ge 0 $), отрицательная и неположительная матрицы.
стохастическая
Неотрицательная матрица, в которой сумма элементов каждой строки равна $ 1 $:
$$
left(begin{array}{cccc}
p_{11} & p_{12} & dots & p_{1n} \
p_{21} & p_{22} & dots & p_{2n} \
& & & \
p_{n1} & p_{n2} & dots & p_{nn}
end{array}
right)
$$
$$sum_{j=1}^n p_{kj}=1 npu k in {1,dots,n } . $$
П
Пример.
$$
left(begin{array}{cccc}
1/3 & 1/2 & 1/6 & 0 \
0 & 1 & 0 & 0\
0.13 & 0.35 & 0.21 & 0.31 \
1/4 & 1/4 & 1/4 & 1/4
end{array}
right)
$$
Используется в теории вероятностей, см.
☞
цепи Маркова.
элементарных преобразований
Для квадратной матрицы $ A_{} $ умножение ее на единичную матрицу $ E_{} $ того же порядка не приводит к изменению матрицы: $ A cdot E = Ecdot A=A_{} $. Теперь «испортим» матрицу $ E_{} $ хотя бы в одном ее элементе и понаблюдаем за результатами аналогичных умножений.
П
Пример. а) Изменяется элемент вне главной диагонали: $ 0_{} $ меняется на какое-то число $ {color{Red}{ alpha} } in mathbb A_{} $.
$$
left(
begin{array}{ccc}
1 & 0 & 0 \
0 & 1 & 0 \
0 & {color{Red}{ alpha} } & 1
end{array}
right)
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right)=
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} + {color{Red}{ alpha} } a_{21} & a_{32} + {color{Red}{ alpha} } a_{22} & a_{33} + {color{Red}{ alpha} } a_{23}
end{array}
right) ;
$$
$$
left(
begin{array}{ccc}
1 & 0 & 0 \
0 & 1 & {color{Red}{ alpha} } \
0 & 0& 1
end{array}
right)
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right)=
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} + {color{Red}{ alpha} } a_{31} & a_{22} + {color{Red}{ alpha} } a_{32} & a_{23} + {color{Red}{ alpha} } a_{33} \
a_{31} & a_{32} & a_{33}
end{array}
right) .
$$
Вывод. Умножение матрицы такого вида ( $ 0_{} $ в $ j_{} $-й строке и $ k_{} $-м столбце матрицы $ E_{} $ меняется на $ {color{Red}{ alpha} } $) слева на матрицу $ A_{} $ эквивалентно прибавлению к $ j_{} $-й строке матрицы $ A_{} $ ее $ k_{} $-й строки, домноженной на $ {color{Red}{ alpha} } $.
б) Изменяется элемент главной диагонали: $ 1_{} $ меняется на какое-то число $ {color{Red}{ alpha} } in mathbb A_{} $.
$$
left(
begin{array}{ccc}
1 & 0 & 0 \
0 & {color{Red}{ alpha} } & 0 \
0 & 0& 1
end{array}
right)
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right)=
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
{color{Red}{ alpha} } a_{21} & {color{Red}{ alpha} } a_{22} & {color{Red}{ alpha} } a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right)
$$
Вывод. Умножение матрицы такого вида ( $ 1_{} $ в $ j_{} $-й строке матрицы $ E_{} $ меняется на $ {color{Red}{ alpha} } $) слева на матрицу $ A_{} $ эквивалентно домножению на $ {color{Red}{ alpha} } $ соответствующей строки матрицы $ A_{} $.
в) Произведем еще одну «экзекуцию» с матрицей $ E_{} $: переставим местами две ее строки. Такая матрица иногда называется матрицей перестановки (и, кстати, является ортогональной ) , что оправдано следующим ее свойством: умножим ее на $ A_{} $:
$$
left(
begin{array}{ccc}
1 & 0 & 0 \
0 & 0 & 1 \
0 & 1& 0
end{array}
right)
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right)=
left(
begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{31} & a_{32} & a_{33} \
a_{21} & a_{22} & a_{23}
end{array}
right)
$$
Вывод. Умножение матрицы такого вида (переставляются $ j_{} $-я и $ k_{} $-я строки матрицы $ E_{} $) слева на матрицу $ A_{} $ эквивалентно перестановке соответствующих строк матрицы $ A_{} $.
♦
Для общего случая матриц порядка $ n_{} $ матрицы, построенные по аналогии с предыдущим примером, называются матрицами элементарных преобразований.
?
Показать, что умножение матриц преобразований справа на матрицу $ A_{} $ эквивалентно соответствующим преобразованиям столбцов матрицы $ A_{} $.
?
Какое действие с матрицей $ A_{} $ оказывает умножение ее на матрицу
$$
left(
begin{array}{ccccc}
0 & 0 & dots & 0 & 1 \
0 & 0 & dots & 1 & 0 \
vdots & & & & vdots \
0 & 1 & dots & 0 & 0 \
1 & 0 & dots & 0 & 0
end{array}
right) ?
$$
Последняя матрица относится к классу матриц, обобщающих класс матриц элементарных преобразований. Матрица $ P_{} $ называется матрицей перестановки если в любой ее строке и любом ее столбце в точности один элемент равен $ 1_{} $ при всех остальных равных $ 0_{} $. Она тесно связана с понятием перестановки элементов. Пусть имеются различные числа14) $ {alpha_1,dots, alpha_n} $. Любое их упорядочивание называется перестановкой. Если имеются две перестановки одного и того же набора чисел, записываемые в виде векторов-строк: $ (x_1,dots,x_{n}) $ и $ (y_1,dots,y_n) $, то они связаны между собой посредством умножения на матрицу перестановки $ P_{} $ порядка $ n_{} $:
$$ (y_1,dots,y_n) =(x_1,dots,x_n)P . $$
Так, к примеру, если $ (y_1,y_2,y_3,y_4)=(x_2,x_4,x_3,x_1) $, то
$$(y_1,y_2,y_3,y_4)=(x_1,x_2,x_3,x_4)
left(begin{array}{cccc}
0 & 0 & 0 & 1 \
1 & 0 & 0 & 0 \
0 & 0 & 1 & 0 \
0 & 1 & 0 & 0
end{array}
right) .
$$
Очевидно действие матрицы перестановки при умножении на произвольную квадратную матрицу $ A_{} $; также очевидно, что результат этого действия эквивалентен последовательным действиям матриц элементарных преобразований, т.е. любая матрица перестановки может быть представлена как произведение матриц элементарных преобразований.
Матрицы элементарных преобразований используются при анализе метода Гаусса решения систем линейных уравнений.
ленточная
Пронумеруем диагонали квадратной матрицы, начиная с главной — в обе стороны. Если все диагонали, начиная с некоторого их номера, будут заполнены нулевыми элементами, то такая матрица называется ленточной. Аналитически:
$$ a_{jk}=0 quad npu quad |j-k| ge L .$$
Минимальное из возможных значений $ L $, при которых последнее будет выполнено, называется шириной ленточной матрицы: в этом случае матрица имеет не более $ 2L-1 $ диагоналей, которые могут содержать ненулевые элементы.
П
Пример. Ленточная матрица ширины $ 1_{} $ является диагональной матрицей; ленточная матрица ширины $ 2_{} $ является трехдиагональной:
$$
left(
begin{array}{lllllllll}
a_{11} & a_{12} & 0 & 0 & 0 & 0 & dots & 0 & 0 \
a_{21} & a_{22} & a_{23} & 0 & 0 & 0 & dots & 0 & 0 \
0 & a_{32} & a_{33} & a_{34} & 0 & 0 & dots & 0 & 0 \
0 & 0 & a_{43} & a_{44} & a_{45} & 0 & dots & 0 & 0 \
vdots & & & & ddots & & & & vdots \
0 & 0 & 0 & 0 & 0 & 0 & dots & a_{n,n-1} & a_{n,n}
end{array}
right).
$$
§
Ленточные матрицы возникают в численных методах решения граничных задач для обыкновенных дифференциальных уравнений; см.
☞
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ.
Часто встречающиеся (“именные”) матрицы
Вандермонда
$$ mathbf V(x_1,dots,x_n)= left[ x_j^{k-1} right]_{j,k=1}^{n}=
left(begin{array}{ccccc}
1 &x_1&x_1^2&ldots&x_1^{n-1}\
1 &x_2&x_2^2&ldots&x_2^{n-1}\
vdots& &&& vdots\
1 &x_n&x_n^2&ldots&x_n^{n-1}
end{array}right)_{ntimes n}
$$
или ей транспонированная. Иногда рассматривают неквадратные матрицы Вандермонда.
§
Подробнее о матрице Вандермонда
☞
ЗДЕСЬ.
Частным случаем матрицы Вандермонда является матрица дискретного преобразования Фурье:
$$
F=left[ varepsilon_j^{k} right]_{j,k=0}^{n-1}=
left( begin{array}{lllll}
1 & 1 & 1 & dots & 1 \
1 & varepsilon_1 & varepsilon_1^2 & dots & varepsilon_1^{n-1} \
1 & varepsilon_2 & varepsilon_2^2 & dots & varepsilon_2^{n-1} \
1 & varepsilon_3 & varepsilon_3^2 & dots & varepsilon_3^{n-1} \
vdots & & & & vdots \
1 & varepsilon_{n-1} & varepsilon_{n-1}^{2} & dots & varepsilon_{n-1}^{n-1}
end{array}
right)_{ntimes n}
quad npu quad varepsilon_j = cos frac{2 pi j}{n} + {mathbf i} , sin frac{2 pi j}{n}
$$
— корне n-й степени из 1. Основываясь на свойстве $ varepsilon_j=varepsilon_1^j $, матрицу часто записывают в эквивалентном виде
$$
F=
left[ varepsilon^{jk} right]_{j,k=0}^{n-1}=
left( begin{array}{lllll}
1 & 1 & 1 & dots & 1 \
1 & varepsilon & varepsilon^2 & dots & varepsilon^{n-1} \
1 & varepsilon^2 & varepsilon^4 & dots & varepsilon^{2(n-1)} \
1 & varepsilon^3 & varepsilon^6 & dots & varepsilon^{3(n-1)} \
vdots & & & & vdots \
1 & varepsilon^{n-1} & varepsilon^{2(n-1)} & dots & varepsilon^{(n-1)^2}
end{array}
right)_{ntimes n} quad npu quad varepsilon = cos frac{2 pi}{n} + {mathbf i} , sin frac{2 pi}{n} .
$$
§
Свойства матрицы дискретного преобразования Фурье
☞
ЗДЕСЬ; ее применение
☞
ТРИГОНОМЕТРИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ.
Гессе
Матрица, составленная из частных производных второго порядка функции $ f(x_1,dots,x_{ell}) $
$$
H (f) = left(
begin{array}{cccc}
{partial^2 f}/{partial x_1^2} & {partial^2 f}/{partial x_1 partial x_2} & dots & {partial^2 f}/{partial x_1 partial x_{ell}} \
{partial^2 f}/{partial x_2 partial x_1} & {partial^2 f}/{partial x_2^2} & dots & {partial^2 f}/{partial x_2 partial x_{ell}} \
dots & && dots \
{partial^2 f}/{partial x_{ell} partial x_1} & {partial^2 f}/{partial x_{ell} partial x_2} & dots & {partial^2 f}/{partial x_{ell}^2}
end{array}
right)= left[ frac{partial^2 f}{partial x_j partial x_k} right]_{j,k=1}^{ell}
$$
(в предположении, что эти производные существуют). Определитель матрицы Гессе называется гессианом.
§
Подробнее о применениях матрицы Гессе к задачам исследования стационарных точек функции на экстремум, а также самой функции на выпуклость
☞
ЗДЕСЬ.
Грама
Пусть в линейном пространстве $ mathbb E $ определено скалярное произведение векторов, которое обозначим $ langle X,Y rangle $.
Матрицей Грама системы векторов $ {X_1,dots,X_{m} } $ называется квадратная матрица
$$
G(X_1,dots,X_m)=
left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \
dots & & & dots \
langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle
end{array}
right)
= left[ langle X_j,X_k rangle right]_{j,k=1}^m
.
$$
Если векторы $ {X_1,dots,X_{n} } $ составляют базис линейного пространства, то задание их матрицы Грама сведет вычисление скалярного произведения произвольных векторов пространства к действию с их координатами:
если
$$X=x_1X_1+ dots +x_nX_n quad u quad Y=y_1X_1+ dots +y_nX_n ,
$$
то
$$
langle X,Y rangle=left(x_1,x_2,dots,x_n right)
left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \
dots & & & dots \
langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle
end{array}
right)
left(
begin{array}{c}
y_1 \
y_2 \
vdots \
y_n
end{array}
right)
.
$$
§
Подробнее о свойствах матрицы Грама и ее применении к задачам вычисления расстояний
☞
ЗДЕСЬ.
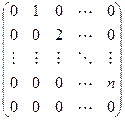
Фробениуса
Матрица
$$
{mathfrak F}=
left( begin{array}{lllllll}
0 & 1 & 0 & 0 & dots & 0 & 0 \
0 & 0 & 1 & 0 & dots & 0 & 0 \
0 & 0 & 0 & 1 & dots & 0 & 0 \
vdots& &&&ddots & & vdots \
0 & 0 & 0 & 0 & dots & 0 & 1 \
a_n & a_{n-1} & a_{n-2} & & dots & a_2 & a_1
end{array} right)_{n times n}
$$
или ей транспонированная. Ее характеристический полином имеет вид
$$ det ({mathfrak F} – x E) = (-1)^n(x^n-a_1x^{n-1}-dots-a_{n}) , . $$
Тем самым, матрица Фробениуса является решением задачи построения матрицы простейшего вида, имеющей заданный характеристический полином. Исходя из этого соображения, матрицу $ {mathfrak F} $ часто называют сопровождающей матрицей полинома15) $ f(x)=x^n-a_1x^{n-1}-a_2x^{n-2}- dots – a_n $.
§
Применение матрицы Фробениуса
☞
РЕШЕНИЕ ЛИНЕЙНОГО РАЗНОСТНОГО УРАВНЕНИЯ.
Якоби
Матрицей Якоби системы из $ m_{} $ функций
$ {f_1(x_1,dots,x_n),dots,f_{m}(x_1,dots,x_n)} $ по переменным $ x_{1},dots,x_n $ называется матрица,
составленная из всевозможных частных производных:
$$
mathbf J = left[ frac{partial f_j}{partial x_k} right]_{j=1,dots,m, atop k=1,dots,n} =
left(
begin{array}{cccc}
{partial f_1}/{partial x_1} & {partial f_1}/{partial x_2} & dots & {partial f_1}/{partial x_n} \
{partial f_2}/{partial x_1} & {partial f_2}/{partial x_2} & dots & {partial f_2}/{partial x_n} \
dots & && dots \
{partial f_m}/{partial x_1} & {partial f_m}/{partial x_2} & dots & {partial f_m}/{partial x_n}
end{array}
right)_{mtimes n} .
$$
В частном случае $ m=1_{} $ матрица Якоби состоит из одной строки:
этот вектор в $ mathbb R_{}^{n} $ или в $ mathbb C^{n} $ называется градиентом функции $ f_{} $ (в точке $ (x_1,dots,x_{n}) $):
$$
operatorname{grad} (f) = left( frac{partial f}{partial x_1},dots, frac{partial f}{partial x_n} right) .
$$
§
Применение матрицы Якоби
☞
ЗДЕСЬ
f
Функции от матрицы
определитель
или детерминант16) определяется для произвольной квадратной матрицы $ A_{} $, и представляет из себя полином от всех ее элементов. Обозначается – либо $ det (A_{}) $, либо $ det A_{} $, либо – в развернутом виде –
$$
left|
begin{array}{cccc}
a_{11} & a_{12} & dots & a_{1n} \
a_{21} & a_{22} & dots & a_{2n} \
dots & & & dots \
a_{n1} & a_{n2} & dots & a_{nn}
end{array}
right|
$$
(матрица ограничивается вертикальными чертами). Имея в виду порядок матрицы $ A_{} $, о ее определителе говорят как об определителе порядка $ n_{} $.
Для $ n=1_{} $:
$$
det (A) = a_{11} ;
$$
для $ n=2_{} $:
$$
det (A) = left|
begin{array}{cc}
a_{11} & a_{12} \
a_{21} & a_{22}
end{array}
right|=a_{11}a_{22}-a_{12}a_{21} ;
$$
для $ n=3_{} $:
$$
det (A) =
left|
begin{array}{lll}
a_{11} & a_{12} & a_{13}\
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
end{array}
right| =
$$
$$
=a_{11}a_{22}a_{33}+a_{12}a_{23} a_{31} +
a_{21}a_{32} a_{13} – a_{31} a_{22} a_{13} – a_{21}a_{12}a_{33} –
a_{11} a_{32} a_{23} ;
$$
для $ n=4_{} $ формула становится громоздкой.
Понятие определителя вводится с целью компактной записи критерия разрешимости системы линейных уравнений
$$
left{
begin{array}{lllll}
a_{11}x_1 &+a_{12}x_2&+ ldots&+a_{1n}x_n &=b_1,\
a_{21}x_1 &+a_{22}x_2&+ ldots&+a_{2n}x_n &=b_2,\
dots & & & dots & \
a_{n1}x_1 &+a_{n2}x_2&+ ldots&+a_{nn}x_n &=b_n.
end{array} right.
$$
и представления ее решения.
Т
Теорема. Если определитель матрицы, составленной из коэффициентов $ a_{jk} $, отличен от нуля, то система имеет единственное решение относительно неизвестных $ x_{1},dots,x_n $.
§
Определение, свойства и применения определителя
☞
ЗДЕСЬ
Для неквадратных матриц понятие определителя не вводится, но имеется понятие миноров матрицы.
Если выбрана подматрица матрицы $ A_{} $ — т.е. взяты ее элементы, стоящие на пересечении
строк с номерами $ i_1,i_2,dots,i_{k} $ и столбцов с номерами $ j_1,dots,j_{ell} $ (номера указаны строго в порядке возрастания) и эта подматрица — квадратная, т.е. $ k=ell $, то ее определитель называется минором матрицы (k-го порядка). Обозначать будем
$$ Aleft( begin{array}{llll} i_1 & i_2 & dots & i_{k} \
j_1 & j_2 & dots & j_{k}
end{array}
right) . $$
след
определяется для произвольной квадратной матрицы $ A_{} $ как сумма элементов ее главной диагонали;
обозначается17) $ operatorname{Sp}(A_{}) $ или $ operatorname{tr}(A_{}) $:
$$ operatorname{Sp}(A)=a_{11}+a_{22}+dots+a_{nn} . $$
Свойства. Для квадратных матриц одинакового порядка имеют место равенства:
a) $ operatorname{Sp}(A+B) = operatorname{Sp}(A) + operatorname{Sp}(B_{}) $;
б) $ operatorname{Sp}(alpha A_{}) = alpha operatorname{Sp}(A) $ для любого числа $ alpha_{} $;
в) $ operatorname{Sp}(AB) = operatorname{Sp}(BA_{}) $;
г) $ operatorname{Sp} (A^{top}) = operatorname{Sp} (A_{}) $
д) $ operatorname{Sp}(A^{top} B) = sum_{j,l=1}^n a_{jk} b_{jk} $
характеристический полином
определяется для произвольной квадратной матрицы $ A_{} $ как $ det (A_{}- x E) $, где $ E_{} $ – единичная матрица одинакового с $ A_{} $ порядка. Если порядок матрицы равен $ n_{} $, то указанный определитель является полиномом степени $ n_{} $ по $ x_{} $.
П
Пример. Для $ n=2_{} $:
$$ det (A-x E)=
begin{vmatrix}
a_{11}-x & a_{12}\
a_{21}& a_{22}-x
end{vmatrix}=x^2-(a_{11}+a_{22})x + (a_{11}a_{22}-a_{12}a_{21}) ;
$$
для $ n=3 $:
$$
det (A-x E)=
begin{vmatrix}
a_{11}-x & a_{12} & a_{13}\
a_{21}& a_{22}-x & a_{23} \
a_{31}& a_{32} & a_{33}-x
end{vmatrix}=
$$
$$
=-x^3+(a_{11}+a_{22}+a_{33})x^2 – left {
begin{vmatrix}
a_{11}& a_{12}\
a_{21}& a_{22}
end{vmatrix}
+begin{vmatrix}
a_{22}& a_{23}\
a_{32}& a_{33}
end{vmatrix}+
begin{vmatrix}
a_{11}& a_{13}\
a_{31}& a_{33}
end{vmatrix}
right }x+
$$
$$
+det A .
$$
§
Структура, свойства и методы вычисления характеристического полинома
☞
ЗДЕСЬ
ранг
определяется для произвольной (не обязательно квадратной) матрицы $ A_{} $ как наибольший порядок ее отличных от нуля миноров. Иначе говоря: $ operatorname{rank} (A_{}) ={mathfrak r}in {mathbb N} $ тогда и только тогда, когда существует ее минор порядка $ {mathfrak r} $, отличный от нуля, а все миноры более высокого порядка равны нулю. Кроме того, полагают ранг нулевой матрицы равным нулю: $ operatorname{rank} ({mathbb O}_{mtimes n}) = 0_{} $.
§
Методы вычисления, свойства и применения ранга матрицы
☞
ЗДЕСЬ
норма
Функция, ставящая в соответствие произвольной квадратной матрице $ A_{} $ порядка $ n_{} $ вещественное число, называется матричной нормой если для нее выполняются следующие аксиомы:
-
$ || A_{} || geq 0 $ (неотрицательность);
-
$ || A_{} || = 0 $ тогда и только тогда, когда $ A_{}=mathbb{O} $ (положительность);
-
$ || alpha A_{} ||=|alpha|cdot || A || $ для всех $ alpha_{}in mathbb{C} $ (абсолютная однородность);
-
$ || A + B_{} || le ||A||+||B|| $ (неравенство треугольника);
-
$ ||AB||le ||A|| cdot ||B_{}|| $.
§
Норма вводится не только для квадратных матриц. Подробнее
☞
ЗДЕСЬ.
Обращение матрицы
Для квадратной матрицы $ A_{} $ матрица $ B_{} $ называется левой обратной, если $ BA=E_{} $, где $ E_{} $ – единичная матрица одинакового порядка с $ A_{} $. Отсутствие свойства коммутативности умножения приводит к необходимости определения еще одной обратной матрицы — правой обратной, т.е. матрицы $ C_{} $ такой, что $ AC= E_{} $. К счастью, необходимость в этом «дублировании» практически сразу пропадает:
Т
Для того, чтобы существовала левая обратная матрица для матрицы $ A_{} $ необходимо и достаточно, чтобы $ det A_{} ne 0 $. В этом случае, левая обратная матрица будет единственной, и будет совпадать с правой обратной.
Для обратной к матрице $ A_{} $ закреплено обозначение $ A_{}^{-1} $, а сама процедура нахождения обратной матрицы называется обращением. Матрица, определитель которой отличен от нуля, называется неособенной или невырожденной или обратимой.
Доказательство. Необходимость условия $ det A_{} ne 0 $ для существования, например, левой обратной матрицы следует из условия
$$ det (B cdot A)= det E quad iff quad (det B) (det A) =1 . $$
Покажем достаточность. Вычислим все алгебраические дополнения к элементам матрицы $ A_{} $, составим из них новую матрицу порядка $ n_{} $ и транспонируем ее. Полученная матрица
$$
operatorname{adj}(A) =left(left[A_{jk} right]_{jk}^n right)^{top} =
left(
begin{array}{llll}
A_{11} &
A_{21}& dots &
A_{n1} \
A_{12} &
A_{22} & dots &
A_{n2} \
dots & & & dots \
A_{1n} &
A_{2n} & dots &
A_{nn}
end{array}
right)
$$
называется взаимной или союзной матрице $ A_{} $. Для любой матрицы $ A_{} $ имеет место равенство
$$
A cdot operatorname{adj}(A) =
left(
begin{array}{cccc}
det A & & & \
& det A & & {mathbb O} \
{mathbb O} & & ddots & \
& & & det A
end{array}
right) = det A cdot E .
$$
Справедливость этого факта следует из теории определителей: сумма произведений элементов строки матрицы на их алгебраические дополнения равна определителю матрицы; а на алгебраические
дополнения к элементам любой другой строки — нулю (см.
☞
ЗДЕСЬ ).
При выполнении условия $ det A_{} ne 0 $ можем взять
$$
A^{-1}=frac{ operatorname{adj}(A) }{det A}=
left(
begin{array}{llll}
frac{A_{11}}{det A} &
frac{A_{21}}{det A} & dots &
frac{A_{n1}}{det A} \
&&& \
frac{A_{12}}{det A} &
frac{A_{22}}{det A} & dots &
frac{A_{n2}}{det A} \
&&& \
vdots & & & vdots \
frac{A_{1n}}{det A} &
frac{A_{2n}}{det A} & dots &
frac{A_{nn}}{det A}
end{array}
right) .
$$
Пока что мы получили правую обратную матрицу: доказано, что она удовлетворяет условию $ A C = E_{} $. Проверка того, что полученная матрица будет являться и левой обратной, т.е. удовлетворяет условию $ C A=E $, производится снова с использованием теоремы о сумме произведений элементов столбца матрицы $ A_{} $ на алгебраические дополнения к другому столбцу той же матрицы (см.
☞
ЗДЕСЬ ). Теперь покажем, единственность полученной обратной матрицы. Предположим, что каким-то другим способом найдена еще одна матрица $ C_1 $ обладающая тем же самым свойством $ A C_1 = E $. Домножим это равенство слева на матрицу $ C_{} $:
$$ C(AC_1) = C E . $$
Операция умножения матриц подчиняется ассоциативному закону, поэтому
$$ (CA) C_1 = C , $$
но, по доказанному ранее, $ CA=E_{} $. И мы получили равенство $ C_1 = C $, доказывающее единственность правой обратной матрицы. Аналогично доказывается единственность и левой обратной.
♦
П
Пример. Вычислить
$$
left( begin{array}{rrr}
4 & 8 & -5\
-4 & 7 &-1 \
-3 & 5 & 1
end{array}
right)^{-1} .
$$
Решение. Вычисляем определитель этой матрицы: $ det A = 99 ne 0 $. Обратная матрица существует. Вычисляем алгебраические дополнения элементов:
$$
overbrace{left| begin{array}{rr}
7 &-1 \
5 & 1
end{array}
right|}^{A_{11}}=12,
overbrace{-left| begin{array}{rrr}
-4 &-1 \
-3 & 1
end{array}
right|}^{A_{12}}=7,
overbrace{left| begin{array}{rrr}
-4 & 7 \
-3 & 5
end{array}
right|}^{A_{13}}=1,
$$
$$
overbrace{-left| begin{array}{rr}
8 &-5 \
5 & 1
end{array}
right|}^{A_{21}}=-33,
overbrace{left| begin{array}{rr}
4 &-5 \
-3 & 1
end{array}
right|}^{A_{22}}=-11,
overbrace{-left| begin{array}{rr}
4 &8 \
-3 & 5
end{array}
right|}^{A_{23}}=-44,
$$
$$
overbrace{left| begin{array}{rr}
8 &-5 \
7 & -1
end{array}
right|}^{A_{31}}=27,
overbrace{-left| begin{array}{rr}
4 &-5 \
-4 & -1
end{array}
right|}^{A_{32}}=24,
overbrace{left| begin{array}{rr}
4 &8 \
-4 & 7
end{array}
right|}^{A_{33}}=60 .
$$
Cоставляем из них матрицу:
$$
left( begin{array}{rrr}
12 & 7 & 1\
-33 & -11 &-44 \
27 & 24 & 60
end{array}
right)
$$
и не забываем ее транспонировать, а также поделить на определитель!
Ответ.
$$
left( begin{array}{rrr}
frac{scriptstyle 4}{scriptstyle 33} &
-frac{scriptstyle 1}{scriptstyle 3} &
frac{scriptstyle 3}{scriptstyle 11} \
&& \
frac{scriptstyle 7}{scriptstyle 99} &
-frac{scriptstyle 1}{scriptstyle 9} &
frac{scriptstyle 8}{scriptstyle 33} \
&& \
frac{scriptstyle 1}{scriptstyle 99} &
-frac{scriptstyle 4}{scriptstyle 9} &
frac{scriptstyle 20}{scriptstyle 33}
end{array}
right) .
$$
?
Показать справедливость следующих свойств операции обращения :
a) $ (A^{-1})^{-1}=A_{} $;
б) $ (Acdot B)^{-1} = B^{-1}A_{}^{-1} $;
в) $ (A_{}^{top})^{-1}=(A^{-1})^{top} $;
г) $ det A_{}^{-1} = (det A)^{-1} $.
Предполагается, что в левой части каждого равенства операции определены.
§
Методы вычисления, свойства и применения обратной матрицы
☞
ЗДЕСЬ
Полином от матрицы и матричный полином
Для квадратной матрицы $ A_{} $ ее $ k_{} $-й степенью ($ k_{}in mathbb N $) называют результат умножения ее на себя $ k_{} $ раз:
$$ A^k = underbrace{Atimes dots times A}_k . $$
В виду ассоциативности операции умножения, скобки в этом произведении можно расставить произвольным образом. Дополнительно полагают $ A^{0} = E $ при ненулевой матрице $ A_{} $ и, в случае существования обратной матрицы, определяют и отрицательную степень:
$$ A^{-k} = (A^{-1})^k . $$
?
Показать, что
a) cтепени матрицы $ A_{} $ коммутируют: $ A^{k} A^{ell}= A^{ell} A^k $;
б) $ det (A^k) = left( det A right)^{k} $.
П
Пример. Вычислить
$$
left( begin{array}{rrr}
-3 & 2 & -3 \
-2 & 3 & -3 \
1 &-1 & 1
end{array}
right)^9
$$
Решение. Чтобы сэкономить на количестве матричных умножений, будем осуществлять их по схеме
$$
left(left(A^2 right)^2right)^2 A .
$$
Имеем
$$
A^2=left( begin{array}{rrr}
2 & 3 & 0 \
-3 & 8 & -6 \
0 &-2 & 1
end{array}
right) quad Rightarrow quad left(A^2 right)^2=
left( begin{array}{rrr}
-5 & 30 & -18 \
-30 & 67 & -54 \
6 &-18 & 13
end{array}
right) quad Rightarrow quad left(left(A^2 right)^2right)^2=
left( begin{array}{rrr}
-983 & 2184 & -1764 \
-2184 & 4561 & -3780 \
588 & -1260 & 1033
end{array}
right)
$$
и окончательно
$$
left(left(A^2 right)^2right)^2A=
left( begin{array}{rrr}
-3183 & 6350 & -5367 \
-6350 & 13095 & -10911 \
1789 & -3637 & 3049
end{array}
right) .
$$
♦
?
Проверить, что для матрицы из предыдущего примера, любая ее степень
$$ B=A^n $$
будет подчиняться условиям: $ b_{12}=-b_{21}^{} $ и $ b_{23}^{}=3 b_{32} $.
Обобщением возведения в степень является операция вычисления полинома от матрицы. Если $ g(x)=b_0x^m+b_1x^{m-1}+dots+b_{m} $ — полином по переменной $ x_{} $, то значением этого полинома на квадратной матрице $ A_{} $ называется матрица
$$ g(A)=b_0A^m +b_1A^{m-1}+dots+b_m E , $$
где $ E_{} $ — единичная матрица того же порядка, что и $ A_{} $.
П
Пример. Вычислить $ g(A)_{} $ для
$$ g(x)= 3,x^4-x^3+2,x^2-4,x-1 quad u quad
A=left( begin{array}{rrr}
1 & -3 & 4 \
3& 1 &8 \
-4 & -8 & 1
end{array}
right) .
$$
Решение. Можно было бы производить вычисления напрямую, но мы снова попытаемся сэкономить на количестве операций, действуя по схеме Хорнера:
$$
g(A)=(((3A-E)A+2E)A-4E)A-E .
$$
$$
B_1 = 3A-E =
left( begin{array}{rrr}
2 & -9 & 12 \
9& 2 & 24 \
-12 & -24 & 2
end{array}
right) ;
$$
$$
B_2=B_1A+2E=
left( begin{array}{rrr}
-71 & -111 & -52 \
-81& -215 & 76 \
-92 & -4 & -236
end{array}
right) ;
$$
$$
B_3=B_2A-4E=
left( begin{array}{rrr}
-200 & 518 & -1224 \
-1030& -584 & -1968 \
840 & 2160 & -640
end{array}
right) ;
$$
$$
g(A)=B_4=B_3A-E=
left( begin{array}{rrr}
6249 & 10910 & 2120 \
5090& 18249 & -10760 \
9880 & 4760 & 19999
end{array}
right)
$$
♦
§
Более подробный анализ структуры и изложение способов вычисления полинома от матрицы (а также таких функций как $ e^x, cos x , sin x ,
sqrt{x} $)
☞
ЗДЕСЬ.
Следующее определение сходно по звучанию с предыдущим, но не совпадает с ним по смыслу. Имеются разночтения в определении matrix polynomial — см. статьи Википедии Polynomial matrix и Matrix polynomial.
Рассмотрим квадратную матрицу, элементами которой являются полиномы над множеством $ mathbb A_{} $ (мы ограничимся случаями, когда это множество совпадает с одним из множеств $ mathbb Z_{},mathbb Q, mathbb R $ или $ mathbb C_{} $).
П
Пример.
$$
A(x)=left(
begin{array}{ccc}
3x^2+4x+1 & x^3 – sqrt{3} & -2,x +1 \
x^2-1 & 7,x^3-x+4 & 6,x^2-3,x+1 \
4,x^3-7,x^2+3,x-2 & 2,x-17 & x^2
end{array}
right) .
$$
Такую матрицу можно представить в виде полинома по $ x_{} $ с матричными коэффициентами:
$$
A(x)= left(
begin{array}{ccc}
0 & 1 & 0 \
0 & 7 & 0 \
4 & 0 & 0
end{array}
right) x^3 +
left(
begin{array}{rcc}
3 & 0 & 0 \
1 & 0 & 6 \
-7 & 0 & 1
end{array}
right) x^2 +
left(
begin{array}{rrr}
4 & 0 & -2 \
0 & -1 & -3 \
3 & 2 & 0
end{array}
right) x
+left(
begin{array}{rrr}
1 & – sqrt{3} & 1 \
-1 & 4 & 1 \
-2 & -17 & 0
end{array}
right) .
$$
В общем случае полиномиальная матрица имеет вид
$$
A(x)=A_0 x^m + A_1 x^{m-1}+dots+A_m ,
$$
где $ A_0,dots,A_{m} $ — квадратные числовые матрицы одинакового порядка $ n_{} $.
Часто полиномиальная матрица называется матричным полиномом по $ x_{} $ (или же полиномом по $ x_{} $ с матричными коэффициентами).
Если при этом $ A_0 ne mathbb O $, то $ n_{} $ называют степенью полиномиальной матрицы. Если,
вдобавок, матрица $ A_{0} $
невырожденная, то матричный полином называется регулярным.
Матричные уравнения
Матрица может быть определена не только явным образом, но и заданием соотношения, которому она должна удовлетворять. Так, к примеру обратная матрица для квадратной матрицы $ A $ фактически определялась как решение матричного уравнения $ AX= E $. Отсутствие свойства коммутативности умножения порождает причудливые комбинации, не имеющие аналогов в скалярном случае.
Уравнение Ляпунова
имеет вид
$$ A^{top}X+XA=C $$
при заданной матрице $ A_{} $ и заданной симметричной матрице $ C_{} $ (обе — квадратные одинакового порядка $ n_{} $),
относительно неизвестной матрицы $ X_{} $, которая разыскивается также во множестве симметричных матриц порядка $ n_{} $.
Имеет важное значение в теории управления.
Уравнение является частным случаем матричного уравнения Сильвестра
$$ AX+XB=C $$
при произвольных квадратных матрицах $ A,B,C_{} $.
!
Далее идет сложный для понимания материал!
Пример. Решить матричное уравнение Сильвестра для матриц второго порядка:
$$ A=left(
begin{array}{cc}
a_{11} & a_{12} \
a_{21} & a_{22}
end{array}
right) ,
B=left(
begin{array}{cc}
b_{11} & b_{12} \
b_{21} & b_{22}
end{array}
right) ,
C=left(
begin{array}{cc}
c_{11} & c_{12} \
c_{21} & c_{22}
end{array}
right) .
$$
Решение. Подставляя в уравнение матрицу
$$
X=left(
begin{array}{cc}
x_{11} & x_{12} \
x_{21} & x_{22}
end{array}
right) ,
$$
с пока неопределенными элементами, получаем систему линейных уравнений, которую тоже запишем в матричном виде:
$$
left( begin{array}{cccc}
a_{11}+b_{11} & a_{12} & b_{21} & 0 \
a_{21} & a_{22}+b_{11} & 0 & b_{21} \
b_{12} & 0 & a_{11}+b_{22} & a_{12} \
0 & b_{12} & a_{21} & a_{22}+b_{22}
end{array}
right)
left( begin{array}{c}
x_{11} \ x_{21} \ x_{12} \ x_{22}
end{array}
right)=
left( begin{array}{c}
c_{11} \ c_{21} \ c_{12} \ c_{22}
end{array}
right)
$$
(матрицы $ X_{} $ и $ C_{} $ «вытянули» в строки). Матрица в левой части имеет порядок $ 4_{} $ и может быть представлена в виде суммы двух матриц:
$$
left( begin{array}{cccc}
a_{11}+b_{11} & a_{12} & b_{21} & 0 \
a_{21} & a_{22}+b_{11} & 0 & b_{21} \
b_{12} & 0 & a_{11}+b_{22} & a_{12} \
0 & b_{12} & a_{21} & a_{22}+b_{22}
end{array}
right)=
left( begin{array}{cccc}
a_{11} & a_{12} & 0 & 0 \
a_{21} & a_{22} & 0 & 0 \
0 & 0 & a_{11} & a_{12} \
0 & 0 & a_{21} & a_{22}
end{array}
right)
+
left( begin{array}{cccc}
b_{11} & 0 & b_{21} & 0 \
0 & b_{11} & 0 & b_{21} \
b_{12} & 0 & b_{22} & 0 \
0 & b_{12} & 0 & b_{22}
end{array}
right) .
$$
Для формализации записи этих двух слагаемых придумана специальная операция
☞
КРОНЕКЕРОВО ПРОИЗВЕДЕНИЕ. Пока не останавливаясь на этом формализме, вычислим определитель: получим крайне громоздкий полином $ 4_{} $-й степени относительно элементов матриц $ A_{} $ и $ B_{} $. Оказывается, этот полином совпадает
с результантом характеристического полинома матрицы $ A_{} $ и характеристического полинома матрицы $ (-B_{}) $:
$$ mathcal R (det(A-lambda E), det(-B-lambda E)) . $$
Если это выражение отличо от нуля, то матричное уравнение $ AX+XB=C $ имеет решение при любой матрице $ C_{} $.
♦
Квадратные уравнения
?
Уравнение $ x^2=-1 $ не имеет решения в вещественных числах. Можно ли утверждать аналогичное для уравнения матричного:
$$X^2=-
left(
begin{array}{rr}
1 & 0 \
0 & 1
end{array}
right) ?
$$
Эта задача — вычисления квадратного корня из матрицы — является частью общей задачи о вычислении аналитической функции от матрицы, т.е. произвольной функции $ g(x) $, представимой в виде сходящегося ряда. Частным случаем задачи является рассмотренная выше задача вычисления полинома от матрицы. Подробнее об этой задаче
☞
ЗДЕСЬ.
Уравнение
$$ A^{top}X+XA-X^{top}BX=C $$
называется матричным уравнением Риккати. Уравнение Ляпунова получается из него при нулевой матрице $ B $.
Матрица квадратичной формы
рассматривается
☞
ЗДЕСЬ
Матрица преобразования координат
— это матрица, связывающая координаты произвольного
вектора $ X_{} $ из $ n_{} $—мерного линейного пространства в двух различных базисах $ {X_1,dots,X_n} $ и $ {{mathfrak X}_1,dots,{mathfrak X}_n} $ этого пространства:
$$X=x_1X_1+dots+x_nX_n={mathfrak x}_1{mathfrak X}_1+dots+{mathfrak x}_n{mathfrak X}_n
.$$
Называется также матрицей перехода от базиса к базису. Подробнее
☞
ЗДЕСЬ.
Матрица линейного отображения
— это матрица, связывающая координаты произвольного вектора $ X_{} $ из линейного пространства $ mathbb V_{} $ с координатами его образа $ Y_{} $ в линейном пространстве $ mathbb W_{} $ при выборе некоторых фиксированных базисов этих пространств.
Подробнее
☞
ЗДЕСЬ.
Задачи
Источники
Координаты вектора в базисе
Пример №1 . Даны векторы ε1(2;1;3), ε2(3;-2;1), ε3(1;-3;-4), X(7;0;7). Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора X в этом базисе.
Решение. Данная задача состоит из двух частей. Сначала необходимо проверить, образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису.
Вычислим определитель матрицы:
∆ = 2*((-2)*(-4) – (-3)*1) – 3*(1*(-4) – (-3)*3) + 1*(1*1 – (-2)*3) = 14
Определитель матрицы равен ∆ =14
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α1α2α3, что имеет место равенство:
X = α1ε1 + α2ε2 + α3ε3
Запишем данное равенство в координатной форме:
(7;0;7) = α(2;1;3) + α(3;-2;1) + α(1;-3;-4)
Используя свойства векторов, получим следующее равенство:
(7;0;7) = (2α1;1α1;3α1😉 + (3α2;-2α2;1α2😉 + (1α3;-3α3;-4α3😉
(7;0;7) = (2α1 + 3α2 + 1α3;1α1 -2α2 -3α3;3α1 + 1α2 -4α3)
По свойству равенства векторов имеем:
2α1 + 3α2 + 1α3 = 7
1α1 -2α2 -3α3 = 0
3α1 + 1α2 -4α3 = 7
Решаем полученную систему уравнений методом Гаусса или методом Крамера.
Ответ:
X = 2ε1 + ε2
В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
Пример №2 . В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
a1=(1;5;3), a2=(2;1;-1), a3=(4;2;1), a4=(17;13;4).
5.1.6. Примеры решения задач по теме «Линейные операторы и квадратичные формы»
Пусть Е1, Е2, Е3, Е4 – базис в векторном пространстве. Разложить вектор
Выпишите матрицу перехода от старого базиса к новому, столбцами которой являются координаты новых базисных векторов в старом базисе. Строки этой матрицы являются коэффициентами в формулах преобразования старых координат через новые.
Выпишем матрицу перехода от старого базиса к новому, столбцами которой являются координаты новых базисных векторов в старом базисе:

Строки этой матрицы являются коэффициентами в формулах преобразования старых координат через новые.
Координаты вектора Х в старом базисе: Х = (1; 2; -1; 3). Пусть в новом базисе он имеет координаты: X = (X, Y, Z, T). Тогда, используя матрицу Т, найдем связь между старыми и новыми координатами:

Следовательно, в новом базисе Х = (-1; 3; -4; 3).
Найти матрицу А’ оператора А:
Искомая матрица А’ = T-1 A T, где Т – матрица перехода из старого базиса к новому.
Искомая матрица А’ = T-1 A T, где Т – матрица перехода из старого базиса к новому. Составим матрицу Т :



Ответ: 
Найти собственные числа и собственные векторы линейного оператора, заданного матрицей

Для определения собственных чисел составьте характеристическое уравнение:
Координаты собственных векторов RI = (Xi, Yi) должны удовлетворять системе уравнений, коэффициенты которых получены из элементов строк определителя, стоящего в левой части характеристического уравнения, при подстановке LI.
Составим характеристическое уравнение:
Найдем собственные векторы:
1) для L = -2 координаты собственного вектора R1 = (X1, Y1) должны удовлетворять системе уравнений, коэффициенты которых получены из элементов строк определителя, стоящего в левой части характеристического уравнения, при подстановке L = -2:
Если Х1 = 1, то У1 = -1, и R1= (1; -1). Остальные собственные векторы коллинеарны вектору (1; -1), и общий вид собственного вектора, соответствующего L = -2: R1 = С1(1; -1), где С1 – произвольная постоянная.
2) для L = 6 координаты собственного вектора R2 (X2; Y2) удовлетворяют системе:
Пусть Х2 = 3, тогда У2 = 5, и R2 = (3; 5). Соответственно общий вид второго собственного вектора: R2 = С2(3; 5).
Ответ: собственные числа L1 = -2, L2 = 6; собственные векторы R1 = С1(1; -1),
В пространстве 3-мерных векторов задан оператор
Где I – базисный вектор декартовой системы координат.
Выяснить геометрический смысл этого оператора.
Множитель Xi – скалярное произведение, то есть число, поэтому вектор (Xi)I коллинеарен оси Ох.
Оператор А переводит произвольно направленный вектор Х в вектор
KI, коллинеарный оси Ох, поскольку первый множитель – скалярное произведение, то есть число. Из определения скалярного произведения следует, что
Следовательно, А – оператор проектирования на ось Ох.
Оператор осуществляет проектирование вектора Х на ось Ох;
Привести матрицу А линейного оператора к диагональному виду и найти соответствующий базис, если
Найдите собственные числа и собственные векторы матрицы линейного оператора, задайте базис из линейно независимых собственных векторов R1, R2, R3 , в котором матрица оператора примет диагональный вид, и составьте матрицу перехода к новому базису.
Найдем собственные векторы, соответствующие полученным собственным числам.
Подставим в строки определителя L = 2 и найдем связь между координатами собственного вектора R2 = (X2, Y2, Z2):
Та же зависимость получается для координат третьего собственного вектора R3 = (X3, Y3, Z3). Выберем значения двух координат каждого из этих векторов так, чтобы R2 и R3 были линейно независимы.
Пусть Х2 = 1, У2 = 0, тогда Z2 = -3, и R2 = (1; 0; -3).
Получен базис из линейно независимых собственных векторов R1, R2, R3 , в котором матрица оператора примет диагональный вид.
Составим матрицу перехода к новому базису:
Найдем матрицу, обратную к Т:

Тогда в базисе из собственных векторов матрица оператора
Ответ: в базисе (1; 1; 1), (1; 0; -3), (0; 1; 3) матрица оператора
Линейный оператор А задан в некотором базисе матрицей
Найти собственные числа и собственные векторы оператора А-1 – оператора, обратного к А.
Собственные числа обратного оператора являются обратными к собственным числам данного оператора, а их собственные векторы одинаковы.
Характеристическое уравнение для А:
Найдем матрицу обратного оператора:

Соответствующее характеристическое уравнение:
Составить матрицу квадратичной формы 3Х2 – 10Ху + 8У2 и найти ее собственные числа.
Матрица квадратичной формы А11Х2 + 2А12Ху + А22У2 является
Симметрической (Aij = Aji) и имеет вид:
В нашей задаче А11 = 3, А12 = -5, А22 = 8. Следовательно,
Составим характеристическое уравнение, корнями которого являются собственные числа:
Ответ: матрица квадратичной формы 
Собственные числа
Найти базис, в котором квадратичная форма 2Х2 + 4Ху + 5У2 будет иметь канонический вид, и указать этот вид.
Канонический вид квадратичной формы:
1) во-первых, не содержит произведения Ху;
2) во-вторых, коэффициенты при Х2 и У2 равны собственным числам матрицы квадратичной формы.
Базис, в котором квадратичная форма имеет канонический вид, состоит из нормированных собственных векторов матрицы квадратичной формы.
Матрица квадратичной формы
Собственные числа: L1 = 1, L2 = 6.
Для L1 = 1 координаты вектора R1 = <X1, Y1> определяются уравнением
Х1 + 2У1 = 0, Х1 = -2У1. Если У1 = 1, то Х1 = -2, и R1 = C<-2; 1>. Найдем значение С из условия, что вектор R1 нормирован, то есть его длина равна 1:
Итак, базис имеет вид:
И в этом базисе квадратичная форма примет вид: L1Х2 + L2У2, то есть Х2 + 6У2.
Ответ: в базисе 
Указать преобразование координат, приводящее квадратичную форму
8Х2 – 12Ху + 17У2 к каноническому виду.
Матрица преобразования координат имеет вид:
Где R1 = (X1, Y1) и R2 = (X2, Y2) – нормированные собственные векторы.
Найдем базис из нормированных собственных векторов.
Составим матрицу перехода к новому базису, столбцами которой будут координаты новых базисных векторов R1, R2 в старом базисе:
Строки этой матрицы определяют коэффициенты уравнений, выражающих старые координаты через новые:
Где Х, У – координаты в старом базисе, а Х’, Y’ – в новом.
Таким образом, найдено искомое преобразование.
Ответ: 
Привести к каноническому виду квадратичную форму 5Х2 – 12Ху.
Матрица преобразования координат имеет вид:
Где R1 = (X1, Y1) и R2 = (X2, Y2) – нормированные собственные векторы. В новом базисе квадратичная форма имеет канонический вид, причем коэффициенты при Х2 и У2 совпадают с собственными числами матрицы квадратичной формы.
Матрица перехода к базису из собственных векторов:
Подставим найденные выражения в квадратичную форму:
Как и следовало ожидать, в новом базисе квадратичная форма имеет канонический вид, причем коэффициенты при Х2 и У2 совпадают с собственными числами матрицы квадратичной формы.
Найти преобразование координат, приводящее квадратичную форму
X2 + Y2 + 5Z2 – 6Xy + 2Xz – 2Yz к каноническому виду.
Матрица преобразования координат:
Для заданной квадратичной формы
Составим и решим характеристическое уравнение:
(Мы не останавливаемся подробно на способах решения уравнений высших порядков. В данном случае, например, один из корней был найден перебором делителей свободного члена, а затем левая часть разложена на множители.)
Найдем нормированные собственные векторы:
Матрица перехода к новому базису:
Задает преобразование координат:
Заметим, что в новых координатах квадратичная форма примет вид:
Где коэффициенты являются собственными числами, стоящими в той же последовательности, что и соответствующие собственные векторы в матрице Т.
Ответ:
Матрица линейного оператора примеры
Построение матрицы по заданной формуле отображения.
Пусть отображение задано с помощью формулы:
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор 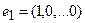
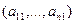
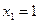
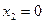
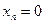
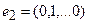
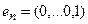
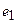
Пример 1. Пусть оператор задан с помощью формулы:
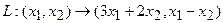
Прежде всего, докажем, что это отображение – действительно линейный оператор.
Отобразим сумму векторов:
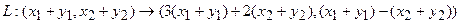
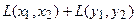
Аналогично для умножения на константу:
Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x1 = 1, x2 = 0, а затем x1 = 0, x2 = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).
Поэтому матрица линейного оператора будет иметь вид:
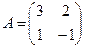
Аналогичным способом решается задача и для 3 и большего количества переменных.
Пример 2. 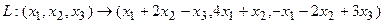
Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).
Матрица линейного оператора:
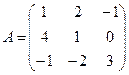
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.
Если задана система 
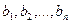
Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.
Пусть 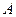
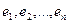
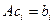
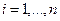
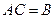
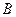
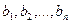
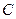
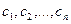
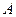
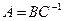
Пример. Найти матрицу линейного оператора, отображающего базис
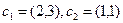
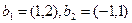
Здесь 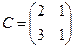
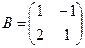
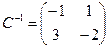
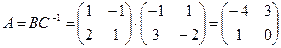
Проверка осуществляется умножением получившейся матрицы на каждый вектор: 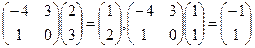
Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.
2.3. Прочие способы нахождения матрицы оператора.
Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида 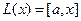
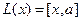
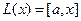
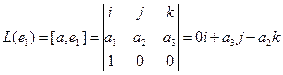
Аналогично, 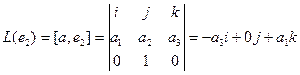
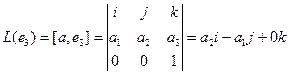
Координаты полученных векторов запишем в виде столбцов матрицы оператора.
Матрица оператора: 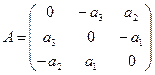
Аналогично можно построить матрицу линейного оператора 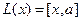
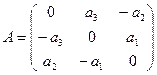
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы 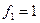
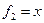
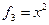
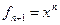
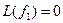
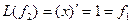
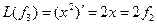
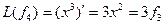
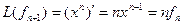
Матрица этого линейного оператора:
Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Матрица линейного оператора
Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:
Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:
Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .
Разложим векторы x и y по базису e 1 ,e 2 . e n :
В силу линейности оператора A можно написать
Заметим, что каждый вектор 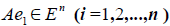
В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:
Получили, что линейному оператору A в данном базисе соответствует квадратная матрица
которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .
Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .
Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .
Примеры линейных операторов
1. В пространстве 2-мерных векторов линейным оператором является правило
связывающее вектор-прообраз 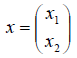
2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.
3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .
Пример: Известны образы базисных векторов E 3 под действием оператора A :
Найти матрицу этого оператора в исходном базисе.
Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем
Действия над операторами
Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.
Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .
Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .
Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.
Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством 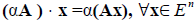
?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.
Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .
Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .
Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .
Рассмотрим матрицы – столбцы:
и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.
a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y
б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x
Свойства умножения линейных операторов вытекают из свойств умножения матриц.
Определение 4. Линейные операторы A и В называются равными, если 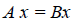
Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 
1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 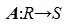
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы 

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов 

Пусть x − произвольный элемент в R. Тогда
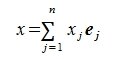 |
(3) |
является разложением x в по базису 
Применим оператор A к базисным векторам 
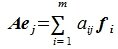 |
(4) |
где aij − координаты полученного вектора в базисе 
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
Сделаем следующее обозначение:
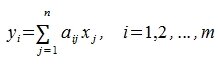 |
(6) |
Тогда равенство (5) примет следующий вид:
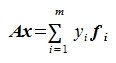 |
(7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе 
Построим матрицу A с элементами aij:
 |
(8) |
Тогда выражение (6) можно записать в матричном виде:
Матрица A называется матрицей линейного оператора в заданных базисах 

2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej= Aej+ Bej= | n | (aij+bij) ej |
| ∑ | ||
| j= 1 |
Следовательно оператору C отвечает матрица 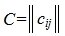
3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
можно записать в виде матричных равенств
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
Учитывая произвольность х, получим
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
[spoiler title=”источники:”]
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/5-1-6-primery-resheniia-zadach-po-teme-lineinye-operatory-i-kvadratichnye-formy
http://planshet-info.ru/kompjutery/matrica-linejnogo-operatora-primery
[/spoiler]
Как найти расположение элемента в матрице
Вопрос:
У меня есть матрица A, что некоторые элементы этой матрицы повторяются. Мне нужно найти места
элемент в этой матрице. Как я могу это сделать?
Благодарю.
Лучший ответ:
Функция find может дать вам индексы столбцов строки.
Например
>> [r c] = find( A == 3 )
Ответ №1
Надеюсь, это поможет. Синтаксис
ind = find(X)
ind = find(X, k)
ind = find(X, k, 'first')
ind = find(X, k, 'last')
[row,col] = find(X, ...)
[row,col,v] = find(X, ...)
Ссылка:
http://www.mathworks.in/help/matlab/ref/find.html
Ответ №2
Я вижу, у вас уже есть ответы на вопрос о том, как найти элементы. Вот как работать с повторяющимися элементами.
Прежде всего, вы можете найти уникальные элементы:
v = [1:4 2:5] % Suppose this is your vector
[v_unique, idx] = unique(v,'first')
v_unique – теперь ваш вектор с удаленными дубликатами. Однако, если вас интересуют местоположения дубликатов, это даст вам список:
setxor(idx,1:numel(v))

 Сообщение было отмечено Ychenyi как решение
Сообщение было отмечено Ychenyi как решение