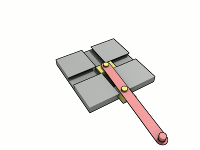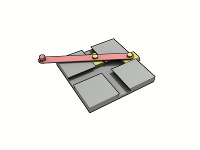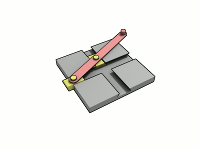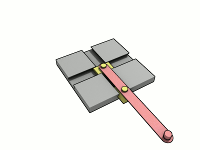
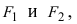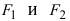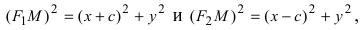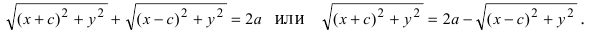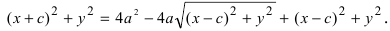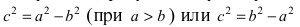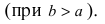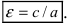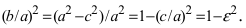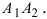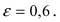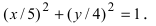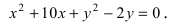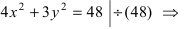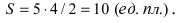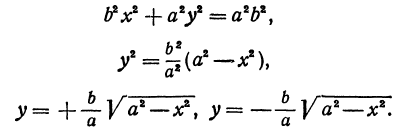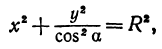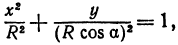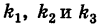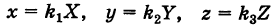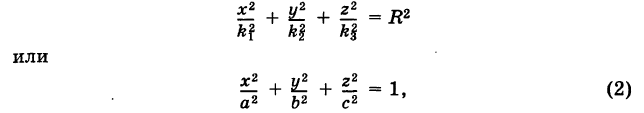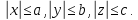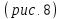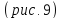Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.
ВНИМАНИЕ! Если Вы искали как найти координаты точки по углу от произвольной прямой и совсем не подразумевали эллипс, то Вам сюда.
Калькулятор точки на эллипсе
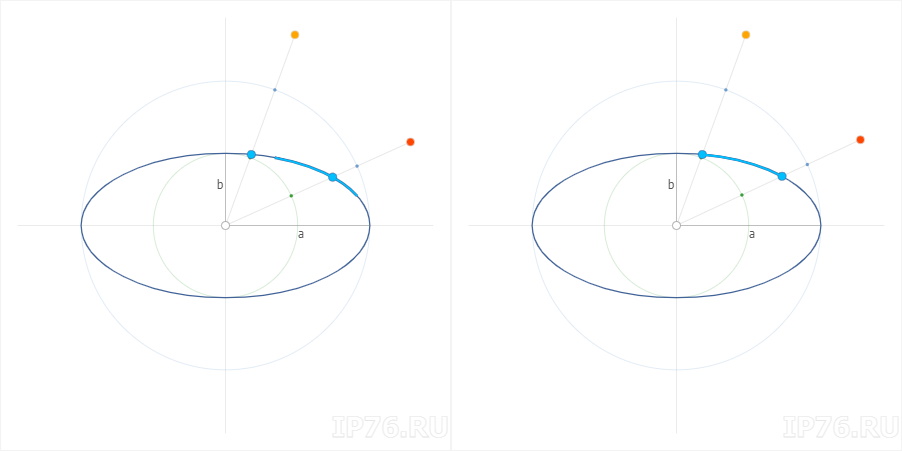
Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.
Маркеры кликабельны и таскабельны.
Если есть вопросы, предложения по калькулятору или заметили ошибку, буду очень рад обратной связиx
Эллипс:
a:
b:
Углы (град.):
Get a better browser, bro…
Параметрическое уравнение эллипса
Обратимся, как обычно, к Википедии. Находим там следующее:
Каноническое уравнение эллипса может быть параметризовано:
Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.
Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.
Подготовка
У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.
Проведем прямую из общего центра [X0;Y0] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X1;Y1] и [X2;Y2].
α – угол между прямой и осью X.
| Малая окружность | X1 = b × cos α | Y1 = b × sin α |
| Большая окружность | X2 = a × cos α | Y2 = a × sin α |
Нахождение зависимости
Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X0;Y0] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.
Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.
Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:
X’ = X2 = a × cos α
Y’ = Y1 = b × sin α
Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.
Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.
Тангенс угла β в этом случае равен:
(3) Тангенс угла β
Используя формулу тангенса произведем дальнейшие преобразования:
(4) Зависимость тангенса α от тангенса β
Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.
Нахождение координат
Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.
Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):
|
//– находим параметр (некий угол) для уравнения — SinCos(Angle,sn,cs); t := ArcTan2(a*sn, b*cs); |
Получившийся в результате вызова ArcTan2 угол есть ничто иное, как параметр t в параметрическом уравнении (1). Подставив его в уравнение, находим координаты точки на эллипсе, отстоящей на заданный угол от оси X.
О параметре
Практический смысл параметра t состоит в том, что это угол окружности до «сплющивания». Этот тот угол окружности, который будет соответствовать точке эллипса при заданном угле. Попытаюсь на практике показать.
В JavaScript’е нет понятия эллипс. Тем более нет понятия дуги эллипса. Но можно нарисовать окружность (через дугу) и «сплющить». Может быть такой номер пройдет и с дугой?
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
// рисует дугу эллипса function drawArcEllipse(ctx, center, a, b, start, finish, colorLine=‘none’, widthLine=0.0, angle=0.0) { if (a==0.0) return; var t1 = start; var t2 = finish; ctx.beginPath(); // сохраняем контекст ctx.save(); // перемещение координат в центр эллипса ctx.translate(center.x, center.y); // поворот плоскости на угол, если требуется if (angle!=0.0) ctx.rotate(angle); // сжимаем по вертикали ctx.scale(1, b/a); // рисуем дугу ctx.arc(0, 0, a, t1, t2); // восстанавливает контекст ctx.restore(); if (colorLine!=‘none’) ctx.strokeStyle = colorLine; if (widthLine>0.0) ctx.lineWidth = widthLine; ctx.stroke(); ctx.closePath(); } |
На рисунке слева видим, что дуга расположена совершенно неправильно. Очевидно, что надо использовать какие-то другие углы. Вот тут на помощь приходит параметр эллипса. Это как раз тот самый угол, который обеспечивает «попадание» в нужный нам угол при «сплющивании» окружности.
Перепишем функцию с учетом нахождения параметра:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
// рисует дугу эллипса function drawArcEllipse(ctx, center, a, b, start, finish, colorLine=‘none’, widthLine=0.0, angle=0.0) { if (a==0.0) return; var sn = Math.sin(start); var cs = Math.cos(start); var t1 = Math.atan2(a*sn, b*cs); sn = Math.sin(finish); cs = Math.cos(finish); var t2 = Math.atan2(a*sn, b*cs); ctx.beginPath(); // сохраняем контекст ctx.save(); // перемещение координат в центр эллипса ctx.translate(center.x, center.y); // поворот плоскости на угол, если требуется if (angle!=0.0) ctx.rotate(angle); // сжимаем по вертикали ctx.scale(1, b/a); // рисуем дугу ctx.arc(0, 0, a, t1, t2); // восстанавливает контекст ctx.restore(); if (colorLine!=‘none’) ctx.strokeStyle = colorLine; if (widthLine>0.0) ctx.lineWidth = widthLine; ctx.stroke(); ctx.closePath(); } |
На рисунке справа видим, что все встало на свои места. Идеальная дуга )
Координаты точки наклонного эллипса
Перенесено в отдельную статью.
Практика
Две функции. Первая находит параметр t по углу. Вторая производит расчет координат. Из второй не вызываю первую, т.к. получится двойное вычисление полуосей. Код не настолько велик, чтобы его нельзя было продублировать.
|
//****************************************************************** // Найти угол, который будет использован в расчете точки на элипсе // Т.е. тот самый параметр t в параметрическом уравнении эллипса: // x = a * cos t // y = b * sin t //****************************************************************** function GetEllipseAngleParam(ARect : TRectF; Angle : Extended) : Extended; var sn,cs : Extended; // синус/косинус a,b : Extended; // полуоси по X/Y begin a := ARect.Width/2; b := ARect.Height/2; SinCos(Angle,sn,cs); result := ArcTan2(a * sn, b * cs); end; |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
//******************************************************************** // Найти координату точки на эллипсе по углу отклонения //******************************************************************** function CalcEllipsePointCoord(ARect : TRectF; Angle : extended) : TPointF; var sn,cs : Extended; // синус/косинус a,b : Extended; // полуоси по X/Y cnt : TPointF; // центр t : Extended; // параметр для уравнения эллипса begin // инициализация полуосей a := ARect.Width/2; b := ARect.Height/2; // центр эллипса cnt := ARect.CenterPoint; // находим параметр (некий угол) для уравнения SinCos(Angle,sn,cs); t := ArcTan2(a * sn, b * cs); // считаем результат по параметрическому уравнению SinCos (t, sn, cs); result.X := cnt.x + a * cs; result.Y := cnt.Y + b * sn; end; |
Скачать исходник + исполнямый файл
Друзья, спасибо за внимание!
Надеюсь, материал после правок стал понятней.
Подписывайтесь на телегу.
Если есть вопросы, с удовольствием отвечу )
Эллипс, его фокусы и главные оси
Эллипс как коническое сечение, его фокусы и директрисы, получаемые геометрически с помощью шаров Данделена.
Э́ллипс (др.-греч. ἔλλειψις «опущение; нехватка, недостаток (эксцентриситета до 1)») — замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость.
Окружность является частным случаем эллипса с эксцентриситетом 
Определение[править | править код]
Эллипс — геометрическое место точек M евклидовой плоскости, для которых сумма расстояний до двух данных точек 

, причём
Другие определения[править | править код]
Эллипс также можно определить как:
- фигуру, которую можно получить из окружности, применяя аффинное преобразование
- ортогональную проекцию окружности на плоскость
- пересечение плоскости и кругового цилиндра.
Связанные определения[править | править код]
- Проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
- Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
- Точка пересечения большой и малой осей эллипса называется его центром.
- Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
- Расстояния
и
от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
- Расстояние
называется фокальным расстоянием.
- Величина
называется эксцентриситетом.
- Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
- Радиус эллипса в данной точке это отрезок, соединяющий центр эллипса с точкой, а также его длина, которая вычисляется по формуле
, где
— угол между радиусом и большой полуосью.
- Фокальным параметром
называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
- Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью:
. Величина, равная
называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент сжатия и эксцентриситет эллипса связаны соотношением
- Для каждого из фокусов существует прямая, называемая директрисой, такая, что отношение расстояния от произвольной точки эллипса до его фокуса к расстоянию от этой точки до данной прямой равно эксцентриситету эллипса. Весь эллипс лежит по ту же сторону от такой прямой, что и фокус. Уравнения директрис эллипса в каноническом виде записываются как
для фокусов
соответственно. Расстояние между фокусом и директрисой равно
.
Соотношения между элементами эллипса[править | править код]
Части эллипса (описание см. в разделе «Связанные определения»)
— большая полуось;
— малая полуось;
— фокальное расстояние (полурасстояние между фокусами);
— фокальный параметр;
— перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
— апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);




|

|

|

|

|

|
|
|---|---|---|---|---|---|---|
 — большая полуось — большая полуось
|

|

|

|

|

|

|
 — малая полуось — малая полуось
|

|

|

|

|

|

|
 — фокальное расстояние — фокальное расстояние
|

|

|

|

|

|

|
 — фокальный параметр — фокальный параметр
|

|

|

|

|

|

|
 — перифокусное расстояние — перифокусное расстояние
|

|

|

|

|

|

|
 — апофокусное расстояние — апофокусное расстояние
|

|

|

|

|

|

|
Координатное представление[править | править код]
Эллипс как кривая второго порядка[править | править код]
Эллипс является центральной невырожденной кривой второго порядка и удовлетворяет общему уравнению вида
при инвариантах 

Соотношения между инвариантами кривой второго порядка и полуосями эллипса (верно только при условии, что центр эллипса совпадает с началом координат и 
Соотношения
Если переписать общее уравнение в виде
то координаты центра эллипса:
угол вращения определяется из выражения
Направления векторов осей:
отсюда
Длины полуосей определяются выражениями
Обратное соотношение — коэффициенты общего уравнения из параметров эллипса — можно получить, подставив в каноническое уравнение (см. раздел ниже) выражение для поворота системы координат на угол Θ и переноса в точку 
Выполнив подстановку и раскрыв скобки, получим следующие выражения для коэффициентов общего уравнения:
Если ввести только угол, а центр эллипса оставить в начале координат, то
Следует заметить, что в уравнении общего вида эллипса, заданного в декартовой системе координат, коэффициенты 

где 
будет выполняться при любом 
Соотношение между инвариантой 
где 

Другие инварианты находятся в следующих соотношениях:
Каноническое уравнение[править | править код]
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением:
Это уравнение называется каноническим уравнением эллипса. Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат[Комм. 1].
Соотношения[править | править код]
Для определённости положим, что
В этом случае величины 

Зная полуоси эллипса, можно вычислить:
- его фокальное расстояние и эксцентриситет
- координаты фокусов эллипса
Эллипс имеет две директрисы, уравнения которых можно записать как
Фокальный параметр (то есть половина длины хорды, проходящей через фокус и перпендикулярной оси эллипса) равен
Фокальные радиусы, то есть расстояния от фокусов до произвольной точки кривой 
Уравнение диаметра, сопряжённого хордам с угловым коэффициентом 
Уравнение касательной к эллипсу в точке 
Условие касания прямой 


Уравнение касательных, проходящих через точку 
Уравнение касательных, имеющих данный угловой коэффициент 
точки касания такой прямой эллипса (или что то же самое, точки эллипса, где касательная имеет угол с тангенсом, равным 
Уравнение нормали в точке 
Уравнения в параметрической форме[править | править код]
Геометрическая иллюстрация параметризации эллипса (анимация)
Каноническое уравнение эллипса может быть параметризовано:
где 
Только в случае окружности (то есть при 

В полярных координатах[править | править код]
Если принять фокус эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах 
где e — эксцентриситет, а p — фокальный параметр.
Знак минус соответствует помещению полюса полярных координат в левый фокус, а знак плюс — в правый.
Вывод уравнения[править | править код]
Пусть r1 и r2 — расстояния до данной точки эллипса от первого и второго фокусов.
Пусть также полюс системы координат находится в первом фокусе, а угол 
Тогда из определения эллипса следует, что
.
Отсюда 
С другой стороны, из теоремы косинусов
Исключая 
Учитывая, что 

Если принять центр эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах 
Длина дуги эллипса (
s) в зависимости от его параметра (
θ)
Длина дуги эллипса[править | править код]
Длина дуги плоской линии определяется по формуле:
Воспользовавшись параметрическим представлением эллипса, получаем следующее выражение:
После замены 
Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к эллиптическому интегралу второго рода 
где 
Приближённые формулы для периметра[править | править код]

Максимальная погрешность этой формулы 


Погрешность всегда положительна.
Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:

Максимальная погрешность этой формулы 


Погрешность также всегда положительна.
Существенно лучшую точность при 
![{displaystyle Lapprox pi left[3(a+b)-{sqrt {(3a+b)(a+3b)}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd919c01064b504e3a2107daeb14e81db8d394ba)
При эксцентриситете эллипса 


Погрешность всегда отрицательна.
Ещё точней оказалась вторая формула Рамануджана:
![{displaystyle Lapprox pi (a+b)left[1+{frac {3left({frac {a-b}{a+b}}right)^{2}}{10+{sqrt {4-3left({frac {a-b}{a+b}}right)^{2}}}}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d67456329cc94bf72277ecc25d1950bfc160c3f)
Точные формулы для периметра[править | править код]
Джеймс Айвори[1] и Фридрих Бессель[2] независимо друг от друга получили формулу для периметра эллипса:
Альтернативная формула
где 

а 

Площадь эллипса и его сегмента[править | править код]
Площадь эллипса вычисляется по формуле
Площадь сегмента между дугой[en], выпуклой влево, и вертикальной хордой, проходящей через точки 

Если эллипс задан уравнением

Другие свойства[править | править код]
- Оптические
- Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
- Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
- Если
и
— фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой
равен углу между этой касательной и прямой
.
- Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
- Эквивалентная формулировка: через середины двух любых параллельных хорд эллипса проходит какой-либо диаметр эллипса. В свою очередь, любой диаметр эллипса всегда проходит через центр эллипса.
- Эволютой эллипса является астроида, вытянутая вдоль вертикальной оси.
- Точки пересечения эллипса с осями являются его вершинами.
- Эксцентриситет эллипса, то есть отношение
характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
- Если эксцентриситет эллипса равен нулю (что то же самое, что фокальное расстояние равно нулю:
), то эллипс вырождается в окружность.
- Если эксцентриситет эллипса равен нулю (что то же самое, что фокальное расстояние равно нулю:
- Экстремальные свойства[5]
-
- где
обозначает площадь фигуры
.
- Более того, равенство достигается в том и только в том случае, если
ограничено эллипсом.
- Более того, равенство достигается в том и только в том случае, если
- Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипсы и только они имеет максимальную аффинную длину.
- где
- Если произвольный эллипс вписан в треугольник ABC и имеет фокусы P и Q, тогда для него справедливо соотношение[6]
- Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (всё время касаясь её) а второй конец лестницы будет скользить по полу (всё время касаясь его), тогда любая фиксированная точка лестницы (не на её концах), будет двигаться по дуге некоторого эллипса. Это свойство остаётся верным, если мы возьмём точку не внутри лестницы-отрезка, а на её мыслимом продолжении. Последнее свойство используется в описанном выше[⇦] эллипсографе.
- Касательная, проходящая через точку
, принадлежащую эллипсу, имеет следующее уравнение:
Построение эллипса[править | править код]
|
|
Построение эллипса с помощью иголок, нитки и карандаша |
Инструментами для рисования эллипса являются:
- эллипсограф
- две иголки, воткнутые в фокусы эллипса и соединённые ниткой длиной 2a, которую оттягивают карандашом. Способ был придуман Джеймсом Максвеллом в возрасте 14 лет и при запросе его отца в Эдинбургское королевское общество оказался ранее неизвестным[7].
При помощи циркуля или циркуля и линейки можно построить любое количество точек, принадлежащих эллипсу, но не весь эллипс целиком.
Эллипсы, связанные с треугольником[править | править код]
- Эллипс Брокара — эллипс с фокусами в точках Брокара
- Эллипс Мандарта
- Эллипс Штейнера
См. также[править | править код]
- Кривая второго порядка
- Парабола
- Каустика
- Эллипсоид
- Эллипсограф
- Гипербола
- Окружность Аполлония
- Овал Кассини
Комментарии[править | править код]
- ↑ Если же в правой части стоит единица со знаком минус, то получившееся уравнение
описывает мнимый эллипс, он не имеет точек на вещественной плоскости.
Примечания[править | править код]
- ↑ Ivory J. A new series for the rectification of the ellipsis (англ.) // Transactions of the Royal Society of Edinburgh. — 1798. — Vol. 4. — P. 177—190. — doi:10.1017/s0080456800030817.
- ↑ Bessel F. W. Über die Berechnung der geographischen Längen und Breiten aus geodätischen Vermesssungen (нем.) // Astron. Nachr.. — 1825. — Bd. 4. — S. 241—254. — doi:10.1002/asna.18260041601. — Bibcode: 1825AN……4..241B. В англ. переводе: Bessel F. W. The calculation of longitude and latitude from geodesic measurements (1825) (англ.) // Astron. Nachr.. — 2010. — Vol. 331. — P. 852—861. — doi:10.1002/asna.201011352. — arXiv:0908.1824.
- ↑ Adlaj S. An eloquent formula for the perimeter of an ellipse (англ.) // Notices of the AMS. — 2012. — Vol. 76, iss. 8. — P. 1094—1099. — doi:10.1090/noti879.
- ↑ Корн, 1978, с. 68.
- ↑ Фейеш Тот Л. Глава II, §§ 4, 6 // Расположения на плоскости, на сфере и в пространстве. — М.: Физматгиз, 1958. — 364 с.
- ↑ Allaire P. R., Zhou J., Yao H. Proving a nineteenth century ellipse identity (англ.) // Mathematical Gazette. — 2012. — Vol. 96, no. 535. — P. 161—165.
- ↑ Карцев В. П. Максвелл. — М.: Молодая гвардия, 1974. (Серия «Жизнь замечательных людей»). С. 26—28.
Литература[править | править код]
- Корн Г., Корн Т. Свойства окружностей, эллипсов, гипербол и парабол // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 70—73.
- Селиванов Д. Ф. Эллипс // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- А. В. Акопян, А. А. Заславский. Геометрические свойства кривых второго порядка, — М.: МЦНМО, 2007. — 136 с.
- И. Бронштейн. Эллипс // Квант, № 9, 1970.
- А. И. Маркушевич. Замечательные кривые // «Популярные лекции по математике», выпуск 4.
Ссылки[править | править код]
- S.Sykora, Approximations of Ellipse Perimeters and of the Complete Elliptic Integral E(x). Review of known formulae (англ.)
- Grard P. Michon. Perimeter of an Ellipse (Final Answers) (англ.), 2000—2005. — 20 c.
- Видео: Как нарисовать эллипс
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 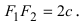
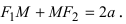
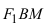
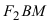
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 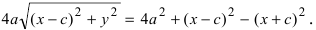
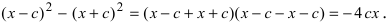
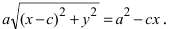
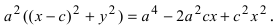
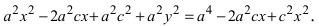
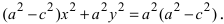
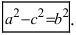
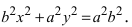
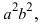
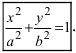
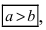
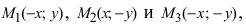
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 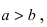
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 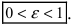
Если 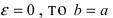
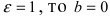
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 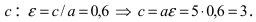
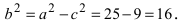
Пример:
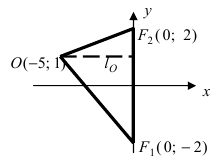
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 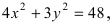
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
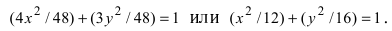
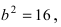
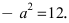
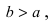
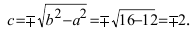
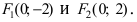
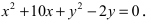
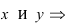
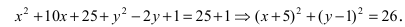
Построим в декартовой системе координат треугольник 
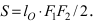
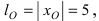
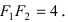
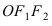
Эллипс в высшей математике
Рассмотрим уравнение
где 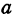
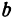
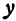
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 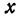
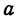
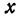
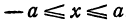
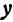
При 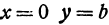
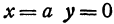
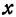

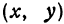
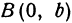
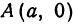
Полученная линия называется эллипсом. Число 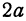
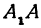
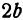
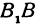
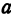
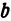
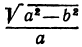
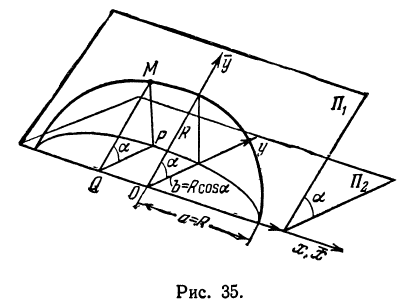
Пример:
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 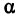
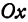
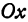
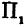
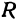
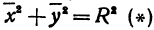
Пусть точка 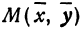
Обозначим проекцию точки 
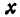
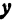
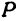

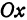
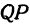
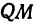
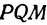
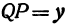
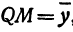
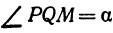
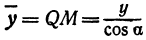

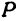
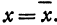
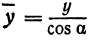
или
а это есть уравнение эллипса с полуосями 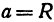
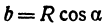
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 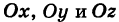
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 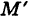
(рис. 206). Отсюда
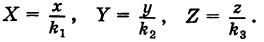
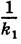
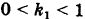
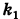
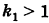
Подставляя эти формулы в уравнение (1), будем иметь
где 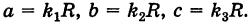
Величины 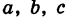
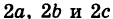
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
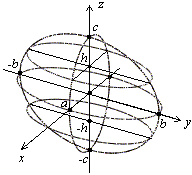
Эллипсоид
(рис.7) (от «эллипс»
и греч. «eidos» — вид) – замкнутая
центральная поверхность
второго порядка. Эллипсоид имеет
центр симметрии –

осями. Точки пересечения координатных
осей с эллипсоидом называются его
вершинами. Сечения эллипсоида плоскостями
являются эллипсами (в частности, всегда
можно указать круговые сечения эллипсоида).
Каноническое уравнение эллипсоида имеет
вид:
–
сфера.
В
сечении эллипсоида плоскостью,
перпендикулярной любой из координатных
осей, получается эллипс.
Форма эллипсоида.
Исследуем
форму эллипсоида. Из уравнения 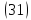
ограничены:
Эллипсоид
обладает тремя плоскостями симметрии,
тремя осями симметрии и центром симметрии.
Ими служат соответственно координатные
плоскости, координатные оси и начало
координат.
Для
выяснения формы эллипсоида рассмотрим
его сечения плоскостями. Найдем линию
пересечения эллипсоида с плоскостью

Так как любая точка плоскости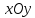
нулевую третью координату,
то координаты точек эллипсоида на
плоскости
уравнению:
Получаем,
что линия пересечения является эллипсом
с полуосями 
Рис.
8.
Сечение
плоскостью
Аналогично,
сечение в плоскости 
дает эллипс:
с
полуосями 

а сечение плоскостью
с
полуосями
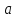
Рис.9.
Сечения эллипсоида координатными
плоскостями
Нарисованный
“каркас” из сечений уже дает
представление об эллипсоиде. Но чтобы
выяснить, как ведет себя поверхность
между нарисованными кривыми, рассмотрим
сечение эллипсоида плоскостью

Эта плоскость параллельна плоскости
пересекает ось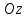
точке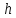
Уравнения этой линии:
Очевидно,
что если

то ни одна точка пространства не может
удовлетворять этой системе: в левой
части первого уравнения стоит
неотрицательное число, а в правой –
отрицательное.
Если

то в сечении получим лишь одну точку

зависимости от знака
Пусть
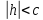
Тогда первое уравнение преобразуем к
виду:
то
есть к виду:
где
Уравнение

эллипсу, задаваемому уравнением
с коэффициентом подобия
полуосями

Ясно, что сечение плоскостью
таким же эллипсом, расположенным
симметрично первому относительно
плоскости
Нарисуем эти сечения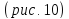
Рис.10.
Дополнительные сечения эллипсоида
Таким
образом, весь эллипсоид составлен из
эллипсов, лежащих в плоскостях,
параллельных плоскости
подобных эллипсу в плоскости

эллипсоида:
Рис.11.
Эллипсоид
Так
же, как для эллипса, точки пересечения
эллипсоида с координатными осями
называются вершинами эллипсоида, центр
симметрии – центром эллипсоида. Числа

полуосями. Если полуоси попарно различны,
то эллипсоид называется трехосным.
Если
две полуоси равны друг другу, то эллипсоид
называется эллипсоидом вращения.
Эллипсоид вращения может быть получен
вращением эллипса вокруг одной из осей.
Например, если

то все сечения эллипсоида плоскостями
будут окружностями. Сам эллипсоид может
быть получен из эллипса:
лежащего
в плоскости

при вращении его вокруг оси
Рис.12.
Эллипсоид
вращения
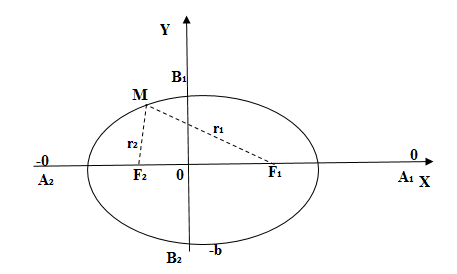
Эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки до двух точек равняется постоянной величине.
Что такое эллипс и фокусное расстояние
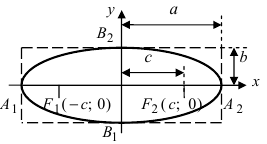
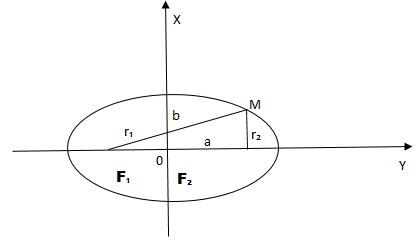
Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .
Обозначим фокусы эллипса и
. Допустим, что расстояние
=
– фокусное расстояние.
Рис. 1
– фокусы .
;
,
– половина расстояния между фокусами;
– большая полуось;
– малая полуось.
Теорема:
Фокусное расстояние и полуоси связаны соотношением:
Если точка находится на пересечении эллипса с вертикальной осью,
(теорема Пифагора). Если же точка
находится на пересечении его с горизонтальной осью,
. Так как по определению сумма
– постоянная величина, то приравнивая получается:
.
Уравнение эллипса
Уравнение элиппса бывает двух видов:
- Каноническое уравнение эллипса.
- Параметрическое уравнение эллипса.
Сначала рассмотрим каноническое уравнение эллипса:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:
Если центр эллипсa смещен в точку с координатами
тогда уравнение:
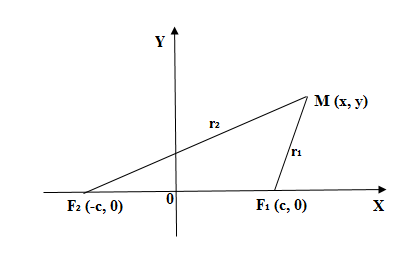
Чтобы получить каноническое уравнение эллипса, разместим и
на оси
симметричной к началу координат. Тогда у фокусов будут такие координаты
и
(см. рис. 2).
Пусть – произвольная точка эллипса. Обозначим через
и
– расстояние от точки
к фокусам. Согласно с определением эллипса:
(1)
Рис. 2
Подставим в (1) ,
и освободимся от иррациональности, подняв обе части к квадрату, получим:
(подносим к квадрату обе части): ,
Обозначим: , получаем каноническое уравнение эллипса:
(2)
Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из у нас получается
. Так как
, тогда
, и поэтому
.
Для построения эллипса обратим внимание, что если точка принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки
тоже удовлетворяют это уравнение: из
.
Точки – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.
Из уравнения (2) находим , для первой четверти
.
Если , тогда
. Если же
, тогда
. Точки
и
, а также симметричные с ними
,
– вершины эллипса, точка
– центр эллипса,
=
большая ось,
– малая ось эллипса.
Если первой четверти, тогда из
получается, что при возрастании
от
к
значение
падает от
к
. (рис. 3)
Параметрическое уравнение выглядит так:
Основные свойства эллипса
Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.
1. Угол между касательной к эллипсу и фокальным радиусом равен углу между касательной и фокальным радиусом
.
2. Уравнение касательной к эллипсу в точке с координатами
:
.
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).
4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами и
у треугольника
, тогда выполняется соотношение:
=
Эксцентриситет эллипса
Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается
Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда
– получается круг. Если же
, тогда
– эллипс превращается в отрезок. В некоторых случаях
. Для фокальных радиусов приведём без доказательства такие формулы:
Рис. 3
Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и
, тогда вычислим
– полуфокусное расстояние.
Строим фокусы и
на расстоянии один от другого
Концы не растянутой нити длиной
закрепляем в точках
и
. Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.
Примеры решения задач
Задача
Задан эллипс уравнением и точки
. Необходимо:
- убедиться, что точки
и
лежат на эллипсе;
- найти полуоси эллипса и координаты его фокусов;
- найти расстояние от точки
к фокусам;
- убедиться, что сумма этих расстояний равна длине большой оси;
- найти эксентриситет эллипса.
Решение
1. Подставим координаты точки
в левую часть уравнения эллипса:
– точка
лежит на эллипсе. Аналогично для
:
точка
лежит на эллипсе.
2. С канонического и данного уравнения
эллипса выходит:
Из равенства
получается:
– полуфокусное расстояние. Координаты фокусов
и
.
3. Найдём фокальные радиусы точки :
4. Найдём сумму , что отвечает определению эллипса.
5. Эксцентриситет находится по формуле .
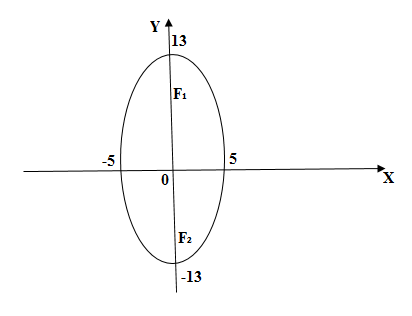
Задача
Найти оси, вершины и фокусы эллипса
Решение
Сведём обычное уравнение к каноническому:
,
. Вершины эллипса в точках
,
,
,
. Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае
больше, чем
, то эллипс, который вытянут вдоль оси
, находим полуфокусное расстояние
.
Фокусы в точках и
. (см. рис. 3)
Рис. 4
Найти оси, вершины и фокусы эллипса или
. Построить эллипс.
Сравнивая последнее уравнение с уравнением (2), у нас получается:
,
. Откуда находим оси эллипса:
,
и координаты вершин:
,
,
,
. Дальше из формулы:
. Значит, фокусами эллипса есть точки:
и
. Для построения эллипса отложим на осях
и
вершины
соответственно соединим их плавной линией, (см. задачу 1).
Замечание! Если в каноническом уравнении большей полуосью будет
, тогда фокусы эллипса будут расположены на оси
и тогда
.











































































![{displaystyle L=pi (a+b)left[1+sum limits _{n=1}^{infty }left[{frac {(2n-1)!!}{(2n-1)cdot 2^{n}cdot n!}}left({frac {a-b}{a+b}}right)^{n}right]^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/183ae8a63e961c04df036bfaf8a44d26edc4d621)