Как найти координаты фокуса параболы онлайн

Как найти координаты фокуса параболы онлайн

bold{mathrm{Basic}} bold{alphabetagamma} bold{mathrm{ABGamma}} bold{sincos} bold{gedivrightarrow} bold{overline{x}spacemathbb{C}forall} bold{sumspaceintspaceproduct} bold{begin{pmatrix}square&square\square&squareend{pmatrix}} bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx}
ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square}
left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec
alpha beta gamma delta zeta eta theta iota kappa lambda mu
nu xi pi rho sigma tau upsilon phi chi psi omega
A B Gamma Delta E Z H Theta K Lambda M
N Xi Pi P Sigma T Upsilon Phi X Psi Omega
sin cos tan cot sec csc sinh cosh tanh coth sech
arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech
begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge
(square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil
overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset
vee wedge neg oplus cap cup square^{c} subset subsete superset supersete
int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod
lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x}
(2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5)
(1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1)
mathrm{Radians} mathrm{Degrees} square! ( ) % mathrm{clear}
arcsin sin sqrt{square} 7 8 9 div
arccos cos ln 4 5 6 times
arctan tan log 1 2 3 –
pi e x^{square} 0 . bold{=} +

Subscribe to verify your answer

Subscribe

Sign in to save notes

Sign in

Number Line

Examples

  • foci (y-2)=3(x-5)^2

  • foci:3x^2+2x+5y-6=0

  • foci:x=y^2

  • foci:(y-3)^2=8(x-5)

  • foci:(x+3)^2=-20(y-1)

  • Show More

Description

Calculate parabola focus points given equation step-by-step

parabola-foci-calculator

en

Related Symbolab blog posts

  • Practice, practice, practice

    Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing…

    Read More

    • Enter a problem

    Save to Notebook!

    Sign in

    Источник

    The directrix is a fixed line used in describing a curve or surface. This curve can be a parabola. Here is a simple online Directrix calculator to find the parabola focus, vertex form and parabola directrix. In this below online Parabola focus directrix calculator just enter the input values in the form of a standard equation, y = ax2 + bx + c to get the result. Use our free online Parabola calculator to solve your academic mathematical and engineering problems.

    The directrix is a fixed line used in describing a curve or surface. This curve can be a parabola. Here is a simple online Directrix calculator to find the parabola focus, vertex form and parabola directrix. In this below online Parabola focus directrix calculator just enter the input values in the form of a standard equation, y = ax2 + bx + c to get the result. Use our free online Parabola calculator to solve your academic mathematical and engineering problems.

    Code to add this calci to your website Expand embed code Minimize embed code

    Formula:

    x = – b / 2a
    y = c – ( ( b2 – 1) / 4a)
    u = – b / 2a
    v = ax2 + bx + c
    d = c – ( ( b2 + 1) / 4a)

    Where,
    a = X2 Coefficient
    b = X Coefficient
    c = Constant
    x = Parabola Focus x-coordinate
    y = Parabola Focus y-coordinate
    u,v = Vertex Form
    d = Parabola Directrix

    All the parabola directrix calculations can be made in easier and quicker manner by using this Parabola directrix calculator.

    Источник
    Консультации по учебе, на самой крупной бирже
    студенческих работ !

    Калькулятор для определения координат правого фокуса параболы.

    Кривая второго порядка задана каноническим уравнением. Определите координаты ее правого фокуса F (для элипса
    или гиперболы) или ее единственного фокуса (для параболы)
    `y^2=16x`

    Кривая второго порядка задана каноническим уравнением. Определите координаты ее правого фокуса F (для элипса или гиперболы) или ее единственного фокуса (для параболы)

    Для решения задач необходимо зарегистрироваться.

    Источник

    Координаты фокуса параболы: как найти, формула

    Содержание:

    • Формулировка параболы в алгебре и геометрии
    • Что такое фокус параболы, определение
    • Как найти фокус параболы

      • Уравнение расчета
      • Чему равны координаты фокуса
    • Абсцисса фокуса параболы
    • Примеры расчета фокусного расстояния в задачах

    Формулировка параболы в алгебре и геометрии

    Определение

    Парабола — совокупность точек на плоскости, расположенных на одинаковом удалении от фокуса F и директрисы d, в которую точка F не входит.

    Парабола

     

    Парабола является коническим сечением, или коникой. Это значит, что она возникает при пересечении плоскости с поверхностью кругового конуса. Плоскость сечения при этом параллельна одной из касательных плоскостей конуса.

    Парабола в конусе

     

    Точка пересечения параболы с ее осью называется вершиной. Она считается началом системы координат, канонической для данной кривой.

    Что такое фокус параболы, определение

    Определение

    Расстояние от точки фокуса до любой точки параболы равняется расстоянию от этой точки к директрисе.

    Если в фокус поместить источник света, все исходящие из него световые лучи после отражения от нее пойдут по прямым, параллельным оси симметрии. И наоборот, все световые лучи, идущие параллельно оси, после отражения от «стенок» кривой соберутся в одной точке. Это оптическое свойство широко применяется в конструкциях прожекторов, фар, фонарей, телескопов-рефлекторов.

    Как найти фокус параболы

    Уравнение расчета

    Каноническое уравнение:

    (y^2;=;2px)

    Парабола на оси

     

    Если расположить параболу слева от оси ординат, уравнение примет вид:

    (y^2;=;-;2px)

    Парабола отрицательное уравнение

     

    Параметр p — расстояние от фокуса до директрисы, которая определяется уравнением:

    (х;=;-frac p2)

    Чтобы узнать расстояние r от любой точки параболы до фокуса, равное ее расстоянию до директрисы, нужно воспользоваться формулой:

    (r;=;frac p2;+;x)

    В полярной системе координат с центром в фокусе и направлением вдоль оси фокальный параметр можно найти по формуле:

    (p;=;rho;times;(1;+;cosleft(varthetaright)))

    Чему равны координаты фокуса

    Фокус будет иметь координаты ((frac p2;;0)).

    Абсцисса фокуса параболы

    Также фокус и параметр p можно искать через так называемую фокальную хорду (Р_1Р_2).

    Хорда параболы

     

    Эта прямая, проходящая через фокус и параллельная директрисе, пересекает параболу в двух точках. Половина длины фокальной хорды будет равна параметру p, являясь абсолютной величиной ординаты любой из точек (Р_1, Р_2).

    Абсцисса каждой из этих точек будет равна абсциссе фокуса (frac p2).

    Для ординаты y каждой из точек (Р_1, Р_2):

    (y^{2;}=;2p;times;frac p2;=;p^2).

    Примеры расчета фокусного расстояния в задачах

    Пример 1

    Определить координаты фокуса параболы (y^{2;}=;4х).

    Решение

    Находим параметр p:

    4 = 2p

    p = 2

    Координаты (1; 0).

    Пример 2

    Определить координаты фокуса параболы (y^{2;}=;6х).

    Решение

    Находим параметр p:

    6 = 2p

    p = 3

    Координаты (1,5; 0).

    Насколько полезной была для вас статья?

    Рейтинг: 2.02 (Голосов: 47)

    Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

    Текст с ошибкой:

    Расскажите, что не так

    Поиск по содержимому

    Источник
    • Home
    • »
    • Geometry
    • »

    Parabola Calculator

    ( Parabola Grapher Online )

    Parabola Vertex Focus Calculator Formulas

    (Y = aX2 + bX + c, a≠0)


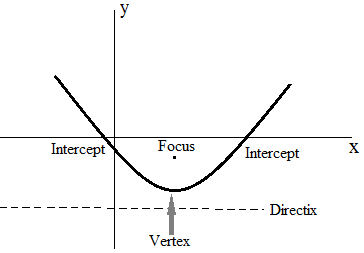
    • Focus X = -b/2a
    • Focus Y = c – (b2 – 1)/4a
    • Vertex X = -b/2a
    • Directrix Y = c – (b2 + 1)/4a
    • X Intercept = -b/2a ± √(b * b – 4ac)/2a,0

    Parabola equation and graph with major axis parallel to y axis. If a>0, parabola is upward, a<0, parabola is downward. If the major axis is parallel to the x axis, interchange x and y during your calculation.

    click

    here for parabola equation solver.

    Segment of a Parabola Calculator

    Segment of a Parabola Formulas

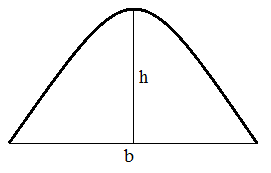
    • Area = 2 * h * b;
    • Arc Length = sqrt(b2 + 16 * h2)/2 + b2 * ln((4 * h + sqrt(b2 + 16 * h2))/b)/(8*h)

    Источник

    Добавить комментарий