| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
фокусы:9x^2+4y^2=1
-
фокусы:16x^2+25y^2=100
-
фокусы:25x^2+4y^2+100x-40y=400
-
фокусы:frac{(x-1)^2}{9}+frac{y^2}{5}=100
- Показать больше
Описание
Пошаговый расчет точек фокусировки эллипса по заданному уравнению
ellipse-function-foci-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Practice, practice, practice
Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Unit Converter
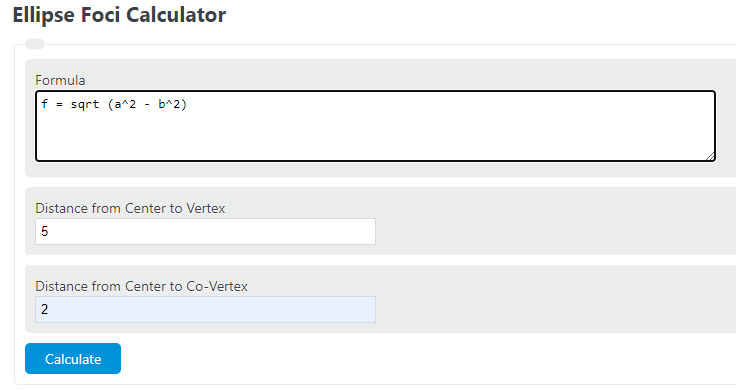
Enter the distance from the center to the vertex and the distance from the center to the co-vertex to determine the ellipse foci. This calculator can also determine the distance from the center to the vertex or co-vertex given the other variables.
- Area of an Oval Calculator
- Eccentricity Calculator
- Centroid Calculator
Ellipse Foci Formula
The following formula is used to calculate the ellipse focus point or foci.
- Where F is the foci
- a is the distance from the center to the vertex (also known as the center to the furthest point)
- b is the distance from the center to the co-vertex (center to shortest point
To calculate an ellipse foci, square the distance from the center to the vertex and square the distance from the center to the co-vertex, subtract the latter from the former, then take the square root of the result.
Ellipse Foci Definition
An ellipse foci is defined as the locus of points in which the sum of the distance to each focus point is constant.
Ellipse Foci Example
How to calculate an ellipse foci?
- First, determine the distance to the vertex.
Measure the furthest distance from the center to the edge of the ellipse.
- Next, determine the distance to the co-vertex.
Measure the closest distance from the center to an edge.
- Finally, calculate the foci.
Using the formula above, calculate the foci.
FAQ
What is an ellipse foci?
An ellipse foci is the distance from the center of an ellipse to it’s focus points and is a measure of the elongation of the ellipse.

Каноническое уравнение эллипса по двум точкам
| Две точки с координатами |
|
Первая координата |
|
Вторая координата |
| Каноническое уравнение эллипса |
| Большая полуось эллипса |
| Малая полуось эллипса |
| Эксцентриситет эллипса |
| Фокусное/фокальное расстояние |
| Коэффициент сжатия |
| Координаты первого фокуса F1(x1:y1) |
| Координаты второго фокуса F2(x2:y2) |
| Фокальный параметр |
| Перифокусное расстояние |
| Апофокусное расстояние |
Уравнение эллипса в каноническом виде имеет вот такой вид.
Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.
Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.
Кроме этого, на этой странице мы получим следующую информацию.
Фокальный параметр – половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса
Значение полуосей – большая полуось 

Эксцентриситет – коэффициент, показывающий насколько его фигура отличается от окружности
Фокальное расстояние
Коэффициент сжатия – отношение длин малой и большой полуосей
Перифокусное расстояние
Апофокусное расстояние
Примеры задач
Cоставить каноническое уравнение эллипса по двум точкам
Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt
и получаем результат
| Каноническое уравнение эллипса |
 |
| Большая полуось эллипса |
|
8.48528137423857 |
| Малая полуось эллипса |
|
5.656854249492381 |
| Эксцентриситет эллипса |
|
0.8958064164776166 |
| Фокусное/фокальное расстояние |
|
32.2490309931942 |
| Коэффициент сжатия |
|
0.4444444444444444 |
| Координаты первого фокуса F1(x1:y1) |
|
-16.1245154965971 : 0 |
| Координаты второго фокуса F2(x2:y2) |
|
16.1245154965971 : 0 |
| Фокальный параметр |
|
3.5555555555555554 |
| Перифокусное расстояние |
|
1.875484503402901 |
| Апофокусное расстояние |
|
34.1245154965971 |
И еще один пример
Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса.
Если мы введем данные в калькулятор получим
 |
| Большая полуось эллипса |
|
5.877538136328849 |
| Малая полуось эллипса |
|
NaN |
Как видно, одна из осей не может быть определена, так как нам придется брать корень квадратный из отрицательного числа, а следовательно одна из осей будет комплексным числом, что быть не может.
Таким образом по этим двум точкам, нельзя построить эллипс.
А что же можно построить? Перейдя по ссылке данной в начале статьи, мы можем увидеть что это каноническое уравнение гиперболы.
Более подробно, про гиперболу есть отдельный калькулятор Каноническое уравнение гиперболы по двум точкам
Удачных расчетов!
-
Определение эллипса.
Начать изучение
-
Фокусы, эксценриситет и директрисы эллипса.
Начать изучение
-
Уравнение касательной к эллипсу.
Начать изучение
Определение эллипса.
Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1label{ref1}
$$
при условии (a geq b > 0).
Из уравнения eqref{ref1} следует, что для всех точек эллипса (|x| leq a) и (|y| leq b). Значит, эллипс лежит в прямоугольнике со сторонами (2a) и (2b).
Точки пересечения эллипса с осями канонической системы координат, имеющие координаты ((a, 0)), ((-a, 0)), ((0, b)) и ((0, -b)), называются вершинами эллипса. Числа (a) и (b) называются соответственно большой и малой полуосями эллипса.
В каноническое уравнение входят только квадраты координат. Поэтому, если координаты ((x, y)) какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты ((-x, y)), ((x, -y)) и ((-x, -y)) точек (M_{1}), (M_{2}) и (M_{3}) (рис. 8.1). Следовательно, справедливо следующее утверждение.
Утверждение 1.
Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.
Внешний вид эллипса проще всего описать сравнением с окружностью радиуса (a) с центром в центре эллипса: (x^{2}+y^{2}=a^{2}). При каждом (x) таком, что (|x| < a), найдутся две точки эллипса с ординатами (pm b sqrt{1-x^{2}/a^{2}}) и две точки окружности с ординатами (pm a sqrt{1-x^{2}/a^{2}}). Пусть точке эллипса соответствует точка окружности с ординатой того же знака. Тогда отношение ординат соответствующих точек равно (b/a). Итак, эллипс получается из окружности таким сжатием ее к оси абсцисс, при котором ординаты всех точек уменьшаются в одном и том же отношении (b/a) (рис. 8.2).
Фокусы, эксценриситет и директрисы эллипса.
У эллипса есть две замечательные точки, которые называются его фокусами.
Определение.
Пусть по определению
$$
c^{2}=a^{2}-b^{2}label{ref2}
$$
и (c geq 0).
Фокусами называются точки (F_{1}) и (F_{2}) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат (рис. 8.3).
Для окружности (c=0), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.
Определение.
Отношение
$$
varepsilon=frac{c}{a}label{ref3}
$$
называется эксцентриситетом эллипса.
Отметим, что (varepsilon < 1).
Утверждение 2.
Расстояние от произвольной точки (M(x, y)), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы (x):
$$
r_{1}=|F_{1}M|=a-varepsilon x, r_{2}=|F_{2}M|=a+varepsilon x.label{ref4}
$$
Доказательство.
Очевидно, что (r_{1}^{2}=(x-c)^{2}+y^{2}). Подставим сюда выражение для (y^{2}), найденное из уравнения эллипса. Мы получим
$$
r_{1}^{2}=x^{2}-2cx+c^{2}+b^{2}-frac{b^{2}x^{2}}{a^{2}}.nonumber
$$
Учитывая равенство eqref{ref2}, это можно преобразовать к виду
$$
r_{1}^{2}=a^{2}-2cx+frac{c^{2}x^{2}}{a^{2}}=(a-varepsilon x)^{2}.nonumber
$$
Так как (x leq a) и (varepsilon < 1), отсюда следует, что справедливо первое из равенств eqref{ref4}: (r_{1}=a-varepsilon x). Второе равенство доказывается аналогично.
Утверждение 3.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса (2a).
Доказательство.
Необходимость. Если мы сложим равенства eqref{ref4} почленно, то увидим, что
$$
r_{1}+r_{2}=2a.label{ref5}
$$
Достаточность. Пусть для точки (M(x, y)) выполнено условие eqref{ref5}, то есть
$$
sqrt{(x-c)^{2}+y^{2}}=2a-sqrt{(x+c)^{2}+y^{2}}.nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^{2}=asqrt{(x+c)^{2}+y^{2}}.label{ref6}
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение eqref{ref2}. Мы придем к (b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}), равносильному уравнению эллипса eqref{ref1}.
С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнения в канонической системе координат (рис. 8.4)
$$
x=frac{a}{varepsilon},\ x=-frac{a}{varepsilon}.label{ref7}
$$
Директрису и фокус, которые лежат по одну сторону от центра, будем считать соответствующими друг другу.
Утверждение 4.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса (varepsilon).
Доказательство.
Докажем это предложение для фокуса (F_{2}(-c, 0)). Пусть (M(x, y)) — произвольная точка эллипса. Расстояние от (M) до директрисы с уравнением (x=-a/varepsilon) по формуле (9) §3 гл. II равно
$$
d_{2}=|x+frac{a}{varepsilon}|=frac{1}{varepsilon}(varepsilon x+a).nonumber
$$
Из формулы eqref{ref4} мы видим теперь, что (r_{2}/d_{2}=varepsilon).
Обратно, пусть для какой-то точки плоскости (r_{2}/d_{2}=varepsilon), то есть
$$
sqrt{(x+c)^{2}+y^{2}}=varepsilon left(x+frac{a}{varepsilon}right).nonumber
$$
Так как (varepsilon=c/a), это равенство легко приводится к виду eqref{ref6}, из которого, как мы знаем, следует уравнение эллипса.
Уравнение касательной к эллипсу.
Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть (M_{0}(x_{0}, y_{0})) — точка на эллипсе и (y_{0} neq 0). Через (M_{0}) проходит график некоторой функции (y=f(x)), который целиком лежит на эллипсе. (Для (y_{0} > 0) это график (f_{1}(x)=bsqrt{1-x^{2}/a^{2}}), для (y_{0} < 0) — график (f_{2}(x)=-bsqrt{1-x^{2}/a^{2}}). Не уточняя знака (y_{0}), обозначим подходящую функцию (f(x)).) Для нее выполнено тождество
$$
frac{x^{2}}{a^{2}}+frac{(f(x))^{2}}{b^{2}}=1.nonumber
$$
Дифференцируем его по (x):
$$
frac{2x}{a^{2}}+frac{2ff’}{b^{2}}=0.nonumber
$$
Подставляя (x=x_{0}) и (f(x_{0}=y_{0})), находим производную от (f) в точке (x_{0}), равную угловому коэффициенту касательной:
$$
f'(x_{0})=frac{b^{2}}{a^{2}} frac{x_{0}}{y_{0}}.nonumber
$$
Теперь мы можем написать уравнение касательной:
$$
y-y_{0}=-frac{b^{2}}{a^{2}} frac{x_{0}}{y_{0}}(x-x_{0}).nonumber
$$
Упрощая это уравнение, учтем, что (b^{2}x_{0}^{2}+a^{2}y_{0}^{2}=a^{2}b^{2}), так как (M_{0}) лежит на эллипсе. Результату можно придать вид
$$
frac{xx_{0}}{a^{2}}+frac{yy_{0}}{b^{2}}=1.label{ref8}
$$
При выводе уравнения eqref{ref8} мы исключили вершины эллипса ((a, 0)) и ((-a, 0)), положив (y_{0} neq 0). Для этих точек оно превращается, соответственно, в уравнения (x=a) и (x=-a). Эти уравнения определяют касательные в вершинах. Проверить это можно, заметив, что в вершинах ж как функция от у достигает экстремума. Предоставим читателю проделать это подробно и показать тем самым, что уравнение eqref{ref8} определяет касательную для любой точки (M_{0}(x_{0}, y_{0})) на эллипсе.
Утверждение 5.
Касательная к эллипсу в точке (M_{0}(x_{0}, y_{0})) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.
Доказательство.
Нам надо сравнить углы (varphi_{1}) и (varphi_{2}), составленные векторами (overrightarrow{F_{1}M_{0}}) и (overrightarrow{F_{2}M_{0}}) с вектором (boldsymbol{n}), перпендикулярным касательной (рис. 8.5). Из уравнения eqref{ref8} находим, что (boldsymbol{n}(x_{0}/a^{2}, y_{0}/b^{2})), и потому
$$
(overrightarrow{F_{1}M_{0}}, boldsymbol{n})=frac{x_{0}}{a^{2}}(x_{0}-c)+frac{y_{0}}{b^{2}}y_{0}=1-frac{x_{0}c}{a^{2}}=frac{a-varepsilon x_{0}}{a}.nonumber
$$
Используя eqref{ref4}, мы получаем отсюда, что (cos varphi_{1}=1/(a|boldsymbol{n}|)). Аналогично находим (cos varphi_{2}=1/(a|boldsymbol{n}|)). Утверждение доказано.
Как видно, одна из осей не может быть определена, так как нам придется брать корень квадратный из отрицательного числа, а следовательно одна из осей будет комплексным числом, что быть не может.
Таким образом по этим двум точкам, нельзя построить эллипс.
А что же можно построить? Перейдя по ссылке данной в начале статьи, мы можем увидеть что это каноническое уравнение гиперболы.
Более подробно, про гиперболу есть отдельный калькулятор Каноническое уравнение гиперболы по двум точкам
Как найти координаты фокусов эллипса
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует “сплюснутость” эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет , а один из фокусов находится в точке (6; 0)
Продолжаем решать задачи на эллипс вместе
Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса
,
где и — расстояния этой точки до директрис и .
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа “эр” с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
1. Окружность. 2Окружностью называется геометрическое место точек, равноудаленных от одной фиксированной точки, называемой центром окружности. Расстояние от произвольной точки окружности до его центра называется радиусом окружности.
g Если центр окружности находится в точке , а радиус равен R, то уравнение окружности имеет вид:
. (3.13)
4Обозначим через (рис. 3.5) произвольную точку окружности. Используя формулу расстояния между двумя токами (3.1) и определение окружности, получим: . Возводя полученное равенство в квадрат, мы получим формулу (3.13).3
2. Эллипс. 2 Эллипсом называется геометрическое место точек, сумма расстояний которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.
Для того, чтобы вывести каноническое (простейшее) уравнение эллипса, примем за ось Ox прямую, соединяющую фокусы F1 и F2. Пусть при этом фокусы будут симметричны относительно начала координат, т.е. будут иметь координаты: и . Здесь через 2с обозначено расстояние между фокусами. Обозначим через x и y координаты произвольной точки М эллипса (рис 3.6). Тогда по определению эллипса, сумма расстояний от точки М до точек F1 и F2 равно константе (обозначим эту константу через 2а).
. (3.14)
Уравнение (3.14) является уравнением эллипса. Упростим данное уравнение, избавившись от квадратных корней. Для этого перенесем один из радикалов в правую часть равенства (3.14) и возведем обе части полученного равенства в квадрат:
,
,
,
.
Возводя последнее равенство в квадрат, получим
, или
,
.
Разделим обе части на :
.
Так как сумма расстояний от произвольной точки эллипса до его фокусов больше расстояния между фокусами, т.е. 2а > 2c, то .
Обозначим через b 2 . Тогда простейшее (каноническое) уравнение эллипса будет иметь вид:
, (3.15)
. (3.16)
Оси координат являются осями симметрии эллипса, заданного уравнением (3.15). Действительно, если точка с текущими координатами (x; y) принадлежит эллипсу, то и точки при любом сочетании знаков принадлежат эллипсу.
2Ось симметрии эллипса, на которой расположены фокусы, называется фокальной осью. Точки пересечения эллипса с его осями симметрии называются вершинами эллипса. Подставляя x = 0 или y = 0 в уравнение эллипса найдем координаты вершин:
2Отрезки А1А2 и B1B2, соединяющие противоположные вершины эллипса, а также их длины 2a и 2b, называют соответственно большой и малой осями эллипса. Числа a и b, называют соответственно большой и малой полуосями эллипса.
2Эксцентриситетом эллипса называется отношение расстояния между фокусами (2с) к большой оси (2a), т.е.
. (3.17)
Так как а и с положительны, причем c
2Отрезок 2a, длина которого равна расстоянию между вершинами гиперболы, называют действительной осью гиперболы. Отрезок 2b называют мнимой осью гиперболы. Числа a и b, называют соответственно действительной и мнимой полуосями гиперболы.
Можно доказать, что прямые линии
(3.23)
являются асимптотами гиперболы, т.е. такими прямыми, к которым неограниченно приближаются точки гиперболы при их неограниченном удалении от начала координат ( ).
2Эксцентриситетом гиперболы называется отношение расстояния между фокусами (2с) к действительной оси (2a), т.е., как и в случае эллипса
. (3.24)
Однако в отличии от эллипса эксцентриситет гиперболы больше единицы.
Если фокусы гиперболы расположены на оси Oy, то в левой части уравнения гиперболы изменятся знаки на противоположные:
. (3.25)
В этом случае полуось b будет действительной, а полуось a – мнимой. Ветви гиперболы будут симметричны относительно оси Oy (рис 3.9). Формулы (3.22) и (3.23) не изменятся, формула (3.24) будет выглядеть следующим образом:
. (3.26)
4. Парабола. Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом и от данной прямой, называемой директрисой (предполагается, что фокус не лежит на директрисе).
Для того, чтобы составить простейшее уравнение параболы примем за ось Ox прямую, проходящую через ее фокус перпендикулярно директрисе, и направленную от директрисы к фокусу. За начало координат примем середину отрезка O от фокуса F до точки А пересечения оси Ox с директрисой. Длина отрезка AF обозначается через p и называется параметром параболы.
В данной системе координат координаты точек А и F будут, соответственно, , . Уравнение директрисы параболы будет . Обозначим через (x; y) координаты произвольной точки М параболы (рис. 3.10). Тогда по определению параболы:
. (3.27)
Возведем обе части равенства (3.27) в квадрат:
, или
, откуда
. (3.28)
Уравнение (3.28) называется каноническим уравнением параболы.
Каноническими являются так же следующие уравнения параболы.
. (3.29)
Ветви параболы, заданной уравнением (3.29), направлены влево, фокус имеет координаты , уравнение директрисы .
. (3.30)
Ветви параболы, заданной уравнением (3.30), направлены вверх, фокус имеет координаты , уравнение директрисы .
. (3.31)
Ветви параболы, заданной уравнением (3.31), направлены вниз, фокус имеет координаты , уравнение директрисы .
Задача 3.3. Найти координаты фокусов и эксцентриситет эллипса:
Решение. В каноническом виде уравнение эллипса выглядит следующим образом: Из этого уравнения видно, что большая полуось эллипса равна а малая полуось равна Расстояние от центра эллипса до его фокусов, находим из формулы (3.16): Таким образом, фокусы эллипса имеют координаты:
Эксцентриситет эллипса найдем по формуле (3.17):
Задача 3.4. Асимптоты гиперболы имеют уравнения и расстояние между фокусами равно 10. Составить каноническое уравнение гиперболы.
Решение. Из условия задачи следует, что
.
Подставляя в равенство (3.22) с = 5 и a = 2b, мы получим уравнение, из которого найдем b:
b 2 = 25 – 4b 2 , 5b 2 = 25, b 2 = 5, . Следовательно, a = 2b = .
Подставляя a 2 = 20 и b 2 = 5 в уравнение (3.21), получим искомое уравнение гиперболы:
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10572 — | 7332 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
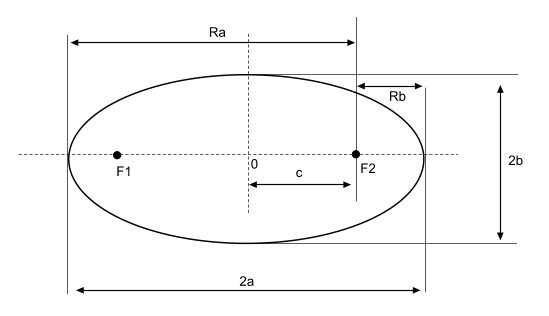
Эллипс – геометрическое место точек M(x;y), сумма расстояний которых до двух данных точек F1F2 имеет одно и то же значение 2a:
точки F1 и F2 – называются фокусами эллипса;
расстояние F1F2 – фокусное расстояние и равно F1F2=2с;
a — большая полуось;
b — малая полуось;
c — фокальный радиус, то есть полу расстояние между фокусами;
p — фокальный параметр;
Rmin – минимальное расстояние от фокуса до точки на эллипсе;
Rmax — максимальное расстояние от фокуса до точки на эллипсе;
где
Длина малой оси эллипса 134 м. Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса
Постройте кривую 4x 2 +9y 2 =36. Найдите фокусы, фокальный параметр и эксцентриситет.
Делим обе части на 36 и получаем каноническое уравнение эллипса
a=3, b=2
c 2 =a 2 -b 2 =3 2 -2 2 =9-4=5
Отсюда находим Фокусы F1(-2,2;0) F2(2,2;0)
Фокальный параметр находим следующим образом
Эксцентриситет эллипса
Пример 3
Постройте кривую . Найдите фокусы и эксцентриситет.
Решение
Уравнение запишем в виде
a=1, b=5
Это уравнение не является каноническим уравнением эллипса, так как b>a, а должно быть b c 2 =a 2 − b 2 =5 2 −1 2 =25 − 1=24
Следовательно, фокусы в системе координат (x’;y’) имеют координаты (-4,9;0) и (4,9;0), а в системе (x;y) координаты
Эксцентриситет эллипса равен
Кривые второго порядка. Эллипс: формулы и задачи
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F – числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) – длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат – в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат – малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность – частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия – эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось – это a = 5 , меньшая полуось – это b = 4 . Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует “сплюснутость” эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
– если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
– если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат – каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет , а один из фокусов находится в точке (6; 0)
Продолжаем решать задачи на эллипс вместе
Если – произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и – расстояния до этой точки от фокусов , то формулы для расстояний – следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже – красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса
,
где и – расстояния этой точки до директрис и .
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e – эксцентриситет и числа “эр” с подстрочными индексами 1 и 2 – искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
[spoiler title=”источники:”]
http://hd01.ru/info/kak-najti-koordinaty-fokusov-jellipsa/
http://function-x.ru/curves_ellipse.html
[/spoiler]






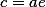


;M_2(3sqrt{1.5}:sqrt{2}))

