Как найти координаты компланарных векторов

Как найти координаты компланарных векторов

Компланарные векторы и условие компланарности

В данной статье мы рассмотрим такие темы, как:

  • определение компланарных векторов;
  • условия компланарности векторов;
  • примеры задач на компланарность векторов.

Определение компланарных векторов

Определение 1

Компланарные векторы — это векторы, которые параллельны одной плоскости или лежат на одной плоскости. 

Примечание

Два любых вектора всегда компланарны, поскольку всегда можно найти плоскости параллельные 2-м произвольным векторам.

Условия компланарности векторов

  • Для 3-х векторов выполняется условие: если смешанное произведение 3-х векторов равно нулю, то эти три вектора компланарны.
  • Для 3-х векторов выполняется условие: если три вектора линейно зависимы, то они компланарны.
  • Для n-векторов выполняется условие: если среди векторов не более 2-х линейно независимых векторов, то они компланарны.

Примеры решения задач на компланарность векторов

Пример 1

Исследуем на компланарность векторы

a¯=(1;2;3), b=(1;1;1) и c¯=(1;2;1)

Как решить?

Векторы будут являться компланарными, если их смешанное произведение равно нулю, поэтому вычисляем смешанное произведение заданных векторов. Для этого составляем определитель, по строкам которого записываются координаты векторов-сомножителей:

(a¯,b¯,c¯)=123111121==1×1×1+1×2×3+2×1×1-1×1×3-2×1×1-1×2×1=2≠0

Отсюда следует, что смешанное произведение не равняется нулю, поэтому векторы не являются компланарными.

Ответ: векторы не являются компланарными.

Пример 2

Докажем, что три вектора

a¯=(1;-1;2), b=(0;1;-1) и c¯=(2;-2;4) компланарны.

Как решить?

Находим смешанное произведение данных векторов:

(a¯,b¯,c¯)=1-1201-12-24==1×1×4+0×(-2)×2+(-1)×(-1)××2-2×1×2-(-2)×(-1)×1-0×(-1)

Из данного примера видно, что смешанное произведение равняется нулю.

Ответ: векторы являются компланарными. 

Пример 3

Проверим, компланарны ли векторы

a¯={1;1;1}, b¯={1;2;0), c¯={0;-1;1}, d¯={3;3;3}.

Как решить?

Необходимо найти количество линейно независимых векторов: записываем значения векторов в матрицу и выполняем элементарные преобразования:

1111200-11333~

Из 2-ой строки вычитаем 1-ю, из 4-ой вычитаем 1-ю, умноженную на 3:

1111-12-10-10-113-33-33-3~11101-10-11000~

К 3-ей строке прибавляем 2-ю:

11101-10+0-1+11+(-1)3-33-33-3~11101-1000000

Поскольку в матрице только две ненулевые строки, делаем вывод, что среди них всего два линейно независимых вектора.

Ответ: векторы являются компланарными, поскольку среди них всего два линейно независимых вектора. 

Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник
Автор статьи

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Понятие компланарности векторов

Для начала рассмотрим, какие вектора называются компланарными.

Определение 1

Два вектора, которые параллельны одной плоскости называются компланарными.

Рассмотри, компланарны ли векторы a, b и c на следующем примере. Пусть нам даны три вектора $overrightarrow{a_1}, overrightarrow{a_2}$ и $overrightarrow{a_3}$. Тогда

  1. Пары векторов $overrightarrow{a_1}, и overrightarrow{a_2}$, $overrightarrow{a_2}$ и $overrightarrow{a_3}$ и $overrightarrow{a_1}$ и $overrightarrow{a_3}$ компланарны между собой.

  2. Если два из этих векторов, к примеру $overrightarrow{a_1}, и overrightarrow{a_2}$, коллинеарны, то векторы $overrightarrow{a_1}, overrightarrow{a_2}$ и $overrightarrow{a_3}$ компланарны.

  3. Если $overrightarrow{a_1}, overrightarrow{a_2}$ и $overrightarrow{a_3}$ лежат в одной плоскости, то они компланарны.

Для дальнейшего рассмотрения напомним следующую теорему.

Произвольный вектор $overrightarrow{p}$ можно разложить по двум неколлинеарным векторам $overrightarrow{a_1}, $ и $overrightarrow{a_2}$ с единственными коэффициентами разложения, то есть

[overrightarrow{p}={alpha }_1overrightarrow{a_1}+{alpha }_2overrightarrow{a_2}]

Теоремы, связанные с условием компланарности трех векторов

Пусть нам даны три вектора $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$.

Теорема 2

Если один из трех данных векторов можно разложить по двум другим векторам, то есть

[overrightarrow{c}=alpha overrightarrow{a}+beta overrightarrow{b}]

где $alpha $ и $beta $ – действительные числа, то векторы $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$ являются компланарными векторами.

Доказательство.

Здесь возможны два случая.

  1. Векторы $overrightarrow{a} и overrightarrow{b}$ – коллинеарные векторы. Но это условие неприменимо, если одна из координат вектора приравнивается нулю.

    В этом случае компланарность векторов $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$ очевидна.

  2. Векторы $overrightarrow{a} и overrightarrow{b}$ не являются коллинеарными.

    Так как вектор $overrightarrow{c}$ имеет свое разложение по двум неколлинеарным векторам $overrightarrow{a} и overrightarrow{b}$. Значит эти векторы попадают под условие теоремы 1, и, следовательно, векторы $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$ лежат в одной плоскости, то есть являются компланарными.

Теорема доказана.

«Компланарные векторы» 👇

Теорема 3

Если три вектора $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$ являются компланарными, а векторы $overrightarrow{a} и overrightarrow{b}$ не являются коллинеарными, то вектор $overrightarrow{c}$ можно единственным образом разложить по векторам $overrightarrow{a} и overrightarrow{b},$ то есть

[overrightarrow{c}=alpha overrightarrow{a}+beta overrightarrow{b}]

Доказательство.

Так как векторы $overrightarrow{a}, overrightarrow{b}$ и $overrightarrow{c}$ компланарны, то значит в произвольной плоскости $gamma $, которой параллельны эти векторы, можно построить векторы $overrightarrow{a’}=overrightarrow{a},$ $overrightarrow{b’}=overrightarrow{b}$ и $overrightarrow{c’}=overrightarrow{c}$. Так как векторы $overrightarrow{a} и overrightarrow{b}$ не коллинеарны, то и векторы $overrightarrow{a’}$ и $overrightarrow{b’}$ не коллинеарны, тогда, по теореме 1, вектор $overrightarrow{c’}$ можно разложить по векторам $overrightarrow{a’}$ и $overrightarrow{b’}$ следующим образом

[overrightarrow{c’}=alpha overrightarrow{a’}+beta overrightarrow{b’}]

Причем это разложение единственно.

Следовательно

[overrightarrow{c}=alpha overrightarrow{a}+beta overrightarrow{b}]

Которое также единственно.

Теорема доказана.

Признак и критерий компланарности векторов

Пусть нам даны векторы $overrightarrow{a}=(a_1,a_2,a_3), overrightarrow{b}=(b_1,b_2,b_3)$ и $overrightarrow{c}=(c_1,c_2,c_3)$. Три вектора будут компланарны, если выполняется следующее условие:

Условие <a href=компланарности векторов. Автор24 — интернет-биржа студенческих работ” />

Рисунок 1. Условие компланарности векторов. Автор24 — интернет-биржа студенческих работ

Пример задачи

Пример 1

Пусть нам дан куб $ABCDA_1B_1C_1D_1$. Разложите вектор $overrightarrow{A_1C_1}$ по векторам $overrightarrow{AB} и overrightarrow{BC}$.

Разложение по векторам. Автор24 — интернет-биржа студенческих работ

Рисунок 2. Разложение по векторам. Автор24 — интернет-биржа студенческих работ

Решение.

Так как плоскости $(ABC)$ и ${(A}_1B_1C_1)$ параллельны, и векторы $overrightarrow{A_1C_1}$, $overrightarrow{AB} и overrightarrow{BC}$ параллельны, следовательно, по определению являются компланарными. Тогда, по теореме 1, вектор $overrightarrow{A_1C_1}$ можно разложить по векторам $overrightarrow{AB} и overrightarrow{BC}$ единственным образом.

Используя свойства сложения двух векторов, получим

[overrightarrow{A_1C_1}=overrightarrow{A_1B_1}+overrightarrow{B_1C_1}]

Так как

[overrightarrow{A_1B_1}=overrightarrow{AB}, overrightarrow{B_1C_1}=overrightarrow{BC}]

Следовательно

[overrightarrow{A_1C_1}=overrightarrow{AB}+overrightarrow{BC}]

Ответ: $overrightarrow{AB}+overrightarrow{BC}$.

Пример 2

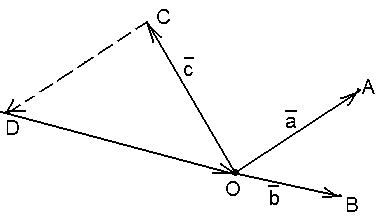
Пусть нам дан параллелепипед. Найти тройки компланарных векторов, изображенных в параллелепипеде на рисунке ниже.

Параллелепипед. Автор24 — интернет-биржа студенческих работ

Рисунок 3. Параллелепипед. Автор24 — интернет-биржа студенческих работ

Решение.

  1. Так как векторы $overrightarrow{OA}, overrightarrow{OB}$ и $overrightarrow{OE}$ лежат в плоскости $(BOA)$ то эти векторы являются компланарными.

  2. Так как векторы $overrightarrow{OC}, overrightarrow{OB}$ и $overrightarrow{{BB}_1}$ лежат в плоскости $(BOC)$ то эти векторы являются компланарными.

  3. Так как векторы $overrightarrow{OC}, overrightarrow{OD}$ и $overrightarrow{OE}$ лежат в плоскости $(COE)$ то эти векторы являются компланарными.

Пример 3

Доказать, что векторы с координатами $left(1, 13, 2right), left(3, -5, 2right)и (5,-1,4)$ компланарны.

Решение.

Применим признак компланарности трех векторов.

Найдем определитель

Нахождение определителя. Автор24 — интернет-биржа студенческих работ

Рисунок 4. Нахождение определителя. Автор24 — интернет-биржа студенческих работ

Следовательно, это векторы компланарны, ч. т. д.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

В данной публикации мы рассмотрим, какие векторы называются компланарными, и перечислим условия для компланарности двух, трех и большего количества векторов. Также разберем примеры решения задач по этой теме.

  • Условия компланарности векторов

  • Пример задачи

Условия компланарности векторов

Векторы, лежащие в одной плоскости или параллельные ей, называются компланарными.

Компланарные векторы

Из определения следует, что любые два вектора компланарны, т.к. всегда можно найти плоскость, параллельную им обоим.

Условия компланарности:

  1. Для трех векторов:
    • Их смешанное произведение равняется нулю.
    • Они линейно зависимы.
  2. Для n-ого количества векторов: среди них не более двух линейно независимых векторов.

Пример задачи

Определим, являются ли векторы a = {2; 5; 8}, b = {1; 4; 3} и c = {6; 7; 1} компланарными.

Решение

Чтобы проверить компланарность векторов с заданными координатами, найдем их смешанное произведение.

Пример смешанного произведения векторов

a · [b x c] = 8 + 90 + 56 – 192 – 42 – 5 = -85

Таким образом, векторы не являются компланарными, т.к. их смешанное произведение не равняется нулю.

Источник

Определение
8. Векторы
называются компланарными,
если их можно отложить в одной плоскости.

Свойства
компланарных векторов.

10.
Коллинеарные векторы компланарны. Иными
словами, во множество всех возможных
компланарных между собой векторов
вместе с каждым его вектором входят все
векторы, коллинеарные с ним. В частности,
нулевой вектор содержится в любом таком
множестве и вместе с каждым вектором в
это множество входит противоположный
ему вектор. Отсюда же следует, что
множество компланарных векторов замкнуто
относительно операции умножения на
действительное число.

20.
Сумма двух векторов есть вектор,
компланарный с ними. Следовательно,
множество компланарных векторов замкнуто
относительно операции сложения.

30.
Три вектора компланарны тогда и только
тогда, когда хотя бы один из них можно
представить в виде линейной комбинации
двух других.

Доказательство.

Пусть векторы
компланарны. Возможны два случая.

1) Среди данных
векторов есть хотя бы одна пара
коллинеарных векторов. Пусть
иколлинеарны. Тогда, по свойствам
коллинеарных векторов, хотя бы один из
них можно выразить через другой. Пусть.
Тогда,
т.е. векторесть линейная комбинация векторови.

2)
Данные векторы попарно не коллинеарны.
Отложим их от одной точки О. Пусть
,,.
Отрезки ОА, ОВ, ОС попарно не параллельны.
Проведём СD
ОА
так, что D

ОВ (прямой ОВ). Тогда получим
,
т.е. векторесть линейная комбинация векторови.

Рис.
9

 Пусть
.
По свойствам 10
и 20
следует, что вектор
компланарен с векторамии.

40.
Если векторы
ине
коллинеарны, то любой компланарный с
ними вектор можно представить в виде
их линейной комбинации.

Теорема 4.
Множество
всех компланарных векторов есть двумерное
векторное пространство над
полем действительных чисел. Базисом
в нём является любая упорядоченная пара
неколлинеарных векторов.

Доказательство
следует из
предыдущих
свойств.

Задача 3. АВСD
и AB1C1D1

два произвольных параллелограмма.

Докажите, что
векторы
,,параллельны одной плоскости.

Решение.
Для решения задачи достаточно показать,
что эти векторы компланарны.

;

;

=

=
()
+ ()
= =.
Так как,
то эти векторы компланарны .

Рис.
10

Теорема 5. Если
векторы
не компланарные, то любой геометрический
вектор можно представить в виде их
линейной комбинации.

Доказательство.
Пусть векторы


не
компланарны. Очевидно, никакие два из
них не являются коллинеарными. Пусть


любой вектор. Возможны два случая.

1) Вектор

компланарен с какой-нибудь парой данных
векторов. Пусть

компланарен с векторами

и
.
Тогда по
свойству 30
компланарных векторов
.

2)
Вектор

не компланарен ни с одной парой данных
векторов. Отложим все четыре вектора
от одной точки О.
пусть
,,и(рис. 11). Проведём (DM)



(M

(AOB))
и (MN)



(N

(OA)).
Тогда
.
Ноколлинеарен вектору,
поэтому.
Аналогично,,.
Следовательно,.

Рис.
11

Теорема 6.
Множество
всех геометрических векторов есть
трёхмерное
векторное пространство
над полем действительных чисел. Базисом
в нём является любая упорядоченная
тройка некомланарных векторов.

Доказательство
следует из
теоремы 5 и свойств компланарных векторов.

В курсе линейной
алгебры (в первом семестре) введены
координаты вектора в данном базисе и
рассмотрены свойства координат. Все
определения и свойства их будут
использоваться в векторных пространствах
геометрических векторов.

Если в векторном
пространстве зафиксированы два базиса
В и
В1,
Т
– матрица перехода от базиса В
к базису В1,
х и
х1
столбцы координат данного вектора
в базисахВ
и В1
соответственно, то х
= Тх1.
Если эти формулы переписать в координатах
во множестве компланарных векторов, то
получим

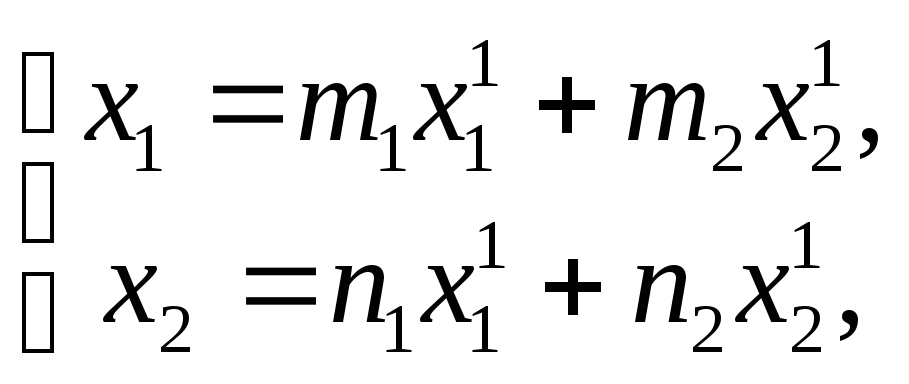где
,.

Во множестве всех
геометрических векторов

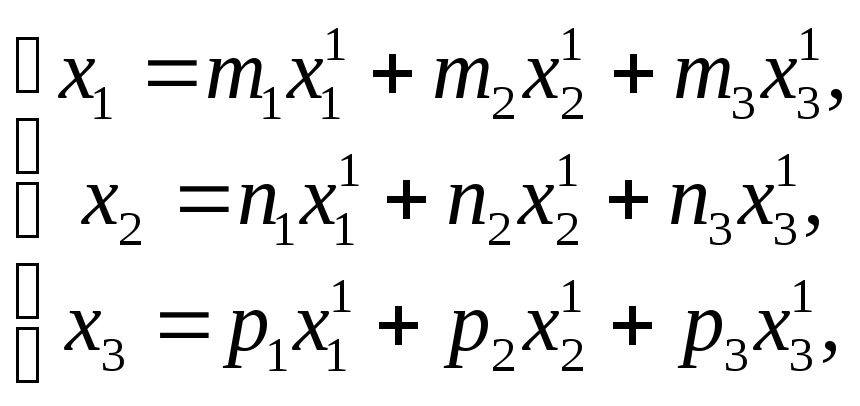где
,,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 1).

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Условия компланарности векторов

  • Для 3-х векторов. Три вектора компланарны если они линейно зависимы.

  • Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.

Примеры задач на компланарность векторов

Пример 1. Проверить компланарны ли три вектора a = {1; 2; 3},
b = {1; 1; 1}, c = {1; 2; 1}.

Решение: найдем смешанное произведение векторов

a · [b × с] =    1     2     3    =
  1     1     1  
  1     2     1  

= 1·1·1 + 1·1·2 + 1·2·3 – 1·1·3 – 1·1·2 – 1·1·2 = 1 + 2 + 6 – 3 – 2 – 2 = 2

Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.

Пример 2. Доказать что три вектора a = {1; 1; 1},
b = {1; 3; 1} и c = {2; 2; 2} компланарны.

Решение: найдем смешанное произведение векторов

a · [b × с] =    1     1     1    =
  1     3     1  
  2     2     2  

= 1·2·3 + 1·1·2 + 1·1·2 – 1·2·3 – 1·1·2 – 1·1·2 = 6 + 2 + 2 – 6 – 2 – 2 = 0

Ответ: вектора компланарны так, как их смешанное произведение равно нулю.

Пример 3. Проверить коллинеарны ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1}, d = {3; 3; 3}.

Решение: найдем количество линейно независимых векторов, для этого запишем значения векторов в матрицу, и выполним над ней элементарные преобразования

(   1     1     1   )  ~
  1     2     0  
  0     -1     1  
  3     3     3  

из 2-рой строки вычтем 1-вую; из 4-той строки вычтем 1-вую умноженную на 3

~  (   1     1     1   )  ~  (   1     1     1   )  ~ 
  1 – 1     2 – 1     0 – 1     0     1     -1  
  0     -1     1     0     -1     1  
  3 – 3     3 – 3     3 – 3     0     0     0  

к 3-тей строке добавим 2-рую

~  (   1     1     1   )  ~  (   1     1     1   )
  0     1     -1     0     1     -1  
  0 + 0     -1 + 1     1 + (-1)     0     0     0  
  3 – 3     3 – 3     3 – 3     0     0     0  

Так как осталось две ненулевые строки, то среди приведенных векторов лишь два линейно независимых вектора.

Ответ: вектора компланарны так, как среди приведенных векторов лишь два линейно независимых вектора.

Источник

Добавить комментарий